Estimating selection through male fitness: three complementary methods illuminate the nature and causes of selection on flowering time

Abstract

Our understanding of selection through male fitness is limited by the resource demands and indirect nature of the best available genetic techniques. Applying complementary, independent approaches to this problem can help clarify evolution through male function. We applied three methods to estimate selection on flowering time through male fitness in experimental populations of the annual plant Brassica rapa: (i) an analysis of mating opportunity based on flower production schedules, (ii) genetic paternity analysis, and (iii) a novel approach based on principles of experimental evolution. Selection differentials estimated by the first method disagreed with those estimated by the other two, indicating that mating opportunity was not the principal driver of selection on flowering time. The genetic and experimental evolution methods exhibited striking agreement overall, but a slight discrepancy between the two suggested that negative environmental covariance between age at flowering and male fitness may have contributed to phenotypic selection. Together, the three methods enriched our understanding of selection on flowering time, from mating opportunity to phenotypic selection to evolutionary response. The novel experimental evolution method may provide a means of examining selection through male fitness when genetic paternity analysis is not possible.

1. Introduction

Flowering plants mate cryptically, copiously and promiscuously. This has led to a potential bias in our understanding of how, and how strongly, natural selection works in the species that stand at the base of virtually all terrestrial food chains. It is relatively easy to approximate a plant's female reproductive success: simply count its seeds. Estimating reproductive success through male function is a far greater challenge. Tracking the success of a plant's pollen in siring offspring is simply not feasible, necessitating less direct and more cumbersome measures. More often than not, fitness through male function is left unexamined. For example, just five of 87 studies reviewed in a recent meta-analysis of selection on flowering time considered any effect on male fitness [1]. Because selection through the two sexual functions can conceivably differ in intensity and direction [2], a focus on seed production alone can lead to a biased view. This paper addresses the gap in our understanding of selection through male fitness by applying complementary methods to estimate selection on flowering time in a manipulative experiment. Each method targets a different point in the progression from phenotypic selection to evolutionary response; their combined use therefore offers a rich understanding of the nature and causes of selection.

The first method is genetic paternity analysis, a mainstay of evolutionary ecology [3–8]. Selection differentials estimated via paternity analysis convey the phenotypic covariance between traits and male fitness. They are, however, inherently more error-prone than those estimated through female fitness, for which the fitness measure (e.g. seeds produced) can be directly observed. Moreover, these differentials alone cannot reveal the causes of selection, nor can they convey capacity for evolutionary response [9,10]. These gaps can be bridged by pairing genetic paternity analysis with additional methods.

The second method assumes siring opportunity is the principal determinant of male fitness. This idea originates in estimates of plant phenotypic gender, in which flower and fruit production schedules are tallied across a population to estimate an individual's opportunity to sire seed [11–13]. Inherent to these calculations is the assumption that all flowers dispense the same amount of pollen, which is then randomly vectored to all available stigmas: the distribution of male and female reproductive effort in a population is the sole determinant of an individual's male fitness. Empirical support for this convenient and common [14–18] assumption is mixed. Some support is provided by genetic paternity analyses detecting increased male fitness among individuals whose peak flower production coincides with peak seed production in a population [19,20]. However, the true determinant of male fitness in such cases could be a correlated, unmeasured trait. We apply a more rigorous test by coupling genetic paternity analysis with a mating opportunities analysis. Because the former captures the total phenotypic covariance between a trait and male fitness, and the latter the covariance between a trait and mating opportunity only, the two can be compared to reveal the relative importance of mating opportunity as an agent of selection.

A third independent estimate of selection through male fitness can be made within the framework of experimental evolution. This technique examines evolutionary change in response to conditions set up by the investigator [21]. It has been applied to plants, for example, to evaluate evolutionary responses to changes in mating opportunity and pollinator service [22,23]. In these studies, response to selection was estimated by rearing seeds representative of the initial and final generations in a common environment, with seeds drawn randomly from all the seeds produced. Observed evolutionary change therefore represented response to selection through both male and female components of fitness. To isolate the male component, we employ an apparently novel, alternative sampling of seeds, sampling uniformly across dams. Sampling the same number of seeds from every dam eliminates variance in female reproductive success. Therefore, in the common environment, any phenotypic difference between parent and offspring generations must be owing to differential siring success. The selection differential can then be calculated when a reliable estimate of heritability is available.

Like genetic paternity analysis, selection estimated using experimental evolution conveys the influence of mating opportunity plus other factors on male fitness. Comparing results of this approach with those of the mating opportunities method therefore provides a second test of the relative importance of mating opportunity in shaping selection through male fitness. Moreover, whereas genetic paternity analysis reveals the phenotypic covariance between a trait and male fitness, the experimental evolution approach describes the genetic covariance only. Comparing these two methods can therefore reveal the relative contributions of genetic and environmental covariances to phenotypic selection. Finally, combining all three approaches clarifies evolutionary dynamics, telling the complete story from siring opportunity to phenotypic selection to evolutionary response [10].

We aimed to understand flowering time evolution through male fitness in experimental populations of the annual plant Brassica rapa. These populations were manipulated to isolate two inherently correlated possible sources of selection on flowering time [8,24]. First, flowering time, which we define as days from emergence to first flowering (‘age at flowering’, AAF), could determine plant condition going into reproduction [25], directly affecting fitness. Second, AAF partially determines the quality of environment experienced during reproduction (e.g. exposure to pollinators [26], frugivores [27] or abiotic stressors [28]), such that selection on AAF comes indirectly through its correlation to Julian date of flowering (JDF). We manipulated the AAF–JDF correlation by staggering the planting dates of families with known genetic values for AAF, creating populations in which AAF and JDF were positively (the presumed natural condition), negatively or uncorrelated (electronic supplementary material, figure S1a–c). In all populations, plants with an early JDF flowered longest, regardless of AAF [8] (electronic supplementary material, figure S1d–f). Intuitively, early-flowering, long-duration plants should enjoy greater mating opportunity than late-flowering, short-duration plants. We therefore expected that the association between AAF and mating opportunity varied across treatments, depending on the correlation between AAF and JDF (electronic supplementary material, figure S1j–l).

The direction of selection on AAF through female fitness in the experimental populations depended on the sign of the AAF–JDF correlation (mean selection differential ± s.e. positive treatment: −0.328 ± 0.057; uncorrelated treatment: −0.028 ± 0.077; negative treatment: +0.164 ± 0.069; n = 5 replicate populations per treatment across two seasons) [24], suggesting that flowering date influenced female fitness more than flowering age. In contrast, genetic paternity analysis revealed that selection through male fitness strongly favoured young AAF when AAF and JDF were uncorrelated (S (95% Bayesian confidence interval) = –0.433 (–0.587, –0.281), n = 1 population) [8]. Selection was comparatively weak in the positive treatment (S = –0.189 (–0.314, –0.066), n = 1), and absent in the negative (S = 0.011 (–0.098, 0.117), n = 1) [8]. Here, we expand our investigation of selection through male fitness to (i) test the role of mating opportunities in shaping selection on AAF through male fitness, (ii) determine the genetic versus environmental basis of phenotypic covariance between flowering time and male fitness, and (iii) assess evolutionary response to phenotypic selection on flowering time through male fitness. These goals are achieved through application of the three methods described above.

The challenges of estimating selection through male fitness are universal. The particular methods we used will be most directly applicable to plants, but our underlying premises extend readily to other systems.

2. Methods

(a). Study system

Brassica rapa is a perfect-flowered, self-incompatible annual naturalized across much of North America [29]. In Eastern Canada, seeds germinate in the spring, and plants begin producing flower buds (bolt) approximately 25 days after emergence; first flowers open approximately 8 days later (E.J.A. 2009, personal observation). Individual flowers persist 1 or 2 days, and flower production continues long after the first fruit have set. Seeds used in this experiment were bulk collected from more than 200 plants sampled from a population of more than 5000 growing at the margins of a fallow field in the Eastern townships of Quebec, Canada, during 2009 (population BBF, 46.15 N, 70.72 W, voucher specimen deposited at the Royal Ontario Museum (TRT)).

(b). Experimental design

We estimated selection on AAF through the male component of fitness in three experimental populations of B. rapa. These were established at the University of Toronto's Koffler Scientific Reserve at Jokers Hill (KSR; 44.02N 79.52 W) as part of a larger experiment aimed at uncovering the causes of selection on flowering time [8,24]. The populations studied here are representatives of three experimental treatments. In the positive correlation treatment, plants genetically inclined to flower at the youngest AAF began flowering on the earliest JDF, and those genetically inclined to flower at an old AAF flowered last. In the negative correlation treatment, the correlation was reversed, so that plants flowering at the oldest age flowered first. In the uncorrelated treatment, AAF varied independently of JDF (electronic supplementary material, figure S1a–c). Temperature and photoperiod decreased over the course of the experiment, indicating that JDF was a reasonable proxy for the environment experienced during reproduction [24]. The field experiment is described in full elsewhere [24]; we provide essential details here.

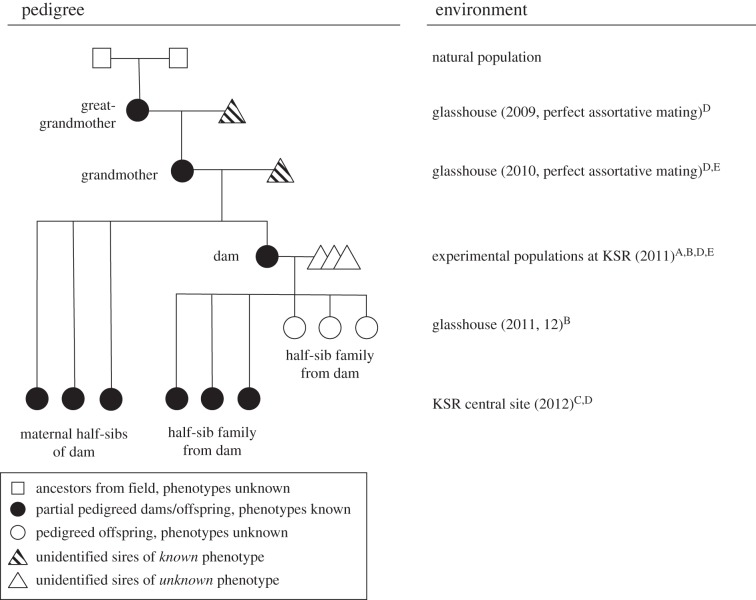
Experimental plants were drawn from a partially pedigreed population (figure 1). To establish the pedigree, we grew approximately 500 field-collected seeds in the University of Toronto glasshouse during autumn 2009, recorded the age at bolting of each individual, and enforced perfect assortative mating by bolting time. Each dam received multiple sires sharing her exact bolting age, and all plants acted as dam and sire. A single seed was planted from each mother, and we recorded bolting time and enforced assortative mating for a second generation. Seeds produced by this generation were used in the field experiment (figure 1). After two generations of perfect assortative mating, dam bolting time was a strong predictor of mean offspring bolting time (standardized mid-parent offspring regression h² = 0.73; electronic supplementary material, figure S2). Age at bolting and AAF are strongly, positively correlated (r = 0.85, p < 0.01, n = 423 plants grown at KSR during 2010). Bolting data could therefore be used to schedule sowing dates such that plants of a required AAF would begin flowering on a desired JDF [24].

Figure 1.

Generations included in this experiment, and the environments in which they were grown. Superscripts following environment descriptors indicate the analyses in which plants were used: A = phenotypes used to estimate male fitness by mating opportunities method; B = leaf tissue used to estimate selection differential by genetic method; C = phenotypes used to estimate response to selection in experimental evolution method; D = phenotypes used to estimate heritability of age at flowering for experimental evolution method; E = sample of seeds produced used to test intergenerational maternal effects.

To set up the 2011 field experiment (figure 1), seeds produced by the 2010 glasshouse generation were planted individually into 164 ml ‘cone-tainer’ pots (Stuewe & Sons, Corvallis, OR). Seedlings were reared under a polyethylene-covered greenhouse at KSR until bolting. Because there was scatter about the offspring–dam AAF regression (electronic supplementary material, figure S2), we planted 4–10 seeds from maternal families representing the target AAF, and chose individuals exhibiting the desired AAF on the required Julian date for transplant into the experiment. Plants were transplanted after bolting but before first flowering. Populations consisted of 56 individuals assigned to random positions on a 7 × 8 grid with 14 cm between positions. Transplants occurred on six dates over a 25-day period, with 4–15 individuals introduced to the population per transplant date [24]. The populations were open pollinated and were situated in old field habitat. They were positioned at least 250 m from one another, often with a forested patch in between. Brassica rapa does not occur naturally at the study site. We therefore assume all mating occurred within populations. We recorded AAF as days between seed planting and flowering. Although two replicate populations per treatment were established during 2011 [24], only one replicate could be evaluated for male fitness given available resources.

(c). Estimating selection through the male component of fitness

(i). Method 1: mating opportunity

The mating opportunity method evaluates each plant's opportunity to sire seeds based on its schedule of flower (pollen) deployment relative to the seed production schedule of its population. We recorded flower and seed production schedules by tagging all inflorescences with a sharkskin jeweller's tag immediately below the lower-most fresh flower every 10 days. This tagging established flower production ‘intervals' within each plant; fruit occurring between two tags must have been sired by another plant in flower during that interval. We counted fresh open flowers on each plant on 3 days within each interval. The sum of counted flowers over an interval estimates the total flowers displayed. Seeds were harvested and weighed by tagging intervals within plants.

To estimate the mass of seed sired by an individual during a given tagging interval, we multiplied the individual's proportional contribution to the total flower production of its population by the mass of seeds that were available for siring at that time. Summing seed mass sired over intervals yields the individual's expected male fitness. Building on formulae presented in [15,30], we used the flower and seed production schedules to estimate a matrix Φ = MF, in which each cell Φ_[j,k] is the expected total mass of seeds with j as dam and k as sire. M represents seed production by maternal plants, with M_[j,d] equal to seed mass produced by mother j during tagging interval d. F is a K × D matrix of the fraction of total flowers produced by father k during interval d, with each column summing to 1. Element F_{[k, d]} is assumed to equal father k's proportional contribution to the interval d pollen pool. To adapt these methods to self-incompatible B. rapa, we calculated a new matrix F_j for each mother j, setting the flower production of k = j to zero each time. Thus, each row Φ_{[j, ]} = M_{[j, ]}F_j. Each column Φ_[,k] sums to the mass of seed expected to have been sired by k based on mating opportunity alone. For each population, we mean relativized this estimate of male fitness, and regressed it against AAF (standardized to a mean of 0 and standard deviation of 1) to estimate the selection differential on AAF [9]. This analysis was carried out in R [31].

(ii). Method 2: genetic paternity analysis

We next estimated selection differentials on AAF through male fitness using full probability genetic paternity models. The results of this analysis have been previously reported [8]; methods are detailed in electronic supplementary material, appendix A. Briefly, all parents and a sample of 500 seeds from each population (figure 1) were characterized at eight microsatellite loci. Dams contributed to the offspring samples in proportion to the mass of seed they produced. The genetic data were analysed in full probability paternity models to estimate the effect of AAF on male fitness using R package MasterBayes [3]. These models simultaneously resolve the pedigree and identify the most likely effects of phenotypic traits on male reproductive success [32]. The phenotypic effects are interpretable as selection differentials [8,33].

(iii). Method 3: experimental evolution

In this analysis, we estimated the response to selection on AAF that occurred during the 2011 season (R) and the heritability of AAF (h²), and then calculated the selection differential (S) required to give rise to the observed response using the breeder's equation, S = R/h² [34,35].

Response to selection

We eliminated phenotypic plasticity as a cause of generational differences in AAF by rearing parental and offspring generations in a common environment. We tested for possible maternal effects on AAF by weighing samples of 10 seeds from each of 35 maternal sibships representing parent and offspring generations (figure 1) as a proxy for maternal investment.

During summer 2012, we grew maternal half-siblings of dams from the 2011 field experiment alongside offspring produced during the field experiment (figure 1). The parental generation was represented by 784 plants per population (14 maternal half-siblings × 56 plants), and the offspring generation was represented by two parallel, overlapping samples. The first, ‘proportional’, sample comprised 784 seeds distributed among mothers in proportion to their aggregate seed mass. The second, ‘uniform’, sample comprised exactly 14 seeds from each mother (14 × 56 = 784 seeds total). In total, we grew approximately 950 offspring per population, with approximately 620 shared between proportional and uniform samples. Because the uniform sample eliminated variance in dam reproductive success, we assume that any change in mean AAF between parents and uniformly sampled offspring occurred via response to selection through male fitness only.

Seeds were planted singly into ‘cone-tainer’ pots on 1 June 2012, and then fully randomized. We reared seedlings under a polyethylene-covered greenhouse at KSR for 12 days before moving all pots outdoors to a site central to the 2011 populations. Plants were fertilized with 15 ml of a 20 : 20 : 20 formula (0.5 g l⁻¹) 10 and 18 days after planting, and were watered daily. We verified that germination failure and other sources of missing data did not bias estimates of response to selection (electronic supplementary material, appendix B).

AAF ranged from 24 to 56 days after planting. On day 40, dried flower buds were found below the first open flowers of seven plants, likely owing to heat stress. We estimated that these would have flowered between days 36 and 40 had buds not been damaged. An additional 298 plants dropped early buds before flowering. Based on their developmental stage, we estimated these would have flowered between days 45 and 48. Finally, flea beetles (Phyllotreta sp.) damaged the primary inflorescence of three plants that would have otherwise likely flowered between days 49 and 52.

The change in mean AAF between parent and offspring generations (R) was estimated using maximum-likelihood estimation to allow inclusion of censored data for damaged plants. For each population, AAF (y_i) was approximated by a gamma distribution and modelled as a function of generation (x_i; parent or offspring)

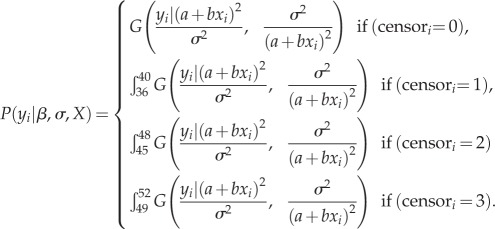The gamma density distribution (G) is defined by the shape parameter ŷ²/σ², and scale parameter σ²/ŷ, where ŷ and σ are the AAF mean and standard deviation, respectively. The mean was modelled as a linear function of the generation x_i: ŷ = a + bx_i. We assumed σ did not vary by generation; this assumption was supported by consistency in σ across populations and offspring samples (electronic supplementary material, appendix C). We solved for a, b and σ (constrained to be greater than 0) using method ‘L-BFGS-B’ of function mle2 in R package bbmle [36]. Parameter b is the estimate of R.

Heritability

We estimated h² using an animal model in R function MCMCglmm [37]. We included in this analysis AAF data and partial pedigree information from all generations for which we had phenotypic information, from 2009 to 2012 (figure 1). AAF was modelled as a function of the fixed effect cohort (2009, 2010, 2011 or 2012, the latter including representatives of parental and offspring generations) and random effects for additive genetic variance (V_A) and non-additive genetic variance plus environmental variance within cohorts (V_E). A posterior distribution for h² is obtained by V_A/(V_A + V_E).

For all cohorts after 2009, we knew every plant's dam with certainty. For the 2010 and 2011 cohorts, we also had partial information about sire phenotypes (figure 1). We investigated h² under two complementary pedigree scenarios. In the first, we assumed that maternal half-siblings in the 2010 and 2011 cohort were full-sibs, with a unique ‘dummy sire ID’ assigned to each family. Dummy sire AAF equalled dam AAF. In the second scenario, we assumed that maternal half-siblings in the 2010 and 2011 cohorts were half-sibs, with a unique ‘dummy sire ID’ for each offspring, and dummy sire AAF again matching dam AAF.

Analyses were run from four starting parametrizations for random effects: (i) 50 : 50 distribution for V_A : V_E; (ii) 95 : 5; (iii) 25 : 75 and (iv) 75 : 25. Each model was run for 330 000 iterations with a burn-in of 30 000 and thinning interval of 300. We verified convergence across starting parametrizations using Gelman diagnostic tests (function gelman.diag(), [37]); the different starting parametrizations yielded nearly identical h² estimates. We retained the posterior distribution from the 50 : 50 starting parametrization for estimating S.

Selection differential

We expressed R in standard deviation units by dividing b by σ. We then divided the standardized R by h² to back-calculate S for uniform and proportional offspring samples for each population. All parameters were estimated with error. We therefore drew 1000 samples of b and σ from a normal distribution with a mean equal to their maximum-likelihood estimate and standard deviation equal to their standard error. We similarly drew 1000 samples of h² from the posterior distribution. Using these samples, we obtained a mean and 95% CI for S.

3. Results

(a). Mating opportunity as a determinant of male fitness

The mating opportunities method predicted strong, but opposite, selection on AAF in the positive and negative correlation populations, with intermediate selection in the uncorrelated population (figure 2a). In other words, mating opportunity decreased with later JDF in all populations, suggesting that flowering environment (JDF) was a better predictor of mating opportunity than flowering time genotype (AAF). This was expected given the negative correlation between JDF and flowering duration (electronic supplementary material, figure S1).

Figure 2.

Selection differentials on age at flowering (AAF; 95%CI) in three populations of Brassica rapa differing in association between AAF and Julian date of flowering (JDF). Differentials estimated using via (a) flowering and seed production schedules (n = 56 plants per population), (b) genetic paternity analysis (n = 56 parents + ∼500 offspring) and (c) comparison of mean AAF in parental and offspring generations (n = 784 parents + 784 offspring per population; offspring sampled uniformly across mothers).

Estimates of selection on AAF derived via the mating opportunity method did not, however, agree with results of the genetic (figure 2b) and experimental evolution methods (figure 2c). The latter two methods found that the strongest selection on AAF occurred in the uncorrelated population, and that the strength of selection in the positive treatment population was intermediate to that in the other two. Despite this disagreement, estimated mating opportunity was positively correlated with genetic estimates of male fitness (r = 0.557, 0.349, 0.482 in positive, uncorrelated and negative population; in each p < 0.01, n = 56). Thus, male fitness does seem to have increased with increased mating opportunity, but this association did not shape selection on AAF.

(b). Genetic and environmental covariance between age at flowering and male fitness

The genetic method reveals phenotypic covariance between AAF and male fitness, whereas the experimental evolution method reveals genetic covariance only. Overall, results of these two methods agreed on the relative strength and directions of selection across populations: selection strongly favoured young AAF in the uncorrelated population, and selection in the positive treatment population was intermediate to that in the other two (figure 2b,c). This agreement suggests a genetic basis to the phenotypic covariance between AAF and male fitness. However, in all populations, differentials estimated by the experimental evolution method were more positive than those estimated by the genetic method (figure 2). This discrepancy is consistent with a common environmental covariance between AAF and male fitness in all populations, acting in addition to genetic covariance (electronic supplementary material, figure S3). By design, the covariance between AAF and the environment experienced during reproduction (JDF) varied among experimental treatments (electronic supplementary material, figure S1a–c). Thus, the hypothesized common environmental covariance, if present, must have occurred early in life, before flowering.

(c). Heritability and response to selection

Heritability (h²) of AAF was 0.506 (0.462–0.522) (mode and 95%HPD interval of posterior distribution) when all offspring produced per maternal plant within the 2009 and 2010 cohort were assumed to be full-sibs. The estimate increased to 0.610 (0.573–0.638) when offspring produced per maternal plant during 2009 and 2010 were assumed to be half-sibs. We used the latter estimate when applying the breeder's equation, noting that S would be stronger if the h² estimate from the full-sib assumption were adopted.

Flowering time evolved following a single generation of selection in the experimental populations. As intended, AAF did not vary among the three parental samples (electronic supplementary material, table S1). Total selection on AAF generated a more than 0.5 days advance in AAF in offspring of the positive and uncorrelated populations, and a nearly 1 day delay in the negative population (table 1a). Responses to selection through male fitness alone were weaker, particularly in the positive population (table 1b). The uncorrelated population exhibited the least difference in response to selection estimated from proportional versus uniform offspring samples (table 1).

Table 1.

Estimated responses to selection on age at flowering (AAF; days, 95% CI) in three experimental populations of Brassica rapa. Responses estimated by comparing the mean AAF of the parental generation to offspring sampled (a) proportionately or (b) uniformly across dams.

population	(a) proportional sample	(b) uniform sample
positive correlation treatment	–0.72 (–1.09, –0.35)	0.15 (–0.23, 0.53)
uncorrelated treatment	–0.65 (–1.00, –0.30)	–0.47 (–0.83, –0.12)
negative correlation treatment	0.86 (0.51, 1.21)	0.46 (0.11, 0.82)

We weighed seeds as a proxy for maternal investment, and compared seed mass across generations to test for possible maternal effects. Seeds representing the offspring generation were heavier than those representing the parental generation (mass per 10 seeds parental ± s.d. = 14.27 ± 3.10 mg; offspring = 15.89 ± 2.74 mg; t₆₈ = –2.30, p = 0.025).

4. Discussion

The three methods emphasized different aspects of selection on AAF. Collectively, their results enrich our understanding of selection on AAF in this experiment.

(a). Mating opportunity contributed little to selection on flowering time

The mating opportunities method found opposing selection in populations representing the positive and negative treatments, and no selection in the uncorrelated treatment (figure 2a). This pattern is entirely consistent with expectations if mating opportunity were the sole determinant of siring success, indicating that mating opportunity was indeed temporally structured in the manner we expected (electronic supplementary material, figure S1). Moreover, mating opportunity was positively correlated with male fitness estimated via the genetic method. Despite this, both the genetic and experimental evolution methods (figure 2b,c) detected patterns of selection on AAF that conflicted with expectations if mating opportunity were paramount (figure 2a). Strong selection for young AAF when AAF was uncorrelated with mating opportunity (figure 2, circles) is particularly convincing in this regard. Thus, mating opportunity did not much influence selection on AAF through male fitness.

Few other studies in plants have explicitly tested associations between mating opportunity, male fitness and selection on phenotypic traits. In an experimental garden of Raphanus sativus, Devlin & Ellstrand [19] found that individuals whose peak flowering coincided with the peak flowering of the most productive dams sired more seed than those peaking earlier or later. They did not test whether this association between mating opportunity and male fitness translated to selection on any trait. Delph & Herlihy [20], however, found that an association between flower size and mating opportunity contributed to selection for small flower size in males of Silene latifolia. Our study has shown that correlation between a trait and mating opportunity will not inevitably drive selection on the trait of interest. In the experimental populations of B. rapa, the male fitness effects of AAF must have extended beyond the effects of AAF on mating opportunity.

(b). Possible early-life environmental covariance between flowering time and male fitness

Agreement between the genetic and experimental evolution methods on the overall pattern of selection on AAF across the three populations was striking. Both detected strong selection for young AAF in the uncorrelated treatment, and a more negative differential in the positive treatment than in the negative (figure 2b,c). However, in all populations, the selection differential estimated by the experimental evolution method was more positive than that estimated by the genetic method. There are at least two possible, non-exclusive causes.

First, maternal effects could have delayed AAF in the offspring generation, biasing the estimated response to selection in the experimental evolution method. In B. rapa, the first seeds produced by a dam develop into plants that flower approximately 0.5 days earlier than the last seeds [15]. Assuming this within-plant effect is attributable to a within-plant decline in maternal investment [38], it is possible that among-generation variation in investment per seed similarly affects AAF. If such maternal effects were responsible for the ‘upwards shift’ in selection differentials in the experimental evolution method, then we might expect seeds representing the offspring generation to be less well provisioned than those representing the parents. However, the greater mass of offspring suggested the opposite. This result does not decisively rule out maternal effects, but neither does it offer immediate support.

Second, the more negative selection differentials by the genetic method could be caused by an unexpected environmental covariance between AAF and male fitness (electronic supplementary material, figure S3). Plants were non-randomly selected for inclusion in the field experiment: we chose individuals whose AAF matched the target AAF for their maternal family. In practice, this led to a tendency to choose early-flowering half-sibs from young-AAF families, and late from old. We made the operating assumption that after two generations of perfect assortative mating, most of the scatter in the dam–offspring regression (electronic supplementary material, figure S2) was due to segregation variance. However, some may have been environmental in origin, caused, for example, by small differences in shading experienced as seedlings. If this unknown environmental factor also affected male fitness, then our process of choosing plants may have given rise to a negative environmental covariance between AAF and male fitness. Such covariance would influence results of the genetic method without affecting the response to selection estimated by experimental evolution (electronic supplementary material, figure S3).

That environmental covariance between traits and fitness contributes to selection on phenotypes is well recognized [39–41], but it is challenging to control for such effects. Rausher [40] proposed forming populations of sibships and regressing family mean fitness on family mean traits to obtain estimates of selection gradients that are not biased by environmental covariance. While this approach has been used in examining selection through female fitness [42], it has not yet been combined with paternity analysis, perhaps because the inclusion of several groups of close relatives in a population would tend to reduce variability at neutral genetic markers. The combined results of genetic and experimental evolution methods here, however, suggest that the possibility of environmental covariance between traits and male fitness merits further consideration.

(c). Flowering time evolution through male fitness

It is not surprising that selection acts on flowering time [1], or that populations are capable of responding to that selection [43,44]. Our study is unique, however, in its comprehensive examination from mating opportunity to phenotypic selection to evolutionary response, and in its focus on male fitness.

The methods employed to describe selection through male fitness each relied in some way on information about female fitness during the 2011 field experiment, which we estimated as a plant's aggregate seed mass. This fitness measure does not account for alternate seed packaging strategies (i.e. many small versus few large seeds), which could yield fitness differences. However, seed size varied less than total seed mass (CV_{mass 10 seeds} = 17%; CV_{total seed mass} = 59%; n = 35 plants used in testing for maternal effects), suggesting that most variation in total seed mass during the 2011 field experiment was due to variation in seed number rather than in seed size. Aggregate seed mass was thus a reasonable female fitness estimate on which to base analyses of selection through male fitness.

The experimental manipulation tested the hypothesis that the environment experienced during reproduction (JDF) shapes selection on AAF through male fitness. Strong selection for young AAF when AAF and JDF were uncorrelated rejected this hypothesis [8]. By comparing results of the genetic and mating opportunities methods, we further excluded mating opportunity as the primary driver of selection on AAF.

We have previously speculated that the unknown factor driving selection for young AAF in the uncorrelated population could be negative covariance between AAF and pollen quality [8]. Such covariance would be masked in the positive and negative populations, because these two treatments affected the date on which pollen of a given AAF was dispersed and deposited on stigmas, but not the identity of competitors: young-AAF pollen competed primarily with young, and old with old [24]. In the uncorrelated population, however, young- and old-AAF pollen circulated at every date, and so should have regularly competed on the same stigmas. Thus, competitive superiority of young-AAF pollen would be most evident in the uncorrelated population, where it would lead to selection for young AAF through male fitness. The experimental evolution results presented here verified the earlier genetic result. Pollen competitive ability has been shown to covary with other traits, such Pgi allozyme type in Clarkia unguiculata [45], but it has not been previously associated with flowering time. The hypothesis that AAF correlates with pollen quality in B. rapa merits further study.

Response to total selection on flowering time in this experiment was rapid, with AAF advancing or decreasing by more than 0.5 days in all populations after just one generation (table 1a). The close agreement between differentials estimated by genetic and experimental evolution methods (figure 2b,c) indicates that uniform offspring sampling succeeded in isolating the response to selection through male fitness. Differences in intensity and direction of selection through male versus female fitness can be inferred by comparing responses estimated from uniform versus proportional samples. In the uncorrelated population, the estimated responses from uniform and proportional samples differed by just 0.18 days (table 1). Thus, nearly all of the 0.65 days response in the proportional sample was due to selection through male fitness, as one would expect given the weak effect of AAF on seed production [24] and strong effect on seed siring (figure 2b) in this population. In contrast, in the positive and negative populations, responses between samples differed by 0.87 and 0.40 days, respectively. These larger differences in response reveal the female fitness advantage of early JDF (young and old AAF, respectively) that occurred in these populations [24]. Comparing phenotypes of offspring sampled uniformly versus proportionately across dams may prove a useful strategy for inferring the nature of selection through male fitness where genetic paternity analysis is not possible.

Estimating selection through male fitness is labour- and resource-intensive, and the estimates obtained are not as certain as those for female fitness, where the fitness measure can be more directly observed. The mating opportunities method was the easiest to implement, but it did not agree with the other two, indicating that male fitness was not determined solely by the number and quality of available mates. Comparing selection estimates generated through genetic and experimental evolution methods prompted intriguing hypotheses about the effects of early-life environment on male fitness. These two methods also hint at correlation between AAF and pollen quality. Using three complementary methods allowed independent verification of the paternity analysis findings, and enriched our overall understanding of selection in this experiment.

Data accessibility

Phenotypic data from the 2011 field experiment are accessible at http://dx.doi.org/10.5061/dryad.nk885. R scripts and data used in mating opportunities method and in experimental evolution method are accessible at http://dx.doi.org/10.5061/dryad.5k4m2. Genetic data and R scripts used in paternity analysis are accessible at http://dx.doi.org/10.5061/dryad.5g5rp/1.

Authors' contributions

Both authors conceived the study, discussed results, crafted the final manuscript and gave final approval for publication. E.J.A. coordinated and executed experiments, analysed data and prepared the initial manuscript draft.

Competing interests

We have no competing interests.

Funding

This research was supported by a Natural Science and Engineering Research Council of Canada (NSERC) Discovery grant to A.E.W., and an NSERC Graduate Scholarship, Ontario Graduate Scholarships in Science and Technology (sponsored by the families of C.E. Eckenwalder and F.M. Hill), and a General Motors Canada Award for Women in Science and Mathematics to E.J.A.