Abstract
Social behaviour may enable organisms to occupy ecological niches that would otherwise be unavailable to them. Here, we test this major evolutionary principle by demonstrating self-organizing social behaviour in the plant-animal, Symsagittifera roscoffensis. These marine aceol flat worms rely for all of their nutrition on the algae within their bodies: hence their common name. We show that individual worms interact with one another to coordinate their movements so that even at low densities they begin to swim in small polarized groups and at increasing densities such flotillas turn into circular mills. We use computer simulations to: (i) determine if real worms interact socially by comparing them with virtual worms that do not interact and (ii) show that the social phase transitions of the real worms can occur based only on local interactions between and among them. We hypothesize that such social behaviour helps the worms to form the dense biofilms or mats observed on certain sun-exposed sandy beaches in the upper intertidal of the East Atlantic and to become in effect a super-organismic seaweed in a habitat where macro-algal seaweeds cannot anchor themselves. Symsagittifera roscoffensis, a model organism in many other areas in biology (including stem cell regeneration), also seems to be an ideal model for understanding how individual behaviours can lead, through collective movement, to social assemblages.
Keywords: social behaviour, circular milling, collective motion
1. Introduction
The study of collective motion is rapidly becoming a major interdisciplinary field in its own right, bringing approaches from statistical physics to social behaviour [1]. This field, at its best, is characterized by cycles of modelling and experimentation on particular study systems that elucidate general principles applicable to, for example, shaken metallic rods through macromolecules, bacterial colonies, amoebae, cells, insects, fish, birds, mammals and human social behaviour [1]. One emergent concept in the field of collective motion is that with increasing density, many flocking systems exhibit a series of phase transitions ranging from isolated individuals through small polarized groups to circular mills and finally static assemblages. In colloids and granular materials, the slowdown of movement with increasing density is known as jamming [2], a transition also observed in human panic evacuation [3]. Systems that exhibit all three of these phase transitions are, however, rare (but see recent work focusing on the last of these transitions in collective cellular movement during metazoan development [4] and reticulate pattern formation in cyanobacteria [5]). Here, we test the idea that a new model system exhibits all three transitions.
Our study model is the marine flat aceol [6] worm Symsagittifera roscoffensis renowned as the plant-animal [7,8]. Adult S. roscoffensis feed on the nutrients produced by the photosynthesizing symbiotic algae living within their bodies. Hence, they seek sites where their algae can photosynthesize [9] more effectively. These worms are typically encountered as biofilms on sandy beaches at low tide [8]. In initial observations of S. roscoffensis transferred at fairly high densities to Petri dishes containing a shallow pool of sea water, we noted a rapid and spontaneous emergence of circular milling behaviour, which, to the best of our knowledge, had not been described before in these worms, very possibly because it may occur only fleetingly at a certain stage of the tidal cycle, for example when S. roscoffensis initially come to the surface on the beaches they inhabit. Hence, the purpose of this paper is to test hypotheses, through cycles of experimentation and modelling, which focus on the transitions in the social behaviour and collective motion of these worms. We determine how individual worms move, how small groups of worms interact with one another and how circular mills form. We propose that circular milling gathers worms together and eventually leads to such high densities that the worms can form continuous biofilms and thus act as if they are a super-organismic seaweed.
One of the most extreme manifestations of collective motion is circular milling. It occurs when individuals in a group are so synchronized that they follow one another nose-to-tail in a complete ring in such a way that their trajectories are almost identical and approximately circular; often there are multiple orbits nested within one another [10,11]. At the outset of modern studies of collective decision-making, circular milling behaviour was seen as a key characteristic of ultra-cohesive group movement [10]. It has been reported, for example, in Bacillus bacteria [12,13], Daphnia [14], processionary caterpillars [15], army ants [16], fish [17,18] and tadpoles [19].
Mechanistically, circular milling typically occurs because an isolated group of individuals follow one another in a continuous ring. In processionary caterpillars and army ants, circular milling is underpinned by individuals laying trails that others follow and reinforce [15,16]. In fish, it occurs because of rules of attraction and alignment [11,20–22]. A recent sophisticated analysis of collective motion in glass prawns demonstrates that a weak form of circular milling can occur in an annular arena because these supposedly non-social Crustacea influence one another's movements even after a substantial delay following an encounter [23].
The functional significance of circular milling is much less clear. Indeed, circular milling seems often to be maladaptive, especially in processionary caterpillars and army ants where individuals may remain trapped in a mill, by more and more trail laying, until they die of exhaustion [16]. In fish, where it occurs fairly frequently, it may serve for predator avoidance [20] through an extreme form of the geometry for the selfish herd [24]. By contrast, in glass prawns, confinement to a doughnut-shaped environment facilitates interactions and generates collective circular motion [23]. In general, however, explanations for circular milling remain elusive. The experimental tractability of the social behaviour and collective motion in S. roscoffensis, we demonstrate here, promises to elucidate the reasons why circular milling occurs both mechanistically and functionally in this species.
First, we examine the characteristics of individual worms including their sizes, their speeds of movement and their behavioural lateralization. Second, we determine if these worms have a tendency to interact even at low densities such that they encounter and line up with one another more frequently than they would if oblivious of others. To do this, we create the first of two computer simulation models to mimic the densities, lengths and rates of movement of real worms in arenas of the same size and shape as used in our experiments with real worms. This first model represents the null hypothesis of no social interaction. Hence, we use simulations of this model to detect potential social behaviours among the real worms. Third, we analyse the occurrence of circular milling as a function of worm density. Fourth, having established through comparisons with the null-hypothesis model that real worms do interact socially, even at low densities, we create the second model based on worms having simple rules of local interactions. The simulations of this second model reproduce the formation of small polarized groups of moving worms that lead, at yet higher densities, to circular mills. Finally, we put forward the hypothesis that the purpose of these circular mills is to enable the worms to congregate into extremely high-density assemblages that then can become biofilms.
2. Material and methods
(a). Study organisms and experimental videos
We collected S. roscoffensis from a northeasterly facing beach on the North East Coast of Guernsey on 17–19 June 2014. The worms were held at ambient temperature in seawater collected from the same site and transferred to arenas for filming. The depth of water within each arena was approximately 2 mm and the worms were swimming freely. Filming at 15 fps with a Canon G7 camera using a resolution of 768 × 1024 pixels per frame followed within minutes of collection to minimize the length of time the worms were held. We made 14 videos of a total of 707 worms. Thirteen of the videos recorded the behaviour of between three and 99 worms in a circular ceramic arena (2875 mm2) for varying values at low density and one recorded 293 worms in a square plastic weighing boat (961 mm2) for a high-density value. The videos were between 164 and 792 s in length.
(b). Characteristics of individual worms
For length measurements, we took still images, in which each worm could be seen clearly, from a representative sample from four of the videos at low worm densities in the circular arenas (excluding two videos with 61 and 99 worms). Using ImageJ software [25], a straight line was drawn across the diameter of the arena in each image to provide a length calibration. We then used the ‘segmented line’ freehand drawing tool, and the ‘fit spline’ option to draw a line from end to end of the worm, matching any curvature, to produce a dataset of worm lengths in millimetres.
For individual trajectories (figure 1a), we tracked worms in their quasi-two-dimensional environment of a shallow pool of seawater in another four videos at low density in the circular arenas using the AnTracks software system [26]. From these trajectories, we extracted length, speed, curvature and handedness to test for any relationship between length and speed, explore the effect of curvature on speed and investigate whether individual behavioural lateralization influences the formation of circular mills.
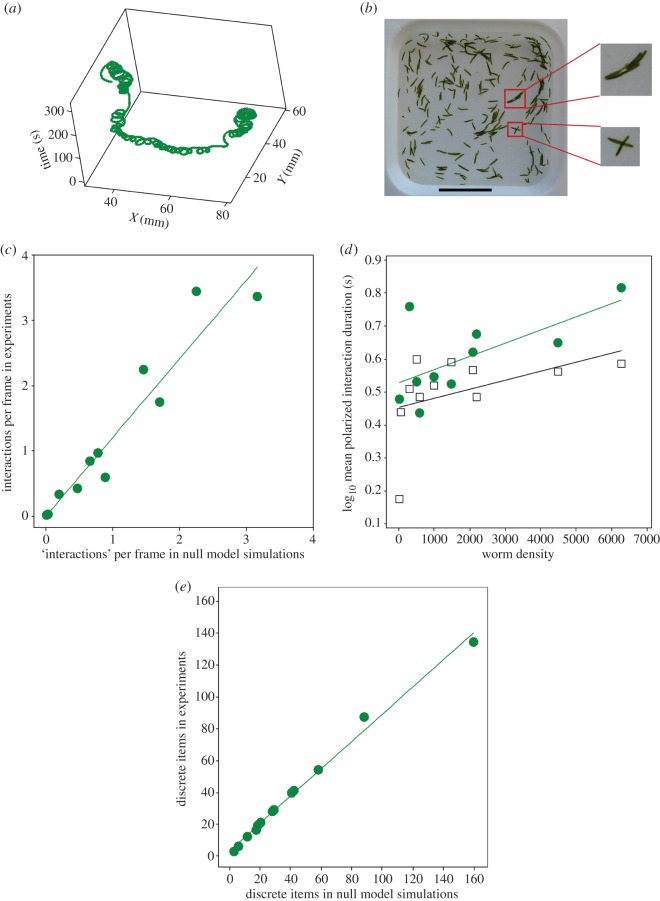
Figure 1.
Movement of individual S. roscoffensis worms and behaviour at intermediate densities. (a) Convoluted trajectory of a single worm. This individual made predominantly anticlockwise movements. (b) Flotilla formation at intermediate densities. The black scale bar at the bottom of the arena represents 10 mm. The upper red square shows a polarized group of four worms moving in the same direction in mutual contact (i.e. a flotilla; see also the upper panel to the right). The lower red square shows two worms crossing over one another (see also the lower panel to the right). (c) Comparison between number of interactions (per frame, both crossings and polarizations, see Material and methods) among worms in experimental videos and number of crossing and polarization events (per frame) in paired null model simulations at low to intermediate densities. The line of best fit passes through the origin and has a slope = 1.205 (t9 = 15.44, p < 0.001), which is significantly greater than 1 (95% CI: 1.029, 1.381; see the electronic supplementary material). Thus, there are more interactions between the real than between the virtual worms. (d) Polarized interaction durations increased among real worms in the experiments (green circles) but not among the virtual worms in the null model simulations (empty squares) which are paired with each experimental video (N = 11). The gradient of the relationship between log10 mean polarization event duration (s) and worm density is significantly different from 0 for the videos (slope = 0.000040, t8 = 2.44, p = 0.040), but not for the null model simulations (slope = 0.000027, t9 = 1.53, p = 0.161). This means that the relationship between polarization event duration and density (see the electronic supplementary material) can be attributed entirely to the data from the worms in the experiments. (e) The worms aggregate more in the experimental videos than in the null model simulations with increasing density as shown by the slope of the regression line being significantly less than 1. (N = 14; data from 13 circular arenas and one densely populated square arena; the latter is represented by the point at the top right.) Thus, there are fewer discrete objects in the videos than in the paired null model simulations. The equation of the line is: no. of discrete items in experiments = 3.19 + 0.858 no. of discrete items in simulations (R2 = 99.2%). The slope is significantly different from 0 (t12 = 38.73, p < 0.001) and significantly smaller than 1 (95% CI: 0.810–0.906; 99% CI: 0.790–0.925; see the electronic supplementary material).
(c). Interactions between worms: frequency
We used the same interval of 2 s (see later for justification) for the analysis of the videos and their paired simulations to minimize any issues of pseudo-replication. As the speeds of the worms in the videos and in the simulations were similar, the chance that the same interactions would be seen in successive frames would be similar, all else being equal, in both the videos and the simulations. Rather than using automated methods to detect worm encounters in the simulations, we used the same human observers to detect interactions both in the simulations and in the experimental videos. It was not difficult for a human observer to count the well-defined crossing and polarization events (see later) on still video frames and simulation bitmap images. Hence, this very simple procedure ensured that the same criteria were applied to both and hence that any differences between them were reproducible.
(i). Experimental videos
The software ‘ImageGrab’ (http://imagegrab.en.softonic.com/, accessed October 2014) was used to take a still image from the videos every 2 s. This interval was chosen to avoid counting the same interaction twice because in 2 s worms on average moved approximately two body lengths (average length = 1.68 mm, see Results; average speed = 1.78 mm s−1; see electronic supplementary material, figure S1). The images were then analysed one by one for the number of interactions. We recognized two types of interaction: (i) crossing—two worms are in direct contact but are not aligned in the same direction, that is, one is crossing over the other (the vertical proximity is approx. 1 mm, given the approximate 0.5 mm diameter of the worms and the 2 mm water depth); (ii) polarization—two worms are swimming in the same direction and orientation, in close proximity (within 1 mm), and in parallel or tandem positions. Such close proximity (within 1 mm) is almost certain to involve interaction even if only owing to disturbance in the physical environment.
Each contact between any two or more worms was counted. Therefore, if a worm had a worm parallel to it on either side, two polarized interactions were counted; similarly, if there were two worms swimming next to each other, and one was also crossing over with a third worm, one crossing and one polarization interaction were recorded. The total number of each interaction type was counted for each video and then divided by the number of analysed images to calculate an average number of interactions per image for a video. The analysis was based on 11 videos (figure 1c,d). The videos of the circular arena with 61 and 99 worms and of the square arena with 293 worms were not included because such high densities made these observations more difficult.
(ii). Simulation of non-interacting worms
The swimming behaviour of individual S. roscoffensis worms was recreated by computer simulation. The scale of the simulation was the same as that of the experimental video and the number of worms, and their lengths were chosen to match specific videos. The worms were made up of 0.2 mm units, which moved through the removal of a unit at the tail end and the replacement of it at the head end, each time changing the head-end angle by up to ±0.1 rad using a uniform distribution.
The simulation was configured so that it would run for the same length of time as the corresponding video and had an option to save bitmaps at set intervals. This function was used to collect the screenshots that were analysed. The bitmap interval was set to 2 s and the number of frames entered so that the simulation run time would match the duration of each video in 2c(i).
The worms were produced in six colours and had a black dot at the leading or ‘head’ end to aid in identifying the direction of movement during analysis (e.g. to determine polarization events).
For each image, the number of crossings and polarization events were recorded. The different colours aided counting the number of worms involved in each event and the marked heads helped to differentiate between parallel worms travelling in the same and different directions. The total number of events was then divided by the number of images as in the video analysis.
(d). Interactions between worms: duration
(i). Experimental videos
We calculated the mean duration of polarization interactions for each of the 11 videos also analysed for interaction frequency. We analysed a maximum of 20 such interactions from each video. A random number generator was used to select 20 if more had been recorded. The video was restarted at the beginning of each interaction and followed through to its end. We calculated each interaction duration as the difference between its start and end frame number.
(ii). Simulation of non-interacting worms
We mimicked the procedure with the videos of real worms as described in 2d(i) with simulations of non-interacting worms. We scrolled through the bitmaps until polarization events were found, and then followed the event from the first to the last image in which it occurred. The number of bitmaps featuring the event was used to produce the event duration in seconds based on the bitmap interval of 500 ms. We thus found the mean event duration for the simulation corresponding to each video.
(e). Interactions between worms: aggregation formation
(i). Experimental videos
We analysed all 14 videos to examine worm clustering (figure 1e). Using ImageGrab, we took a screenshot from the videos every 20 s. In each image, the number of clusters was counted. We defined clusters as occurring when two or more worms were in direct contact.
(ii). Simulation of non-interacting worms
The cluster counts for the simulation were performed by a modified version of the simulation program. The bitmaps of the simulation at 20 s intervals were loaded and then the program counted the number of clusters per bitmap.
(f). Circular milling as a function of density
The presence or absence of circular milling was recorded in 100 × 100 mm Petri dishes. Five were used for each of 17 dilution series making 85 data points altogether for density. The worms were pipetted with sea water into a plastic beaker to produce a high density of S. roscoffensis worms in approximately 50 ml of water. This was enough to complete one dilution series as follows: 8 ml was pipetted into the first Petri dish and then 4, 2, 1 and 0.5 ml into the second to fifth Petri dish, respectively. The mixture in the beaker was consistently and evenly stirred throughout the pipetting process to ensure the mixture of S. roscoffensis and sea water was as homogeneous as possible. Sea water collected from the habitat of S. roscoffensis was then added to each Petri dish to make the total volume of water in each up to 40 ml. At time zero, all of the Petri dishes were agitated to ensure that there were no mills present at the beginning of the experiment.
We observed the group of Petri dishes for 60 min and recorded the presence or absence of circular mills in each during that period. If a circular mill was seen, further observation of that Petri dish ceased at that time. Thus for each of the 85 density values, we recorded a value of 1 if at least one mill formed and a value of 0 if no mills formed over the 60-min-period of observation. At the end of the observations a photograph was taken of the most dilute dish of each series and the number of S. roscoffensis worms was counted with ImageJ. The numbers in the other Petri dishes were estimated from the number counted in the most dilute dish.
With worms collected at the same field site as described above but in June 2015, we studied the directionality of circular milling by again video recording them in plastic arenas. These data were also used in our analysis of the possible effect of arena walls on the formation of circular mills (electronic supplementary material, figure S5).
(g). Simulation of interacting worms
The simulation took place in a circular arena containing N ≤ 10 000 worms placed initially at random. Each worm consisted of a pair of jointed rods each 5 units long with an angle between them up to ±0.05 rad. At fixed time intervals, dt, the worm was advanced by a distance s = vdt(1−gc) along its circumscribed circle, where v was the worm's standard straight-line speed, c its instantaneous curvature and g a constant describing how the worm slows when turning. The final angle of the head section was then chosen from the existing one and four alternative random directions within ±0.15 rad of the tail direction and on the basis of which of these five options best accommodated the head with respect to the heads and tails of neighbouring worms.
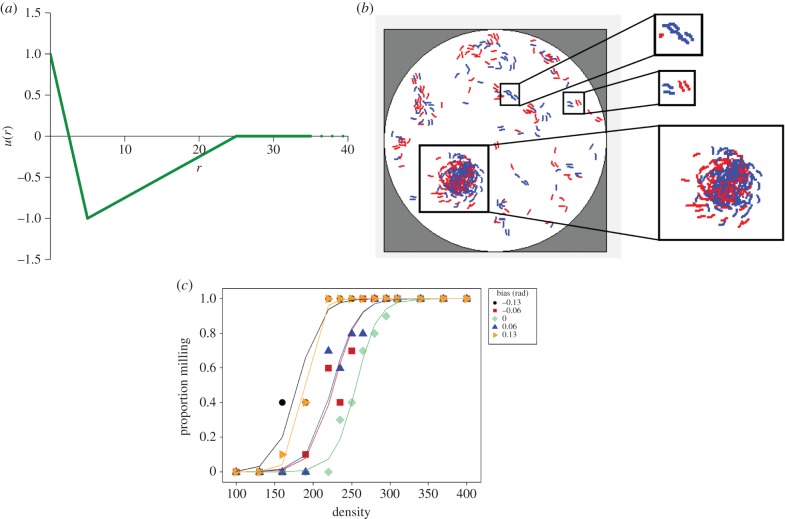
For each candidate position of the head, we calculated the energy U = Σλu(r), where the summation was taken with respect to the head and tail positions of all other worms within rmax and r was the relevant separation (electronic supplementary material, figure S4). We used an approximation of the Lennard–Jones model for pairwise interaction (figure 3a), as commonly used in such simulations [1]:
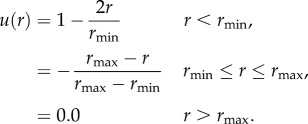 |
Figure 3.
Simulation of interacting worms. (a) Potential energy curve, an approximation of the Lennard–Jones model [1], used for pairwise interactions in the simulation of interacting worms; u(r): potential energy function, u(r) > 0: repulsion; u(r) < 0: attraction; r: range of interaction; at rmin = 5 attraction is at its maximum and rmax = 25 is the maximum range for any interaction (see electronic supplementary material, figure S4, for pseudocode). (b) The results of one simulation showing one circular mill (lower sub-panel) and several flotillas (examples in the top two sub-panels; worms in blue or red are temporarily moving clockwise or anticlockwise, respectively; note, these simulations have neither left not right biases in the movements of individual worms). (c) Self-organizing circular mills in the simulations as a function of density for different levels of lateral bias (rad) in the movement of individual worms; the bias range −0.13 to 0.13 rad goes from clockwise to anticlockwise with 0.00 rad representing no bias. There was a significant effect of density on the proportion of simulations with milling (out of 10 simulations for each value of density); note density here (i.e. the number of worms per simulation arena) cannot be directly compared to density of the real worms in a volume of sea water. For each of the five levels of bias, the proportion of simulations with milling increased by 7% (95% CI: 6–9%, p < 0.001, see the electronic supplementary material) with every additional worm. However, the inflection points differed; the inflection point for no bias (0.00 rad) was significantly different from the other four, whereas the inflection points for clockwise and anticlockwise biases of the same magnitude (−0.13 and 0.13 rad or −0.06 and 0.06 rad) were not significantly different from each other and significantly different from the rest (electronic supplementary material, table S1).
The multiplier λ took the value 1.0 for head–tail calculations. For head–head calculations, we used λ = 0.5 if the tails of the two worms were separated by more than the length of a worm, otherwise λ = 2.0. This weighting factor favoured polarized (head-to-head) alignment. The lowest of these energies was adopted for the new head position.
After each set of recalculations, the worms' identification numbers were shuffled to avoid undue influence by any one of them, and a simple reflection procedure ensured that worms stayed within the arena.
The values adopted for the various constants had been based where possible on measurements of real worms and translated into the artificial arena (electronic supplementary material, figure S4).
The circular arena had a radius of 200 units and given that the virtual and real worms had a length of 10 units and on average 1.68 mm, respectively, this represented an arena of radius 33.6 mm and an area of 3547 mm2.
We used the same simulation model in our analysis of the effect of arena boundaries on the formation of circular mills (electronic supplementary material, figure S5).
3. Results
(a). Characteristics of individual worms
The worms in our samples had a mean length of 1.68 mm (s.e. = 0.075 mm, N = 57) with the smallest being 0.54 mm and the largest 2.91 mm long. Their speed was well within the distribution measured by other methods in earlier studies [9]. It increased significantly with length but rather weakly and there was much variation (electronic supplementary material, figure S1). At low density in the circular arenas, the convoluted trajectories of individual worms were significantly biased towards clockwise movements (33 in a sample of 41, binomial two-tailed test, p = 0.0001; electronic supplementary material, figure S2, but see figure 1a for an anticlockwise example). Their speed declined markedly as a function of body curvature (electronic supplementary material, figure S3a,b) which in turn set their future trajectories.
(b). Interactions between worms
To test if the worms have a tendency to interact with one another, we compared the paired videos of the real worms and the simulations of non-interacting and non-laterally biased worms to determine if the real worms have either more or fewer interactions than the purely random encounters of the simulated worms. This comparison revealed that the real worms actively interact with one another even at rather low densities (figure 1c).
We considered two or more worms to be potentially interacting, either in the experimental videos or in the simulations, when they were less than 1 mm apart. Indeed, when this condition is met, typically the worms might be crossing over one another or swimming in the same direction with their bodies in parallel (the latter included worms that were closely following one another, as if in tandem). Such parallel similarly orientated movement, either side by side or following, is known as polarization [18].
The worms interacted with one another disproportionately more frequently as their density increased (figure 1b). The durations of individual polarization events increased with worm density among the real but not among the virtual worms in the null model simulation (figure 1d). As densities increased, several of the worms became involved in the same polarization interaction. In this way, they began to form small cohesive fleets, which we call flotillas (figure 1b).
Real worms maintained contact with one another so frequently with increasing densities that counting the number of isolated objects (single worms plus groups of touching worms) in freeze frames of experimental videos versus simulations showed a significant difference in the numbers of observed discrete entities (figure 1e). In short, there were significantly fewer (but bigger) aggregations among the real worms than among the virtual worms because they associated more with increasing density.
(c). Circular milling and directionality as a function of density
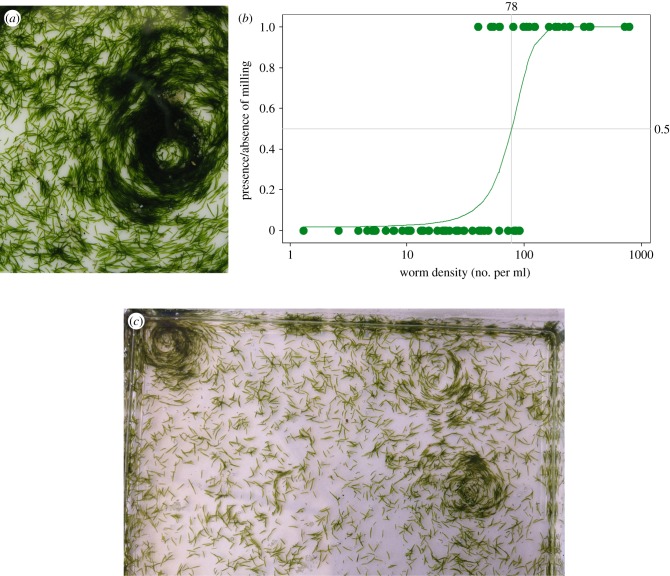
The separate experiments with different densities of worms in the 100 × 100 mm Petri dishes showed that the likelihood of circular milling in S. roscoffensis (figure 2a) increases abruptly as a function of increasing density (figure 2b). When they began to form, the initial diameter of these circular mills was of the order of about 10 mm and they were often well away from the dish edge (figure 2c). If anything, they are more likely to form near the centre (electronic supplementary material, figure S5). Thus, the circular milling of these worms does not occur because they are responding to the boundaries of their arena as a template; rather they occur because the worms are influencing one another's movements.
Figure 2.
Symsagittifera roscoffensis worms exhibit milling as a step function of increasing density. (a) A circular mill in a small arena. (b) The relationship between worm density (no. per ml) and the presence or absence of circular mills (1 and 0, respectively); green circles: data, black line: predicted probabilities from the fitted binary logistic regression model log(π/(1 − π)) = −4.126 + 0.053x, where π is the probability of milling and x is worm density. The model predicts that with every additional worm per ml, the probability of milling increases on average by 5% (95% CI: 3–8%) and that at density above 78 worms ml−1, the presence of milling becomes more likely than not (see the electronic supplementary material). (c) Part of a 100 × 100 mm Petri dish where three circular mills have formed.
Our observations from June 2015 showed that out of 45 circular mills all but one were clockwise.
(d). Simulation modelling of interacting worms
Symsagittifera roscoffensis worms may only be able to detect one another at very short distances. Hence, we produced a new computer simulation of these worms' movements with only very local interactions between them (figure 3a and electronic supplementary material, figure S4) to determine how the observed phase transitions, that is from solitary worms, to polarized flotillas, to large circular mills might occur through self-organization [17]. Because we knew the size and speed of the real worms (electronic supplementary material, figure S1) and the effect of curvature on their speeds (electronic supplementary material, figure S3), there were few arbitrary parameters. We observed flotillas and milling (figure 3b) with reasonable choices for the elapsed time per iteration, the maximum range of any interaction and the separation at which the potential energy is at a minimum (figure 3a and electronic supplementary material, figure S4). The likelihood of milling after a given time interval as a function of N (figure 3c) was similar qualitatively to the experimental data (figure 2b).
The behavioural lateralization of individual worms is likely to promote the probability of circular milling at lower densities (figure 3c).
4. Discussion
Through cycles of experimentation and modelling, we have been able to demonstrate how individual worms move at low densities, how they begin to interact with one another and how with increasing density this leads to circular milling behaviour.
The worms propel themselves through the action of cilia on their surface. However, they also have muscles that determine the curvature of their bodies and hence the curvature of their trajectories [8]. Such small average changes in speed with length may occur because drag will be proportional to surface area, as is the number of cilia, whose combined power combats such drag [27]. This might explain why worms of different sizes, but all of similar proportions, move at surprisingly similar speeds.
Clearly, the behaviours leading to circular mill formation begin to be seen even at fairly low densities; namely worms influencing one another's movements to form lasting parallel formations and aggregations. Such social behaviour becomes ever more common with increasing worm density (figure 2b).
The rather constant average speeds of the worms, despite substantial differences in body lengths (electronic supplementary material, figure S1), and their tendencies to turn in the same clockwise directions (electronic supplementary material, figure S2) seem to be adaptations that favour circular milling (figure 3c). Individual worms exhibit behavioural lateralization such that they move in a clockwise direction; the vast majority of circular mills (44 of the 45 observed in 2015) have a clockwise rotation and simulations show that circular milling will occur at lower densities when individual worms have the same directional biases.
In contrast to other organisms, such as starlings [28,29], that show collective group movements, these worms may only be able to detect one another at very short distances and hence our simulations of potentially interacting worms are based only on relatively local interactions between the worms. These simulations replicate the circular milling seen among the real worms at relatively high densities (figure 3b,c). Thus we have been able to establish how the movements of, and simple local interactions between, individuals contribute to the self-organizing emergent properties and phase transitions of large groups [17].
So far we have examined what factors favour circular milling in these plant-animals from a mechanistic view point. Now we will consider its possible adaptive value. Circular milling appears to be maladaptive in army ants and processionary caterpillars. Furthermore, in the non-social glass prawns, where it arises under environmental conditions which facilitate interaction during motion around a ring, it also seems to serve no apparent purpose [23]. However, we hypothesize that, where they are adaptive, circular mills may act as a positive-feedback vortex to capture the highest possible local densities of organisms for protection by numbers or other social advantages. In the case of S. roscoffensis considered here circular milling may enable these plant-animals to form very dense biofilms or mats that allow them to behave collectively as a social seaweed and colonize sandy beaches (figure 4a,b) where traditional macro-algal seaweeds would be unable to anchor a holdfast. We hypothesize these mats enable the worms to stabilize their positions in pools of seepage sea water on sandy beaches (figure 4b), by sharing a more or less continuous mucous sheath. The sharing of such a relatively thick mucous sheet may also enable the worms to benefit from sunlight on both of their sides at once as their underside receives solar energy reflected from the substrate [8].
Figure 4.
Dense mat formation of S. roscoffensis on a Guernsey beach. (a) The worms are in the drainage channel (from 7 to 2 o′clock) around the circular rock which is approximately 15 cm across. The rock is an anchor for the holdfasts of the macro-algae in the photograph, whereas the worms will burrow into the sand on the incoming tide. (b) A close-up of a mat revealing heterogeneity in worm density.
Recently, it has been shown that individual S. roscoffensis worms move towards light intensities that may be detrimental to the maximum photosynthetic rates of their symbiotic algae [9]. Our findings here may help to resolve this paradox because these worms are very likely to form dense aggregates at high light intensities and may take it in turns to be sheltered or exposed by burrowing inside or onto the surface of such social conglomerates. Such behaviour, using conspecific aggregations as living shields against environmental extremes, is seen, for example, in emperor penguins who form rotating huddles as protection against extreme Antarctic winds [30,31]. The worms are likely to find greater individual safety in these hugely dense aggregations and may even be able to defend themselves collectively through the mass production of dimethylsulfoniopropionate [8,32,33].
Our demonstration of social behaviour, with multiple phase transitions, in S. roscoffensis fills a missing tier in the long list of organisms in which collective motion has been observed [1,34]. We confidently predict that the diversity of organisms exhibiting social collective motion, at all levels of biological complexity, will continue to grow for the foreseeable future and that the importance of social behaviour as a major evolutionary transition [35] will be increasingly recognized.
Supplementary Material
Acknowledgements
We thank Ann Coquelin for her help and kindness in providing facilities for our work in Guernsey. We gratefully acknowledge two anonymous referees for their helpful comments.
Ethics
All S. roscoffensis worms were returned to the place on the shore from where they were collected after the experiments.
Data accessibility
All data associated with this paper can be found at the designated Dryad depository: http://dx.doi.org/10.5061/dryad.1n70s.
Authors' contributions
N.R.F. initiated and designed the study, A.W. conducted the modelling, K.A.J.G. and A.R.G. carried out the experiments, V.V. and H.P. analysed the experimental videos, C.D. and M.L.G. helped with the experiments, M.C.S. provided the tracking software, A.B.S.F. carried out the statistical analysis. N.R.F., A.W. and A.B.S.F. drafted the paper. All authors contributed to revisions.
Competing interests
We declare we have no competing interests.
Funding
We thank our respective departments for support.
References
- 1.Vicsek T, Zafeiris A. 2012. Collective motion. Phys. Rep. 517, 71–140. ( 10.1016/j.physrep.2012.03.004) [DOI] [Google Scholar]
- 2.Biroli G. 2007. Jamming: a new kind of phase transition? Nat. Phys. 3, 222–223. ( 10.1038/nphys580) [DOI] [Google Scholar]
- 3.Helbing D, Farkas IJ, Vicsek T. 2000. Simulating dynamical features of escape panic. Nature 407, 487–490. ( 10.1038/35035023) [DOI] [PubMed] [Google Scholar]
- 4.Sadati M, Taheri Qazvini N, Krishnan R, Park CY, Fredberg JJ. 2013. Collective migration and cell jamming. Differentiation 86, 121–125. ( 10.1016/j.diff.2013.02.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tamulonis C, Kaandorp J. 2014. A model of filamentous cyanobacteria leading to reticulate pattern formation. Life 4, 433–456. ( 10.3390/life4030433) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bourlat SJ, Hejnol A. 2009. Acoels. Curr. Biol. 19, R279–R280. ( 10.1016/j.cub.2009.02.045) [DOI] [PubMed] [Google Scholar]
- 7.Keeble F. 1910. Plant-animals: a study in symbiosis. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 8.Bailly X, et al. 2014. The chimerical and multifaceted marine acoel Symsagittifera roscoffensis: from photosymbiosis to brain regeneration. Front. Microbiol. 5, 1–13. ( 10.3389/fmicb.2014.00498) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nissen M, Shcherbakov D, Heyer A, Brummer F, Schill RO. 2015. Behaviour of the plathelminth Symsagittifera roscoffensis under different light conditions and the consequences for the symbiotic algae Tetraselmis convolutae. J. Exp. Biol. 218, 1693–1698. ( 10.1242/jeb.110429) [DOI] [PubMed] [Google Scholar]
- 10.Deneubourg JL, Goss S. 1989. Collective patterns and decision-making. Ethol. Ecol. Evol. 1, 295–311. ( 10.1080/08927014.1989.9525500) [DOI] [Google Scholar]
- 11.Lukeman R, Li YX, Edelstein-Keshet L. 2009. A conceptual model for milling formations in biological aggregates. Bull. Math. Biol. 71, 352–382. ( 10.1007/s11538-008-9365-7) [DOI] [PubMed] [Google Scholar]
- 12.Ben-Jacob E, Cohen I, Czirók A, Vicsek T, Gutnick DL. 1997. Chemomodulation of cellular movement, collective formation of vortices by swarming bacteria, and colonial development. Phys. A Stat. Mech. Appl. 238, 181–197. ( 10.1016/S0378-4371(96)00457-8) [DOI] [Google Scholar]
- 13.Sokolov A, Apodaca MM, Grzybowski BA, Aranson IS. 2010. Swimming bacteria power microscopic gears. Proc. Natl Acad. Sci. USA 107, 969–974. ( 10.1073/pnas.0913015107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ordemann A, Balazsi G, Caspari E, Moss F. 2003. Daphnia swarms: from single agent dynamics to collective vortex formation. In Proc. SPIE vol. 5110, Fluctuations and Noise in Biological, Biophysical, and Biomedical Systems, 30 April 2003 (eds SM Bezrukov, H Frauenfelder, F Moss), pp. 172–179. Bellingham, WA: Int. Soc. for Optical Engineering. [Google Scholar]
- 15.Fabre J-H, Legros GV. 1879. Souvenirs entomologiques: études sur l'instinct et les moeurs des insectes/J.-H. Fabre. Paris, France: Marie Léonard. [Google Scholar]
- 16.Franks NR, Gomez N, Goss S, Deneubourg JL. 1991. The blind leading the blind in army ant raid patterns: testing a model of self-organization (Hymenoptera: Formicidae). J. Insect Behav. 4, 583–607. ( 10.1007/BF01048072) [DOI] [Google Scholar]
- 17.Camazine S, Deneubourg JL, Franks NR, Sneyd NR, Theraulaz G, Bonabeau E. 2001. Self-organization in biological systems (Princeton studies in complexity). Princeton, NJ: Princeton University Press. [Google Scholar]
- 18.Soria M, Freon P, Chabanet P. 2007. Schooling properties of an obligate and a facultative fish species. J. Fish Biol. 71, 1257–1269. ( 10.1111/j.1095-8649.2007.01554.x) [DOI] [Google Scholar]
- 19.Bazazi S, Pfennig KS, Handegard NO, Couzin ID. 2012. Vortex formation and foraging in polyphenic spadefoot toad tadpoles. Behav. Ecol. Sociobiol. 66, 879–889. ( 10.1007/s00265-012-1336-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Couzin ID, Krause J, James R, Ruxton GD, Franks NR. 2002. Collective memory and spatial sorting in animal groups. J. Theor. Biol. 218, 1–11. ( 10.1006/yjtbi.3065) [DOI] [PubMed] [Google Scholar]
- 21.Couzin ID, Krause J, Franks NR, Levin SA. 2005. Effective leadership and decision-making in animal groups on the move. Nature 433, 513–516. ( 10.1038/nature03236) [DOI] [PubMed] [Google Scholar]
- 22.Calovi DS, Lopez U, Ngo S, Sire C, Chaté H, Theraulaz G. 2014. Swarming, schooling, milling: phase diagram of a data-driven fish school model. New J. Phys. 16, 015026 ( 10.1088/1367-2630/16/1/015026) [DOI] [Google Scholar]
- 23.Mann RP, Perna A, Strömbom D, Garnett R, Herbert-Read JE, Sumpter DJT, Ward AJW. 2013. Multi-scale inference of interaction rules in animal groups using Bayesian model selection. PLoS Comput. Biol. 9, e1002961 ( 10.1371/journal.pcbi.1002961) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hamilton WD. 1971. Geometry for the selfish herd. J. Theor. Biol. 31, 295–311. ( 10.1016/0022-5193(71)90189-5) [DOI] [PubMed] [Google Scholar]
- 25.Schneider CA, Rasband WS, Eliceiri KW. 2012. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675. ( 10.1038/nmeth.2089) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stumpe MC.2012. AnTracks. See http://www.antracks.org .
- 27.Alexander RM. 1970. Functional design in fishes. London, UK: Hutchinson University Library. [Google Scholar]
- 28.Cavagna A, Cimarelli A, Giardina I, Parisi G, Santagati R, Stefanini F, Viale M. 2010. Scale-free correlations in starling flocks. Proc. Natl Acad. Sci. USA 107, 11 865–11 870. ( 10.1073/pnas.1005766107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pearce DJG, Miller AM, Rowlands G, Turner MS. 2014. Role of projection in the control of bird flocks. Proc. Natl Acad. Sci. USA 111, 10 422–10 426. ( 10.1073/pnas.1402202111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ancel A, Visser H, Handrich Y, Masman D, Maho YL. 1997. Energy saving in huddling penguins. Nature. 385, 304–305. ( 10.1038/385304a0) [DOI] [Google Scholar]
- 31.Gerum RC, Fabry B, Metzner C, Beaulieu M, Ancel A, Zitterbart DP. 2013. The origin of traveling waves in an emperor penguin huddle. New J. Phys. 15, 125022 ( 10.1088/1367-2630/15/12/125022) [DOI] [Google Scholar]
- 32.Raina J-B, et al. 2013. DMSP biosynthesis by an animal and its role in coral thermal stress response. Nature 502, 677–680. ( 10.1038/nature12677) [DOI] [PubMed] [Google Scholar]
- 33.Wolfe GV, Steinke M, Kirst GO. 1997. Grazing-activated chemical defence in a unicellular marine alga. Nat. 387, 894–897. ( 10.1038/43168) [DOI] [Google Scholar]
- 34.Sumpter DJT. 2010. Collective animal behaviour. Princeton, NJ: Princeton University Press. [Google Scholar]
- 35.Maynard Smith J, Szathmary E. 1995. The major transitions in evolution. Oxford, UK: Oxford University Press. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data associated with this paper can be found at the designated Dryad depository: http://dx.doi.org/10.5061/dryad.1n70s.