Photoacoustics with coherent light

Abstract

Since its introduction in the mid-nineties, photoacoustic imaging of biological tissue has been one of the fastest growing biomedical imaging modality, and its basic principles are now considered as well established. In particular, light propagation in photoacoustic imaging is generally considered from the perspective of transport theory. However, recent breakthroughs in optics have shown that coherent light propagating through optically scattering medium could be manipulated towards novel imaging approaches. In this article, we first provide an introduction to the relevant concepts in the field, and then review the recent works showing that it is possible to exploit the coherence of light in conjunction with photoacoustics. We illustrate how the photoacoustic effect can be used as a powerful feedback mechanism for optical wavefront shaping in complex media, and conversely show how the coherence of light can be exploited to enhance photoacoustic imaging, for instance in terms of spatial resolution or for designing minimally invasive endoscopic devices. Finally, we discuss the current challenges and perspectives down the road towards practical applications in the field of photoacoustic imaging.

1. Introduction

Photoacoustic imaging of biological tissue is a fast developing multi-wave imaging modality that couples light excitation to acoustic detection, via the photoacoustic effect, to yield images of optical absorption [1], [2], [3], [4]. The photoacoustic effect consists in light absorption followed by acoustic emission, via thermo-elastic stress-generation. It was first used in the field of optical absorption spectroscopy, and has been introduced for biomedical applications in the mid-90s [5], [6], [7]. The general principle of photoacoustic imaging is the following: the sample to be imaged is illuminated by pulsed light (for most implementations), and acoustic waves generated from illuminated absorbing regions are detected by acoustic sensors. Depending on the situation, the resolution can be limited either by the acoustic or by the optical wavelength. Photoacoustic imaging was first developed for deep tissue optical imaging in the so-called acoustic-resolution regime, to overcome the loss of optical resolution caused by optical scattering. Due to multiple scattering of light in biological tissue, optical-resolution imaging based on ballistic light is limited to depths typically less than one millimetre [1], and the resolution of optical techniques based solely on multiply scattered light (such as Diffuse Optical Tomography [8]) is on the order of the imaging depth. On the other hand, ultrasound is very weakly scattered in biological tissue, and therefore photoacoustic waves can be used to reconstruct images of optical absorption with the resolution of ultrasound, which inversely scales with its frequency. The resolution and penetration depth for deep tissue acoustic-resolution photoacoustic imaging is ultimately limited by the attenuation of light and sound. In the spectral region 600-900 nm, the so-called “optical window” where absorption is minimal in tissues, the amount of multiply scattered light decreases exponentially with an effective attenuation length of about 1 cm [2]. The acoustic attenuation in tissue increases linearly with frequency, with a typical value of 0.5 dB cm⁻¹ MHz⁻¹. As a consequence of both light and sound attenuation, the penetration depth of photoacoustic imaging turns out to typically scale linearly with the acoustic-resolution, with a maximum depth-to-resolution ratio of about 200 [1], [4]. Another regime of photoacoustic imaging is optical-resolution photoacoustic microscopy, for which light is focused and raster-scanned over the sample to make a point-by-point photoacoustic image with a resolution given by the optical spot size [9]. This regime is only possible at shallow depth, where ballistic light is still present and can be focused to the optical diffraction limit. Over both the optical- and acoustic-resolution regimes, the depth-to-resolution ratio of photoacoustic imaging is typically in the 100-200 range, a combined consequence of both optical and ultrasound attenuation.

Because multiple scattering of light is an inescapable process during the propagation of light in complex media such as biological tissue (sec. 2.2), it has long been considered as a nuisance one wants to get rid of. In the last decade, it has however been demonstrated that multiple scattering could actually be exploited for optical imaging at unprecedented depth. This blooming field of research leveraged on the coherence properties of multiple scattered light (such as the formation of optical speckle patterns [10], sec. 2.3) and the possibility to control such properties thanks to the manipulation of light impinging on the medium: optical wavefront shaping has allowed focusing and imaging at optical resolution through strongly scattering materials [11] (sec. 2.4). In the field of photoacoustic imaging, up until recently, light has usually been considered from the sole point of view of the absorption of optical energy. Lasers have therefore been widely used as powerful and flexible sources of optical energy. In optical-resolution microscopy, spatial coherence is the necessary condition to focus down to a diffraction spot. However, coherence properties of lasers also confer specific properties to multiple scattering, at the core of phenomena such as the formation of optical speckle patterns, and open the possibility of manipulating scattered light with optical wavefront shaping. This paper reviews the recent research efforts led over the past few years to exploit and take advantage of the photoacoustic effect in conjunction with coherent illumination in the multiple scattering regime. We first introduce general concepts regarding both photoacoustics and light propagation in scattering media (Sec. 2), which will be extensively used in the rest of the paper. The two following sections then review the use of the photoacoustic effect as a feedback mechanism for optical wavefront shaping (Sec. 3) and how coherent light may enhanced photoacoustic imaging with speckle illumination or optical wavefront shaping (Sec. 4). We finally discuss the current limitations and envision some perspectives in the field.

2. Background

2.1. Photoacoustics: from light absorption to sound generation

In the context of photoacoustic imaging of soft biological tissue, one of the simplest and widely used theoretical description of the photoacoustic effect can be summarized by the following equation [12], [3]

$$\left[\frac{{\partial }^2}{\partial t^2}-c_s^2{\nabla }^2\right]p(\text{r},t)=\mathrm{\Gamma }\frac{\partial H}{\partial t}(\text{r},t)$$ (1)

where p(r, t) is the photoacoustic pressure field, and H(r, t) is a heating function that corresponds to the thermal energy converted from optical absorption, per unit volume and time per unit time. Eq. (1) assumes that the medium is acoustically and thermally homogeneous (with c_s the speed of sound, and Γ the Gruneisen coefficient which quantifies the efficiency of the photoacoustic generation by thermal expansion [3]), while the optical properties of the medium (hence H) may vary spatially. It also assumes that thermal diffusion may be neglected over the spatial and temporal scales of interest (i.e. heat-confinement assumption [3]), which is usually true for most situations encountered in photoacoustic imaging and will be considered fulfilled in this paper. This equation simply states that the heating following (optical) absorption appears as a source term in the acoustic wave equation, and therefore leads to the generation and propagation of acoustic waves.

H(r, t) is proportional to the optical intensity I(r, t), with some coefficient representative of the optical absorption. Importantly, time t in Eq. (1) refers to the time evolution of the optical intensity, which by definition is proportional to the square of the electric field averaged over a few optical periods. Using the complex notation for electric fields with slowly time-varying envelopes, the optical intensity may be written as I(r, t) ∝ |E(r, t)|², where the proportionality constant reflects local dielectric properties. In strongly scattering media such as biological tissue, there is no simple description for I(r, t) and E(r, t). The propagation of the electric field may be described by Maxwell's equations in which material properties strongly vary in space, with scattering caused by local variations of the index of refraction. While it is impossible in practice to obtain a full description of E(r, t) at the microscopic level, due to the very complex propagation process, light propagation in multiply scattering media may however be described with statistical approaches, further discussed in the following sections.

2.2. Light transport in multiple scattering media

The most widely used approach to model light propagation for the photoacoustic imaging of biological tissue is based on transport theory. In this framework, the physical quantity of interest is the fluence rate, which represents a local ensemble-averaged value of the optical intensity. Depending on the desired accuracy and scales of interest, several approaches may be used to describe the flow of optical energy with a transport approach. Numerical approaches include Monte-Carlo simulations of random walks used to describe the paths followed by the optical energy [13], and analytical models include the radiative transfer equation or the diffusion equation [14]. These approaches all have in common to describe the propagation of the optical energy based on scattering and absorption, defined as macroscopic values such as the absorption coefficient μ_a and the scattering coefficient μ_s. The simplest form of the transport theory in a macroscopically homogeneous medium is given by the following diffusion equation [14]

$$\left[\frac{1}{c}\frac{\partial }{\partial t}-\frac{1}{3({\mu }_a+{\mu }_s^{\prime })}{\nabla }^2\right]{\mathrm{\Phi }}_r(\text{r},t)=-{\mu }_a(\text{r}){\mathrm{\Phi }}_r(\text{r},t)$$ (2)

where Φ_r(r, t) is the optical fluence rate, defined as the energy per unit area per unit time integrated over all directions. Eq. (2) states that the fluence rate obeys a classical diffusion equation, with a loss term that reflects optical absorption, and a diffusion coefficient $D=\frac{1}{3({\mu }_a+{\mu }_s^{\prime })}$ that only depends on scattering and absorption. In D, ${\mu }_s^{\prime }$ is the reduced scattering coefficient, defined as ${\mu }_s^{\prime }={\mu }_s(1-g)$ where g reflects the scattering anisotropy [14]. The transport mean free path $l^{*}=1/{\mu }_s^{\prime }$ and the absorption length l_a = 1/μ_a are also often used as the spatial scales relevant respectively for multiple scattering and absorption. In biological tissue in the near infrared (the “optical window”), l^* and l_a are of the order of 1 mm and 10 cm respectively [15]. Eq. (2) can be derived from the radiative transfer equation (RTE), which is a more elaborate (and large scale) description of the energy transport based on the radiance L(r, s, t), i.e. a quantity that takes into account the direction s of the energy flux. It is out of the scope here to discuss the RTE (further details may be found in [14] for instance), but suffice it to mention that the fluence rate (that obeys Eq (2) under the diffusion approximation) is defined from the radiance by Φ_r(r, t) = ∫_4πL(r, s, t)dΩ.

Under the assumption that light propagation may be described by the transport theory, the fluence rate is the important physical quantity for photoacoustic imaging as the heating function H(r, t) may be readily expressed as

$$H(\text{r},t)={\mu }_a(\text{r}){\mathrm{\Phi }}_r(\text{r},t)$$ (3)

When the fluence rate Φ_r(r, t) may be decomposed as Φ_r(r, t)=Φ(r)f(t), the following widely used form of the photoacoustic wave equation is obtained:

$$\left[\frac{{\partial }^2}{\partial t^2}-c_s^2{\nabla }^2\right]p(\text{r},t)=\mathrm{\Gamma }{\mu }_a(\text{r})\mathrm{\Phi }(\text{r})\frac{\partial f(t)}{\partial t}$$ (4)

In most practical implementations of photoacoustic imaging, f(t) is a pulsed function (normalized such that ∫f(t)dt = 1), and μ_a(r)Φ(r) is the amount of absorbed energy per unit volume. For very short pulse (such as to verify the so-called stress-confinement condition [3], [16]), it can be shown that the forward photoacoustic problem described by Eq. (4) may be re-formulated as a source-free initial value problem, with an initial condition given by

$$p(\text{r},t=0)=p_0(\text{r})=\mathrm{\Gamma }{\mu }_a(\text{r})\mathrm{\Phi }(\text{r})$$ (5)

The stress-confinement condition is fulfilled when the pulse duration is much shorter that the characteristic acoustic propagation time within the medium, which for nanosecond pulses is verified with absorbers with typical dimensions larger than a few micrometers. The solution p(r, t) corresponding to pulses f(t) with finite duration may be obtained straightforwardly from the temporal convolution of the solution to Eq. (5) with f(t). This formulation shows that the appropriate resolution of the inverse problem based on the measurements of pressure waveforms provides a reconstruction of μ_a(r)Φ(r). In other words, under the stress-confinement assumption, the initial pressure build-up is proportional both to the local absorption coefficient and to the local fluence.

Although the formulation of the photoacoustic effect based on Eqs. (3) and (4) is one of the most widely used in photoacoustic imaging, it is inherently limited to situations where the propagation of light may be described appropriately by use of the light fluence Φ(r). While such situations are indeed the most commonly encountered in photoacoustic imaging, there however exist situations where the light fluence is not appropriate to describe phenomena of interests. As may be demonstrated from rigorous derivations of the diffusion equation from first principles in disordered media [17], [18], Φ(r, t) corresponds to a theoretical averaged value of the optical intensity, averaged over an ensemble of realizations of the disorder. In practice where experiments are performed with one given medium (one realization), a good approximation to Φ(r, t) is a spatial average of the optical intensity I(r, t) over a volume with typical linear dimensions of the order of a few wavelengths. As a consequence, Φ(r, t) is a physical quantity that does not take into account higher-order spatial correlations of the optical field. In particular Φ(r, t) does not take into account phenomena such as speckle patterns that exist when interference takes place between various propagation paths followed by sufficiently coherent light, as introduced in the following section.

2.3. Optical speckle

2.3.1. Definition

The phenomenon commonly called “speckle” refers to the granular structure of the intensity field I(r, t) that results from the seemingly random interference of a multitude of field amplitudes from different propagation paths [19], [20], [10]. Speckle patterns are observed in various configurations, including scattering by rough surfaces, propagation through scattering media and propagation inside multiple scattering media such as biological tissue. An illustration of a typical speckle pattern is given further in Fig. 5. As discussed below, speckle patterns are only observed when the light source has sufficient temporal and spatial coherence. Mathematically, the intensity at a given point I(r, t) may be written as a sum of a large number of complex amplitudes contributions as

$$I(\text{r},t)\propto |\sum _{\mathrm{path}k}{A}_k(\text{r},t)e^{i{\varphi }_k(\text{r},t)}{|}^2$$ (6)

where A_k and ϕ_k are the amplitude and phase of the electric field for path k.

Fig. 5.

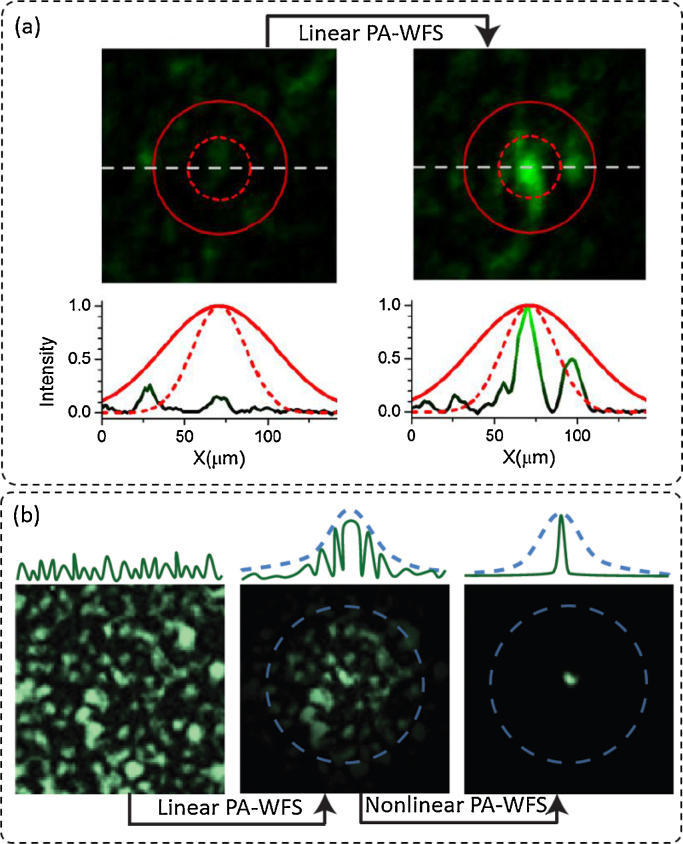
Illustration of sub-acoustic resolution optical focusing with photoacoustic-guided wavefront shaping with homogeneously absorbing samples, adapted from [69] and [70]. (a) The red circles show the approximate filtered transducer focal region (80 MHz, -6 dB, dashed line) and focal spot size at the frequency peak of the detected photoacoustic response (50 MHz, -6 dB, solid line). Left: optical speckle field (intensity) without optimized wavefront. Right: optical focus (intensity) generated by the optimized wavefront. The authors proposed that the sub-acoustic resolution optical focusing is achieved thanks to the non-uniform spatial response of the ultrasound transducer that would favor optical modes at the center [69]. (b) By using nonlinear photoacoustic-guided wavefront shaping, [70] performed sub-acoustic resolution optical focusing with a final optical enhancement factor of ∼6000. Linear PA-WFS first provided focusing with a enhancement of ∼60, and subsequent nonlinear PA-WFS provided an additional factor of ∼100. Figure (a) adapted with permission from [69], 2015 NPG. Figure (b) adapted with permission from [70], 2015 NPG.

2.3.2. Properties of an ideal speckle

We first consider the ideal case of perfectly coherent (monochromatic) light with angular frequency ω₀ that has undergone multiple propagation paths. Under this assumption, the intensity at a given point is stationary with = I(r) ∝|∑_{path k}A_k(r)e^iϕ_k(r)|². We further consider the case of a fully-developed speckle, i.e. the phases {ϕ_k} are uniformly distributed over [0 ; 2π], which has extremely well defined statistical properties. The first-order statistics of a fully-developed speckle field is described by the distribution of its intensity, which obeys the following negative exponential statistics [20], [10]

$$p_I(I)=\left\{\begin{array}{cc}\frac{1}{\langle I\rangle }exp\left(-\frac{I}{\langle I\rangle }\right)\hfill & I\ge 0\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right)$$ (7)

An important property of the above probability distribution is that its standard deviation σ_I is equal to its mean 〈I〉. As a consequence, fully developed speckle patterns have a contrast σ_I/〈I〉 = 1. While this probability function refers to an ensemble statistics over realizations of disorder, it is often realistic in practice to assume ergodocity and to consider that this ensemble statistics also describes the statistics over spatial position in the speckle field. This contrast of 1 is an example of a simple though fundamental feature of multiply scattered coherent light which is discarded by the transport theory: a homogeneous speckle field (p_I independent of r) translates into a constant fluence rate Φ(r) = 〈I〉 in the transport theory (N.B. The fluence rate is also often called accordingly the optical intensity, although it represents only an averaged intensity strictly speaking). A useful propertie of speckle is that the addition of N uncorrelated speckle intensity patterns will result in a speckle with a reduced contrast of $1/\sqrt{N}$ [19]. As a consequence, with spatially or temporally incoherent illumination, the intensity distribution is smoothed toward the mean intensity value from the transport theory.

Furthermore, the analysis of the spatial autocorrelation of a stationary speckle pattern provides the typical dimensions of a speckle “grain”, another major property of speckle, which depend on the considered geometry. Two configurations are of particular interest in the context of this review. The first one is a free-space propagation geometry, which corresponds for instance to the observation at some distance of the scattering by a rough surface or propagation through a scattering layer. In this case, the typical transverse linear dimension of a speckle grain is given by [10]:

$${\varphi }_s\sim \lambda \frac{z}{D}$$ (8)

where λ is the optical wavelength, z is the distance from the scatterer to the transverse imaging plane, D is the typical lateral dimension of the illuminated surface of the scattering object. The exact value of the numerical prefactor (close to one) in Eq. (8) depends on the illumination distribution on the scattering object. Along the main direction of propagation, the typical longitudinal dimension is given by [10]:

$$l_s\sim 7\lambda {\left(\frac{z}{D}\right)}^2$$ (9)

The exact value of the numerical prefactor in Eq. (9) also depends on the illumination distribution on the scattering object. This prefactor is close to 7 for a circular aperture of diameter D, close to 5 for a square of side D. The dimensions given by the formulas (8) and (9) (valid only for small values of $\frac{z}{D}$) are identical to those of the diffraction-limited focal spot of a lens with aperture D and focal distance z. The second important situation for the speckle grain size is inside a multiply scattering medium. There, due to the fact that the speckle is formed from contributions from all directions, the speckle grain is isotropic, with a typical linear dimension dictated solely by the wavelength and given by

$${\varphi }_s^{\mathrm{inside}}\sim \frac{\lambda }{2}$$ (10)

which is also the dimension of a diffraction-limited focal spot obtained with a full 4π aperture.

The contrast value of 1 discussed above is in fact only true in a scalar model, i.e. for linearly polarized light. For fully polarized light undergoing multiple scattering [10], the polarization is also mixed [21]. In paraxial free-space configuration geometry with $\frac{z}{D}\ll 1$, one can consider that there are two uncorrelated and fully developped speckle intensity patterns associated to two orthogonal polarizations in the imaging plane, which add up incoherently, and the resulting contrast is reduced to $1/\sqrt{2}$. Deep inside a multiple scattering medium, the 3-D speckle intensity results from the incoherent summation of the three possible polarizations and the contrast is further reduced to $1/\sqrt{3}$. Moreover, it has been assumed so far that the propagation medium is stationary, and that the speckle pattern is therefore stationary in time. For media whose properties may vary in time, such soft matter or biological tissue, the previous description of speckle patterns with monochromatic light remains valid provided that the intensity field are measured over integration time much smaller than any characteristic time of motion in the scattering medium.

2.3.3. Speckle with partially coherent light

A general condition to observe speckle patterns is that the coherence length of the light is larger than the largest path differences involved in the interference patterns. The coherence length l_c may be defined as the maximum length difference between two different paths in order to still observe interference, and is a direct consequence of the coherence time τ_c of a light source (l_c = c × τ_c) [20]. The temporal coherence of a light source is related to the spectral linewidth Δν of its spectral power density, with τ_c being proportional to $\frac{1}{\mathrm{\Delta }\nu }$ (with a proportionality constant that depends on the shape of the linewidth). For a Lorentzian line, ${\tau }_c=\frac{1}{\pi \mathrm{\Delta }\nu }$, and the coherence length is therefore

$$l_c=c\times {\tau }_c=\frac{c}{\pi \mathrm{\Delta }\nu }$$ (11)

If the coherence length is too short compared to the typical range of propagation paths, some of the partial waves corresponding to the terms in the summation in Eq. (6) cannot interfere coherently at position r, giving rise to incoherent sums of speckles, thus leading to a loss of contrast. If one considers light propagation through a slab of thickness L, the range of propagation paths in the multiple scattering regime (i.e. L ≫ l^*) scales as $\frac{L^2}{l^{*}}$ [23]. As a consequence, a condition to obtain a well contrasted speckle pattern after the propagation of light with coherence length l_c through a thickness L of a multiply scattering media with transport mean free path l^* is

$$l_c\gg \frac{L^2}{l^{*}}$$ (12)

This condition may also be written in the time or frequency domain as ${\tau }_c\sim \frac{1}{\mathrm{\Delta }\nu }\gg \frac{L^2}{c{l}^{*}}$, where$\frac{L^2}{c{l}^{*}}$ is the Thouless time [24], corresponding to the light storage time in the medium and to the temporal spreading of a light pulse after a diffusive propagation through a distance L. As an order of magnitude, the coherence length required to obtain a well-contrasted speckle pattern inside or through 3 cm of biological tissue is typically $l_c\sim \frac{{(3\mathrm{cm})}^2}{1\mathrm{mm}}\sim 1\mathrm{m}$. For pulsed light, a coherence length l_c ∼ 1m corresponds to a minimal pulse duration ${\tau }_p\sim \frac{l_c}{c}\sim 3\mathrm{ns}$. Therefore, whereas light coherence is generally neglected in photoacoustics, sufficiently coherent pulsed light does lead to coherent effects such as speckle patterns through or inside strongly scattering media. Before reviewing the recent investigations aimed at coupling photoacoustics and coherence effects, we briefly introduce the main principles of optical wavefront shaping in complex media, a field that has developed very rapidly over the past few years [11].

2.4. Optical wavefront shaping with multiply scattered light

2.4.1. Principles

Although multiple scattering may appear stochastic, as illustrated by the random appearance of speckle patterns, it is deterministic in nature. However, the deterministic propagation of coherent light trough strongly scattering media is driven by a huge number of parameters that reflect the complex nature of the multiple scattering process. For instance, the speckle pattern that arises from an illumination area A after propagation through a thick scattering medium is typically described by a number of parameters N (often referred to as the number of modes) that scales as $\frac{2\pi A}{{\lambda }^2}$, which for visible light corresponds typically to 10 million modes per square millimetre [11]. As a consequence, it has long been thought that the techniques of adaptive optics (which involves measuring and controlling the phase and/or amplitude of the wavefronts of light with a given number of degrees of freedom (DOF)) were limited to situations where the distortions of optical wavefront could be described or compensated for with a relatively small number of modes, comparable to the number of DOF provided by the optical devices. The pioneering demonstration of spatial focusing through a strongly scattering layer by Vellekoop and Mosk [22] has however shown that adaptive optics could in fact be extended to situations where one controls only a limited numbers of DOF compared to the total number of mode involved in the propagation: it was demonstrated in this work that optical wavefront shaping with N_DOF degrees of freedom allowed enhancing the intensity of a single speckle grain by a factor η ∝ N_DOF relatively to the intensity of each speckle grain in the diffuse background, while the ratio N_DOF/N ≪ 1 only dictates the ratio of the intensity within the enhanced spot to the total transmitted intensity.

Schematics of the experiment performed by Vellekoop and Mosk [22] are shown in Fig. 1. The key principle at the core of this experiment is that the transmitted electric field E_m in the CCD camera plane is a linear combination of the electric fields E_n = A_ne^iϕ_n coming from the N_DOF pixels of the spatial light modulator (SLM):

$$E_m=\sum _{n=1}^{N_{\mathrm{DOF}}}{t}_{\mathrm{mn}}{A}_n{e}^{i{\varphi }_n}$$ (13)

where A_n and ϕ_n are the amplitude and phase of the light reflected from the nth input pixel, and t_mn is the complex transmission matrix between the transmitted (output) field and the SLM (input) field [22]. Optical wavefront shaping essentially consists in first measuring transmitted output values, followed by appropriately setting the phase and/or amplitude (depending on the type of control provided by the spatial light modulator) of the input field in order to obtain a targeted pattern in the output field. Several approaches have been investigated to implement optical wavefront shaping with strongly scattering media, based either on optimization or measurement of a transmission matrix, as discussed in the two following sections.

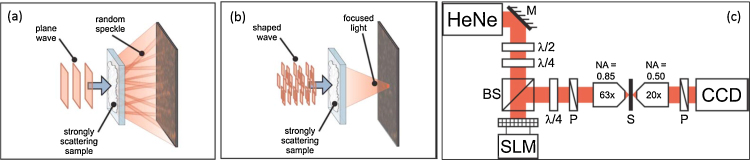
Fig. 1.

General illustration of optical wavefront shaping through a strongly scattering sample. (a) A coherent plane is multiply scattered through a strongly scattering sample, yielding a speckle pattern propagating in free-space to the observation plane. (b) Optical wavefront shaping of the incident wave allows focusing light through the scattering sample. (c) Experimental setup used to perform optical wavefront shaping in the pioneer experiment by Vellekoop and Mosk [22]. The values of the phase on each pixel of the spatial light modulator (SLM) were found one by one with an optimization algorithm based on a feedback signal measured on the camera (CCD). Figure reproduced with permission from [22], 2007 OSA.

2.4.2. Optimization-based optical wavefront shaping

In their pioneering experiment, Vellekoop and Mosk [22] demonstrated focusing towards a single speckle grain by use of an optimization approach: with the typical dimension of speckle grains matched to that of the measurement pixel size, the phases ϕ_n of each input electric field E_n corresponding to the n-th mode were cycled sequentially from 0 to 2π, and the phase values that maximized the intensity on a given pixel of the camera are recorded for each input mode. After this procedure, the phases of all the input modes are set simultaneously to their recorded optimal value, resulting in a strong constructive interference at the chosen speckle grain as all the terms t_mnA_ne^iϕ_n are in phase [22], effectively forming a very strong focus. The authors were able to enhance the light intensity of a targeted speckle grain by a factor 1000 through a 10-μm thick layer of rutile (TiO₂) with a transport mean free path of 0.55 μm.

A key parameter when optimizing the light intensity is the dimension of the targeted detection area relatively to that of the speckle grain. When a number N_s of speckle grains are contained within the targeted area, the intensity enhancement factor is typically divided by N_s as the focusing is spread over the N_s speckle grains, and therefore scales as $\eta \propto \frac{N_{\mathrm{DOF}}}{N_s}$ [25]. Moreover, when the targeted area contains several speckle grains, the global effect of a phase modulation of a single input mode is decreased compared to that obtained for a single speckle grain, as the phases on each speckle grain are uncorrelated. As a consequence, the possibility to detect intensity modulation in the target region depends on the signal-to-noise ratio and decreases with the number N_s of independent speckle grains in the detection area. Note that stemming from the initial work of Vellekoop and Mosk [22], several algorithms have been proposed, in order to improve the focusing efficiency in low SNR scenarios [26], to improve focusing speed [27], [28] or to adapt to different modulation schemes [29]. The main limitation of optimization approaches is that the whole optimization procedure has to be repeated for each desired target pattern, leading to very long measurement times in practice if several target patterns are required.

2.4.3. Wavefront shaping with the transmission matrix

Following the initial demonstration of optical wavefront shaping by use of an optimization approach, Popoff and coworkers demonstrated the first measurement with a strongly scattering layer of an optical transmission matrix t_mn with over 60,000 elements [30]. To do so, the transmitted speckle patterns were measured over the camera plane for a set of orthogonal input modes that form a full basis for all the possible SLM modes. As the camera records only the optical intensity, an interferometric approach was implemented to retrieve the phase and amplitude information from intensity measurements: an unshaped part of the beam reflected off an unmodulated region on the SLM is used as a reference beam, and the phase of each controlled SLM input mode is varied from 0 to 2π in order to retrieve the amplitude and phase of the matrix element. For each input mode n, the phases and amplitudes of the intensity modulations measured on all the output pixels of the camera provides a measurement of the column t_mn = |t_mn|e^iϕ_mn of the transmission matrix. Repeating these measurements for all possible input mode provides the transmission matrix between the pixels of the camera and the pixels of the SLM. From the transmission matrix, one can predict the amplitude and phase required on each input mode in order to obtained any desired output pattern in the camera plane, via inversion or phase-conjugation of the transmission matrix [31]. As the simplest example, Eq. (13) shows that focusing light onto the m^th output pixel may simply be obtained with a phase-only SLM by setting the phase of each n^th input mode to ϕ_n = − ϕ_mn: doing so, all the terms in Eq. (13) end up in phase, resulting in focusing towards the m^th output pixel. The result is therefore similar to that obtained with the optimization approach; however the key advantage of the transmission matrix approach is that once the transmission matrix is measured, input patterns may be computed for any desired transmitted pattern, while the optimization approach requires to measure the optimized input patterns for each desired output pattern.

2.4.4. Discussion

Wavefront shaping in biological tissues is currently a very active field of research. While this review focuses on photoacoustics-related works, other imaging modalities are explored in parallel, in particular multiphoton fluorescence [32], [33], [34], [35] and coherent imaging techniques such as optical coherence tomography or tomographic phase microscopy [36]. At a more basic level, different strategies and technologies are explored for faster or more efficient wavefront shaping, beyond the slow liquid crystal technology, from MEMS-based devices [28], [37], [29] to fast photorefractive materials [38] or acousto-optics modulators [39]. Radically novel concepts, such as compressive sensing [40] or non-invasive imaging [41], [42] also emerge as potentially interesting techniques to apply to photoacoustic imaging. The memory effect, an old concept from mesoscopic physics that states that for a thin sample a optimized focus can be scanned over a small volume [43], [44], has recently been characterized in biological tissues [45], [46], [47] and also hold promises for better and faster wavefront shaping-based imaging.

Analogous to the case of multiple scattering media, a speckle pattern is also observed at the output of a multimode fiber when illuminated by coherent light at the input. Following the first proof-of-concepts related to multiple scattering media, wavefront shaping has therefore also rapidly been applied to light manipulation through multi-mode fibers [48], [49], [50], [51]. As multi-mode fibers have a much smaller footprint than bundles of single-mode fibers (for an equivalent number of modes), these works opened important perspectives step towards the miniaturization of devices for optical endomicroscopy. Recent developments in the fields of photoacoustic endoscopy are presented in section 4.2.

3. Photoacoustic-guided optical wavefront shaping

All implementations of optical wavefront shaping require some feedback signal from the targeted region. A feedback mechanism for optical wavefront shaping should provide some sensing of the optical intensity. Appropriate mechanisms include direct intensity measurement with a camera or optical detector, or the use of some “guide star” following the approach in adaptive optics for astronomy [53]. While the use of a camera or detector limits wavefront shaping towards region outside the scattering media [22], [30], [32], [54], the “guide star” approach may be implemented inside a scattering sample. Fluorescent or second-harmonic “guide stars” have been successfully investigated as feedback mechanisms [55], [25], but these approaches, in addition to being invasive, only allows focusing in the vicinity of a single static target. Ultrasound tagging via the acousto-optic effect is a promising approach that offers dynamic and flexible control, which has been the subject of several recent investigations [56], [57], [58], [59], [60], [61], [38]. In this approach, the selective detection of tagged photons followed by phase-conjugation allows to backpropagate light towards the ultrasound focus where the tagging via acousto-optic modulation occured. This has the advantage to allow single shot digital phase conjugation, i.e. finding the optimal wavefront to refocus on the guide-star without a long learning process (like optimization or transmission matrix), and therefore refocusing in a single refresh frame of the spatial light modulator. This was for instance demonstrated by Liu and coworkers who demonstrated focusing in tissues with 5.6 ms decorrelation time [38]. Although this approach is in principle compatible with in vivo imaging, the activation of a local guide star by acoustic tagging is limited to a single ultrasound focal zone, and scanning is required to focused light at various directions, requiring in turns long acquisition times.

As introduced in Sec. 2.1, the photoacoustic effect is sensitive to the absorption of optical energy, and therefore provides a mechanism to sense both the optical absorption and the optical intensity inside multiple scattering media. Based on its sensitivity to optical absorption, photoacoustic-guided wavefront shaping has first been investigated for ultrasound wavefront shaping, to focus acoustic waves towards optical absorbers with time-reversal approaches [62], [63]. Photoacoustic-guided wavefront shaping was later applied in the context of acousto-optic imaging in the presence of acoustic abberations [64]. In 2011, Kong and coworkers first demonstrated the use of the photoacoustic effect as a feedback mechanism for optical wavefront shaping [52], triggering significant research efforts towards photoacoustic-guided optical wavefront shaping. Analogous to wavefront shaping with the other feedback mechanisms introduced above, two main approaches have been used to implement photoacoustic-guided optical wavefront shaping (PA-WFS), either based on optimization or transmission matrix, as reviewed in the two following sections.

3.1. Photoacoustic-guided optical wavefront shaping with optimization

In their pioneering work [52], Kong and coworkers followed the optimization approach initially proposed by Vellekoop and Mosk [22], as illustrated on Fig. 2. The target plane consisted of a glass layer covered with graphite particles, placed behind the scattering layer. Different concentrations and types of absorbers were used to demonstrate photoacoustic-guided wavefront shaping: the authors first demonstrated optical tracking and focusing towards the 41 μm-diameter focal zone of a 75 MHz ultrasound transducer with a homogeneously absorbing layer, in clear water. Experiments with single microparticles (10 μm or 50 μm in diameter) isolated within the 90 μm-diameter focal zone of a 40 MHz ultrasound transducer confirmed that the enhancement of the optimized photoacoustic signal decreased with the number of optical speckle grains (with grain size about 2 μm) within the absorbing target, in qualitative agreement with what is predicted for the optical enhancement factor. Typical enhancement for the photoacoutic signal ranged from 5 to 10, with the larger enhancements observed for the smallest particles. Interestingly, it was shown that with a speckle size of 1 μm and a 10 μm-diameter graphite particle, it was not possible to observe any enhancement with the available 140 degree of freedom provided by the deformable mirror used for the experiment [52].

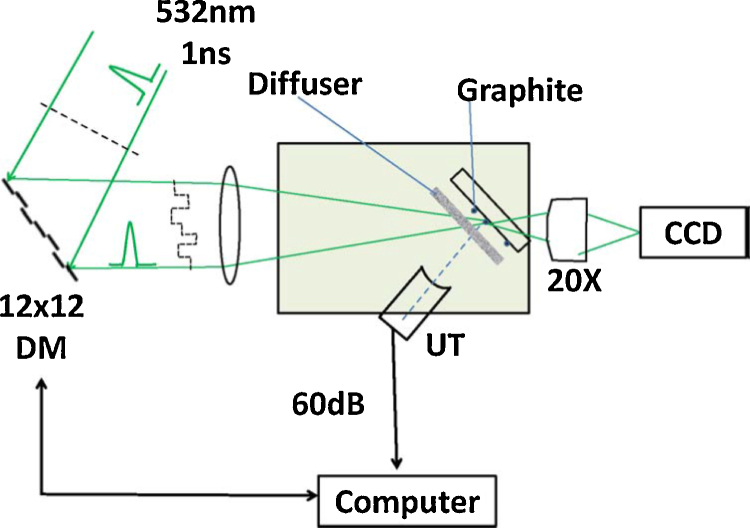
Fig. 2.

Experimental setup used by Kong and coworkers [52] to demonstrate optical wavefront shaping with a deformable mirror (DM) through a scattering media with photoacoustic feedback. A glass slide covered with absorbing graphite particles was placed behind the scattering layer, and a high frequency ultrasound transducer (UT) was focused on the absorbing slide to measure the photoacoustic signal from its focal region. The photoacoustic signal was used as a feedback signal for the optimization procedure driving the DM. The CCD camera was only used here to verify the light intensity distribution on the absorbing layer after the optimization. Figure reproduced with permission from [52], 2011 OSA.

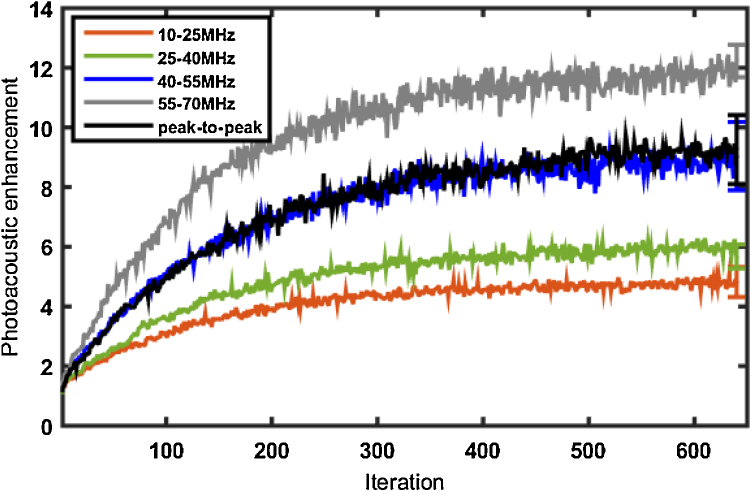
This pioneering work was rapidly followed by several investigations of photoacoustic-guided optical wavefront shaping. In all the works reviewed in this section, the experimental setups are similar to that introduced by Kong and coworkers: in particular, photoacoustic feedback signals are measured from speckle patterns produced in a free-space geometry after propagation through a scattering sample. Importantly, the size of the speckle grains is systematically adjusted to match the typical dimension of the ultrasound focus by setting the distance between the scattering sample and the measurement plane (see Sec. 2.3 on the properties of optical speckle patterns). The spatial light modulators or deformable mirrors used to perform wavefront shaping were used in a reflection configuration, as in Figs. 1 and 2. Following the approach proposed by Kong and coworkers [52], Caravaca-Aguirre and coworkers used a genetic algorithm to perform PA-WFS and enhance the light intensity behind a scattering layer by one order of magnitude [65], as illustrated in Fig. 3. Their study, aimed at improving photoacoustic imaging, is further discussed in Sec. 4. Chaigne and coworkers [66] further demonstrated that the large bandwidth of photoacoustic signals could be exploited in the frequency domain to adjust the dimensions of the photoacoustic focal zone. By iterative optimization of the highest frequency components (55-70 MHz band) of the broadband photoacoustic signals measured with a transducer with central frequence 27 MHz, the authors obtained a photoacoustic enhancement factor of about ×12, higher than the enhancement obtained with optimization in lower frequency bands (ranging from ×4 to ×8) or from peak-to-peak amplitude measurements (×8), as illustrated in Fig. 4. To maximize the sensitivity of photoacoustic measurement to phase modulation of the light beam, the optimization algorithm used a Hadamard basis vectors as the basis for the input modes (instead of the canonical pixel basis) of a 140-element deformable mirror [66]. Moreover, by simultaneously monitoring the evolution of the speckle pattern during the optimization process, it was confirmed experimentally that the optimization with the highest photoacoustic frequencies lead to a tighter optical focus than what was obtained by optimization with the lower frequency components.

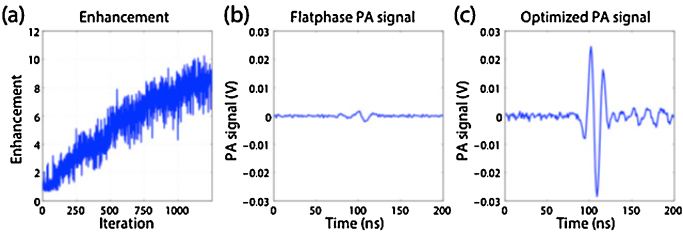
Fig. 3.

Illustration of the photoacoustic signal enhancement obtained with optimization-based photoacoustic-guided optical wavefront shaping. (a) Evolution of the photoacoustic enhancement with the optimization process, based on a genetic algorithm. (b) Photoacoustic signal prior to wavefront shaping. (c) Enhanced photoacoustic signal obtained for the optimal input wavefront. Figure reproduced with permission from [65], 2013 OSA.

Fig. 4.

Evolution of the photoacoustic enhancement factor by optical wavefront shaping during the optimization process, with different feedback values. In addition to the usual peak-to-peak photoacoustic amplitude as feedback signal, RMS values over several frequency bands computed from a Fourier analysis were used as alternative photoacoustic feedback values. For each feedback quantity, the photoacoustic enhancement factor was computed by normalizing the optimized quantity by its value under homogeneous illumination. Figure reproduced with permission from [66], 2014 OSA.

A key advantage of the photoacoustic effect as a feedback mechanism is that the sensing may be performed simultaneously over the whole measurement volume, by use of imaging ultrasound arrays. With a spherical matrix array of 256 piezoelectric transducers, Deán-Ben and co-workers demonstrated photoacoustic-guided optical wavefront shaping by optimizing photoacoustic signals from selected targets of a 3D photoacoustic image, by means of a genetic algorithm [67]. PA-WFS is usually limited in speed by either the laser pulse repetition frequency or the refresh rate of the adaptive optics device. In the context of photoacoustic flowmetry, Tay and coworkers investigated the potential of digital micromirror devices (DMD), which are binary amplitude modulators, towards rapid PA-WFS [68]: a combination of Hadamard multiplexing with multiple binary-amplitude illumination patterns was implemented to perform wavefront shaping based on the photoacoustic signal measured with a 10 MHz spherically focused transducer, and an intensity enhancement of a factor 14 was obtained. Although the DMD refresh rate was as high as 22 kHz, the optimization approach remained very long (typically two hours) because of a SNR issue. This study however demonstrated the potential of using DMD for PA-WFS.

One specific feature of photoacoustic sensing for optical wavefront shaping arises from the possibility to create an optical focus smaller than the ultrasound resolution [69], [70] (see Fig. 5), thus opening the possibility for super-resolution photoacoustic imaging. When several optical speckle grains are present within the ultrasound resolution spot, the feedback signal mixes the information coming from individual speckles. However, based on the non-uniform spatial sensitivity across the ultrasound focal region, it has been suggested that the spatially non-uniform photoacoustic feedback tends to localize the optimized optical intensity to a single speckle smaller than the acoustic focus, by preferentially weighting the single optical speckle closest to the center of the ultrasound focus during the optimization [69](see Fig. 5.a). As a consequence, an optical enhancement factor of 24 was reported for the optimized optical grain, about three times higher than the photoacoustic enhancement factor which averages the optical enhancement over all the optical speckles present in the focal spot. Possible applications of this sub-acoustic resolution optical focusing are further discussed in Sec. 4.2. While this effect was first reported in the context of linear photoacoustics, where the photoacoustic amplitude is proportional to the absorbed optical intensity as described by Eq. (1), Lai and coworkers introduced a nonlinear PA-WFS with a dual-pulse illumination scheme [70]. In short, this approach exploits the change in photoacoustic conversion efficiency between two consecutive intense illuminations to produce a feedback signal that is nonlinearly related the optical intensity: the first illumination pulse creates a photoacoustic signal that is linearly related to the optical intensity, but also changes the value of the Grüneisen coefficient Γ involved in the second illumination pulse. The change in the Grüneisen coefficient is caused by the temperature increase that follows the first illumination pulse [71], [70]. As a consequence, the feedback signal defined as the difference of the photoacoustic amplitudes of the two consecutive pulses varies nonlinearly with the optical intensity. As a result, optimization based on such a nonlinear feedback signal strongly favors focusing towards a single optical speckle grain rather than distributing the optical intensity evenly over all the speckle grains inside the acoustic focus spot. This effect had first been demonstrated with optical wavefront shaping based on nonlinear feedback from two-photon fluorescence [34], [33]. With nonlinear PA-WFS, Lai and coworkers achieved focusing to a single optical speckle grain 10 times smaller than the acoustic focus, with an optical intensity enhancement factor of ∼6000 and a photoacoustic enhancement factor of ∼60 (see Fig. 5.b).

3.2. The photoacoustic transmission matrix

Following the transmission matrix approach proposed in optics [30], introduced in Sec. 2.4, the measurement of a photoacoustic transmission matrix was demonstrated for PA-WFS with both 1D and 2D photoacoustic images [73], [72]. The concept is strictly similar to that in optics, except that the pixels of the optical camera are replaced by the pixels of the photoacoustic image, which values are linearly related to the local optical intensity.

The method was first implemented with the time-resolved photoacoustic signal from a single-element transducer processed as a 1D photoacoustic image [73], and was rapidly extended to 2D photoacoustic images reconstructed from signals acquired with a conventional linear ultrasound array [72]. The typical experimental setup used to acquire the photoacoustic transmission matrix from 2D photoacoustic images is shown in Fig. 6, along with typical results. Fig. 6(b) shows the photoacoustic image of an absorbing leaf skeleton (photograph shown in Fig. 6(a), obtained by averaging the various photoacoustic images obtained during the measurement of the transmission matrix. The absence of horizontally oriented features in Fig. 6(b) is a consequence of the limited view configuration, where the ultrasound probe mostly detect waves propagating upwards, and is further discussed in Sec. 4. As opposed to the optimization approach, the photoacoustic transmission matrix approach can be used to focus light at any desired location after the matrix has been measured: Fig. 6(c) is a zoom on the blue region of Fig. 6(b), showing a target region outlined in red. Fig. 6(d) illustrates the light intensity enhancement (typically 6 times) after the SLM input pattern has been set to focus light towards the target region based on the knowledge of the photoacoustic transmission matrix. As an additional illustration of the power of the matrix approach, it was also shown that a singular value decomposition (SVD) of the photoacoustic transmission matrix provides a mean for automatically identifying signals from the most absorbing targets [73]. In contrast with optimization approaches, the transmission matrix approach rely on the assumption that the measured signal is proportional to the intensity. It therefore cannot benefit from non-linearities or non-uniformities of the acoustic response for sub-acoustic resolution focusing.

Fig. 6.

Illustration of photoacoustic-guided optical wavefront shaping based on the photoacoustic transmission matrix. The laser pulse is reflected off a spatial light modulator (SLM) before propagating through a scattering medium and illuminating an absorbing sample. 2D photoacoustic images are reconstructed from the photoacoustic signals measured with a linear ultrasound array. A photoacoustic transmission matrix was measured between the pixels of the 2D-photoacoustic image and the pixels of the SLM. (a) Photograph of the absorbing sample (dyed leaf skeleton). (b) Conventional photoacoustic image equivalent to that obtained under homogeneous illumination. (c) Zoom on the blue inset in (b). (d) Photoacoustic image obtained after setting the SLM pixels to selectively focus light onto the targeted region indicated in red, based on prior measurements of the photoacoustic transmission matrix. A photoacoustic enhancement factor of about 6 was observed in the targeted region. Figures (a), (b), (c) and (d) adapted from [72], 2014 OSA.

4. Enhancing photoacoustic imaging with coherent light

In the previous section, we reported results for which the photoacoustic effect was used as feedback mechanism for optical wavefront shaping of coherent light. In this section, we now illustrate how photoacousting imaging may directly benefit from effects based on the coherence of light, such as speckle illumination or optical wavefront shaping. Generally speaking, the ultimate objective of photoacoustic imaging is to quantitatively reconstruct the distribution of optical absorption, described via the absorption coefficient μ_a(r). This objective has usually been pursued by considering that μ_a(r)Φ_r(r, t) is the relevant quantity, where the fluence rate Φ(r, t) is a spatially smooth function, in particular usually smoother than μ_a(r). However, if the coherence of light is to be taken into account, the local optical intensity I(r, t) is the appropriate physical quantity, as discussed in Sec. 2.3. From a theoretical point of view, the relevant photoacoustic equation for coherent light should then read

$$\left[\frac{{\partial }^2}{\partial t^2}-c_s^2{\nabla }^2\right]p(\text{r},t)=\mathrm{\Gamma }{\mu }_a(\text{r})\frac{\partial I}{\partial t}(\text{r},t)$$ (14)

where I(r, t) is generally a speckle pattern (and assuming that the optical absorption may still be described by some function μ_a(r)). As opposed to the fluence rate Φ(r, t), I(r, t) is strongly spatially varying over the typical dimensions of the optical speckle grain (i.e. half the optical wavelength inside scattering media), and can vary from pulse to pulse. In particular, in many cases I(r, t) will usually vary spatially at least as fast or faster than μ_a(r) and than the acoustic resolution. In such situations, the photoacoustic signals are expected to bear the signature of speckle patterns. In addition, because optical wavefront shaping provides a means to control I(r, t) through or inside strongly scattering media, it allows controlling additional degrees of freedom relatively to the sample illumination, as opposed to conventional photoacoustic imaging based solely on the fluence rate. The two following sections illustrate how both multiple speckle illumination and wavefront shaping may be exploited to improve photoacoustic imaging.

4.1. Exploiting multiple speckle illumination

As discussed above, photoacoustic waves generated from a sample illuminated with an optical speckle pattern bear some information on μ_a(r)I(r, t). As a consequence, the general features of photoacoustic sources such as their frequency content or directivity may be strongly affected by a speckle illumination. By using multiple speckle illumination, Gateau and coworkers have shown that both limited-view and frequency filtering artefacts could be compensated for with appropriate processing of the corresponding multiple photoacoustic images, as illustrated in Fig. 7 for three types of samples (a), (b) and (c). The experiments were conducted with a setup similar to that shown in Fig. 6, with a spatial light modulator (segmented MEMS mirror) for the sample (b) [72], and with a rotating diffuser instead of the MEMS for the samples (a) and (c) [74]. 2D photoacoustic images were reconstructed from ultrasound signals acquired with a linear ultrasound array (128 elements, 20 MHz central frequency). The images (a1), (b1) and (c1) correspond to photographs of the absorbing samples. The images (a2), (b2) and (c2) correspond to the conventional photoacoustic images that would be obtained with homogeneous illumination with incoherent light (in practice, they were obtained by averaging the photoacoustic signals obtained under various illumination patterns with coherent light). These images illustrate the limited-view artefacts associated with directional photoacoustic source: the ultrasound array located above the samples can only measure the photoacoustic waves that propagates upwards, i.e. the waves emitted by horizontally-oriented elements or boundaries. Moreover, image (c2) illustrates how the low frequency content associated with the low spatial frequency content of the large and homogeneous absorbing disk are filtered out by the high-frequency transducer array (central frequency about 20 MHz [74]). However, when multiple speckle illumination is used, the heterogeneous spatial distribution of the light intensity breaks the amplitude correlation among the ultrasound waves generated by each point-like absorber throughout the structure: the fluctuation of the photoacoustic signals from one illumination to the other may be interpreted as fluctuation signals emitted from fluctuating point-like sources (with size that of the speckle grain) that generate high-frequency and omnidirectional photoacoustic waves. Images (a3), (b3) and (c3) are fluctuation images computed from the photoacoustic images obtained under all the multiple speckle illuminations, illustrating how both high-pass filtering and limited view artefact can be overcome by taking advantage of multiple speckle illumination enabled by the use of coherent light.

Fig. 7.

Photoacoustic imaging with multiple speckle illumination. The experimental setup is similar to that of Fig. 6. Three types of absorbing samples are illuminated with multiple speckle illumination, by either using a SLM or a moving diffuser. (a1), (b1) and (c1) are photographs of the absorbing samples. (a2), (b2) and (c2) are conventional photoacoustic images equivalent to those obtained under homogeneous illumination. (a3), (b3) and (c3) are fluctuation images computed from the photoacoustic images obtained under all the multiple speckle illuminations. The fluctuations images reveal otherwise invisible features on the conventional images, because of directivity or frequency bandwidth issues. Figures (a) and (c) adapted with permission from [74], 2013 OSA. Figure (b) adapted with permission from [72], 2014 OSA.

While multiple speckle illumination was initially used in photoacoustic to palliate visibility issues, it also has a tremendous potential for super-resolution imaging. Indeed, when a sample is illuminated with multiple uncorrelated speckle patterns, optical absorbers separated by more than one speckle diameter behave as uncorrelated sources of fluctuating photoacoustic signals. The super-resolution optical fluctuation imaging (SOFI) technique developed for fluorescence microscopy [76] indicates that a higher-order statistical analysis of temporal fluctuations caused by fluctuating sources provides a way to resolve uncorrelated sources within a same optical diffraction spot. This principle, initially demonstrated with blinking fluorophores to break the optical diffraction limit, was very recently adapted and demonstrated in the context of photoacoustic imaging to break the acoustic diffraction limit [75]. As illustrated in Fig. 8, a second-order analysis of optical speckle-induced photoacoustic fluctuations was shown to provide super-resolved photoacoustic images. The resolution enhancement with raw (prior to deconvolution) images was about 1.4, as expected from the analysis of second-order statistics with a Gaussian-like point spread function [76], and was estimated to about 1.8 after deconvolution was performed on the images. As implemented in SOFI, the analysis of higher-order statistics is expected to further provide higher resolution enhancement and is currently being investigated.

Fig. 8.

Super-resolution photoacoustic fluctuation imaging with multiple speckle illumination. The experimental setup is similar to that of Fig. 6. (a) Conventional photoacoustic imaging. (b) Super-resolution photo-acoustic image, obtained by computing a variance image from multiple speckle illumination. (c) Photograph of the sample, made of 100-μm diameter beads. (d) Cross-sections, blue curve: conventional image, red curve: square root of variance image. Scale bars: 200 μm. Figure reproduced with permission from [75], 2016 OSA.

4.2. Exploiting optical wavefront shaping through scattering samples

Although the photoacoustic effect has first been proposed in the context of optical wavefront shaping as a way to provide a feedback mechanism, optical wavefront shaping clearly offers a tremendous potential to improve photoacoustic imaging. Because coherent light can be manipulated through or inside strongly scattering media, the distribution of the light intensity in tissue is not limited to that predicted by the transport theory, and may furthermore be significantly increased locally comparatively to the diffuse regime. As a consequence in the context of photoacoustic imaging, whose performances in terms of depth-to-resolution is fundamentally limited by the signal to noise ratio, the optical intensity enhancement enabled by optical wavefront shaping opens up the possibility to increase the penetration depth and/or the resolution.

The first demonstrations of the potential of optical wavefront shaping to improve photoacoustic imaging were reported in two publications from the same group [65], [69]. In both investigations, the authors first optimized the local fluence behind a static diffuser by PA-WFS with optimization based on a genetic algorithm, and then scanned the absorbing sample behind the static diffuser to obtain a photoacoustic image. The photoacoustic effect was therefore used first as a feedback mechanism for wavefront shaping, as discussed in Sec. 3.1 and illustrated in Fig. 3, and then the optimized light distribution was scanned relatively to the absorbing sample to obtain enhanced photoacoustic images. The first type of enhancement that was reported consisted in a significant increase of the signal-to-noise ratio [65]. Moreover, as previously discussed in Sec. 3.1, because the optical focus may be smaller than the acoustic focal spot, sub-acoustic resolution photoacoustic images were also reported, as illustrated in Fig. 9. Fig. 9(a) show a photograph of the sweat bee wing sample used in the study. Fig. 9(b) is the conventional photoacoustic image of the sample obtained with uniform illumination, whereas Fig. 9(c) is the photoacoustic image obtained by scanning the sample across the optical spot optimized with PA-WFS. Note also that scanning an optical diffraction spot over an absorbing sample should also reduce limited view and limited bandwidth artefacts, although such a feature has not be reported yet.

Fig. 9.

Enhancement of photoacoustic imaging with optical wavefront shaping. (a) Photograph of the absorbing sample (sweet bee wing). (b) Conventional acoustic-resolution photoacoustic image obtained under homogeneous illumination. (c) Photoacoustic image obtained by scanning the sample relatively to a fixed scattering layer traversed by a fixed optimized optical wavefront. The resolution is that of the optimized optical focus shown in Fig. 5(a). Figure adapted with permission from [69], 2015 NPG.

Although promising, these preliminary results were however obtained in a rather unrealistic configuration for imaging where the purely absorbing object to image was scanned relatively to a static scattering object. Additional promising preliminary results were also reported by Conkey and coworkers [69], obtained by scanning the transducer instead of scanning the scattering sample: it was shown that by optimizing the photoacoustic amplitude at each point of a 1D scan over a simple 1D absorbing pattern, the photoacoustic image obtained from optimized signals exhibits an improved resolution as compared to the conventional image under homogeneous or single random illumination. This improved resolution was attributed to the narrower spatial point spread function, similarly to what was observed on a homogeneously absorbing sample (see Fig. 5(a)). Achieving enhanced photoacoustic imaging by performing wavefront shaping inside the object to image however remains to be demonstrated. In addition to the approach investigated by Conkey and coworkers [69], alternative approaches towards this goal include the use of the acousto-optic effect to first enhance the optical intensity and then scan the optimized spot to form a photoacoustic image, or the development of iterative approaches where an initial conventional photoacoustic image could then be used to perform PA-WFS and consequently improve the signal-to-noise ratio of further photoacoustic images to improve their resolution.

4.3. Photoacoustic microendoscopy with multi-mode optical waveguides

In the field of photoacoustic imaging, optical-resolution photoacoustic endoscopy was first introduced by use of bundles of single-mode fibers by Hajireza and coworkers [78], [79], and was further investigated with various approaches including multiple optical and acoustic components [80], [81] or all-optical components [82] assembled in a cathether housing. With these approaches, the diameter of the probes typically ranges from 1 mm to 4 mm and the resolution ranges from 5 μm to 20 μm. As introduced in Sec. 2.4, optical wavefront shaping has been investigated to manipulate or deal with light propagation in multi-mode optical fibers [48], [49], [50], [51], an important step towards the miniaturization of optical endoscopes. The principle of a miniaturized photoacoustic endomicroscope endowed with optical wavefront shaping was first demonstrated by focusing and scanning pulsed coherent light through a 220 μm-diameter multimode fiber [77], based on a phase conjugation approach [51]. As illustrated in Fig. 10, an absorbing wire was imaged with diffraction limited optical resolution (around 1.5 μm) at the distal tip of a multimode fiber. However, the photoacoustic signals were detected through water with a 20 MHz ultrasound transducer, a situation not relevant for imaging inside biological tissue which strongly attenuates high-frequency ultrasound. Consequently, Simandoux and coworkers [83] demonstrated the use of a water-filled silica capillary as a multi-mode optical waveguide for optical excitation and a quasi-monomode acoustic waveguide to collect the photoacoustic wave with a reduced attenuation, through a 3-cm thick fat layer. The use of such a capillary to simultaneously perform optical wavefront shaping with optical digital phase conjugation and photoacoustic detection was further demonstrated in a recent study highlighting the potential of such capillaries for multi-modal optical imaging [84].

Fig. 10.

Photoacoustic endomicroscopy with optical wavefront shaping through a multimode fiber. (a) Schematic of the experimental setup. Focusing and scanning a diffraction-limited optical spot at the distal tip of the fiber was obtained by use of optical digital phase conjugation at the proximal tip. A spherically focused 20 MHz ultrasound transducer was used to detect photoacoustic signals from an absorbing sample placed in water in front of the distal tip. (b) Photograph of the absorbing samples (a knot between two absorbing nylon threads). (c) Optical resolution (∼ 1.5 μm) photoacoustic image obtained by scanning the focused optical spot across the field of view. Figure adapted with permission from [77], 2013 AIP.

5. Discussion and conclusion

The several recent investigations reviewed above illustrate how coupling photoacoustics and light coherence enables new horizons in several directions. On the one hand, the photoacoustic effect provides a valuable feedback mechanism for optical wavefront shaping, that allows in principle sensing inside scattering media via remote ultrasound detection. On the other hand, photoacoustic imaging may take advantage from the properties of light coherence, via the possibility to use multiple speckle illumination or to manipulate light distribution with optical wavefront shaping.

Although recent publications demonstrated promising proof-of-concepts experiments, several challenges lay ahead to bridge the gap between such proof of concepts and practical applications. As a fundamental limitation of all the demonstrations reviewed above where the photoacoustic effect is used to sense speckle patterns, the typical size of the optical speckle grain was made much larger than λ/2 and comparable to the ultrasound resolution. Doing so, the number of independent optical speckle grains within the ultrasound resolution cell was kept relatively small, either to allow sensing fluctuations from multiple speckle illumination with a sufficient signal-to-noise ratio or to demonstrate significant light intensity enhancement by wavefront shaping with a relatively low number of degrees of freedom. However, controlling the size of the optical speckle grains is only possible with free-space propagation, usually by adjusting the distance between the scattering object to the sample plane. Inside biological tissue, the typical speckle size cannot be controlled anymore, as it is dictated solely by the optical wavelength λ_optics. If one considers a 3D ultrasound focal spot with typical linear dimension λ_ultrasound, the number N_s of independent 3D optical speckle grains within this focal spot is expected to scale as $N_s\sim {\left(\frac{{\lambda }_{\mathrm{ultrasound}}}{{\lambda }_{\mathrm{optics}}}\right)}^2$. For photoacoustic sensing with several tens of MHz ultrasound, which has been demonstrated up to several mm in tissue [85], λ_ultrasound is of the order of a few tens of microns, and the number of independent speckle grains within the ultrasound focal spot may be as high as several thousand to ten thousand. The photoacoustic detection of speckle fluctuations with grain size as small as 2 μm was demonstrated through a scattering diffuser with 20 MHz ultrasound propagating through water with sufficient SNR to provide fluctuation images [74], but exploiting multiple speckle illumination inside scattering media has yet to be demonstrated. Similarly, photoacoustic-guided optical wavefront shaping has only been demonstrated with significant optical enhancement factor through scattering samples with speckle grain enlarged by free-space propagation [65], [66], [67], [68], [69], [70], [72], [73], as for acousto-optic-guided wavefront shaping experiments [56], [57], [58], [59], [60], [61]. By studying the influence of the absorber size with a fixed speckle grain size, it was recently confirmed experimentally that the efficiency of photoacoustic-guided wavefront shaping decreases rapidly when the typical absorber dimension is large compared to the speckle size: with a speckle size of about 30 μm (generated via free-space propagation), the photoacoustic enhancement was reduced to less than 1.5 for spherical absorbers 400 μm in diameter [86], in agreement with earlier qualitative observations by Kong and coworkers [52].

There are several possible directions towards enabling the principles reviewed above inside scattering samples. The photoacoustic effect, as opposed to acousto-optic modulation, only takes place in the presence of optical absorption. While this is certainly one drawback of photoacoustic sensing of light intensity, as no information can be retrieved from absorption-free regions, it may however be turned into an advantage for PA-WFS: for PA-WFS, the relevant number of independent speckle grains to consider within the ultrasound focal spot is that overlapping the distribution of optical absorbers. Therefore, if optical absorbers are sparse enough at the scale of the ultrasound focal spot, it is expected that the number of relevant speckle grains to sense or control with wavefront shaping may remain relatively low. Sparse distributions of absorbers may occur in tissue for instance either for blood microvessels or exogenous contrast agents at relatively low concentrations. For a given distribution of photoacoustics sources, reducing the size of the ultrasound sensing region via increasing the detection frequency is the most straightforward option, but this remains limited by the ultrasound attenuation. As the signal-to-noise ratio is the fundamental limitation, either because a small fluctuation has to be detected over a large signal (large number N_s of independent relevant speckle grains) or because a small signal is involved (very high ultrasound frequency to reduce N_s), there is a strong need for ultrasound transducers optimized for photoacoustic sensing, both in terms of sensitivity and bandwidth. The transducers that have been used so far in proof-of-principle experiments are commercially available ones, with standard technologies usually developed for pulse-echo measurement and not necessarily optimized for photoacoustic detection. The tremendous development of biomedical photoacoustic imaging will hopefully trigger the development of dedicated transducers, which could bring photoacoustics with coherent light closer to practical applications.

Regarding optical wavefront shaping, fast light manipulation is needed for in vivo tissue application, in which various types of motion leads to speckle decorrelation with time scales as short as a few millisecond [87]. The most recent research efforts towards fast wave front shaping involve the use of digital micromirrors (DMD) [28], [88], [89], [90], [37]. It is expected that the significant research efforts and very rapid progresses made in the field will continue to stimulate the development of new devices with both fast refresh rates and millions of pixel with flexible amplitude and/or phase control, that will in return benefit the field of photoacoustics with coherent light.

Exploiting light coherence in photoacoustics also requires appropriate laser sources. For pulsed light, a minimal coherence length l_c ∼ 1 m corresponds to a minimal pulse duration ${\tau }_p\sim \frac{l_c}{c}\sim 3\mathrm{ns}$. In the context of photoacoustic imaging with multiply scattered coherent light, this shows that pulses of at least a few nanoseconds must be used if the effect of coherence is to be exploited at centimeters depth in biological tissue. However, not all nanosecond-pulse laser have a nanosecond temporal coherence. For instance, the Q-switched nanosecond-pulse lasers widely used for deep photoacoustic imaging usually have a coherence length no longer that a few millimeters. While lasers such as Nd:YAG pulsed lasers may be injected with a single-longitudinal-mode seed laser with a large coherence length to obtain pulses with a coherence time of a few nanoseconds, this approach may not be readily extended to tunable laser sources based on optical parametric oscillators (OPO). So far, 532 nm is the only wavelength that has been used to perform the proof-of-concepts experiments reviewed in this paper. There is thus a clear need of new tunable and coherent laser sources in the so-called therapeutic window (600-900 nm) where light can penetrate deep into biological tissue. Narrowband OPO with a coherence length of a few centimeters exist, but this approach remains quite scarce, expensive and not yet very robust and reliable.

In summary, the coupling between the photoacoustic effect and propagation of multiply scattered coherent light opens up new horizons for both optical wavefront shaping and photoacoustic imaging. On the one hand, the photoacoustic effect offers a unique feedback mechanism for optical wavefront shaping or optical imaging with speckle illumination. On the other hand, the possibility to exploit the enormous number of degrees of freedom of multiply scattered coherent light with optical wavefront shaping and/or multiple speckle illumination offers exciting opportunities to break the current depth-to-resolution ratio of non-invasive photoacoustic imaging and/or to make photoacoustic endomicroscopy minimally invasive.

Conflicts of interest

The authors declare that there are no conflicts of interest.

Biographies

Emmanuel Bossy has been an Associate Professor at ESPCI Paris and Institut Lanvegin in Paris, France, since 2004. For the academic year 2015-2016, he is currently an Invited Professor at the Ecole Polytechnique Fédérale de Lausanne, in the Optics Laboratory and Laboratory of Applied Photonics Devices. In 2016, he joins the Laboratoire Interdisciplinaire de Physique (LIPhy) at the Université Grenoble Alpes. His general research field is wave propagation and imaging in complex media, and his work includes photoacoustic imaging, acousto-optic imaging and non-destructive testing with ultrasound. He received his Ph.D. degree in 2003 from the Université Pierre et Marie Curie for his contributions to quantitative ultrasonic characterization of bone, and was a post-doctoral research fellow at Boston University from 2003 to 2004 where his research oriented towards biomedical imaging techniques that couple light and sound.

Sylvain Gigan is currently a Professor at Université Pierre et Marie Curie, and a researcher at Laboratoire Kastler-Brossel, at the Physics Department of ENS, in Paris, France, where he leads the team “optical imaging in complex and biological media”. He is a member of the Institut Universitaire de France. He holds a PhD in quantum Optics under the direction of Claude Fabre, and has been successively a postdoctoral researcher in quantum information in Vienna in the group of Markus Aspelmeyer, and an Associate Professor at ESPCI Paris and Institut Langevin in Paris, France.