Robust Sliding Mode Control Based on GA Optimization and CMAC Compensation for Lower Limb Exoskeleton

Abstract

A lower limb assistive exoskeleton is designed to help operators walk or carry payloads. The exoskeleton is required to shadow human motion intent accurately and compliantly to prevent incoordination. If the user's intention is estimated accurately, a precise position control strategy will improve collaboration between the user and the exoskeleton. In this paper, a hybrid position control scheme, combining sliding mode control (SMC) with a cerebellar model articulation controller (CMAC) neural network, is proposed to control the exoskeleton to react appropriately to human motion intent. A genetic algorithm (GA) is utilized to determine the optimal sliding surface and the sliding control law to improve performance of SMC. The proposed control strategy (SMC_GA_CMAC) is compared with three other types of approaches, that is, conventional SMC without optimization, optimal SMC with GA (SMC_GA), and SMC with CMAC compensation (SMC_CMAC), all of which are employed to track the desired joint angular position which is deduced from Clinical Gait Analysis (CGA) data. Position tracking performance is investigated with cosimulation using ADAMS and MATLAB/SIMULINK in two cases, of which the first case is without disturbances while the second case is with a bounded disturbance. The cosimulation results show the effectiveness of the proposed control strategy which can be employed in similar exoskeleton systems.

1. Introduction

The lower extremity exoskeleton, which began in the late 1960s, is an electromechanical structure worn by human users as an intelligent device for performance assistance and enhancement. In recent years, wearable robots have attracted interests of many researchers widely. The Berkeley Lower Extremity Exoskeleton (BLEEX) was designed to assist people in walking for carrying load, which could walk at the speed of 0.9 m/s while carrying 34 kg payload [1]. A mechanical leg has seven DOFs (three at the hip, one at the knee, and three at the ankle), of which four DOFs are actuated by valve-based hydraulic actuation systems [2]. However, these many active DOFs make the system complex and heavy, weighing 38 kg. The latter exoskeletons, that is, ExoHiker, ExoClimber, and HULC, simplify mechanical structure and reduce the number of active DOFs while carrying more payloads up to 68 kg–90 kg [3]. Hybrid Assistive Limb (HAL), proposed by the University of Tsukuba in Japan, has two active DOFs at the hip joint and knee joint, which are controlled according to collected electrical signals from muscles [4]. HAL is used to help users carry load and assist disabled people in walking [5, 6]. An underactuated exoskeleton system is designed based on appropriate criteria to help infantry soldiers walk on different terrain, where active joints are applied to the knee joints while other joints are passive [7]. Moreno et al. studied and analyzed the human interaction with wearable lower limb exoskeleton, where the robot gathered information from the sensors in order to detect human actions and subjects also modified their gait patterns to obtain the desired responses from the exoskeleton [8].

Although many kinds of lower limb exoskeleton robots are studied, the human-exoskeleton collaborative movement is quite complex and difficult due to nonlinear characteristics of dynamic model and uncertainties, for example, external disturbance and involuntary movements. To achieve the goal of making exoskeletons providing assistance for human beings, a consistent dynamic tracking performance is required to maneuver exoskeletons in an efficient, smooth, and continuous manner [9]. The control procedure can be divided into two steps, acquiring human motion intent with human-robot interaction (HRI) and following the human motion intent accurately.

When the wearer wants to move, the central controller sends control signals to enforce the exoskeleton to follow commanded signals, during which HRI decreases. A crucial issue of control is to follow the estimated human motion intent accurately. The more accurate the intention tracking is, the more compliantly the exoskeleton works. The precise motion control of robotic manipulators has received considerable attention from many robotics researchers and its challenges continue to limit overall control performance because of structured and unstructured uncertainties [10]. In exoskeletons, the structured uncertainties contain payload variations, while unstructured uncertainties contain sensor noises, joint friction, and external disturbances. There are many approaches for position control approaches to deal with uncertainties such as robust control [11, 12], adaptive control [13, 14], intelligent control [15], and sliding mode control [16].

SMC is a robust control approach that drives state trajectory to predefined sliding surface by using discontinuous control inputs [17], which is used to improve control performance for robotic manipulators with model uncertainties such as parameter perturbations, unknown joint frictions and inertias, and external disturbances [18]. It is notable that its overall performance is superior to general PID control algorithm [19]. The process of designing a SMC controller has two steps: defining suitable sliding surfaces and designing discontinuous control laws [13]. Parameters of SMC should be chosen suitably to obtain optimal performance. Some common optimization methods are provided and applied in robots, for example, GA [20], particle swarm optimization (PSO) [21], ant colony optimization (ACO) [22], and evolutionary algorithm (EA) [23]. GA is simple to be implemented and is capable of locating global optimal solutions [24], which is utilized to optimize the structure of intelligent methods [25, 26]. The decoupled SMC as a supervisory controller is applied in accordance with PID control, whose parameters are tuned using GA, to enhance tracking performance and eliminate the chattering problem [27]. The gain switch and sliding surface constant parameters are selected by GA so that the designed SMC can achieve satisfactory performance [28]. However, GA is only used to optimize parameters of sliding surfaces or SMC control laws. In this work, we use GA to optimize all parameters of the sliding surface and the control law at the same time.

The optimal SMC can deal with uncertainties to achieve satisfactory performance. To improve tracking performance, CMAC is added as a compensation item with property of fast learning capability. The CMAC proposed first by Albus [29] is similar to the mode of human cerebellum, which is an autoassociative memory feed-forward neural network. Compared with other feed-forward neural networks, it has faster convergence speed [30]. The approach which uses CMAC as a compensation item with SMC is applied in position control of robotic manipulators [31]. In this work, we propose to combine optimal SMC using GA and CMAC compensation to form the hybrid position control strategy.

The remainder of this paper is organized as follows. The specific system under study is given in the second section. In Section 3, the proposed control strategy is explained in details. Cosimulations using the proposed approach and results analysis are presented in the fourth section. Conclusions are drawn in the final section.

2. Problem Formulations

2.1. Exoskeleton Configuration

Based on principles in biological design, the designed exoskeleton is required to retain adaptability to multifunctionality of human lower limbs. An available powerful tool when designing an assistive exoskeleton is the enormous Clinical Gait Analysis (CGA) data on human walking [32]. With CGA data [33], our designed exoskeleton is shown in Figure 1. As Figure 1 shows, there are two active joints of a single leg in sagittal plane, which are knee joint and hip joint actuated by hydraulic actuation system.

Figure 1.

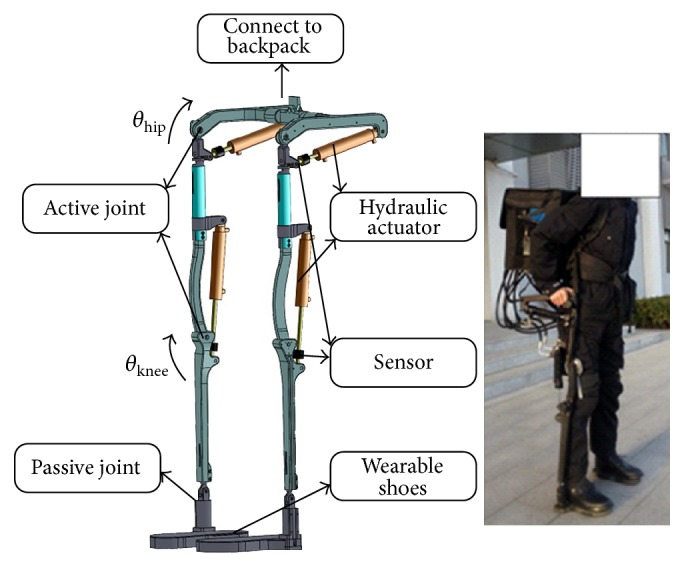
Prototype of lower limb powered exoskeleton. There are two active joints of each leg in walking direction, which are represented as θ_hip and θ_knee. All auxiliary facilities are packaged in the backpack.

2.2. Mathematical Model of Exoskeleton

For multirigid system, Euler-Lagrange is a frequently used method for modeling of robotic manipulators. The exoskeleton is a typical human-robot collaboration system, which includes the user's lower limbs and mechanical limbs which are tied together at the interaction cuffs. Mathematical model of a single leg of exoskeleton is obtained because of its symmetry structure. Without loss of generality, the dynamic equation of the swing leg of exoskeleton robot can be expressed as follows:

$$\begin{array}{c}\mathbf{M}\left(\mathbf{q}\right)\ddot{\mathbf{q}}+\mathbf{C}\left(\mathbf{q},\dot{\mathbf{q}}\right)\dot{\mathbf{q}}+\mathbf{G}\left(\mathbf{q}\right)+\mathbf{D}=\mathbf{T},\end{array}$$ (1)

where M(q) ∈ R^n×n is the symmetric definite inertial matrix; $\mathit{C}\left(\mathit{q},\dot{\mathit{q}}\right)\in R^{n\times n}$ is the Coriolis and centrifugal force matrix; G(q) ∈ R^n×1 is the gravitational force matrix; T ∈ R^n×1 is the control input vector; D ∈ R^n×1 denotes unmodeled dynamics and external disturbances.

For dynamics model in (1), several properties are presented as the following [34].

Property 1 . —

Matrix M(q) is symmetric and positive definite.

Property 2 . —

Matrix $\dot{\mathit{M}}(\mathit{q})-\mathrm{2}\mathit{C}(q,\dot{q})$ is a skew-symmetric matrix if ∀ε ∈ Rⁿ, ${\epsilon }^T(\dot{\mathit{M}}(\mathit{q})-\mathrm{2}\mathit{C}(q,\dot{q}))\epsilon =\mathrm{0}$.

Property 3 . —

There exist finite scalars δ_i > 0,  i = 1,…, 4 such that ‖M(q)‖ ≤ δ₁,  $‖\mathit{C}(\mathit{q},\dot{\mathit{q}})‖\le {\delta }_{\mathrm{2}}$,  ‖G(q)‖ ≤ δ₃, and ‖D‖ ≤ δ₄, which means all items in dynamic model are bounded.

In the position control of robotic manipulators, we define trajectory tracking error as

$$\begin{array}{c}\mathbf{e}={\mathbf{q}}_d-\mathbf{q},\end{array}$$ (2)

where e is the tracking error, q_d is reference trajectory, and q is actual trajectory. Based on (2), we can obtain

$$\begin{array}{c}\dot{\mathbf{e}}={\dot{\mathbf{q}}}_d-\dot{\mathbf{q}},\\ \\ \ddot{\mathbf{e}}={\ddot{\mathbf{q}}}_d-\ddot{\mathbf{q}},\\ \end{array}$$ (3)

where $\dot{\mathit{e}}$ and $\ddot{\mathit{e}}$ is the first and second derivative of e,  ${\dot{\mathit{q}}}_d$ and ${\ddot{\mathit{q}}}_d$ are angular velocity and acceleration vector of command input, and $\dot{\mathit{q}}$ and $\ddot{\mathit{q}}$ are that of actual output, respectively, all of which are bounded.

3. Control Strategy Design

3.1. Sliding Mode Control

A general SMC design consists of two steps: the sliding surface design and the control law construction. The purpose of the SMC is to track the trajectory specified by human intention and maintain system trajectory in the sliding surfaces [18]. Considering that there exist uncertainties including unmodeled frictions, variation of parameters, and external disturbances, the robustness should be an important concern in the controller design for exoskeleton system. The general sliding surface is defined as $\mathit{s}=\dot{\mathit{e}}+\mathit{A}\mathit{e}$. To improve robustness of controller, a designed integral sliding surface is represented as follows [35]:

$$\begin{array}{c}\mathbf{s}=\dot{\mathbf{e}}+\mathbf{A}\mathbf{e}+\mathbf{H}\underset{\mathrm{0}}{\overset{ts}{{\displaystyle \int }}}\mathbf{e}\hspace{0.17em}dt,\end{array}$$ (4)

where A and H are positive definite matrix. Then $\dot{\mathit{s}}$ can be derived:

$$\begin{array}{c}\dot{\mathbf{s}}=\ddot{\mathbf{e}}+\mathbf{A}\dot{\mathbf{e}}+\mathbf{H}\mathbf{e}.\end{array}$$ (5)

As the second design stage of SMC, the control laws should be chosen, which should be satisfied with the existence condition of SMC [36]:

$$\begin{array}{c}{\mathbf{s}}^T\dot{\mathbf{s}}<\mathrm{0}.\end{array}$$ (6)

For the exoskeleton system under study, we define the SMC control law as follows:

$$\begin{array}{c}\mathbf{u}=\mathbf{M}\left(q\right){\ddot{\mathbf{q}}}_d-\left({\mathbf{T}}_d-\mathbf{C}\left(q,\dot{q}\right)\dot{\mathbf{q}}\right)+\mathbf{M}\left(q\right)\mathbf{A}\dot{\mathbf{e}}\\ +\mathbf{M}\left(q\right)\mathbf{H}\mathbf{e}+\mathbf{C}\left(q,\dot{q}\right)\mathbf{s}+\mathbf{\epsilon }\mathrm{sgn}\left(\mathbf{s}\right)+\mathbf{K}\mathbf{s},\end{array}$$ (7)

where T_d = D − G(q), ε and K are positive definite matrices, and sgn⁡(s) is a symbolic function which is shown as follows:

$$\begin{array}{c}\mathrm{sgn}\left(\mathbf{s}\right)=\left\{\begin{array}{cc}\mathrm{1},\hfill & \mathbf{s}>\mathrm{0},\hfill \\ \mathrm{0},\hfill & \mathbf{s}=\mathrm{0},\hfill \\ -\mathrm{1},\hfill & \mathbf{s}<\mathrm{0}.\hfill \end{array}\right.\end{array}$$ (8)

The SMC algorithm has chattering phenomena, which affects the accuracy of position control much. In order to eliminate chattering, the continuous function θ(s) with relay characteristics is used to replace the function of symbolic function sgn⁡(s) to restrict the trajectory in a boundary layer of ideal sliding mode [37]. Then (7) can be rewritten as

$$\begin{array}{c}\mathbf{u}=\mathbf{M}\left(q\right){\ddot{\mathbf{q}}}_d-\left({\mathbf{T}}_d-\mathbf{C}\left(q,\dot{q}\right)\dot{\mathbf{q}}\right)+\mathbf{M}\left(q\right)\mathbf{A}\dot{\mathbf{e}}\\ +\mathbf{M}\left(q\right)\mathbf{H}\mathbf{e}+\mathbf{C}\left(q,\dot{q}\right)\mathbf{s}+\mathbf{\epsilon }\theta \left(\mathbf{s}\right)+\mathbf{K}\mathbf{s},\end{array}$$ (9)

where θ(s) = s/(‖s‖ + σ), σ > 0. Before stability analysis, Barbalat lemma is shown as the following [38].

Barbalat Lemma. If a differentiable function f(t) has a limit as t → ∞, and if $\dot{f}(t)$ is uniformly continuous, then f(t) → 0 as t → ∞.

Theorem 1 . —

The proposed controller (9) guarantees asymptotic convergence to zero, both of the trajectory tracking errors and sliding surfaces. Namely, the system is globally stable; that is, when t → ∞,  e → 0,  s → 0.

Proof —

Lyapunov function is defined as

$$\begin{array}{c}\mathbf{V}=\frac{\mathrm{1}}{\mathrm{2}}{\mathbf{s}}^T\mathbf{M}\left(q\right)\mathbf{s}.\end{array}$$ (10)

Differentiating V with respect to time yields

$$\begin{array}{c}\dot{\mathbf{V}}={\mathbf{s}}^T\mathbf{M}\left(q\right)\dot{\mathbf{s}}+\frac{\mathrm{1}}{\mathrm{2}}{\mathbf{s}}^T\dot{\mathbf{M}}\left(q\right)\mathbf{s}.\end{array}$$ (11)

Considering Property 2, then

$$\begin{array}{c}{\mathbf{s}}^T\left(\frac{\mathrm{1}}{\mathrm{2}}\dot{\mathbf{M}}\left(q\right)-\mathbf{C}\left(q,\dot{q}\right)\right)\mathbf{s}=\mathrm{0}.\end{array}$$ (12)

Combining (10)–(12), one can get

$$\begin{array}{c}\dot{\mathbf{V}}={\mathbf{s}}^T\left(\mathbf{M}\left(q\right)\dot{\mathbf{s}}+\mathbf{C}\left(q,\dot{q}\right)\mathbf{s}\right)={\mathbf{s}}^T\left(\mathbf{M}\left(q\right)\left({\ddot{\mathbf{q}}}_d-\ddot{\mathbf{q}}\right)+\mathbf{M}\left(q\right)\mathbf{A}\dot{\mathbf{e}}+\mathbf{M}\left(q\right)He+\mathbf{C}\left(q,\dot{q}\right)\mathbf{s}\right).\end{array}$$ (13)

And $\ddot{\mathit{q}}$ can be solved by

$$\begin{array}{c}\ddot{\mathbf{q}}=\mathbf{M}{\left(q\right)}^{-\mathrm{1}}\left(\mathbf{T}+{\mathbf{T}}_d-\mathbf{C}\left(q,\dot{q}\right)\dot{\mathbf{q}}\right).\end{array}$$ (14)

Substituting (14) into (13), then

$$\begin{array}{c}\dot{\mathbf{V}}={\mathbf{s}}^T\left(\mathbf{M}\left(q\right){\ddot{\mathbf{q}}}_d-\left(\mathbf{T}+{\mathbf{T}}_d-\mathbf{C}\left(q,\dot{q}\right)\dot{\mathbf{q}}\right)+\mathbf{M}\left(q\right)\mathbf{A}\dot{\mathbf{e}}+\mathbf{M}\left(q\right)\mathbf{H}\mathbf{e}+\mathbf{C}\left(q,\dot{q}\right)\mathbf{s}\right).\end{array}$$ (15)

Substituting (7) into (15), we can obtain

$$\begin{array}{c}\dot{\mathbf{V}}={\mathbf{s}}^T\left(-\mathbf{\epsilon }\theta \left(\mathbf{s}\right)-\mathbf{K}\mathbf{s}\right).\end{array}$$ (16)

It is easy to know that K and ε are positive definite matrices; therefore s^TKs > 0,  s^Tθ(s) > 0; then $\dot{\mathit{V}}<\mathrm{0}$. Hence, the system is globally stable. With the Barbalat lemma, s → 0 as t → ∞; then one knows e → 0 and $\dot{\mathit{e}}\to \mathrm{0}$ as t → ∞. This control law could realize convergence of the trajectory tracking error to zero.

3.2. Genetic Algorithm

In SMC, those constant parameters existing in sliding surfaces and control laws, which are A,  H,  K, and ε in (9), determine the overall performance. Hence, it is necessary to find the optimal values of them using optimization algorithm. GA is an adaptive heuristic search algorithm that mimics the process of natural selection and uses biological evolution to develop a series of search space points toward an optimal solution. There are five components that are required to implement GA: representation, initialization, fitness function, genetic operators, and genetic parameters [39].

A simple GA involves three types of operator: selection, crossover, and mutation [40]. Selection is a probabilistic process for selecting chromosomes in the population using their fitness values. The chromosome with larger fitness value is likely to be selected to reproduce. Crossover is the process of randomly choosing a locus and swaps the characters either left or right of this locus between two chromosomes to create two offspring. The probability of crossover occurring for the parent chromosomes is usually set to a large value (e.g., 0.8). Mutation is to randomly flip some of the bits by changing “0” to “1” or vice versa, with a small probability (e.g., 0.001) which maintains genetic diversity to guarantee that GA can come to better solution. The process of GA optimization is shown in Figure 2. As Figure 2 shows, there are parameters such as the size of population and generation and the length of code that should be initialized; then the process of selection, crossover, and mutation is preceded until the convergence conditions are satisfied.

Figure 2.

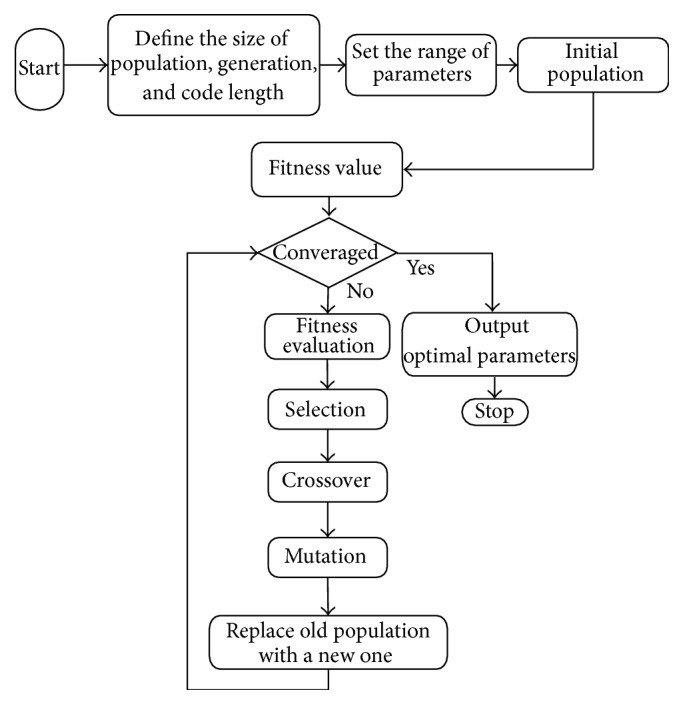
The process of GA optimization, when the convergence condition is satisfied, the optimal parameters will be obtained.

3.3. SMC with GA Optimization

Based on that discussed above, the fitness function should be confirmed before implementing GA to SMC. The goal of SMC is to achieve precise trajectory tracking for robotic manipulators; that is, the smaller the trajectory errors are, the more effective the controller is. Those parameters to be optimized are relevant to trajectory error; hence the fitness function is defined as follows:

$$\begin{array}{c}J\left(\mathbf{A},\mathbf{H},\mathbf{K},\mathbf{\epsilon }\right)={\displaystyle \sum }_{k=\mathrm{0}}^{\infty }{‖\mathbf{e}\left(k\right)‖}^{\mathrm{2}}.\end{array}$$ (17)

With the fitness function, those parameters can be found with the minimization of tracking errors during the trajectory tracking using the designed control law. In the search space of GA, the SMC will have optimal parameters when the fitness function has minimum values. The algorithm of SMC optimized by GA is shown as Algorithm 1 in Appendix A.

Algorithm 1.

Optimize SMC with GA. (Notation: q_hd(k) and q_kd(k) represent desired trajectory of hip joint and knee joint, resp.)

3.4. CMAC Neural Network

The CMAC neural network has three steps: projecting an input into association area, compressing memory cell through Hash coding, and calculating the output as a scalar product of the memory area [41], which is shown in Figure 3. The output of CMAC can be expressed as follows [42]:

$$\begin{array}{c}{\mathbf{y}}_s={\mathbf{C}}_s^T\mathbf{H}\mathbf{W}\\ =\left[\begin{array}{cccc}{c}_{s,\mathrm{1}}& c_{s,\mathrm{2}}& \cdots & c_{s,N_h}\end{array}\right]\left[\begin{array}{ccc}{h}_{\mathrm{1,1}}& \cdots & h_{\mathrm{1},M_p}\\ ⋮& & ⋮\\ h_{N_h,\mathrm{1}}& \cdots & h_{N_h,M_p}\end{array}\right]\left[\begin{array}{c}{\omega }_{\mathrm{1}}\\ {\omega }_{\mathrm{2}}\\ ⋮\\ {\omega }_{M_p}\end{array}\right],\end{array}$$ (18)

where C_s is an association vector projected by input vector, W is the weight vector, H is the matrix of Hash coding, M_p is the number of Hash vector, N_h is the number of association vector, and h_ij = 1 represents ith association unit response to jth Hash unit.

Figure 3.

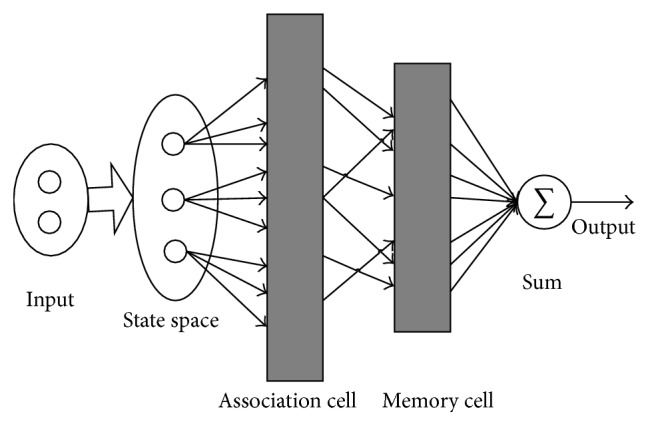
Structure of CMAC neural network.

Similar to other neural networks, the weight parameters should be updated using Least Square Method (LSM). The updating process is expressed as follows:

$$\begin{array}{c}\mathrm{\Delta }\mathbf{W}=\frac{\eta }{N_h}{\mathbf{A}}_{s-\mathrm{1}}\left({\widehat{\mathbf{y}}}_{s-\mathrm{1}}-{\mathbf{A}}_{s-\mathrm{1}}^T{\mathbf{W}}_{s-\mathrm{1}}\right),\\ \\ \mathbf{W}\left(k+\mathrm{1}\right)=\mathbf{W}\left(k\right)+\mathrm{\Delta }\mathbf{W}+\alpha \left(\mathbf{W}\left(k+\mathrm{1}\right)-\mathbf{W}\left(k\right)\right),\\ \end{array}$$ (19)

where ΔW is the weight vector increment, η is the learning rate, A_s−1^T = C_s−1^TH, ${\widehat{y}}_{s-\mathrm{1}}$ is the target output, and α is the inertial parameter.

CMAC was originally proposed to be applied into control problems by Miller III et al. [43]. The CMAC control loop is usually added to traditional control loops, where the traditional controller actuates the plant stably and the CMAC helps to improve control preciseness without affecting the traditional control loop [44, 45]. In other words, the CMAC control is usually added as a compensation item of traditional control method. The algorithm of the hybrid control strategy combining SMC and CMAC is shown as Algorithm 2 in Appendix B.

Algorithm 2.

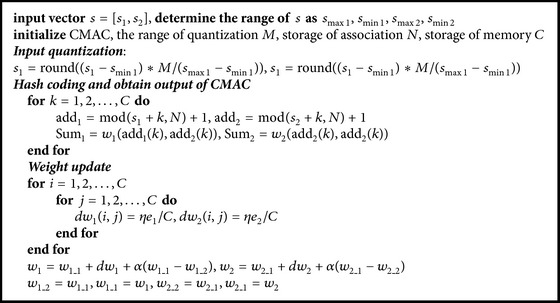
The process of CMAC neural network. (Notation: the input is sliding surface and the output is the compensation control vector.)

3.5. Combination of GA Optimization-Based SMC and CMAC Neural Network

Based on discussion above, we can combine SMC, GA, and CMAC neural network into a hybrid control strategy, which is called SMC_GA_CMAC. We can write the proposed control law based on (9) as follows:

$$\begin{array}{c}\mathbf{u}={\mathbf{K}}_c{\mathbf{U}}_c+\mathbf{M}\left(q\right){\ddot{\mathbf{q}}}_d-\left({\mathbf{T}}_d-\mathbf{C}\left(q,\dot{q}\right)\dot{\mathbf{q}}\right)\\ +\mathbf{M}\left(q\right){\mathbf{A}}_{\text{GA}}\dot{\mathbf{e}}+\mathbf{M}\left(q\right){\mathbf{H}}_{\text{GA}}\mathbf{e}+\mathbf{C}\left(q,\dot{q}\right)\mathbf{s}+{\mathbf{\epsilon }}_{\text{GA}}\theta \left(\mathbf{s}\right)+{\mathbf{\text{K}}}_{\text{GA}}\mathbf{s},\end{array}$$ (20)

where U_c represents the output of CMAC neural network, K_c ∈ R^n×1 is a positive definite matrix, and A_GA, H_GA,  ε_GA, and K_GA are matrices optimized using GA. With the reaching condition (6), the output of CMAC U_c has constraint as the following:

$$\begin{array}{c}{\mathbf{U}}_c=\left\{\begin{array}{cc}{\mathbf{U}}_c,\hfill & \text{if\hspace{0.17em}\hspace{0.17em}}{\mathbf{s}}^T{\mathbf{U}}_c\ge \mathrm{0},\hfill \\ -{\mathbf{U}}_c,\hfill & \text{if\hspace{0.17em}\hspace{0.17em}}{\mathbf{s}}^T{\mathbf{U}}_c<\mathrm{0}.\hfill \end{array}\right.\end{array}$$ (21)

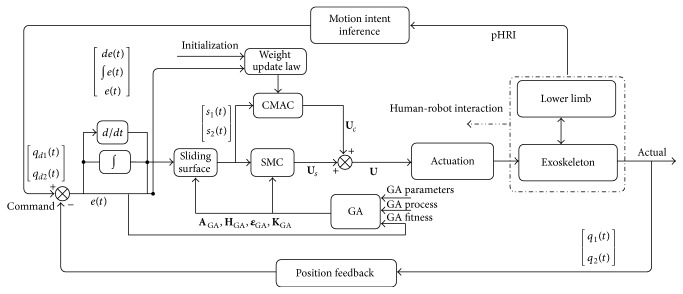
For the exoskeleton system, the control diagram is illustrated as Figure 4 shows. As Figure 4 shows, GA is employed to obtain the optimal parameters A_GA,  K_GA,  H_GA, and ε_GA to construct optimized SMC. The CMAC's input is the sliding surface and its weight updating is derived from minimizing the tracking error. The output of the proposed control law is U = U_s + K_cU_c, of which U_s is the main output provided by SMC_GA and U_c is the compensation output provided by CMAC.

Figure 4.

The control diagram of the proposed method for the exoskeleton system.

4. Simulations with the Proposed Control Strategy

In this section, the proposed method is examined through simulations. The simulation results, which are from application into controlling the swing leg of the exoskeleton using the proposed algorithms, are presented. As Figure 1 shows, the active DOFs are hip joint and knee joint, while the ankle joint is passive. Based on (1), the dynamics model of swing leg can be expressed as

$$\begin{array}{c}\mathbf{M}{\left(q\right)}_{\text{exo}}\ddot{\mathbf{q}}+\mathbf{C}{\left(q,\dot{q}\right)}_{\text{exo}}\dot{\mathbf{q}}+\mathbf{G}{\left(q\right)}_{\text{exo}}=\mathbf{T},\end{array}$$ (22)

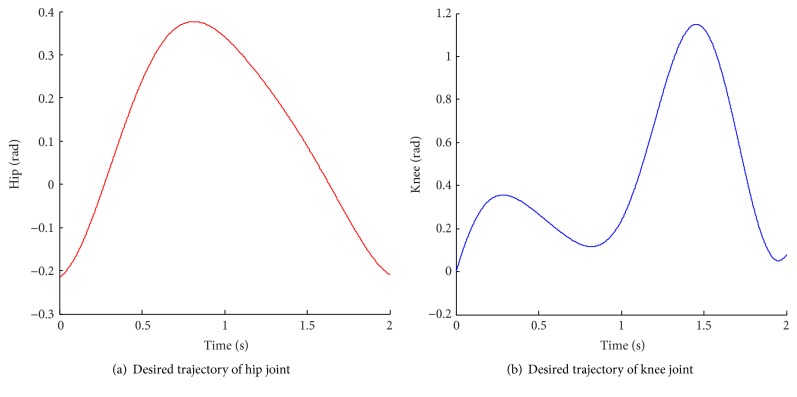
where M(q)_exo ∈ R^2×2, $\mathit{C}{\left(q,\dot{q}\right)}_{\text{exo}}\in R^{\mathrm{2}\times \mathrm{2}}$, G(q)_exo ∈ R^2×1, $\ddot{\mathit{q}}\in {\mathit{R}}^{\mathrm{2}\times \mathrm{1}}$, $\dot{\mathit{q}}\in {\mathit{R}}^{\mathrm{2}\times \mathrm{1}}$, and T ∈ R^2×1. In simulations, the desired angular position of lower limb joints stems from the CGA data as Figure 5 shows. The period of the cyclical gait is 2 seconds and we will obtain the fitting expression with respect to time

$$\begin{array}{c}{q}_{\text{hip}}\left(t\right)=\mathrm{3.85}\cos \left(\mathrm{0.330}t+\mathrm{2.14}\right)\\ +\mathrm{71.6}\cos \left(\mathrm{3.49}t-\mathrm{1.88}\right)\\ +\mathrm{41.0}\cos \left(\mathrm{4.68}t-\mathrm{0.3}\right),\\ q_{\text{knee}}\left(t\right)=\mathrm{40.9}\cos \left(\mathrm{1.04}t-\mathrm{0.208}\right)\\ +\mathrm{157}\cos \left(\mathrm{5.82}-\mathrm{0.047}\right)\\ +\mathrm{82.3}\cos \left(\mathrm{7.49}t-\mathrm{4.13}\right),\end{array}$$ (23)

where q_hip(t) and q_knee(t) are the desired angular position of hip joint and knee joint, respectively.

Figure 5.

The desired joint trajectory of human lower limb movement. The initial posture is in the vertical direction.

To investigate the effectiveness and robustness of the proposed scheme, two simulation cases are considered: without disturbances (Case One) and with bounded disturbances (Case Two). The external disturbance D(t) is a function of time which is assumed to have an upper bound:

$$\begin{array}{c}D\left(t\right)=a\sin \left(\pi t\right),‖a‖\le \mathrm{1}.\end{array}$$ (24)

For recording the respective performances, the root mean square error (RSME) is defined to examine control performance as follows:

$$\begin{array}{c}\text{RSME}=\sqrt{{\displaystyle \sum }_{k=\mathrm{1}}^N\frac{{‖e\left(k\right)‖}^{\mathrm{2}}}{N}},\end{array}$$ (25)

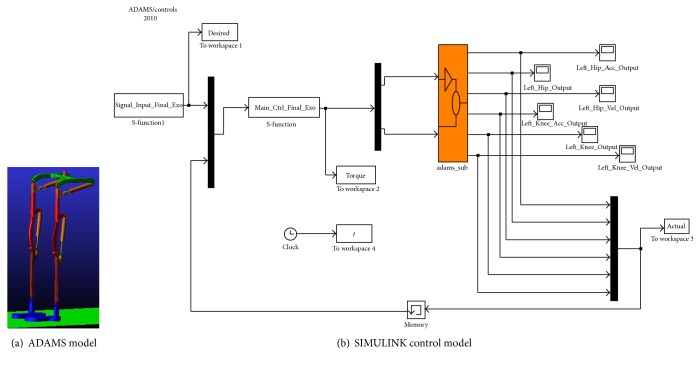
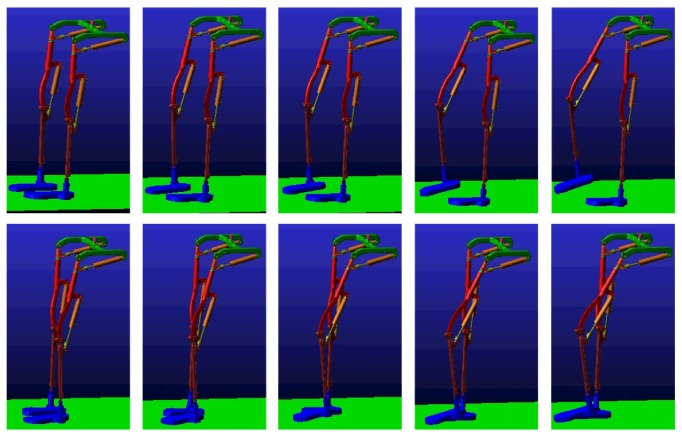
where N is the size of error vector. We integrate ADAMS and MATLAB/SIMULINK to control the exoskeleton using the proposed control strategy, which is shown in Figure 6. As Figure 6 shows, there are six output variables from ADAMS model which are angular position, velocity, and acceleration of knee joint and hip joint of a swing leg while the designed controller in MATLAB outputs two control torques into ADAMS model. Figure 6(a) shows the exoskeleton model in ADAMS and Figure 6(b) shows the control scheme in SIMULINK. The designed controller produces control signals transferred to ADAMS while the kinematics information of exoskeleton joints is measured in ADAMS and returned back to MATLAB workspace. Through creating a communication block between MATLAB and ADAMS, the dynamics movements in gait cycles are shown in Figure 7, which illustrates the level ground walking for the lower extremity exoskeleton.

Figure 6.

Cosimulation using ADAMS and MATLAB for exoskeleton robot.

Figure 7.

ADAMS effect pictures of gait cycles for lower extremity exoskeleton.

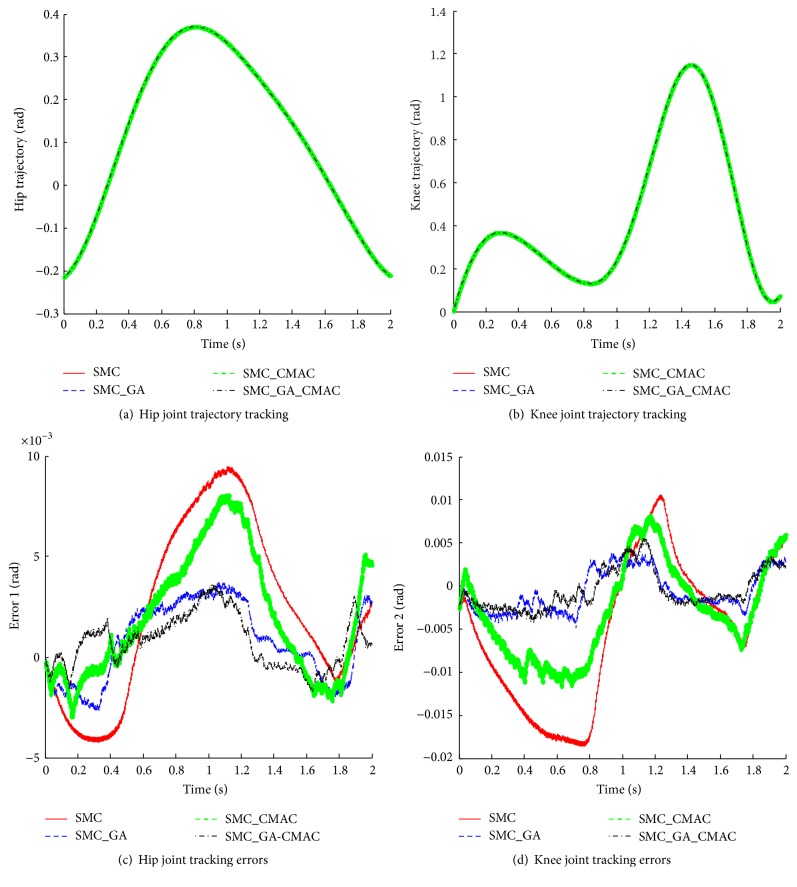
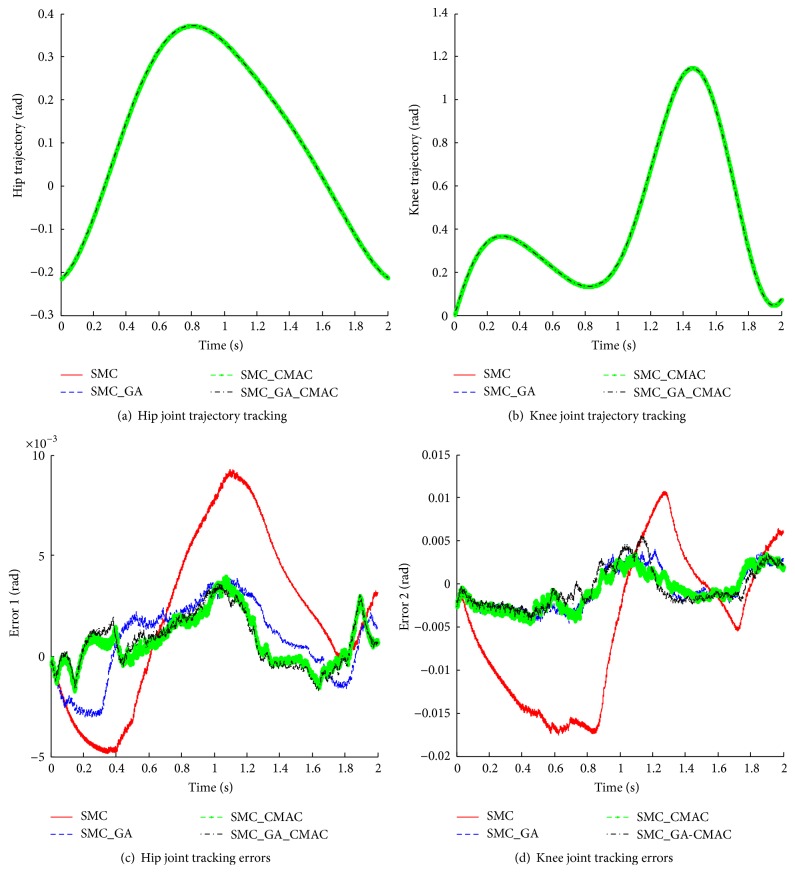
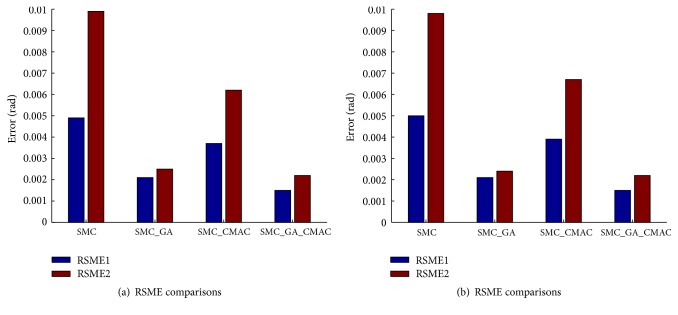
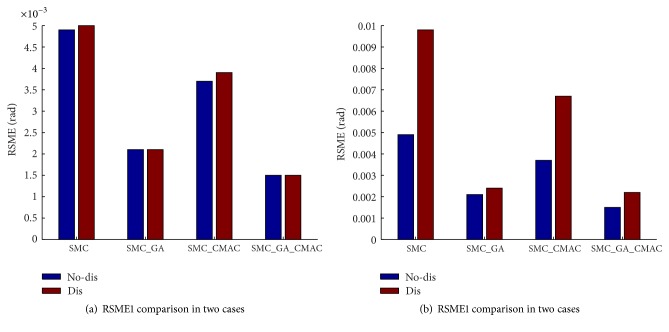
The comparisons between the proposed control scheme and conventional SMC, SMC with CMAC (SMC_CMAC) neural network, and optimal SMC with GA (SMC_GA) are conducted. The simulated comparisons, containing tracking positions and tracking errors of SMC, SMC_GA, SMC_CMAC, and SMC_GA_CMAC in Case One and Case Two, are depicted in Figures 8 and 9. As Figure 8 shows, Figures 8(a) and 8(c) represent the joint trajectory tracking of hip joint and knee joint while Figures 8(b) and 8(d) show tracking error comparisons of those two joints using four kinds of controllers separately. It can be seen that all of controllers can achieve good tracking performance and the conventional SMC without optimization has the largest tracking errors. Similarly, the angular position tracking and tracking errors comparisons in Case Two are depicted in Figures 9(a)–9(d). As Figure 9 shows, the desired joint angular trajectory also can be tracked well. To evaluate the control performances of Case One and Case Two, RSME comparisons using four controllers are depicted in Figures 10 and 11. Figure 10(a) gives RSME of two joint tracking errors in Case One while Figure 10(b) describes that in Case Two. In two cases, the performance sequence from worse to better should be SMC, SMC_CMAC, SMC_GA, and SMC_GA_CMAC. Figure 11(a) illustrates the RSME comparison of hip joint while Figure 11(b) illustrates that of knee joint. In Figures 10 and 11, the RSME do not change much; hence the proposed control strategy still works when there exists external disturbance.

Figure 8.

The performance comparisons using four methods in Case One.

Figure 9.

The performance comparisons using four methods in Case Two.

Figure 10.

RSME comparisons in Case One (without disturbance) and Case Two (with bounded disturbance), respectively. RSME1 is for the hip joint while RSME2 is for the knee joint.

Figure 11.

RSME1 and RSME2 comparisons in two cases. Icon “No-dis” means Case One and “Dis” means Case Two, respectively.

If the RSME is treated as a benchmark, the improvement percent (IMP) of performance with four kinds of controllers in Case One and Case Two is displayed in Tables 1 and 2. As the two tables show, the proposed control strategy will gain the highest improvement percentages of 69.4% and 76.8% for hip joint and knee joint separately in Case One while they change to be 68.1% and 76.8% in Case Two. Tables 1 and 2 illustrate that the SMC_GA is inferior to SMC_GA_CMAC but has better performance than SMC_CMAC, while the SMC_CMAC is superior to SMC. Therefore, the proposed control strategy is robust and effective whether the exoskeleton system dynamics suffer from bounded external disturbance or not.

Table 1.

Accuracy improvement comparison (Case One).

Control methods	IMP for hip joint (%)	IMP for knee joint (%)
SMC	0	0
SMC_GA	57.1%	74.5%
SMC_CMAC	24.5%	37.4%
SMC_GA_CMAC	69.4%	76.8%

Table 2.

Accuracy improvement comparison (Case Two).

Control methods	IMP for hip joint (%)	IMP for knee joint (%)
SMC	0	0
SMC_GA	55.3%	75.2%
SMC_CMAC	17.4%	31.7%
SMC_GA_CMAC	68.1%	76.8%

5. Conclusions

For lower limb assistive exoskeletons, precise position control is very important for the human-exoskeleton collaboration. In this paper, a hybrid position control strategy SMC_GA_CMAC is proposed to follow human limb joints trajectory for the exoskeleton. GA is used to find the optimal structure of SMC and CMAC neural network is implemented as the compensation to improve tracking performance. The proposed SMC_GA_CMAC control strategy is proven to be stable with Lyapunov function and features better tracking performance compared with SMC, SMC_GA, and SMC_CMAC. The proposed control algorithm has guaranteed the requirement for high accuracy of position control for robotic manipulators suffering from dynamics uncertainties. The hybrid control strategy SMC_GA_CMAC is more suitable to control the exoskeleton to follow human motion intent under the occurrence of uncertainties. In addition, the proposed method will be investigated and explored in the real exoskeleton prototype in the near future.

Future study will be focused on the optimization of CMAC to overcome its drawbacks because of the binary input mapping character, which can be addressed by intelligent approaches such as fuzzy logic in cosimulation. The human motion intent estimation is also a crucial challenge, which will be investigated using machine learning methods.

Appendix

A. SMC Optimization Using GA

See Algorithm 1.

B. CMAC Neural Network Compensation

See Algorithm 2.

Competing Interests

The authors declare that they have no competing interests.