Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Mar 30;6:23731. doi: 10.1038/srep23731

Transmission-Type 2-Bit Programmable Metasurface for Single-Sensor and Single-Frequency Microwave Imaging

Yun Bo Li 1, Lian Lin Li 2, Bai Bing Xu 1, Wei Wu 1, Rui Yuan Wu 1, Xiang Wan 1, Qiang Cheng 1, Tie Jun Cui 1,a
PMCID: PMC4812328  PMID: 27025907

Abstract

The programmable and digital metamaterials or metasurfaces presented recently have huge potentials in designing real-time-controlled electromagnetic devices. Here, we propose the first transmission-type 2-bit programmable coding metasurface for single-sensor and single- frequency imaging in the microwave frequency. Compared with the existing single-sensor imagers composed of active spatial modulators with their units controlled independently, we introduce randomly programmable metasurface to transform the masks of modulators, in which their rows and columns are controlled simultaneously so that the complexity and cost of the imaging system can be reduced drastically. Different from the single-sensor approach using the frequency agility, the proposed imaging system makes use of variable modulators under single frequency, which can avoid the object dispersion. In order to realize the transmission-type 2-bit programmable metasurface, we propose a two-layer binary coding unit, which is convenient for changing the voltages in rows and columns to switch the diodes in the top and bottom layers, respectively. In our imaging measurements, we generate the random codes by computer to achieve different transmission patterns, which can support enough multiple modes to solve the inverse-scattering problem in the single-sensor imaging. Simple experimental results are presented in the microwave frequency, validating our new single-sensor and single-frequency imaging system.

The theory and technology of the electromagnetic imaging have been well developed in recent years and many new cutting-edge imaging methods have been proposed, one of which is the well-known single-sensor (or single-radar) imaging1. This imaging method is associated with the wavefront reconstruction or inverse scattering problem in the imaging area. The single-sensor system has only one detecting source instead of a source array. To change the modes of the single source, different radiation or receiving patterns are required to reconstruct the objects by solving matrix equations. Thus, the kernel issue in developing the single-sensor imaging system is to generate randomly multiple-mode modulators or masks2,3,4. The masks can also be considered as spatial filters, in which the unit cell’s transmission performance should be varied under the frequency or electronic controls. Recently, an excellent contribution on the single-sensor imaging by using dispersive metamaterials5,6,7,8 has been reported by Hunt et al.9. Then reconfigurable spatial light modulators (SLMs) based on metamaterial absorbers10,11 have been applied to realize reflection-type single-pixel imaging in the terahertz regime12. Sequentially, two-dimensional (2D) holographic metasurfaces have been presented to reconstruct the planar objects13,14. Combining with the metasurfaces which can flexibly manipulate electromagnetic characteristics of modulators, the single-sensor imaging system will have tremendous potentials and opportunities to promote the imaging performance.

Metasurfaces15,16,17,18,19,20,21,22,23,24,25 have many advantages over bulk metamaterials, such as the low loss, low cost, and low profile, and hence have overwhelmingly attracted the scientists and engineers in recent years. A number of outstanding results have been presented, including the generalized Snell’s law18, Huygens metasurface21 and cascaded transmit-array24. The above three new concepts or technologies can extremely increase the ability in designing the spatial modulators26,27, which are the important components for the imaging system and spatial signal processing. The design of spatial modulators using metasurfaces requires that the unit cells with changing texture sizes can overlap 360-degree phase variance under the high transmission rate. For the generalized Snell’s law which introduces the concept of phase discontinuities, the transmission rate is limited to 25% under the cross polarization27. For the Huygens metasurfaces, the unit cells are hard to design to satisfy the electric and magnetic resonances under the same frequency. Owing to the high transmission rate and easy realization, the cascaded transmit-array metasurfaces are frequently adopted as the spatial modulators, although they suffer from the thick unit cells composed of multiple layers.

In the imaging area, metamaterials with the negative index of refraction were introduced to realize the perfect image under the ideal case28, which opens the door for metamaterial imaging. Based on the theory of amplifying evanescent waves28, super- and hyper-lenses have been proposed29,30,31,32, which can achieve super-resolution imaging in experiments. Distinguished from the super/hyper-lens approaches28,29,30,31,32, metamaterials or metasurfaces have also contributions in the wave-front reconstruction or calculation imaging. More recently, the holographic imaging has rapidly developed by using metasurfaces33, which can generate arbitrary optical images with different recordings of the hologram. Ni et al. presented the thinnest hologram to modulate both amplitudes and phases in the visual band, which produces high-resolution and low-noise images with the aids of complementary V-type nano-antennas34. Simultaneously, by using the plasmonic metasurfaces, Zhang et al. have reconstructed images of complex objects in the optical band with eliminating the undesired effects of multiple diffractions35, and also made the meta-hologram reach 80% conversion efficiency between two circular-polarization states36.

More recently, coding, digital, and programmable metamaterials have been presented37,38, providing a new way to describe metamaterial. In the reflection-type 1-bit programmable metamaterial37, the unit cells were controlled by the field programmable gate array (FPGA) to reach zero reflection phase (“0” state) or 180-degree reflection phase (“1” state). Then the reflections and scattering of electromagnetic waves can be manipulated by changing the “0” and “1” states of each unit cell in real time by FPGA, realizing instant switch among different functionalities, such as single-beam reflection, multi-beam scattering, and diffusions37. However, transmission-type programmable metamaterial has not been reported yet, which has more application potentials.

In this article, we propose a novel transmission-type 2-bit programmable metasurface and then present a single-sensor and single-frequency imaging system in the microwave frequency, which makes use of only one sensor with multi-mode measurements to reconstruct the object. In our design, the coding unit contains two layers, which is convenient for changing the voltages in rows and columns to switch the diodes in the top and bottom layers. We use computer to manipulate FPGA to deliver the random binary codes “0” and “1” for switching the diode states on the unit cells, which results in the change of transmission features of the whole metasurface. Due to the dyadic states in each layer of the unit cell, the whole aperture can be made 2-bit coding programmable. For the transmission performance of the 2-bit units, we need enough phase variety between coding units to keep high transmission amplitudes. Then, excited by a single horn antenna (i.e. the single sensor), the 2-bit programmable metasurface can randomly modulate and generate many different transmission patterns, which can provide adequate modes to solve the inverse scattering problem in the microwave imaging system. Compared with the recently excellent work for terahertz single-pixel imaging based on SLMs12, we can control the rows and columns of the metasurface aperture simultaneously using the 2-bit programmable coding metasurface, instead of tuning all unit cells independently12. For instance, for an N × N-element metasurface, we need only 2N random controls to the row and column, instead of N2 independent controls to all elements12, which will reduce the costs and complexities of the imaging system significantly. Compared with the pioneer work on single-sensor imaging methods to transform the masks controlled by frequency using dispersive and resonance metasurfaces9,13,14, the proposed programmable imaging system with variable modulators under single frequency can avoid the object dispersion.

Results and Discussions

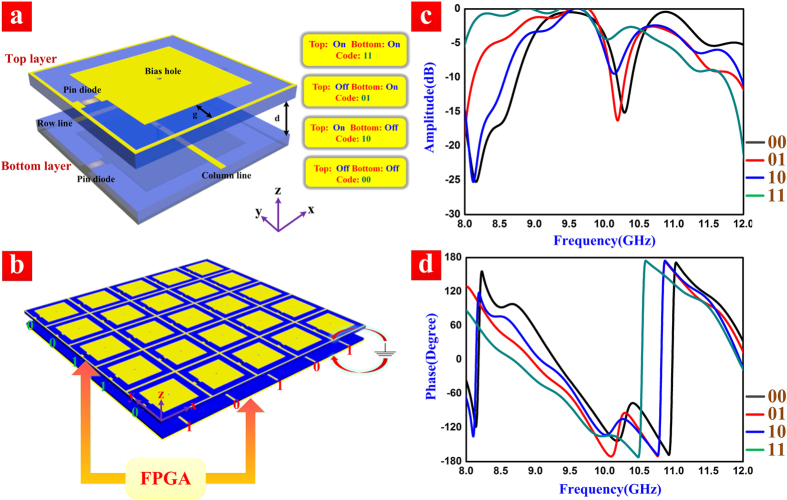
To realize the single-sensor and single-frequency imaging system, the core task is to propose the programmable spatial modulators controlled by digital codes. We choose here the transmit-array metasurface with high transmission amplitude and large phase variety as our spatial modulators. The unit cell of the programmable metasurface has two layers, as shown in Fig. 1(a), in which each layer contains a switchable diode. For conveniently grounding, we use a metallic fishnet texture39 in the edges of the unit cell. The positive voltages are loaded through via holes. On the top layer of the unit cell, the back feeding line is horizontal; while on the bottom layer, the back feeding line is vertical, which will perform the controls of rows and columns, respectively. We choose a commercially available “SMP 1320-079LF” as the switchable diode, whose parameters are introduced in the legend of Fig. 1. When positive voltage is loaded though via hole, we define the state of the diode as “On”; when no voltage is loaded, the state is defined as “Off”. Thus, according to the structure of the two-layer unit cell, there are four states in the whole texture due to the dual responses in each layer. We indicate the four states as 2-bit binary codes: “11”, “01”, “10”, and “00”, respectively.

Figure 1.

Figure 1

Open in a new tab

(a)The diagram of the 2-bit coding unit cell. The period of the unit is 14 mm, and a commercial printed circuit board F4B is chosen as the dielectric substrate (blue areas) with the relative permittivity of 2.2 and the thickness of 1 mm. The texture has two layers: the top layer and the bottom layer, which have mirror-symmetrical geometries except of the feeding lines. The two layers are separated by air with the gap of d = 3 mm. The pin diodes are connected between the fishnets in the outer rings and the middle metallic patches, which are insulated by the size of g = 2 mm. (b) The 2-bit programmable coding metasurface for our single-sensor and single-frequency imaging, in which FPGA can randomly deliver the binary codes (0 or 3.3 V voltage) on rows (green) and columns (red), simultaneously. (c,d) The simulated amplitudes (c) and phases (d) of transmission characteristics of the 2-bit coding unit cell with different states.

Here, we want to reconstruct the objects under a single frequency between 9 to 10 GHz. For this purpose, we first extract the parameters of the pin diode in this frequency band. An “R-L-C” series model is assumed and the extracted results are R = 0.06 Ω, L = 0.45 nH, and C = 0.25 pF when the loaded voltage is 0 V; and R = 0.17 Ω, L = 0.89 nH, and C = 2.75 pF when the loaded voltage is 3.3 V. By importing the “R-L-C” parameters into the commercial software, CST Microwave Studio, we can simulate the transmission performance of the unit cell (S21), as shown in Fig. 1(c,d). Here, different codes mean different states of the Pin diodes in the upper and lower layers of the unit cell. Hence the current distributions of the unit cell under different codes are varied, which lead to affect the transmission coefficients. The parameter sweeping method is used to design the 2-bit unit cells based on the full-wave simulations by loading the lumped circuit. The simulation results indicate that the 2-bit coding unit has good features of high-amplitude transmissions and enough phase shifts in the considered frequency band, which satisfy the requirements to our single-sensor imaging. Based on the unit-cell design, we create a 5 × 5 transmission-type programmable metasurface, as illustrated in Fig. 1(b). The thickness of the metasurface is 5 mm, which is close to λ/7 (λ is the wavelength at 9 GHz). We use FPGA to deliver the randomly binary codes, which control the high and zero voltages on the row and column lines to generate the 2-bit coding. Though each metasurface unit cell is not controlled individually, the row and column of the metasurface are manipulated simultaneously so that all unit cells possessing on their own spatial positions have independent 2-bit random codes.

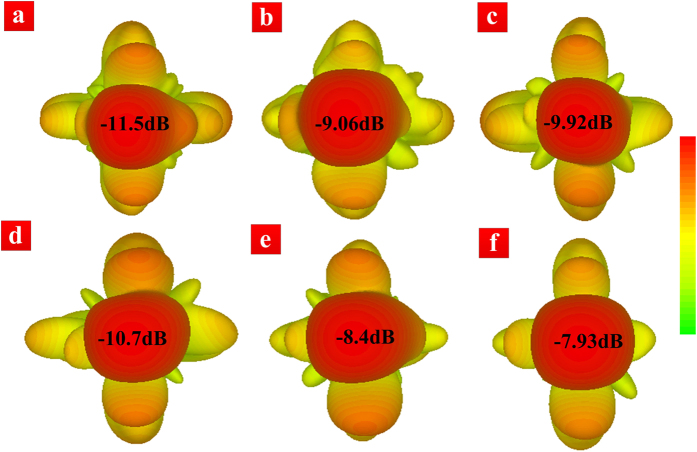
In fact, we can generate many groups of “row and column” binary codes to randomly modulate the masks of the transmission-type programmable metasurface. Figure 2(a–f) illustrate some selected transmission patterns through the metasurface obtained by full-wave numerical simulations. From Fig. 2(a–f), we find that the appearances and gains of the transmission patterns are both discriminative under different programmable modulations. The results clearly demonstrate that, by using the proposed method (controlling “row and column” simultaneously) to manipulate the metasurface masks, we can obtain many different transmitting and receiving patterns, which are the essential for the single-sensor image reconstruction.

Figure 2. The transmission patterns (i. e., forward radar cross sections) in the far-field region with different programmable scenarios at 9.2 GHz, in which the values of relative transmission gains are given.

Figure 2

Open in a new tab

(a) Row codes: 00000; Column codes: 10000. (b) Row codes: 01100; Column codes: 10110. (c) Row codes: 00001; Column codes: 11001. (d) Row codes: 10000; Column codes: 10001. (e) Row codes: 11001; Column codes: 11100. (f) Row codes: 11101; Column codes: 10111.

For the single-sensor and single-frequency imaging system, we need many different measurement modes, and thus many different metasurface patterns, to constitute a generalized system response matrix, which characterizes the signal sensed by the horn antenna for a given configuration of metasurface illuminated by the same horn antenna. The actual measurement signals under a given metasurface mode is related to the original object-area vector σ = (σi), i = 1, 2, …, N, through the generalized system response matrix G = (Gpj), p = 1, 2, …, P, j = 1, 2, …, N. The relationship amongs σ, G and the measurement data V = (V(p)i), p = 1, 2, …, P, is expressed as

graphic file with name srep23731-m1.jpg

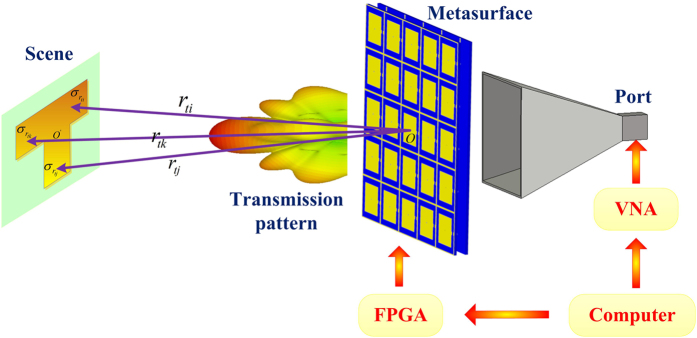
To interpret the establishment of Eq. (1), as shown in Fig. 3, O is the original point of global coordinate system, which is the central point of the programmable metasurface aperture as well, and O′ is the central point of the image scene. For the metasurface with the pth pattern (p = 1, 2, … P, P indicates the total number of metasurface patterns for the whole imaging) configured by FPGA, the electrical field radiated from the horn antenna after experiencing through the metasurface reads37:

Figure 3. The schematic of the proposed single-sensor and single-frequency microwave imaging system, in which the horn antenna is considered as the single sensor, while the vector network analyzer (VNA) can be treated as the transmitter and receiver.

Figure 3

Open in a new tab
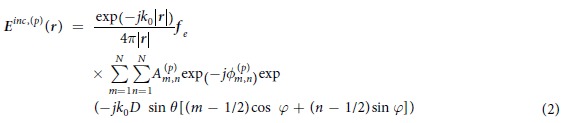graphic file with name srep23731-m2.jpg

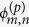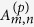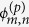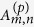The quantities Inline graphic and Inline graphic correspond to the phase and amplitude distributions, respectively, which are caused by the illumination of horn antenna, over the (m,n)th metasurface unit with the pth metasurface configuration. It remains an open and challenging problem to determine Inline graphic and Inline graphic with the acceptable accuracy for the imaging purpose because of the really complicated interactions among the metasurface elements and the microwave signal diffracted from the horn antenna. The summation involved in Eq. (2) is performed across the whole radiation elements of the metasurface. Other parameters introduced in Eq. (2) are explained as follows, i.e., fe denotes the radiation pattern of unit, k0 is the operational wavenumber in free space, D is the size of the element and θ and φ are associated with polar and azimuth angles of r, respectively. For notable convenience, Eq. (2) is formally rewritten as

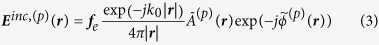graphic file with name srep23731-m7.jpg

With such illumination as descripted by Eq. (2) or Eq. (3), the current Js(r′) induced on the surface of the conducting object is

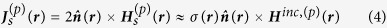graphic file with name srep23731-m8.jpg

Herein, 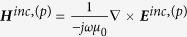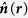Inline graphic, Inline graphic is the normal direction on the conducting object surface, and σ(r′) = 2 is associated with the conducting pixel, and being zero otherwise. It is noted that the geometrical optical approximation has been explicitly made for the smooth object in the second equality of Eq. (4). Now, following the standard Huygens’s principle, we can immediately arrive at the scattered electrical field emerged from the probed object illuminated by Eq. (2), namely,

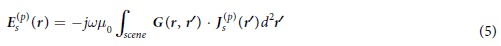graphic file with name srep23731-m11.jpg

Herein, the dyadic Green’s function reads

graphic file with name srep23731-m12.jpg

where Inline graphic is the scalar Green’s function in free space.

With the use of the reciprocal property, the signal sensed by the horn antenna is:

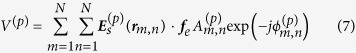graphic file with name srep23731-m14.jpg

Combing Eqs (2, 3, 4, 5) with Eq. (7) leads to following linear expression relating the observation V(p) and the reflectivity of probed object σ(r′), namely,

graphic file with name srep23731-m15.jpg

where

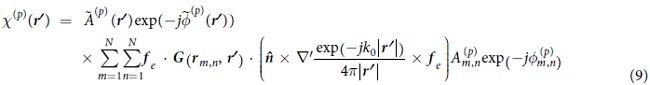graphic file with name srep23731-m16.jpg

For the purpose of numerical operation, the image scene is evenly divided into N sub-areas, in each the sub-RCS is defined as σj(j = 0, 1…N). In order to avoid introducing too many notations, Gpj(p = 0,1…P; j = 0, 1…N), calculated from Eq. (9), is used to represent the system response relating the pth observation and the jth pixel. Then, Eq. (8) can be cased into the compact form (Eq. (1)) after stacking all P measurements corresponding to P metasurface patterns.

In our design, both P and N are equal to 5 × 5 = 25 and the matrix G is composed of 25 × 25 = 625 units. Eq. (1) can be rewritten as V = Gσ for short. Hence it is obvious that σ = G−1V when the matrix G is a square matrix. That is to say, if the object area to be reconstructed has 25 sub-object areas, the times of measurements must be 25 for solving the unknown sub-objects by using the directly inverse operation. Thus, the main purpose of the multi-times measurements under different programmable transmission modes is to build up the matrix equation.

According to the theory of single-sensor imaging, we present the flow chart of the whole imaging system, as shown in Fig. 3. Here, the computer is the brain of the imaging system, which can control the vector network analyzer (VNA) and FPGA to further control the single source (i.e., the horn antenna) and the transmission-type programmable metasurface, respectively. We set the object to be reconstructed in the far-field region. First, the computer emits the random “row and column” binary codes stored in FPGA to complete the mask modulations. Then, the computer sends the orders of transmission and receiving to VNA. This situation can be considered as the single-times measurement in the imaging system. To build up the matrix equation, we should make 25 times (in this design) measurements under different programmable coding patterns at the same frequency. However, the unknown generalized system response matrix should be calibrated before the imaging experiments. To distinguish with the former metamaterial-based single-sensor imaging system, we apply the pin diodes controlled by voltages to change the transmission performance of the metasurface at single frequency, instead of using the dispersive characteristics of metasurfaces to avoid the object dispersion.

To further validate the new method of the single-sensor and single-frequency imaging system, we fabricate a sample of the transmission-type programmable metasurface and complete the imaging experiments. The sample is composed of 10 × 10 = 100 elements with the size of 140 × 140 mm2. However, in our experiment we can only use 5 × 5 = 25 elements in the center of the metasurface, which are efficiently illuminated by the horn antenna. Sufficiently different (or random) transmission patterns for the imaging system are generated by using the programmable coding elements. Considering to the exclusive calibration time of the generalized system response matrix, we only divide the object area to be solved into 25 sub-areas, and the size of each sub-area is 20 × 20 mm2 (the resolution is about 2λ/3 at 9 GHz). More elements of the sample should be used if we want to reconstruct a bigger field of view (FOV) with high efficiency.

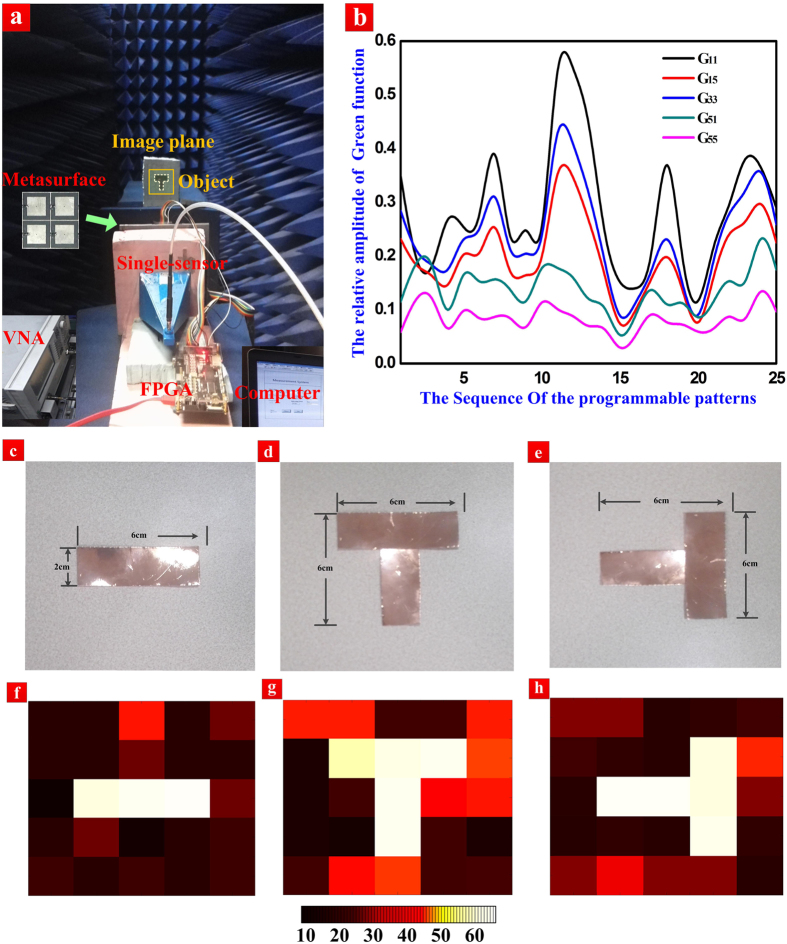
It is very important to calibrate the generalized system response matrix with regard to the imaging system by changing the transmission patterns. There exist two methods to get such matrix: 1) Acquire the near-filed currents on the imaging aperture, and then the far-filed transmission and receiving patterns will be obtained by applying the spatial Fourier transform; 2) Move a regular small metallic object for calibration in all sub-areas on the imaging plane to obtain the transmission and receiving performance in the manner of point-to-point scanning, which are the information of the system response function. According to the practicability, we choose the second method to make calibration, but the calibration process is complicated and time-consuming. The Labview software is applied to connect VNA (Agilent N5230C) and FPGA to the computer, which is also used to control the transmission and sampling of signals. We adopt the technology of background cancellation and loading the hardware time-domain gate to eliminate the effect of background noise. The intermediate frequency bandwidth is reduced for filtering the random noise in experiments. Figure 4(b) shows some calibration results of the generalized system response matrix under the change of coding patterns.

Figure 4.

Figure 4

Open in a new tab

(a) The single-sensor and single-frequency imaging system based on the 2-bit programmable coding metasurface. (b) The sampled information of the generalized system response matrix (G11, G15, G33, G51, and G55) calibrated under the 25 different programmable patterns in our measurements. For each randomly varied curve, it can prove that the diodes are working in the experiments. (c–e) The photographs of three metallic objects: the horizontal bar (c), the T-type object (d), and the T-type object rotated by 90 degrees (e). (f–h) The imaging results of the three metallic objects at 9.2 GHz: the horizontal bar (f), the T-type object (g), and the T-type object rotated by 90 degrees (h).

From Fig. 4(b), we observe that the generalized system response matrix in each sub-area has irregular (or random) variety under different programmable coding patterns, and thus it is appropriate for reconstructing the object based on our imaging system. In experiments shown in Fig. 4(a), we have reconstructed three metallic objects: a horizontal bar, a T-type object, and a T-type object rotated by 90 degrees, as displayed in Fig. 4(c–e). The experimental imaging results at 9.2 GHz are presented in Fig. 4(f–h), which clearly validates the efficiency of the single-sensor and single-frequency imaging system.

Conclusions

We have proposed a new transmission-type 2-bit programmable coding metasurface and further built up a single-sensor and single-frequency microwave imaging system. In design of the imaging system, we have realized to change the masks randomly using the programmable metasurface, in which the rows and columns can be controlled simultaneously by the binary codes. Compared to the conventional methods of single-sensor imaging, in which all unit cells are manipulated independently, the proposed imaging system can greatly reduced the cost and complexity of the feeding circuits. Because it is based on the single-frequency reconstruction without the frequency agility, this imaging system also avoids the object dispersion. The 2-bit programmable coding metasurface is composed of transmission-type elements to realize many different transmission patterns, which are the essential parts for solving the inverse problem in the single-sensor and single-frequency imaging. The proposed method is not only applicable for the far-filed imaging, but also for the near-field imaging, which will be studied in our future work. The new imaging system may also be extended to the terahertz frequencies.

Additional Information

How to cite this article: Li, Y. B. et al. Transmission-Type 2-Bit Programmable Metasurface for Single-Sensor and Single-Frequency Microwave Imaging. Sci. Rep. 6, 23731; doi: 10.1038/srep23731 (2016).

Acknowledgments

This work was supported by the National Science Foundation of China (61571117, 61138001, 61302018 and 61401089), 111 Project (111-2-05), and the Scientific Research Foundation of Graduate School of Southeast University (No. YBJJ1435).

Footnotes

Author Contributions Y.B.L., L.L.L., B.B.X., W.W., R.Y.W., X.W., Q.C. and T.J.C. completed the theoretical analysis and the measurement. Y.B.L. and T.J.C. wrote the manuscript.

References

  1. Duarte M. F. et al. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag 25, 83 (2008). [Google Scholar]
  2. Chan W. L. et al. a spatial light modulator for terahertz beams. Appl. Phys. Lett. 94, 213511 (2009). [Google Scholar]
  3. Watts C. M., Liu X. & Padilla W. J. Metamaterial electromagnetic wave absorbers. Adv. Opt. Mater. 24, 98 (2012). [DOI] [PubMed] [Google Scholar]
  4. Sensale-Rodriguez B. et al. Terahertz imaging employing graphene modulator arrays. Opt. Express. 21, 2324 (2013). [DOI] [PubMed] [Google Scholar]
  5. Smith D. R., Pendry J. B. & Wiltshire M. C. K. Metamaterials and Negative Refractive Index. Science 305, 788 (2004). [DOI] [PubMed] [Google Scholar]
  6. Schurig D. et al. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 314, 977 (2006). [DOI] [PubMed] [Google Scholar]
  7. Lai Y., Chen H. Y., Zhang Z. Q. & Chan C. T. Complementary Media Invisibility Cloak that Cloaks Objects at a Distance Outside the Cloaking Shell. Phys. Rev. Lett. 102, 093901 (2009). [DOI] [PubMed] [Google Scholar]
  8. Luo Y., Zhang J. J. B., Wu I. & Chen H. S. Interaction of an electromagnetic wave with a cone-shaped invisibility cloak and polarization rotator. Phys. Rev. B 78, 125108 (2008). [Google Scholar]
  9. Hunt J. et al., Metamaterial apertures for computational imaging. Science 339, 310 (2013). [DOI] [PubMed] [Google Scholar]
  10. Landy N. I., Sajuyigbe S., Mock J. J., Smith D. R. & Padilla W. J. Perfect metamaterial absorber. Phys. Rev. Lett. 100, 207402 (2008). [DOI] [PubMed] [Google Scholar]
  11. Chen H. T. et al. Antireflection coating using metamaterials and identification of its mechanism. Phys. Rev. Lett. 105, 073901 (2010). [DOI] [PubMed] [Google Scholar]
  12. Watts C. M. et al. Terahertz compressive imaging with metamaterial spatial light modulators. Nat. Photonics. 8, 605 (2014). [Google Scholar]
  13. Lipworth G. et al. Metamaterial apertures for coherent computational imaging on the physical layer. J. Opt. Soc. Am. A 30, 1603 (2013). [DOI] [PubMed] [Google Scholar]
  14. Hunt J. et al. Metamaterial microwave holographic imaging system. J. Opt. Soc. Am. A 31, 2109 (2014). [DOI] [PubMed] [Google Scholar]
  15. Holloway C. L. M., Mohamed A., Kuester E. F. & Dienstfrey A. Reflection and transmission properties of a metafilm: With an application to a controllable surface composed of resonant particles. IEEE Trans. Antennas Propag. 47, 853 (2005). [Google Scholar]
  16. Holloway C. L. et al. An Overview of the Theory and Applications of Metasurfaces: The Two-Dimensional Equivalents of Metamaterials. IEEE Trans. Antennas Propag. 54, 10 (2012). [Google Scholar]
  17. Sun S. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 11, 426 (2012). [DOI] [PubMed] [Google Scholar]
  18. Yu N. et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333 (2011). [DOI] [PubMed] [Google Scholar]
  19. Yu N. & Capasso F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139 (2014). [DOI] [PubMed] [Google Scholar]
  20. Liu L. X. et al. Broadband Metasurfaces with Simultaneous Control of Phase and Amplitude. Adv. Mater. 26, 5031 (2014). [DOI] [PubMed] [Google Scholar]
  21. Pfeiffer C. & Grbic A. Metamaterial Huygens’ Surfaces: Tailoring Wave Fronts with Reflectionless Sheets. Phys. Rev. Lett. 110, 197401 (2013). [DOI] [PubMed] [Google Scholar]
  22. Germain D., Seetharamdoo D., Burokur S. N. & De Lustrac A. Phase-compensated metasurface for a conformal microwave antenna. Appl. Phys. Lett. 103, 124102 (2013). [Google Scholar]
  23. Li Y. B., Wan X., Cai B. G., Cheng Q. & Cui T. J. Frequency-controls of electromagnetic multi-beam radiations and beam scanning by metasurfaces. Sci. Rep. 4, 6921 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Pfeiffer C. & Grbic A. Cascaded metasurfaces for complete phase and polarization control. Appl. Phys. Lett. 102, 231116 (2013). [Google Scholar]
  25. Li Y. B., Cai B. G., Wan X. & Cui T. J. Diffraction-Free Surface Waves by Metasurfaces, Opt. Lett. 39, 5888 (2014). [DOI] [PubMed] [Google Scholar]
  26. Jiang S. et al. Controlling the Polarization State of Light with a Dispersion-Free Metastructure. Phys. Rev. X. 4, 041042 (2014). [Google Scholar]
  27. Monticone F., Estakhri N. M. & Alu A. Full Control of Nanoscale Optical Transmission with a Composite Metascreen. Phys. Rev. Lett. 110, 203903 (2013). [DOI] [PubMed] [Google Scholar]
  28. Pendry J. B. Negative Refraction Makes a Perfect Lens, Phys. Rev. Lett. 85, 3966 (2000). [DOI] [PubMed] [Google Scholar]
  29. Fang N., Lee H., Sun C. & Zhang X. Sub–Diffraction-Limited Optical Imaging with a Silver Superlens. Science 308, 534 (2005). [DOI] [PubMed] [Google Scholar]
  30. Zhang X. & Liu Z. Superlenses to overcome the diffraction limit. Nat. Mater. 7, 435 (2008). [DOI] [PubMed] [Google Scholar]
  31. Jiang W. et al. Broadband All-Dielectric Magnifying Lens for Far-Field High-Resolution Imaging. Adv. Mater. 25, 6963 (2013). [DOI] [PubMed] [Google Scholar]
  32. Ma C. & Liu Z. A super resolution metalens with phase compensation mechanism. Appl. Phys. Lett. 96, 183103 (2010). [Google Scholar]
  33. Lee W. H. Sampled Fourier Transform Hologram Generated by Computer. Appl. Opt. 9, 639 (1970). [DOI] [PubMed] [Google Scholar]
  34. Ni X., Kildishev A. V. & Shalaev V. M. Metasurface holograms for visible light. Nat. Commun. 4, 2807 (2013). [Google Scholar]
  35. Huang L. et al. Three-dimensional optical holography using a plasmonic metasurface, Nat. Commun. 4, 2808 (2013). [Google Scholar]
  36. Zheng G. et al. Metasurface holograms reaching 80% efficiency. Nat. Nanotech. 10, 308 (2015). [DOI] [PubMed] [Google Scholar]
  37. Cui T. J., Qi M. Q., Wan X., Zhao J. & Cheng Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light: Sci. & Appl. 3, e218 (2014). [Google Scholar]
  38. Giovampaola C. D. & Engheta N. Digital metamaterials. Nat. Mater. 13, 1115 (2014). [DOI] [PubMed] [Google Scholar]
  39. Kafesaki M. et al. Left-handed metamaterials: The fishnet structure and its variations. Phys. Rev. B 75, 235114 (2007). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES