Significance
Humans mount an antibody-mediated immune response against influenza viruses that can be recalled. Nevertheless, individuals can suffer from recurrent influenza infections as viruses can change their antigenic properties by altering their surface glycoproteins. This antigenic evolution requires frequent update of seasonal influenza vaccines. To inform vaccine updates, laboratories that contribute to the World Health Organization Global Influenza Surveillance and Response System assess the antigenic phenotypes of circulating viruses. Based on the relationship of antigenic distance to genetic differences between viruses, we developed a model to interpret measured antigenic data and predict the properties of viruses that have not been characterized antigenically and explore the model’s value in predicting the future composition of influenza virus populations.
Keywords: evolution, antigenic distance, phylogenetic tree
Abstract
Human seasonal influenza viruses evolve rapidly, enabling the virus population to evade immunity and reinfect previously infected individuals. Antigenic properties are largely determined by the surface glycoprotein hemagglutinin (HA), and amino acid substitutions at exposed epitope sites in HA mediate loss of recognition by antibodies. Here, we show that antigenic differences measured through serological assay data are well described by a sum of antigenic changes along the path connecting viruses in a phylogenetic tree. This mapping onto the tree allows prediction of antigenicity from HA sequence data alone. The mapping can further be used to make predictions about the makeup of the future A(H3N2) seasonal influenza virus population, and we compare predictions between models with serological and sequence data. To make timely model output readily available, we developed a web browser-based application that visualizes antigenic data on a continuously updated phylogeny.
Seasonal influenza viruses evade immunity in the human population through frequent amino acid substitutions in their hemagglutinin (HA) and neuraminidase (NA) surface glycoproteins (1). To maintain efficacy, vaccines against seasonal influenza viruses need to be updated frequently to match the antigenic properties of the circulating viruses. To facilitate informed vaccine strain selection, the genotypes and antigenic properties of circulating viruses are continuously monitored by the World Health Organization (WHO) Global Influenza Surveillance and Response System (GISRS), with a substantial portion of the virological characterizations being performed by the WHO influenza Collaborating Centers (WHO CCs) (2).
Antigenic properties of influenza viruses are measured in hemagglutination inhibition (HI) assays (3) that record the minimal antiserum concentration (titer) necessary to prevent crosslinking of red blood cells by a standardized amount of virus based on hemagglutinating units. An antiserum is typically obtained from a single ferret infected with a particular reference virus. For a panel of test viruses, the HI titer is determined by a series of twofold dilutions of each antiserum. An antiserum is typically potent against the homologous virus (the reference virus used to produce the antiserum), but higher concentrations (and hence lower titers) are frequently required to prevent hemagglutination by other (heterologous) test viruses. HI titers typically decrease with increasing genetic distance between reference and test viruses (1).
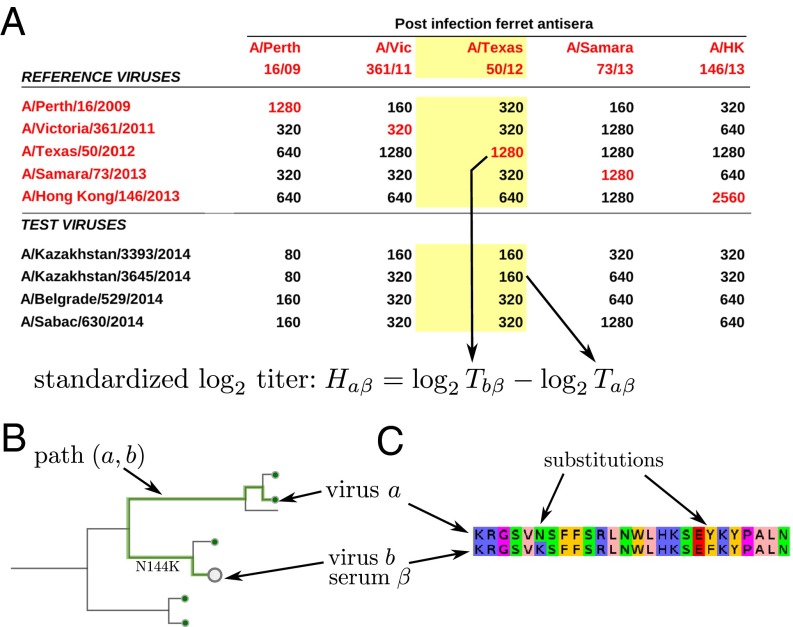
Given multiple antisera raised against different reference viruses and a panel of test viruses, WHO CCs routinely measure the HI titers of all combinations of test viruses a and sera β, resulting in a matrix of HI titers (see Fig. 1A). The HI titer of a test virus a using antiserum β raised against the reference virus b is typically standardized as , i.e., the difference in the number of twofold dilutions between homologous and heterologous titer. Standardized titers from many HI assays can be visualized in two dimensions via multidimensional scaling—an approach termed “antigenic cartography” (4). Although standard cartography does not use sequence information, sequences have been used as priors for positions in a Bayesian version of multidimensional scaling (5). To infer contributions of individual amino acid substitutions to antigenic evolution, Harvey et al. and Sun et al. (6, 7) have used models that predict HI titer differences by comparing sequences of reference and test viruses.
Fig. 1.
Antigenic data and models for HI titers. (A) A typical table reporting HI titer data. Each number in the table is the maximum dilution at which the antiserum (column) inhibited hemagglutination of red blood cells by a virus (row). The red numbers on the diagonal indicate homologous titers. A typical HI assay consists of all reciprocal measurements of the available antisera and reference viruses, and a number of test viruses that are measured against all antisera, but for which no homologous antiserum exists. To make measurements using different antisera comparable, we define standardized log-transformed titers relative to the homologous titer. (B) Each HI titer between antiserum α and virus b can be associated with a path on the tree connecting the reference and test viruses a and b, respectively, indicated as a thick line. The tree model seeks to explain the antigenic differences as additive contributions of branches. (C) In the substitution model, the sum over branches on the tree is replaced by a sum of contributions of amino acid substitutions.
Here, we show that antigenic properties of seasonal influenza viruses are accurately described by a model based on the phylogenetic tree structure of their HA sequences. We use the model to show that HI titers have a largely symmetric and tree-like structure that can be used to define an antigenic distance between viruses. We show that large-effect substitutions account for about half of the total antigenic change and that the effect of specific substitutions is dependent on the genetic background in which they occur. We further investigate the ability of HI measurements to predict dominant clades in the next influenza season. To visualize antigenic properties on the phylogenetic tree, we have integrated the models of antigenic distances and the raw HI titer data into nextflu.org—an interactive real-time tracking tool for influenza virus evolution (8).
This comprehensive summary of HA sequences from past and current influenza viruses linked to their antigenic properties has the potential to inform vaccine strain selections and facilitate efforts to predict successful influenza lineages (9–13).
Results
We use two related models that predict HI titers from sequences. The first—the tree model—explains standardized HI titers as a sum of contributions associated with internal branches in the phylogenetic tree that connect the reference virus b and the test virus a (see Fig. 1B). The second—the substitution model—explains HI titers in terms of a sum of contributions associated with amino acid substitutions between reference and test virus (see Fig. 1C). These two models are similar but complement each other in a few aspects that we discuss further below. In addition to contributions associated with branches or substitutions, measured HI titers depend on the overall reactivity of individual antisera and viruses in HI assays. In the model, we account for this variability through “antiserum potency,” which raises or lowers the expected titer of all HI measurements against an antiserum, and “virus avidity,” which raises or lowers the expected titer of all HI measurements against a virus.
Specifically, in the tree model, the measured standardized titer between virus a and antiserum β (corresponding to the reference virus b) is modeled by defined as
| [1] |
where , , and denote the avidity of virus a, the potency of antiserum β, and the genetic component of HI titer differences, respectively. The latter is decomposed into a sum of contributions along internal branches i in the path separating the test (a) and reference viruses (b), i.e., . In the substitution model, the sum over branches is replaced by a sum over amino acid substitutions between reference and test viruses. The parameters of our model are determined by fitting the model to available HI titer measurements while penalizing large values for the parameters.
The virus avidity accounts for systematic variations of HI titers of virus a across multiple antisera, i.e., a row of the HI matrix in Fig. 1. Within our model, can be positive or negative. Large absolute values of are penalized by adding a term proportional to to the cost function (-norm regularization). Similarly, the antiserum potency captures variation in HI titers of antiserum β across many test viruses, i.e., a column of the HI matrix. Part of the latter variation is already removed by using standardized titers relative to the homologous titer , but systematic variation remains that is absorbed by . Potencies are regularized by their -norm, as well, and allowed to be positive or negative.
Titers tend to decrease with increasing genetic distance between the reference and test virus. We therefore constrain the contributions to be nonnegative. While similar, the tree and substitution models differ slightly in how the genetic component of HI titers is parameterized. The tree model associates one term with each branch, and the contribution of the branch is independent of the direction of the path running through the branch. The substitution model associates a nonnegative effect with each amino acid difference— is modeled as a weighted sum of amino acid differences between reference virus b and test virus a. We give the model the additional freedom of independent effects for forward and backward substitutions, e.g., F159S vs. S159F.
In contrast to the potencies and avidities, we regularize the using their -norm, i.e., the contribute to cost function via their absolute value rather than their square. This regularization encourages a sparse model in which a minority of explain most antigenic evolution while many . Only internal branches of the tree or substitutions observed in more than one virus are candidates for nonzero contributions. Contributions of terminal branches or singletons can be absorbed into the virus avidities. For a detailed description of the models and inference procedures, see Material and Methods.
The Tree and Substitution Models Accurately Predict HI Titers.
We evaluated the performance of the models in predicting HI titers for different influenza lineages A(H3N2), A(H1N1)pdm09, B/Yam, and B/Vic. We trained the models on 90% of the data and used the remaining measurements to validate the models as in ref. 5. The number of viruses, number of antisera, HI measurements, etc., for each lineage are provided as Table S1.
Table S1.
Virus, antisera, and parameter count for the different time intervals and influenza virus lineages
| Lineage | Time interval | Model | Number of viruses | Number of test viruses | Number of ref viruses | Number of antisera | Number of HI titers | Number of genetic parameters | Number of s nonzero genetic parameters |
| H3N2 | 3 y | tree | 1,985 | 720 | 15 | 31 | 3,626 | 235 | 56 |
| H3N2 | 3 y | mutation | 1,985 | 720 | 15 | 31 | 3,626 | 44 | 24 |
| H3N2 | 6 y | tree | 2,658 | 1,442 | 31 | 74 | 10,676 | 472 | 146 |
| H3N2 | 6 y | mutation | 2,658 | 1,442 | 31 | 74 | 10,676 | 94 | 44 |
| H3N2 | 12 y | tree | 2,502 | 1,772 | 69 | 233 | 15,925 | 610 | 231 |
| H3N2 | 12 y | mutation | 2,502 | 1,772 | 69 | 233 | 15,925 | 143 | 73 |
| H3N2 | 20 y | tree | 3,283 | 1,935 | 98 | 299 | 17,490 | 698 | 266 |
| H3N2 | 20 y | mutation | 3,283 | 1,935 | 98 | 299 | 17,490 | 225 | 105 |
| H1N1pdm09 | 7 y | tree | 2,441 | 908 | 8 | 12 | 2,776 | 296 | 62 |
| H1N1pdm09 | 7 y | mutation | 2,441 | 908 | 8 | 12 | 2,776 | 60 | 18 |
| Vic | 6 y | tree | 1,929 | 303 | 4 | 9 | 534 | 131 | 23 |
| Vic | 6 y | mutation | 1,929 | 303 | 4 | 9 | 534 | 12 | 5 |
| Vic | 12 y | tree | 1,425 | 400 | 16 | 61 | 2,501 | 176 | 53 |
| Vic | 12 y | mutation | 1,425 | 400 | 16 | 61 | 2,501 | 30 | 19 |
| Vic | 20 y | tree | 1,676 | 471 | 26 | 87 | 2,792 | 206 | 64 |
| Vic | 20 y | mutation | 1,676 | 471 | 26 | 87 | 2,792 | 44 | 22 |
| Yam | 3 y | tree | 1,572 | 77 | 2 | 5 | 153 | 31 | 8 |
| Yam | 3 y | mutation | 1,572 | 77 | 2 | 5 | 153 | 2 | 2 |
| Yam | 6 y | tree | 1,750 | 304 | 9 | 20 | 1,304 | 121 | 28 |
| Yam | 6 y | mutation | 1,750 | 304 | 9 | 20 | 1,304 | 34 | 12 |
| Yam | 12 y | tree | 1,384 | 352 | 15 | 52 | 2,751 | 147 | 39 |
| Yam | 12 y | mutation | 1,384 | 352 | 15 | 52 | 2,751 | 44 | 17 |
| Yam | 20 y | tree | 1,811 | 422 | 24 | 72 | 2,789 | 188 | 57 |
| Yam | 20 y | mutation | 1,811 | 422 | 24 | 72 | 2,789 | 70 | 25 |
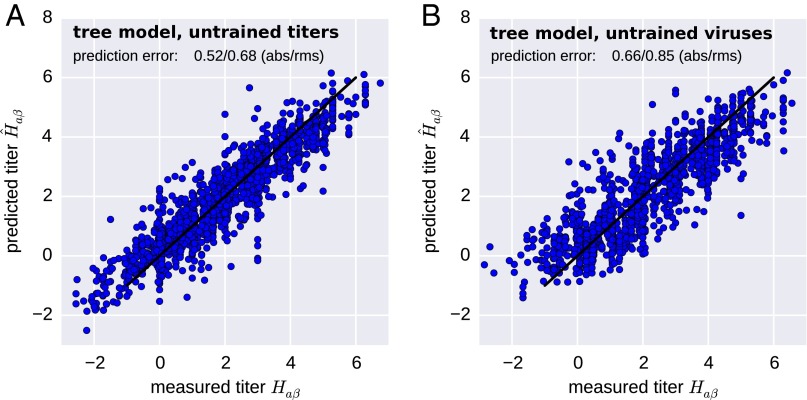
We found that the models were able to predict titers of antiserum−virus combinations to an accuracy of approximately titer levels for A(H3N2) with somewhat lower accuracy for the influenza B lineages (Table 1 and Fig. 2A).
Table 1.
Prediction accuracy of the tree and substitution models across influenza viruses
| Model | Tree | Substitution | ||
| Untrained unit | Titer | Virus | Titer | Virus |
| A(H3N2) (12 y) | 0.52 | 0.66 | 0.5 | 0.73 |
| A(H1N1)pdm09 (7 y) | 0.44 | 0.72 | 0.45 | 0.9 |
| B/Yam (12 y) | 0.64 | 0.88 | 0.65 | 1.0 |
| B/Vic (12 y) | 0.77 | 0.8 | 0.73 | 0.84 |
“Titer” and “virus” in the row “Untrained unit” refer to predictions for test sets in which individual titer measurements or all measurements involving a particular virus, respectively, were omitted from the training data.
Fig. 2.
A(H3N2) HI titers are accurately predicted by the tree model. The figure scatters predicted titers (y axis) against a test set of measurements not used for training of the model (x axis). This test set either consists of (A) a random sample of 10% of all measurements or (B) all measurements for 10% of all viruses. In the latter, no avidity can be estimated for viruses in the test set because these viruses are completely absent from the training data ( is assumed). Hence prediction accuracy is lower but still comparable to the measurement accuracy. The figure shows data obtained using a 12-y set of A(H3N2) viruses. Other time intervals and lineages are predicted similarly well.
To quantify the prediction accuracy for viruses for which no antigenic data exist, we selected 10% of the viruses and excluded all measurements involving these viruses from the training data. Both models predicted titers for viruses not part of the training set to an accuracy of approximately titer levels (Table 1 and Fig. 2B). Having completely excluded a virus from the training data implies that no avidity of a virus can be estimated (and is used instead). The increased prediction error is therefore largely due to virus-to-virus variability that is not captured by the HA phylogeny.
To infer the genetic component of an HI titer, the relevant branches in the tree or the substitutions that separate test and reference virus have to be constrained by measurements in the training data set. For a completely novel clade in the tree, the model would predict HI titers equal to that of the base of the clade for all subtending viruses. Similarly, accurate inferences by the substitution model require the effects of the relevant substitutions to be constrained by training data.
Using the tree and substitution models, we can predict HI titers for every combination of antiserum and virus in a phylogenetic tree (with prediction confidence varying by quality and amount of antigenic data). Because the substitution or branch effects pick up antigenic changes associated with a larger number of antiserum−virus pairs, whereas antiserum potencies and virus avidities absorb serum- and virus-specific variation, the resulting model of antigenic distances is a smoothed and coarse-grained description of the HI titer data.
Note that the model correctly predicts titers in excess of homologous titers (negative values in Fig. 2A). These higher titers often coincide with large negative virus avidities, which explains the absence of titers predicted to be strongly negative in Fig. 2B, where no virus avidities are available.
Cumulative Antigenic Evolution.
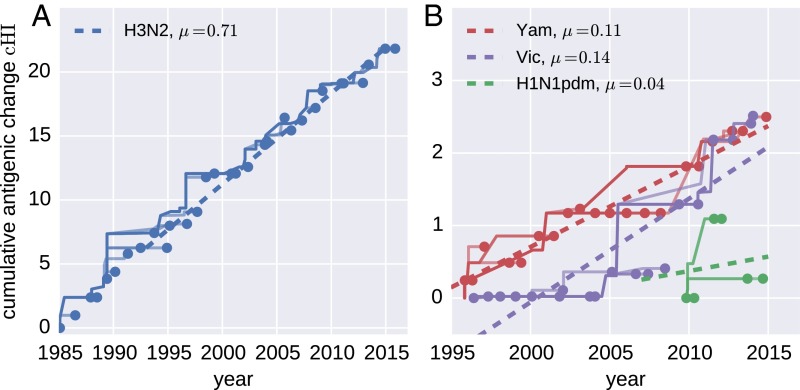
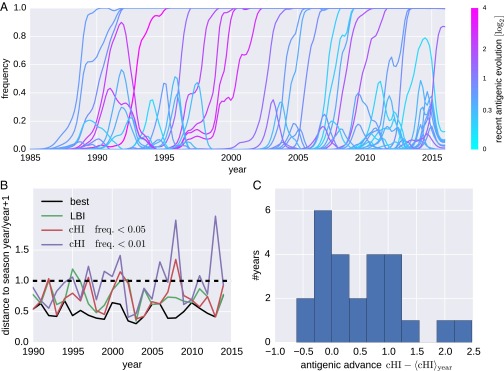
By summing all contributions to antigenic change on branches on the path between a virus and the root of the tree, we can estimate the total past antigenic change, , for each node in the tree. This cumulative antigenic change is roughly comparable to “dimension 1” in antigenic cartography (more precisely analogous to the length of a path on the map corresponding to the trunk of the tree). Our models infer that A(H3N2) viruses advance by ∼0.7 titer units per year (Fig. 3A), whereas influenza B virus lineages advance 0.15 (Vic) and 0.1 (Yam) units per year (Fig. 3B). Previous estimates of these rates using cartography (5) suggested higher absolute values, but the relative magnitude of rates in different lineages were found to be similar. Forcing the antigenic distance matrix into two dimensions causes distortions that might result in an exaggeration of the distances. Very little consistent temporal change in antigenic properties is observed in A(H1N1)pdm09 (Fig. 3B).
Fig. 3.
Cumulative antigenic change (cHI) from phylogeny root to tips across influenza viruses. (A) A(H3N2) antigenic evolution over the past 30 y. The trunk of the tree is shown as a thick line, and side branches are shown as thin lines. The dashed straight line indicates the linear regression vs. time. (B) The corresponding traces for the two influenza B lineages (past 20 y) and A(H1N1)pdm09 (past 7 y).
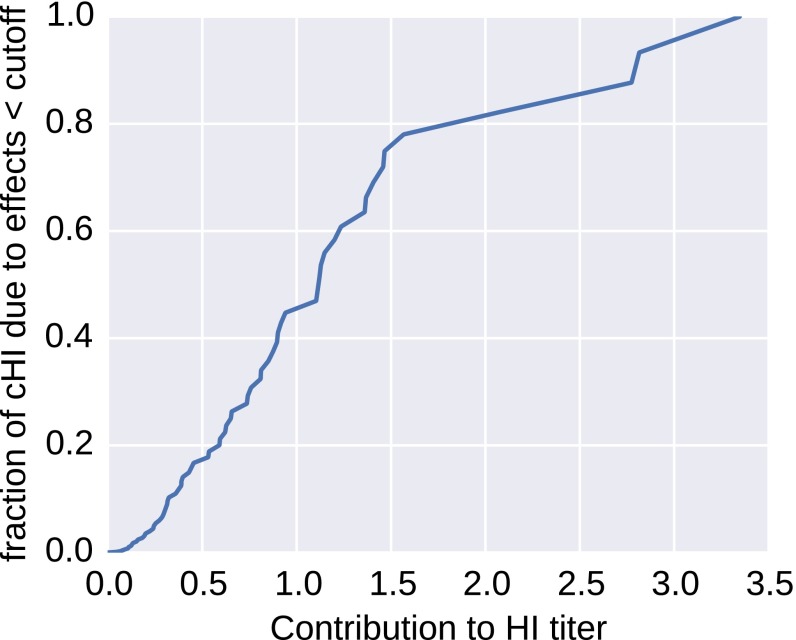
We estimate that, for A(H3N2) viruses, approximately half the cumulative antigenic evolution is due to a large number of substitutions with effects smaller than one unit, whereas 20% is accounted for by a few substitutions with effects greater than two units (Fig. S1). However, some of the largest effects are associated with clusters of colinear amino acid substitutions, and their individual effects cannot be resolved.
Fig. S1.
Contributions of small and large effect substitution to antigenic evolution. About half of antigenic change is attributed to mutations with effects smaller than one unit. The figure shows the fraction antigenic change by common mutations with effects smaller than the cutoff on the horizontal axis.
As we have shown, the two models of HI titers accurately predict HI titers of all seasonal influenza virus lineages. However, A(H3N2) viruses have been monitored more closely and over a larger number of years than the other lineages. We therefore focus subsequent analysis of the structure of antigenic space and the dynamics of antigenic evolution on A(H3N2).
HI Titers Define an Approximate Distance.
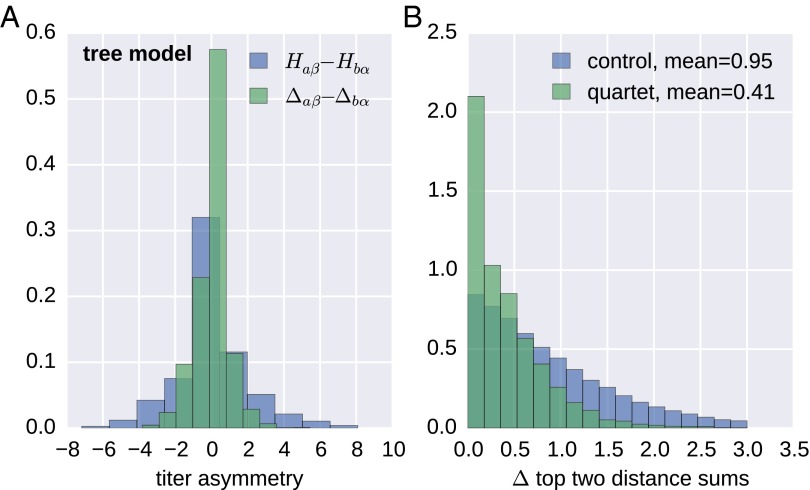
To further evaluate the approach of partitioning a titer into an antiserum, a virus, and a symmetric tree component , we considered all reciprocal titer measurements, i.e., pairs of viruses against which antisera α, β have been raised and that have been measured against each other. Subtracting the virus avidities and antiserum potency contributions from titers, the remainders Δaβ = Haβ − va − pβ and Δbα should reduce the titers to the symmetric tree component . Fig. 4A compares the distribution of Δaβ − Δbα with the uncorrected difference between the reciprocal titers for A(H3N2). Although raw reciprocal titer measurements often differ by several titer units (SD 2.0), the corrected tree component was symmetric to within one unit (SD 0.9), comparable to the accuracy of HI titer measurements.
Fig. 4.
H3N2 HI titers define an approximate a distance on the tree. (A) Reciprocal HI titer measurements often differ by several units (histogram of ). After subtracting avidities and potencies, the remainder Δaβ − Δbα is almost symmetric, with deviations on the order of the measurement accuracy (SD 0.95). (B) On a tree, the two largest sums of distances within antisera/virus quartets are equal (see HI Titers Define an Approximate Distance). B shows the distribution of the absolute value of the difference of the top two distance sums for quartets and for three random distance sums. Those from quartets have a much smaller deviation. A and B both show results for A(H3N2) viruses from the last 12 years.
The degree to which titer distances have tree-like properties can be tested using the following quartet rule: Take any four leaves and construct the sum of the distances , and . If the distances are given by a tree, the two largest of the three sums of distances will be equal. The quartet rule can only be tested on sets of viruses for which all pairwise distances have been inferred. Hence, we determined maximal “cliques” of reference antisera, the activities of which had been measured against all other reference viruses within the clique. Out of these cliques, we repeatedly selected, at random, four viruses, calculated the three distance sums, and compared the largest and second largest distance sum. As a control, we constructed the analogous distribution for triplets of random variables with the same distribution as the distance sums, but without the dependence via the tree: We obtained three sums of two distances by three times randomly drawing four antisera. Both distributions are shown in Fig. 4B. The difference between the largest and second largest of these distance sums of quartets has a mean of 0.41 titer levels, whereas the control has a mean of 0.96 titer levels. The similarity of the largest and second largest sums supports a tree-like structure underlying observed HI distances.
Amino Acid Substitutions Associated with Titer Drops.
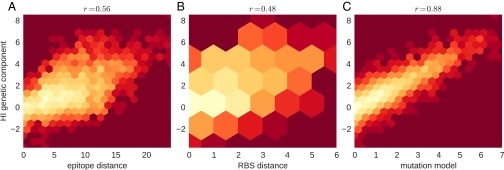
The majority of antigenic evolution tends to occur at a subset of sites (14, 15). Seven positions near the HA receptor binding site (Koel 7) have been shown to account for major historic antigenic transitions (16). However, the number of substitutions at epitope sites or Koel 7 sites alone is a poor predictor of antigenic distance, with values of about 0.25 (Fig. S2), possibly because the effect of a substitution depends on the genetic background (HA sequence) in which it occurs.
Fig. S2.
Determinants of corrected HI titers (y axis) of A(H3N2) viruses. (A) Correlation of corrected HI titers with the number of substitutions at mapped epitope sites between reference and test virus. Similarly, B shows this correlation for the distance at receptor binding sites, and C shows the correlation with the genetic component of the substitution model. Neither epitope or RBS distance explain much of the titer variation (Pearson correlation coefficient above the panels).
Within the substitution model, we can explicitly associate antigenic changes with amino acid substitutions. Table S2 shows the top contributions for A(H3N2) for sequences estimated from sets of sequences and the associated HI titers in five overlapping 10-y intervals. Most of the largest contributions coincide with substitutions at Koel 7 sites. When a substitution is present in the same context in overlapping time intervals, the estimated effects tend to be similar (K189N, K135E, K158R, K140E, Y159F)—provided there are enough data to constrain the model.
Table S2.
The 55 largest inferred antigenic effects of substitutions in HA1 for A(H3N2) in the past 30 y as inferred by the substitution model in overlapping 10 y intervals
| Substitutions | 1985–1995 | 1990–2000 | 1995–2005 | 2000–2010 | 2005–2016 |
| K156E* | — | 3.4 | — | — | — |
| K158N/N189K* | — | — | — | 2.59 | 3.28 |
| C1R*,† | — | 3.23 | — | — | — |
| K189N* | — | — | — | 2.96 | 2.45 |
| S262N | — | 2.48 | 0.0 | — | 0.05 |
| K158R* | — | — | — | 1.95 | 2.01 |
| C2*,† | — | — | 1.98 | — | — |
| K135G | 1.95 | 1.95 | — | — | — |
| C1*,† | — | 1.94 | — | — | — |
| N145K* | 1.91 | 0.0 | 0.48 | 0.53 | — |
| K140E | — | — | 1.59 | 1.33 | — |
| K193N* | 1.56 | — | — | — | — |
| H155Y/R189K* | 1.55 | — | — | — | — |
| I186S | 1.54 | — | — | — | — |
| V186G | — | — | — | 0.0 | 1.52 |
| Y155H/K189R* | 1.48 | — | — | — | — |
| K145N* | 0.0 | 0.0 | 1.45 | 1.2 | — |
| S193F/D225N* | — | — | — | 1.4 | — |
| S133D/E156K* | — | 1.37 | — | — | — |
| T135G | — | 1.34 | — | — | — |
| R189S* | 1.28 | 0.93 | — | — | — |
| C3† | 1.27 | — | — | — | — |
| T262N | 1.25 | 0.35 | — | — | — |
| S157L | 0.09 | 0.7 | — | — | 1.23 |
| E190D | 0.0 | 1.21 | — | — | — |
| N121T | — | — | 1.2 | — | — |
| K135T | — | 1.19 | — | — | — |
| K156E/D190E* | 1.18 | — | — | — | — |
| S133D | 1.16 | — | — | — | — |
| T135K | — | 0.0 | 1.16 | — | — |
| K140I | — | — | — | 1.15 | 1.1 |
| Q156H* | — | — | 1.14 | 0.75 | — |
| K62E/N276K | — | — | 1.11 | — | — |
| G186S | — | — | 1.07 | — | — |
| N144K | — | — | — | 1.06 | 0.0 |
| L226V | — | 0.22 | 1.06 | — | — |
| K144D | — | — | — | — | 1.06 |
| M260I | — | — | — | 1.05 | 0.0 |
| F159Y* | — | — | 0.25 | 0.39 | 1.04 |
| S193N* | 1.03 | — | 0.46 | 0.0 | — |
| S189R* | — | 0.98 | — | — | — |
| T212S | — | — | — | — | 0.98 |
| K135E | 0.94 | 0.88 | — | — | — |
| T212A | — | — | — | 0.94 | 0.59 |
| C4*,† | — | — | 0.92 | 0.15 | — |
| K156H* | — | — | 0.91 | — | — |
| R142G | — | — | 0.91 | 0.32 | 0.23 |
| M242I | — | — | 0.91 | — | — |
| Y159F* | — | — | 0.91 | 0.81 | 0.0 |
| I112V/S193F* | — | — | — | — | 0.88 |
| N145S* | — | — | — | 0.21 | 0.88 |
| F159S* | — | — | — | — | 0.88 |
| L157S/S189R* | 0.87 | — | — | — | — |
| S159Y* | 0.0 | — | — | — | 0.85 |
| K144N | — | — | — | — | 0.85 |
When several substitutions always occurred together, a combined effect is shown. Columns involving substitutions at Koel 7 sites are marked with an asterisk. A dash indicates the absence of the substitution in a particular time interval. The substitutions are sorted by the maximum across time intervals.
C1: K62E, V144I, K156Q, E158K, V196A, N276K; C1R: E62K, N121T, S124G, N133D, R142G, I144V, Q156K, K158E, A196V, K276N, i.e., largely the reverse of cluster C1; C2: S124G, N133D, I144V, Q156K, K276N a subset of cluster C1; C3: K82E, E83K, A131T, R299K; C4: I25L, Q75H, T131A, T155H.
By and large, the effects we infer are compatible with those associated with cluster transitions determined in ref. 16. For example, the transition from the Sichuan/87 (SI87) cluster to the Beijing/89 (BE89) cluster involved the substitution N145K, for which we infer an effect of 1.91 antigenic units (each unit is equal to a twofold decrease in HI titer). Together with minor effects associated with N193S, I186S, and G135N, this comes close to the map distance 3.9 units. For the transition from SI87 to Beijing/92 (BE92), the substitution model estimates a distance of 4.5 units that is associated with many almost simultaneous substitutions—hence the exact assignment remains difficult to pin down. The map distance corresponding to this cluster transition is 7.8 units, whereas the typical titer drop is ∼5 units and hence closer to the estimate of the tree or substitution model. The transition from BE92 to Wuhan/95 (WU95) is gradual, with several substitutions of intermediate magnitude. From WU95 to Sydney/97 (SY97), we estimate a distance of ∼3 units of which 2 units are attributed to the set of substitutions: K62E/V144I/K156Q/E158K/V196A/N276K (C1). These substitutions account for 3.6 units in cartography. Lastly, the transition from SY97 to Fujian/02 (FU02) is attributed to Q156H (1.1 units as in ref. 16) and N121T. Most of the distances we infer between clusters are smaller than those estimated in cartography, which is compatible with our finding of overall reduced antigenic drift when modeling antigenic evolution in many dimensions (see below).
The inferred effects of substitutions suggest substantial dependence on genetic background and the specific amino acid change. For HA1 position 145, the back and forth between asparagine (N) and lysine (K) is associated with different effects in 1989–1992, and 2004. Interestingly, the inferred effect of the forward substitutions (N145K in 1989–1992 and K145N in 2004) is large in these instances, whereas the inferred effect for the backward direction is small. Some substitutions at Koel 7 positions have very small effects, such as, for example, S189N. Other substitutions at these positions have large effects but don’t spread. K158R, for example, shows up repeatedly and is associated with a 2-unit titer drop without ever reaching high frequencies. A full table of all inferred effects for substitutions at particular positions in overlapping 10-y intervals is given as Dataset S1 and the 55 largest effects are given in Table S2. However, the interpretation of effects is sometimes difficult due to colinearities between substitutions.
Limitations of the Models.
The tree and substitution model perform similarly in terms of accuracy, as summarized in Table 1, which is expected because branches of the tree are associated with substitutions and vice versa. In particular circumstances, however, one model is more accurate than the other, and the two models complement each other in a number of situations.
The tree model assumes that titers are additive along the tree. Although this is, in general, a reasonable assumption, it is violated when the same amino acid position is mutated multiple times in different parts of the tree. As a recent example, independent substitutions at HA1 position 159 of A(H3N2) viruses define different genetic/antigenic clades: F159Y defining clade 3C.2a and F159S defining clade 3C.3a. The distances between viruses in these clades are not necessarily a sum of the effects associated with the branches separating the clades, because one substitution at position 159 masks the other. In such cases, the substitution model tends to be more accurate, as it has the additional freedom to introduce the Y159S substitution (and the reverse) that directly differentiates viruses in these clades.
Similarly, the substitution model fails when the same substitution (as opposed to different substitutions at the same position) occurred in different places on the tree in different genetic backgrounds, which is common in sequence ensembles covering long time periods. The model will fit a single effect, even though the effect of the substitution might be background-dependent. Furthermore, the substitution model tends to be inaccurate when predicting titers for test viruses that predate the reference virus. Such “back-in-time” measurements are underrepresented in the data, and although the forward substitution might have a large effect assigned, the few back-in-time measurements do not provide enough support to include the reverse substitutions into the model. The tree model does not suffer from this problem, as effects are assumed to be symmetric.
By and large, the models accurately predict measured HI titers (Fig. 2), and deviations affect only isolated clades, typically, when very few measurements are available to constrain the model. The visualization described in Visualization of Antigenic Evolution allows a direct side-by-side comparison of the two models and the measurements, which makes it easy to identify such isolated inaccuracies.
Antigenic Change and the Success of Clades.
Antigenic changes result in viruses able to reinfect individuals with immunity to previously circulating viruses. Intuitively, large antigenic changes should therefore be positively selected for and rapidly spread through the virus population. We investigated the relationship between the amount of antigenic change and success of clades in the phylogenetic tree. Fig. 5 shows frequency trajectories of clades reaching at least 10% at one time, and color indicates the magnitude of the antigenic change that accumulated along the ancestral lineage over the preceding 6 mo. Consistent with expectation, large antigenic changes fix more often than small antigenic changes. However, there are also several clades that evolved antigenically but failed to spread. Extinction of transiently successful clades could be due to fitness cost associated with the substitutions responsible for antigenic change or could be the result of competition of multiple antigenically advanced clades (17–19).
Fig. 5.
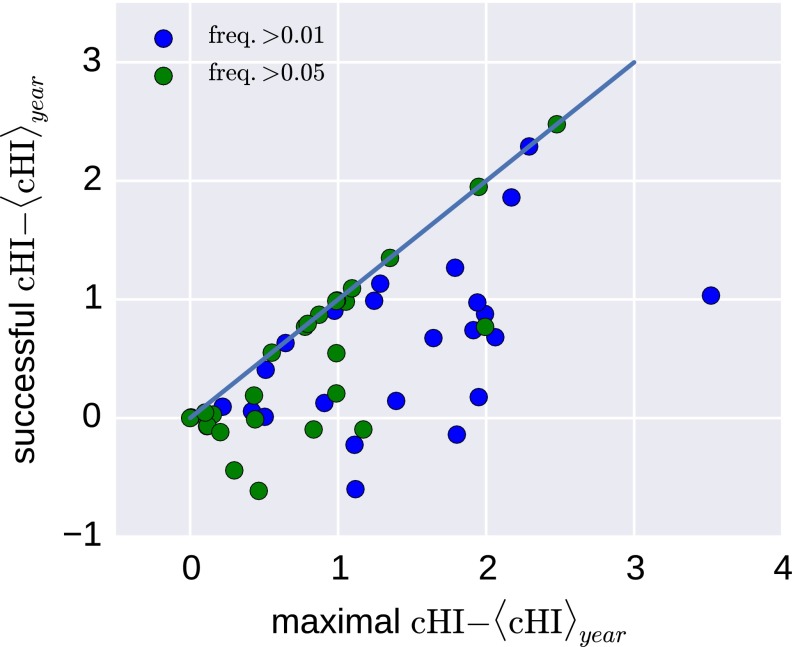
Antigenic evolution and the success of A(H3N2) clades. (A) Trajectories of clades colored by inferred cumulative antigenic evolution in the past 6 mo on branches ancestral to the clade. The majority of the clades with substantial recent antigenic change fix, but several antigenically evolved branches go extinct. B quantifies the power of cumulative antigenic change () to predict clade success. B shows the nucleotide distances of clades with maximal among clades that account for at least 1% and 5% of all viruses. Predictions based on maximal LBI are also shown. Distances are relative to the average distance between present and future populations shown as the dashed line at 1. The solid black line indicates the distances of the best possible pick in each year. Predictions based on maximal LBI and are correlated, but maximal is sensitive to false positives (highest scoring clades that go extinct). (C) Histogram of centered of the clade closest to the next season for each year, suggesting that successful clades tend to be antigenically advanced.
For each season, we determined the clade with highest Local Branching Index [LBI, a predictor of clade success (10)] and the clade with the largest antigenic advancement () relative to all other viruses in a season. We restricted the latter to clades that account for at least 5% of available sequences for the given season. For each of these clades, Fig. 5B shows genetic distance to the virus population of the following season. Antigenic advance as measured by is predictive of which lineage would dominate the following season: The distance to the future population of the most antigenically advanced clade is significantly below the population average (dashed line in Fig. 5B). Predictions by and LBI are comparable in quality and are correlated. However, clades with maximal are sometimes far from the future population, suggesting that a predictor based on antigenic phenotype alone readily generates false positives, i.e., highest scoring clades that go extinct; the problem becomes worse when smaller clades are included (threshold lowered to % of all sequences). Nevertheless, successful clades tend to be antigenically advanced. Fig. 5C shows the distribution of of clades closest to the next season. These clades tend to have larger than cocirculating viruses. These results suggest that correlates with spread of a clade but is not the only factor determining clade success (see also Fig. S3).
Fig. S3.
Success versus antigenic advancement. In many years, the most antigenically advanced clade (highest ) is not the clade dominating the next season. The figure shows the maximally observed centered vs. the centered of the successful clade for each year from 1990 to 2014.
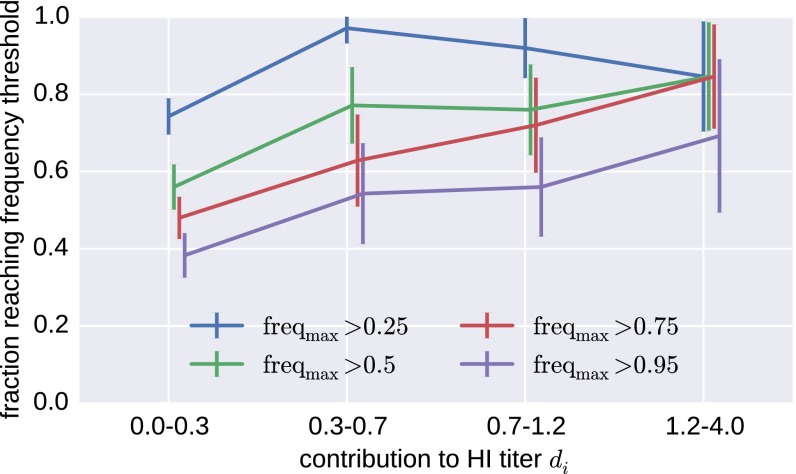
As an alternative to clades in the tree, Fig. 6 shows the probability of a substitution reaching a certain frequency as a function of its inferred antigenic effect. The probability to rise to a high frequency increases with antigenic effect, but even substitutions with very large effect can fail to spread—an effect that limits predictive power. This occasional lack of fixation happens despite the fact that antigenic effects of successful substitutions are more likely to be detected.
Fig. 6.
Substitutions with large antigenic effect fix preferentially. The figure shows the fraction of all substitutions in A(H3N2) that reach the indicated frequency for different magnitudes of the inferred antigenic effect of this substitution. The plot combines data from substitution models fitted to five overlapping 10-y intervals from 1985 to 2015 and contains all substitutions that reach at least 10% population frequency. There are few substitutions in the highest HI category; error bars show SDs of boot strap replicates of substitutions.
Visualization of Antigenic Evolution.
Antigenic evolution can be visualized by mapping titer distances into the plane using a variant of multidimensional scaling (4). This 2D representation, however, is not readily superimposed with the sequence evolution of the viruses. Instead of squeezing the sequence evolution onto the plane (5), we map the HI titer data onto the phylogenetic tree using nextflu (8).
The application nextflu tracks, in near-real time, the evolution of seasonal influenza viruses and allows users to explore recent changes at particular positions, spot rapidly growing clades, and analyze the geographic distribution of viruses. We have integrated the tree and sequence models of titer data into nextflu’s Python-based processing pipeline augur. The titer data and the models are exported along with the tree and visualized using auspice, the JavaScript-based front end of nextflu. The resulting visualization is available at nextflu.org/h3n2/3y/, and Fig. 7 shows a screen shot.
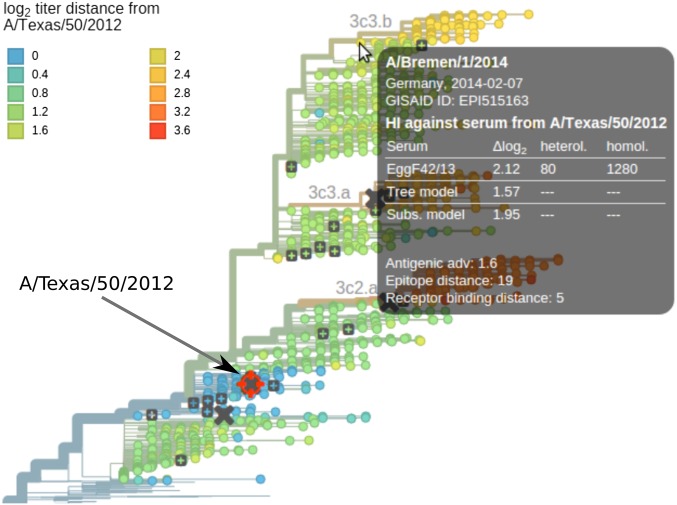
Fig. 7.
Visualization of antigenic evolution on the tree. Tree tips are colored according to the predicted titer distance relative the focal virus (A/Texas/50/2012 in this case). The tool tip shows titers relative to all available antisera and titer predictions as a table. Each reference virus (gray squares) can be chosen by clicking with the mouse, upon which the tree color is updated. Crosses indicate vaccine strains. The tool tip shows all available measurements and the predictions by both models, and the color averages measurements relative to different antisera. Visualizations are available for all seasonal influenza lineages.
This web visualization allows exploration of HI distance relative to specific antisera. All reference viruses against which antisera have been raised are indicated by gray squares. A focal reference virus can be chosen by clicking on one of these squares, thereby coloring the tree according to the average antigenic distance between viruses and antisera raised against the focal virus. Tooltips—information boxes that pop up when the mouse hovers over a virus—display all available measurements along with the predicted titers relative to the focal virus. The normalized and log-scaled titers can be optionally corrected using estimates of antiserum potency and virus avidity.
The tree can be colored either by measured titers (which are available only for a subset of the viruses) or the predictions by either the tree model or the substitution model. Toggling between coloring by measured and predicted titers gives an intuitive visual impression of the noise in titer data and possible inaccuracies of the model predictions.
In addition to titer measurements and titer predictions, the website allows coloring of the tree according to the antigenic evolution that accumulated along branches starting from the root of the tree. The latter is similar to dimension one in antigenic cartography.
Discussion
We have shown that antigenic evolution of seasonal influenza viruses can be accurately predicted from HA sequences using models parameterized by branches separating test and reference virus in a phylogenetic tree or by amino acid substitutions separating the two sequences. Both of these models predict titers with similar or better accuracy than cartographic approaches (4). In addition to prediction of HI titers, the models and the mapping of HI data onto the HA phylogeny provide insight into the structure of antigenic space and allowed us to investigate the relationship between antigenic evolution and clade success.
Previous analyses had concluded that two dimensions provide the optimal embedding for antigenic evolution of human seasonal H3N2 viruses, and adding additional dimensions did not improve the predictive power (4, 5). Here we find that a model based on the tree structure—effectively infinite dimensional—predicts titers with similar or better accuracy. This apparent discrepancy has its roots in the number of parameters necessary to specify the model. A d-dimensional antigenic map of V viruses and S antisera has location parameters. If, in addition to locations, avidities and potencies are inferred, the parameter count increases by . Because the number of parameters increases rapidly with the number of dimensions of the map, the predictive power can decrease at high d due to overfitting. In contrast, the tree model requires only one parameter for every internal branch in the tree (of which there are, at most, ) and parameters for avidities and potencies. In practice, the number of internal branches B is substantially lower than (often severalfold) due to the many polytomies in the tree. For A(H3N2) viruses from the past 12 y, HI data were available for 1,772 out of a total of 2,502 viruses in the tree. Of the 610 internal branches constrained by HI data, 231 branches were inferred to affect HI titers (with effects >0.001). Hence, with substantially fewer parameters, we achieve a better or comparable fit to the data than cartography, which suggests that the phylogenetic tree is a more natural space for antigenic change. We corroborated this interpretation by explicitly testing “treeness” using quartet distances and symmetry between reciprocal measurements (Fig. 4).
We find substantial differences in the overall rate of antigenic evolution across viruses with fast antigenic drift in H3N2 and slow antigenic drift within both influenza B lineages, in agreement with ref. 5. Overall, antigenic drift estimated by our method tends to be somewhat lower, in particular for influenza B. This discrepancy in drift is likely due to the different model space: The phylogenetic tree provides more freedom for different clades to evolve in different directions, and antigenic distances are accommodated on side branches rather than the trunk. On a 2D antigenic map, however, the space for side branches and subclusters is limited, such that more antigenic distance is picked up by the backbone of the map.
Current efforts to predict the evolution and dynamics of seasonal influenza viruses (9–13) are based solely on virus HA sequences. By mapping the phenotypic HI data onto sequences and phylogenetic trees, it should be possible to improve prediction accuracy. Using HI data to predict is, however, not as straightforward as it might seem, and, by itself, it does not predict better than the sequence-based LBI predictor (10). HA substitutions associated with large antigenic changes have a higher probability of fixation, but many causing substantial antigenic change (e.g., K158R) fail to spread in the population. Similarly, in many years, clades that are antigenically more distant from previously circulating viruses die out. The high frequency of such “false positives” interferes with the use of HI measurements for early detection of emerging strains that are the likely founders of future generations of the virus. We observe substantial false positives at the 1% clade frequency level, but fewer false positives at the 5% frequency level (Fig. 5B). However, using a 5% frequency threshold results in the loss of much of the early detection capacity, limiting HI-based prediction to the regime accessible to the sequence-based genealogy approaches, such as LBI.
The main challenge is hence to find a way to reduce the false positive rate in HI-based prediction. Success of strains with smaller HA antigenic advancement over the ones with a larger advancement could be rationalized in two ways: (i) by some alternative improvement of infectivity, immune system avoidance, or lower mutational load or (ii) by a fitness cost associated with a large antigenic effect substitutions. Competition between clades in terms of antigenic advancement and mutational load has been demonstrated in computational models (18) and is the basis of recent efforts to predict influenza virus evolution (9). Supporting the second scenario, it is known that adaptive mutations are sometimes not tolerated in certain genetic backgrounds because they destabilize the encoded protein and further stabilizing mutations are required to compensate for the loss of virus fitness (17, 20) and have also been studied in computational models (19). Better understanding of the context dependence of large antigenic effect HA substitutions may therefore be a promising path toward reducing the false positive rate and improving prediction capacity. The problem of false positive detection is also seen at the Koel 7 positions: Although most past dramatic changes in antigenic phenotype are associated with substitutions at these positions, they do not always have antigenic effects and/or may fail to spread. Hence Koel 7 substitutions alone are poor predictors of clade success.
In conclusion, our study demonstrates that HI data integrate naturally onto the sequence-derived phylogeny of the virus. Although, at present, HI-based prediction does not outperform sequence-based methods, better understanding of genetic context dependence of HI data may provide a path toward improved performance. Characterizing HA substitutions that have historically been associated with antigenic transitions and placing HI data directly into genealogical context may also help with optimizing targeted acquisition of HI data.
Materials and Methods
Data HA Sequences of Influenza.
A and B viruses isolated from humans were downloaded from the Global Initiative on Sharing Avian Influenza Data (GISAID). Accession numbers of all sequences are provided as Datasets S2−S5. We collected HI data from references (4, 21, 22) and annual and interim reports of the WHO CC London between 2002 and 2015 (23–35). HI data before 2011 were curated in ref. 5. Original HI data tables are available from the website of the Worldwide Influenza Centre at the Francis Crick Institute at https://www.crick.ac.uk/research/worldwide-influenza-centre/annual-and-interim-reports/.
Although the modalities of HI assays have changed over the years (red blood cells from different species, addition of NA inhibitors, etc.), we find that the model describes data spanning many years with reasonable accuracy. This insensitivity of the model is likely due to the fact that differences in HI assay methodologies can largely be absorbed in the model terms for antiserum potency and virus avidity. However, the most recent data, largely provided by WHO CC London, are modeled with greater accuracy.
Data Processing and Model Fit.
The data processing pipeline is based on nextflu (8), which subsamples viruses, aligns sequences, and builds a phylogenetic tree. To make use of as much HI data as possible, viruses that are antigenically characterized were preferentially included. This pipeline was modified for the current purpose to enforce the inclusion of all strains for which antigenic data were available. Then, in addition to the standard “augur” pipeline of nextflu, the tree and substitution models were fitted to the HI data as follows.
For each combination of virus i and antiserum α, we define standardized log titer as , where is the titer of antiserum to reference virus b required to inhibit virus a and is the homologous titer. In case multiple measurements are available, we average the standardized log titers. When no homologous titer is available, the maximal titer is used as a proxy for the homologous titer. The path between test virus a and reference virus b extends over branches of the phylogeny , where each branch makes a contribution . Our model of HI titers between viruses a and serum β is defined in Eq. 1. The parameters , , and are then estimated by minimizing the cost function
| [2] |
subject to the constraints . To avoid overfitting, the different parameters of the model are regularized by the last three terms in Eq. 2. Large titer drops are penalized with their absolute value multiplied by λ ( regularization), which results in a sparse model in which most branches have no titer drop (36). Similarily, the antiserum and virus avidities are -regularized by γ and δ, penalizing very large values without enforcing sparsity. This constrained minimization can be cast into a canonical convex optimization problem and solved efficiently; see below. In the substitution model, the sum over the path in the tree is replaced by a sum over amino acid differences in HA1. Sets of substitutions that always occur together are merged and treated as one compound substitution. The inference of the substitution model parameters is done in the same way as for the tree model (see refs. 6 and 7 for a similar approach). Because there are only a small number of antisera and differences in antiserum potency are often on the order of one or two antigenic units, δ was assigned a small value of 0.2; was used to regularize branch or substitution, and for virus effects. The quality of the fit depends weakly on these parameters.
The total numbers of adjustable parameters are S antiserum potencies, V avidities of viruses, and M internal branches of the tree, of which there are, at most, , but typically fewer due to many polytomies in the trees. In practice, only a fraction of the branches have nonzero branch effects, and the total number of nonzero parameters is not much larger than the number of test viruses. In the substitution model, the number of nonsingleton substitutions found in an HA1 alignment is typically on the order of 100, most of which are inferred to have no antigenic effect.
This optimization of Eq. 2 can be cast into a canonical quadratic programming problem of the form
| [3] |
where is the vector of unknowns, and the matrix and the vector specify the cost function. The matrix and the vector encode inequality constraints on .
To formulate Eq. 2 in this canonical form, we concatenate the titer drops associated with internal branches i of the tree, the potencies of each antiserum, and avidities of virus isolates into a single vector ,
| [4] |
where B are the number of branches in the tree connecting measurements, V is the number of viruses with titer measurements, and S are the number of antisera. Next, we construct a large binary matrix of dimension , where N is the total number of measurements. Each row of the matrix codes for a titer prediction . Using the double index to label measurements, entries of are given by
| [5] |
i.e., for all s that correspond to a branch of the path , the virus avidity , and the antiserum potency ; otherwise, . All titer predictions of Eq. 1 are hence given by
| [6] |
where is the vector of parameters.
Using these definitions, the cost function Eq. 2 can be written as
| [7] |
subject to for . Dropping constant terms and defining
| [8] |
we have
| [9] |
To enfore the regularization and the positivity of the titer drops corresponding to , , we define inequality constraints
| [10] |
for , which forces all titer drops to be positive. In addition, we set
| [11] |
and add λ to to penalize large effects. With these definitions, we have cast Eq. 2 in the form of Eq. 3. The resulting quadratic programming problem is then solved with cvxopt by M. Andersen and L. Vandenberghe.
The HI titer data and the inferred model parameters are integrated into the json data structure describing the tree or saved in an additional data file for later visualization using auspice.
Visualization.
The HI titer coloring and tool tips is implemented via straightforward extension of nextflu’s visualization software auspice. In addition to the standard nextflu tree display, a structure showing the positions at which the substitution model inferred large contribution to antigenic change are shown on the pages for each individual virus lineage. The structures are visualized with JSmol (37). For H3N2, we use structure 5HMG (38); for H1N1pdm, we use 4LXV (39); and, for the influenza B Victoria and Yamagata lineages, we use 4FQM (40) and 4M40 (41). The structure visualization is available at hi.nextflu.org/H3N2/3y/.
SI Text
We acknowledge the authors and originating and submitting laboratories of the sequences from GISAID’s EpiFlu Database on which this research is based. The laboratories and institutions are as follows: WHO Collaborating Centre for Reference and Research on Influenza, Victorian Infectious Diseases Reference Laboratory, Australia; WHO Collaborating Centre for Reference and Research on Influenza, Chinese National Influenza Center, China; WHO Collaborating Centre for Reference and Research on Influenza, National Institute of Infectious Diseases, Japan; WHO Collaborating Centre for Reference and Research on Influenza, National Institute for Medical Research, United Kingdom; WHO Collaborating Centre for the Surveillance, Epidemiology and Control of Influenza, Centers for Disease Control and Prevention, United States; ADImmune Corporation, Taiwan; ADPH Bureau of Clinical Laboratories, United States; Aichi Prefectural Institute of Public Health, Japan; Akershus University Hospital, Norway; Akita Research Center for Public Health and Environment, Japan; Alabama State Laboratory, United States; Alaska State Public Health Laboratory, United States; Alaska State Virology Laboratory, United States; Aomori Prefectural Institute of Public Health and Environment, Japan; Aristotelian University of Thessaloniki, Greece; Arizona Department of Health Services, United States; Arkansas Children's Hospital, United States; Arkansas Department of Health, United States; Auckland Healthcare, New Zealand; Auckland Hospital, New Zealand; Austin Health, Australia; Baylor College of Medicine, United States; California Department of Health Services, United States; Canberra Hospital, Australia; Cantacuzino Institute, Romania; Canterbury Health Services, New Zealand; Caribbean Epidemiology Center, Trinidad and Tobago; CDC GAP Nigeria, Nigeria; CDC-Kenya, Kenya; CEMIC University Hospital, Argentina; CENETROP, Plurinationial State of Bolivia; Center for Disease Control, Taiwan; Center for Public Health and Environment, Hiroshima Prefectural Technology Research Institute, Japan; Central Health Laboratory, Mauritius; Central Laboratory of Public Health, Paraguay; Central Public Health Laboratory, Ministry of Health, Oman; Central Public Health Laboratory, Palestinian Territory; Central Public Health Laboratory, Papua New Guinea; Central Research Institute for Epidemiology, Russian Federation; Centre for Diseases Control and Prevention, Armenia; Centre for Infections, Health Protection Agency, United Kingdom; Centre Pasteur du Cameroun, Cameroon; Chiba City Institute of Health and Environment, Japan; Chiba Prefectural Institute of Public Health, Japan; Childrens Hospital Westmead, Australia; Chuuk State Hospital, Federated States of Micronesia; City of El Paso Department of Public Health, United States; Clinical Virology Unit, CDIM, Australia; Colorado Department of Health Laboratory, United States; Connecticut Department of Public Health, United States; Contiguo a Hospital Rosales, El Salvador; Croatian Institute of Public Health, Croatia; CRR Virus Influenza Region Sud, France; CRR Virus Influenza Region Sud, Guyana; CSL Ltd., United States; Dallas County Health and Human Services, United States; DC Public Health Laboratory, United States; Delaware Public Health Laboratory, United States; Departamento de Laboratorio de Salud Publica, Uruguay; Department of Virology, Medical University Vienna, Austria; Disease Investigation Centre Wates, Australia; Drammen Hospital/Vestreviken HF, Norway; Ehime Prefecture Institute of Public Health and Environmental Science, Japan; Erasmus Medical Center, Netherlands; Erasmus University of Rotterdam, Netherlands; Ethiopian Health and Nutrition Research Institute, Ethiopia; Evanston Hospital and NorthShore University, United States; Facultad de Medicina, Spain; Fiji Centre for Communicable Disease Control, Fiji; Florida Department of Health, United States; Fukui Prefectural Institute of Public Health, Japan; Fukuoka City Institute for Hygiene and the Environment, Japan; Fukuoka Institute of Public Health and Environmental Sciences, Japan; Fukushima Prefectural Institute of Public Health, Japan; Gart Naval General Hospital, United Kingdom; Georgia Public Health Laboratory, United States; Gifu Municipal Institute of Public Health, Japan; Gifu Prefectural Institute of Health and Environmental Sciences, Japan; Government Virus Unit, Hong Kong; Gunma Prefectural Institute of Public Health and Environmental Sciences, Japan; Hamamatsu City Health Environment Research Center, Japan; Haukeland University Hospital, Department of Microbiology, Norway; Headquarters British Gurkhas Nepal, Nepal; Health Forde, Department of Microbiology, Norway; Health Protection Agency, United Kingdom; Health Protection Inspectorate, Estonia; Hellenic Pasteur Institute, Greece; Hiroshima City Institute of Public Health, Japan; Hokkaido Institute of Public Health, Japan; Hopital Cantonal Universitaire de Geneves, Switzerland; Hopital Charles Nicolle, Tunisia; Hospital Clinic de Barcelona, Spain; Hospital Universitari Vall d'Hebron, Spain; Houston Department of Health and Human Services, United States; Hyogo Prefectural Institute of Public Health and Consumer Sciences, Japan; Ibaraki Prefectural Institute of Public Health, Japan; Illinois Department of Public Health, United States; Indiana State Department of Health Laboratories, United States; Infectology Center of Latvia, Latvia; Innlandet Hospital Trust, Division Lillehammer, Department for Microbiology, Norway; INSA National Institute of Health Portugal, Portugal; Institut National d'Hygiene, Morocco; Institut Pasteur d'Algerie, Algeria; Institut Pasteur de Dakar, Senegal; Institut Pasteur de Madagascar, Madagascar; Institut Pasteur in Cambodia, Cambodia; Institut Pasteur New Caledonia, New Caledonia; Institut Pasteur, France; Institut Pasteur, Saudi Arabia; Institut Penyelidikan Perubatan, Malaysia; Institute National D'Hygiene, Togo; Institute of Environmental Science and Research, New Zealand; Institute of Environmental Science and Research, Tonga; Institute of Epidemiology and Infectious Diseases, Ukraine; Institute of Epidemiology Disease Control and Research, Bangladesh; Institute of Immunology and Virology Torlak, Serbia; Institute of Medical and Veterinary Science, Australia; Institute of Public Health, Serbia; Institute of Public Health, Albania; Institute of Public Health, Montenegro; Institute Pasteur du Cambodia, Cambodia; Instituto Adolfo Lutz, Brazil; Instituto Conmemorativo Gorgas de Estudios de la Salud, Panama; Instituto de Salud Carlos III, Spain; Instituto de Salud Publica de Chile, Chile; Instituto Nacional de Enfermedades Infecciosas, Argentina; Instituto Nacional de Higiene Rafael Rangel, Venezuela, Bolivia; Instituto Nacional de Laboratoriosde Salud, Bolivia; Instituto Nacional de Salud de Columbia, Colombia; Instituto Nacional de Saude, Portugal; Iowa State Hygienic Laboratory, United States; IRSS, Burkina Faso; Ishikawa Prefectural Institute of Public Health and Environmental Science, Japan; ISS, Italy; Istanbul University, Turkey; Istituto Superiore di Sanità, Italy; Ivanovsky Research Institute of Virology RAMS, Russian Federation; Jiangsu Provincial Center for Disease Control and Prevention, China; John Hunter Hospital, Australia; Kagawa Prefectural Research Institute for Environmental Sciences and Public Health, Japan; Kagoshima Prefectural Institute for Environmental Research and Public Health, Japan; Kanagawa Prefectural Institute of Public Health, Japan; Kansas Department of Health and Environment, United States; Kawasaki City Institute of Public Health, Japan; Kentucky Division of Laboratory Services, United States; Kitakyusyu City Institute of Enviromental Sciences, Japan; Kobe Institute of Health, Japan; Kochi Public Health and Sanitation Institute, Japan; Kumamoto City Environmental Research Center, Japan; Kumamoto Prefectural Institute of Public Health and Environmental Science, Japan; Kyoto City Institute of Health and Environmental Sciences, Japan; Kyoto Prefectural Institute of Public Health and Environment, Japan; Laboratoire National de Sante Publique, Haiti; Laboratoire National de Sante, Luxembourg; Laboratório Central do Estado do Paraná, Brazil; Laboratorio Central do Estado do Rio de Janeiro, Brazil; Laboratorio de Investigacion/Centro de Educacion Medica y Amistad Dominico Japones, Dominican Republic; Laboratorio De Saude Publico, Macao; Laboratorio de Virologia, Direccion de Microbiologia, Nicaragua; Laboratorio de Virus Respiratorio, Mexico; Laboratorio Nacional de Influenza, Costa Rica; Laboratorio Nacional De Salud Guatemala, Guatemala; Laboratorio Nacional de Virologia, Honduras; Laboratory Directorate, Jordan; Laboratory for Virology, National Institute of Public Health, Slovenia; Laboratory of Influenza and ILI, Belarus; Laboratório Central de Saúde Pública do Rio Grande do Sul, Brazil; Landspitali - University Hospital, Iceland; Lithuanian AIDS Center Laboratory, Lithuania; Los Angeles Quarantine Station, CDC Quarantine Epidemiology and Surveillance Team, United States; Louisiana Department of Health and Hospitals, United States; Maine Health and Environmental Testing Laboratory, United States; Malbran, Argentina; Marshfield Clinic Research Foundation, United States; Maryland Department of Health and Mental Hygiene, United States; Massachusetts Department of Public Health, United States; Mater Dei Hospital, Malta; Medical Research Institute, Sri Lanka; Medical University Vienna, Austria; Melbourne Pathology, Australia; Michigan Department of Community Health, United States; Mie Prefecture Health and Environment Research Institute, Japan; Mikrobiologisk Laboratorium, Sykehuset i Vestfold, Norway; Ministry of Health and Population, Egypt; Ministry of Health of Ukraine, Ukraine; Ministry of Health, Bahrain; Ministry of Health, Kiribati; Ministry of Health, Lao, People's Democratic Republic; Ministry of Health, NIHRD, Indonesia; Ministry of Health, Oman; Minnesota Department of Health, United States; Mississippi Public Health Laboratory, United States; Missouri Department. of Health & Senior Services, United States; Miyagi Prefectural Institute of Public Health and Environment, Japan; Miyazaki Prefectural Institute for Public Health and Environment, Japan; Molde Hospital, Laboratory for Medical Microbiology, Norway; Molecular Diagnostics Unit, United Kingdom; Monash Medical Centre, Australia; Montana Laboratory Services Bureau, United States; Montana Public Health Laboratory, United States; Nagano City Health Center, Japan; Nagano Environmental Conservation Research Institute, Japan; Nagoya City Public Health Research Institute, Japan; Nara Prefectural Institute for Hygiene and Environment, Japan; National Center for Communicable Diseases, Mongolia; National Center for Laboratory and Epidemiology, Laos; National Centre for Disease Control, Mongolia; National Centre for Disease Control and Public Health, Georgia; National Centre for Preventive Medicine, Republic of Moldova; National Centre for Scientific Services for Virology and Vector Borne Diseases, Fiji; National Health Laboratory, Japan; National Health Laboratory, Myanmar; National Influenza Center French Guiana and French Indies, French Guiana; National Influenza Center, Brazil; National Influenza Center, Mongolia; National Influenza Centre for Northern Greece, Greece; National Influenza Centre of Iraq, Iraq; National Influenza Laboratory, United Republic of Tanzania; National Influenza Reference Laboratory, Nigeria; National Insitut of Hygien, Morocco; National Institute for Biological Standards and Control, United States; National Institute for Communicable Disease, South Africa; National Institute for Health and Welfare, Finland; National Institute of Health Research and Development, Indonesia; National Institute of Health, Republic of Korea; National Institute of Health, Pakistan; National Institute of Hygiene and Epidemiology, Vietnam; National Institute of Public Health - National Institute of Hygiene, Poland; National Institute of Public Health, Czech Republic; National Institute of Virology, India; National Microbiology Laboratory, Health Canada, Canada; National Public Health Institute of Slovakia, Slovakia; National Public Health Laboratory, Cambodia; National Public Health Laboratory, Ministry of Health, Singapore, Singapore; National Public Health Laboratory, Nepal; National Public Health Laboratory, Singapore; National Reference Laboratory, Kazakhstan; National University Hospital, Singapore; National Virology Laboratory, Center Microbiological Investigations, Kyrgyzstan; National Virus Reference Laboratory, Ireland; Naval Health Research Center, United States; Nebraska Public Health Laboratory, United States; Nevada State Health Laboratory, United States; New Hampshire Public Health Laboratories, United States; New Jersey Department of Health & Senior Services, United States; New Mexico Department of Health, United States; New York City Department of Health, United States; New York Medical College, United States; New York State Department of Health, United States; Nicosia General Hospital, Cyprus; Niigata City Institute of Public Health and Environment, Japan; Niigata Prefectural Institute of Public Health and Environmental Sciences, Japan; Niigata University, Japan; Nordlandssykehuset, Norway; North Carolina State Laboratory of Public Health, United States; North Dakota Department of Health, United States; Norwegian Institute of Public Health, Norway; Ohio Department of Health Laboratories, United States; Oita Prefectural Institute of Health and Environment, Japan; Okayama Prefectural Institute for Environmental Science and Public Health, Japan; Okinawa Prefectural Institute of Health and Environment, Japan; Oklahoma State Department of Health, United States; Ontario Agency for Health Protection and Promotion, Canada; Oregon Public Health Laboratory, United States; Osaka City Institute of Public Health and Environmental Sciences, Japan; Osaka Prefectural Institute of Public Health, Japan; Oslo University Hospital, Ulleval Hospital, Department of Microbiology, Norway; Ostfold Hospital - Fredrikstad, Department of Microbiology, Norway; Oswaldo Cruz Institute - FIOCRUZ - Laboratory of Respiratory Viruses and Measles, Brazil; Papua New Guinea Institute of Medical Research, Papua New Guinea; Pasteur Institut of Cote d'Ivoire, Cote d'Ivoire; Pasteur Institute, Influenza Laboratory, Vietnam; Pathwest QE II Medical Centre, Australia; Pennsylvania Department of Health, United States; Prince of Wales Hospital, Australia; Princess Margaret Hospital for Children, Australia; Public Health Laboratory Services Branch, Centre for Health Protection, Hong Kong; Public Health Laboratory, Barbados; Puerto Rico Department of Health, Puerto Rico; Qasya Diagnostic Services Sdn Bhd, Brunei; Queensland Health Scientific Services, Australia; Refik Saydam National Public Health Agency, Turkey; Regent Seven Seas Cruises, United States; Royal Victoria Hospital, United Kingdom; Republic Institute for Health Protection, the former Yogoslav Republic of Macedonia; Republic of Nauru Hospital, Nauru; Research Institute for Environmental Sciences and Public Health of Iwate Prefecture, Japan; Research Institute of Tropical Medicine, Philippines; Rhode Island Department of Health, United States; RIVM National Institute for Public Health and Environment, The Netherlands; Robert-Koch-Institute, Germany; Royal Chidrens Hospital, Australia; Royal Darwin Hospital, Australia; Royal Hobart Hospital, Australia; Royal Melbourne Hospital, Australia; Russian Academy of Medical Sciences, Russian Federation; Rwanda Biomedical Center, National Reference Laboratory, Rwanda; Saga Prefectural Institute of Public Health and Pharmaceutical Research, Japan; Sagamihara City Laboratory of Public Health, Japan; Saitama City Institute of Health Science and Research, Japan; Saitama Institute of Public Health, Japan; Sakai City Institute of Public Health, Japan; San Antonio Metropolitan Health, United States; Sapporo City Institute of Public Health, Japan; Scientific Institute of Public Health, Belgium; Seattle & King County Public Health Laboratory, United States; Sendai City Institute of Public Health, Japan; Servicio de Microbiología Clínica Universidad de Navarra, Spain; Servicio de Microbiología Complejo Hospitalario de Navarra, Spain; Servicio de Microbiología Hospital Central Universitario de Asturias, Spain; Servicio de Microbiología Hospital Donostia, Spain; Servicio de Microbiología Hospital Meixoeiro, Spain; Servicio de Microbiología Hospital Miguel Servet, Spain; Servicio de Microbiología Hospital Ramón y Cajal, Spain; Servicio de Microbiología Hospital San Pedro de Alcántara, Spain; Servicio de Microbiología Hospital Santa María Nai, Spain; Servicio de Microbiología Hospital Universitario de Gran Canaria Doctor Negrín, Spain; Servicio de Microbiología Hospital Universitario Son Espases, Spain; Servicio de Microbiología Hospital Virgen de la Arrixaca, Spain; Servicio de Microbiología Hospital Virgen de las Nieves, Spain; Servicio de Virosis Respiratorias INEI-ANLIS Carlos G. Malbran, Argentina; Shiga Prefectural Institute of Public Health, Japan; Shimane Prefectural Institute of Public Health and Environmental Science, Japan; Shizuoka City Institute of Environmental Sciences and Public Health, Japan; Shizuoka Institute of Environment and Hygiene, Japan; Singapore General Hospital, Singapore; Sorlandet Sykehus HF, Department of Medical Microbiology, Norway; South Carolina Department of Health, United States; South Dakota Public Health Laboratory, United States; Southern Nevada Public Health Laboratory, United States; Spokane Regional Health District, United States; St. Judes Childrens Research Hospital, United States; St. Olavs Hospital HF, Department of Medical Microbiology, Norway; State Agency, Infectology Center of Latvia, Latvia; State of Hawaii Department of Health, United States; State of Idaho Bureau of Laboratories, United States; State Research Center of Virology and Biotechnology Vector, Russian Federation; Statens Serum Institute, Denmark; Stavanger Universitetssykehus, Avdeling for Medisinsk Mikrobiologi, Norway; Subdireccion General de Epidemiologia y Vigilancia de la Salud, Spain; Subdirección General de Epidemiología y Vigilancia de la Salud, Spain; Swedish Institute for Infectious Disease Control, Sweden; Swedish National Institute for Communicable Disease Control, Sweden; Taiwan CDC, Taiwan; Tan Tock Seng Hospital, Singapore; Tehran University of Medical Sciences, Iran; Tennessee Department of Health Laboratory-Nashville, United States; Texas Childrens Hospital, United States; Texas Department of State Health Services, United States; Thai National Influenza Center, Thailand; Thailand MOPH-US CDC Collaboration, Thailand; The Nebraska Medical Center, United States; Tochigi Prefectural Institute of Public Health and Environmental Science, Japan; Tokushima Prefectural Centre for Public Health and Environmental Sciences, Japan; Tokyo Metropolitan Institute of Public Health, Japan; Tottori Prefectural Institute of Public Health and Environmental Science, Japan; Toyama Institute of Health, Japan; U.S. Air Force School of Aerospace Medicine, United States; US Naval Medical Research Unit No. 3, Egypt; Uganda Virus Research Institute, National Influenza Center, Uganda; Universidad de Valladolid, Spain; Università Cattolica del Sacro Cuore, Italy; Universitetssykehuset Nord-Norge HF, Norway; University Malaya, Malaysia; University of Florence, Italy; University of Genoa, Italy; University of Ghana, Ghana; University of Michigan SPH EPID, United States; University of Parma, Italy; University of Perugia, Italy; University of Pittsburgh Medical Center Microbiology Laboratory, United States; University of Sarajevo, Bosnia and Herzegovina; University of Sassari, Italy; University of the West Indies, Jamaica; University of Vienna, Austria; University of Virginia, Medical Labs/Microbiology, United States; University Teaching Hospital, Zambia; UPMC-CLB Department of Microbiology, United States; US Army Medical Research Unit - Kenya, GEIS Human Influenza Program, Kenya; USAMC-AFRIMS Department of Virology, Cambodia; Utah Department of Health, United States; Utah Public Health Laboratory, United States; Utsunomiya City Institute of Public Health and Environment Science, Japan; VACSERA, Egypt; Vermont Department of Health Laboratory, United States; Victorian Infectious Diseases Reference Laboratory, Australia; Virginia Division of Consolidated Laboratories, United States; Wakayama City Institute of Public Health, Japan; Wakayama Prefectural Research Center of Environment and Public Health, Japan; Washington State Public Health Laboratory, United States; West Virginia Office of Laboratory Services, United States; Westchester County Department of Laboratories & Research, United States; Westmead Hospital, Australia; WHO National Influenza Centre Russian Federation, Russian Federation; WHO National Influenza Centre, National Institute of Medical Research, Thailand; WHO National Influenza Centre, Norway; Wisconsin State Laboratory of Hygiene, United States; Wyoming Public Health Laboratory, United States; Yamagata Prefectural Institute of Public Health, Japan;Yamaguchi Prefectural Institute of Public Health and Environment, Japan; Yamanashi Institute for Public Health, Japan; Yap State Hospital, Micronesia; Yokohama City Institute of Health, Japan; and Yokosuka Institute of Public Health, Japan.
Supplementary Material
Acknowledgments
We are grateful to John McCauley for making HI titer data available and for valuable feedback on this manuscript. We also acknowledge the researchers at the originating and submitting laboratories who generated the sequence data, downloaded from Global Initiative on Sharing Avian Influenza Data’s (GISAID) EpiFlu Database, on which this research is based. We gratefully acknowledge the network of World Health Organization (WHO) National Influenza Centres, comprising the WHO Global Influenza Surveillance and Response System (GISRS), for providing the influenza viruses used in this study and the WHO CCs that produced the wealth of HI titer data analyzed here. The work of the WIC (RSD) was supported by the Medical Research Council under Programme U117512723. A full list of all laboratories that contributed to the data used here is available at nextflu.org/acknowledgements/ and in SI Text. This work is supported by the ERC though Stg-260686, by the NIH through U54 GM111274, by the Simons Foundation Grant 326844, and by a University Research Fellowship from the Royal Society.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1525578113/-/DCSupplemental.
References
- 1.Hay AJ, Gregory V, Douglas AR, Lin YP. The evolution of human influenza viruses. Philos Trans R Soc Lond B Biol Sci. 2001;356(1416):1861–1870. doi: 10.1098/rstb.2001.0999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Barr IG, et al. Writing Committee of the World Health Organization Consultation on Northern Hemisphere Influenza Vaccine Composition for 2013–2014 WHO recommendations for the viruses used in the 2013-2014 Northern Hemisphere influenza vaccine: Epidemiology, antigenic and genetic characteristics of influenza A(H1N1)pdm09, A(H3N2) and B influenza viruses collected from October 2012 to January 2013. Vaccine. 2014;32(37):4713–4725. doi: 10.1016/j.vaccine.2014.02.014. [DOI] [PubMed] [Google Scholar]
- 3.Hirst GK. The quantitative determination of influenza virus and antibodies by means of red cell agglutination. J Exp Med. 1942;75(1):49–64. doi: 10.1084/jem.75.1.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Smith DJ, et al. Mapping the antigenic and genetic evolution of influenza virus. Science. 2004;305(5682):371–376. doi: 10.1126/science.1097211. [DOI] [PubMed] [Google Scholar]
- 5.Bedford T, et al. Integrating influenza antigenic dynamics with molecular evolution. eLife. 2014;3:e01914. doi: 10.7554/eLife.01914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Harvey WT, et al. 2014. Identifying the genetic basis of antigenic change in influenza A(H1n1). arXiv:1404.4197.
- 7.Sun H, et al. Using sequence data to infer the antigenicity of influenza virus. MBio. 2013;4(4):e00230-–13. doi: 10.1128/mBio.00230-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Neher RA, Bedford T. nextflu: Real-time tracking of seasonal influenza virus evolution in humans. Bioinformatics. 2015;31(21):3546–3548. doi: 10.1093/bioinformatics/btv381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Łuksza M, Lässig M. A predictive fitness model for influenza. Nature. 2014;507(7490):57–61. doi: 10.1038/nature13087. [DOI] [PubMed] [Google Scholar]
- 10.Neher RA, Russell CA, Shraiman BI. Predicting evolution from the shape of genealogical trees. eLife. 2014;3:e03568. doi: 10.7554/eLife.03568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Steinbrück L, McHardy AC. Allele dynamics plots for the study of evolutionary dynamics in viral populations. Nucleic Acids Res. 2011;39(1):e4. doi: 10.1093/nar/gkq909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.He J, Deem MW. Low-dimensional clustering detects incipient dominant influenza strain clusters. Protein Eng Des Sel. 2010;23(12):935–946. doi: 10.1093/protein/gzq078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Steinbrück L, Klingen TR, McHardy AC. Computational prediction of vaccine strains for human influenza A (H3n2) viruses. J Virol. 2014;88(20):12123–12132. doi: 10.1128/JVI.01861-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shih ACC, Hsiao TC, Ho MS, Li WH. Simultaneous amino acid substitutions at antigenic sites drive influenza A hemagglutinin evolution. Proc Natl Acad Sci USA. 2007;104(15):6283–6288. doi: 10.1073/pnas.0701396104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Muñoz ET, Deem MW. Epitope analysis for influenza vaccine design. Vaccine. 2005;23(9):1144–1148. doi: 10.1016/j.vaccine.2004.08.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Koel BF, et al. Substitutions near the receptor binding site determine major antigenic change during influenza virus evolution. Science. 2013;342(6161):976–979. doi: 10.1126/science.1244730. [DOI] [PubMed] [Google Scholar]
- 17.Gong LI, Suchard MA, Bloom JD. Stability-mediated epistasis constrains the evolution of an influenza protein. eLife. 2013;2:e00631. doi: 10.7554/eLife.00631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Koelle K, Rasmussen DA. The effects of a deleterious mutation load on patterns of influenza A/H3n2’s antigenic evolution in humans. eLife. 2015;4:e07361. doi: 10.7554/eLife.07361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kucharski A, Gog JR. Influenza emergence in the face of evolutionary constraints. Proc R Soc Lond B Biol Sci. 2012;279(1729):645–652. doi: 10.1098/rspb.2011.1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Thyagarajan B, Bloom JD. The inherent mutational tolerance and antigenic evolvability of influenza hemagglutinin. eLife. 2014;3:e03300. doi: 10.7554/eLife.03300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Russell CA, et al. The global circulation of seasonal influenza A (H3N2) viruses. Science. 2008;320(5874):340–346. doi: 10.1126/science.1154137. [DOI] [PubMed] [Google Scholar]
- 22.Barr IG, et al. Writing Committee of the World Health Organization Consultation on Northern Hemisphere Influenza Vaccine Composition for 2009-2010 Epidemiological, antigenic and genetic characteristics of seasonal influenza A(H1N1), A(H3N2) and B influenza viruses: basis for the WHO recommendation on the composition of influenza vaccines for use in the 2009-2010 northern hemisphere season. Vaccine. 2010;28(5):1156–1167. doi: 10.1016/j.vaccine.2009.11.043. [DOI] [PubMed] [Google Scholar]
- 23.Hay AJ, Lin YP, Gregory V, Bennet M. Annual Report. Natl Inst Med Res; London: 2002. [Google Scholar]
- 24.Hay A, et al. Characteristics of Human Influenza AH1N1, AH3N2, and B Viruses Isolated September 2007 to February 2008. Natl Inst Med Res; London: 2008. [Google Scholar]
- 25.Hay A, et al. Antigenic and Genetic Characteristics of Human Influenza A(H1N1), A(H3N2) and B Viruses Isolated During October 2008 to February 2009. Natl Inst Med Res; London: 2009. [Google Scholar]
- 26.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Northern Hemisphere. Natl Inst Med Res; London: 2010. [Google Scholar]
- 27.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Southern Hemisphere. Natl Inst Med Res; London: 2010. [Google Scholar]
- 28.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Southern Hemisphere. Natl Inst Med Res; London: 2011. [Google Scholar]
- 29.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Northern Hemisphere. Natl Inst Med Res; London: 2012. [Google Scholar]
- 30.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Southern Hemisphere. Natl Inst Med Res; London: 2012. [Google Scholar]
- 31.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Northern Hemisphere. Natl Inst Med Res; London: 2013. [Google Scholar]
- 32.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Southern Hemisphere. Natl Inst Med Res; London: 2013. [Google Scholar]
- 33.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Northern Hemisphere. Natl Inst Med Res; London: 2014. [Google Scholar]
- 34.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Southern Hemisphere. Natl Inst Med Res; London: 2014. [Google Scholar]
- 35.McCauley J, et al. Report Prepared for the WHO Annual Consultation on the Composition of Influenza Vaccine for the Northern Hemisphere. Natl Inst Med Res; London: 2015. [Google Scholar]
- 36.Candes E, Tao T. Decoding by linear programming. IEEE Trans Inf Theory. 2005;51(12):4203–4215. [Google Scholar]
- 37. JSmol Developers (2015) JSmol: An open-source HTML5 viewer for chemical structures in 3D. Available at https://sourceforge.net/projects/jsmol. Accessed March 8, 2015.
- 38.Weis WI, Brünger AT, Skehel JJ, Wiley DC. Refinement of the influenza virus hemagglutinin by simulated annealing. J Mol Biol. 1990;212(4):737–761. doi: 10.1016/0022-2836(90)90234-D. [DOI] [PubMed] [Google Scholar]
- 39.Yang H, et al. Structural stability of influenza A(H1N1)pdm09 virus hemagglutinins. J Virol. 2014;88(9):4828–4838. doi: 10.1128/JVI.02278-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dreyfus C, et al. Highly conserved protective epitopes on influenza B viruses. Science. 2012;337(6100):1343–1348. doi: 10.1126/science.1222908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ni F, Kondrashkina E, Wang Q. Structural basis for the divergent evolution of influenza B virus hemagglutinin. Virology. 2013;446(1-2):112–122. doi: 10.1016/j.virol.2013.07.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.