Computer vision cracks the leaf code

Significance

The botanical value of angiosperm leaf shape and venation (“leaf architecture”) is well known, but the astounding complexity and variation of leaves have thwarted efforts to access this underused resource. This challenge is central for paleobotany because most angiosperm fossils are isolated, unidentified leaves. We here demonstrate that a computer vision algorithm trained on several thousand images of diverse cleared leaves successfully learns leaf-architectural features, then categorizes novel specimens into natural botanical groups above the species level. The system also produces heat maps to display the locations of numerous novel, informative leaf characters in a visually intuitive way. With assistance from computer vision, the systematic and paleobotanical value of leaves is ready to increase significantly.

Abstract

Understanding the extremely variable, complex shape and venation characters of angiosperm leaves is one of the most challenging problems in botany. Machine learning offers opportunities to analyze large numbers of specimens, to discover novel leaf features of angiosperm clades that may have phylogenetic significance, and to use those characters to classify unknowns. Previous computer vision approaches have primarily focused on leaf identification at the species level. It remains an open question whether learning and classification are possible among major evolutionary groups such as families and orders, which usually contain hundreds to thousands of species each and exhibit many times the foliar variation of individual species. Here, we tested whether a computer vision algorithm could use a database of 7,597 leaf images from 2,001 genera to learn features of botanical families and orders, then classify novel images. The images are of cleared leaves, specimens that are chemically bleached, then stained to reveal venation. Machine learning was used to learn a codebook of visual elements representing leaf shape and venation patterns. The resulting automated system learned to classify images into families and orders with a success rate many times greater than chance. Of direct botanical interest, the responses of diagnostic features can be visualized on leaf images as heat maps, which are likely to prompt recognition and evolutionary interpretation of a wealth of novel morphological characters. With assistance from computer vision, leaves are poised to make numerous new contributions to systematic and paleobotanical studies.

Leaves are the most abundant and frequently fossilized plant organs. However, understanding the evolutionary signals of angiosperm leaf architecture (shape and venation) remains a significant, largely unmet challenge in botany and paleobotany (1–3). Leaves show tremendous variation among the hundreds of thousands of angiosperm species, and a single leaf can contain many thousands of vein junctions. Numerous living angiosperm clades supported by DNA data do not have consistently recognized leaf or even reproductive characters (4); the clades’ fossil records are often lacking or poorly known (5) but are probably “hiding in plain sight” among the millions of fossil leaves curated at museums. Leaf fossils are most commonly preserved in isolation, lacking standard botanical cues such as arrangement, organization, stipules, trichomes, and color (6). Moreover, improved ability to identify living foliage would advance field botany because most plants flower and fruit infrequently (7, 8).

The only major survey of leaf architectural variation is more than 40 y old (1), long preceding the reorganization of angiosperm phylogeny based on molecular data (9, 10). Traditional leaf architectural methods (11, 12) are extremely labor-intensive, inhibiting detailed analyses of leaf variation across angiosperms; accordingly, recent studies have been limited in taxonomic and character coverage (3, 13, 14). Modern machine learning and computer vision methods offer a transformative opportunity, enabling the quantitative assessment of leaf features at a scale never before remotely possible. Many significant computer vision contributions have focused on leaf identification by analyzing leaf-shape variation among species (15–19), and there is community interest in approaching this problem through crowd-sourcing of images and machine-identification contests (see www.imageclef.org). Nevertheless, very few studies have made use of leaf venation (20, 21), and none has attempted automated learning and classification above the species level that may reveal characters with evolutionary significance. There is a developing literature on extraction and quantitative analyses of whole-leaf venation networks (22–25). However, those techniques mostly have not addressed identification problems, and they are methodologically limited to nearly undamaged leaves, which are rare in nature and especially in the fossil record.

Despite the numerous difficulties involved in analyzing leaf architecture, experienced botanists regularly identify leaves to species and higher taxonomic categories quickly and correctly, often without the use of verbally defined characters (“leaf gestalt”). Here, we attempt to automate leaf gestalt, using computer vision and machine learning on a database of several thousand cleared-leaf images to test whether an algorithm can generalize across diverse genera and species to learn, recognize, and reveal features of major angiosperm clades. This challenge is wholly different from that of identifying species, as typically practiced in the computer vision field (see above discussion), because the leaf variation within a species is nearly insignificant compared with that among species within a family or order, as seen in example leaf pairs from various families (Fig. 1). Nevertheless, generations of botanists and paleobotanists have emphasized the recognizability of leaf traits at the family and higher levels (1, 7, 26). We test this fundamental supposition by asking whether a machine vision algorithm can perform a comparable task, learning from examples of large evolutionary categories (families or orders) to correctly discriminate other members of those lineages. We then visualize the machine outputs to display which regions of individual leaves are botanically informative for correct assignment above the species level.

Fig. 1.

Representative heat maps on selected pairs of leaves from analyzed families, showing typical variation among species within families. Red intensity indicates the diagnostic importance of an individual codebook element at a leaf location for classifying the leaf into the correct family in the scenario of Fig. 3A. The locations and intensities correspond to the maximum classifier weights associated with the individual codebook elements (Materials and Methods). For readability, only coefficients associated with the 1 × 1 scale of the spatial pyramid grid are shown; most elements have zero activation on a given leaf. Background areas show some responses to minute stray objects. All images are shown with equal longest dimensions (here, height), as processed by the machine-vision system; see Dataset S1 for scaling data. Specimens from Wolfe National Cleared Leaf Collection as follows. First row, left to right: Anacardiaceae, Comocladia acuminata, Wolfe (catalog no. 8197) and Campnosperma minus (catalog no. 8193); Fabaceae, Bauhinia glabra (catalog no. 30215) and Dussia micranthera (catalog no. 9838). Second row: Myrtaceae, Myrcia multiflora (catalog no. 3543) and Campomanesia guaviroba (catalog no. 3514); Fagaceae, Quercus lobata (catalog no. 1366) and Chrysolepis sempervirens (catalog no. 7103). Third row: Rosaceae, Prunus subhirtella (catalog no. 8794) and Heteromeles arbutifolia (catalog no. 11992); Melastomataceae, Conostegia caelestis (catalog no. 7575) and Memecylon normandii (catalog no. 14338). Fourth row: Lauraceae, Sassafras albidum (catalog no. 771) and Aiouea saligna (catalog no. 2423); Annonaceae, Neostenanthera hamata (catalog no. 4481) and Monanthotaxis fornicata (catalog no. 2866). Extended heat-map outputs are hosted on Figshare, dx.doi.org/10.6084/m9.figshare.1521157.

To train the system (see Materials and Methods for details), we vetted and manually prepared 7,597 images of vouchered, cleared angiosperm leaves from 2,001 phylogenetically diverse genera and ca. 6,949 species from around the world, and we updated nomenclature to the Angiosperm Phylogeny Group (APG) III system (10). Cleared leaves (Fig. 1) are mounted specimens whose laminar tissues have been chemically altered and then stained to allow close study of venation patterns in addition to the leaf outlines. Importantly, we did not, except in severe cases (Materials and Methods), exclude leaves with common imperfections such as bubbles or crystallization in the mounting medium, leaf damage (insect, fungal, mechanical), or imaging defects (poor focus, background artifacts). Four sets of images were processed for the analyses: those from the (i) 19 families and (ii) 14 orders with minimum sample sizes of 100 images each and those from the (iii) 29 families and (iv) 19 orders with minimum sample sizes of 50 images each. In all analyses, random halves of the image sets were used to train the system and the other half to test, and this procedure was repeated 10 times. Accuracy measures correspond to averages and SDs across these 10 repetitions.

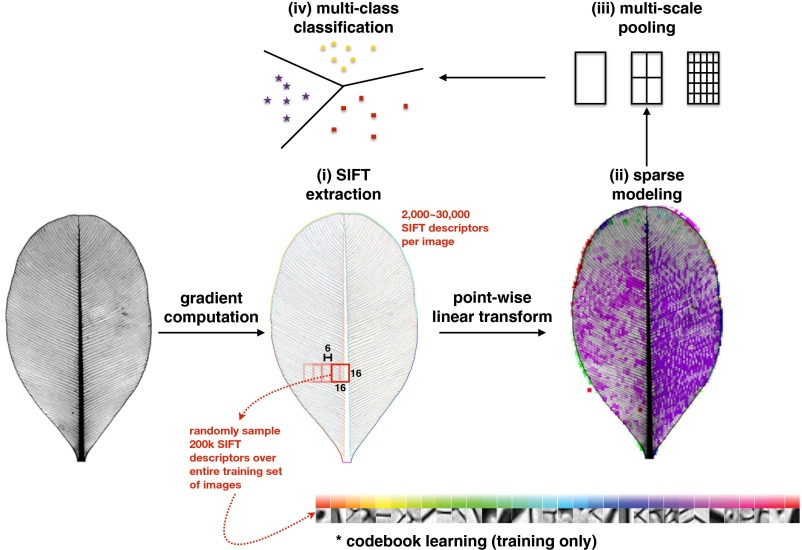
The computer vision algorithm (see Materials and Methods for details; Fig. S1) used a sparse coding approach, which learns a codebook (Fig. 2) from training images and uses it to represent a leaf image as a linear combination of a small number of elements (27). Similar methods have been applied to a variety of problems (28–30). Of interest here regarding “leaf gestalt,” seminal work in vision science (27) showed that training a sparse coding model on images of natural scenes resulted in receptive fields that resemble those of the mammalian visual cortex. Our approach used Scale Invariant Feature Transform (SIFT) visual descriptors (31) extracted from individual locations on the training leaf images to learn a codebook (Fig. 2) and then to model each location as a linear combination of the codebook elements. Support Vector Machine (SVM) (32), a machine-learning classifier, was trained on the pooled maximum coefficients for each codebook element and the associated taxonomic labels (families or orders). Training resulted in a classification function that was applied to predict familial and ordinal identifications of novel images. Heat maps of visualized diagnostic responses were generated directly on individual leaf images (Fig. 1).

Fig. S1.

Computer vision system summary.

Fig. 2.

Learned visual codebook (n =1,024 coding elements) obtained from one random split of the image library. Ten splits were done to compute the reported accuracies (Table 1). A few codebook elements are moiré dots from background areas of scanned book pages (see Materials and Methods). Precisely visualizing the codebook is an unsolved problem, and we used a computational approximation (38) to produce this figure.

To our knowledge, no prior approach has adopted this powerful combination of tools for leaf identification, used cleared leaves or analyzed leaf venation for thousands of species, attempted to learn and discriminate traits of evolutionary lineages above the species level, or directly visualized informative new characters.

Results

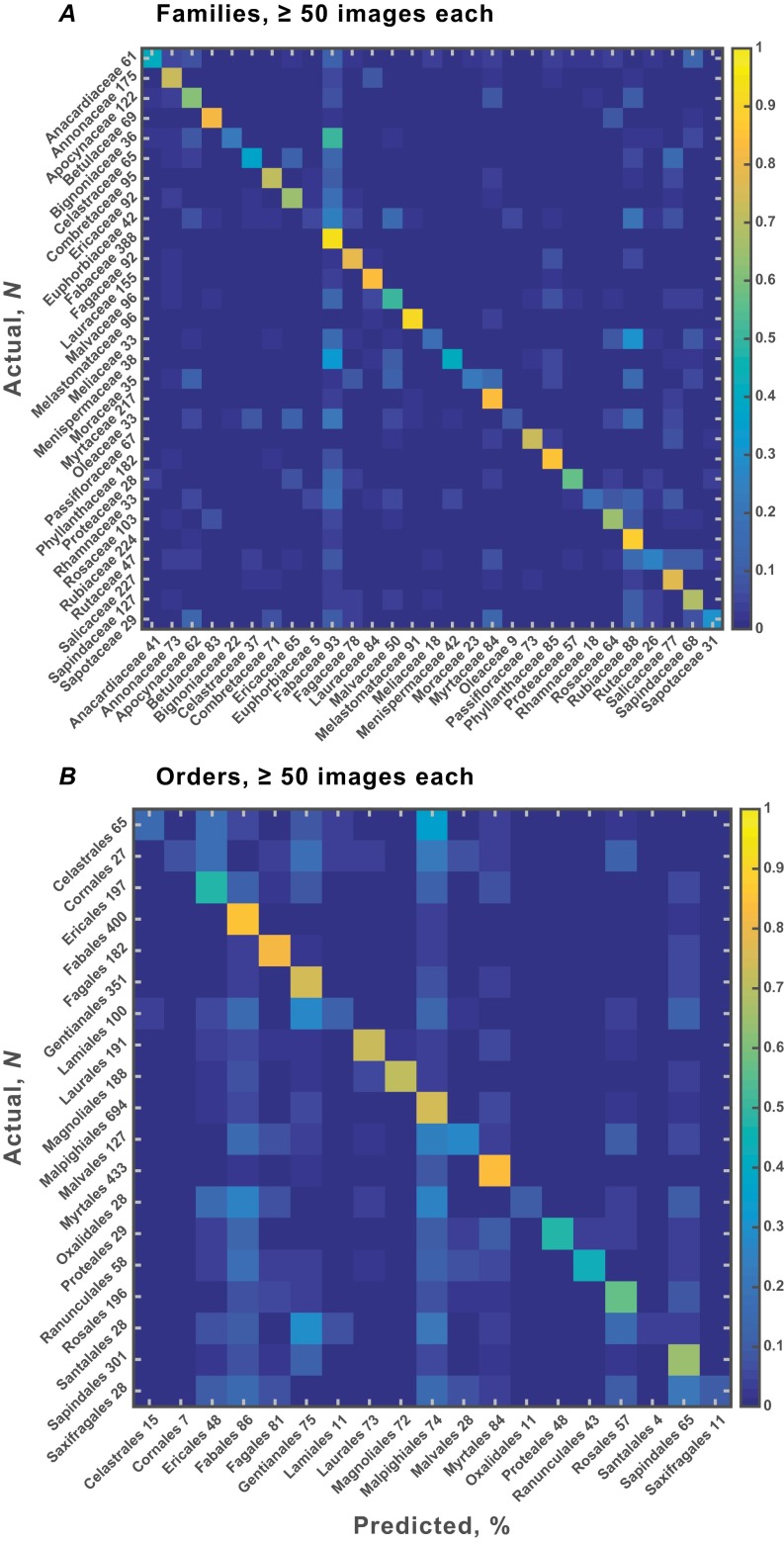
Classification accuracy was very high (Fig. 3 and Fig. S2), especially considering the well-known challenges of identifying leaves to higher taxa visually and the deliberate inclusion of many imperfect specimens and low-quality images. Accuracy for the 19 families with ≥100 images was 72.14 ± 0.75%, ca. 13 times better than random chance (5.61 ± 0.54%; accuracy is defined as the grand mean and SD of the 10 trial averages of the diagonal values of the confusion matrices, as in Fig. 3). Thus, the algorithm successfully generalized across a few thousand highly variable genera and species to recognize major evolutionary groups of plants (see also Materials and Methods, Success in Generalization of Learning across Taxonomic Categories and Collections). Significantly, the system scored high accuracies (>70%) for several families that are not usually considered recognizable from isolated blades, including Combretaceae, Phyllanthaceae, and Rubiaceae. Of great biological interest, our heat maps directly illustrate leaf features that are diagnostic for classification (Fig. 1; extended heat-map outputs are hosted on Figshare, dx.doi.org/10.6084/m9.figshare.1521157).

Fig. 3.

Confusion matrices for family (A) and order (B) classification at the 100-image minimum per category. Colors indicate the proportion of images from the actual categories at left that the algorithm classified into the predicted categories along bottom of each graph (also see Fig. S2 and Dataset S1). Based on a single randomized test trial (of 10 total) on half of the image set, following training on the other half. Note that the sample sizes (N) shown along the left sides equal half the total processed because the sample sizes represent the number of testing samples used, which is half the total number of samples available for each training/test split. Numbers along horizontal axes show the percentage correctly identified. For example, at top left corner, 36% of 61 Anacardiaceae leaves (22 of the 61 leaves) were correctly identified to that family. Identification (chance) accuracies and SDs across 10 trials show negligible variance (see also Table 1): (A) 72.14 ± 0.75% (5.61 ± 0.54%) for 19 families; (B) 57.26 ± 0.81% (7.27 ± 0.44%) for 14 orders.

Fig. S2.

Confusion matrices for family (A) and order (B) classification at the 50-image minima, as in Fig. 3. Identification (chance) accuracies and SDs: (A) 55.84 ± 0.86% (3.53 ± 0.34%), for 29 families; (B) 46.14 ± 0.79% (5.17 ± 0.17%), for 19 orders.

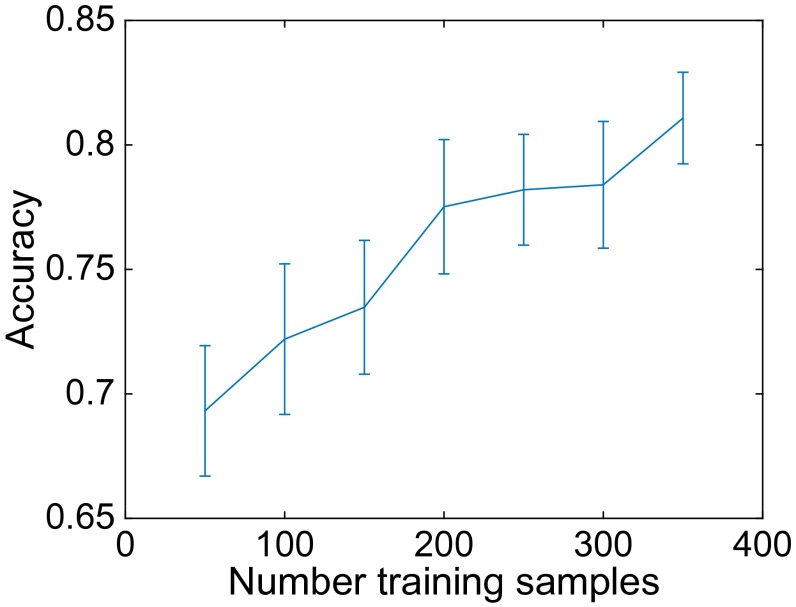
Accuracy at the ordinal level was also many times greater than chance. This result partly reflects the recognition of the constituent families rather than generalization across families to recognize orders; however, even after testing for this effect, there was still a significant signal for generalization (Materials and Methods). On first principles, generalization across genera to recognize families should be more successful, as seen here, than generalization across families to distinguish orders. The genera within a family are usually much more closely related to each other, and thus likely to be phenotypically similar, than are the families within an order. Hypothetically, an increased number of well-sampled families in targeted orders would allow improved recognition of orders and generalization across families (see also Fig. S3). Artifacts specific to particular image sets contributed noise but were largely overcome (Materials and Methods), boding well for applying the system to a range of new and challenging datasets.

Fig. S3.

System accuracy as a function of the number of training samples available per category, for five orders with at least 400 images each (Fabales, Gentianales, Malpighiales, Myrtales, and Sapindales).

For a benchmark comparison, we classified the images from the 19 families in Fig. 3A via holistic analysis of leaf shape alone. We compared the well-known shape-context algorithm (15) (Materials and Methods) with our sparse coding algorithm on extracted leaf outlines. For family classification at the 100-image minimum, shape context performed above random chance (12.44 ± 0.74% vs. 5.61 ± 0.54% chance result) but below sparse coding of the same outlines (27.94 ± 0.85%), and both scored far below sparse coding of images with venation (ca. 72%; Fig. 3A). These results help to demonstrate the diagnostic significance of both leaf venation and shape. The importance of leaf venation is long established (26). However, the results from leaf outlines refute the widely held view, seen in many of the hundreds of papers cited in the extended bibliography of ref. 33, that leaf shape is principally selected by climate and that phylogeny plays a negligible role.

Discussion

All of our results validate the hypotheses that higher plant taxa contain numerous diagnostic leaf characters and that computers can acquire, generalize, and use this knowledge. In addition to the potential for computer-assisted recognition of living and fossil leaves, our algorithm represents an appealing, novel approach to leaf architecture. Conventional leaf architecture (12) currently employs ca. 50 characters to describe a range of characters that are usually visible over large areas of a specimen, from patterns of shape and major venation to categories of fine venation and marginal configuration. Scoring these characters requires immense manual effort, and their systematic significance is poorly understood. In sharp contrast, the learned codebook elements derived here encode small leaf features, mostly corresponding to previously undescribed orientations and junctions of venation and leaf margins (Fig. 2); the codebooks and diagnostic significance values (Fig. 1) are automatically generated.

Our heat maps (Fig. 1 and extended outputs at dx.doi.org/10.6084/m9.figshare.1521157) provide a trove of novel information for developing botanical characters that probably have phylogenetic significance as well as for visual training (improved “gestalt”). The dark red patches on the heat maps indicate leaf locations with the most significant diagnostic responses to codebook elements, providing numerous leads for the conventional study of previously overlooked patterns. Diagnostic features appear to occur most often at tertiary and higher-order vein junctions, as well as along the margins and associated fine venation of both toothed and untoothed leaves. Close examination of the heat maps reveals variation among families. For example, responses at leaf teeth are strongest along basal tooth flanks in Fagaceae and Salicaceae, versus tooth apices in Rosaceae; in Ericaceae, responses are located at teeth and on minute marginal variations that do not form teeth. Responses at margins tend to be concentrated in the medial third of the lamina in Annonaceae and Combretaceae versus the distal half in Fabaceae, Phyllanthaceae, and Rubiaceae. Tertiary-vein junctions are significant across groups, with apparently higher sensitivity at junctions with primary veins in Fagaceae, perhaps reflecting the tendency toward zigzag midveins in that family; with secondary and intersecondary veins in Apocynaceae and Betulaceae; and with other tertiaries and finer veins in several families such as Anacardiaceae. Correspondingly, many Anacardiaceae are known for having unusual tertiary venation (13, 34).

Many of the analyzed families have numerous species with visually distinctive, generally holistic traits that are widely applied in field identification (1, 7, 8). Examples include acute basal secondary veins and low vein density in Lauraceae; palmate venation in Malvaceae; the prevalence of multiple, strongly curving primary veins in Melastomataceae; the distinctive perimarginal veins of Myrtaceae; and the characteristic (1) teeth of Betulaceae, Fagaceae, Rosaceae, and Salicaceae. However, the small image regions used here mostly bypassed these patterns, and using larger image regions (by down-sampling the images) significantly reduced accuracy (Table 1). Nevertheless, the novel, fine-scale features will probably improve understanding of conventional characters. For example, the leaf margins of Melastomataceae show diagnostic responses and generally follow the trends of the well-known, strongly curving primary veins. The perimarginal vein configurations of Myrtaceae appear quite responsive, especially the little-studied (35) ultimate venation. Leaf teeth are closer in size to the patches and are often “hot,” but the leaf teeth’s responsive areas are difficult to relate to the standard tooth-type classifications (1), which are now ripe for revision.

Table 1.

Identification accuracies at varying image resolutions

Scenario	64	128	256	512	768	1,024	1,536	2,048
Families, ≥100 images, %	15.82 ± 3.17	40.50 ± 1.17	58.07 ± 0.93	67.57 ± 0.86	71.54 ± 0.67	72.14 ± 0.75	73.43 ± 0.92	72.08 ± 7.27
Orders, ≥100 images, %	10.56 ± 1.85	29.37 ± 1.67	44.51 ± 0.87	52.95 ± 0.78	57.21 ± 0.97	57.26 ± 0.81	58.54 ± 0.23	60.40 ± 1.70

Analyses in this study were all done at 1,024-pixel resolution (Fig. 3). The resolution is pixels along longest dimension. Uncertainties are SDs.

In sum, along with the demonstration that computers can recognize major clades of angiosperms from leaf images and the promising outlook for computer-assisted leaf classification, our results have opened a tap of novel, valuable botanical characters. With an increased image library and testing on well-preserved fossils, analyses from heat-map data are likely to achieve the longstanding goals of quantifying leaf-phylogenetic signal across angiosperms and systematic placements of large numbers of fossil leaves.

Materials and Methods

Cleared Leaf Dataset.

We assembled a dataset of 7,597 vetted images of cleared leaves (or leaflets for compound leaves), representing nearly as many species, from 2,001 genera and ca. 6,949 species collected around the world (Dataset S1). The images mostly represent woody angiosperms and come from three herbarium-vouchered sources: (i) the Jack A. Wolfe USGS National Cleared Leaf Collection, housed at the Smithsonian Institution, 5,063 images (clearedleavesdb.org); (ii) our scans of the E. P. Klucking Leaf Venation Patterns book series (36), 2,305 images; and (iii) the Daniel Axelrod Cleared Leaf Collection, University of California, Berkeley, 229 images (ucmp.berkeley.edu/science/clearedleaf.php). Images used were those with white space present around the leaf, more than ca. 85% of leaf visible, midvein not folded or discontinuously broken, and at least some tertiary venation visible. Importantly, we did not screen other common sources of noise such as tears, folds in the lamina, insect or fungal damage, and bubbles or crystallization in the mounting medium. Many images from the Klucking series were of notably low quality and bore a moiré pattern from printing.

The selection of taxonomic groups was entirely opportunistic, based on the cleared-leaf resources available. However, the resulting collection is highly diverse phylogenetically because Wolfe, Klucking, and Axelrod each attempted to maximize their coverage of genera within families. We considered families with at least 100 images and randomly split the images from each family so that one half was used to train the classifier and the other to test the system (random halving was used as a conservative splitting procedure; we note that increasing the relative proportion of training images further increased accuracies in all scenarios). This cutoff yielded 19 families selected with at least 100 images each (Fig. 3A): Anacardiaceae, Annonaceae, Apocynaceae, Betulaceae, Celastraceae, Combretaceae, Ericaceae, Fabaceae, Fagaceae, Lauraceae, Malvaceae, Melastomataceae, Myrtaceae, Passifloraceae, Phyllanthaceae, Rosaceae, Rubiaceae, Salicaceae, and Sapindaceae. We also attempted a lower cutoff of 50 images per family, adding 10 additional families (Fig. S2A): Bignoniaceae, Euphorbiaceae, Meliaceae, Menispermaceae, Moraceae, Oleaceae, Proteaceae, Rhamnaceae, Rutaceae, and Sapotaceae. We repeated the random-halving procedure 10 times and here report the mean accuracy and SD over all 10 splits (Fig. 3 and Fig. S2). We conducted a similar protocol for classification at the ordinal level, yielding 14 APG III orders selected at the 100 image minimum (Fig. 3B): Celastrales, Ericales, Fabales, Fagales, Gentianales, Lamiales, Laurales, Magnoliales, Malpighiales, Malvales, Myrtales, Ranunculales, Rosales, and Sapindales. We also attempted a lower cutoff of 50 images per order, adding five more orders (Fig. S2B): Cornales, Oxalidales, Proteales, Santalales, and Saxifragales.

We prepared each image manually to focus processing power on the leaf blades and to minimize uninformative variation. We rotated images to have vertical leaf orientation, cropped them to an approximately uniform white-space border, adjusted them to gray-scale with roughly consistent contrast, removed petioles, and erased most background objects. Sets of all prepared images are available on request from P.W. All images were resized so that their maximum width or height dimension was 1,024 pixels, maintaining the original aspect ratio. This resolution offered the optimal balance between performance and computing cost (Table 1). We updated generic names using multiple standard sources and revised familial and ordinal assignments using APG III (10).

The resulting collection (Dataset S1) contains images of 182 angiosperm families, 19 of them with ≥100 images each and totaling 5,314 images (Fig. 3A). We considered each family as an independent category in the computer vision system, regardless of its relationships with the other groups, thus testing the traditional idea (1, 7, 36) that leaves within angiosperm families have visually similar features despite the enormous morphological variation among constituent genera and species.

Computer Vision Algorithm.

We analyzed leaf architecture using a sparse coding learning approach (code in Dataset S2). This method aims to represent image spaces with linear combinations of a small number of elements (27) from a visual codebook that is learned from training images. In our approach (Fig. S1), adapted from ref. 28, SIFT visual descriptors (31) were first extracted from all database images. These 128-dimensional descriptors were computed from small (16 × 16 pixel) image patches that are densely sampled (with a stride of 6 pixels corresponding to a 10-pixel overlap between sampled patches). This process resulted in about 2,000 to ∼30,000 SIFT descriptors generated per image, depending on image size. We then executed 10 random splits of the image set into training and testing halves as described above. For each split, the algorithm randomly sampled 200,000 SIFT descriptors from the training set to learn an overcomplete codebook of d =1,024 elements (Fig. 2) using the SPArse Modeling Software (SPAMS) toolbox (spams-devel.gforge.inria.fr).

Next, we applied a point-wise linear transform to both the training and test images: for a given location within an image, the corresponding SIFT descriptor was modeled as a linear combination of the learned codebook elements. After this step, each image location became associated with a set of d coefficients, each corresponding to a different codebook element. Because of the sparsity constraint, at any location only a few of these coefficients are nonzero. We subsequently implemented a multiscale spatial pyramid (28), whereby a maximum was computed for each coefficient over all locations, within each cell of a pyramid of grids placed across the whole image at three different scales (1 × 1, 2 × 2, and 4 × 4 grids, totaling 21 cells). For each input image, this maximum pooling operation resulted in d max coefficient values for each of the 21 cells. Concatenating these 21 values for each of the d = 1,024 coefficients yielded a 21,504-dimensional feature vector for each input image. SVM (32) was then trained using the feature vectors from a training set of leaf images and their associated taxonomic labels (families or orders). The resulting learned classification function was then applied to predict family or order identifications for a testing set of leaves from their feature vectors. Here, we used the LIBSVM software (https://csie.ntu.edu.tw/∼cjlin/libsvm), using a multiclass setting with a radial basis function kernel. Chance level was assessed using random permutations of the taxonomic labels of the training images.

Success in Generalization of Learning Across Taxonomic Categories and Collections.

To assess the robustness of the machine-vision system, we evaluated the extent to which the algorithm succeeds in generalizing recognition across taxonomic categories versus basing its decisions primarily on detecting the presence or absence of constituent subcategories that it has learned [i.e., (i) families within orders and (ii) genera within families]. We addressed this issue by redoing the analyses with and without systematic separation of the respective subcategories among each training vs. testing half, with 10 repetitions as in the main experiments.

To test the first case, generalization across families to detect orders, we conducted an experiment in which we selected all orders that each had at least two families with at least 50 images apiece, namely Ericales, Fagales, Gentianales, Lamiales, Malpighiales, Myrtales, Rosales, and Sapindales. We eliminated any remaining families with fewer than 50 images each and then trained and tested the system in two scenarios. First, half the leaf images from each order was randomly selected for inclusion in the training pool, regardless of family membership, whereas the other half was used in the testing pool, thus allowing family overlaps (accuracy of order recognition: 67.49 ± 0.88%; chance level 12.38 ± 0.77%). Second, half the families from each order was randomly selected for training and the remaining families for testing, thus excluding overlaps (accuracy of order recognition: 26.52 ± 2.33%; chance level: 12.31 ± 1.72%). The fact that the system accuracy was much larger for the first than the second scenario suggests comparatively low success in generalization across families, but the success rate was still more than double that of chance. Thus, ordinal classification in the machine-vision system has a substantial contribution from generalization at the family level, but even with these small numbers of families per order, there is still a significant signal for generalization across families.

To test the second case, generalization across genera to recognize families, we conducted a similar experiment in which we selected the families that each contain at least two genera that (i) each have at least 25 images and (ii) together total at least 100 images. The resulting six families were Combretaceae, Ericaceae, Lauraceae, Myrtaceae, Phyllanthaceae, and Salicaceae. After eliminating remaining genera with fewer than 25 images each, we trained and tested the system in two scenarios. First, half the images from each family were randomly sampled for training, regardless of genus, whereas the other half was used for testing, thus allowing generic overlaps (accuracy of family recognition: 88.01 ± 0.93%; chance level: 16.37 ± 3.09%). Second, the training and testing samples were obtained by randomly selecting half the genera for the training pool and those remaining for the testing pool; in other words, no overlap of genera was allowed between the training and testing halves (accuracy of family recognition: 70.59 ± 3.73%; chance level: 17.37 ± 1.83%). The fact that accuracy was larger for the first scenario but remained very significantly above chance for the second suggests that the system exhibits robust generalization across genera to recognize families, and is not, for example, dependent on well-sampled genera such as Acer (maples, Sapindaceae) and Quercus (oaks, Fagaceae). The higher possibility of identification errors for genera than for families on the original samples biases against this positive result, which confirms conventional wisdom regarding the general identifiability of families as well as the potential for machine vision to recognize finer taxonomic levels.

We also explored the extent to which the machine-vision system may be exploiting possible biases associated with individual collections, such as the moiré printing pattern in the Klucking images. We conducted an experiment in which we selected all orders that had at least 50 images each in both the Klucking and the Wolfe collections, namely Laurales, Magnoliales, Malpighiales, Malvales, and Myrtales. We trained and tested the system in three scenarios, following the same methods that we used in the main experiments. First, we trained on the Klucking and tested on the Wolfe image collection (accuracy of order recognition: 37.44 ± 0.66%; chance level: 19.40 ± 3.53%). Second, we trained on the Wolfe and tested on the Klucking collection (accuracy of order recognition: 41.12 ± 0.94%; chance level: 20.04 ± 5.00%). Third, we combined the two sources and randomly sampled half the images from each order for training and half for testing (accuracy of order recognition: 64.68 ± 2.65%; chance level: 18.96 ± 3.78%). The higher accuracy in scenario 3 suggests that biases exist (e.g., image background) that can be picked up by the system. However, the significant generalization of the system in scenarios 1 and 2, especially when taking into account the overall much lower image quality of the Klucking collection, suggests that these biases only account for a small fraction of the overall system accuracy.

Benchmark Using Shape Context.

The shape-context algorithm has been successfully used for species-level leaf classification (15). We tested both the shape-context and sparse-coding algorithms on leaf outlines extracted from the same image subset used for the 19 family, 100-image-minimum scenario shown in Fig. 3A. Leaves were segmented automatically by combining the Berkeley contours detection system (37) with second-order Gaussian derivative filters, and the corresponding closed boundary was then filled to obtain foreground masks. Shape-context features were then extracted from the leaf silhouette, following the approach of Ling and Jacobs (15). Leaf contours were sampled uniformly at 128 landmark points, and shape-context descriptors were extracted at every sampled point, using source code available online (www.dabi.temple.edu/∼hbling/code_data.htm). This procedure led to a 96 × 128 dimensional visual representation (the shape context) for each leaf image. Matching between two leaves’ shape contexts was obtained through dynamic programming, where matching cost is used to measure similarity. The pairwise similarities were then used to derive a Kernel matrix that was fed to an SVM, which was trained and tested using the same pipeline as for the sparse model described in Materials and Methods, Computer Vision Algorithm.