Quantum communication complexity advantage implies violation of a Bell inequality

Significance

For many communication complexity problems the quantum strategies, distinguished by using Bell nonlocal correlations, provide exponential advantage over the best possible classical strategies. Conversely, for any Bell nonlocal correlations there exists a communication complexity problem that is solved more efficiently using the former. Despite many efforts, there were only two problems for which one could certify that any strategy that outperforms the classical one must harbor Bell nonlocal correlations. We prove that any large advantage over the best known classical strategy makes use of Bell nonlocal correlations. Thus, we provide the missing link to the fundamental equivalence between Bell nonlocality and quantum advantage.

Abstract

We obtain a general connection between a large quantum advantage in communication complexity and Bell nonlocality. We show that given any protocol offering a sufficiently large quantum advantage in communication complexity, there exists a way of obtaining measurement statistics that violate some Bell inequality. Our main tool is port-based teleportation. If the gap between quantum and classical communication complexity can grow arbitrarily large, the ratio of the quantum value to the classical value of the Bell quantity becomes unbounded with the increase in the number of inputs and outputs.

The key element that distinguishes classical from quantum information theory is quantum correlations. The first attempt to quantify their strength was quantitatively expressed in Bell’s theorem (1). They are similar to classical correlations in that one cannot take advantage of them to perform superluminal communication, yet every attempt to explain such correlations from the point of view of classical theory—namely, to find a local hidden variable model—is impossible. For a long time the existence of quantum correlations was merely of interest to philosophically minded physicists and was considered an exotic peculiarity, rather than a useful resource for practical problems in physics or computer science. This has changed dramatically in recent years—it became apparent that quantum correlations can be used as a resource for a number of distributed information processing tasks (2–4), producing surprising results (5, 6).

One area where using quantum correlations has wide-reaching practical implications is communication complexity. A typical instance of a communication complexity problem features two parties, Alice and Bob, who are given binary inputs x and y. They wish to compute the value of $f\left(x,y\right)$ by exchanging messages between each other. The minimum amount of communication required to accomplish the task by exchanging classical bits (with bounded probability of success) is called classical communication complexity, denoted as $C\left(f\right)$.

There are two ways to account for the communication complexity of computing a function when we want to make use of quantum correlations. In the first one, Alice and Bob share any number of instances of the maximally entangled state ${|{\mathrm{\Psi }}^{-}\rangle }_{AB}=\left(1/\sqrt{2}\right){\left(|01\rangle -|10\rangle \right)}_{AB}$ beforehand and are allowed to exchange classical bits to solve the problem. Another approach is to have no preshared entanglement, but instead allow Alice and Bob to exchange qubits. The latter type of protocol can always be converted to the former with preshared entanglement and classical communication. We denote the quantum communication complexity of computing the function $f\left(x,y\right)$ (with bounded probability of success) by $Q\left(f\right)$.

For a large number of problems, the respective quantum communication complexity is much lower compared with its classical counterpart (4, 7). In such cases, we say that there exists a quantum advantage for communication complexity. In other words, one achieves a quantum advantage if the quantum communication complexity of the function is lower than its corresponding classical communication complexity.

One of the most striking example of quantum advantage is the famous Raz problem (5, 8), where quantum communication complexity is exponentially smaller than classical. Another example is the “hidden matching” problem for which the quantum advantage leads to one of the strongest possible violations of the Bell inequality (9). The latter inequality plays an important role in detecting quantum correlations and certifying the genuinely quantum nature of resources at hand. Previously, to obtain an unbounded violation of a particular Bell inequality one resorted to problems with the exponential quantum advantage. Here, we show that one can achieve the same result, using only polynomial quantum advantage.

As a matter of fact, the very first protocols offering quantum advantage were based on a quantum violation of certain Bell inequalities (6). It was even shown that for a very large class of multiparty Bell inequalities, correlations that violate them lead to a quantum advantage (perhaps, for a peculiar function) (10). This indicates that Bell nonlocality often leads to a quantum advantage. However, there are more and more communication protocols that offer a quantum advantage, but, nevertheless, they are not known to violate any Bell inequality.

It has long been suspected (6) that quantum communication complexity and Bell nonlocality are the two sides of the same coin. Although it is possible to convert a Bell nonlocality testing experiment to the communication complexity instance, the reverse has been known only for some particular examples. The question is whether this relationship holds in general, namely, Is quantum communication inherently equivalent to Bell nonlocality when solving communication complexity problems?

Until now, there were only two concrete examples where one could certify quantum correlations in the context of communication complexity by providing a quantum state and a set of measurements whose statistics violate some Bell inequality. The first case is the “hidden matching” problem and the second one is a theorem, which states that a special subset of protocols that provide quantum advantage also implies the violation of local realism (6). To get the violation of Bell inequalities obtained from the examples above, one had to perform an involved analysis that relied on a problem-specific set of symmetries. Thus, such an approach cannot be generalized to an arbitrary protocol for achieving a quantum advantage in the communication complexity problem.

In this paper, we show that given any (sufficiently large) quantum advantage in communication complexity, there exists a way of obtaining measurement statistics that violate some linear Bell inequality. This completely resolves the question about the equivalence between the quantum communication and Bell nonlocality: Whenever a protocol computes the value of the function $f\left(x,y\right)$ better than the best classical protocol, even with a gap that is only quadratic, then there must exist a Bell inequality that is violated.

We provide a universal method that takes a protocol that achieves the quantum advantage in any single- or multiround communication complexity problem and uses it to derive the violation of some linear Bell inequality. This method can be generalized to a setting with more than two parties. Our Bell inequalities lead to a so-called unbounded violation (11): The ratio of the quantum value to the classical value of the Bell quantity can grow arbitrarily large with the increase of the number of inputs and outputs, whenever the ratio of $C\left(f\right)$ and ${\left(Q\left(f\right)\right)}^2$ grows too. In particular, an exponential advantage leads to an exponential ratio.

Our method consists of two parts. In the first part, we use the quantum protocol based on the given communication complexity game to construct a set of quantum measurements on a maximally entangled state The central ingredient of our construction is the recently discovered port-based teleportation (12, 13). In the second part, given a protocol that computes a function f by using $Q\left(f\right)$ qubits, and the optimal classical error probability achievable with ${\left(Q\left(f\right)\right)}^2$ bits, we construct the corresponding linear Bell inequality that is subsequently violated by the above quantum measurements.

For one-way communication complexity problems we develop a much simpler method that is based on the remote state preparation and results in a nonlinear Bell inequality.

Quantum Communication Complexity Protocol

We start by defining a general quantum multiround communication protocol. Two parties, Alice and Bob, receive inputs $x\in X={\left\{\mathrm{0,1}\right\}}^n$ and $y\in Y={\left\{\mathrm{0,1}\right\}}^n$ according to some distribution μ and their goal is to compute the function $f:X\times Y\to \left\{\mathrm{0,1}\right\}$ by exchanging qubits over multiple rounds. We further use subscripts for the system names to denote the round number. The parties proceed as follows:

• i)Alice applies $U_x^{A_0\to M_1{A}_1}$ on her local state ${\rho }_{A_0}$ and sends ${\rho }_{M_1}$ to Bob. In general, $M_1$ may be entangled with $A_1$, which remains with Alice.
• ii)Bob performs $U_y^{M_1{B}_0\to M_2{B}_1}$ on the state ${\rho }_{M_1}\otimes {\sigma }_{B_0}$. Then he sends back the system $M_2$ to Alice, keeping $B_1$.
• iii)Parties repeat steps i and ii for $r-1$ rounds. In the last round, instead of communicating back to Alice, Bob measures the observable $o_y$ and outputs the value of the function f. The observable $o_y$ acts on the system $M_{2r-1}$ and Bob’s memory $B_{r-1}$.

The above protocol may be transformed to the form where a one-qubit system is exchanged between Alice and Bob at any round. To achieve this, we split the Q-qubit message from Alice to Bob (or vice versa) into Q rounds of one-qubit transmission and modify the protocol as follows. We start from the initial state, which has the form

$$|{\rho }_A^M\rangle |{\theta }_A^C\rangle |{\sigma }_B^M\rangle ,$$ [1]

where $|{\rho }_A^M\rangle$ and $|{\sigma }_B^M\rangle$ describe the memory registers that belong to Alice and Bob, respectively. The state $|{\theta }_A^C\rangle$, initially in state $|\theta \rangle =|0\rangle$ with Alice, is a one-qubit system that is used for message passing from Alice to Bob and vice versa. In each round, Alice applies $U_x^i$ to $\rho \otimes \theta$, and Bob applies $U_y^i$ to $\sigma \otimes \theta$. In the last round, instead of applying a unitary transformation, Bob performs a measurement. One may view unitaries $U_x^i$ and $U_y^i$ as controlled gates acting on the memory with the one-qubit register acting as a control. This implies that for given x, in round i the state of Alice’s memory is spanned on at most $2^i$ orthogonal vectors. This observation will be crucial for the construction of a compressed-memory quantum protocol. Thus, we can transform any given protocol that requires Q qubits of communication into one that makes use of $2Q$ one-qubit exchanges.

From an Arbitrary Protocol to a Compressed-Memory Protocol

One shortcoming of the above protocols is that both players possess a local memory, possibly entangled with the message, which can span an arbitrary number of qubits and therefore could be much too big to properly handle in other parts of our construction. We solve this problem by converting an arbitrary protocol, as described above, to a protocol where we can upper bound the maximum size of the local memory.

The following proposition, which is a consequence of the Yao–Kremer lemma (3, 14), shows that it is possible to compress the parties’ local memory each step and that therefore the size of the local memory can be assumed to be at most the total communication. We include the proof in Supporting Information, section IV.

Proposition 1.

For any Q-qubit quantum communication protocol (without prior entanglement) there exists a Q-qubit quantum communication protocol for which Alice and Bob can encode their local memory on at most Q qubits each.

Quantum Measurements from the Quantum Communication Complexity Protocol

We now show how to convert a multiround compressed-memory protocol for computing $f\left(x,y\right)$, which gives a quantum advantage to the violation of a linear Bell inequality. There exist two different protocols to achieve this. The first protocol is based on the recently introduced method of port-based teleportation, which we briefly review in the next section. The second method, discussed at the end of this paper, relies on remote state preparation (15). We base our construction on the port-based teleportation because unlike the remote state preparation it is easily extendible to the multiround protocol and also gives rise to a linear Bell inequality.

Port-Based Teleportation

In deterministic port-based teleportation, the two parties share N pairs of maximally entangled qudits ${|{\mathrm{\Psi }}^{-}\rangle }_{A_1{B}_1}\otimes \cdots \otimes {|{\mathrm{\Psi }}^{-}\rangle }_{A_N{B}_N}$, each of which is called a “port.” To transmit the state ${|{\mathrm{\Psi }}^{\text{in}}\rangle }_{A_0}$, the sender performs the square-root teleportation measurement given by a set of positive operator valued measure (POVM) elements ${\left\{\mathrm{\Pi }\right\}}_{i=1}^N$ (precisely defined in equation 27 of ref. 13) on all of the systems $A_i$, $i=0,\dots ,N$, obtaining the result $z=1\dots N$. Then, he or she communicates z to the receiver who traces out the subsystems $B_1\dots B_{z-1}{B}_{z+1}\dots B_N$ and remains with the teleported state ${|{\mathrm{\Psi }}^{\text{out}}\rangle }_{B_z}$ in the subsystem $B_z$. Teleportation always succeeds and the fidelity of the teleported state with the original is $F\left({|{\mathrm{\Psi }}^{\text{in}}\rangle }_{A_0},{|{\mathrm{\Psi }}^{\text{out}}\rangle }_{B_z}\right)\ge 1-d^2/N$. The cost of the classical communication from sender to receiver is equal to $c={\log }_{2}N$. The distinctive feature of this protocol is that unlike with original teleportation, it does not require a correction on the receiver’s side.

Constructing Quantum Measurements

Using port-based teleportation we can now construct the relevant quantum measurements. Parties start with the initial state [1] and perform the following protocol:

• i)Alice applies $U_x^{A_0\to M_1{A}_1}$ on her local state ${\rho }_{A_0}$. She obtains the state of size $Q_1=\log \hspace{0.17em}\text{dim}{M}_1+\log \hspace{0.17em}\text{dim}{A}_1$, which is teleported to Bob at once, using $N_1$ ports each of dimension $2^{Q_1}$. This consumes $N_1$ ports. Alice does not communicate the classical teleportation outcomes $\left\{i_1^A\right\}$, $\left|\left\{i_1^A\right\}\right|=N_1$ with $i_1^A\in \left\{1,\dots ,N_1\right\}$ to Bob.
• ii)Bob applies the local unitary $U_y^{M_1{B}_0\to M_2{B}_1}$ to each of the ports (he does not know the value of $i_1$) and teleports each of the $N_1$ states one-by-one by applying the teleportation measurement using $N_2$ ports each of the dimension $2^{Q_2}$, where $Q_2=\log \hspace{0.17em}\text{dim}{M}_2+\log \hspace{0.17em}\text{dim}{B}_1+\log \hspace{0.17em}\text{dim}{A}_1$. This consumes $N_1{N}_2$ ports. Bob keeps the set of $N_2$ teleportation outcomes $\left\{i_{1,1}^B,\dots ,i_{1,N_2}^B\right\}$, $\left|\left\{i_{\mathrm{1,1}}^B,\dots ,i_{1,N_2}^B\right\}\right|=N_1{N}_2$, where for each $j=1\dots N_2$, $i_{1,j}^B\in \left\{1,\dots ,N_2\right\}$.
• iii)Parties repeat steps i and ii for $r-1$ rounds.

At the end of the protocol we obtain the set of measurements that map the generic communication protocol into the set of correlations,

$$p(\left\{i_1^A\right\},\left\{i_{\mathrm{1,1}}^B,\dots ,i_{1,N_1}^B\right\},\left\{i_{\mathrm{2,1}}^A,\dots ,i_{2,N_1\hspace{0.17em}{N}_2}^A\right\},\dots ,\left\{i_{r,1}^B,\dots ,i_{r,N_1\hspace{0.17em}{N}_2\dots N_{2r-1}}^B\right\},\left\{o_1,\dots ,o_{N_1\hspace{0.17em}{N}_2\dots N_r}\right\}|x,y),$$ [2]

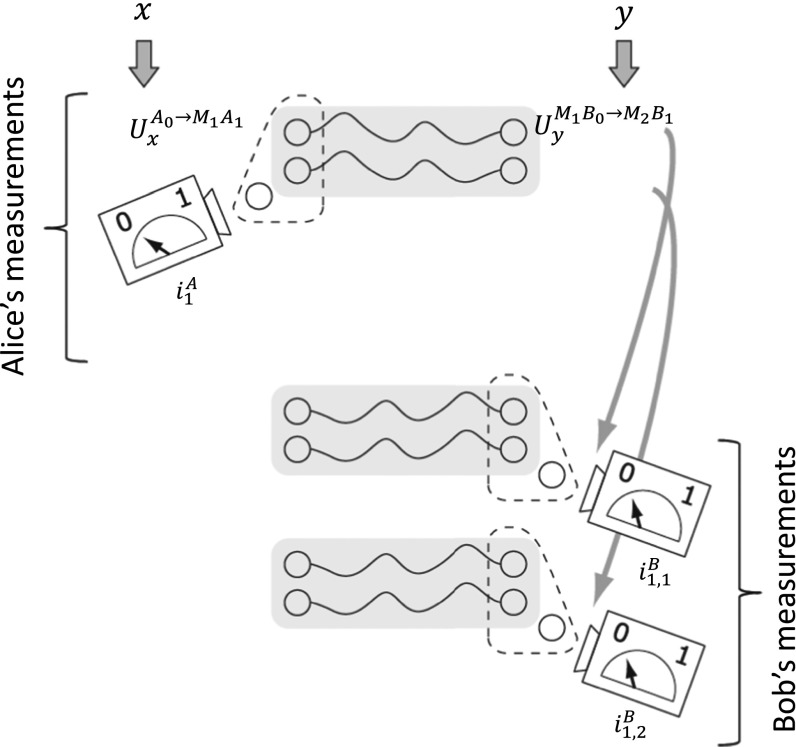
where $\left\{o_j\right\}$ are the final teleportation measurements in round r on Bob’s side. An important feature of this construction is that all of the quantum measurements are performed simultaneously but the classical information exchange happens sequentially. A single round of the protocol is depicted in Fig. 1 and the entire protocol is depicted in Fig. 2.

Fig. 1.

The structure of a single round of the protocol. Alice applies $U_x$ to her system, which if followed by Bob’s unitary $U_y$. Bob has no information about the outcome of Alice’s port-based teleportation, $i_1^A$, so he teleports each of his qudit subsystems individually, obtaining $i_{\mathrm{1,1}}^B$, $i_{\mathrm{1,2}}^B$,….

Fig. 2.

Constructing quantum measurements. A and B denote Alice’s and Bob’s local subsystems, respectively. Each measurement $M_i$, $i=1,\dots ,r_{2r-1}$ represents the square-root measurement in the port-based teleportation (12).

Simulating the Quantum Protocol

The last part of the puzzle is a method of simulating the compressed-memory quantum protocol, using the above correlations and classical communication.

Lemma 1.

Given a protocol for computing f that uses Q qubits of communication and achieves the success probability $p_{\text{succ}}\ge 1/2+\mathit{ϵ}$, $\mathit{ϵ}>0$, one can simulate it using correlations [2] and $10Q^2$ bits of classical communication with the success probability $p_{\text{succ}}\ge 1/2+{\left(1-2^{-Q}\right)}^{2Q}\mathit{ϵ}$.

Proof:

Having access to correlations [2], Alice and Bob exchange their respective outcomes of the teleportation measurements that amount to ${\log }_2{N}_1{N}_2{N}_3\dots N_{2r-1}$ bits of communication. This finalizes the port-based teleportation and thus simulates the corresponding quantum protocol. After exchange, Bob returns $o_L$, where L denotes the last index that he received from Alice.

The above protocol is equivalent to $2r$ rounds of port-based teleportation used for the compressed-memory protocol. Because by the compression of Proposition 1 for every round i the dimension of the teleported state $Q_i$ is at most $2^{2Q+1}$ (the message is encoded in 1 qubit and the local memories are encoded in Q qubits each), we set ${\log }_2{N}_i=5Q$ so that the fidelity of teleportation on each step is $F\ge \left(1-2^{-Q}\right)$. Then the protocol has success probability $p_{\text{succ}}\ge 1/2+F^{2r}\mathit{ϵ}$, where $p_{\text{succ}}\ge 1/2+\mathit{ϵ}$ is the success probability of the original quantum protocol. Bounding the number of rounds r by the total amount of quantum communication Q, we get $p_{\text{succ}}\ge 1/2+1/2{\left(1-2^{-Q}\right)}^{2Q}\mathit{ϵ}$. Thus, the total amount of classical communication is bounded above by $10Q^2$.

$\square$

Construction of a Bell Inequality and Its Violation

Let us sum up the whole construction. First, we start with a quantum multiround protocol to compute f that uses quantum communication and no shared entanglement. This protocol requires Q qubits of communication and achieves $p_{\text{succ}}\ge 1/2+\mathit{ϵ}$. In this protocol, Alice and Bob may use an arbitrary amount of local quantum memory between rounds. Second, we convert it to the protocol with compressed local quantum memory, where the latter can be encoded in Q qubits. The compressed protocol is then used to obtain correlations in the form [2]. These correlations together with classical communication are used to recover the original communication complexity protocol that computes f. This protocol uses $O\left(Q^2\right)$ bits of classical communication and achieves success probability $p_{\text{succ}}\ge 1/2+{\left(1-2^{-Q}\right)}^{2Q}\mathit{ϵ}$.

Now, if for a function $f\left(x,y\right)$ there exists a gap between $C\left(f\right)$ and ${\left(Q\left(f\right)\right)}^2$ with $p_{\text{succ}}=1/2+\delta$ for the classical communication complexity protocol, and $\delta \ll \mathit{ϵ}$—then we observe the quantum violation of the Bell inequality of the form

$${\displaystyle \sum _{x,y}\mu \left(x,y\right)}{\displaystyle \sum _{q\in \mathcal{P}}p\left(o_q=f\left(x,y\right)|x,y\right)}\le \frac{1}{2}+\delta ,$$ [3]

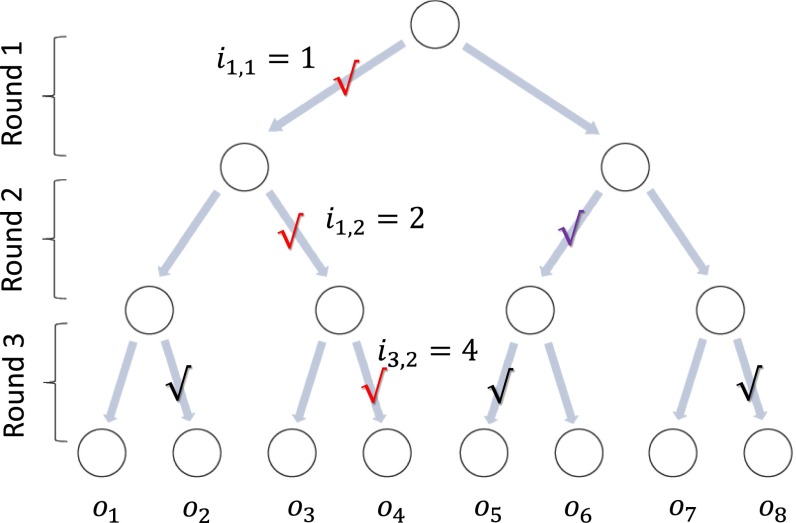
where μ is a probability measure on $X\times Y$, the set $\mathcal{P}$ denotes the set of all paths from the root to the leaves of length $2r-1$ of the tree formed by the subsequent outputs of Alice and Bob in the protocol, and $p\left(o_q=f\left(x,y\right)|x,y\right)$ is the marginal probability that comes from summing over all indexes that do not explicitly appear in the path q (Fig. 3). With the exception of the last level, every node on the ith level has $N_i$ children that correspond to the outcome of the ith round of teleportation. The index of the first node in the path corresponds to the state being on Alice’s side and each subsequent index corresponds to the state being either on Alice’s or on Bob’s side in the alternating manner. The leaves of the tree correspond to the outcomes of Bob’s binary observable, which is his guess of the value of the function $f\left(x,y\right)$. (Note that in the Bell inequality, only special outputs appear—those given by the paths of length $2r-1$ from the root to the leaves—whereas in general, outputs will be given by all sequences composed of choosing one node from every level.)

Fig. 3.

Exchange of the information after simultaneous teleportations to reveal the path of the teleported system in a three-round protocol. After Alice’s teleportation measurement in the first round the state ended up in port 1. Then, Bob teleports each of the two ports from the array that he used in the previous round, obtaining the outcomes 2 and 3 for ports 1 and 2, respectively. Finally, Alice performs a teleportation measurement for each of her four ports, obtaining the outcomes $\mathrm{2,4,5,8}$ for the ports $\mathrm{1,2,3,4}$, respectively. A defines a path q to be a sequence of teleportation outcomes: $q=\left\{i_{\mathrm{1,1}}=1,i_{\mathrm{2,1}}=2,i_{\mathrm{3,2}}=4\right\}$. The last node of the path points to the system, whose outcome provides Bob’s guess. Recall that the measurements are performed at the same time, and the sequential multiround protocol consists only of the exchange of classical information obtained after teleportation. The latter is required to identify the last node of the path, which is used to make a guess about the value of the function.

The Bell inequality [3] is the central quantity of this paper. The left-hand side of the inequality constitutes the maximal success probability of guessing the value of f that can be achieved with the correlations of the form [2]. If this success probability turns out to be greater than the maximal success probability attained by the best classical protocol (the right-hand side of the inequality), this implies that correlations [3] reveal Bell nonlocality.

Large Violation of a Bell Inequality from Communication Complexity

We now show how to combine the above ingredients to get the main result: Whenever $C\left(f\right)\gg {\left(Q\left(f\right)\right)}^2$, we obtain an unbounded violation of the Bell inequality—the ratio of the quantum to the classical value of our Bell inequality grows arbitrarily when we increase the number of inputs and outputs (6, 9, 11, 16–18).

To state and proof the main theorem we summarize the above results in the following sequence of steps:

• i)Given a quantum protocol with advantage that uses Q bits of communication and achieves $p_{\text{succ}}=1/2+\mathit{ϵ}$, we convert it (using Proposition 1) to the memoryless protocol that uses $10Q^2$ bits of communication and achieves the same success probability.
• ii)From the memoryless protocol using measurements and quantum state we obtain the set of quantum correlations $R_q$.
• iii)
  Using $R_q$ and $10Q^2$ bits of classical communication, we obtain a new protocol $\overline{P}$ that achieves

  $$p_{\text{succ}}\ge \frac{1}{2}+{\left(1-2^{-Q}\right)}^{2Q}\mathit{ϵ}.$$

  Recall that all of the above measurements are done simultaneously, but the exchange of the corresponding classical information happens sequentially.
• iv)
  We turn protocol $\overline{P}$ into a Bell inequality. To this end, we consider a general construction of Bell inequality given any function $f\left(x,y\right)$ and a protocol P that uses communication and correlations. Namely, denote $f_P\left(a,b,x,y\right)$ to be a guess of $f\left(x,y\right)$ determined by the protocol for given inputs $\left(x,y\right)$ and outputs $\left(a,b\right)$. Then, consider the probability of success of guessing the correct value of the function f parameterized by the correlations R,

  $$\begin{array}{c}{p}_{f,P}^{\text{succ}}\left(R\right)=\text{Prob}\left[f_P\left(a,b,x,y\right)=f\left(x,y\right)\right]=\\ {\displaystyle \sum _{x,y}\mu \left(x,y\right)}{\displaystyle \sum _{a,b}R\left(ab|xy\right){\mathbb{I}}_{\left\{f_P\left(a,b,x,y\right)=f\left(x,y\right)\right\}}},\end{array}$$ [4]

  where $\mathbb{I}(\cdot )$ is the indicator function. Our Bell inequality will simply be a shifted value of guessing probability

$$B_{f,P}\left(R\right)=p_{f,P}^{\text{succ}}\left(R\right)-\frac{1}{2}.$$ [5]

• v)
  We consider the behavior of the above Bell inequality on classical correlations $R_{\text{cl}}$ as a function of the amount of communication used by $\overline{P}$. To this end we apply Lemma 3 (proved in Supporting Information, section I), which states that given an arbitrary protocol P that uses $C_P$ bits of communication, we have

  $$B_{f,P}\left(R_{\text{cl}}\right)\le \sqrt{\frac{3C_P}{C\left(f,2/3\right)}}.$$

  We apply it to our protocol $\overline{P}$.

Our main claim is contained in Theorem 1:

Theorem 1.

Suppose two parties can compute a function f, using the protocol P with Q qubits of communication and the success probability $2/3$. Then there exist a quantum correlation $R_q$ and a Bell inequality $B_{f,P}$ such that

$$\frac{B_{f,P}\left(R_q\right)}{B_{f,P}\left(R_{\text{cl}}\right)}\ge \frac{\sqrt{C\left(f,2/3\right)}}{6\sqrt{30}Q}{\left(1-2^{-Q}\right)}^{2Q},$$ [6]

where $C\left(f,2/3\right)$ is the classical communication complexity of f with probability $2/3$, and $R_{\text{cl}}$ stands for arbitrary classical correlation.

Remark:

Theorem 1 implies that if $Q^2$ is sufficiently smaller than C (i.e., when we have a sufficiently large quantum advantage in communication complexity), then we obtain violation of a Bell inequality.

Proof:

Given the protocol P of computing f with success probability $2/3=1/2+1/6$ (where we set $\mathit{ϵ}=1/6$) while using Q qubits of communication, we consider protocol $\overline{P}$ from item iii, which uses $10Q^2$ bits of communication with the same probability of success. If applied to correlations $R_q$ of item ii and using Lemma 1 above, it achieves the success probability $1/2+{\left(1-2^{-Q}\right)}^{2Q}\left(1/6\right)$. Thus, the Bell inequality $B_{f,\overline{P}}$ constructed in item v evaluated on $R_q$ gives

$$B_{f,\overline{P}}\left(R_q\right)\ge {\left(1-2^{-Q}\right)}^{2Q}\frac{1}{6}.$$ [7]

The next step is to check the value of the same Bell inequality on classical correlations $R_{\text{cl}}$. To this end, we apply item v with $P=\overline{P}$, and $C_P=10Q^2$, obtaining that for any classical correlations $R_{\text{cl}}$

$$B_{f,\overline{P}}\left(R_{\text{cl}}\right)\le \sqrt{\frac{30Q^2}{C\left(f,2/3\right)}}.$$ [8]

We put together Eqs. 7 and 8, obtaining the required bound for the ratio of Bell value on our particular quantum correlation $R_q$ and arbitrary classical correlation $R_{\text{cl}}$:

$$\frac{B_{f,\overline{P}}\left(R_q\right)}{B_{f,\overline{P}}\left(R_{\text{cl}}\right)}\ge \frac{\sqrt{C\left(f,2/3\right)}}{6\sqrt{30}Q}{\left(1-2^{-Q}\right)}^{2Q}.$$ [9]

$\mathrm{\square }$

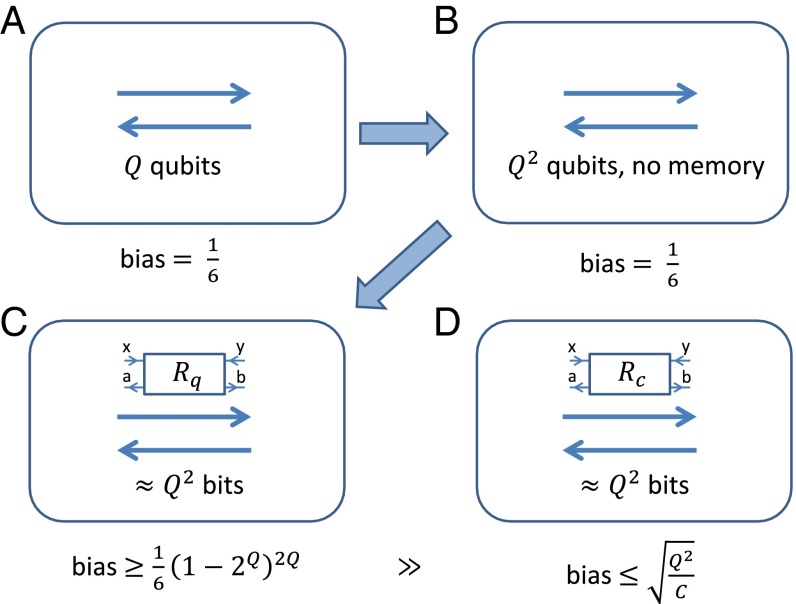
For $C\left(f,2/3\right)\gg Q$ the right-hand side becomes large, implying large violation of a Bell inequality. The diagrammatic proof of Theorem 1 is depicted in Fig. 4.

Fig. 4.

The scheme of the proof of Theorem 1. (A) an initial protocol evaluating function f with bias $1/6$, using Q qubits; (B) memoryless protocol, with the same bias, using $Q^2$ qubits; (C) protocol $\overline{P}$ using quantum correlations and $Q^2$ qubits, with bias still about $1/6$; (D) protocol $\overline{P}$ gives small bias for any classical correlation $R_c$ if $Q^2$ is sufficiently smaller than $C\left(f,2/3\right)$.

We provide several examples to demonstrate the power of our result.

Examples

Both of the examples are based on an explicit communication complexity problem called “vector in subspace” that was first introduced in ref. 5. In this problem, Alice and Bob receive the n-dimensional vector v and the description of $n/2$-dimensional subspace H, respectively, with the promise that either $v\in H$ or $v\in H^{\perp }$. The aim of the game is to determine which subspace v belongs to by exchanging messages between the parties. We consider two variants of the problem below.

Vector in Subspace Problem with One-Way Communication.

In this protocol, there is only one round of communication from Alice to Bob. Also, the local memory is not used. The deterministic quantum protocol requires $\log n$ qubits of communication (where n is the length of the vector in the problem), whereas the classical communication complexity is $C\left(f,2/3\right)=\mathrm{\Omega }\left(\sqrt[3]{n}\right)$ (8).

Knowing the quantum protocol P explicitly, we obtain a stronger Bell inequality because we do not need to invoke any approximations. Using $5\log n$ bits of communication and correlations [2], we can achieve the quantum success probability of $p_q=1/2+1/2{\left(1-2^{-5\hspace{0.17em}\log n}\right)}^{10\hspace{0.17em}\log n}$, whereas the classical protocol using the same amount of communication achieves $p_c=1/2+\delta$, where ${\delta }^2\le 5\log n/A\sqrt[3]{n}$, for some constant A. Thus, the ratio of quantum to classical values of the Bell inequality given in Theorem 1 is

$$\frac{B\left(R_q\right)}{B\left(R_{\text{cl}}\right)}=\frac{1/2\left(1-1/n\right)}{\sqrt{5\hspace{0.17em}\log \hspace{0.17em}n/A\sqrt[3]{n}}}=\mathrm{\Omega }\left(\frac{\sqrt[6]{n}}{\sqrt{\log \hspace{0.17em}n}}\right),$$ [10]

where we use $B\equiv B_{f,P}$ when it does not lead to ambiguity.

Vector in Subspace Problem with Two-Way Communication [Raz Original Problem (5)].

In this protocol, Alice sends Bob a quantum state of size $\log n$ (where n is the length of the vector in the problem) and then receives a state of the same size. As in the previous example, the parties do not use any local memory. There exists a deterministic quantum protocol for this problem. The classical communication complexity is $C\left(f,2/3\right)=\mathrm{\Omega }\left(\sqrt[4]{n}/\log n\right)$. But using only $10\log n$ qubits of communication and correlations [2], we get $p_q=1/2+{\left(1-2^{-\log n}\right)}^2$. The classical protocol using the same amount of communication achieves $p_c=1/2+\delta$, where ${\delta }^2\le c\left(10{\log }^{2}n/\sqrt[4]{n}\right)$, for some constant A. Thus, the ratio of quantum to classical Bell values is

$$\frac{B\left(R_q\right)}{B\left(R_{\text{cl}}\right)}=\frac{1/2{\left(1-1/n\right)}^2}{\sqrt{10A{\log }^{2}n/\sqrt[4]{n}}}=\mathrm{\Omega }\left(\frac{\sqrt[8]{n}}{\log n}\right).$$ [11]

One-Way Communication Complexity Problems.

We now detail the scenario when Alice is allowed to send a single message to Bob to introduce a very different approach to obtain the violation of a Bell inequality. In this case, state preparation protocol on Alice’s side followed by the measurement of a quantum state by Bob will suffice. Also, there is no need for the local quantum memory on either side because one does not have to preserve the state of the communication protocol. Therefore, the role of the port-based teleportation is played by the remote state preparation.

One marked difference of this approach is that it consumes a significantly smaller amount of entanglement. Also, in this setting, we obtain the nonlinear Bell inequality that explicitly features the probability of Bob guessing the communication from Alice—something that is not possible using the method that relies on the port-based teleportation.

We first outline the remote state preparation protocol and then construct the relevant Bell inequalities below.

Remote State Preparation.

In the remote state preparation, Alice and Bob share a maximally entangled qudit state ${|{\mathrm{\Phi }}^{+}\rangle }_{AB}=\left(1/\sqrt{d}\right){\displaystyle {\sum }_{i=0}^{d-1}{|i\rangle }_A{|i\rangle }_B}$. Alice wants to prepare a known quantum state $|\varphi \rangle$ on Bob’s side by acting only on her share of the qudit, requiring no postprocessing on his side. To achieve this, she performs a measurement with elements $\left\{|\varphi *\rangle \langle \varphi *|,\mathbb{I}-|\varphi *\rangle \langle \varphi *|\right\}$, where $|\varphi *\rangle$ is a conjugation of $|\varphi \rangle$ in the computational basis, on her part of ${|{\mathrm{\Phi }}^{+}\rangle }_{AB}$, followed by the communication of the classical outcome to Bob if she measured $|\varphi *\rangle \langle \varphi *|$ (we denote this outcome as 1). This protocol has a very low probability of success, 1/d. We discuss the techniques to amplify it in Supporting Information, section II.

Correlations.

Applying the remote state preparation protocol to our communication complexity problem, we obtain the correlations

$$p\left(a,b|x,y\right)=\text{tr}\left[\left(M_x^a\otimes M_y^b\right){\rho }_{AB}\right],$$ [12]

where $\left\{M_x^a\right\}$ are the POVM elements from the remote state preparation and $\left\{M_y^b\right\}$ describes Bob’s measurements on the shared state ${\rho }_{AB}$. In the current setup, the number of the binary observables of Alice and Bob is equal to the number of inputs x and y. The correlations [12] are obtained by acting on a single instance of the entangled state whereas the multiround approach uses in the order of $2^Q$ states. Merging m instances together, we obtain the set of correlations

$$p\left(\left\{i\right\},\left\{o_1,\dots ,o_N\right\}|x,y\right),$$ [13]

where $i\in I$, $I=\left\{1,\dots ,m\right\}$ denotes the case when the remote state preparation succeeds and $\left\{o_i\right\}$ are the respective outputs. Thus, our Bell inequality may be written in the form [3]:

$${\displaystyle \sum _{x,y}\mu \left(x,y\right)}{\displaystyle \sum _{i\in I}p\left(i,o_i=f\left(x,y\right)|x,y\right)}\le \frac{1}{2}+\delta .$$ [14]

Nonlinear Bell Inequality.

Here we derive a Bell inequality for the case where the parties have the option to abort at any stage of the protocol. Our inequality turns out to be nonlinear and will depend only on two parameters, $p_A$ and $p_B$, defined as follows:

• •
  $p_A$—probability that Alice succeeded, i.e., her outcome is 1 (averaged over all observables by the measure μ):

  $$p_A={\displaystyle \sum _{x,y}\mu \left(x,y\right)p\left(a=1|x,y\right)}.$$ [15]

  This probability turns out to be equal to Bob successfully “guessing” the communication from Alice in the absence of communication from the latter.
• •
  $p_B$—conditional probability that Bob’s outcome is equal to value of the function, given that Alice succeeded:

  $$p_B={\displaystyle \sum _{x,y}\mu \left(x,y\right)p\left(b=f\left(x,y\right)|x,y,a=1\right)}.$$ [16]

Using roughly $m\approx 1/p_A$ instances of the state ${\rho }_{AB}$, Alice obtains one successful outcome $a=1$ on average. Then, Alice communicates to Bob this successful instance.

To obtain the inequality, we show how Alice and Bob may guess the correct value of the function. In this setup, as in the previous case, Alice uses $m\approx 1/p_A$ instances of the state ${\rho }_{AB}$. Then Alice communicates to Bob the first instance where the outcome appeared, using $\log m\approx -\log p_A$ bits. Finally, Bob looks at the outcome for the successful instance and with probability $p_B$ obtains the value of the function f.

If Alice and Bob share a state that admits a local-realistic description, then the used communication cannot be smaller than the value $C\left(p_B,n\right)$, because it is the optimal value attainable by classical means. Thus, for any local-realistic state, we must necessarily have

$$\log \frac{1}{p_A}\mathrm{\gtrsim }C\left(p_B,n\right).$$ [17]

See Supporting Information, section III for further details.

Discussion

Examples show that our protocol produces large violations that are a bit weaker than the best known ones such as $n/{\log }^{2}n$ (16) or $\sqrt{n}/\log n$ (9). This seems to be the price for its universality. However, it is an interesting open question, whether one can find a communication complexity protocol, such that the obtained Bell inequality would admit more dramatic violation than what is currently achievable. Another challenge is to decrease the amount of entanglement used to violate our Bell inequalities, which in our construction is exponential in the quantum communication complexity of the given problem. Similarly, the output size grows exponentially, which gives rise to the question of whether there exists a more efficient method of exhibiting the Bell nonlocality of quantum communication complexity schemes. The last two challenges could be addressed by devising a more efficient teleportation protocol or improving one of the existing ones (19). Finally, our method does not cover the protocols with initial entanglement. This is quite paradoxical, because protocols that use initial entanglement should be Bell nonlocal even more explicitly. It is therefore desirable to search for a method of demonstrating the Bell nonlocality of such protocols.

I) Proof of Lemma

Lemma 3.

For a protocol P supplemented by classical correlations $R_c$ and using $C_P$ bits of communication, the shifted success probability of computing f is bounded above as

$$B_{f,P}\left(R_c\right)\le \sqrt{\frac{C_P}{C\left(f,2/3\right)}}.$$ [S1]

Proof:

Consider the success probability of the protocol P in the statement of Lemma 3 after the exchange of $C_P$ messages:

$$p_c=\frac{1}{2}+B_{f,P}\left(R_c\right)\le \frac{2}{3}.$$ [S2]

To express the ratio [S1] we need to find $B_{f,P}\left(R_c\right)$ in terms of communication complexity. We achieve this by using the amplification argument (see Supporting Information, section II for the proof), which boosts the success probability to 2/3 at the expense of sending at most $C\left(f,p_c\right)$ bits of communication:

$$\begin{array}{c}C\left(f,p_c\right)\ge \frac{1}{3}{\left(p_c-\frac{1}{2}\right)}^{2}C\left(f,\frac{2}{3}\right)\\ =\frac{1}{3}{\left(B_{f,P}\left(R_c\right)\right)}^{2}C\left(f,\frac{2}{3}\right).\end{array}$$ [S3]

Thus,

$$B_{f,P}\left(R_c\right)\le \sqrt{\frac{3C\left(f,p_c\right)}{C\left(f,2/3\right)}}=\sqrt{\frac{3C_P}{C\left(f,2/3\right)}}.$$ [S4]

$\square$

II) Communication Complexity for Arbitrary Success Probability from Communication Complexity for Fixed Success Probability

Here we use the amplification (pumping) argument, which is a well-known technique for increasing the success probability of a randomized protocol (20) by repetition, and prove the following bound for the communication required by a randomized algorithm,

$$C\left(f,p_{\text{S}}\right)\ge \frac{1}{3}{\left(p_{\text{S}}-\frac{1}{2}\right)}^{2}C\left(f,\frac{2}{3}\right),$$ [S5]

where $C\left(f,p_{\text{S}}\right)$ stands for communication complexity of an arbitrary (quantum or classical) randomized protocol. The bound is valid for $1/2<p_{\text{S}}<2/3$. We use the pumping argument to show that a smaller $C\left(f,p_{\text{S}}\right)$ would enable one to construct a protocol that uses less communication than $C\left(f,2/3\right)$ and achieves $p_{\text{S}}=2/3$ and hence leads to a contradiction.

Let protocol $\mathrm{\Pi }$ use $C\left(1/2+ϵ\right)$ bits of communication to achieve $p_{\text{S}}=1/2+\mathit{ϵ}$. Let us consider protocol $\mathrm{\Pi }\prime$ in which Alice and Bob repeat protocol $\mathrm{\Pi }$ l times and then Bob returns as an answer the most common output of $\mathrm{\Pi }$. Because we are restricted to Boolean functions, the success probability $p_{\text{S}}\prime$ of $\mathrm{\Pi }\prime$ is equal to the probability that protocol $\mathrm{\Pi }$ gives the correct answer no less than $\lceil l/2\rceil +1$ times. By the Chernoff bound we get

$$p_{\text{S}}\prime \ge 1-\exp \left(-\frac{1}{2}l{\mathit{ϵ}}^2\right).$$ [S6]

Because we require that $p_{\text{S}}\prime \ge 2/3$, we get that

$$l\ge \frac{3}{{ϵ}^2}.$$ [S7]

From the communication complexity bound, it is known that to achieve $p_{\text{S}}=2/3$, the protocol $\mathrm{\Pi }\prime$ requires at least $C\left(f,2/3\right)$ bits of communication. On the other hand, protocol $\mathrm{\Pi }\prime$ repeats protocol $\mathrm{\Pi }$ l times and uses $lC\left(f,1/2+\mathit{ϵ}\right)$ bits of communication. Putting this together, we have

$$lC\left(f,\frac{1}{2}+\mathit{ϵ}\right)\ge C\left(f,\frac{2}{3}\right).$$ [S8]

Using relation [S7] we get finally

$$C\left(f,\frac{1}{2}+\mathit{ϵ}\right)\ge \frac{{\mathit{ϵ}}^2}{3}C\left(f,\frac{2}{3}\right).$$ [S9]

For $1/2+\mathit{ϵ}=2/3$ our estimation leads to a communication complexity bound of $1/108C\left(f,2/3\right)$ which is much below the true value. This discrepancy comes from the nonoptimality of the pumping protocol.

III) Rigorous Derivation of the Nonlinear Bell Inequality and Its Violation

We now derive the nonlinear Bell inequality

$$\lceil \log 1/p_A+\log \log 1/\delta \rceil +1\ge C_{\mu }\left(f,n,\left(1-\delta \right)p_A+\delta /2\right),$$ [S10]

where the classical communication complexity $C\left(f,p\right)$ is additionally parameterized by μ and the size of the problem n. First, we construct a one-way protocol with classical communication that makes use of shared entanglement given the set of correlations. We restrict ourselves to the family of correlations $p\left(a,b|x,y\right)$ with $x,y\in {\left\{\mathrm{0,1}\right\}}^n$, $a,b\in \left\{\mathrm{0,1}\right\}$. As usual, $a=1$ is interpreted as the success on Alice’s side. When the latter occurs, we expect b to hold the value of the function $b=f\left(x,y\right)$. This restriction does not limit the generality because we may always take negation of $a,b,x,y$, which is a local operation.

We show that for any correlation $p\left(a,b|x,y\right)$, characterized by n, $p_A$, and $p_B$ (defined in the main text) leads to the protocol ${\mathrm{\Pi }}_B$ solving a problem of size n, using $\lceil \log 1/p_A+\log \log \delta \rceil +1$ bits of communication and achieving $p_{\text{S}}^{\mu }=\left(1-\delta \right)p_B+\delta /2$ for the initial probability distribution $\mu \left(x,y\right)$.

Protocol ${\mathrm{\Pi }}_B$ works as follows. Let Alice and Bob share $\lceil k/p_A\rceil$ copies of the correlations. They use their inputs x, y to select the appropriate measurements. Alice sends to Bob the index i of the first correlation where she obtained $a=1$. Then, Bob estimates b for the respective correlation i and returns it as an output of protocol ${\mathrm{\Pi }}_B$. In the case when none of the boxes returned $a=1$, Alice outputs ABORT and Bob returns a random bit.

The protocol requires $\lceil \log \hspace{0.17em}k/p_A\rceil$ bits of communication to encode i of the box and 1 extra bit to encode the message ABORT. The probability that Alice gets $a=1$ for at least one instance is $1-{\left(1-p_A\right)}^{k/p_A}\ge 1-2^{-k}$. For this case Bob returns $b=f\left(x,y\right)$ with the probability $p_B$. If Bob receives ABORT, he returns the proper value with probability $1/2$. Putting $\delta =2^{-k}$ we get an overall success probability of $p_{\text{S}}^{\mu }=\left(1-\delta \right)p_B+\delta /2$ with communication of $\lceil \log 1/p_A+\log \log 1/\delta \rceil +1$ bits.

For all of the correlations with the local hidden variable model we get

$$\lceil \log 1/p_A+\log \log 1/\delta \rceil +1\ge C_{\mu }\left(f,n,\left(1-\delta \right)p_B+\delta /2\right).$$ [S11]

In the case when the communication complexity is given only for the fixed probability of success $p_{\text{S}}=2/3$, by the pumping argument and the fact that $C_{\mu }\left(2/3,n\right)\mathrm{\le }{C}_{\mu }\left(p_{\text{S}},n\right)$ for $p_{\text{S}}\ge 2/3$ we obtain

$$\lceil \log 1/p_A+\log \log 1/\delta \rceil +1$$ [S12]

$$\ge \{\begin{array}{c}\frac{1}{3}{\left(\left(1-\delta \right)p_B+\delta /2-\frac{1}{2}\right)}^2{C}_{\mu }\left(\frac{2}{3},n\right),\hspace{1em}\text{if\hspace{0.17em}}\left(1-\delta \right)p_B+\delta /2\le \frac{2}{3},\\ C_{\mu }\left(\frac{2}{3},n\right),\hspace{1em}\text{if\hspace{0.17em}}\left(1-\delta \right)p_B+\delta /2>\frac{2}{3}.\end{array}$$

Using the fact that correlations obtained from a quantum protocol with communication complexity Q and success probability $p_{\text{S}}$ are characterized by $p_A=2^{-Q}$ and $p_B=p_{\text{S}}$ and inserting them into [S11], we make the following observation:

Observation 1.

Let $C_{\mu }\left(f,n,p_{\text{S}}^C\right)$ be defined as in Eq. S10. If correlations obtained by construction of Eq. 2 in the main text from a quantum protocol with success probability $p_{\text{S}}$ and communication complexity Q do not violate the Bell inequality [S11], then

$$Q\left(f,n,p_{\text{S}}\right)\ge \underset{\delta }{\text{max}}\left(C_{\mu }\left(f,n,\left(1-\delta \right)p_{\text{S}}+\delta /2\right)-\log \log 1/\delta \right)-2.$$ [S13]

To witness the violation of a Bell inequality constructed for a particular function f, it suffices to know how $C_{\mu }\left(f,n,p_{\text{S}}^C\right)$ dominates over $Q_{\mu }\left(f,n,p_{\text{S}}^Q\right)$ for some fixed $p_{\text{S}}^Q\ge p_{\text{S}}^C$. [Function $g\left(n\right)$ dominates $h\left(n\right)$ if for any constant k there exists $n_0$ such that for any $n>n_0$ we have $kg\left(n\right)\ge h\left(n\right)$.]

IV) Memory Compression of Quantum Communication Protocols

We convert an arbitrary quantum communication protocol into one where on each round Alice and Bob compress their memory and teleport it alongside the message. This ensures that they do not store any information associated with the message between the rounds.

The theoretical underpinning of such conversion is Lemma 2, proved by Yao (3) and Kremer (14) (also ref. 21, lemma 7.2.1 and ref. 22, appendix A). Lemma 2 applies to protocols where only a single qubit is sent per round. One can also derive a version of the latter where the message size is variable per round, which gives a more efficient memoryless version of protocols that need only a small number of rounds.

Lemma 2.

The state of an $\ell$-qubit protocol (without prior entanglement) on input $\left(x,y\right)$ can be written as

$${\displaystyle \sum _{i\in {\left\{\mathrm{0,1}\right\}}^{\ell }}{\alpha }_i\left(x\right){\beta }_i\left(y\right)|A_i\left(x\right)\rangle |i_{\ell }\rangle |B_i\left(y\right)\rangle ,}$$

where the ${\alpha }_i\left(x\right)$ and ${\beta }_i\left(y\right)$ are complex numbers of magnitude $\le 1$, the $|A_i\left(x\right)\rangle ,|B_i\left(y\right)\rangle$ are unit vectors belonging to Alice and Bob, respectively, and $i_{\ell }$ denotes the last bit of the $\ell$-bit string i.

Consider the state description given by Lemma 2 for our quantum protocol after m rounds. Let ${\left\{|A_i\left(x\right)\rangle \right\}}_{i\in {\left\{\mathrm{0,1}\right\}}^l}$ describe Alice’s local states encoded in k qubits, for some k. Because there are only $2^m$ different vectors $|A_i\left(x\right)\rangle$, there exists a unitary $U_m\left(x\right)$ and a collection of m-qubit states $|{\widehat{A}}_i\left(x\right)\rangle$ such that for all $i\in {\left\{\mathrm{0,1}\right\}}^m$ we have $U_m\left(x\right)|A_i\left(x\right)\rangle ={|0\rangle }^{\otimes \left(k-m\right)}|{\widehat{A}}_i\left(x\right)\rangle$. [More precisely, we can find some orthonormal basis $|e_i\left(x\right)\rangle$ for the space spanned by the (not necessarily orthogonal) $|A_i\left(x\right)\rangle$, which consists of at most $2^m$ basis vectors. Then we can write $U_m\left(x\right)={\displaystyle \sum _{i\in {\left\{\mathrm{0,1}\right\}}^m}|0\mathrm{\dots }0i\rangle }\langle e_i\left(x\right)|+T,$ where T is the completion of the unitary transformation on the orthogonal complement of the subspace spanned by the $|e_i\left(x\right)\rangle$ vectors, to the orthogonal complement of the subspace spanned by the $|0\mathrm{\dots }0i\rangle$ vectors.] Similarly on Bob’s side there exists a unitary $V_m\left(y\right)$ such that $V_m\left(y\right)|B_i\left(y\right)\rangle ={|0\rangle }^{\otimes \left(k\prime -m\right)}|{\widehat{B}}_i\left(y\right)\rangle$, where $k\prime$ is the number of qubits used to encode Bob’s local state ${\left\{|B_i\left(x\right)\rangle \right\}}_{i\in {\left\{\mathrm{0,1}\right\}}^l}$ in the original protocol and every $|{\widehat{B}}_i\left(y\right)\rangle$ is an m-qubit state.

Therefore, the state of the protocol after m rounds can be written as

$$\left(U_m{\left(x\right)}^{†}\otimes V_m{\left(y\right)}^{†}\right)\times \left[{|0\dots 0\rangle }_A{|0\dots 0\rangle }_B{\displaystyle \sum _{i\in {\left\{\mathrm{0,1}\right\}}^m}{\alpha }_i\left(x\right){\beta }_i\left(y\right)|{\widehat{A}}_i\left(x\right)\rangle |i_m\rangle |{\widehat{B}}_i\left(y\right)\rangle }\right],$$

where ${|0\dots 0\rangle }_A$ and ${|0\dots 0\rangle }_B$ are the trivial local states on Alice and Bob, respectively. Then all of the local memory of the m-round protocol can be encoded in m qubits. This proves Proposition 1 in the main text.