Energy landscape in protein folding and unfolding

Significance

Protein folding represents an open question in science, and the free-energy landscape framework is one way to describe it. In particular, the role played by water in the processes is of special interest. To clarify these issues we study, during folding–unfolding, the temperature evolution of the magnetization for hydrophilic and hydrophobic groups of hydrated lysozyme using NMR spectroscopy. Our findings confirm the validity of the theoretical scenario of a process dominated by different energetic routes, also explaining the water role in the protein configuration stability. We also highlight that the protein native state limit is represented by the water singular temperature that characterizes its compressibility and expansivity and is the origin of the thermodynamical anomalies of its liquid state.

Abstract

We use ¹H NMR to probe the energy landscape in the protein folding and unfolding process. Using the scheme $\rightleftarrows$ reversible unfolded (intermediate) $\to$ irreversible unfolded (denatured) state, we study the thermal denaturation of hydrated lysozyme that occurs when the temperature is increased. Using thermal cycles in the range $295<T<365$ K and following different trajectories along the protein energy surface, we observe that the hydrophilic (the amide NH) and hydrophobic (methyl CH₃ and methine CH) peptide groups evolve and exhibit different behaviors. We also discuss the role of water and hydrogen bonding in the protein configurational stability.

An intriguing problem of statistical physics concerns the evolutionary pathways that molecular systems follow as they form mesoscale structures and exhibit new functional behaviors (1). An example of this problem is the self-organization of biosystems that evolve from basic molecules. This challenging subject is studied by using a variety of theoretical methods (2–4). The free-energy landscape model is nowadays the most used to describe such phenomena and especially the aging of the protein folding mechanism (1, 5, 6), i.e., the way in which proteins fold to their native state and then unfold (protein denaturation) (6, 7). The model is based on the idea that in complex materials and systems there are many thermodynamical configurations in which the free-energy surface exhibits a number of local minima separated by barriers, i.e., as the system explores its phase space the trajectory of its evolution is an alternating sequence of local energy minima and saddle points (transition states), which are associated with the positions of all of the system particles. A trajectory thus specifies the path of the system as it evolves by moving across its energy landscape.

A peptide is a linear chain of amino acids, and globular proteins are polypeptide chains that fold into their native conformation. During the folding process a polypeptide undergoes many conformational changes and there is a significant decrease in the system configurational entropy as the native state is approached. To understand folding we focus on how proteins search conformational space. The process is accompanied by many microscopic reactions, the nature of which is determined by the specifics of the energy surface. Thus, the characteristics of the energy surface of a polypeptide chain are the key to a quantitative understanding of folding. Although the degrees of freedom of a polypeptide chain allow an enormously large number of possible configurations, “constraints” on the energy decrease these configurations visited in the folding reaction to a limited number (8). Understanding the free-energy surface (“landscape”) enables us to understand the folding process. A balance between the potential energy and the configurational entropy leads to a free-energy barrier that generates the two-state folding behavior usually observed in small proteins. The potential energy decreases as the native state is approached and favors folding, but decreasing the entropy of the configuration is unfavorable to folding.

The thermodynamics and kinetics of folding and unfolding have been intensively studied by molecular dynamics (MD) simulation (9, 10) and different experimental techniques (11–16). Whereas MD simulations directly model peptide conformational transitions in terms of the energy landscape, experiments supply useful but limited information, revealing some details in the structure and the collective dynamics of protein, both dry and in solution. Examples of this include the spectroscopic techniques (e.g., NMR, neutron, X-ray, Raman, and FTIR) that supply data on structure and dynamical modes of the protein, and the calorimetric measurements that follow the reversible folding–unfolding as far as irreversible denaturation (9, 10). The protein dynamics have been studied from the glass state in the deep supercooled regime ($T<200$ K) to the completely denatured state ($T\simeq 350$ K) by proving the essential role of the hydration water. As for bulk water, hydrogen bond (HB) interactions strongly determine the properties of these systems, for which water is not simply a solvent but is also an integral and active component, i.e., it is itself an important “biomolecule” that plays both a dynamic and structural role (17). Hence, HB interactions are the key to understanding water’s properties and how water functions in biological environments (18).

Among the different experimental methods, calorimetry, by monitoring the process reaction rates, focuses directly the energetic properties of the hydrated proteins folding–unfolding mechanism and measures the enthalpy and entropy behaviors. Unlike common chemical reaction rates, which increase as the temperature is increased, the rate constant of the protein folding reaction initially increases on increasing T, by following an Arrhenius law goes to a maximum, and then decreases as the temperature continues to increase (19). This latter situation is also well-described in MD simulations (20). The activation enthalpy is thus T-dependent and the corresponding protein specific heat, $C_P\left(T\right)$, exhibits large changes: first it increases with T, reaches a maximum, and then decreases. Hence a $C_P\left(T\right)$ plot against T exhibits an endothermic peak whose area is related to the enthalpy of transformation of the protein. Such a behavior is also strongly influenced by the protein hydrophobic side chains and hydration water (19, 21, 22).

NMR spectroscopy instead can be used to follow folding (or unfolding) processes by probing interactions as they form at the level of individual residues, and to compare the findings obtained with simulations (13, 23–25). NMR studies involve investigation of the equilibrium conversion between native and denatured states resulting from a protein being subjected to heat, extremes of pH, or chemical denaturants. The kinetics of the process may limit the observations. If the folding occurs on a time scale for which spectra can be measured and recorded sequentially, the spectral changes accompanying the reaction can be monitored at the individual residue level and thus be accurately studied. Recently, new methods have been developed to probe very fast processes or by slowing down the protein folding kinetics by means of proper reactants.

One example of ¹H NMR spectroscopy in which the protein folding can be properly detailed is represented by a real-time study of bovine α-lactalbumin (BLA) refolding, at 293 K, where spectra show significant resonance changes from methyl and methine groups of aromatic residues (25). In this case the experimental strategy was in the control of the Ca²⁺ concentration for which the folding kinetics can vary over several orders of magnitude. The BLA refolding was initiated by a pH jump (in the absence of Ca²⁺) by injecting a solution at pH 8.8 containing a proper buffer into a protein solution at pH 2.0. In such a way the ¹H NMR spectra were recorded at incremented time points (between 1.2 s and 10.3 min, with steps of 10 ms) after initiation of refolding. Such an approach, in enlarging the folding kinetics, represents the potentiality of the NMR methodology in its capability of monitoring specific aspects of the folding, like the protein structural changes, the energetic configurations, and the role of the hydration water.

Here, to study the folding–unfolding of hydrated lysozyme we use a different approach based on its thermal denaturation. More precisely, to quantify the behavior of the protein hydrophilic (the amide NH) and hydrophobic (methyl and methine) groups, during the folding–unfolding process, we use as control variable the temperature, which slows the process kinetics to many hours. The goal is to determine the topography of the protein energy landscape by following different trajectories along the energy surface. This allows us also to consider explicitly the role of water and hydrogen bonding in protein configurational stability.

Results

Thermal denaturation of lysozyme occurs according to the scheme, native state (N) $\rightleftarrows$ reversible unfolded (intermediate) state (RU) $\to$ irreversible unfolded (denatured) state (IU); N $\rightleftarrows$ RU $\to$ IU (21, 22). This is consistent with the general view that the first step in the denaturation of small one-domain globular proteins, e.g., lysozyme, is a reversible conformational (unfolding) transition, and the second step is an irreversible denaturation. Studies performed in the $290<T<370$ K range have revealed that the observed $C_P\left(T\right)$ peak is caused by heat absorption when the equilibrium constant between the native lysozyme state and a conformational different intermediate state increases with T (26, 27). The $C_P^{\text{max}}\left(T\right)$ peak temperature is $T_D=$ 347 K and seems to represent the reversibility limit. Lysozyme at a hydration level of $h=0.3$ has a water monolayer covering its surface (27). As described in Methods, we have conducted the experiments using different heating/cooling cycles exploring completely or partially the folding process N $\rightleftarrows$ RU $\to$ IU. Briefly, cycles A (295 K$\to 365$ K$\to 297$ K) and B (296 K$\to 366$ K$\to 298$ K) follow the complete denaturation starting from the native state with steps of $\mathrm{\Delta }T=2$ K. Cycle C (295 K$\to 320$ K $\to 298$ K) operates only inside the native N state with $\mathrm{\Delta }T=1$ K. Cycles D (310 K$\to 349$ K $\to 310$ K) and E (310 K $\to 343$ K$\to 310$ K) work inside the N $\rightleftarrows$ RU $\to$ IU and N $\rightleftarrows$ RU regions, respectively, with $\mathrm{\Delta }T=1$ K.

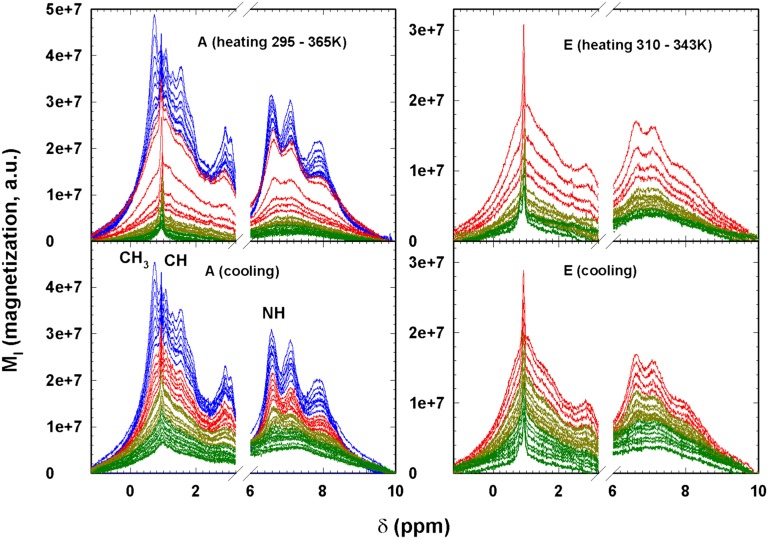
Fig. 1 shows the NMR spectra of the hydrated protein for two thermal cycles after the water contribution has been extracted. In case A the thermal evolution moves from the native state (N) to the fully denatured state (295–365 K), and vice versa. In case E the protein is in the N $\rightleftarrows$ RU phase (310–343 K). From the spectra in cycle A in the heating phase (shown in red), a marked change in the T region around $C_P^{\text{max}}\left(T\right)$ (337–347 K) occurs. Thus, Fig. 1 shows that the folding–unfolding reaction at the individual residue level can be quantitatively monitored, and it supplies the details of the system energy configurations. Among the several residues observable in the ¹H NMR spectra in Fig. 1, we considered the hydrophilic (the amide NH) and hydrophobic (CH₃ and CH) side-chain groups centered at chemical shifts $\delta \simeq 6.7$ ppm, $\delta \simeq 0.8$ ppm, and $\delta \simeq 0.94$ ppm, respectively (28).

Fig. 1.

Protein ¹H NMR spectra (magnetization versus the chemical shift) of cycles A (Left) and E (Right). (Top) Spectra in the heating phase; (Bottom) spectra in the cooling phase. Cycle A regards the complete thermal denaturation of lysozyme, whereas cycle E deals with the reversible evolution from the native to the unfolded (intermediate) state. In both cycles the spectral evolution from the native to the denatured state is reported in different colors just to clarify the protein thermal behavior. The spectra of the native state are reported in green, those of the RU region before the onset of the $C_P\left(T\right)$ peak ($320-336$ K) in dark yellow, the spectra above this region up to the $C_P^{\text{max}}\left(T\right)$ ($337-347$ K) are in red, and finally spectra in the irreversible denatured region (IU) are in blue.

Data Analysis and Discussion.

The hydrogens attached to the amide nitrogen atoms of peptide via HB (29–31) rapidly exchange with solvent hydrogen atoms in unfolded states, but are often protected from exchange when the protein folding is the result of the involvement of amides in the HBs and burial in the protein interior. It is well known that the HBs of water molecules—with the carbonyl oxygen (C = O) and an amide N–H molecular group—trigger the biomolecular activity of the protein peptides. The most stable water–protein configuration has two HBs: (i) a water proton donor bond to the carbonyl oxygen and (ii) an amide N–H proton donor bond to the water oxygen (29–31). In protein folding, the water HBs play a role in protein–protein binding and in molecular recognition. In short, water acts as an HB “glue” between the carbonylic and amidic groups in a protein (31), and during the folding phase the formation of hydrophobic clusters compensates for the loss of system configurational entropy.

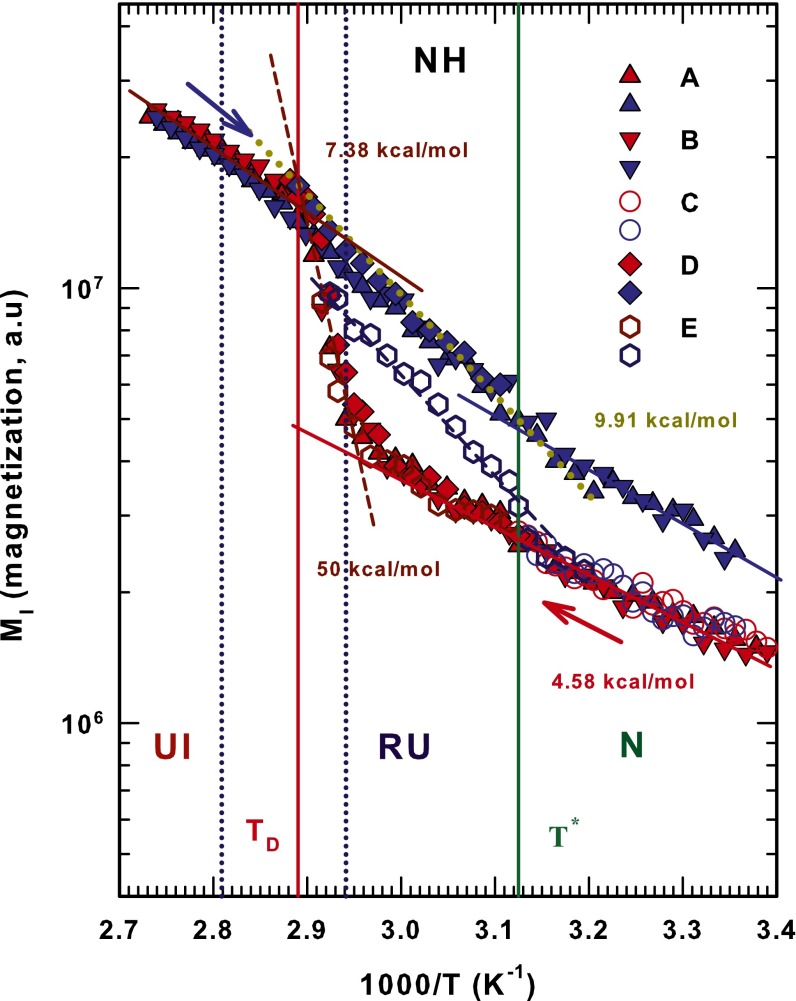
Hence, the protein stability is strongly dependent on the HB strength (or lifetime) that decreases by increasing temperature. It is just this change in the HB strength that determines the thermodynamic properties of the hydrated protein and the corresponding heat capacity effects (30). All of this is reflected in Fig. 1. Figs. 2–4 show an Arrhenius plot [the log of the measured magnetization $M_I\left(T\right)$ vs. $1/T$] that provides a detailed analysis of the different energetic behaviors of the protein groups, namely hydrophilic (the amide NH) and hydrophobic (methyl and methine) groups, evaluated using the procedure described in Methods.

Fig. 2.

AR representation of the measured magnetization values of the hydrophilic amide groups (NH). Data for all five different studied thermal cycles (A, B, C, D, and E) are illustrated. The characteristic temperatures $T^{*}$ and $T_D$ are also reported. Lines represent AR behaviors; the corresponding activation energies $E_A$ are indicated in kcal/mol. Cycles A, B, and D deal with a complete denaturation; C operates in the native protein state (N), whereas E refers to the native and intermediate states (N$\rightleftarrows$ RU).

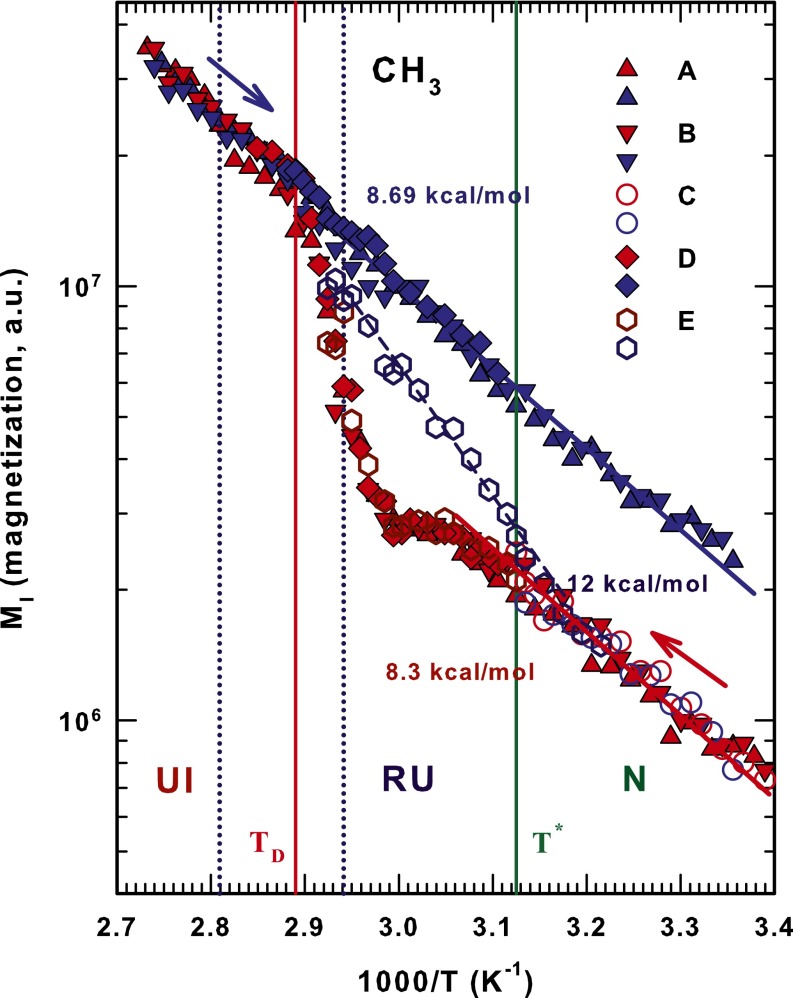
Fig. 4.

Protein methine ($\text{CH}$) magnetization, $M_I\left(T\right)$, for all of the different thermal cycles. Lines and symbols are the same as previously used.

Fig. 2 deals with the Arrhenius representation of the measured magnetization values [$M_I\left(T\right)$] of the hydrophilic amide groups. All five different thermal cycles (A, B, C, D, and E) studied are illustrated. There is a large T interval in A and B for which the complete protein denaturation can be studied, and a smaller T interval in C and D. All figures show the $T_D$ and $T^{*}$ temperatures. $T^{*}$ is the compressibility minimum temperature of bulk water. It is invariant with increasing pressure, and coincides with the cross-over point at which thermal expansion is found to be constant with pressure (32). $T^{*}$ also signals the breakdown of the tetrahedral structure of water (33) and the limit of the protein native state (34). Above $T^{*}$ water becomes a “simple” liquid and thus a bad solvent (32). Fig. 2 shows the T region of the lysozyme-water configurational $C_P\left(T\right)$ peak (dotted line) (26, 27). The overall behavior of cycles A, B, and D is essentially the same. By increasing T, $M_I\left(T\right)$ exhibits a pure Arrhenius (AR) behavior (with an activation energy $E_A\simeq 4.58\hspace{0.5em}\text{kcal}/\text{mol}$) up to the onset of the $C_P\left(T\right)$ peak. Above that it presents a marked increase [super-Arrhenius (SA) in character] that stops at approximately $T_D$, after which it evolves again according to the AR law ($E_A\simeq 7.38\hspace{0.5em}\text{kcal}/\text{mol}$) up to 365 K, where the thermal cycle is inverted. During the cooling phase the energetic behavior of this amide group is about the same as the heating phase up to $T_D$. At the lowest temperatures, $M_I\left(T\right)$ shows two other AR behaviors: (i) one that stops near $T^{*}$ with $E_A\simeq 9.91\hspace{0.5em}\text{kcal}/\text{mol}$ and (ii) one at $T<T^{*}$ that differs somewhat from that of the heating phase in the same T range. Note that cycle D inverts (in T after the heating phase) above $T_D$ and denatures in the same way as A and B. Cycle C operating in the native state shows complete reversibility and thus has the same activation energy as the other cycles during the early heating phase. Note that the energy behavior shown in cycle E reverses at $T=343$ K, i.e., 4 K below $T_D$, but $M_I\left(T\right)$ in the heating phase exhibits the same behavior as the corresponding behavior in cycles A, B, and D and, in the cooling phase, differs completely because it recovers its native behavior as it nears $T^{*}$. All of this demonstrates the energetic behavior of the hydrophilic protein group NH in a cycle that operates reversibly between the N native state and the RU state (as in cycle E). We evaluate the energy ($E_A$) and enthalpy difference between the native and unfolded state (in cycles A, B, and D) and the energy of the reversible unfolding (in cycle E). We find $\simeq 50$ kcal/mol for the first case and $\simeq 12$ kcal/mol for the second, values that agree with those calculated for lysozyme (58 kcal/mol and 14 kcal/mol) and for globular proteins (35).

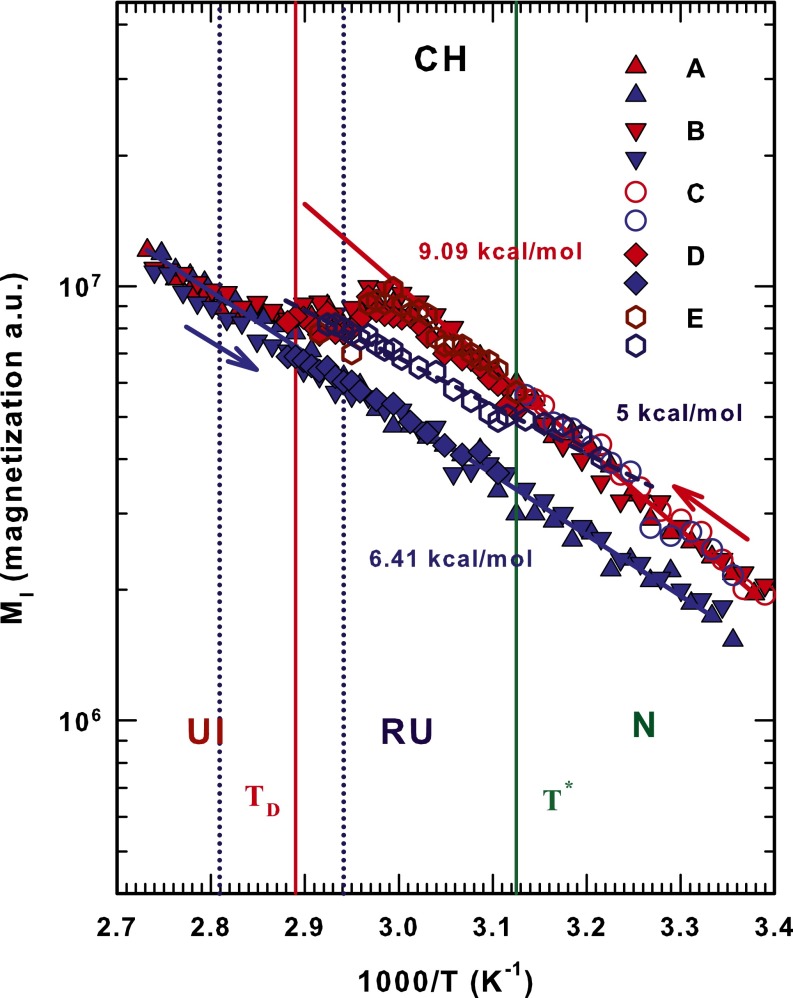
Fig. 3 shows the thermal behavior of the methyl (CH₃) lysozyme groups and reports all of the studied cycles. Note that there are qualitative similarities with the amide groups but that the differing energies indicate a different pathway in both the irreversible denaturation and the reversible unfolding. In the first case the cooling phase appears to be fully AR across the wide T range with $E_A\simeq 8.69$ kcal/mol. In the cooling side of the RU region $E_A\simeq 12\hspace{0.5em}\text{kcal}/\text{mol}$. In the heating phase the N region has an $E_A\simeq 8.3\hspace{0.5em}\text{kcal}/\text{mol}$, the AR behavior stops at $T^{*}$, and in the RU region a weak maximum appears at $\simeq 330$ K, after which $M_I\left(T\right)$ assumes the values of the irreversible denatured phase and rapidly increases to $T_D$.

Fig. 3.

Thermal evolution of the magnetization, $M_I\left(T\right)$, of the protein methyl (${\text{CH}}_3$) groups for all of the studied thermal cycles. Lines and symbols are the same as used in Fig. 2.

Fig. 4 shows $M_I\left(T\right)$ for methine (CH) that in the heating phase is larger than that of the cooling phase. Unlike the amide and methyl polypeptide groups, which are more mobile in the fully denatured phase (IU), i.e., the protein is an open polyelectrolyte and the water a bad solvent, the methine groups are more mobile during the heating phase of the RU region than in the IU phase. This confirms that the hydrophobic groups are buried during protein folding—more so in CH₃ than in CH—and that they are affected by the presence of solvent hydrogen atoms. However, in cycles A, B, and C the methine groups exhibit AR behavior in the cooling phase ($E_A\simeq 6.41$ kcal/mol), and their thermal evolution during the heating phase is more complex. Within the native region the heating phase has an AR evolution ($E_A\simeq 9.09$ kcal/mol) that stops near $T^{*}$, $M_I\left(T\right)$ has a maximum at $T\simeq 330$ K and then decreases to a minimum at $T_D$ and further evolves, exhibiting AR behavior that is nearly identical to that of the cooling phase. In cycle D the methine $M_I\left(T\right)$ recovers (from the RU phase) the thermal trend of the native state, which is an AR behavior with $E_A\simeq 5$ kcal/mol.

$T^{*}$ strongly affects protein folding; it marks the cross-over in bulk water from “normal” liquid behavior when $T>T^{*}$ to behavior characterized by thermodynamic anomalies when $T<T^{*}$. In particular, $T^{*}$ indicates a “singular and universal expansivity point” related to the balance between the entropy and volume cross-correlations $\langle \delta S\delta V\rangle$. In normal liquids $\delta S$ and $\delta V$ fluctuations become smaller as T decreases and they are positively correlated, but in water they become more pronounced at $T^{*}$ and are anticorrelated at the density maximum (at ambient pressure). Structurally $T^{*}$ is identified as the onset temperature of HB clustering (32). Such transport properties as self-diffusion data in the high-temperature regime of bulk water $D_s\left(T\right)$ indicate that $T^{*}$ signals a new dynamic cross-over. Specifically, when T deceases the dynamics change and there is a shift from AR to SA behavior. We used the Adam–Gibbs approach, connected $D_s$ to the configurational entropy $S_c$, and found that at this temperature the local order of water becomes more structured (36). Note that there is a violation of the Stokes–Einstein relationship for $T>T^{*}$ in the first NMR measurement of the proton diffusion in water as a function of T (33). This physical effect of $T^{*}$ in bulk water is also found in confined water. In protein hydration and internal water it is the internal water that “drives” the protein structure from a globular configuration to an open, unfolded configuration. The mechanism for this is the HB structure shared by water, carbonyl oxygen (C = O), and amidic proton (N–H). Figs. 2–4 show that our findings confirm this picture. They also show that above $T^{*}$ as $T_D$ is approached the role of hydration water becomes increasingly important and causes irreversible unfolding in the biopolymer. In the reversibility interval between $T^{*}$ and $T_D$ that defines the interval of the reversibility, the HB structure of the protein side chains enables the internal water to impose a persistent folded structure. All of the measured activation energies quantitatively confirm this picture.

In summary, this study reports the energetic evolution that occurs during the folding and unfolding of separate peptide hydrophilic and hydrophobic groups in single-layer hydrated lysozyme. After studying different thermal cycles, including those that are reversible and those involving complete denaturation, we find that protein properties during this process are strongly affected by different energetic routes.

A comparison between the behavior of these three peptide groups confirms that HBs play a role in protein folding. Evidence for this rests not only in the activation energy values that are of the same order of magnitude as in the HBs, but also in the thermal behavior of the methine groups, specifically in their magnetization $M_I\left(T\right)$ behavior in the N and the RU phases. The higher molecular mobility is caused by the burial effect of the HBs on the hydrophobic groups, which is particularly strong in the case of the methyl groups.

The two forms of protein water, hydration water and internal water, are essential in protein folding. Because all water in the unfolded state belongs to the solvent, hydrogens in the amide groups with peptide bonds interact rapidly via HBs with water. When the protein folds these interactions involve only internal water, which is linked with amides and buries the protein interiors. Thus, clusters of hydrophobic residues are formed in the folded protein and the methine groups are more mobile than the methyl groups.

Methods

We used hen egg white lysozyme at the hydration level $h=0.3$ prepared according to a precise procedure (27). The enzymatic activity in lysozyme is very low up to $h\sim 0.2$, but when h is increased from 0.2 to 0.5 the activity increases sharply. The hydration level was determined by thermogravimetric analysis and also confirmed by directly measuring the weight of the absorbed water. This hydration level corresponds to a monolayer coverage on the protein surface. For each experimental run we used different samples.

Hydrated lysozyme has been studied at ambient pressure and different temperatures (essentially in the $290<T<370$ K range) by using a Bruker AVANCE 700-MHz NMR spectrometer. We focused on the ¹H NMR spectra obtained from free-induction decay, and explored the hydrated protein as a function of temperature in heating–cooling cycles with an accuracy of $\pm 0.1$ K by using the T dependence of the chemical shift of ethylene glycol as a T standard. The spectroscopic experimental technique was “magic angle spinning” (37). The NMR signal intensity $M_I$ is directly related to the system equilibrium magnetization $M_0$, which is related to the susceptibility ${\chi }_0$, which depends linearly on the total number of mobile spins per unit volume, on the mean-square value of the nuclear magnetic moment, and on $1/T$ (the Curie law); hence, the spectra were corrected for the Curie effect.

We used different heating and cooling cycles to explore, completely or partially, the folding process N $\rightleftarrows$ RU $\to$ IU. (i) In cycles A and B we began in the native state and studied the entire process up to complete denaturation. In cycle A the hydrated lysozyme was heated from 295 to 365 K and then cooled down to 297 K, and in cycle B cycle from 296 to 366 K and down to 298 K. In both the warming and the cooling cycles the spectra were measured using steps of $\mathrm{\Delta }T=2$ K. (ii) Cycle C operates inside the native N state. (iii) Cycle D operates inside the N $\rightleftarrows$ RU $\to$ IU region and cycle E inside the N $\rightleftarrows$ RU region. We started both cycles at the sample heating temperature (310 K), but cycle D was inverted immediately above $T_D$ at $T=349$ K and the cooling in cycle E was initiated at 343 K (4 K below $T_D$).

To avoid unwanted abrupt T changes, heating and cooling steps were executed slowly and were ∼20 min in duration. Fig. 1 shows all of the spectra (magnetization intensity $M_I$ versus chemical shift δ in the $-1.2$–10-ppm range) of cycle A (Left) and cycle E (Right) after subtracting from the spectra the central contribution due to water. Both the spectra in the heating phase (Top) and the cooling phase (Bottom) are shown. Fig. 1 also shows the many different contributions made by different protein chemical groups when $M_I$ is increased by increasing T. During the cooling phase the reverse is true. Note that in cycle A the starting spectra and the final spectra (at the same temperature, 297 K) differ to the extent that the spectral evolutions during the heating and cooling phases differ. To clarify the temperature spectral evolution, the different phases are color-coded: the native state spectra in green, the RU region before the $C_P\left(T\right)$ peak at 320–336 K in dark yellow, the spectra above this region up to the $C_P^{\text{max}}\left(T\right)$ at 337–347 K in red, and the irreversible denatured (IU) region in blue. Note that in the heating phase of the cycle A spectra the corresponding $M_I$ rapidly increases in the interval $339<T<351$ K immediately inside the temperature range of the $C_P\left(T\right)$ peak, and in the cooling phase $M_I$ seems to continuously evolve with T. In contrast, cycle E exhibits a different thermal evolution in which the initial and final spectra are essentially the same, indicating that we were in the N $\rightleftarrows$ RU region, that $T_D$ represents the limit of the reversibility, and that the thermal evolution appears to be continuous in both the heating and cooling phases. Note that in the cooling phase we collected spectra in steps of $\mathrm{\Delta }T=1$ K.

To obtain the thermal behavior of hydrophilic (the amide NH) and hydrophobic (methyl CH₃ and methine CH) groups, we performed a spectral deconvolution in terms of their Lorentzian contributions by examining all of the spectra contributions shown in Fig. 1. For all of the measured spectra we used an AR plot to analyze the $M_I$ of the three groups centered at chemical shifts NH $\simeq 6.7$ ppm, CH₃ ≃ 0.8 ppm, and CH $\simeq 0.94$ ppm. The results in Figs. 2–4 are shown for the same $M_I$-reduced temperature ($\mathrm{1,000}/T$) intervals, and are explicitly indicated for the N and IU regions.