Noise-driven growth rate gain in clonal cellular populations

Significance

Differences between individuals exist even in the absence of genetic differences, e.g., in identical twins. Over the last decade, experiments have shown that even genetically identical microbes exhibit large cell-to-cell differences. In particular, the timing of cell division events is highly variable between single bacterial cells. The effect of this variability on long-term growth and survival of bacteria, however, remains elusive. Here, we present a striking finding showing that a bacterial population grows faster on average than its constituent cells. To explain this counterintuitive result, we present a mathematical model that precisely predicts our measurements. Furthermore, we show an empirical growth law that constrains the maximal growth rate of Escherichia coli.

Abstract

Cellular populations in both nature and the laboratory are composed of phenotypically heterogeneous individuals that compete with each other resulting in complex population dynamics. Predicting population growth characteristics based on knowledge of heterogeneous single-cell dynamics remains challenging. By observing groups of cells for hundreds of generations at single-cell resolution, we reveal that growth noise causes clonal populations of Escherichia coli to double faster than the mean doubling time of their constituent single cells across a broad set of balanced-growth conditions. We show that the population-level growth rate gain as well as age structures of populations and of cell lineages in competition are predictable. Furthermore, we theoretically reveal that the growth rate gain can be linked with the relative entropy of lineage generation time distributions. Unexpectedly, we find an empirical linear relation between the means and the variances of generation times across conditions, which provides a general constraint on maximal growth rates. Together, these results demonstrate a fundamental benefit of noise for population growth, and identify a growth law that sets a “speed limit” for proliferation.

Cell growth is an important physiological process that underlies the fitness of organisms. In exponentially growing cell populations, proliferation is usually quantified using the bulk population growth rate, which is assumed to represent the average growth rate of single cells within a population. In addition, basic growth laws exist that relate ribosome function and metabolic efficiency, macromolecular composition, and cell size of the culture as a whole to the bulk population growth rate (1–3). Population growth rate is therefore a quantity of primary importance that reports cellular physiological states and fitness.

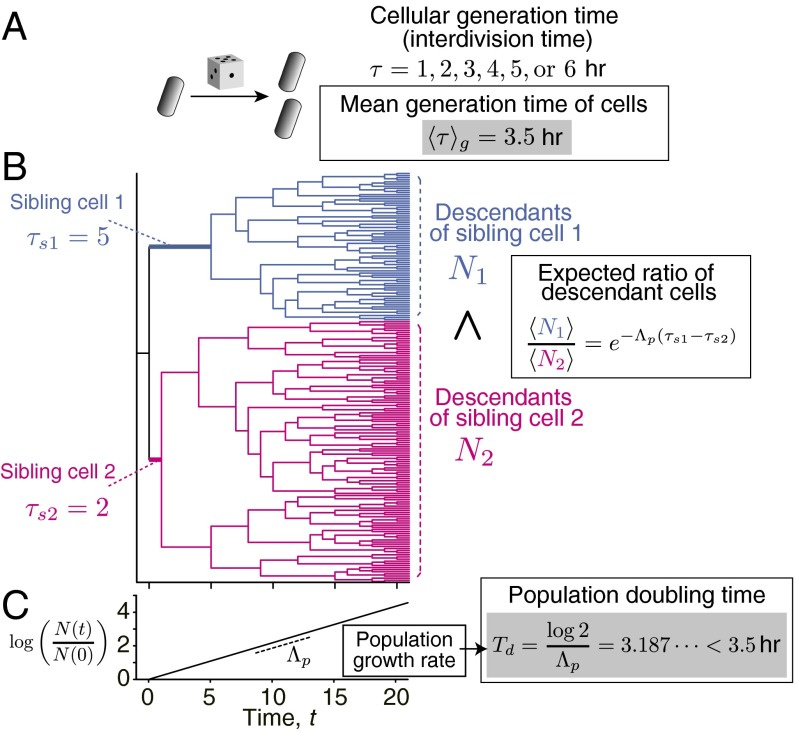
However, at the single-cell level, growth-related parameters such as the division time interval and division cell size are heterogeneous even in a clonal population growing at a constant rate (4–9). Such “growth noise” causes concurrently living cells to compete within the population for representation among its future descendants. For example, if two sibling cells born from the same mother cell had different division intervals, the faster dividing sibling is likely to have more descendants in the future population compared with its slower dividing sister, despite the fact that progenies of both siblings may proliferate equally well (Fig. 1). Intrapopulation competition complicates single-cell analysis because any growth-correlated quantities measured over the population deviate from intrinsic single-cell properties (10–12). In the case of the toy model described in Fig. 1, cells are assumed to determine their generation times (division interval) randomly by roll of a dice. The mean of intrinsic cellular generation time is thus $\left(1+2+\cdots +6\right)/6=3.5$ h, but population doubling time, which is the time required for a population to double the number of cells, is in fact 3.2 h. This counterintuitive result is a direct consequence of growth noise in a population. Indeed, as we will see, the population doubling time can only equal the mean generation time when no variability of generation time exists at the single-cell level. Population growth rate is determined not only by an average of single cells but also by the details of heterogeneity within a population. Therefore, understanding how population growth rates and other properties arise from single-cell heterogeneity poses a fundamental challenge to single-cell biology.

Fig. 1.

Competition within a population caused by growth noise and its consequence to population growth rate. (A) Toy model of cell proliferation. Here, we consider a model of cell proliferation in which all of the cells in a population determine their generation time (interdivision time) randomly by throwing a dice to learn the consequences of intrapopulation growth noise. In this setting, cells can take either of the six possible choices of generation time, $\tau =\mathrm{1,2},\cdots ,6$ h, with the equal probability of 1/6. The mean generation time is thus ${\langle \tau \rangle }_g$= 3.5 h. (B) Example of pedigree tree showing competition between sibling cells. In this tree, two sibling cells were born from the common mother cell at t = 0 h, and divided with different generation times (sibling cell 1: τ_s1 = 5 h; and sibling cell 2: τ_s2 = 2 h). The descendant cells from the both sibling cells follow the same rule of cell divisions irrespectively of the ancestral generation time. The difference of generation time between the sibling cells 1 and 2 was caused just by chance, but the expected number of descendant cells becomes larger for the fast dividing sibling cell. The ratio of the expected number of descendant cells from those sibling cells at a certain future time point is $\langle N_1\rangle /\langle N_2\rangle =e^{-{\mathrm{\Lambda }}_p\left({\tau }_{s1}-{\tau }_{s2}\right)}$, where Λ_p is the population growth rate. (C) Growth of cell population. When all of the cells in the population follow the same division rule in A, the number of cells in the population grows exponentially. The rate of this exponential growth is the “population growth rate,” Λ_p. The time required for the population to double the number of cells is the “population doubling time,” T_d, i.e., $N\left(t\right)=N\left(0\right)2^{t/T_d}$. Therefore, T_d = ln2/Λ_p. An interesting consequence of stochasticity in generation time is that population doubling time becomes smaller than the mean generation time, i.e., T_d <${\langle \tau \rangle }_g$. In the case of the dice population, T_d = 3.187 h, which is indeed smaller than ${\langle \tau \rangle }_g$= 3.5 h.

A classical study of theoretical and experimental microbiology attempted to reveal the discrepancies between mean cellular generation times and population doubling times in real bacterial populations (13). Experimental methods and techniques available at that time, however, hampered reliable tests. Recently, the techniques of single-cell time-lapse microscopy have advanced to a great extent, revealing the heterogeneous and stochastic nature of single-cell dynamics quantitatively (14). With the aid of microfluidic platforms, tracking single cells over many generations in controlled constant or changing environments has also become feasible, providing insights into the mechanisms of cell size homeostasis and stress responses (3, 6, 7, 9, 15–22).

In this study, through microfluidics time-lapse microscopy and single-cell analysis on large-scale, single-cell lineage trees, we reveal that clonal populations of Escherichia coli indeed grow with a doubling time that is smaller than the mean doubling time of their constituent cells under broad, balanced-growth conditions. We show that the observed growth rate gains and population age structures are predictable from cellular generation time distributions based on a simple age-structured population model. Furthermore, we reveal unique features of long single-cell lineages within populations in competition, and provide a history-based formulation that connects growth rate gain with a measure of statistical deviation between isolated and competing lineages. Finally, we demonstrate a linear relation between the means and the variances of generation time across conditions, which constrains the maximum growth rate of this organism.

Results

Microfluidics Time-Lapse Microscopy Reveals Long-Term Single-Cell Lineage Tree Structures.

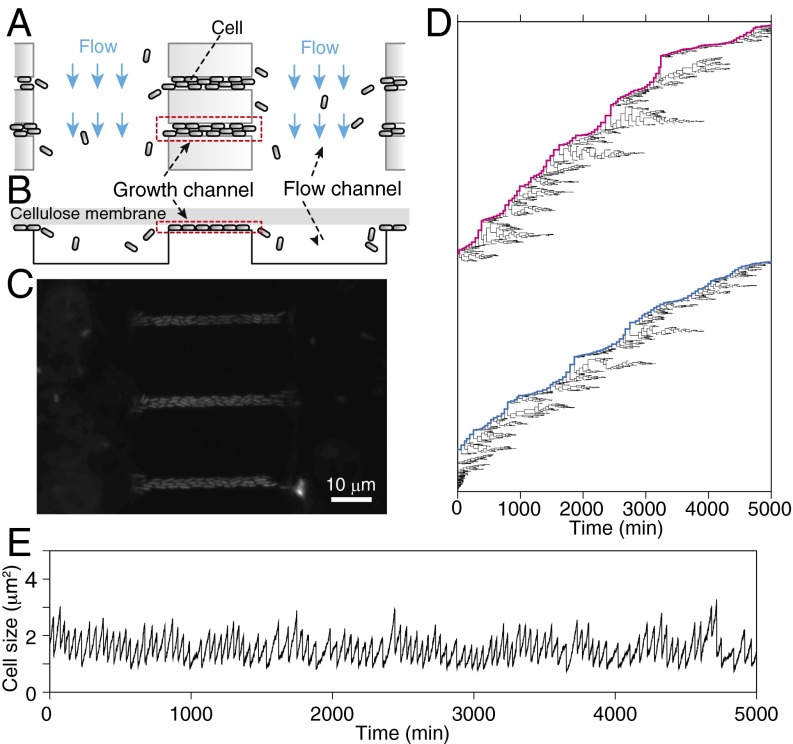
To investigate the role and the consequences of intrapopulation growth noise, we developed a custom microfluidics device for single-cell analysis, which we call the “dynamics cytometer” (Fig. 2 A–C, SI Appendix, Fig. S1, and Movie S1). The dynamics cytometer is similar to the previously reported polydimethylsiloxane (PDMS)-based microfluidics devices designed for long-term single-cell observation (7, 9, 15, 18–21). The important differences are (i) the microchannels are directly created on a glass coverslip, not on PDMS; and (ii) the channel region is covered by a semipermeable membrane (SI Appendix, Fig. S1) via biotin–streptavidin bonding by chemically decorating the surface of a microfabricated glass coverslip with biotin and membrane with streptavidin (23). The narrow and shallow growth channels can harbor 25 ∼ 40 cells at a time. A small fraction of the cells within growth channels are constantly removed to the wide and deep flow channels, which maintains the number of cells in the growth channels nearly constant. In contrast to the “mother machine” (7), the width of the growth channels is wider than a single-cell width, and both ends are open to flow channels. This configuration introduces competition among cells to remain within the growth channels, which is an important feature of this device for evaluating growth properties of both single cells and the population. Fresh medium is constantly supplied to the cells both from the flows in the flow channels and above the membrane, allowing efficient environmental control. Cellular growth rates in this device were indeed stable during the entire period of observation (SI Appendix, Fig. S2). Furthermore, the statistics of cellular growth were indistinguishable across different locations within the growth channels (SI Appendix, Fig. S3), which confirms efficient control of environmental conditions around the cells. Using this device, we observed clonal proliferation processes of E. coli in constant environments by time-lapse microscopy, obtaining large-scale single-cell lineage tree structures (Fig. 2D and SI Appendix, Fig. S4) as well as dynamics of cell size along long, single-cell lineages (Fig. 2E and SI Appendix, Fig. S5).

Fig. 2.

Single-cell growth measurement with dynamics cytometer. (A) Schematic drawing of the dynamics cytometer. In this device, we used the two types of microchannels etched on a coverslip. The narrow and shallow “growth channels” can harbor 25∼40 cells for time-lapse observation. The proliferation of the cells in the growth channels ejects a portion of the cells to the wide and deep “flow channels.” The flow in the flow channels removes the cells from the device. (B) Cross-section view of A. The channel region is covered by a flat semipermeable cellulose membrane with both ends of the flow channels left open to introduce medium flow (see also SI Appendix, Fig. S1C). The membrane restricts the cells to grow in a monolayer within the growth channels, which facilitates cell detection in image analysis. (C) A micrograph of E. coli in the device. (D) Single-cell pedigree of a population of E. coli (F3 rpsL-gfp strain) in a constant environment for 5,000 min (∼100 generations). The bifurcations of the lines indicate cell division, and the end points indicate cell removal from the growth channels. The magenta and blue lines indicate the single-cell lineages that remained in the growth channels for 5,000 min. The trees are obtained from the population proliferating in a single growth channel under a constant flow of M9 minimum medium supplemented with 0.2% glucose at 37 °C. (E) The time course transitions of cell size along the long single-cell lineage. This lineage corresponds to the top lineage in D. See also SI Appendix, Figs. S1–S5.

Analysis of Single-Cell Lineage Trees Reveals That Cell Populations Grow Faster than Their Constituent Single Cells.

Large-scale single-cell lineage trees obtained by the dynamics cytometer contain sufficient information for determining population growth rates and cellular generation time distributions, to which we applied a careful measurement analysis described in SI Appendix. For population growth rate, we first evaluated the instantaneous division rate as $\mathrm{\Lambda }\left(t\right)=\left(1/\mathrm{\Delta }t\right)\mathrm{l}\text{n}\left(\left(N\left(t\right)+D\left(t\right)\right)/N\left(t\right)\right)$, where Δt is the time-lapse interval; N(t) is the number of cells in the growth channels at time t; and D(t) is the number of cells that divided between t and t + Δt. Note that N(t) + D(t) is the number of cells at t + Δt when no cell is removed from the population. Population growth rate Λ_p is then measured as the average of Λ(t), i.e., ${\mathrm{\Lambda }}_p={\displaystyle {\sum }_{i=0}^{n-1}\mathrm{\Lambda }\left(i\mathrm{\Delta }t\right)/n}$, where n is the number of time points in the measurements, yielding the population doubling time $T_d=\mathrm{l}\mathrm{n}2/{\mathrm{\Lambda }}_p$.

A cell’s generation time is the age τ at which a newborn cell will divide next (here “age” means time elapsed since the previous division), which is a random variable with probability distribution function g(τ). The generation time distribution is related to the age-specific division rate b(τ) by $g\left(\tau \right)=b\left(\tau \right)\mathrm{e}\mathrm{x}\text{p}\left[-{\displaystyle {\int }_0^{\tau }b\left(\tau \prime \right)d\tau \prime }\right]$ (SI Appendix). Thus, knowing b(τ) determines g(τ) as well. We measured the age-specific division rate from the single-cell data using $b\left(\tau \right)=\left(-1/\mathrm{\Delta }t\right)\mathrm{l}\text{n}\left(\left(N_a\left(\tau \right)-D_a\left(\tau \right)\right)/N_a\left(\tau \right)\right)$, where N_a(τ) is the number of cells that reached age τ, and D_a(τ) is the number of cells that divided between age τ and τ + Δt. We confirmed by simulation that these statistical estimators provide precise measures of population growth rate and generation time distributions both with and without cell removal (SI Appendix, Figs. S6–S10). Note that all of the information above is obtained directly from lineage tree structures without any fitting to elongation curves. Indeed, our precise measurement of Λ_p demonstrates that comparison between population growth rate and simple mean of individual cells’ elongation rate within a population requires attention because they often report significantly different values (SI Appendix, Table S1).

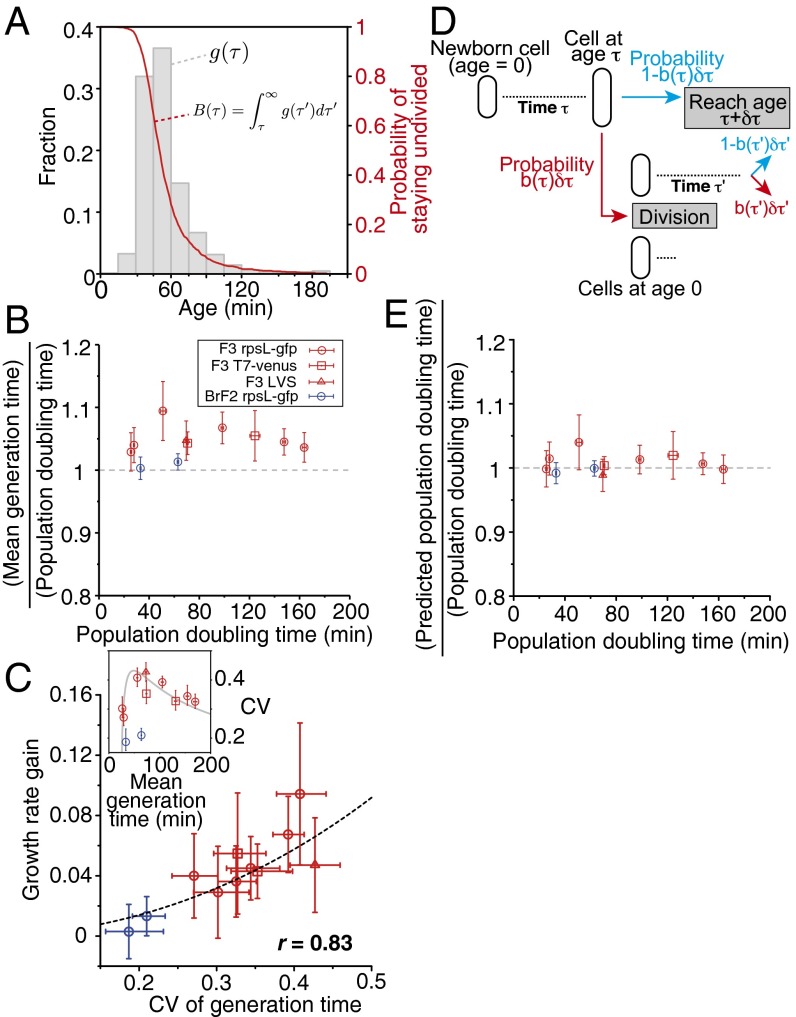
Using the validated growth parameters above, we evaluated generation time distributions (Fig. 3A and SI Appendix, Fig. S11) and population growth rates of four E. coli strains listed in SI Appendix, Table S2, under several culture conditions, in which temperature and nutrient supplements were altered. Under those conditions, the mean of unbiased cellular generation time ranged from 26 to 170 min. The measured generation time distributions were asymmetric and similar to gamma distributions [=${\tau }^{k-1}{e}^{-\tau /\theta }/\mathrm{\Gamma }\left(k\right){\theta }^k$, where k and θ are shape and scale parameters], although significant deviations existed especially in the tails (SI Appendix, Fig. S11). Comparison showed that the mean generation time ${\langle \tau \rangle }_g$ was greater than population doubling time T_d in most cases (Fig. 3B), which means that clonal populations grow faster than the constituent single cells on average under a broad range of constant environmental conditions. The relative gain of population growth rate was positively correlated with the noise [coefficient of variation (CV)] of the generation time distributions (Fig. 3C), indicating that generation time noise increases population growth rate.

Fig. 3.

Relationships between generation time distribution and population doubling time. (A) An example of generation time distribution obtained from the lineage tree structures in Fig. 2D. The gray histogram shows the probability distribution constructed from the lineage trees containing 3,285 cells (corresponding to the left axis), and the red curve shows the survival function (corresponding to the right axis), which represents the probability for a cell to remain undivided until the age on the x axis. In this example, the mean generation time was 55.9 min [54.8–57.0 min, 95% bootstrap confidence interval (CI)], and the coefficient of variation (CV) was 0.39 (0.37–0.41). (B) Ratios of mean cellular generation time to population doubling time plotted against population doubling time. The red points are for the three W3110 derivative strains (circle, F3 rpsL-gfp; square, F3 T7-venus; and triangle, F3 LVS), and blue for the B/r derivative strain, BrF2. Error bars represent 2SD bootstrap error ranges. (C) Relationship between CV of generation time and growth rate gain. Growth rate gain is defined as $\left({\langle \tau \rangle }_g-T_d\right)/T_d=\left({\mathrm{\Lambda }}_p-\lambda \right)/\lambda$, where $\lambda =\mathrm{l}\text{n}\hspace{0.17em}2/{\langle \tau \rangle }_g$ is single-cell growth rate, and corresponds to the distance of the points from the y = 1 line in B. Error bars on x axis are 95% bootstrap CI, and those on y axis are 2SD bootstrap error ranges estimated from the errors in ${\langle \tau \rangle }_g$ and T_d. The correspondence between the point types and the strains is the same as in B. The black broken curve represents the relation when generation time distributions are gamma [$y=\left(\left(2^{x^2}-1\right)/x^2\mathrm{l}\text{n}\hspace{0.17em}2\right)-1={\displaystyle {\sum }_{i=1}^{\infty }\left({\left(\mathrm{l}\text{n}\hspace{0.17em}2\right)}^i/\left(\left(i+1\right)!\right)\right)x^{2i}}$, where x is CV and y is growth rate gain]. (Inset) Relationship between mean and CV of generation time. The gray curve represents the trend for the F3 strains expected from the linear relation between mean and variance of generation time in Fig. 6. Error bars are 95% bootstrap CI. (D) Schematic explanation of age-structured population model. In this model, cells are assumed to divide according to age-specific division probability b(τ)δτ, and each division produces two newborn cells with the age τ = 0, which increase their age and divide again probabilistically according to the same b(τ)δτ. (E) Ratios of theoretically predicted population doubling time to experimental value. Population doubling time was predicted from generation time distribution based on the Euler–Lotka equation [1]. Error bars on x axis are 95% bootstrap CI, and those on the y axis are 2SD bootstrap error ranges. See also SI Appendix, Table S1 and Figs. S6–S12.

Growth Rate Gain and Population Age Structures Can Be Predicted from Generation Time Distributions.

To gain further insights into the observed growth rate gain, we compared the experimental results with the prediction of an age-structured population model (Fig. 3D) (12, 13, 24) in which cells divide according to an age-dependent division probability. An important prediction of this model is that the generation time distribution g(τ) and population growth rate Λ_p must satisfy the so-called Euler–Lotka equation:

$${\displaystyle \underset{0}{\overset{\infty }{\int }}2g\left(\tau \right)e^{-{\mathrm{\Lambda }}_p\tau }d\tau }=1$$ [1]

(see SI Appendix for derivation). This equation allows us to calculate Λ_p using knowledge of g(τ). We thus calculated Λ_p^(theory) [=ln(2)/T_d^(theory)] from experimentally obtained g(τ) according to the computational method described in SI Appendix, finding good agreement with the directly measured value (Fig. 3E). When generation time follows a gamma distribution, i.e., $g\left(\tau \right)={\tau }^{k-1}{e}^{-\tau /\theta }/\mathrm{\Gamma }\left(k\right){\theta }^k$, where k and θ are shape and scale parameters, Eq. 1 is analytically solvable, and growth rate gain is determined solely by the CV. Despite the fact that the generation time distributions were not perfectly gamma, the result in Fig. 3C agrees in trend with this relation.

In addition to population growth rate, this simple model predicts the steady-state age distribution of the population as follows:

$${\psi }_p\left(\tau \right)=2{\mathrm{\Lambda }}_p{e}^{-{\mathrm{\Lambda }}_p\tau }\underset{\tau }{\overset{\infty }{\int }}g\left(\tau \prime \right)d\tau \prime$$ [2]

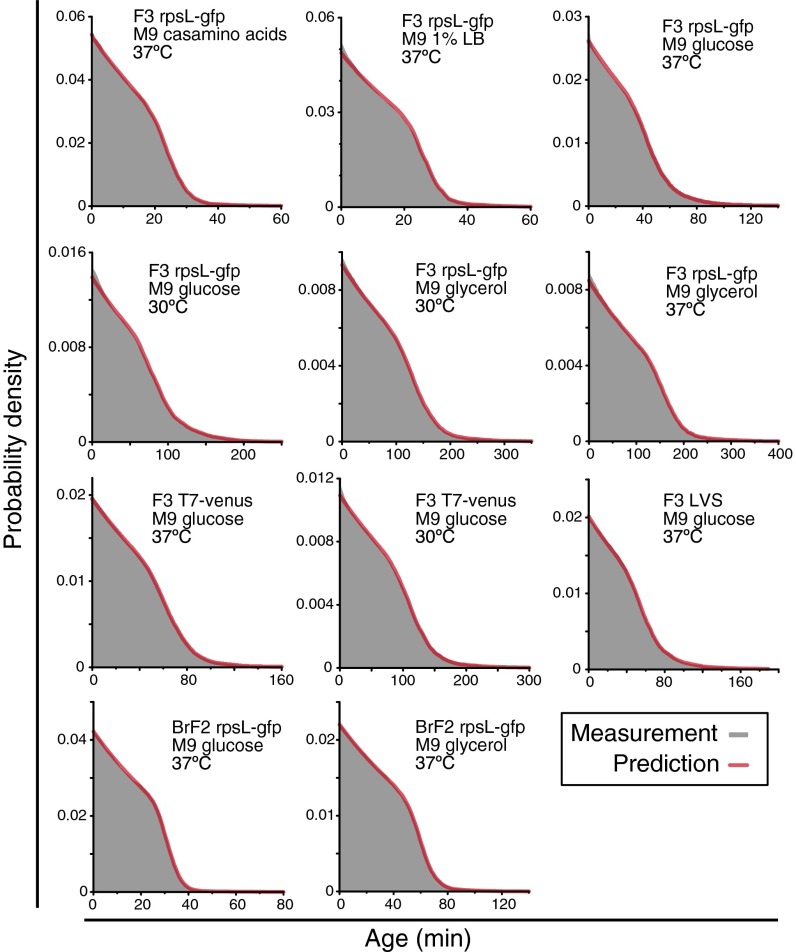
(SI Appendix). This equation shows that the generation time distribution of single cells determines the age distribution of the population because Λ_p is itself determined by g(τ) using [1]. We compared experimentally measured age distributions of the population with those predicted from g(τ) using [2] according to the method described in SI Appendix, finding excellent agreement in all of the conditions without any adjustable parameters (Fig. 4).

Fig. 4.

Comparison of age distributions between measurements and theoretical predictions. The gray distributions represent the experimentally measured population age distributions, and the magenta curves the theoretical predictions from the generation time distribution based on the relation [2]. Strain and culture conditions are indicated in each panel.

Age Distributions Along Long Single-Cell Lineages in Populations Exhibit Optimal Lineage Statistics.

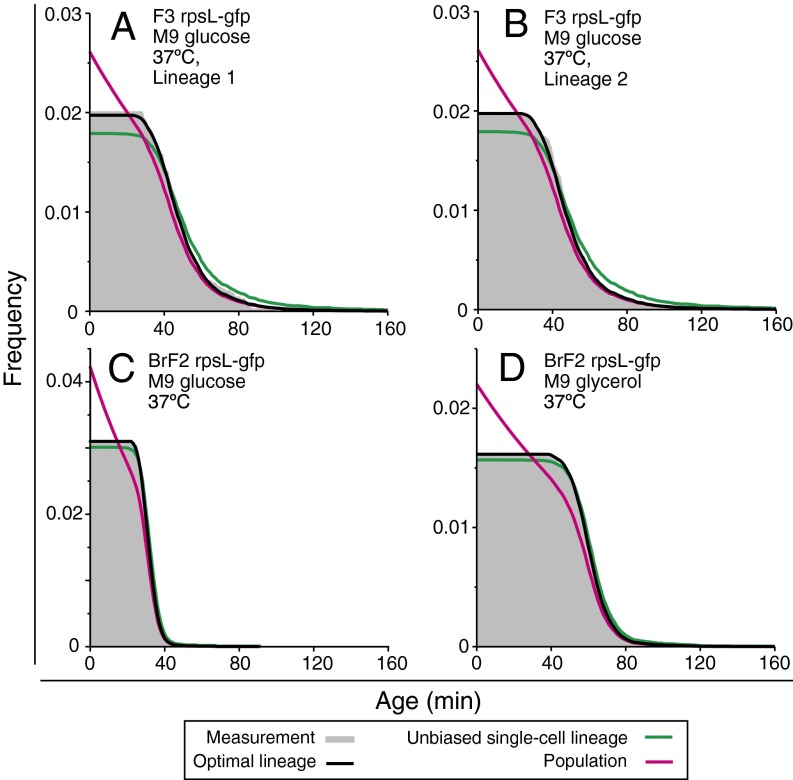
In addition to population growth rates and age distributions, the model makes testable predictions regarding the histories of individual cells within a population. Theoretical analysis of the cell proliferation process from the viewpoint of cellular lineages shows that the distribution $g^{*}\left(\tau \right)\hspace{0.17em}=2g\left(\tau \right)e^{-{\mathrm{\Lambda }}_p\tau }$, which appeared in [1], is in fact the typical generation time distribution along a lineage extracted by randomly choosing a descendant cell and tracking back to its ancestor over many generations (SI Appendix). We previously showed that the distribution g*(τ) corresponds to a set of lineages that optimize the population growth rate (12); hence we call such lineages “optimal lineages.” Importantly, optimal lineages possess a generation time distribution that is distinct from that of single cells in isolation. Focusing on the experimental datasets in which we were able to obtain lineages longer than 100 generations, we confirmed that their age distributions correspond to that of optimal lineages, rather than that of single cells in isolation (Fig. 5).

Fig. 5.

Age distributions along single cell lineages. (A and B) Age distributions along two long single-cell lineages of F3 rpsL-gfp cultured in M9 glucose medium at 37 °C. The gray distributions represent the experimentally measured age distributions along two independent lineages, which correspond to the top lineages of the two tree clusters in Fig. 2D. The green curves represent the predicted age distribution for single-cell lineages in isolation and black for optimal lineages within a population. The magenta curves represent the predicted population age distribution shown in Fig. 4. (C and D) Age distribution along a long lineage of BrF2 strain cultured in M9 glucose medium at 37 °C (C) and in M9 glycerol medium at 37 °C (D).

Analyzing the cell proliferation processes from the viewpoint of cell lineages offers an illuminating mathematical interpretation of these differences, as we prove within the context of the simple age-structured model that

$$\frac{{\langle \tau \rangle }_g-T_d}{T_d}=D\left[g\hspace{0.17em}\left|\right|\hspace{0.17em}{g}^{*}\right],$$

$$\frac{T_d-{\langle \tau \rangle }_{g^{*}}}{T_d}=D\left[g^{*}\hspace{0.17em}\left|\right|\hspace{0.17em}g\right],$$

$$\frac{{\langle \tau \rangle }_g-{\langle \tau \rangle }_{g^{*}}}{T_d}=D\left[g\hspace{0.17em}\left|\right|\hspace{0.17em}{g}^{*}\right]+D\left[g^{*}\hspace{0.17em}\left|\right|\hspace{0.17em}g\right],$$

where $D\left[g\left|\right|g^{*}\right]\equiv {\displaystyle {\int }_0^{\infty }g\left(\tau \right)\mathrm{l}\text{o}{\text{g}}_2\left(g\left(\tau \right)/g^{*}\left(\tau \right)\right)d\tau }$ is the Kullback–Leibler divergence (relative entropy), a nonnegative quantity that measures the dissimilarity between two probability distributions (SI Appendix). Noting that $g^{*}\left(\tau \right)$ is the typical lineage generation time distribution within a population, we can understand from the above relations that growth rate differences are linked with the different statistics along cell lineages in isolation and within a population. The advantage of the lineage viewpoint in analyzing population dynamics has been explored theoretically (12, 25–28); our study provides an experimental foundation behind this powerful concept.

The Means and the Variances of Generation Time Across Conditions Are Linearly Related.

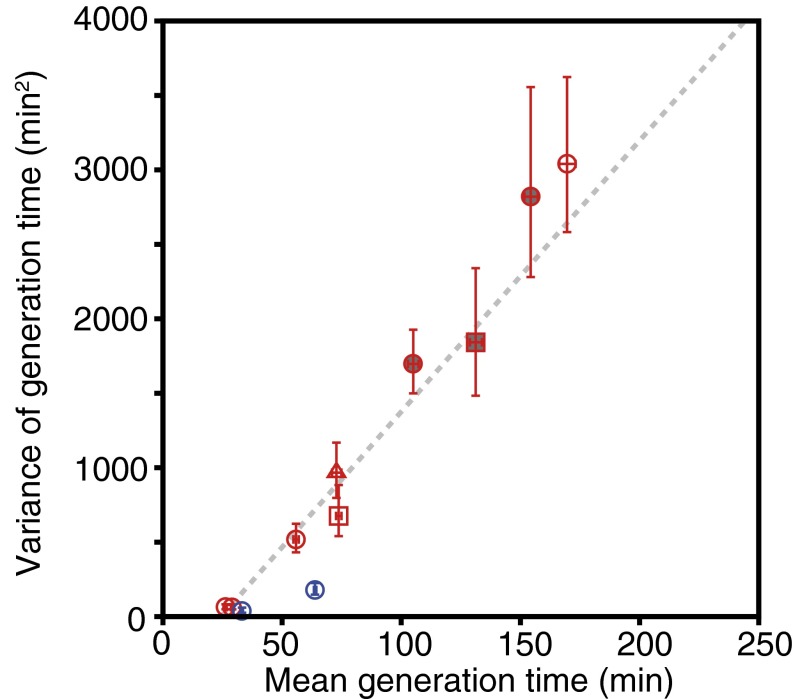
The relations we examined thus far do not impose any constraints on generation time distributions. However, we noticed that the means and variances of the three E. coli strains derived from W3110 (F3 series) were approximately linearly related (Fig. 6). In general, such a relation suggests that the dominant contribution to stochasticity in the cell division time may arise from a number of discrete steps within the cell division cycle, each contributing comparable and largely independent portions of the variance in timing. If the number of steps increases as growth conditions deteriorate, a linear mean–variance scaling relation would arise. It is noteworthy that the X intercept of the linear scaling relation is positive (24.4 ± 0.8 min) and close to the minimum generation time of E. coli in rich media (∼20 min). Thus, this relation may be relevant for establishing the upper bound of growth rate of these strains in any constant environments. Because the X intercept is positive, the CV of generation time is expected to take the maximum value at an intermediate position, where the mean generation time is twice the minimum (X-intercept value). This is indeed seen in Fig. 3C (Inset). The variances of BrF2 strain were significantly smaller than this trend, suggesting that the intrinsic level of generation time heterogeneity is strain specific.

Fig. 6.

Linear relation between mean and variance of generation time. The red points are for the three W3110 derivative strains (circle, F3 rpsL-gfp; square, F3 T7-venus; and triangle, F3 LVS), and blue for the B/r derivative strain, BrF2. The filled red points represent the data taken at 30 °C. The gray trend line represents the linear fit for the red points (F3 strains): y = a (x − b); a = 18.2 ± 1.6 min, and b = 24.4 ± 0.8 min. Error bars are 95% bootstrap CI.

Discussion

The growth of cells constitutes an important physiological process that contributes critically to the fitness of an organism, while also imposing global constraints on intracellular gene expression levels (29), metabolic efficiency (1), and macromolecular composition (2). Most studies on cellular growth have referred to bulk population growth rates in measurements, but recent research on the heterogeneous and stochastic nature of growth at the single-cell level poses new, fundamental questions regarding (i) how precisely the insights gained through population measurements apply to single-cell properties (3), and (ii) how single cells as a whole bring about the observed population properties (12, 13). Our study tackled the latter issue both experimentally and theoretically, showing that a simple age-structured population model explains the intricate relationships between the growth rates of the cells and the population.

The result that the growth rate gain increases with the CV of generation time (Fig. 3C) clearly demonstrates the importance of growth noise in determining population growth rate. This suggests that there are two routes for an organism to evolve to a higher population growth rate in a constant environment: one is simply to decrease the mean generation time; and the other is to increase the heterogeneity of generation times in a population. In reality, a single mutation may affect both mean and variance of generation times simultaneously, resulting in a synergetic or antagonistic effect on the population growth rate. Discriminative measurements on these two contributions have never been performed to our knowledge. In experimental evolution, an increase of population growth rate has usually been attributed exclusively to the change of mean growth properties; measuring single-cell growth heterogeneity over the course of an evolutionary process may reveal the dominant contribution to an increase of population growth rate at each step of the evolutionary trajectories.

The measurements in this study are restricted to the stress-free conditions where cells can grow and divide stably for hundreds of generations. Generally, cells placed in stressful environments show increased levels of phenotypic heterogeneity (16, 30). One apparent role of large phenotypic heterogeneity is to increase the chance of producing fitter individuals to be selectively amplified within a population. Additionally, as our results suggest, heterogeneity increases the population growth rate achievable for a fixed, mean generation time, a result that may clarify the role of stress-induced phenotypic heterogeneity observed in previous experiments.

It is remarkable that a simple population model, using only an age-dependent cell division process, can explain the relationships between the growth rates of cells and the population across such broad culture conditions. We attribute this to having focused only on the age-related growth parameters and cell division statistics, while not modeling cell-size related parameters. Indeed, cell size at birth and generation time are weakly correlated negatively (Pearson correlation coefficient, −0.48 ∼ −0.22; SI Appendix, Fig. S12), and this effect must be considered to account for cell size stability (3, 31–35). Nevertheless, our results suggest that, as far as age-related parameters and population growth rates are concerned, cell size information does not play a predominant role in E. coli over a broad set of culture conditions. It is also important to note that this model assumes no correlation of generation time between mother and daughter cells. Generally, positive mother–daughter correlation increases population growth rate, and negative correlation decreases it (13). However, our experimental results show that mother–daughter correlations of generation time are weak: a positive correlation of 0.2 would increase population growth rate by ∼2% (13), and most of the observed correlations are below this level (SI Appendix, Table S5).

With regard to cell size stability, our study highlights the importance of lineage differences. As recognized by previous studies (6, 7), a small fraction of E. coli cells in clonal populations often become filamentous even in constant environments. We also observed such filamentous cells in our measurements across the population (SI Appendix, Fig. S5 A and B), but importantly these cells are rarely observed along the optimal lineages (Fig. 2E and SI Appendix, Fig. S5). This is likely due to the tail of g*(τ), which decays faster than g(τ) by the factor $e^{-{\mathrm{\Lambda }}_p\tau }$, and thus strongly reduces the probability of observing in the optimal lineages a long generation time associated with filamentous states.

The linear relation between the means and the variances of generation time in Fig. 6 suggests that we can predict the noise levels of generation time only from the means without knowing the details about the environments. A similar idea has been proposed in several recent studies. For example, Iyer-Biswas et al. (31, 36) proposed that the distributions of generation time normalized by their means collapses onto the universal curve based on their experiments with Caulobacter crescentus cultured under various temperature conditions, and that an autocatalytic cycle model for cell cycle control might account for this scaling property. Similarly, Taheri-Araghi et al. (3) proposed the scaling of generation time distribution based on their single-cell analysis on E. coli growth under different nutrient conditions at a fixed temperature, and presented the adder model, which assumes that cells achieve cell size homeostasis by adding a constant size between birth and division irrespective of birth size. For this simple scaling rule to be valid, the CVs of generation time must be constant irrespective of the environmental conditions, and the SDs become proportional to the means. However, our results in Fig. 3C (Inset) and Fig. 6 do not follow this rule. Thus, our results suggest that the scaling rule breaks down in some culture conditions and/or organisms not explored in the previous studies. It should be noted that the mean–variance linear relation is tested only for the W3110-derived strains in our study; characterizing which rule is obeyed by different strains and organisms might be a fruitful subject for future evolutionary study.

In summary, our measurements have established a predictive framework that bridges from single-cell properties to population-level dynamics in conditions where cells can grow stably. The same approach can be used to discover rules that govern growth in severe stress environments, including antibiotics and chemotherapeutics, and to investigate the generality and prevalence of single-cell and population growth laws across strains, species, cell types, and environments.

Materials and Methods

Cell Strains and Culture Conditions.

We used W3110 and B/r derivative E. coli strains in this study (SI Appendix, Table S2). Cells were grown in M9 minimal medium. The culture conditions were changed by different nutrient supplements and temperature as listed in SI Appendix, Table S3. See SI Appendix for details.

Single-Cell Time-Lapse Observation.

We implemented time-lapse observation of E. coli proliferating in the dynamics cytometer using Nikon Ti-E microscope controlled by micromanager (https://micro-manager.org/). The time-lapse images were analyzed by a custom macro of ImageJ (imagej.nih.gov/ij/), and the exported data were further analyzed using a custom C-program. See SI Appendix for details.