Population-based 3D genome structure analysis reveals driving forces in spatial genome organization

Significance

We provide a method for population-based structure modeling of whole diploid genomes using Hi-C data. The method considers the stochastic nature of chromosome structures, which allows a detailed analysis of the dynamic landscape of genome organizations. We predict and experimentally validate the presence of chromosome-specific higher-order centromere clusters, which can play a key role in the spatial organization of the human genome, specifically influencing the overall chromosome positioning, as well as the preference of specific chromosome conformations. Our approach generate predictive structural models of diploid genomes from Hi-C data, which can provide insights into the guiding principles of 3D genome organizations.

Abstract

Conformation capture technologies (e.g., Hi-C) chart physical interactions between chromatin regions on a genome-wide scale. However, the structural variability of the genome between cells poses a great challenge to interpreting ensemble-averaged Hi-C data, particularly for long-range and interchromosomal interactions. Here, we present a probabilistic approach for deconvoluting Hi-C data into a model population of distinct diploid 3D genome structures, which facilitates the detection of chromatin interactions likely to co-occur in individual cells. Our approach incorporates the stochastic nature of chromosome conformations and allows a detailed analysis of alternative chromatin structure states. For example, we predict and experimentally confirm the presence of large centromere clusters with distinct chromosome compositions varying between individual cells. The stability of these clusters varies greatly with their chromosome identities. We show that these chromosome-specific clusters can play a key role in the overall chromosome positioning in the nucleus and stabilizing specific chromatin interactions. By explicitly considering genome structural variability, our population-based method provides an important tool for revealing novel insights into the key factors shaping the spatial genome organization.

The 3D structural organization of the genome plays a key role in nuclear functions such as gene expression and DNA replication (1–3). Thanks to the recent development of genome-wide chromosome conformation capture methods [Hi-C (4–13), TCC (14), and single-cell (15) and in situ Hi-C (16)], close chromatin contacts can now be identified at increasing resolution, providing new insight into genome organization. These methods measure the relative frequencies of chromosome interactions averaged over a large population of cells. However, individual 3D genome structures can vary dramatically from cell to cell even within an isogenic sample, especially with respect to long-range interactions (15, 17, 18). This structural variability poses a great challenge to the interpretation of ensemble-averaged Hi-C data (14, 19–23) and prevents the direct detection of cooperative interactions co-occurring in the same cell. This problem is particularly evident for long-range (cis) and interchromosomal (trans) interactions, which are generally observed at relatively low frequencies and are therefore present only in a small subset of individual cells at any given time (3, 11, 15). Despite their low frequencies, long-range and interchromosome interaction patterns are not random noise. In fact, these interactions are more informative than short-range interactions in determining the global genome architectures in cells and are often functionally relevant—interactions between transcriptionally active regions are often interchromosomal in nature (14). Owing to their variable nature, long-range and trans interactions can be part of alternative, structurally different conformations, which makes their interpretation in form of consensus structures impossible. However, inferring which of the long-range interactions co-occur in the same cell from ensemble Hi-C data remains a major challenge.

These challenges cannot be easily overcome even by the new single-cell Hi-C technology (15), because it currently detects only a relatively small fraction of chromatin interactions in a cell. Also, one might need to profile many thousands of cells before the data cover a statistically representative spectrum of genome structures. It is therefore highly beneficial to develop methods that use ensemble-averaged Hi-C data to infer cooperative long-range chromatin interactions, which in turn would allow reconstruction of a set of genome structures that accurately captures a genome’s structural variability.

The majority of structure modeling approaches are based on the assumption that the contact data arise from a single 3D consensus structure or family of structures, each satisfying the complete Hi-C dataset. These methods relate Hi-C contact frequencies to distances, assuming that a lower contact frequency corresponds to a larger distance between loci in 3D space, which requires additional (often arbitrary) assumptions (6, 12, 24–30). The major limitation of these methods is that the generated consensus structures do not represent single instances of actual genome structures and cannot capture the variable nature of long-range and trans chromatin interactions in different structural states. Further underlining this problem, no single 3D model from these approaches can simultaneously satisfy all of the derived distances or incorporate all of the contacts measured by the Hi-C experiments.

To address this problem we recently introduced the concept of population-based genome structure calculation to explicitly model the genome structure variability between cells using Hi-C data (14, 31). In contrast to consensus structure modeling, a population of thousands of genome structures is generated in which the cumulated contacts of all of the structures recapitulates the Hi-C matrix, rather than each structure individually. The approach does not require a functional relation between the frequencies of contacts and spatial distances. Other more recent 3D modeling efforts also use ensembles of structures for considering structural variability in the models. However, these approaches are currently only applicable to relatively small chromatin fragments with sizes in the range of topological domains (i.e., ∼1 Mb) or individual chromosomes and have not been applied to model entire diploid genomes (19, 20, 22, 23, 32).

Building on our previous method, here we introduce an improved population-based modeling approach and formulate a probabilistic framework to model a population of 3D structures of entire diploid genomes from Hi-C data. The key improvements in the new approach are an iterative probabilistic optimization framework, which now allows the inference of cooperative chromatin interactions co-occurring in the same cells. We determine the genome structure population by maximizing the likelihood function for observing the Hi-C data. Because the problem does not have a closed-form solution, numerical routines are needed to approximate the solution. We propose an iterative procedure to maximize local approximations of the likelihood function, which produces a population of genome structures whose chromatin domain contacts are statistically consistent with the Hi-C data. The result is the best approximation of the underlying true population of genome structures, given the available data.

To determine the true population of genome structures underlying the Hi-C data would require knowing which exact chromatin contacts are present in each cell. The Hi-C data cannot provide this information, but it is possible to approximate the underlying 3D genome structures given additional information. Here, we show that embedding the genome in 3D space enables such an approximation by facilitating the inference of likely cooperative interactions. In 3D space the presence of some chromatin contacts induces structural changes that may make some additional contacts in the same structure more probable, whereas other contacts less likely. Moreover, in a single structure, each chromatin region can form only a limited number of interactions and is confined to the nucleus. These constraints and considerations effectively restrict the conformational freedom of the chromosomes and permit us to infer likely cooperativity between subsets of the observed chromatin interactions, which in turn helps deconvoluting the Hi-C data into a set of plausible structural states.

Our method distinguishes between interactions involving two chromosome homologs and therefore is capable of generating structure populations for entire diploid genomes, which also allows direct assessment of our findings with image analysis techniques. Further, because the generated population contains many different structural states, it can accommodate all of the observed chromatin interactions, including those that would be mutually exclusive in a single structure. Our method is sufficiently flexible to integrate additional experimental information from various data sources, such as imaging or lamina DamID experiments, into the log-likelihood function in the future. Finally, our method is applicable at various levels of resolution.

As a case study, we tested our new method on human lymphoblastoid cells, for which imaging data are available for structure assessment. We generated a population of 3D structures that correctly predicts many features of the lymphoblastoid genome known from imaging experiments, including the distributions of interchromosomal distances between gene loci as well as the preferred nuclear locations of the chromosomes. Most importantly, our analysis revealed the existence of specific higher-order interchromosomal chromatin clusters. Most prominently, we observe chromosome-specific centromere clusters, which can vary in their composition between cells. A centromere is typically found in alternative centromere clusters in different cells and certain centromere combinations are found substantially more often than others, demonstrating a chromosome-specific interaction mode. We find that the propensity for centromere cluster formation affects a chromosome’s overall nuclear positioning, influences its chromosome conformations, and facilitates stable interchromosomal chromatin interaction patterns between certain chromosome regions. We proof the existence of centromere clusters through X-ray tomography experiments and confirm the predicted relative frequencies of specific centromere clusters by 3D FISH experiments. Our observations point to an important functional role of centromere clusters and raise an important hypothesis, namely that modulating the preference for specific centromere–centromere interactions can change the fate of a chromosome’s location in the interphase nucleus as well as stabilize interchromosomal interaction patterns and therefore can help establish cell-type-specific genome architectures.

Results

Population-Based Genome Structure Modeling by Maximum Likelihood Estimation.

Chromosomes are segmented into chromatin domains according to their Hi-C contact patterns. Here, the structure resolution is set at the level of chromatin macrodomains (∼3.5 Mb), defined from the data by a constrained clustering algorithm, for a total of 1,332 domains for the diploid genome (SI Appendix, section A.4 and Fig. S1). Our aim is to generate a large population of 3D genome structures whose macrodomain contacts reproduce the genome-wide Hi-C data (Fig. 1). In other words, we want to construct a population of genome structures (represented by their macrodomain coordinates X) in which the formation of contacts between N chromosome domains is statistically consistent with the normalized contact probability matrix $\mathbf{A}={\left(a_{IJ}\right)}_{N\times N}$ derived from Hi-C experiments (SI Appendix, section A.3.5). We formulate this requirement as a maximum likelihood estimation problem to generate the structure population model X (Materials and Methods).

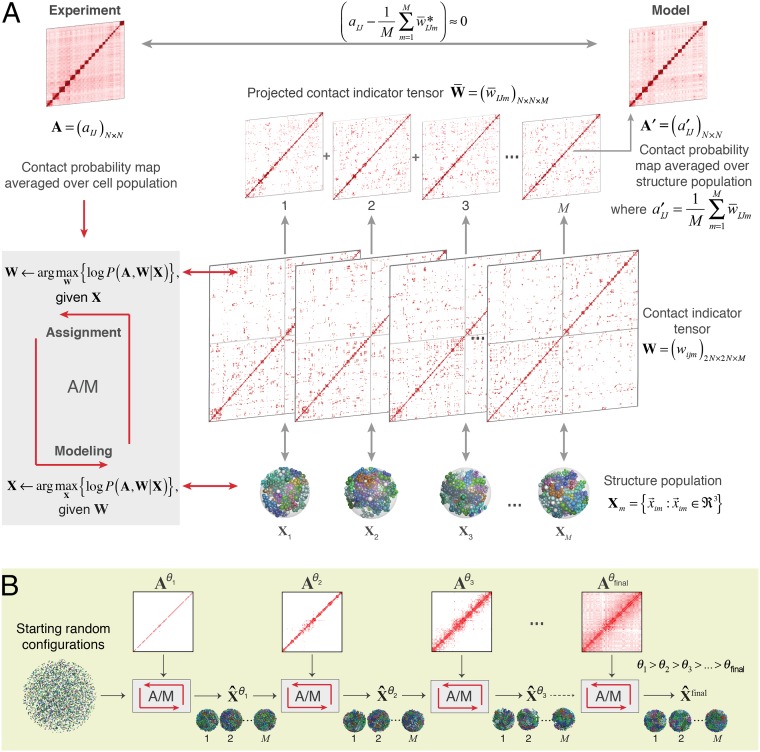
Fig. 1.

Schematic of the population-based genome structure modeling approach. (A) A population of M genome structures is constructed, in which the formation of contacts between chromosome domains over all structures is statistically consistent with the contact probability matrix A, derived from Hi-C experiments (Materials and Methods). We formulate this problem as a maximum likelihood estimation problem. Because the Hi-C data A are incomplete, we introduce the “contact indicator tensor” W, a binary third-order tensor that can complete the missing contact information in A. That is, W specifies which domain contacts exist in which structures of the population and also distinguishes between contacts from homologous chromosome copies. Also shown is the “projected contact indicator tensor,” $\overline{\mathbf{W}}$, derived from W by projecting its diploid genome representation to its haploid representation (SI Appendix). (B) The maximum likelihood optimization is achieved through a stepwise iterative process, where we gradually increase the optimization hardness by gradually adding contacts of the matrix ${\mathbf{A}}^{\theta }={\left(a_{IJ}^{\theta }\right)}_{N\times N}$ with decreasing contact probability threshold θ. This process generates a structure population that is consistent with the Hi-C data (SI Appendix).

The ensemble Hi-C data are contact frequencies averaged over a population of cells, so they cannot reveal which contacts coexist in the same 3D structure. Therefore, we introduce a latent variable, the “contact indicator tensor” $\mathbf{W}={\left(w_{ijm}\right)}_{2N\times 2N\times M}$. This is a binary, third-order tensor that specifies which domain contacts belong to each of the M structures in the model population and also distinguishes contacts from homologous chromosome copies (i.e., each domain has two copies and so there are 2N homologous domain copies). We can jointly approximate the structure population X and the contact indicator tensor W by maximizing the log-likelihood $\log \mathit{ℒ}\left(\mathbf{X}\right|\mathbf{A},\mathbf{W})=\log P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)$.

Obviously, the ensemble-based Hi-C data are not sufficient to derive the true contact tensor W and the structure population X. However, given additional information it is possible to approximate the best solution of W and X for a given Hi-C dataset. Representing the genome domains in 3D space already substantially constrains the conformational freedom of chromosomes and restricts possible Hi-C contact assignments. For instance, the presence of certain chromatin contacts in a structure influences the probability of observing other contacts in the same structure. In addition, volume exclusion introduces the requirement that no two domains can overlap whereas all domains must be confined inside the nuclear volume. Taken together, such constraints can facilitate a structure-based deconvolution of the Hi-C data and an approximation of X that closely reproduces many known structural features of the genome, which were not included as input information.

To solve this problem, we design an iterative procedure to maximize the log-likelihood function. Each iteration consists of two steps (Fig. 1A):

• •
  Assignment step (A-step): Given the current estimated model X^(k), estimate the latent variable W^(k+1) by maximizing the log-likelihood over all possible values of W.

  $${\mathbf{W}}^{(k+1)}=\arg \underset{\mathbf{W}}{\max }\left\{\log P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)\right\},\hspace{1em}\text{given}\hspace{0.17em}\mathbf{X}={\mathbf{X}}^{\left(k\right)}$$
• •
  Modeling step (M-step): Given the current estimated latent variable W^(k+1), find the model X^(k+1) that maximizes the log-likelihood function.

  $${\mathbf{X}}^{(k+1)}=\arg \underset{\mathbf{X}}{\max }\left\{\log P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)\right\},\hspace{1em}\text{given}\hspace{0.17em}\mathbf{W}={\mathbf{W}}^{(k+1)}$$

In our new approach we use a stepwise optimization strategy to gradually increase the optimization hardness (Fig. 1B), which facilitates the detection of cooperative interactions in genome structures. The idea is to begin by estimating a structure population ${\widehat{X}}^{\theta }$ that at first reproduces only the most frequent interactions according to the contact probability matrix A (e.g., above a threshold θ; a_IJ ≥ θ), so that interactions with contact probabilities lower than a certain value θ are ignored (for example, we can start with θ = 1). Then, using this structure population as the initial condition, we add contacts with lower probabilities (e.g., θ = 0.8, that are contacts present in 80% of all structures) and perform another round of optimization. In other words, the contacts in A are added gradually to the structure population X and tensor W, and the iterative optimization (A/M-steps) is applied after each allocation to achieve the convergence of $\left({\widehat{\mathbf{X}}}^{\theta },{\widehat{\mathbf{W}}}^{\theta }\right)$. Because errors in the conformation capture detection are expected to have low frequencies, we stop at the threshold θ = 0.01 to reduce the effect of experimental noise in the calculations.

In the A-step, we use an efficient heuristic strategy to estimate W by using information from the structure population generated in the previous M-step. We assume that assignments of a given chromatin contact across the contact indicator tensor W are more likely realized in those genome structures in which the corresponding chromatin domains are already closer in 3D space. In particular, for each potential contact between domains I and J, we determine a cutoff activation distance $d_{IJ}^{\text{act}}$ based on the distribution of all distances for this pair in all structures of the model population (SI Appendix, Fig. S1C). The cutoff distance is defined such that the probability $P(d_{IJ}\le d_{IJ}^{\text{act}})$ equals to $a_{IJ}$ and is used to estimate the contact indicators.

In the M-step, maximizing $\log P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)$ can be reduced to maximize only $\log P\left(\mathbf{W}|\mathbf{X}\right)$, because A and W are known and $P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)=P\left(\mathbf{A}|\mathbf{W}\right)P\left(\mathbf{W}|\mathbf{X}\right)$. We use simulated annealing dynamics and conjugate gradient optimizations to generate a population of 3D genome structures X for which all of the chromatin contacts in W are physically realized in the genome structures, indicating that the likelihoods of all contacts in the structure population are maximized to approximately one. We implemented the structure optimization tools within the Integrated Modeling Platform (33, 34). We applied our method to human lymphoblastoid cells, using TCC experiments with a fivefold increase in sequencing coverage in comparison with our work reported in ref. 14. We also applied our method to more recent high-resolution in situ Hi-C data from the Lieberman Aiden laboratory (16), which confirmed our conclusions (see SI Appendix, section A.9).

Assessment of Our Structure Population with a Diverse Collection of Experimental Data.

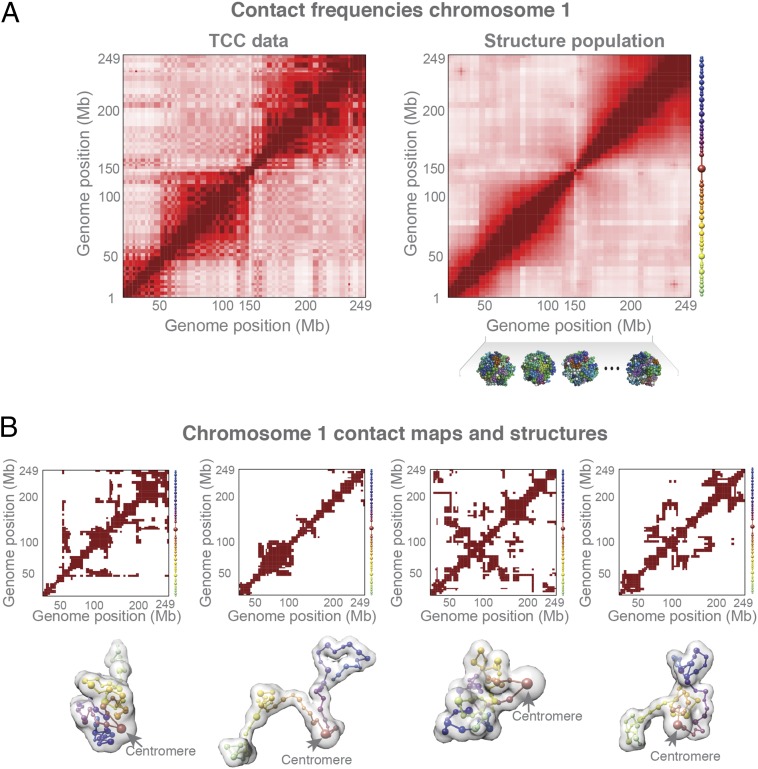
The contact probability map from our structures (i.e., the probability of finding a specific contact in the structure population) agrees very well with those derived from the TCC data (Fig. 2A and SI Appendix, Fig. S2A; row-based Pearson’s r = 0.956). Interchromosomal contact probabilities show a relatively high correlation (Pearson’s r = 0.75), which is comparable to the correlation between normalized interchromosomal contacts from replicate Hi-C experiments (35, 36). Chromosome structures can fold differently in the population, which allows for the stochastic nature of chromosome conformations (Fig. 2B), whereas the cumulative chromatin interactions across the population reproduce the observed Hi-C interaction matrix (Fig. 2A). All our results are highly reproducible in independent replicate simulations, with almost identical contact probability maps and almost identical average radial positions of all of the domains (all Pearson’s r > 0.99, P values negligible; see SI Appendix, section A.6 for details on population size convergence and reproducibility).

Fig. 2.

Structure population. (A) Comparison of the normalized contact probability maps from the TCC experiment (Left) and structure populations (Right) of chromosome 1. On the right side of the heat map are spheres representing the corresponding chromatin domains for chromosome 1. (B) An example of the conformational variability between chromosome structures in the population. These are randomly selected structures of chromosome 1 from the model population (Bottom) and their respective domain contact maps (Top). The translucent surface of each structure represents the volume of the chromosome models, and the connection between sphere centers represents their sequence order in the chromosome (color codes according to their sequence position on chromosome, as in A).

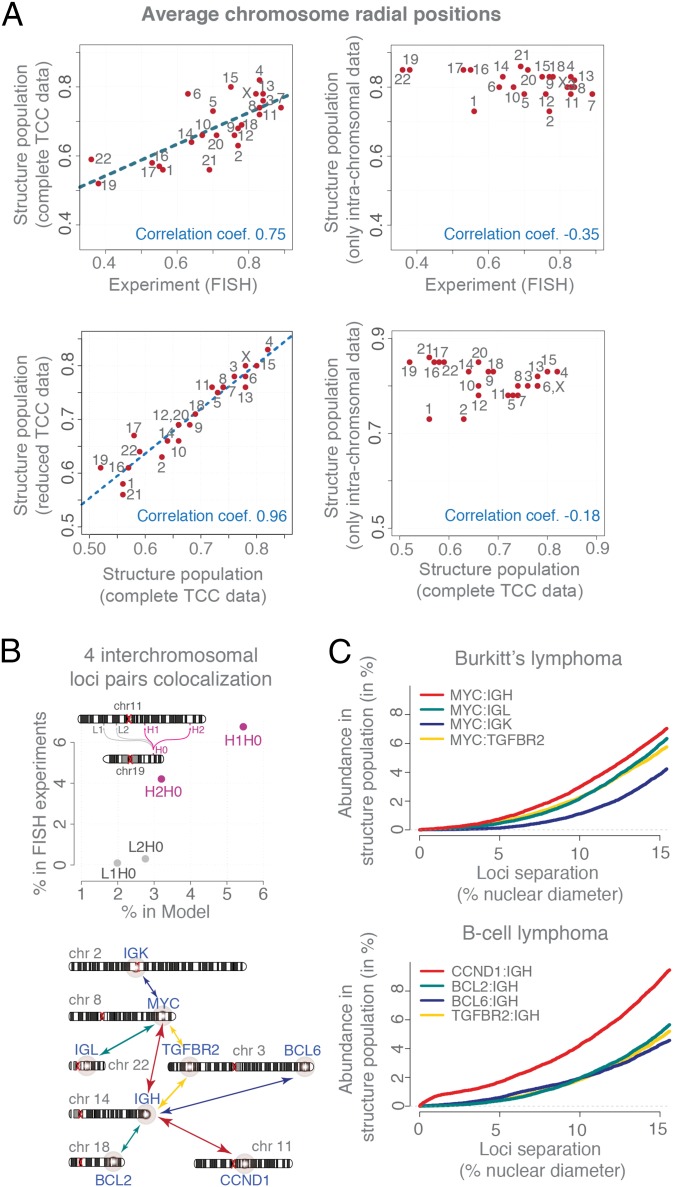
In the structure population, the distribution of each chromosome’s radial distance to the nuclear center shows a distinct maximum, revealing a preferred radial position for the chromosome territory. These positions agree very well with those measured in FISH experiments (37) (Pearson’s r = 0.75, P = 4.2e-5) (Fig. 3A, Top Left). As expected, small, transcriptionally active, gene-rich chromosomes are generally located more centrally in our structures, whereas gene-poor chromosomes are located closer to the nuclear envelope (NE), confirming also previous studies (14, 37). When we generate a structure population without interchromosomal contact data, the chromosome positions do not agree with FISH experiments (Pearson’s r = −0.3; Fig. 3A, Top Right), demonstrating the importance of interchromosomal contacts in constraining the global chromosome organization in our structures.

Fig. 3.

Model assessment. (A) (Top Left) Comparison of the average radial chromosome positions from FISH experiments (37) and the structure population. The dashed line shows a linear fit. (Top Right) The average radial chromosome positions in a structure population generated by including only intrachromosomal TCC contacts (but no interchromosomal contacts). (Bottom Left) Comparison of the average radial chromosome positions between structure populations generated with the complete and a reduced TCC datasets (which contain all intrachromosomal TCC contacts and only those interchromosomal contacts formed by subcentromeric regions). (Bottom Right) Comparison of the averaged radial chromosome positions between structure populations generated with the complete TCC dataset and one structure population generated with a TCC dataset without any interchromosomal interactions. (B) Comparison of the colocation propensity for four interchromosomal loci pairs [formed by four loci on chromosome 11 (H1, H2, L1, and L2) and one on chromosome 19 (H0)] between FISH experiments (14) and the structure population. The colocalization cutoff distance was chosen to be 1 μm. (C) The cumulative distance distributions of eight translocation-prone interchromosomal gene pairs calculated from the structure population for comparison with 3D FISH experiments by Roix et al. (38). The order of gene-pair colocation propensity agrees well with FISH experiments taken from Roix et al. (38) (plots of the experimental data are shown for visual comparison in SI Appendix, Fig. S2C).

Next, we compared the frequencies with which several gene loci (from different chromosomes) are spatially colocalized in the model population with those from 3D FISH experiments measured over a population of cells. Specifically, we measured four interchromosomal 3D distances between a locus on chromosome 19 and 4 other gene loci on chromosome 11. These loci pairs have no known functional connection (14). Two pairs of loci were in close spatial proximity substantially more frequently than the other two, which is in good agreement with the FISH experiments (14). Our structure population captured correctly the rank order of the colocalization frequency among the four pairs (Fig. 3B), even though interchromosomal interactions are generally present at low frequencies. Next, we measured 3D distances between the IGH gene locus (on chromosome 14) and 4 other gene loci on four different chromosomes (i.e., 3, 11, 18, and 22). We also measured distances between the MYC gene locus (on chromosome 8) and four other gene loci on four different chromosomes (i.e., 2, 3, 14, and 22) (Fig. 3C). The spatial proximity of these eight loci pairs has been previously studied by 3D FISH experiments because of their relevance in chromosome translocation events occurring in Burkitt’s and B-cell lymphomas (38). The FISH experiments were performed on at least 500 cells, revealing a distinct distribution of distances for each locus pair (38). The cumulative frequency of 3D distances in our structure population agrees very well with those from the FISH experiments (ref. 38 and SI Appendix, Fig. S2C). In agreement with experiment our structure population predicts the correct loci pairs (MYC:IGH and IGH:CCND1) to be consistently in closer proximity at a higher frequency in the population. Also for the other loci pairs our structure population predicts well the relative frequency of loci distances (that is, the fraction of cells having two loci within a certain distances). For example the relative order of the cumulative distances are correctly predicted between all of the loci and the MYC locus (Fig. 3C). The correct prediction of interchromosomal distances is challenging and relies on an accurate description of the entire genome organization. The level of agreement between predicted and measured interchromosomal gene distances is a good indication of the predictive value of our models. Next, we focus our analysis on the role of centromeres in shaping the spatial genome organization.

Nuclear Locations of Centromeres.

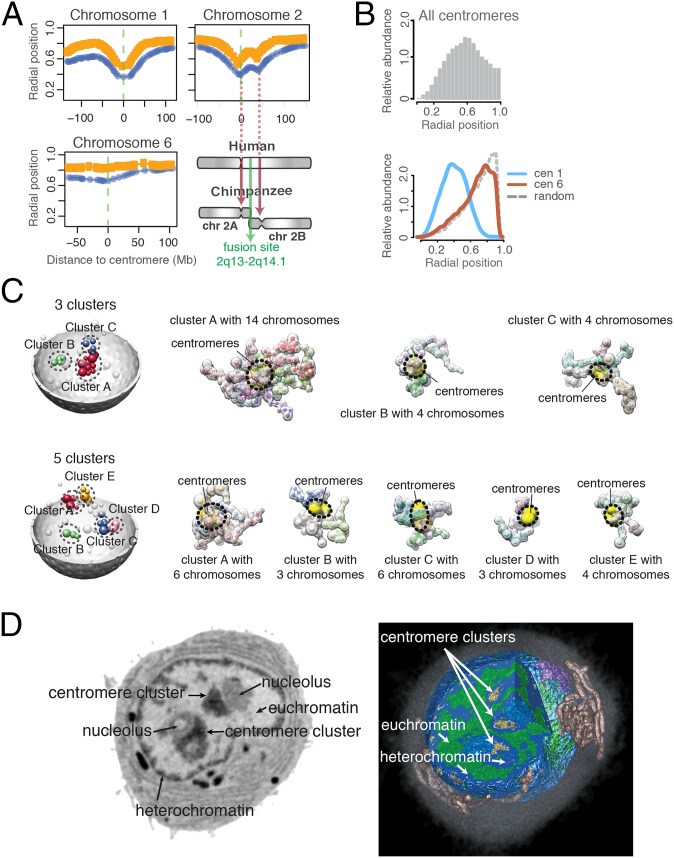
When calculating the average radial position of each domain in a single chromosome, an interesting pattern emerges: For most chromosomes, the centromeres often have the innermost average position among its chromosome domains (Fig. 4A and SI Appendix, Fig. S3), even though no radial constraints were imposed on these regions. The extent of this “V-shaped” pattern varies among chromosomes. It is pronounced in some chromosomes (e.g., chromosomes 1 and 2) and weak in others (e.g., chromosomes 6 and 16). For a few chromosomes, the V shape is pronounced in only one of the two homologs (e.g., chromosome X). A few subtelomeric regions show similar but weaker behavior, in that they have smaller radial positions than other regions in the same chromosome arm. Interestingly, chromosome 2 shows a distinct double-V pattern with a second local minimum, predicting a centromere-like behavior at position 2q21.3–2q22.1 (∼40–50 Mb downstream from the centromere on the q-arm). We noticed that human chromosome 2 evolved from primates by a head-to-head fusion event of two chromosomes (39). The second minimum observed in our structure population is located at exactly the position where a vestigial second centromere would be expected from the evolution event.

Fig. 4.

Chromosome arrangements and centromere clusters. (A) The median radial position of each domain in a chromosome, calculated separately for the radially innermost (blue curve) and outermost chromosome copy (orange curve) in a cell. Centromeres at position 0 are marked with a green dashed line. Regions near the centromeres are often closest to the nuclear interior, making a characteristic V shape. Chromosome 2 shows a double-V pattern with a second local minimum at the position of a possible vestigial second centromere. Chromosome 2 evolved from primates by a fusion event of two chromosomes (see SI Appendix, Fig. S3 for plots of all chromosomes.) (B) (Top) Histogram of radial positions for all centromeres. (Bottom) Comparison of the centromere radial distributions for chromosomes 1 and 6, as well as randomly placed points in a nucleus. (C) Illustration of different centromere clusters observed in the structure population with one genome structure containing three (Top) and the other five clusters (Bottom). (Left) Centromere spheres are colored based on their cluster membership; unclustered centromeres are white. (Right) Chromosomes of the clustered centromeres are shown by their excluded volume. A dashed circle and yellow surfaces indicates the location of the centromeres. (D) Soft X-ray tomography images of a lymphoblastoid cell. (Left) One orthoslice (virtual section) from the soft X-ray tomographic reconstruction of an intact and unstained lymphoblastoid cell shows two clusters of centromeric heterochromatin (arrows). (Right) Three-dimensional rendered view of the same cell that has been segmented and color-coded to show mitochondria (copper) and the Golgi apparatus (lilac) in the cytoplasm surrounding the nucleus. The cross-section is composed of three orthogonal slices and reveals both heterochromatin (shades of light to dark blue reflect increasing degrees of compaction) and euchromatin (green). The highest-absorbing centromeric heterochromatin (golden) is seen toward the central regions of the nucleus.

Overall, the radial distribution of centromeres is generally increased toward the interior regions (Fig. 4B), consistent with observations in FISH experiments (40). However, we can show that the radial distributions vary largely, with some centromeres (e.g., chromosome 1) showing distinctly increased location probabilities at central regions, whereas those of some other chromosomes (e.g., chromosome 6) seem almost uniformly distributed throughout the nucleus (Fig. 4B).

Centromeres Form Higher-Order Clusters.

Centromeres interact with each other, as is evident from the Hi-C data analysis. However, no study addressed the question of whether centromeres form higher-order clusters in this cell type (i.e., the colocalization of three or more centromeres), and which centromeres participate in such clusters and what role clusters play in organizing the interphase genome structure in human cells. We are now in a position to study the higher-order clustering of centromeres in individual cells. We observe that about half of the centromeres in a structure are part of a higher-order cluster (with more than three colocalizing centromeres) (SI Appendix, section A.5.1). The majority of structures (∼80%) contain between two and four such clusters (SI Appendix, Fig. S4A). The cluster size varies widely, with a median of five centromeres (SI Appendix, Fig. S4B). Naturally, smaller clusters are observed more frequently than larger ones and only rarely does a cluster contain more than 20 centromeres; such large clusters are observed in less than 4% of the population. Several clusters are shown in Fig. 4C, illustrating the stochastic nature of centromere clustering in the structure population.

Cryo-X-Ray Tomography Confirms the Presence of Centromere Clusters.

Although higher-order centromere clusters have been observed in some other cell types and species (6, 8, 9, 35, 36, 40–44), in GM12878 cells they have not been characterized yet to our knowledge. To confirm the presence, size, and locations of higher-order clusters experimentally we performed cryo soft X-ray tomography experiments (cryo-SXT) on lymphoblastoid cells (GM12878). Cryo-SXT is a quantitative imaging technique that produces 3D tomographic reconstructions of entire cells in a near-native state. We previously demonstrated the potential of cryo-SXT to detect pericentromeric heterochromatin foci in the nuclei (45). Pericentromeric heterochromatin has higher linear absorption coefficients (LAC) (between 0.34–0.36 µm⁻¹) than the rest of the heterochromatin, which allows their distinction from other heterochromatic regions and euchromatin (46). Our experiments on lymphoblastoid cells revealed clusters of pericentromeric heterochromatin in the interior regions of the nucleus, consistent with our findings (Fig. 4D). Among the 10 imaged intact cells, the majorities (70%) have three and the remaining cells two interior large clusters, in close agreement with our predictions. The measured volume of these regions indicates that centromeres of approximately three to five chromosomes could participate in the formation of these foci. Also, the number and size of these centromere foci vary between individual cells, similar to our findings. These findings are therefore qualitatively in good agreement with our structure models and confirm the predicted centromeric clusters, which can also localize to central regions of the nucleus.

Centromere Clusters Are Specific with Respect to Chromosome Compositions.

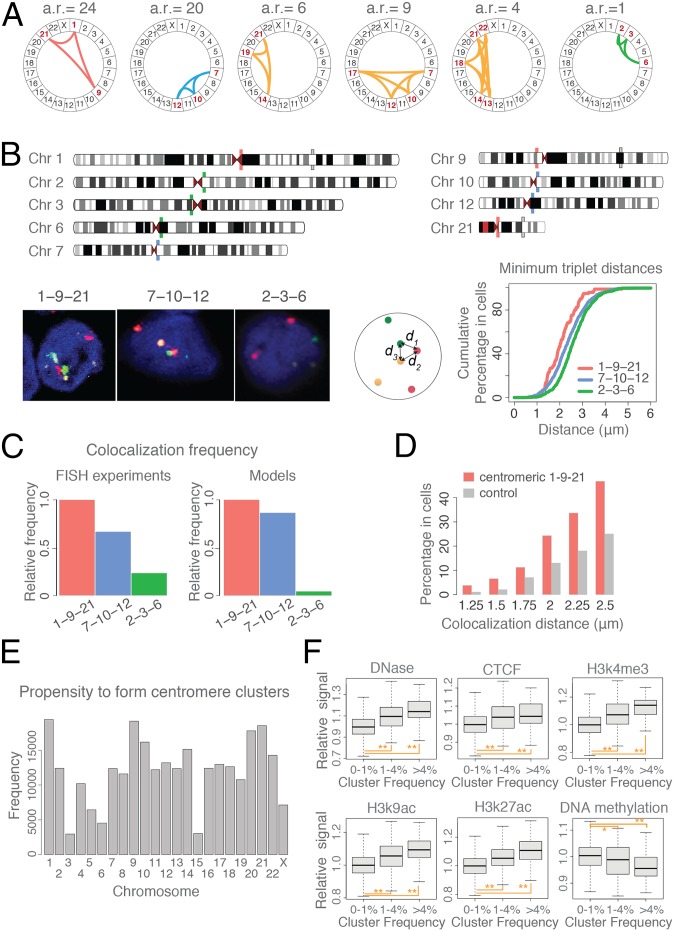
We asked whether the 23 chromosomes have different probabilities to participate in centromere clusters. To detect the frequency of clusters with distinct chromosome identities in the population, we translated each genome structure into a centromere interaction graph and applied a frequent dense-subgraph mining algorithm (47). The algorithm revealed 798 specific centromere cluster combinations (i.e., frequent cluster patterns; Materials and Methods) observed in at least 1% of the population (SI Appendix, Fig. S4E). Many possible centromere cluster combinations are never observed. Only about 18% of all possible three-chromosome combinations exist as centromere clusters. Other clusters are found with relatively high frequencies. For example, the centromere cluster of chromosomes 7, 10, and 12 occurs more frequently than the cluster of chromosomes 2, 3, and 6, but less frequently than the cluster formed by chromosomes 1, 9, and 21 (Fig. 5A). To test the chromosome-specific nature of our predicted centromere clusters, we performed 3D FISH experiments for these three centromere clusters (Fig. 5B) (SI Appendix, section A.10). To compare the colocalization propensity of centromeres in the three clusters we first calculated the cumulative percentage of cells with respect to the probe triplet distances (Fig. 5B). As predicted by our models, the FISH experiments confirm that centromeres 1, 9, and 21 are consistently more frequently at smaller distances to each other than those of centromeres 7, 10, and 12, while centromeres 2, 3, and 6 are least frequently in proximity to each other among the three clusters (Fig. 5B). We then quantified the relative frequencies of centromere colocalization for the three clusters in the cell population. Our model predicts very well the relative cluster frequencies seen in FISH experiments (Fig. 5C). In FISH experiments, the centromere cluster 1–9–21 shows the highest frequency among all three clusters. The observed frequency for cluster 7–10–12 is only 67% of the frequency for cluster 1–9–21, whereas the frequency of cluster 2–3–6 is only 23% of the frequency for cluster 1–9–21. In the model, the rank order of frequencies is identical. The highest frequency is observed for cluster 1–9–21. The frequency of cluster 7–10–12 is only 86% and the frequency of cluster 2–3–6 is only 4% of the frequency observed for cluster 1–9–21, respectively (Fig. 5C). Additionally, we tested whether the centromeres are the main points of interactions for the chromosome cluster 1–9–21. We found that the three markers located in the pericentromeric regions of chromosomes 1, 9, and 21 showed substantially higher colocalization frequency (approximately threefold at distance threshold 1.5 μm; Fig. 5D and SI Appendix, Fig. S9) than a control group of markers located at more distal regions from centromeres on the same chromosomes (56.8, 61.5, and 18.3 Mb away from centromere on chromosomes 1, 9, and 21, respectively; SI Appendix, section A.10). The cumulative probe triplet distances are consistently smaller for the subcentromeric probe cluster than for the control probes at more distant locations from the centromeres. The FISH experiments confirm that centromeres are the likely points of interactions for chromosome cluster 1–9–21.

Fig. 5.

Centromere clusters are chromosome-specific. (A) A selection of centromere clusters detected in the structure population at different frequencies and shown as circos plots (labels are chromosome names). The abundance ratio (a.r.) is the relative cluster frequency in the population with respect to frequency of cluster 2–3–6. (B) Three-dimensional FISH assessment of centromere clusters. (Upper) Schematic view of the genomic locations of all FISH probes. (Lower Left) Images of the three-color FISH experiments with probes in green, red, and yellow. Chromosomal DNA was counterstained in blue with DAPI. (Lower Middle) Cumulative percentage of cells with respect to the smallest probe triplet distances in a cell for each cluster. The “triplet distance” is defined as the smallest averaged sum of all three distances between three different probes: (d1 + d2 + d3)/3. (Lower Right) (C) The relative frequencies of the three clusters in FISH experiments (Left) and structure population (Right). A cluster is defined if all of the three distances between all three probes are less than 1.5 μm in a single cell. (D) Histogram of colocalization frequencies with varying distance threshold for probes located adjacent to centromeric regions of chromosomes 1, 9, and 21 (orange probes in B, Upper) and a control group of markers located at more distal regions from the centromere (gray probes in B, Upper) (see also SI Appendix, Fig. S9). (E) Histogram of the propensity of centromeres to be found in centromere clusters (i.e., the relative abundance of a chromosome in all centromere clusters with frequencies ≥1%). (F) Comparison of the epigenetic signatures in the subcentromeric regions (+5 and −5 Mb from centromere) of frequent and infrequent centromere clusters (Materials and Methods and SI Appendix, Table S4). The enrichments of some epigenetic signatures are correlated with the centromere cluster abundance ratio. Statistical significance is indicated by *P values < 0.005 and **P values <1.e-6 (one-sided Wilcoxon tests). (See SI Appendix, Fig. S4F for more chromatin factors.)

In our model, individual chromosomes differ substantially in their propensity to form centromere clusters. Among the frequent centromeres to cluster in our structure population are those from chromosomes 1, 9, 10, 14, 20, 21, and 22 (Fig. 5E). We conclude that centromere cluster formation is highly specific in nature.

We then asked whether the stability of specific centromere clusters is mirrored by the presence of the same epigenetic markers in the subcentromeric regions of these chromosomes (i.e., regions within 5 Mb of the centromere borders). The gene density, gene expression levels, and constitutive heterochromatin marker (H3K9me3) are similar for all clusters of both high and low frequencies (SI Appendix, Fig. S4F). However, the signal intensities of other histone modifications are clearly correlated with cluster frequency: Positive correlations are found for markers associated with open chromatin structure and chromatin activation, such as DNase hypersensitivity regions, and CTCF binding, and histone modifications H3K4me1, H3K4me3, H3K9ac, and H3K27ac (Fig. 5F and SI Appendix, Fig. S4F). Negative correlation is found for DNA methylation signals, which is depleted in clusters with higher frequency.

We also noticed other factors that contribute to the cluster stabilization. Human acrocentric chromosomes (i.e., 13–15, 20, and 21) bear nucleolus organizer regions (NORs) on their short chromosome arms close to the centromeres (48). We noticed that about two-thirds of our detected centromere clusters contain at least one (and about half at least two) NOR-bearing chromosomes. Therefore, a large portion of the centromere clusters in the structure population is likely to be connected to nucleoli (SI Appendix, Fig. S4 C and D). Indeed, our cryo-SXT experiments confirm this prediction (Fig. 4D). Due to their distinct linear-absorption coefficients cryo-SXT can visualize the locations of nucleoli. About two-thirds of all interior centromere clusters (∼70%) are associated with nucleoli (Fig. 4D).

Centromere Clustering As a Driving Force for Chromosome Positioning.

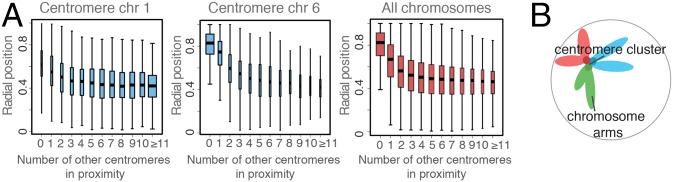
Next we analyze the spatial localizations of higher-order centromere clusters. First of all, we note that if a centromere is part of a larger centromere cluster, it is more likely to be positioned toward the nuclear interior. Indeed, a centromere’s radial position is strongly correlated with the number of other centromeres that it interacts with (Fig. 6A). In other words, when comparing the radial centromere position of the same chromosome in different structures, we observe a smaller radial position for this chromosome when it participates in a larger centromere cluster. This trend is similar for all of the chromosomes (SI Appendix, Fig. S5). However, the likelihood of forming a large cluster varies among chromosomes, which explains the differences in their average centromere positions (Fig. 4B).

Fig. 6.

Centromere clusters are often in the nuclear interior. (A) Box-and-whisker plots showing the distribution of radial positions of a centromere as a function of the number of other centromeres it is in contact with. The widths of the boxes are proportional to the square root of the sample size. Displayed here are plots for chromosomes 1 and 6 and centromeres from all chromosomes combined (see SI Appendix, Fig. S5A). (B) Schematic diagram of a centromere cluster, illustrating that centromeres in a central cluster are often shielded by their chromosome arms from approaching positions close to the NE.

So, why do centromeres in larger clusters prefer interior locations in the nucleus if they are not explicitly tethered to the nuclear envelope? Inspection of the model structures reveals that clustered centromeres tend to be located in the central regions of the corresponding chromosome cluster (Fig. 4C). The centromeres are naturally shielded from approaching the outer nuclear regions by the chromosome arms that radiate outward from the cluster center (Fig. 6B). Therefore, the nuclear volume accessible to the centromeres decreases with increasing cluster size and with the size of the corresponding chromosomes. In other words, due to their restricted accessible volume, clustered centromeres are more often found close to the nuclear interior than nonclustered centromeres, which can access a larger nuclear volume.

Our observations therefore indicate that centromere clustering can be a driving force for positioning some chromosomes toward the nuclear interior. To test this hypothesis, we calculated another structure population using a modified TCC dataset containing all intrachromosomal interactions and only those interchromosomal interactions formed by subcentromeric regions. This criterion excludes nearly 70% of the original TCC data (SI Appendix, Fig. S2A). Strikingly, the genome structures produced in this model accurately reproduce all radial chromosome positions (Pearson’s correlation r = 0.96) (Fig. 3A, Bottom Left). Moreover, this model correctly predicts the contact probabilities of significant interchromosomal interactions (Pearson’s r = 0.67, P = 3.2e-14) for regions within ∼17 Mb from the centromeres, which were excluded from the TCC data when generating this model. Also, the resulting genome-wide contact probability map generally resembles those of the complete data model (SI Appendix, Fig. S2A; Pearson’s r = 0.954). Removing also the subcentromeric interactions from the TCC data produces genome structures with incorrect radial positioning of the chromosomes (Fig. 3A, Bottom Right). We also tested a model with nonspecific centromere–centromere interactions. In this model, we include all intrachromosomal interactions and include only interchromosomal interactions formed between subcentromeric regions with uniform contact probability for each subcentromeric pair (SI Appendix, section A.8). The contact probability is chosen so that the total number of subcentromeric contacts is identical to the original model. The structure population generated with this model did not reproduce the correct radial positioning (SI Appendix, Fig. S2B), supporting the notion that specific centromere interactions could play an important role in chromosome positioning inside the nucleus.

Centromere clustering often induces a more V-shaped chromosome conformation (with centromere at the hinge positions) (Fig. 6B). With increasing cluster sizes, the angle between the clustered chromosome arms tends to decrease (favoring more V-shaped chromosome conformations) (SI Appendix, Fig. S5B), whereas the chromosome arms tend to be more extended (SI Appendix, Fig. S5C). These effects are likely a result of crowding at the cluster centers. Our structures can effectively explain several other findings in the Hi-C data. Subcentromeric regions show relatively high interchromosomal contact probability (ICP, defined as the fraction of interchromosomal contacts among all its contacts) (14) (SI Appendix, Fig. S6). These interchromosomal contacts are formed largely with other subcentromeric regions (14, 36). Indeed, as seen in the structural models (Fig. 4C), crowding in the cluster centers effectively shields subcentromeric regions from interactions with their own chromosome arms, while at the same time restricting interchromosomal interactions largely to subcentromeres of other chromosomes explaining the unusual ICP values for these chromatin regions (14, 36).

Discussion

We introduced a probabilistic framework for deconvoluting ensemble Hi-C data into a population of genome structures whose chromatin contact probabilities are statistically consistent with the Hi-C data. Our models have predictive value. They reproduce remarkably well many known structural properties of the human lymphoblastoid cell genome, even though these were not included as input constraints and are not readily observable in the TCC data. By considering the stochastic nature of chromosome conformations, our models allow a detailed structural analysis of genomes. Here, we focused on the structural role of centromeres and make several interesting findings. We observed the presence of large higher-order centromere clusters in our models and confirmed their presence by Cryo-SXT experiments. However, not all of the chromosomes participate equally likely in centromere clusters and specific combinations of chromosomes are found more often in clusters than others. It remains to be seen what factors are responsible for the chromosome-specific nature of centromere clustering. We showed that histone modifications that are typically associated with more open chromatin in the subcentromeric regions of a chromosome correlate positively with the frequency of this centromere to form stable clusters. Also, the formation of nucleoli may be initiated by centromere clusters. Interestingly, we observe a correlation between the centromere cluster size and its radial position. In other words, if a centromere is in a larger cluster it is more likely to be positioned in the nuclear interior than if the same centromere is part of a smaller cluster. These observations indicate that centromere clustering can shape the interphase genome architecture by imposing strong geometrical constraints on chromosome positioning. Notably, in other organisms, such as yeasts (6, 44, 49–52) and Drosophila melanogaster (8, 9), centromere clustering plays a prominent role in shaping the interphase genome structures. A model based on interchromosomal interactions formed by only subcentromeric regions suffices to reproduce the correct radial positions of all chromosomes. These results raise an interesting hypothesis, namely, that modulating the preferences for centromere–centromere interactions could change the fate of a chromosome’s location, thereby helping establish cell-type-specific genome architectures. Notably, it has been suggested that centromere clustering is a particular feature in undifferentiated cells. Modulating the probability of a chromosome to form centromere clusters during differentiation may contribute to establishing the location preferences of chromosomes in different cell types.

Here, we studied the genome structures at ∼3.5-Mb resolution and focused our analysis on centromere interactions. Our method allows a detailed analysis of the dynamic landscape of genome organization, which is currently not explored by other structure-based methods. In future, our method could be applied at higher resolution [for instance at the levels of “contact domains” (16)], which will chart a more detailed description of the genome structure landscape. Moreover, currently we only included Hi-C data in our analysis. However, to increase accuracy, precision, and coverage in our models it is necessary to integrate all available data sources in future. Our current method provides the first step in this direction by providing a flexible framework for data-driven genome structure modeling.

Materials and Methods

Population-Based Structure Modeling Approach.

The population-based structural modeling approach is a probabilistic framework to generate a large number of genome 3D structures (i.e., the structure population) whose chromatin domain contacts are statistically consistent with the input experimental TCC data. Our structure population represents a deconvolution of the ensemble-averaged TCC data into a population of individual structures and represents the most likely approximation of the true structure population given all of the available data. Our method distinguishes between interactions involving two chromosome homologs and therefore can generate structure populations of entire diploid genomes. Further, because the generated population can contain different structural states, it can accommodate all of the experimentally observed chromatin interactions, including those that would be mutually exclusive in a single structure.

Chromatin is represented at the level of chromosome domains, which were inferred from the TCC data as described previously (14). We represent the genome at the level of macrodomains at about 3.5-Mb resolution (SI Appendix, section A.4).

We formulated the genome structure optimization problem as a maximization of the likelihood $P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)$, where A is the domain contact probability matrix derived from the observed TCC data (SI Appendix, section A.3), X is the model representing the population of genome structures, and W is the latent indicator variable of all diploid chromatin domain contacts across the population. To solve this large-scale model estimation problem, we designed an iterative optimization algorithm with a series of optimization strategies for efficient and scalable model estimation. In addition, here we introduce a stepwise strategy that is developed to efficiently guide the genome structure search process by gradually incorporating all chromatin contacts starting from high to low contact probabilities. The idea is to begin by estimating a structure population that at first reproduces the most frequent interactions, then, by using the resulting structure population as the initial condition, we gradually increase the number of constrained contacts with decreasing contact probabilities, followed at each iterative step by additional rounds of structure optimizations.

Probabilistic Model and Problem Formulation of the Structure Population.

Our model, the structure population, is defined as a set of M diploid genome structures X = {X₁, X₂, …, X_M}, where the m-th structure X_m is a set of 3D vectors representing the center coordinates of 2N domain spheres ${\mathbf{X}}_m=\left\{{\overrightarrow{x}}_{im}:{\overrightarrow{x}}_{im}\in {\Re }^3,i=1,\hspace{0.17em}2\hspace{0.17em}\mathrm{...},\hspace{0.17em}2N\right\}$. N is the number of domains (SI Appendix, section A.4), and each domain has two homologous copies. The contact probability matrix $\mathbf{A}={\left(a_{IJ}\right)}_{N\times N}$ for N domains is derived from the TCC data (SI Appendix, section A.3) and is the probability that a direct contact between domains I and J exists in a structure of the population (note that capital letter indices I and J relate to domains without distinguishing between two homologous copies, whereas lowercase letter indices i, i′ and j, j′ distinguish between two copies). Given $\mathbf{A}={\left(a_{IJ}\right)}_{N\times N}$ we aim to estimate the structure population X such that the likelihood $P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)$ is maximized. $\mathbf{W}={\left(w_{ijm}\right)}_{2N\times 2N\times M}$ is the contact indicator tensor, which is the latent variable complementing the missing information in the TCC data (A) and includes the contacts of all homologous domains in each structure of the population (i.e., $w_{ijm}=1$ indicates the contact between domain spheres i and j in structure m; $w_{ijm}=0$ otherwise) (Fig. 1A). The dependence relationship between these variables is given as $\mathbf{X}\to \mathbf{W}\to \mathbf{A}$, because W is a detailed expansion of A at the diploid representation and single-cell level and X is the structure population that is consistent to W. Therefore, the likelihood $P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)$ can be expanded to $P\left(\mathbf{A}|\mathbf{W}\right)P\left(\mathbf{W}|\mathbf{X}\right)$ according to this relationship. In detail, $P\left(\mathbf{W}|\mathbf{X}\right)$ can be expanded to $P\left(\mathbf{W}|\mathbf{X}\right)={\displaystyle {\prod }_{m=1}^M{\displaystyle {\prod }_{\begin{array}{l}i,j=1\\ i\ne j\end{array}}^{2N}P\left(w_{ijm}|{\overrightarrow{x}}_{im},{\overrightarrow{x}}_{jm}\right)}}$, where we have

$$P\left(w_{ijm}|{\overrightarrow{x}}_{im},{\overrightarrow{x}}_{jm}\right)=P{(w_{ijm}=1|{\overrightarrow{x}}_{im},{\overrightarrow{x}}_{jm})}^{w_{ijm}}P{(w_{ijm}=0|{\overrightarrow{x}}_{im},{\overrightarrow{x}}_{jm})}^{1-w_{ijm}}.$$ [1]

We modeled a contact between two domain spheres i and j as a variant of the rectified or truncated normal distribution (see SI Appendix, section A.1.2). $P\left(\mathbf{A}|\mathbf{W}\right)$ can be expanded as $P\left(\mathbf{A}|\mathbf{W}\right)={\displaystyle {\prod }_{I,J}P\left(a_{IJ}\right|a{\prime }_{IJ})}$, where $a{\prime }_{IJ}$ is the contact probability of the domain pair I and J computed from W. We then model each $a_{IJ}$ as $a_{IJ}=a{\prime }_{IJ}+{\epsilon }_{IJ}$, where ${\epsilon }_{IJ}$ are independent and identical normally distributed random variables with mean zero (${\epsilon }_{IJ}\sim 0$) (SI Appendix, section A.1.3).

With these probabilistic models, we can maximize the log-likelihood $\log P(\mathbf{A},\mathbf{W}|\mathbf{X})$, expressed as below:

$$\log P(\mathbf{A},\mathbf{W}|\mathbf{X})=\log P\left(\mathbf{A}|\mathbf{W}\right)+\log P\left(\mathbf{W}|\mathbf{X}\right)={\displaystyle \sum _{\begin{array}{l}I,J=1\\ I\ne J\end{array}}^N\log P\left(a_{IJ}\right|a{\prime }_{IJ})}+{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{\begin{array}{l}i,j=1\\ i\ne j\end{array}}^{2N}\log P\left(w_{ijm}|{\overrightarrow{x}}_{im},{\overrightarrow{x}}_{jm}\right)}}.$$ [2]

In addition to the TCC data, we also consider additional information about the genome organization. These data are included in form of spatial constraints acting on the 2N domain spheres: (i) a nuclear volume constraint that forces all spheres to lie inside the nuclear volume (${\Vert {\overrightarrow{x}}_{im}\Vert }_2<R_{\text{nuc}}$, where R_nuc is the nuclear radius); (ii) excluded volume constraints that prevent the overlap between any two spheres i and j, that is, ${\Vert {\overrightarrow{x}}_{im}-{\overrightarrow{x}}_{jm}\Vert }_2\ge (R_i^x+R_j^x)$ where $R_i^x$ is the excluded volume radius of sphere i (SI Appendix, section A.1.1); and (iii) information from 3D FISH experiment, which showed that the telomere on q-arm of chromosome 4 is in proximity to the NE (53). Accordingly we add a constraint to the q-arm telomere domain (${\overrightarrow{x}}_{4\text{qtel}}$) of chromosome 4 to be located close to the NE (${\Vert {\overrightarrow{x}}_{4\text{qtel}}\Vert }_2>0.75R_{\text{nuc}}$). Note that, without losing generalization, we use the origin (0,0,0) as the nuclear center, thus ${\Vert \overrightarrow{x}\Vert }_2$ is equivalent to the distance from the nuclear center. In summary, the maximum likelihood problem is formally expressed as follows:

$$\begin{array}{l}\widehat{\mathit{X}}=\arg \underset{\mathit{X}}{\max }\underset{\mathbf{W}}{\max }\left\{\log \mathrm{P}(\mathit{A},\mathbf{W}|\mathit{X})\right\}\\ \text{subject\hspace{0.17em}to\hspace{0.17em}}\{\begin{array}{l}\text{spatial\hspace{0.17em}constraint\hspace{0.17em}I:\hspace{0.17em}nuclear\hspace{0.17em}volume\hspace{0.17em}constraints}\\ \text{spatial\hspace{0.17em}constraint\hspace{0.17em}II:\hspace{0.17em}excluded\hspace{0.17em}volume\hspace{0.17em}constraints}\\ \text{spatial\hspace{0.17em}constraint\hspace{0.17em}III:\hspace{0.17em}}4\text{qtel}-\text{NE\hspace{0.17em}proximity\hspace{0.17em}restraints}\end{array}.\end{array}$$ [3]

Note that, in principal we could add more knowledge-based constraints into this formulation.

Optimization Procedure.

We designed an iterative optimization procedure to solve this maximum likelihood estimation problem. Because our problem does not have a closed-form solution, numerical routines and heuristic strategies are needed to efficiently approximate the solution. This is an efficient iterative solver to alternately optimize W and X while holding the other fixed. We refer to this iterative cycle as the A/M (Assignment/Modeling) steps (Fig. 1A) and this procedure as the A/M algorithm, which are described as follows:

• Initialization step: an initial model estimate X⁽⁰⁾ is needed to start the iterative procedure at the very first optimization step. We first initialize random points for domain positions (spherically uniformly distributed inside the nuclear volume) and then optimize them to satisfy the three spatial constraints in Eq. 3 to get X⁽⁰⁾ (Fig. 1B).

• Assignment step (A-step): Given the current estimated model X^(k), estimate the latent variable W by maximizing the log-likelihood over all possible values of W:

$${\mathbf{W}}^{(k+1)}=\arg \underset{\mathbf{W}}{\max }\left\{\log P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)\right\},\hspace{1em}\text{given}\hspace{0.17em}\mathbf{X}={\mathbf{X}}^{\left(k\right)}.$$ [4]

• Modeling step (M-step): Given the current estimated latent variable W^(k+1), find the model X^(k+1) that maximizes the log-likelihood of the data A. A new structure population will be generated in which all assigned contacts in W will be physically present in the structure population X:

$${\mathbf{X}}^{(k+1)}=\arg \underset{\mathbf{X}}{\max }\left\{\log P\left(\mathbf{A},\mathbf{W}|\mathbf{X}\right)\right\},\hspace{1em}\text{given}\hspace{0.17em}\mathbf{W}={\mathbf{W}}^{(k+1)}.$$ [5]

• Iterative A/M steps until convergence (detailed convergence criteria refers to SI Appendix, section A.1.7).

We extensively exploited the parallelism and algorithmic heuristics underlying the A/M steps, which can largely speed up the procedure and make the implementation scalable for the large-scale TCC data.

Stepwise optimization strategy for efficiently guiding the search process.

The probability of observing a given contact in a specific structure is increased (or decreased) by the presence of another contact in the same structure. For example, a certain chromosome contact brings also other chromosome regions into spatial proximity to each other, which in turn enhances their chances of contacting each other in the same structure rather than in a structure where the corresponding domains are far apart from each other and cannot be brought into spatial proximity. This contact cooperativity facilitates our optimization heuristics: (i) An initial model X that already fits a portion of domain contacts in A can guide a more efficient search of the optimum W than a random structure and (ii) gradually fitting an increasing number of domain contacts (from the highest to the lowest contact probabilities A) can effectively guide the search to the best solution. We therefore designed a stepwise strategy to use these two heuristics. Specifically, we start the first optimization step by using only the most frequent contacts ${\mathbf{A}}^{{\theta }_1}$ (using only $a_{IJ}\ge {\theta }_1$ and ${\theta }_1$= 1.0) as input to obtain ${\widehat{\mathbf{X}}}^{{\theta }_1}$, which reproduces ${\mathbf{A}}^{{\theta }_1}$ (i.e., the structure population contains all physical domain contacts according to the experimental contact probability). Then ${\widehat{\mathbf{X}}}^{{\theta }_1}$ is used as the initial model of the next round of optimization for ${\mathbf{A}}^{{\theta }_2}$, which includes all domain contacts with lower contact probabilities (i.e., using only $a_{IJ}\ge {\theta }_2$ and ${\theta }_2<{\theta }_1$). This in turn leads to the refined structured population ${\widehat{\mathbf{X}}}^{{\theta }_2}$, which covers more domain contacts than ${\widehat{X}}^{{\theta }_1}$. We repeat this process, each time adding more domain contacts to the input data (${\mathbf{A}}^{\theta }$ with lower $\theta$), until ${\mathbf{A}}^{\theta }$ is almost close to A. Because errors in the conformation capture detection are expected to have low frequencies, we typically stop at the threshold θ = 0.01 to reduce the effect of experimental noise in the calculations. The final solution represents the best approximation of the true structure population by reproducing most elements of A. This stepwise procedure is illustrated in Fig. 1B.

Parallel and efficient optimization heuristics for the contact assignment step.

The A-step optimization problem is to “find the contact indicator tensor W whose derived contact probability $a{\prime }_{IJ}$ best matches the observed $a_{IJ}$ for every domain pair I and J″ (Fig. 1). We designed an efficient heuristic, that is, a distance threshold method, to approximate the solution. We assume that the assignments of a given chromatin contact across the contact indicator tensor W are more likely realized in those genome structures in which the corresponding chromatin domains are already closer in 3D space. Our empirical results have shown its effectiveness and a detailed procedure and explanation of this heuristics is described in SI Appendix, section A.1.6. Here, it is briefly summarized as a process of determining the distance threshold $d_{IJ}^{\text{act}}$ for each domain pair (I, J), based on the empirical distribution of all distances between their homologous copies across all structures of the population. Then we determine W based on $d_{IJ}^{\text{act}}$. This process is easily implemented in parallel, because the distance threshold of each domain pair can be independently calculated.

Parallel and efficient numerical approximation for the modeling step.

Given the current estimated contacts of W, the M-step reconstructs the structure population X that best matches W. In the M-step, because A and W are known, its maximization problem in Eq. 5 can be reduced to $\max \log P\left(\mathbf{W}|\mathbf{X}\right)$, which can be further decomposed to the subproblem $\max \log P\left({\mathbf{W}}_m|{\mathbf{X}}_m\right)$ for every structure m in the population, where $P\left({\mathbf{W}}_m|{\mathbf{X}}_m\right)={\displaystyle {\prod }_{i,j}P\left(w_{ijm}|{\overrightarrow{x}}_{im},{\overrightarrow{x}}_{jm}\right)}$ and ${\mathbf{W}}_m$ is the contact indicator matrix of structure m. Therefore, each individual structure can be independently optimized in parallel. To efficiently optimize an individual structure, we used simulated annealing dynamics and conjugate gradient optimizations.

Detection of Centromere Cluster Recurrence Pattern.

To identify the centromere clusters that frequently occur in structures of the population, we performed the following procedure:

• i)Construct M = 10,000 centromere interaction networks from the structure population. Each network corresponds to a structure, each node represents a centromere, and two nodes are connected by an edge if the distance between the centromere domains i and j is d_threshold ≤ 2($R_i^x+R_j^x$).
• ii)Construct M “projected” centromere interaction networks, in which the two homologous centromere copies are represented by a single node. An edge between two nodes is present when there is at least one contact between any of the two corresponding homologous centromere copies.
• iii)To identify the frequently clustered centromeres, we represent the M projected networks as a third-order tensor and apply our tensor-based recurrent heavy subgraph discovery algorithm (47). We suppose that each heavy subgraph (i) should consist of ≥3 nodes, (ii) occurs in at least ≥1% of the structures in the population, and (iii) has a minimum network density 0.7.
• iv)Among all projected frequent centromere clusters detected in step iii we only consider those that exist in the original “unprojected” networks.

Cryo-SXT.

Detailed experimental procedures of the cryo-SXT imaging of Lymphoblastoid cells (GM12878) are described in SI Appendix, section A.11. Projection images were collected at 517 eV using XM-2, the National Center for X-ray Tomography soft X-ray microscope at the Advanced Light Source of Lawrence Berkeley National Laboratory. For each dataset, 180 projection images were collected sequentially around a rotation axis in 1° increments. Projection images were manually aligned using IMOD software by tracking gold fiducial markers on adjacent images (54) and tomographic reconstructions were calculated using the iterative reconstruction method (55, 56). LAC values were determined as described previously (57).

Experimental Methods and Data Processing.

The details of the TCC experiment, data processing including matrix construction, data normalizations, genome representations, and analysis methods are described in SI Appendix, section A.3. The 3D FISH experiments and probe information are described in SI Appendix, section A.10.

Data Accession Code.

The TCC dataset as binary contact catalogs are publicly available in NCBI Sequence Read Archive repository under accession no. SRX030110.