Allosteric switch regulates protein–protein binding through collective motion

Significance

Within biological molecules, a change in shape at one site affecting a distant site is called allostery, and is a process critical for sustaining life. At the atomic level, the means of communication is often not well understood. We identify a previously unidentified way for allostery to occur through collective motion of an entire protein structure. Together with newly developed computational algorithms, we determine atomic structures representing this previously invisible allosteric motion. This allosteric network is shown to be an intrinsic property of the protein and important for enabling binding to different protein partners. The nature of this motion, along with the tools we developed to detect it, should prove invaluable for understanding living organisms and developing new therapeutics.

Abstract

Many biological processes depend on allosteric communication between different parts of a protein, but the role of internal protein motion in propagating signals through the structure remains largely unknown. Through an experimental and computational analysis of the ground state dynamics in ubiquitin, we identify a collective global motion that is specifically linked to a conformational switch distant from the binding interface. This allosteric coupling is also present in crystal structures and is found to facilitate multispecificity, particularly binding to the ubiquitin-specific protease (USP) family of deubiquitinases. The collective motion that enables this allosteric communication does not affect binding through localized changes but, instead, depends on expansion and contraction of the entire protein domain. The characterization of these collective motions represents a promising avenue for finding and manipulating allosteric networks.

Intermolecular interactions are one of the key mechanisms by which proteins mediate their biological functions. For many proteins, these interactions are enhanced or suppressed by allosteric networks that couple distant regions together (1). The mechanisms by which these networks function are just starting to be understood (2–4), and many of the important details have yet to be uncovered. In particular, the role of intrinsic protein motion and kinetics remains particularly poorly characterized. A number of structural ensembles representing ubiquitin motion have been recently proposed (5–9). Additionally, it has been suggested that through motion at the binding interface, its free state visits the same conformations found in complex with its many binding partners (5, 10). However, it remains an unanswered question if the dynamics that enable this multispecificity are only clustered around the canonical binding interface or whether this motion is allosterically coupled to the rest of the protein, especially given the presence of motion at distal sites (11).

Results

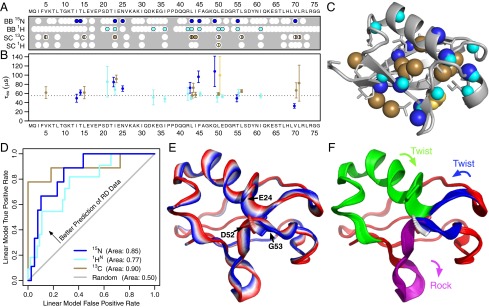
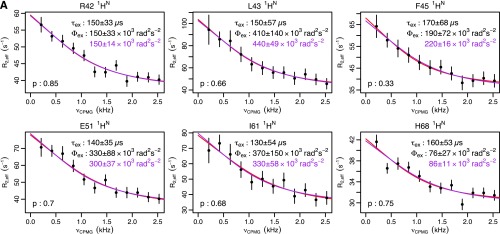
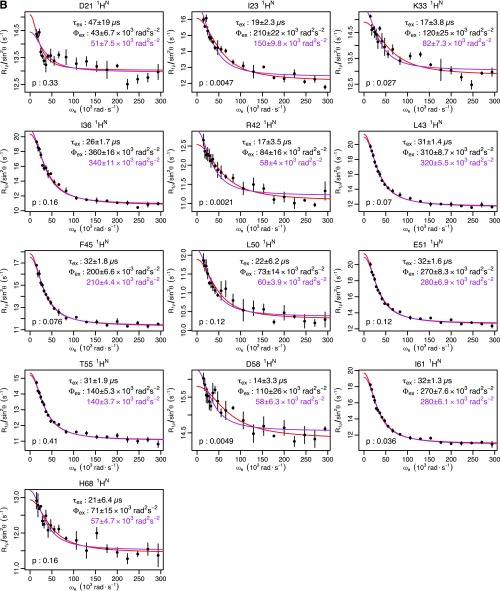
To answer this question and to provide a detailed structural picture of the underlying mechanism, we applied recently developed high-power relaxation dispersion (RD) experiments (12, 13) to both the backbone amide proton (¹H^N) and nitrogen (¹⁵N) nuclei of ubiquitin. This survey yielded a nearly twofold increase in the number of nuclei where RD had been previously observed (11–14) (from 17 to 31; Fig. 1A and Fig. S1). When fit individually, the full set of backbone and side-chain nuclei shows a consistent time scale of motion [exchange lifetime (τ_ex) = 55 μs; Fig. 1B]. Furthermore, the nuclei showing exchange are spread throughout the structure (Fig. 1C). Put together, these data suggest that the motions are not independent but share a common molecular mechanism.

Fig. 1.

Single collective mode explains the majority of the RD data. (A) Thirty-one different nuclei show statistically significant RD at 277 K and are spread across the primary sequence of ubiquitin. White circles indicate residues for which measuring an RD curve was possible. Where two labeled methyl groups were present in the same residue, shaded semicircles indicate the respective methyl(s) showing dispersion. (B) When fit individually, most nuclei show a similar exchange lifetime (τ_ex) that is consistent with the globally fit value of 55 μs (dotted line). (C) Nuclei showing RD are distributed throughout the structure, suggesting concerted motion of the whole structure. (D) ROC curves show that an optimized collective mode can predict a significant fraction of the ¹⁵N, ¹H^N, and ¹³C RD data (P = 0.027; Fig. S3). The straight gray line indicates a random prediction. (E) Interpolation of the backbone from one extreme of the concerted motion vector (blue) to the other (red). The rotating peptide bond between Asp 52 and Gly 53 is shown with a stick representation, along with the Cα-Cβ vector of Glu 24. (F) Optimized motional mode contains several semirigid substructures, each indicated by a different color (Movie S1).

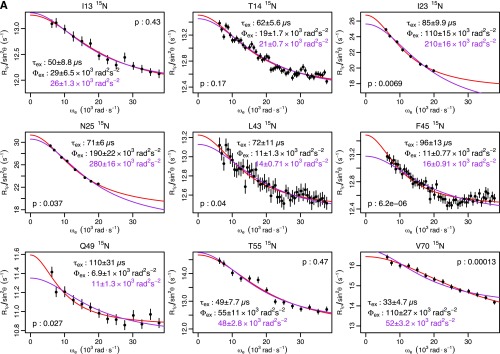
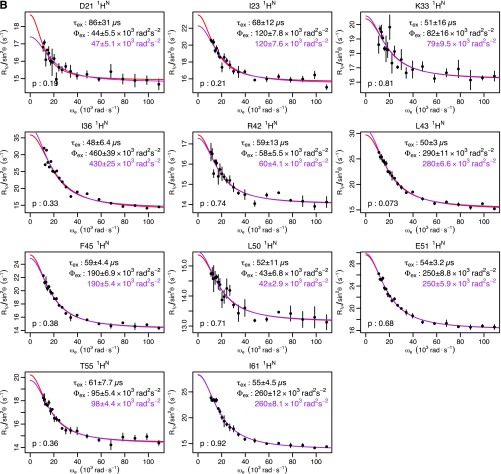
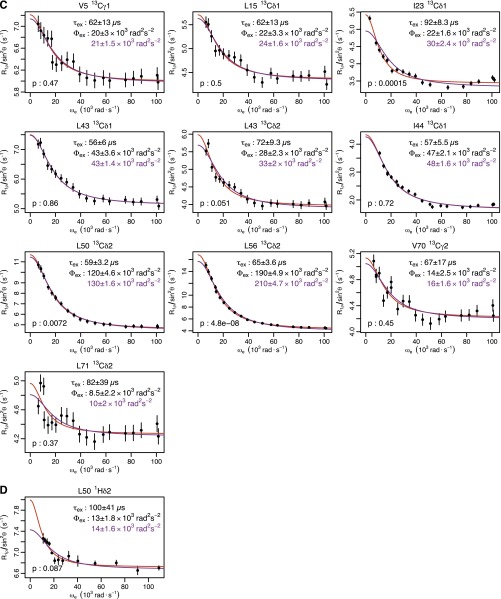
Fig. S1.

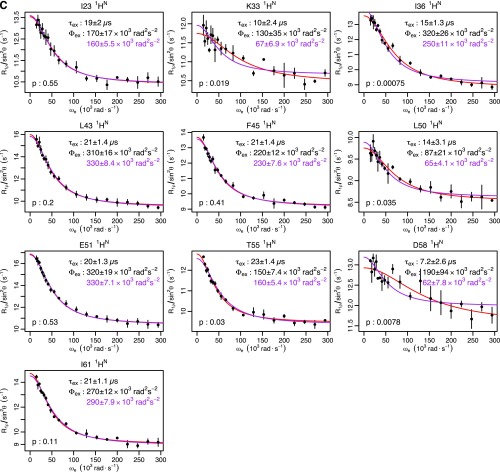
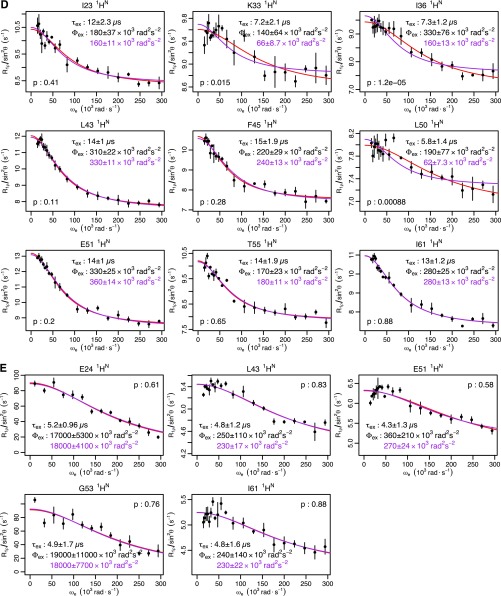
Ubiquitin R_1ρ data at 277 K. Individual fits are shown in red, with the parameters shown in black. Global fits with a single τ_ex (55 μs) are shown, along with the corresponding Φ_ex in purple. F test P values between fits are also shown. (A) Backbone ¹⁵N: T14, L43, and F45 are from this study. I23 and N25 are from previous work (14). I13, Q49, T55, and V70 are from previous work (12). (B) Backbone ¹H^N from this study. (C) Methyl ¹³C from previous work (13). (D) Methyl ¹H from previous work (13).

To determine whether the RD data could be modeled using a single collective motion, we developed a computational method to take a set of molecular dynamics (MD) simulations (10) and derive an optimized linear mode of motion that best explains the RD data (Fig. S2). For all types of nuclei, the resulting collective mode, termed the “RD fit MD mode,” predicts the RD data much better than expected for a random model (Fig. 1D and Figs. S3 and S4). The RD fit MD mode therefore represents a detailed structural model for the reaction coordinate along which much of the microsecond motion takes place (Fig. 1E). This mode is one of the first atomic models for a fast exchange transition in the ground state, whereas other models of motions in the microsecond range have involved the interconversion between a ground state and excited states having distinct chemical shifts (15, 16). A clustering analysis of the RD fit MD mode shows that the motion can be separated into several different regions that maintain a relatively stable internal structure (Fig. 1F). Two adjacent regions twist in opposite directions against one another, whereas another region moves in a rocking motion.

Fig. S2.

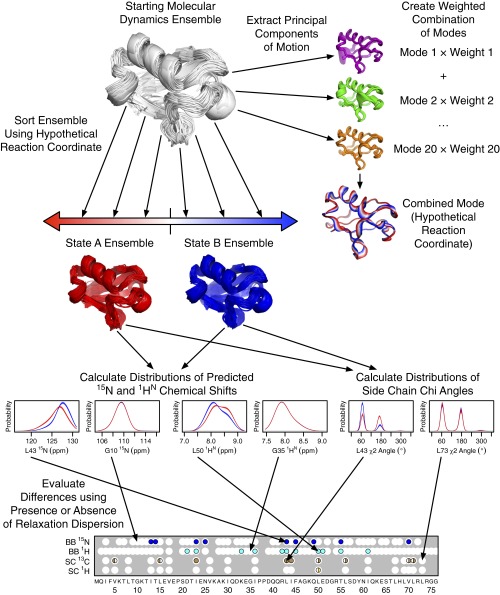
Scheme for generating RD fit MD mode. In this study, a MD ensemble was used, but in principle, any ensemble with sufficiently dense sampling could be used. Error bars in the distributions of predicted chemical shifts or χ-angles are indicated by shaded regions around the lines. The differences between the distributions (shown in Fig. S4) were calculated by determining the area between the error bars of the two distributions.

Fig. S3.

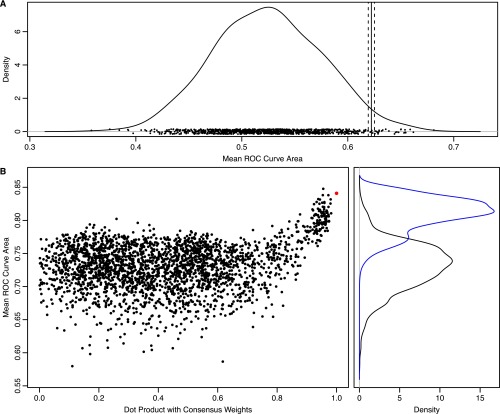
Cross-validation of RD fit MD mode fitting. (A) Distribution of cross-validated mean ROC curve areas for shuffled experimental RD data. The distribution is derived using kernel density estimation with a Gaussian smoothing kernel having an SD equal to the average SE of the underlying data points (0.015). The underlying data points are shown at the base of the plot. The mean ROC curve area for unshuffled experimental data is shown as a solid vertical line, along with the associated SE (dashed vertical lines). The probability of observing a shuffled value larger than the unshuffled value is 0.027. (B) Rescoring of the different weight vectors derived from the cross-validation runs using the full set of experimental data (Left, black points) produces a multimodal distribution with a secondary peak having a higher mean ROC curve area (Right, black curve). Consensus weights were determined using PCA with a weighted covariance matrix strongly biased toward points in the secondary peak. The distribution of mean ROC curve areas using those weights is shown in blue. The consensus weights produce a higher mean ROC curve area (red point) than all but one of the cross-validation weights. The single best set of cross-validation weights is very similar to the consensus weights. The differences between the consensus weights and the different cross-validation weights are shown using the absolute value of the dot product of the respective vectors. This plot shows strong funnel-like behavior (upside down because higher values are better), suggesting that the consensus weights are close to the global minimum of the optimization landscape.

Fig. S4.

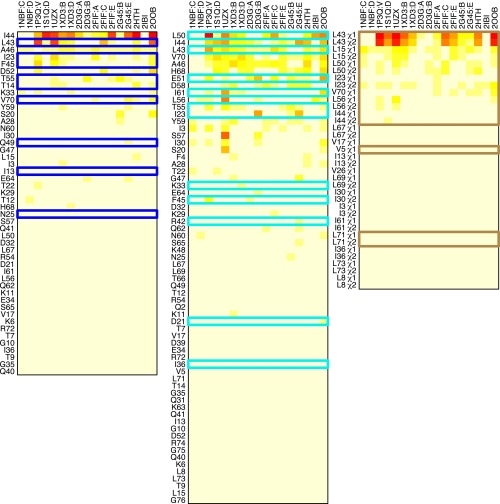
Chemical shift and χ-angle differences predicted using the RD fit MD mode. Distribution differences between MD simulation subensembles (red and blue in Fig. S2) are shown for predicted amide ¹⁵N chemical shifts (Left), predicted amide ¹H^N chemical shifts (Middle), and side-chain χ-angles (Right). Red indicates the greatest difference, and pale yellow indicates the least difference. Columns correspond to MD simulations started from the indicated PDB structure and chain. Rows are sorted by the mean difference for each residue. Residues with significant experimentally observed RD (i.e., those residues for which there should be larger differences in predicted chemical shifts or χ-angles) are outlined with colored rectangles. If the predictions were perfect, there would be a single colored rectangle at the top of each grid, and it would be possible to set a threshold having a 100% true-positive rate without any false-positive rate.

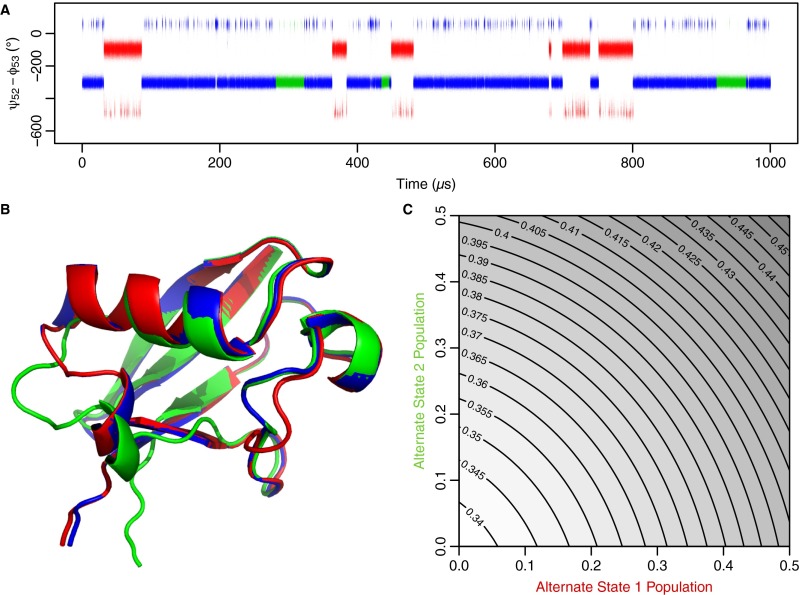
Located at the intersection of these regions, the peptide bond between D52 and G53 undergoes a discrete flip in orientation, unlike the relatively continuous motion observed elsewhere. This flip is also observed if experimental data for residues within 5 Å of D52 and G53 are excluded from fitting the optimized mode. Both orientations of this peptide bond have been observed crystallographically (17, 18) (Fig. 2). In addition, a previous study using mutagenesis and extreme pH values suggested that rotation of this peptide bond may explain the microsecond motion observed in two nearby residues (19). Microsecond motions in this region have also been observed with heteronuclear double-resonance (20) and solid-state RD (21) experiments. Furthermore, in the 100-ns simulations used for modeling the RD fit MD mode, peptide flipping was the structural feature with the slowest time scale, with flips occurring in 21 of 170 independent simulations (Fig. S5). It is also observed in a recently published 1-ms ubiquitin simulation (22) (Fig. S6). Taken together, the flip of the D52-G53 peptide bond emerges as one of the key parts of the concerted motion.

Fig. 2.

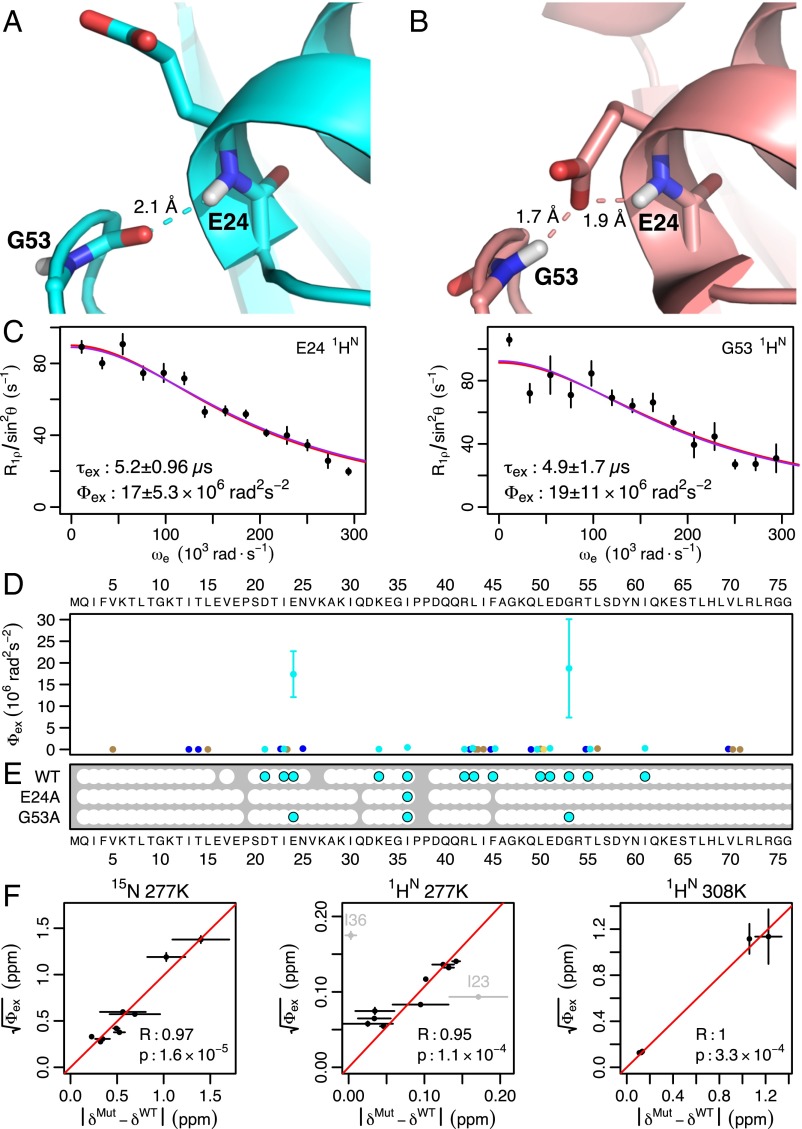
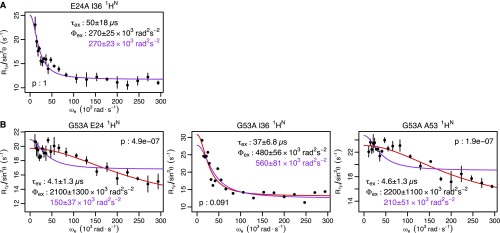
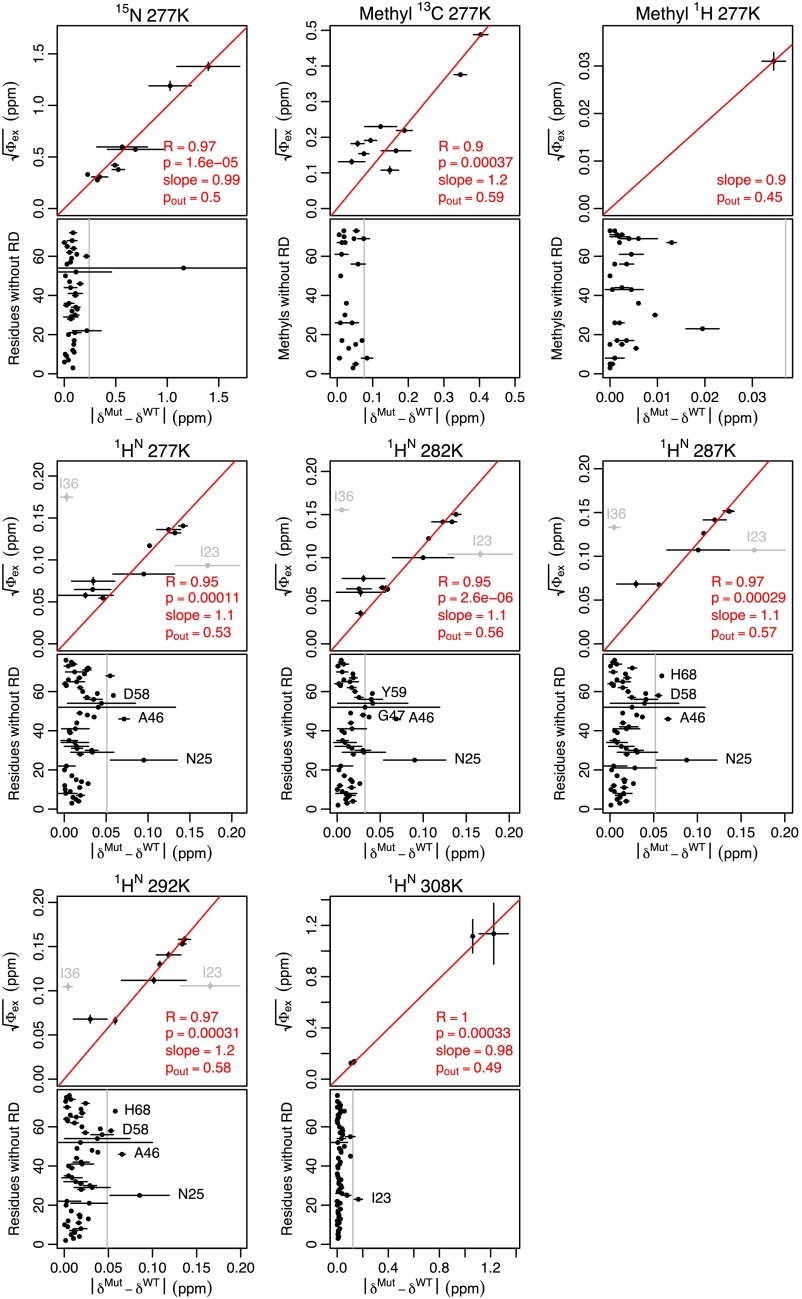
High-power RD and mutation confirms peptide bond flipping as an integral part of the collective motion. (A) In most crystal structures, the G53 backbone NH points out. (B) In a subset of crystal structures, the G53 NH points in. (C) Although the E24 and G53 NH resonances are invisible at 277 K (τ_ex ≈ 55 μs), high-power RD at 308 K speeds up the exchange process and shows these two protons exchanging at the same rate as L43, E51, and I61 (τ_ex ≈ 5 μs; Fig. S7E). Individual fits (red lines) are indistinguishable from a global fit to the five residues (purple lines). (D) Chemical shift variance (Φ_ex) for E24 and G53 (at 308 K) is one to two orders of magnitude greater than any other nucleus (at 277 K), in agreement with the large chemical shift difference expected. (E) When either E24 or G53 is mutated to suppress the NH-in state, ¹H^N RD becomes undetectable at nearly all residues except I36. Although the G53A mutant shows some RD at residues 24 and 53, Φ_ex values lowered by a factor of 10 or more suggest a 20-fold reduction in the population of the NH-in state (Figs. S7E and S8B). (F) Chemical shift differences between mutant and WT ($\left|{\delta }^{Mut}-{\delta }^{WT}\right|$) are highly correlated with $\sqrt{{\mathrm{\Phi }}_{ex}}$, confirming coupling between the collective motion and the peptide bond. The red line shows the best fit through the origin. I23 was excluded because of its proximity to the mutations, and I36 was excluded because its motion is independent of the peptide bond.

Fig. S5.

Peptide flipping is observed in 100-ns AMBER ff99SB trajectories. In the 100-ns simulations, the peptide bond between residues D52 and G53 rarely flips (indicated by arrows). The orientation is quantified by the difference between the ψ₅₂ and ϕ₅₃ dihedral angles. When the amide proton is pointed toward the α-helix and can hydrogen-bond with E24, the difference is ∼80°. When the amide proton is pointed out into solvent, the difference is approximately −320°. Each of the 10 replicate simulations is shown with a different color. Lightened colors are used to show the first 10 ns of each simulation, which were discarded for calculation of the χ-angle and chemical shift distributions. Despite the peptide bond rotation being one of the slowest processes in the simulations, its rate is ∼100-fold faster than is observed experimentally. This difference suggests that either the barrier in the simulation is too small (perhaps on account of the torsional potential) or that the individual states are understabilized (due to hydrogen bonding or other features) on the order of 1–3 kcal/mol.

Fig. S6.

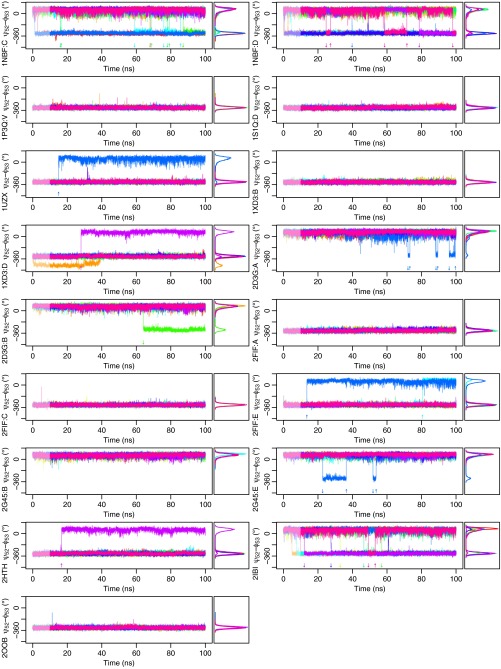
Peptide flipping is observed in a 1-μs CHARMM22* trajectory. (A) Numerous peptide flips between NH-out (−320°) and NH-in (80°) are observed in the dominant state of the trajectory (blue). The peptide flip is also observed in two alternate states (red and blue). (B) Dominant state (blue) is similar to all known crystal structures and is 70% populated. The first alternate state corresponds to a local structural change around residues 50–54 (red, 20%). The second involves unfolding of the last turn of the α-helix (blue, 10%). This unfolding may be responsible for the ¹H^N RD observed at I36. (C) Population of at least one of these states is thought to be overestimated (22), which is in agreement with our own analysis showing that RDC data are best fit when alternate states 1 and 2 are both assigned a population of zero. Contour lines give the respective Q-factors. Like the AMBER ff99SB trajectories, the rates of peptide bond flipping are about 100-fold faster than in the experiments, likely due to similar inaccuracies in the underlying force field of around 1–3 kcal/mol.

When the NH group of the D52-G53 peptide bond is pointed outward into the solvent (the “NH-out” state; Fig. 2A), the ¹H^N nuclei of E24 and G53 are hydrogen-bonded with neutral species (namely, water or an amide carbonyl group). By contrast, when the NH group points in toward the protein (the “NH-in” state; Fig. 2B), both nuclei make hydrogen bonds with the negatively charged side chain of E24. The chemical shift difference between these states should be quite large and result in significant RD. At 277 K, where the initial data were collected, the E24 and G53 amide proton peaks are severely broadened and undetectable. At 308 K, the peaks are visible and our high-power RD experiments (13) indeed reveal significant RD for both nuclei. Their time scales exactly coincide with other residues exhibiting RD at both 277 K and 308 K (Fig. 2C and Fig. S7). Furthermore, the chemical shift variance (Φ_ex) for these two nuclei is at least an order of magnitude greater than any others we observed (Fig. 2D), in agreement with the expected large chemical shift change.

Fig. S7.

Ubiquitin CPMG and R_1ρ data at other temperatures. Individual fits are shown in red, with the parameters shown in black. Global fits with a single τ_ex value are shown, along with the corresponding Φ_ex value in purple. F test P values between fits are also shown. (A) Backbone ¹H^N CPMG at 262 K (global τ_ex = 150 μs). (B) Backbone ¹H^N R_1ρ at 282 K (global τ_ex = 29 μs). (C) Backbone ¹H^N R_1ρ at 287 K (global τ_ex = 20 μs). (D) Backbone ¹H^N R_1ρ at 292 K (global τ_ex = 13 μs). (E) Backbone ¹H^N R_1ρ at 308 K (global τ_ex = 5.0 μs).

To investigate the necessity of the peptide flip for this collective ubiquitin motion, we used two mutants, E24A and G53A, that have been shown to inhibit the NH-in state (19). In the presence of these mutants, ¹H^N RD is either abolished or significantly attenuated (at least by a factor of 10) at all but one residue (Fig. 2E and Fig. S8). This observation suggests that although at least two processes occur on the microsecond time scale [peptide flipping and motion around I36 (22–24)], peptide flipping is directly coupled with the majority of the conformational fluctuation throughout the structure. This finding is further supported by the temperature dependence of ¹H^N RD, in which the majority of residues show profiles that coincide with E24 and G53 (Fig. S9). Finally, the chemical shift differences between the WT and mutant proteins almost entirely explain the RD magnitudes observed at all but one of the nuclei (Fig. 2F and Fig. S10). In addition to confirming the linkage between the peptide flip and the concerted motion, a comparison of the mutant chemical shifts and Φ_ex values show that the population of each state is ∼50% (Fig. S10), indicating that the motion is occurring in the ground state of the protein.

Fig. S8.

Ubiquitin mutant R_1ρ data. Individual fits are shown in red, with the parameters shown in black. Global fits with a single τ_ex value are shown, along with the corresponding Φ_ex value in purple. F test P values between fits are also shown. (A) E24A backbone ¹H^N of I36 at 277 K (global τ_ex = 50 μs). (B) G53A backbone ¹H^N at 277K (global τ_ex = 27 μs). Ten of 11 residues where RD is observed in WT (Fig. S1B) do not show RD in the mutants. I36 still shows RD for both mutants, suggesting it reports a different process, possibly unwinding of the α-helix that has been observed experimentally (23, 24) and in simulations (22). The I36 ¹H^N time scales are consistent for WT (τ_ex = 48 ± 6 μs) and both mutants. For the G53A mutant, the RD at E24 and A53 is about 10-fold faster than WT (55 μs). The Φ_ex value for these two nuclei is reduced about 10-fold over the Φ_ex value observed at 308 K (Fig. S7E), suggesting that the population of the NH-in state is reduced ∼20-fold over WT. A similar 10-fold reduction of the Φ_ex values observed for WT at 277 K would drop the 10 residues not observed in the G53A mutant below the detection threshold, explaining their disappearance.

Fig. S9.

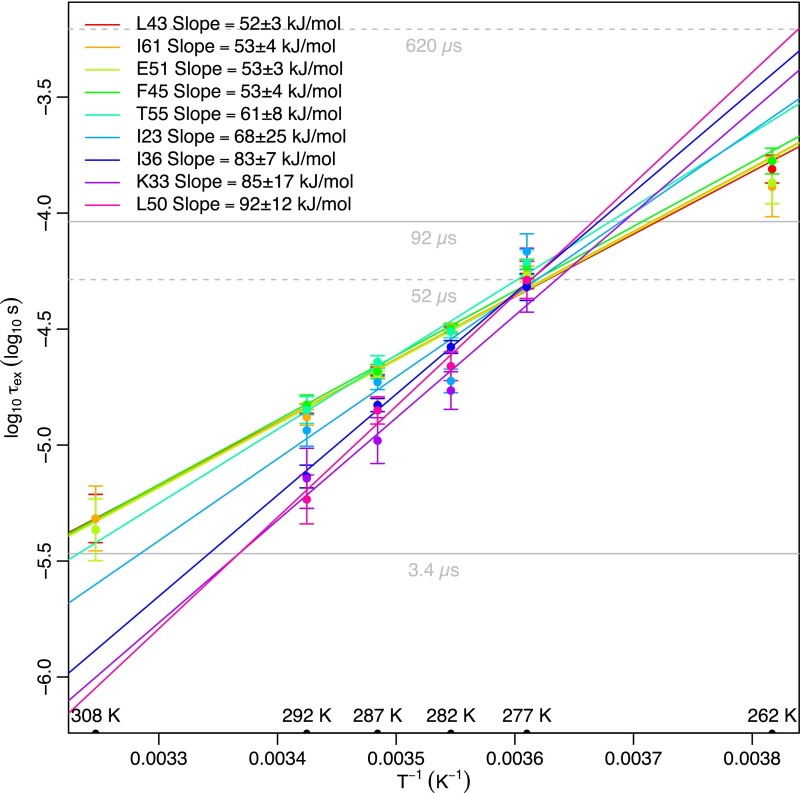
Temperature dependence of RD time scales. L43, I61, E51, F45, T55, and I23 all show the same temperature dependence, within error. At 308 K, the time scales of L43, E51, and I61 coincide with E24 and G53 (Fig. S7E), supporting a direct linkage between all these residues. The temperature dependence of I36, K33, and L50 is somewhat perturbed, suggesting that they may report, in full or in part, on some other process. For I36, this interpretation is supported by mutational data (Fig. 2E). Solid and dashed gray lines indicate the accessible time scales for the R_1ρ and CPMG experiments, respectively.

Fig. S10.

Mutant chemical shifts explain backbone RD and give state populations. ¹⁵N, methyl ¹³C, and ¹H^N chemical shift differences between mutant (E24A and G53A) and WT ($\left|{\delta }^{Mut}-{\delta }^{WT}\right|$) are highly correlated with the observed chemical shift fluctuations from RD ($\sqrt{{\mathrm{\Phi }}_{ex}}$) at all temperatures. The ${\delta }^{Mut}$ values are taken from the mean of the E24A and G53A chemical shifts, with the range of the two mutants covered by the error bars. The ${\mathrm{\Phi }}_{ex}$ values are taken from the global fits. Each plot includes Pearson’s product moment correlation coefficient (R), along with the probability of observing such a value at random if the two parameters were uncorrelated (p). Assuming the mutants are entirely in the NH-out state, it can be shown that $p_{out}=1/\left({\left({\delta }^{Mut}-{\delta }^{WT}\right)}^2/{\mathrm{\Phi }}_{ex}+1\right)=1/\left(1/slop{e}^2+1\right)$. This equation indicates that a slope of 1 will yield a $p_{out}$ of 0.5. The listed populations come from this equation. Because there is only one methyl ¹H data point, only the slope and population are shown. Because ¹H^N I36 reports on a different exchange process, it was excluded from correlation and population analysis. ¹H^N I23 was also excluded because it is very close to both mutations and likely includes chemical shift changes due to the mutations themselves and not just the peptide conformation. At each temperature, the lower plot gives the chemical shift changes for residues where it was possible to obtain RD data but significant RD was not observed. Labeled residues have error bars that do not overlap with the error bar of the residue showing the smallest ${\mathrm{\Phi }}_{ex}$ (vertical gray line). A46, D58, Y59, and H68 all show RD, but the error margins on the parameters are too large to be considered significant (data not shown). N25 does not show RD, but it is also very close to the mutations and likely to include chemical shift changes directly from the mutations.

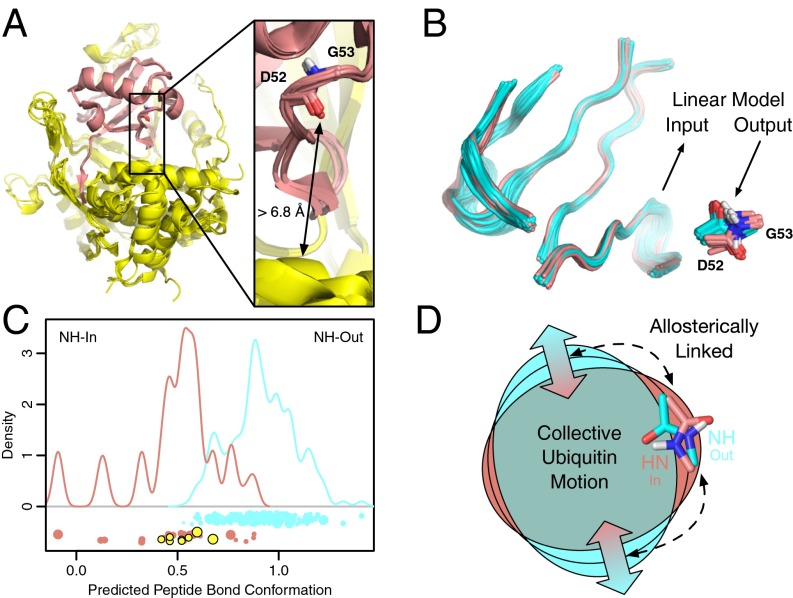
To determine how this collective motion influences binding and other functions of ubiquitin (e.g., presence of different covalent linkages), we performed an extensive structural bioinformatics survey of known ubiquitin crystal structures. Because the peptide bond conformation was the most recognizable feature of the collective mode, we used its conformation as a “marker” for structural discrimination. The most significant relationship we found was the universal association between the NH-in state and binding to the ubiquitin-specific protease (USP) family of deubiquitinases (Fig. S11). This association has been previously noted (18) and is surprising because the peptide bond is at least 6.8 Å from any USP (Fig. 3A).

Fig. S11.

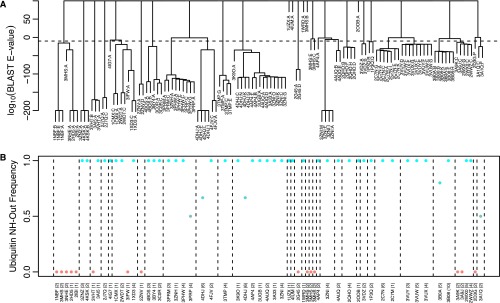
Complexes with USP deubiquitinases always show NH-in conformations. (A) Nonubiquitin sequences from high-resolution (<2.4 Å) structures of ubiquitin complexes were extracted and clustered using the log₁₀ of their BLAST E-values. The PDB identifier and chain containing each nonubiquitin sequence are shown. Groups of sequences were generated using a log₁₀ E-value cutoff of −10. (B) For the PDB structures in each group, all unique sets of ubiquitin coordinates were extracted, including all copies in the asymmetrical unit and all alternates. The frequency of finding an NH-out conformation is shown (colored by conformation: entirely NH-in, pink; and entirely NH-out, cyan), with the number of coordinate sets used given in parentheses. The leftmost group is entirely NH-in and corresponds to the USP family of deubiquitinases.

Fig. 3.

Peptide flipping is allosterically linked to distant residues at the USP binding interface. (A) In all high-resolution (<2.4 Å) complexes between USP deubiquitinases (yellow) and ubiquitin (pink), the G53 backbone NH points into the protein, whereas most other ubiquitin complexes show the NH pointing out toward solvent (Fig. S11). This conformation occurs despite the peptide group being at least 6.8 Å from the USP in all structures (Movie S2). (B) Linkage between the peptide conformation (in, pink; out, cyan) and the backbone of the ubiquitin residues interacting with the USP can be tested by training a PLS linear model using other ubiquitin structures not bound to a USP. (C) The resulting model shows good discrimination between NH-in (pink) and NH-out (cyan) structures. The USP-bound ubiquitin structures (yellow), which were not used for training, are almost completely separated from NH-out conformations. (D) This separation indicates that there is a specific allosteric coupling between the peptide bond conformation and the binding interface, which is very likely mediated by the collective motion. The same color coding is used as in B and C.

Given that when free in solution, changes in the peptide bond affect residues throughout ubiquitin, we hypothesized that specific conformations of residues at the USP-ubiquitin binding interface could be allosterically associated with the NH-in state. To test this hypothesis using completely independent data, we assembled a set of 217 distinct ubiquitin conformations from 70 high-resolution crystal structures in the Protein Data Bank (PDB). We used partial least squares (PLS) functional mode analysis (FMA) (25, 26) to train a linear model to predict the peptide bond conformation solely from the coordinates of residues that interact with USPs, thus excluding the peptide flip region (Fig. 3B). The ability of the resulting model, termed the “peptide fit PDB mode,” to distinguish NH-in from NH-out states based solely on the binding interface indicates a strong allosteric coupling between opposite sides of the protein (Fig. 3 and Fig. S12). Furthermore, the peptide fit PDB mode shares a number of common features and shows a statistically significant correlation (P < 0.001) with the RD fit MD mode (Fig. S13), indicating that the long-distance structural correlations present in crystal structures are similar to the long-distance structural correlations observed in solution.

Fig. S12.

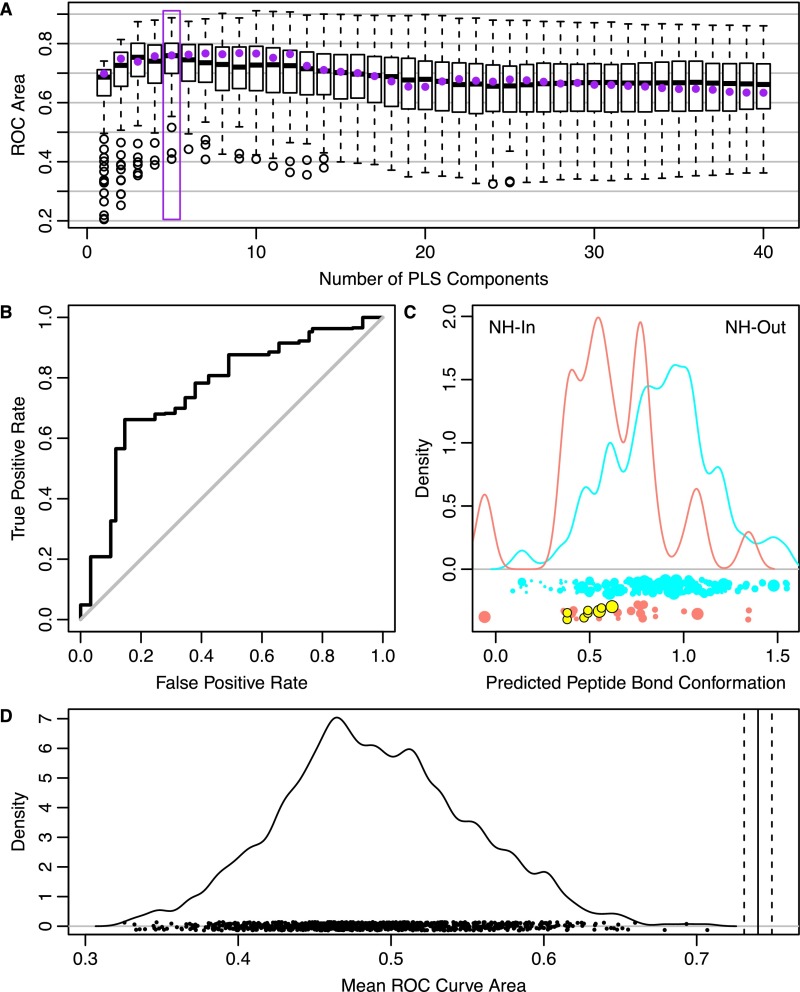
Cross-validation of peptide fit PDB mode fitting. (A) One hundred random twofold cross-validation runs were performed with the constraint that groups shown in Fig. S11B not be split between cross-validation groups. For each of these runs, ROC areas were calculated for models that incorporated differing numbers of PLS components. The box plots show the distributions of these ROC areas, with the line giving the median, the box giving the interquartile range, whiskers giving the most extreme data point within 1.5 times the interquartile range, and circles giving data points outside that range. The maximum median ROC area was observed with five PLS components (purple box). This number of components was used in training subsequent models (Fig. 3). A representative cross-validation model was selected whose ROC area was closest to the median ROC area (at five PLS components). All ROC areas for this model are shown with purple points. (B) ROC plot for the representative model shows that it is significantly more predictive than random (gray diagonal line). (C) Distribution of cross-validated projection values for NH-in (pink) and NH-out (cyan) structures shows moderate overlap between predictions, indicating the USP-interacting residues partially explain the peptide bond conformation. Projection values for USP structures are shown in yellow. In training, the contribution of a set of ubiquitin coordinates was weighted inversely by how many sets of coordinates were in a given PDB structure. The weighting is indicated by the size of the point below the distribution. (D) Average cross-validated ROC area (0.74 ± 0.01, solid and dashed vertical lines) is highly unlikely (P < 0.001) to have occurred by random chance, based on additional cross-validation runs with shuffled input data. The mean cross-validated ROC curve areas (each from 100 different cross-validation groupings) from 1,000 different sets of shuffled peptide bond conformations are shown as points along the x axis. The distribution of these points was determined by kernel density estimation using a Gaussian smoothing kernel with the SD (0.006) taken from the average SE of the 1,000 points. Because none of the shuffled data points exceeds the unshuffled value, the P value is estimated as being less than 1/1,000.

Fig. S13.

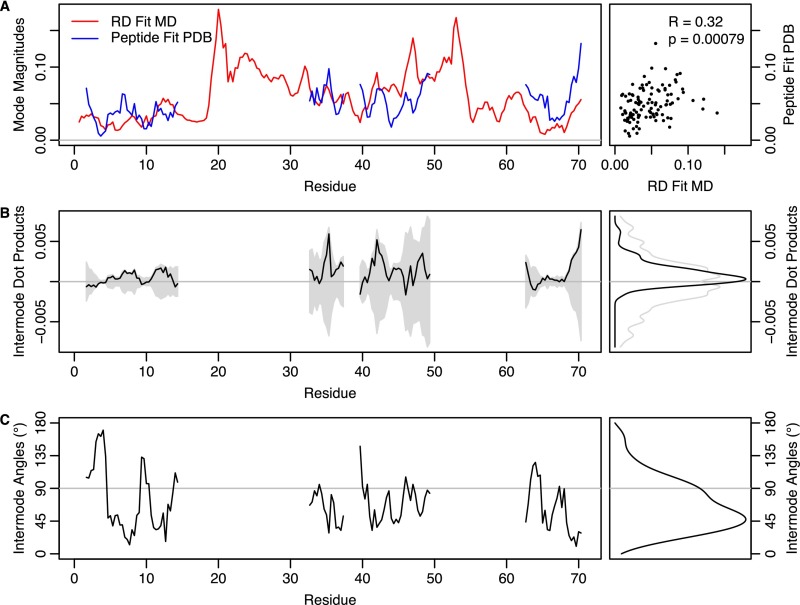
RD fit MD mode and peptide fit PDB mode are similar. The magnitudes and directions of motion for every atom (backbone N, Cα, C) were extracted from both the RD fit MD mode and peptide fit PDB mode. (A) Magnitudes of the RD fit MD mode (red) do coincide with magnitudes of the peptide fit PDB mode (blue). The correlation is modest (R = 0.32) but statistically significant (P = 0.00079). (B) Mostly positive (84 of 108) per-atom dot products between modes indicate that the majority of atoms move in similar directions in both modes (Wilcoxon signed rank: P = 9.9 × 10⁻¹¹). The shaded area indicates the range of possible per-atom dot products, given the magnitudes shown in A. (C) Peak angular difference between per-atom directions of motion is ∼45°.

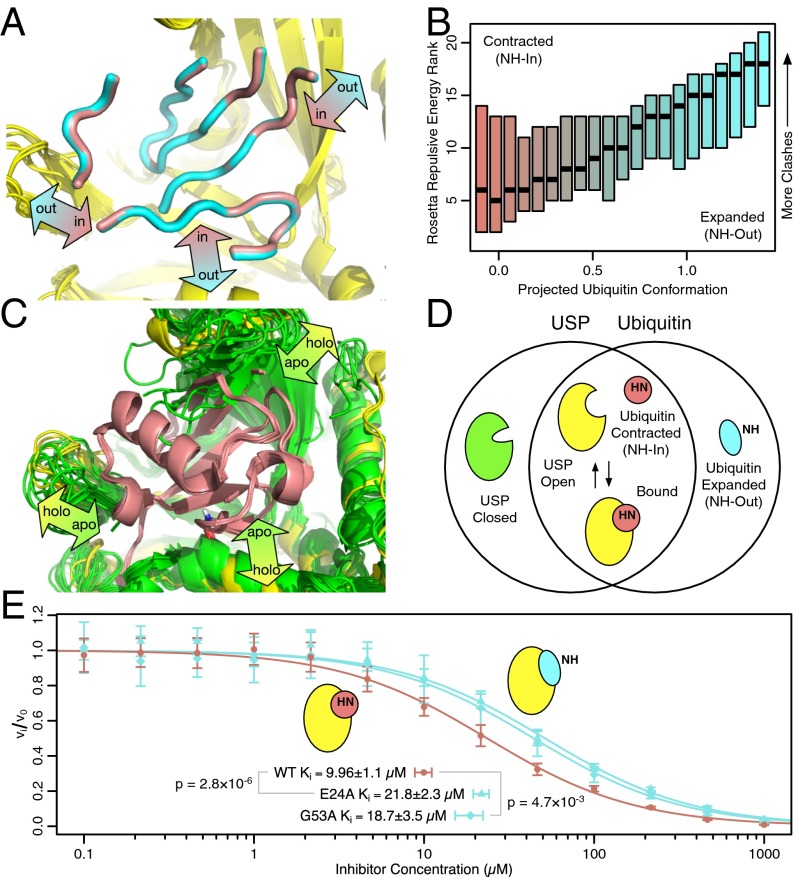
A visual examination of the model shows that NH-out conformations are associated with subtle expansion of ubiquitin around the binding interface, whereas NH-in conformations are contracted (Fig. 4A). The greatest expansion was 0.95 Å (from NH-in to NH-out), which was observed between the Cα atom of residue 35 and the amide nitrogen of residue 49. To determine if contraction confers an energetic benefit for USP binding, we used Rosetta software to determine whether shifting expanded NH-out conformations to be more NH-in–like relieved atomic overlaps with the USP (or vice versa). There is a clear trend where the expanded NH-out state has significantly more clashes with the USP than the contracted NH-in state (Fig. 4B). Given the relative subtlety of the expansion and contraction, it is somewhat surprising that the USPs do not accommodate binding to the expanded NH-out state. A possible explanation comes from comparison of the conformations of USP with (holo) and without (apo) ubiquitin bound (Fig. 4C). The crystal structures strongly suggest that USPs energetically favor a closed conformation that occludes ubiquitin binding. By adopting a contracted NH-in conformation, ubiquitin reduces the amount of USP opening required for binding. In that way, both proteins appear to adapt their conformations mutually to establish a complementary binding interaction (Fig. 4D). The greater USP structural heterogeneity suggests that it is more flexible than ubiquitin and able to deform more to accommodate binding.

Fig. 4.

Peptide flipping allosterically regulates USP binding. (A) Interpolation between extremes of the linear model shows that ubiquitin tends to contract around the binding interface when the peptide flips in (Movie S3). (B) Moving ubiquitin structures along this linear model either relieves or induces clashes with a ubiquitin-bound USP structure (3NHE), depending on whether the structures are made more NH-in–like or NH-out–like. For all 217 high-resolution ubiquitin structures, a series of USP/ubiquitin complex structures was generated at points along the linear model. A box plot of the resulting Rosetta repulsive energy ranks (1 = least clashes, 21 = most clashes) at each point shows the median (black bar) and interquartile range (box, colored by conformational state). (C) Comparison of apo- (green) and holo- (yellow) USP structures shows that the unliganded binding site must expand in complementary directions to accommodate ubiquitin binding. (D) USP-ubiquitin binding involves mutual complementary structural rearrangements of both partners. For ubiquitin, binding is allosterically modulated by motion of a peptide bond distant from the binding interface. (E) As predicted, a kinetic inhibition assay shows mutants that stay in the NH-out state (E24A and G53A, cyan) bind USP2 more weakly than WT (pink), which can accommodate an NH-in conformation.

To verify the hypothesis that the orientation of the peptide bond is linked to the contraction/expansion of ubiquitin, which in turn modulates USP binding, we used the E24A and G53A ubiquitin mutants. Because both mutants strongly favor the NH-out state, they should put ubiquitin in an expanded conformation with less affinity for USPs. An inhibition assay with USP2 indicates that this is indeed the case. Both mutants show twofold weaker affinity (∼0.4 kcal/mol) for USP2 than WT (Fig. 4E). Although this change may seem like a moderate effect, it is actually surprisingly large and highly significant when one considers that it is allosterically triggered by the simple rotation of a solvent-exposed peptide bond on a distal side of the protein.

There are clear precedents for subtle conformational shifts affecting interactions between ubiquitin and its binding partners. Several recent studies have designed mutations in and around the core of ubiquitin to shift its conformational equilibrium toward or away from binding-competent states (27–30). In one case, the mutations introduced widespread millisecond time-scale motions that were not present in WT (29). Together with mutations at the surface of ubiquitin, it is now possible to create synthetic ubiquitin variants capable of perturbing ubiquitin interactions in vivo (28, 31).

The characterization of this collective motion helps to narrow the time scale of other important ubiquitin motions further. For instance, the “pincer mode” between the β1-β2 and β3-α2 loops is important for allowing ubiquitin to bind to different interaction partners (5, 10). However, in the optimized collective mode determined here, there is very little motion in those two loops. Indeed, when the weights of the individual modes are examined, the weight for mode 1 (which corresponds to the pincer mode) is nearly zero. Thus, it is highly likely that the pincer mode moves on a time scale faster than the RD detection limit but slower than the tumbling time of ubiquitin, putting the time scale in the tens to hundreds of nanoseconds. Indeed, the peptide flip motion is also slower than the pincer mode in MD trajectories from two different studies (10, 22).

Discussion

This study revealed an allosteric switch affecting protein–protein binding through collective protein motion at the microsecond time scale. This collective motion was extensively characterized and validated using a combination of techniques, including high-power NMR RD, X-ray crystallography, computer simulation, and enzyme inhibitor assays. Whereas most known microsecond to millisecond time-scale motions involve excursions to excited, lowly populated states, this motion occurs between two ground state ensembles with nearly equal populations (NH-in and NH-out). Strikingly, the peptide bond conformation is allosterically coupled through a diverse set of interactions that triggers contraction/expansion of the entire domain. This type of global domain motion reveals a previously unidentified mechanism for modulating protein affinity. The presence of this allosteric network suggests there may be heretofore undiscovered ways in which macromolecular assemblies and covalent linkages regulate ubiquitin binding. More broadly, this study demonstrates how relatively modest changes in hydrogen bond networks and the protein backbone can bring about distant changes in protein conformation and binding affinity. This observation points toward potential strategies for the rational design of allosteric mutations or ligands.

Methods

Sample Preparation, NMR, and USP2 Inhibition Assays.

Protein sample preparation (32), R_1ρ (12, 33, 34) and Carr–Purcell–Meiboom–Gill (CPMG) (35–37) experiments, and USP2 inhibition assays (32) were adapted from the cited work. Further details and other data analysis procedures are provided in SI Methods.

Predicting RD from MD Snapshots and Principal Component Analysis Eigenvectors.

The method we developed was inspired by FMA (25), in which a linear combination of modes from principal component analysis (PCA) is derived that corresponds to some functional property that can be assigned to each structural snapshot. By contrast, our new algorithm was designed to find a combination of PCA modes that, together, produces a collective motion along which only nuclei showing RD vary their chemical shifts (Fig. S2).

Previous MD simulations of ubiquitin as a free monomer (10) were used to approximate the solution state ensemble. For those simulations, 17 starting conformations were taken from distinct structures of ubiquitin in complex with different binding partners. From each starting structure, 10 separate 100-ns simulations were performed in GROMACS 4 with the amber99sb force field. Snapshots were recorded every 10 ps, and the first 10 ns of each simulation was excluded to allow structural relaxation from the bound form.

To estimate whether chemical shifts of individual nuclei would be affected by structural rearrangements, different metrics were used depending on the specific nuclei involved. For backbone amide nitrogens and protons, chemical shifts were predicted using SHFTX+ version 1.07 (38). Because methyl carbon chemical shift predictions have traditionally performed poorly, and because previous results suggested that rotamer effects were the primary source of methyl carbon chemical shift perturbation (13), we used side-chain χ-angles as a proxy for methyl chemical shifts.

The optimization algorithm involved evaluating the ability of many possible linear modes of motion (each representing a hypothetical reaction coordinate) to predict which residues showed RD. Given a hypothetical mode for evaluation and a single MD trajectory, the algorithm first projected all of the snapshots of that trajectory onto the linear mode. From this projection, two subensembles were assembled, one containing snapshots with negative projection values and the other with snapshots having positive projection values. These ensembles represent the two states in an assumed two-state exchange process.

For each of the two subensembles, distributions of chemical shifts or side-chain χ-angles were calculated using kernel density estimation with a Gaussian smoothing function (SDs of 1 ppm, 0.15 ppm, and 5°, respectively, for amide nitrogens, amide protons, and χ-angles). Differences between the distributions for the two states should indicate a probable chemical shift change. To ensure that only statistically significant differences were taken into account, distributions for the 10 independent simulations from each starting structure were averaged and error bars were calculated by taking the SE. The differences in distributions of the two states were then quantified by calculating the area between the error bars. Because the area under each distribution is 1, the difference ranges from 0 (totally overlapping error bars) to 2 (totally distinct distributions with no error).

The mean difference for each residue and nucleus type was calculated by averaging over the differences from the 17 starting structures. For amide nitrogens, amide protons, and the methyl carbons of Val residues, these differences are represented by a single row of values shown in Fig. S4. For the methyl carbons of Ile and Leu residues, the average was taken over both the χ1- and χ2-angles, corresponding to the two rows of data shown in Fig. S4.

To determine the degree to which residues with detectable RD also showed larger distribution differences, receiver operator characteristic (ROC) curves were calculated. These curves were constructed by sorting residues by the mean distribution difference and calculating the true-positive and false-positive rates for all possible cutoffs. The area under the ROC curve was used to quantify the prediction quality, with 1 corresponding to a perfect prediction and 0.5 corresponding to a random prediction.

Optimizing a Single Collective Mode to Explain the RD Data.

Using the protocol described above, one can then investigate how well individual PCA modes explain the RD data, with the goal of identifying a collective motion that represents a reaction coordinate along which ubiquitin moves on the microsecond time scale. We reasoned that an optimized linear combination of PCA modes might explain the RD data better than any single PCA mode. To construct a vector of weights for this linear combination of PCs, we used a two-step procedure. In the first step, the magnitudes of the weights were assigned. For each of the first 20 previously determined PCA modes (10), the mean ROC curve value was calculated. The mode with the highest mean area was assigned a magnitude of 1, the mode with the lowest mean area was assigned a magnitude of 0, and all other modes were assigned magnitudes by linear interpolation between those values. To normalize differences in variance captured by the modes, the magnitudes were then divided by the corresponding eigenvalues. In the second step, the signs of the weights were assigned. The mode with the highest weight was given a positive sign. The remaining weights were assigned with a greedy algorithm in which modes with successively lower weights were added one at a time with whichever sign gave the highest average ROC curve area.

Cross-Validation of the Optimization Procedure.

To determine whether the optimized collective mode could predict the observation of RD in residues excluded from training, we used a “leave 20% out” cross-validation procedure. Before optimization, a randomly chosen testing set of 20% of the positive (RD observed) and 20% of the negative (RD not observed) residues was excluded for each type of nuclei. The optimization procedure was then performed using the remaining 80% of residues. The small size of the testing set led to significant variance in the mean ROC curve area for different testing sets. Therefore, we repeated the cross-validation procedure 2,500 times to yield a mean overall ROC curve area of 0.622 ± 0.003, compared with a mean overall ROC curve area of 0.84 without cross-validation.

To estimate the statistical significance of observing that value over the background distribution of random ROC curve areas (usually assumed to average around 0.5), we repeated the cross-validation scheme with 1,000 sets of shuffled experimental data. Residues were shuffled within groups, with the groups defined by the availability of RD data. For instance, residues with amide nitrogen, amide proton, and methyl carbon data were shuffled together in one group, whereas residues with only amide nitrogen and proton data but no methyl carbon data were shuffled in a different group. For each set of shuffled experimental data, the cross-validation procedure was performed 50 times. The resulting distribution of mean ROC curve areas is shown in Fig. S3. This distribution indicates that the probability of observing a ROC curve area better than 0.622 at random is 0.027, making it unlikely that the predictive accuracy of the model is observed by chance.

Generation of Consensus Weights.

The set of weights determined during the cross-validation procedure (using the unshuffled data) was rescored with the complete set of experimental data. The resulting distribution of ROC areas is shown in Fig. S3A (black line). Within that distribution, a secondary population of high ROC areas was observed. To determine a consensus vector for that set of weights, a biased PCA was performed. Before consensus PCA, all weights were multiplied by the corresponding eigenvalues from the original PCA (the same as those eigenvalues used in the first step of the optimization procedure above). A weighted covariance matrix was then calculated without centering (i.e., assuming a mean of 0 for each weight). Given a vector of mean ROC areas (A) and the vector of weights (W), the covariance matrix was calculated with the formula W_i = (A_i − min(A))¹⁵. The distribution of ROC areas reweighted with that vector is shown in Fig. S3B (blue line). After eigendecomposition of the covariance matrix, the eigenvector with the highest eigenvalue was selected. The consensus set of weights was determined by normalizing that eigenvector through division by the original PCA eigenvalues. The model produced with these weights was termed the RD fit MD mode and is different from the peptide fit PDB mode described below.

To determine whether peptide flipping would also be seen if a different set of MD trajectories were used, we repeated the fitting procedure with snapshots from the dominant state of the CHARMM22* MD trajectory (22) (Fig. S6). The resulting mode also showed peptide flipping as a prominent feature and significant similarities in per-atom magnitudes (Pearson’s product moment correlation coefficient: P = 1.4 × 10⁻⁵; as in Fig. S13A) and intermode dot products (Wilcoxon signed rank: P = 9.3 × 10⁻⁷; as in Fig. S13B) to the RD fit MD mode trained with the AMBER ff99SB trajectories.

Analysis of Peptide Flipping in PDB Structures.

We started with a set of 122 PDB crystal structures having 370 distinct ubiquitin backbone conformations for residues 1–70 (taking into account multiple copies within the asymmetrical unit and alternate models). Using data from Uppsala Electron-Density Server (39), we manually inspected the region around the D52-G53 peptide bond for each structure to check whether its conformation could be unambiguously assigned. The electron density of the E24 side chain was used as evidence for either an NH-out (Fig. 2A) or NH-in (Fig. 2B) hydrogen bond network. A resolution cutoff of 2.4 Å best discriminated between the conformations that we thought could or could not be assigned. To avoid bias, we then ignored the manual inspection and only analyzed structures having a resolution <2.4 Å, which yielded a set of 70 PDB structures and 217 distinct ubiquitin conformations.

From these structures, we extracted all nonubiquitin sequences, which were clustered by the log₁₀ of their BLAST E-values and divided into groups using a log₁₀ cutoff of −10, such that pairs of sequences with log₁₀ E-values less than −10 were grouped together. For every PDB structure, we determined the fraction of ubiquitin structures having an NH-out peptide conformation. The largest group having no NH-out conformations was the USP family of deubiquitinases. In subsequent structural analysis using this dataset, individual ubiquitin conformations were weighted such that the total weight from all conformations in a given PDB structure was the same as the total weight from any other PDB structure.

PLS FMA.

A residue from ubiquitin (PDB ID code 3MHS chain D) was selected for PLS FMA (25, 26) if any of its atoms was within 5 Å of a USP (PDB ID code 3MHS chain A) or if both of its adjacent residues were within 5 Å of the USP. This selection included the following 36 residues: Q2–T14, K33–P37, Q40–Q49, and K63–V70. The N, Cα, and C backbone coordinates were used for training following subtraction of the mean coordinate values. NH-in ubiquitin conformations were assigned a value of 0, and NH-out conformations were assigned a value of 1.

To determine whether these coordinates could be used to predict the peptide bond conformation, we used complete twofold cross-validation. We restricted the randomized cross-validation groups such that all of the conformations from a given PDB structure or structure group (Fig. S11B) were restricted to being entirely within a single cross-validation group. Cross-validation was repeated 100 times with 1–40 PLS components, and the predictions were evaluated with ROC areas. The best median ROC curve area was found with five PLS components. After cross-validation, the model was retrained (with five PLS components) using all structures except the structures from USP deubiquitinases. This model, which was restricted to 36 residues, was termed the peptide fit PDB mode. To determine if the resolution of the structures had an effect on the mode, we repeated the training procedure with a resolution cutoff of 2.0 Å (136 distinct ubiquitin conformations vs. 217 at 2.4 Å). The resulting mode showed significant similarities in per-atom magnitudes (Pearson’s product moment correlation coefficient: P = 7.6 × 10⁻⁷; as in Fig. S13A) and intermode dot products (Wilcoxon signed rank: P = 3.1 × 10⁻¹⁶; as in Fig. S13B) to the peptide fit PDB mode trained with a cutoff of 2.4 Å. Therefore, the choice of cutoff did not have a large impact on the PDB-derived mode.

Rosetta Structural Modeling.

To determine whether the NH-out conformations showed more steric clashes with USP than NH-in conformations, we used Rosetta with the Talaris2013 score function to rebuild ubiquitin side chains in the context of a high-resolution USP2 structure bound to ubiquitin (1.26 Å, 3NHE). First, each of the generated ubiquitin conformations was placed into the USP2 binding site. Next, RosettaScripts (40) was used to repack and then apply four cycles of rotamer trial minimization to all ubiquitin residues and all USP2 residues whose side chains were within 5 Å of ubiquitin. This procedure was repeated 10 times per conformation. PyRosetta (41) was then used to extract intermolecular repulsive energies between ubiquitin and USP2. Because the role of the β1-β2 loop (residues 8–10) in binding has been previously characterized (10), we excluded the repulsive energies from that loop. The lowest of the 10 repulsive energies for each ubiquitin conformation were then used for analysis.

SI Methods

Sample Preparation.

Perdeuterated, ¹⁵N-labeled WT and mutant ubiquitin was expressed in Escherichia coli adapted to 100% D₂O Toronto minimal medium supplemented with D₇-glucose as a carbon source and ¹⁵N-NH₄Cl as a nitrogen source. The ubiquitin mutants E24A and E53A were generated by PCR-based, site-directed mutagenesis using the QuikChange II Kit (Agilent) following the instructions of the supplier. The catalytic core of USP2 (amino acids 259–605) was expressed and purified following published protocols (32).

NMR.

The ¹⁵N R_1ρ measurements were conducted using uniformly ¹⁵N-labeled ubiquitin in 90% (vol/vol) H₂O/10% (vol/vol) D₂O. The procedure used here followed previously published methods (12, 33). Field strengths were varied from 1,000 to 6,000 Hz. Rates were determined using a two-point sampling scheme in which one reference experiment was recorded without any spin-lock period and another with a spin-lock applied for 120 ms. The errors in rates were propagated from noise in the spectra. In this study, data for T14, L43, and F45 were acquired, adding to the six previously measured dispersion curves (Fig. S1A).

The ¹H^N R_1ρ was collected using a U-[¹⁵N]–labeled sample of perdeuterated ubiquitin in 90% (vol/vol) H₂O/10% (vol/vol) D₂O. For the measurement of ¹H R_1ρ, the experiments used follow previous methods (34). Spin-lock frequencies were varied from 1,000–10,000 Hz (277 K for WT) or 27,000 Hz (other temperatures and mutants), and were calibrated by measuring ¹H 90° pulse lengths at their corresponding power levels. Field strengths and offsets were chosen such that tilt angles of ∼35° were used for all points to minimize the nuclear Overhauser effect (NOE) and rotating frame nuclear Overhauser effects (ROE) that can lead to pseudodispersion profiles (34). The experiments were carried out in an interleaved fashion, where the used delay, field strength, and offset were randomly varied. With the current experimental parameters, the overall change in the temperature was less than 1 K. Relaxation rates were determined using a three-point sampling scheme with spin-lock relaxation delays of 5, 65, and 125 ms. Rate errors were estimated using residuals from the three-point fits. Mean R_1ρ and ω_eff (effective radio frequency field) values were determined using equations 5 and 6, respectively, from the study by Eichmüller and Skrynnikov (34). For each experiment, 56–188 (indirect dimension) and 1,024 (direct dimension) complex points were acquired. Four transients for each increment were collected with recycle delays of 2.3 s (277 K for WT) or 2 s (other temperatures and mutants), yielding a total experiment time of 17–58 min per data point. For E24 and G53 RD curves acquired at 308 K, the sweep width was increased from 23.5 ppm (used in other experiments) to 49.3 ppm, and a six-point sampling scheme was used with spin-lock relaxation delays of 5, 14, 23, 32, 41, and 50 ms. All ¹H^N experiments were conducted on a Bruker spectrometer operating at a ¹H frequency of 600 MHz.

The ¹H^N Carr–Purcell–Meiboom–Gill (CPMG) measurements were conducted on a U-[¹⁵N] and U-[²H] selectively ¹³C-labeled (CHD₂) sample of perdeuterated ubiquitin in 90% (vol/vol) H₂O/10% (vol/vol) D₂O. The sample was loaded in nine capillaries placed into a 5-mm sample tube similar to a previously published method (14). Supercooled CPMG experiments were acquired at 262 K using a relaxation compensated approach with the CPMG period following t₁ evolution (35) and phase cycling of the refocusing pulses (36, 37). The CPMG frequency (ν_CPMG) was varied from 211 to 2,526 Hz during a constant time period (T_CP) of 19 ms. For each experiment, 128 (indirect dimension) and 1,024 (direct dimension) complex points were acquired with a recycle delay of 1 s. For the CPMG experiments, 60 transients were collected for a total experiment time of 315 min per ν_CPMG point. For the reference experiment without the CPMG block, eight transients were collected for a total experiment time of 45 min. Rate errors were propagated from spectral noise. Effective relaxation rates (R_2,eff) were fit assuming fast exchange using the following formula:

$$R_{2,\text{eff}}=R_2+{\mathrm{\Phi }}_{ex}{\tau }_{ex}\left(1-4{\nu }_{CPMG}{\tau }_{ex}\tanh \frac{1}{4{\nu }_{CPMG}{\tau }_{ex}}\right).$$

NMR data processing and peak quantification were done with NMRPipe. Peak intensities for E24 and G53 at 308 K were calculated by taking the maximum spectral intensity in a region around the peak positions. R_1ρ parameter fitting, error estimation, and determination of significant amounts of dispersion were done as previously described (13). CPMG data were processed in the same manner.

Optimizing a Single Collective Mode to Explain the RD Data.

We also tested a third step in which the resulting weights were further refined using Nelder–Mead optimization. Although this technique produced higher ROC curve areas for the training data, it did not produce better ROC curves using the cross-validation procedure described in Methods, Cross-Validation of the Optimization Procedure. Therefore, we did not use this procedure in a final determination of optimized weights. Using the same cross-validation scheme, we determined that the optimal number of PCA modes to include in the optimization was 20. The top 20 eigenvectors covered 78% of the variance and 37% of the SD (i.e., atomic displacement) in the underlying coordinates.

Clustering RD Fit MD Mode into Semirigid Bodies.

To identify a set of semirigid bodies in the RD fit MD mode, residues were first clustered into contiguous segments along the amino acid sequence and then clustered into discontinuous groups of segments. Backbone rmsds between the minimum and maximum projections were used for clustering. For contiguous segment clustering, residues were initially put into single-residue segments. Using a greedy algorithm, the pairs of adjacent segments having the lowest combined rmsd were successively merged. A cutoff of 0.35 Å was used to create 11 contiguous segments for group clustering. Clustering of these segments into discontinuous groups was done with the same greedy algorithm, except that merged groups were no longer required to be adjacent in sequence. A cutoff of 0.7 Å was used to create four rigid bodies.

Analysis of Peptide Flipping in MD Trajectories.

For every snapshot of the 100-ns AMBER ff99SB MD trajectories (10) or the 1-ms CHARMM22* MD trajectory (22), we calculated the ψ-backbone dihedral angle of D52 and the ϕ-backbone dihedral angle of G53. To ensure that structural transitions did not wrap around this periodic ψ/ϕ-space, the angles were normalized in the following manner. First, both angles were mapped onto the range 0–360°. Second, for any ψ_i/ϕ_i-pair whose sum was greater than 350°, ψ_i was set to ψ_i − 360. Under this normalization, ψ_i − ϕ_i is centered around 80° in the NH-in conformation and −320° in the NH-out conformation.

For the CHARMM22* trajectory, the alternate states were identified by inspection of the rmsds of residues 51–53 (alternate state 1) and residues 31–41 (alternate state 2). Q-factors were determined from a combined set of backbone NH, backbone NC, and side-chain residual dipolar couplings (RDCs), using a single alignment tensor for all RDCs in a given alignment medium. To do so, a five-element B vector was first calculated (42) for each internuclear vector in every snapshot in the trajectory. From these vectors, average B vectors for each state were then calculated. The landscape of Q-factors was determined by varying the weights applied to the average B vectors for each state.

PLS FMA.

To enable Rosetta structural modeling of the entire core ubiquitin structure (residues 1–70), we first calculated projection values for the 209 non–USP-bound ubiquitin conformations onto the peptide fit PDB mode. We then used these projection values (instead of the previous 0 or 1 assignments) to train a new PLS model using the backbone N, CA, and C atoms of residues 1–70. The use of 40 PLS components resulted in near-exact reproduction of the peptide fit PDB mode projection values. For each of the 217 crystallographic conformations, we used this PLS model to generate 21 synthetic conformations evenly interpolated from the minimum (NH-in) to the maximum (NH-out) projection value.

USP2 Inhibition Assays.

USP2 inhibition assays were performed similar to previously described assays (32), in which WT and modified ubiquitin constructs inhibit cleavage of 7-amido-4-methylcoumarin (AMC) C-terminally linked to WT ubiquitin. The final reaction buffer included 100 mM NaCl, 50 mM Hepes (pH 7.6), 25 μM ZnCl₂, 5 mM DTT, and 8% DMSO. Thirty-microliter reactions were performed at 25 °C in low-volume, 384-well, black with clear bottom NBS microplates (Corning). Initial rates of fluorescence increase were monitored with a PHERAstar FS microplate reader (BMG Labtech) using a 340-nm/470-nm filter pair. The USP2 concentration was determined from its absorbance at 280 nm and kept fixed at 1.5 nM for all reactions. For K_m determination, concentrations of ubiquitin-AMC (Boston Biochem) were log-spaced from 0.002 to 9.3 μM (12 points in duplicate), without the presence of inhibitor. For determination of K_i values, the concentrations of WT, E24A, and G53A ubiquitin were log-spaced from 0.1 to 1,000 μM (13 points in triplicate), with a fixed concentration of 2 μM ubiquitin-AMC substrate. Inhibitor concentrations were determined by mass. Kinetic parameters were calculated by simultaneously fitting the maximum velocity (V_max), Michaelis–Menten constant (K_m), and inhibition constants ($K_{\text{i},\mathrm{W}\mathrm{T}}$, $K_{\text{i},\mathrm{E}\mathrm{24}\mathrm{A}}$, and $K_{\text{i},\mathrm{G}\mathrm{53}\mathrm{A}}$), with the following equation:

$$V=\frac{V_{\text{max}}\left[S\right]}{K_{\text{m}}\left(1+\left[I_{\mathrm{W}\mathrm{T}}\right]/K_{\text{i},\mathrm{W}\mathrm{T}}+\left[I_{\mathrm{E}\mathrm{24}\mathrm{A}}\right]/K_{\text{i},\mathrm{E}\mathrm{24}\mathrm{A}}+\left[I_{\mathrm{G}\mathrm{53}\mathrm{A}}\right]/K_{\text{i},\mathrm{G}\mathrm{53}\mathrm{A}}\right)+\left[S\right].}$$

Input data included the initial reaction velocities ($V$), substrate concentrations ($\left[S\right]$), and inhibitor concentrations ($\left[I_{\mathrm{W}\mathrm{T}}\right]$, $\left[I_{\mathrm{E}\mathrm{24}\mathrm{A}}\right]$, and $\left[I_{\mathrm{G}\mathrm{53}\mathrm{A}}\right]$, with no more than one inhibitor per reaction). After this global fitting, errors in the inhibition constants were analytically determined by individually fitting each K_i with values of V_max and K_m taken from the global fit. For pairs of sample data (WT/E24A or WT/G53A), ANOVA F test P values were determined by comparing a fit to the global equation with one where the K_i was assumed to be the same for both samples. For these fits, V_max and K_m were also taken from the initial global fit.