A grid-based backbone correction to the ff12SB protein force field for implicit-solvent simulations

Abstract

Force fields, such as Amber’s ff12SB, can be fairly accurate models of the physical forces in proteins and other biomolecules. When coupled with accurate solvation models, force fields are able to bring insight into the conformational preferences, transitions, pathways and free energies for these biomolecules. When computational speed/cost matters implicit solvent is often used -- at the cost of accuracy. We present an empirical grid-like correction term –in the spirit of cMAPs-- to the combination of the ff12SB protein force field and the GBneck2 implicit solvent model. Ff12SB-cMAP is parameterized on experimental helicity data. We provide validation on a set of peptides and proteins. Ff12SB-cMAP successfully improves the secondary structure biases observed in ff12SB+Gbneck2. Ff12SB-cMAP can be downloaded (https://github.com/laufercenter/Amap.git) and used within the Amber package. It can improve the agreement of force fields + implicit solvent with experiments.

Introduction

Atomistic force fields can have small systematic errors when using implicit-solvent models

Atomistic force fields are widely used to simulate a broad range of biomolecular structures and properties¹. These force fields are usually most accurate when combined with explicit water solvent modeling. However, implicit-solvent modeling is often used instead when computational efficiency is needed. This is particularly important in cases where the numbers of explicit waters added are too large for computations (e.g. protein folding starting from extended chains) or when using advanced sampling methods that scale with the number of particles (N) (e.g. the number of replicas needed for replica exchange is proportional to the square root of N)². For example, recently implicit solvent modeling has been used to fold several small proteins³ on lab-sized computer clusters. The computational requirement is orders of magnitude larger when explicit solvent is used⁴.

On the one hand, implicit water has the disadvantage of lacking the details of explicit water models, in treating hydrogen bonding or bridging waters or dipole reorientation⁵, for example. On the other hand, implicit water is computationally efficient, and often useful for simulating large systems. In our experience, simulations of protein folding using ff12SB⁶ and GBneck2⁷ show secondary-structure biases favoring helical conformations. Some of the limitations in this specific combination might come from: (1) ff12SB backbone parameters were derived to improve experimental agreement of the alanine backbone in combination with explicit solvent, (2) known deficiencies of GB implicit solvent and absence of a surface area term^3,7,8 (3) absence of coupling terms between backbone dihedrals (Φ and Ψ).

In this work we aim at a correction term for the combination of protein force field (ff12SB)⁶ and implicit solvent (GBneck2)⁷ that improves agreement with experimental data. This correction term acts as a way to cancel the errors of coupling this specific force field and implicit solvent and is not expected to be transferable to other force field/solvent combinations. We adopt an approach that has been used extensively in the parameterization of Charmm 22 and beyond which is to introduce coupling between backbone dihedrals with a spline based correction map (cMAP)^9–12. Correction maps have already been used in the past as a way to cancel errors arising from combining an implicit solvent model with a force field¹². To disambiguate the different cMAPS available for different force fields¹³ we call this map ff12SB-cMAP.

We show that rather than deriving an individual correction map for each amino acid, it is enough to make two corrections. The first applies to alanine, which is less helical than expected. Glycine and proline need no correction. The second correction applies to the rest of the amino acids, which are too helical in simulations. The resulting force field exhibits improved behavior in the folding of small peptides and has been used successfully for predicting native structures of proteins in the presence¹⁴ and absence¹⁵ of experimental data.

Theoretical Background

The ff12SB-CMAP Approach

There is no unique or perfect approach for deriving a grid correction to the force field. Hence, we first outline below the philosophy and approach that we use to evaluate agreement with experimental data. Next, we outline the training set that we use to develop the correction maps. We then validate our resulting empirical correction on two test sets: (1) folding of small peptides and (2) stability of protein native states.

Correction maps represent an energetic modification to the force field. For every X(ϕ,ψ) there is an energetic correction that has been tabulated in a grid. C-splines¹⁶ are then used to derive forces. In that way, the corresponding correction can be used for molecular dynamics simulations or similar techniques.

Ideally, this correction to the force field would be derived by considering the “real” free energy map of each amino acid and comparing them with maps derived from simulations. Unfortunately, we cannot access the “real” energy map, but we can find approximations to it: (1) from quantum mechanics or (2) from the plethora of protein structures deposited in the PDB or (3) from other experimental data. We have opted for a hybrid approach, in which we first use data for all amino acids (except proline, glycine and pre-proline) present in a set of high resolution crystal structures selected by the Richardson lab¹⁷ (top500) to evaluate weaknesses in the standard energy profiles for the ff12SB force field. Then, guided by these results, we use experimental data for helical propensities (α region) and folding simulations (β region) to develop correction maps that are used in subsequent simulations.

We first make a 2D histogram of populations for phi and psi dihedral values based on amino acids from the top500 dataset that are not involved in secondary structures. The Boltzmann relation is used for deriving a qualitative approximation to the free energy maps based on populations¹⁸ (see Figure 1 and methods). Regions with low populations are not accurately represented in this model, so we only look at regions where the predicted energy is no further than 5 kcal/mol away from the lowest energy structure. We compare these qualitative maps to those derived from simulations of trialanine (see methods),¹⁹ using the same 5kcal/mol threshold for the free energies (see methods). We use trialanine because it is too short to form secondary structures, and we make the approximation that the ensemble of structures sampled by trialanine is representative of the presented in coil regions of protein structures. At this level of approximation, we can compare the shapes of the two maps and the relative depths of the minima around the beta (β) and alpha regions (α), which are statistically better represented in the top500 than other regions of the map (see Figure 1). Even though we are only using this approach to qualitatively identify problematic regions in this work, there are several statistical potentials in the literature that have used similar approaches for refining structures, scoring and sampling^20,21,22.

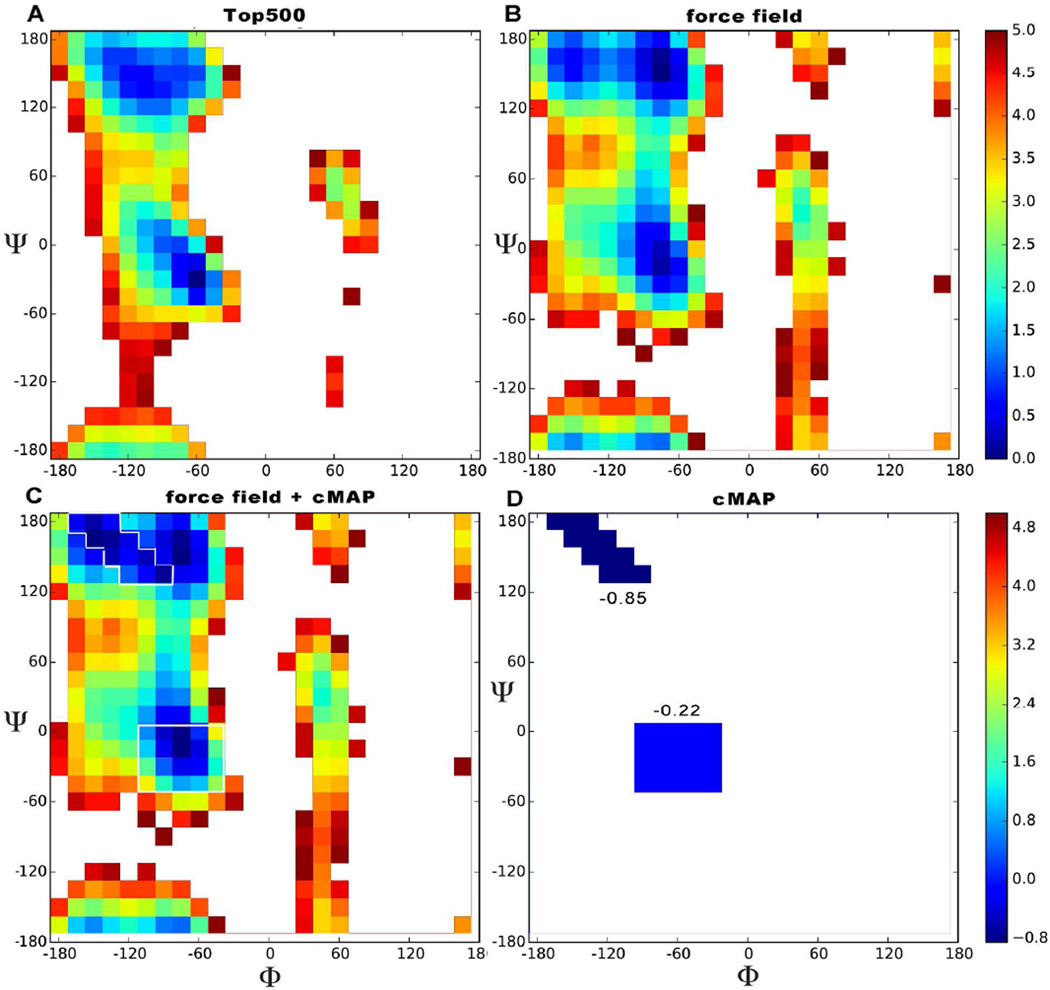
Figure 1.

Free energy ϕ,ψ map. The color scale indicates relative energies with respect to the lowest energy conformation. Energies are truncated at 5 kcal/mol. The experimental plot (A) was derived from data from the top500 dataset by looking at all the non glycine, proline or pre-proline residues, binning them in a 2D histogram, counting populations and using the Boltzmann relation to estimate free energies. The calculated plot (B) was derived from simulations of trialanine (ff12SB force field + Gbneck2 implicit solvent). Plot C shows the effect of ff12SB-cMAP on top of ff12SB for Alanine; the regions directly influenced by cMAP are outlined in white for clarity. The cMAP energy correction we apply is shown by itself in panel D.

Results and discussion

The shape of the Ramachandran differs between current-model simulations and experiments

The important minima comprising the various stable basins: alpha (α), beta (β), polyproline type II (ppII) and left-handed alpha (Lα) conformations can be identified in both experiment and simulations (see Fig. 1 and Fig. S1,S2). The differences between simulations and experiment are mainly in the shapes of the Ramachandran maps surrounding these metastable regions. The forbidden region is quite different in the two maps, in particular the region between α and Lα is much narrower and is tilted clockwise in the simulated map. Examining the α region, we can see that not only is the simulated basin broader and more diffuse, it has also some specific features: a favorable region (Φ ∈ [−180, −120]) not identified in the PDB and the region in between alpha and ppII is different: the force field stabilizes the region near alpha, whereas in the pdb it is the area near ppII that is more stable. Likewise the Lα region has substantial additional density trailing down into the Ψ ∈ [−180,0] region. Finally, the β region is smaller and rounder than in experiment, it is also less favorable than ppII. On the other hand, ppII structures are more favorable than in experiment. Due to the assumptions discussed above, differences between the map derived from the PDB and the one derived from simulations are expected^23,24. We compare backbone preferences for residues not involved in secondary structure – rather than all amino acids-- to understand the natural tendencies of backbones when not influenced by stabilization from hydrogen bonds in α-helices or β-strands. Ideally the position of the global minima and the predicted relative populations of the different basins should be roughly the same both in experiment and in simulation. However, the current combination of force field and implicit solvent does not satisfy this, favoring helical conformations (see Figure 2, panel A). Hence, we derive ff12SB-cMAP to modify the potential in the α and β regions in order to recover the observed experimental balance between the two.

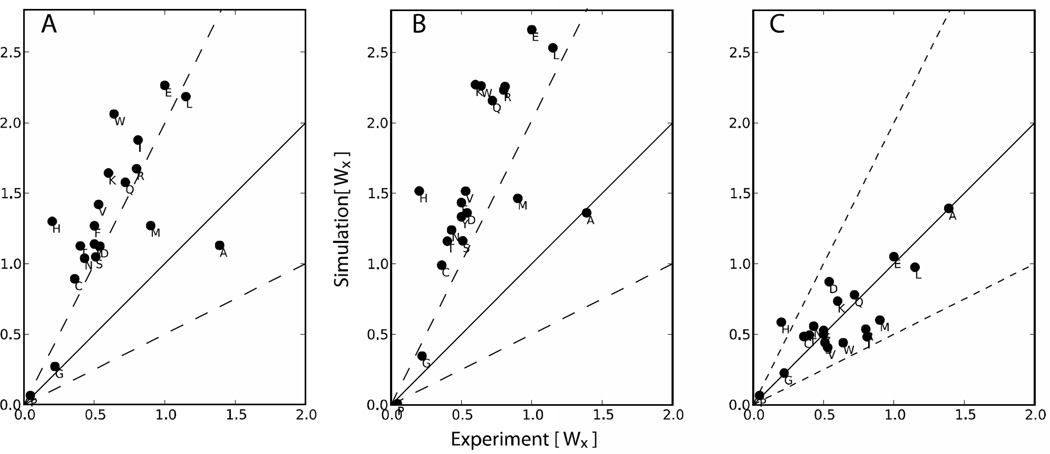
Figure 2.

Computational vs. experimental helical propensities for the 20 amino acids. The black line indicates perfect agreement between theory and experiment. Dotted lines on each side correspond to having helical propensity (Wx) theoretical values that are double (or half) of the experimental ones. This corresponds to a k_BT*ln(2)≈0.41 error in free energy. Panels A: ff12SB, B:ff12SB+ CMAP on Alanine; C: ff12SB+ CMAP.

In summary, high-resolution structures from the top500 suggest that there is a helical bias in the force field, but not how to correct it. In the next section we describe what training set we used to correct it.

TRAINING SET

We aim to improve the balance between the helical (α) and extended (β) regions of the conformational landscape. Hence, only ff12SB-cMAP corrections for those regions (see methods) will be derived.

Helical propensities can be calculated for each amino acid from experiments²⁵. These propensities can also be calculated from computations by following the approach outlined by Best and coworkers²⁶. We try to match the tendencies from experiment and computation iteratively by systematically applying a grid correction to the helical region, running new simulations and comparing to experiment.

There is no similar experimental propensity data to correct the β-region. Hence, we use folding simulations of protein G using restraints. The restraints guide the protein towards native in such a way that if the force field has the right balance between β-strands and α-helices the native topology should form¹⁴.

Modifying the force field for the α or β regions independently has an overall effect on the α / β balance. Hence, an iterative approach is used until both the experimental helicities and successful folding are achieved.

Correction of helical propensities and comparing to experimental data

The helix-forming region of the Ramachandran map is defined as ϕ ∈ [−100,−30] and Ψ ∈ [−67,−7]. This is the region were we will apply the grid correction.

In both cases a peptide system is studied where a guest residue is introduced. By changing only the guest residue, the effect on helicity from each amino acid can be estimated. There are some differences in the peptides used for the experimental²⁵ (WK_m^tL₃-A₉XA₉-^tL₃K_m; where m is 6 or 8 and X represents each amino acid and ^tL₃ represents tert-Leucine) and computationally (AAXAA)₃^26,27 peptides. In particular in computations, the peptide is placed three times in the 15-mer to improve statistics, but in some cases with large side chains this can lead to side chain interactions not possible in the experiment (e.g. tryptophan). Both the experimental data and our computations are post-processed by using the Lifson-Roig model^28,29 (see methods) which returns two parameters (w,v) corresponding to helix extension (w) and helix nucleation (v). They are specific to each amino acid, and a comparison between experiments and computation is shown in Figure 2.

Initially, we ran this procedure by simulating the peptides with the unmodified ff12SB force field to explore the helical tendencies of the different amino acids (Figure 2A). We saw three general patterns: alanine is not helical enough, glycine and proline are in good agreement with experiments, and all the other amino acids have a strong helix bias. Because alanine is the basis for the peptides in our test set, we made a correction grid that only accounts for alanine residues. All (AAXAA)₃ simulations were repeated with this correction (Figure 2B). Our goal was then to make the rest of the amino acids have values between two times and half the experimental value (corresponding to an error of 0.69 k_BT). These thresholds are shown as dashed lines in Figure 2B.

To do this without over fitting we notice that most amino acids are off by a similar amount (linear trend in the plot), hence we derive a correction map that involves all amino acids except glycine, proline or alanine. This yields corrected helical propensities, but we have no information for the β-region. In the next section we show how we address this region. Fixing both regions is an iterative process, and the end result for helicities is seen in Figure 2C.

Since experimental information on the (AAXAA)₃ peptide system is only available for X=Q³⁰, we have used the dataset derived from the (WK_m^tL₃-A₉XA₉-^tL₃K_m) peptides²⁵. Although the helicity of the different amino acids should be transferable to different systems, there are possible problems with side chains of guest residues interacting in the (AAXAA)₃ system. We have observed this not to be an issue for most amino acids. However, tryptophan does tend to create conformations where the three Trp residues are interacting with each other, usually via stacking interactions. By using the same grid correction on all non-glycine, proline or alanine residues we avoid some of the problems of over fitting to different computational and experimental systems.

Correction of the β-region using folding simulations

Deriving a correction term to improve the relative stability of the β-region is more difficult since there is no direct or indirect experimental data we can use. Instead, we have used a procedure based in the methodology that first identified the problem: simulations of protein folding guided by structural data (see methods for details). We use protein G, a small 56 residues protein containing both a helix and four β-strands. We apply restraints¹⁴ (see methods, Fig. S3 and table 1) that guide the protein toward the folded state. The number of restraints is defined to be sparse and uses flat bottom potentials in such a way that it does not over-constrain the system. The restraints guide the system to topologies close to native and --if the force field is accurate-- the structure will rapidly equilibrate to the native conformation. Using this approach we circumvent the slow kinetics of folding. We assess the success by looking at RMSD distributions for simulations of equal length with different grid corrections. The larger the population beneath a certain threshold the more accurately the force field behaves.

Table 1.

Pairs of residues chosen as contacts for folding simulations of protein G and their distance in the native state. Two folding simulations were attempted, in the first all contacts in this table were used, in the second, only the ones in bold were used.

Residue number	Residue number	1GB1 Cα-Cα distance (Å)
8	13	4.90
46	51	5.04
4	17	4.27
42	55	5.56
44	53	5.10
6	15	4.32
2	19	4.41
39	56	5.63
9	39	5.92
8	55	4.61
6	53	4.40
4	51	4.36

We prepared different grid correction strengths (βff12SB-CMAP=(0, −0.25, −0.50, −0.75 and −1.00 kcal/mol)) for the β-region (see Fig. 1). Using the RMSD as a success criteria, we chose −0.75kcal/mol as the initial β-map correction (see Fig. S4).

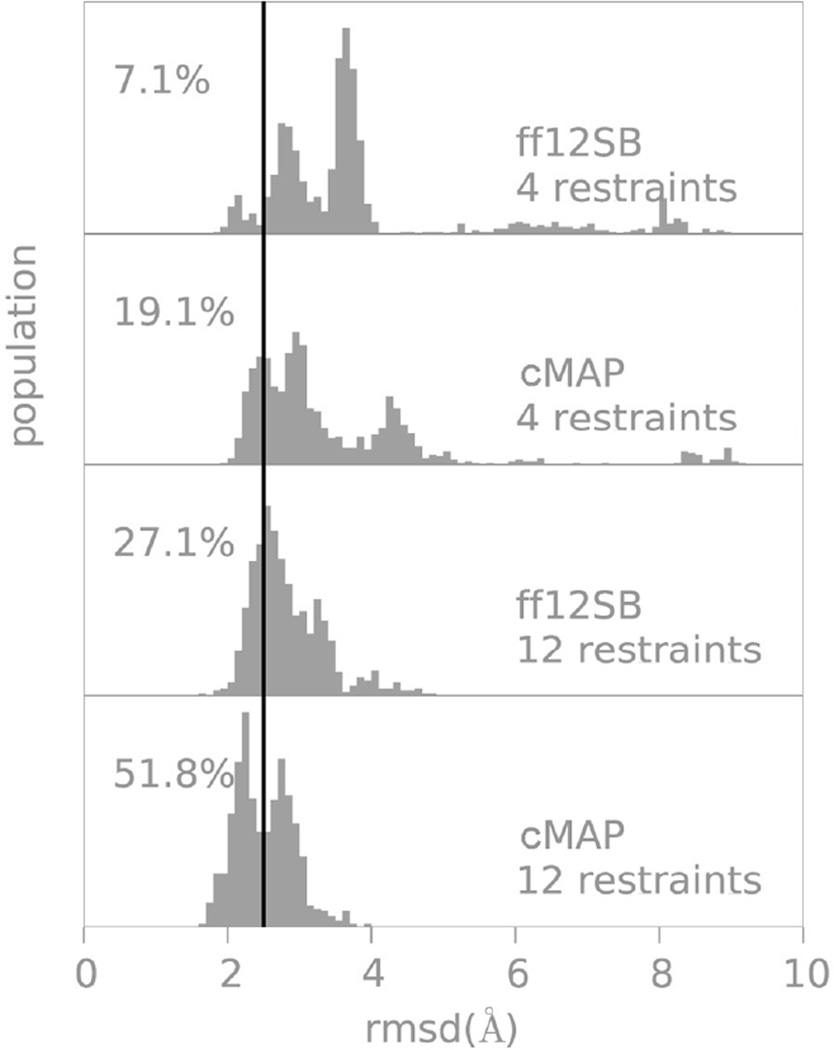
However, the limitation of fixing the α and β regions independently is that changes in either one alter the overall balance between helical and extended conformations. Hence, the helical propensities need to be recalculated (data not shown). We iterated several times to obtain parameters that reproduced both helicity and folding with the constraints that we did not want to deviate significantly from the initial solutions. The final parameters are shown in Table S1 and can be downloaded online (https://github.com/laufercenter/Amap.git). The helical propensities with the last set of parameters can be observed in Figure 2C. Figure 3 shows the RMSD distribution obtained by folding protein G with two different set of restraints: we first used 12 restraints to guide to the correct topology and as a more stringent test took a subset of 4 restraints. Using fewer restraints places more demands on the force field. In both cases we show that our final set of corrections is a significant improvement to the initial force field (nearly doubling the population close to native).

Figure 3.

RMSD distributions from native in protein G folding simulations with different force fields and number of restraints. The percentages refer to the RMSD populations below 2.5Å sampled in the last 50 ns of a 60 ns restrained folding trajectory. We use a stringent value of 2.5Å as a cutoff since the use of restraints already favor a native like topology; notice that in all cases most conformations are within 4Å from the experimental structure.

In order to check for the sensitivity of the parameters to small changes in the ff12SB-cMAP we used a perturbational approach³¹ (see Figure S5 and Methods). We conclude that the parameters are robust to small changes and that the currently derived ff12SB-cMAP sits in an optimal region.

TESTING ff12SB-cMAP

We used two different test systems to assess the quality of the ff12SB-cMAP correction. We first checked that simulations of native proteins did not systematically diverge from the experimentally determined native structure of a set of proteins. If our correction is appropriate then we expect the native state to be kinetically stable; therefore, simulations should not diverge substantially from the native state. Second, a more stringent test is to look at the ability of the original/corrected force fields to reproduce secondary structure preferences of seven small peptides starting from extended conformations.

Native stability tests: proteins are stable with FF12SB-CMAP

One of the main difficulties in identifying the shortcomings in force field-implicit solvent simulations is that in native-like simulations, proteins are usually stable in the sub-microsecond timescale. Indeed, the corrections we applied to the force field are small, meaning that there are subtle effects that displace the overall balance of the force field (see Figure 1). The first test of the force field is to see if native structures are stable in the 100 ns timescale. In native-like simulations, the entropic penalty for forming secondary structure is already paid. Hence, the balance of interacting hydrogen bonds, hydrophobic effect, salt bridges, and others present in the native structure might be enough to keep native states stable for long periods of simulation time.

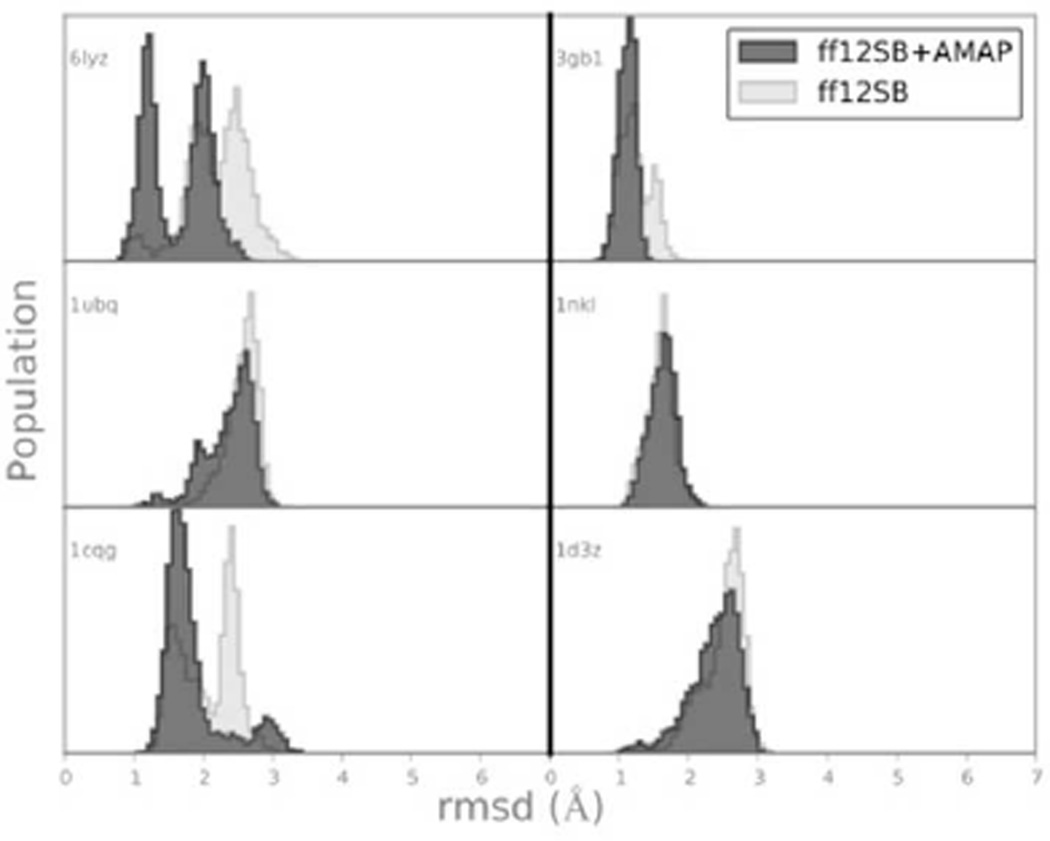
We chose six representative structures from the pdb (1nkl, 6lyz, 3gb1, 1ubq, 1cqg and 1d3z) and ran simulations starting from the native structure with and without ff12SB-cMAP. We assessed success as RMSD distributions referenced to the native structure being close to native. Force field failures can be identified by increasingly larger RMSD values with respect to the native structure.

Figure 4 shows the results in terms of Cα RMSD from the native structure. Overall both force fields have similar behavior, remaining for the majority of the simulation time within 3.0 Å to the native state. Figure S6 shows the propensity for each amino acid along each protein’s chain to be in either helical or extended conformation. As expected, most of the differences with the crystal structure remain in loop regions. As noted by others³ development of more accurate non-polar terms in solvation methods might further increase protein stability.

Figure 4.

All residue, Cα rmsd distribution from native state (x-ray and NMR structures from the PDB). All 350 ns long simulations were started from the experimental structure.

Peptides fold to correct structures with ff12SB-CMAP

Folding simulations are more challenging tests of thermodynamic quality of force fields, and they can unveil deeper problems in secondary structure preferences. For this purpose we simulated seven different peptides^32–41 that have been reported to have a particular fold in solution (some of them –such as Trp-cage or trpzip2– are considered miniproteins). We chose three systems that fold into hairpins and three that fold into helices, with an additional system that has been crystallized as both an α-helix and β-hairpin in the same crystal (see Table 2). The main challenge in comparing with experiment is that it is not clear what percentage of the time these peptides should be structured in solution, and even what the exact structure should be in some cases.

Table 2.

Peptides used and their corresponding native structures. Residue numbers indicate which part of the corresponding PDB was used.

Name	Sequence	Structure	Pdb id
Matα2/MCM1EK	VFNVVTQDMINKST	α-helix/β-hairpin	1MNM (residue 115–128)	39
EK peptide	YAEAAKAAEAAKAF	α-helix	Ideal (Circular Dichroism; 40% helical)32,42
Ribonuclease A C-peptide analog	AETAAAKFLRAHA	α-helix	5RSA analog34,40
Tc5b	NLYIQWLKDGGPSSGRPPPS	α-helix/coil	1L2Y36
Protein G C-termini	GEWTYDDATKTFTVTE	β-hairpin	1GB135 (residue 41–56)	41
Trpzip2	SWTWENGKWTWK	β-hairpin	1HRX38
Nrf2 peptide	AQLQLDEETGEFLPIQ	β-hairpin	2FLU (resid 72–l87)	33

We performed simulations using ff12SB with and without ff12SB-cMAP, in both cases using the GbNeck2⁷ solvent model as described in Methods. Their tendency to fold correctly was assessed by quantifying the overall tendency to adopt different kinds of secondary structure (see Table S1), the individual tendencies of each amino acid in the sequence and the consensus fold of the sequence.

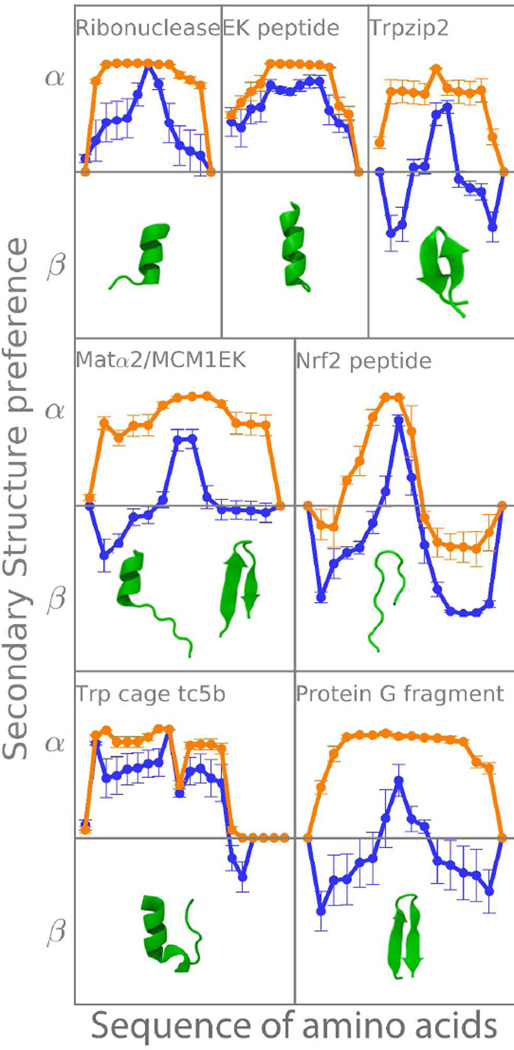
Table S1 shows that the helix forming tendencies remain the same with both force fields for peptides that are supposed to be helical (EK, Ribo and Tc5b). The biggest difference between force fields comes from the ability to form β-strands (labeled ProtG, Nrf2 and Trpzip in Table S1). For ff12SB we detect strand formation only in Nrf2, whereas with ff12SB-CMAP the experimental tendency is captured in all cases. Trpzip2 experimental structure is a hairpin, but in simulations the population of hairpin is not dominant (see Table S1). This difference is not surprising as Trpzip2 is a structure with a higher amount of tryptophan than most proteins, where stacking interactions play an important role and where not including a non-polar term to the solvation energy in our simulations is likely to account for the differences observed⁷. Looking at the RMSD to native of tripzip2 with time (see Figure S7) we observe structures closer than 1.5 Å to native 24% of the time when using ff12SB-cMAP (see Figure S7). As a final descriptor for these peptides, the population of turns (Table S1) increases in ff12SB-cMAP simulations in all cases where hairpins are formed.

The individual amino acid tendencies to form α/β in each sequence are shown in Figure 5 (defined as $\frac{\mathrm{\Delta }G}{k_{B}T}=\text{log }\left(\frac{\mathit{\text{helical population}}+0.01}{\mathit{\text{extended population}}+0.01}\right)$ for each amino acid in each peptide; where the 0.01 semi count ensures that we never take the log of 0). With this definition, values >0 favor the formation of helices, <0 formation of extended strands and =0 means there is no overall preference for either one. Both force fields have a favorable tendency towards helical for peptides that are experimentally determined to be helical. However, the standard deviations (calculated as the standard deviation after dividing the trajectories in 5 blocks of equal length), are very different. Ff12SB has very small deviations, indicating a strong tendency to sample only one kind of conformation, whereas with the correction term greater standard deviations indicate the ability to sample different structures in these REMD trajectories.

Figure 5.

Tendencies for helical (>0) or extended conformations (<0) for each amino acid in different peptides. Different force field's tendencies are shown, as well as the experimental structure for comparison (see table 1). Orange: ff12SB, blue: ff12SB-CMAP. Error bars correspond to one standard deviation as calculated from dividing the trajectory in 5 blocks.

The rest of the peptides can form hairpins and are mostly misrepresented by the original force field. With ff12SB-cMAP, these propensity plots (Figure 5) have a characteristic ‘W’ shape. The valleys in this “W” correspond to parts of the peptide that are in extended conformation and the peaks correspond to turns and termini.

Interestingly, the MAT peptide has been crystallized as both a hairpin and a helix in identical conditions (they are both present inside the same crystal structure)³⁹. In this case we would expect an overall ΔG≈0⁴³. In Figure 5, the C-termini has a ΔG≈0 reflecting the possibility of being in helical or extended conformation. The turn region is never extended in the hairpin, so the overall preference is for being helical in the plot and the N-termini –which is never helical— favors the beta region. Without an ff12SB-cMAP term, the structure is helical throughout the simulation for all amino acid positions.

These results showcase the use of ff12SB-cMAP to correct for secondary structure tendencies and to be helpful in folding simulations. We have successfully used this modified force field in several protein folding studies¹⁴. An alternative way to use the benefits of the new force fields with correct backbone helical propensities in implicit solvent is to combine ff99SB backbone parameters with ff14SB side chain parameters^3,6.

COMPUTATIONAL METHODS

Here we define the experimental and computational data we use to compare ϕ/ψ and SSE tendencies between force fields and experiment.

Deriving an experimental Ramachandran plot from the top500 data

We used the top500 dataset from Duke university for the Ramachandran plots based on high resolution crystal structures to compare the features of the protein’s energy surface (http://kinemage.biochem.duke.edu/databases/top500.php)¹⁷. This data allows us to represent the tendencies for all amino acids whether they are involved in secondary structure or not and separate special cases like glycine and proline. From the population densities in the Ramachandran plot, an approximation to the shape of the free energy can be built qualitatively to compare to force fields by binning the space and using eq. 1.

$$\mathrm{\Delta }{G}_i=-k_{B}T\text{ log}\frac{N_i}{N}$$ (eq. 1)

Where all symbols have their usual meaning. To transform between populations and energies we consider an arbitrary effective temperature for the crystal ensemble of 300K⁴⁴. While not strictly correct, it nevertheless provides a qualitative guide to what the experimentally derived energy map looks like.

Tripeptides allow us to identify the force field’s preferences

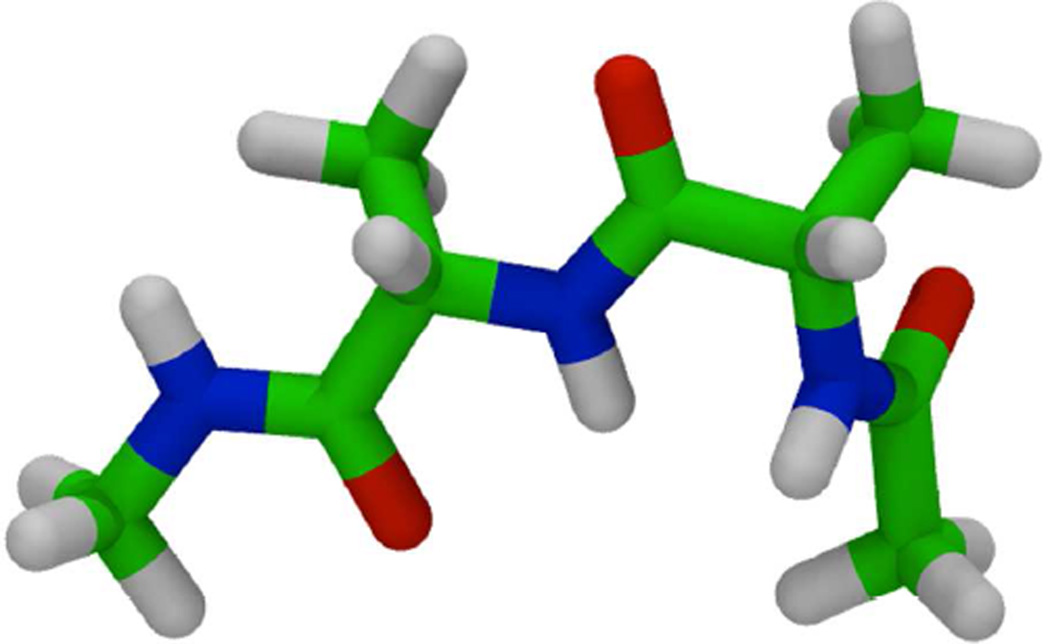
The Ramachandran maps of alanine, glycine and proline were studied with molecular dynamics simulations on small tripeptides (see Fig. 6) both in explicit (TIP3P water model⁴⁵) and implicit water (IGB=8⁷ and mbondi=3 Born radii); no solvent accessible term was used to reproduce the non-polar term. We set a 2 fs time step, with a Langevin thermostat⁴⁶ (coupling constant of 1ps⁻¹) and temperature of 300K. Additionally, the explicit simulation parameters included the use of periodic boundary conditions and particle mesh Ewald⁴⁷. The Berendsen algorithm⁴⁸ was used to keep temperature and pressure in explicit solvent, both with a coupling time of 1ps.

Figure 6.

Blocked tri-alanine peptide as a model system.

Each tripeptide was simulated in 6 independent replicas, roughly 2µs (6 µs) total simulation time in explicit (implicit) solvent. All simulations were performed with the GPU accelerated version of AMBER^49,50.

Ff12SB-CMAP

Grid corrections have already been reported for explicit^10,51,52 and implicit¹² solvent, and here we follow the same form. For each residue, the energy is modified according to a grid-based correction on the ϕ/ψ torsion angles in the Ramanchandran space. Forces and energies are obtained from bicubic spline interpolation (see the original cMAP⁹ paper for details). We defined 24×24 bin grids (resolution of 15° for each dihedral) as in the original cMAP⁹. Additionally, the machinery to run calculations with cMAP like grids is already in place in popular molecular dynamics packages^13,53–56, making the application of ff12SB-cMAP straightfoward. Ff12SB-cMAP can be obtained from the github (https://github.com/laufercenter/Amap.git).

Ff12SB-CMAP Sensitivity

Using thermodynamic perturbation theory³¹ the helical propensity of the test set of ploy-peptides was computed as function of the scaling of the ff12SB-cMAP corrections. Test sets were obtained scaling alpha and beta region corrections from 80% to 120% of the original one in steps of 2%. The coefficient of determination (R2) between the result of every set of parameters and experimental results was used to assess the quality of the set (see Figure S5).

Helical propensities are a good way to match force field and experimental behavior

We compared experimental helical propensities²⁵ with computational ones in a similar fashion to Best and coworkers²⁶. We simulated the (AAXAA)₃ peptide, with X representing each of the 20 amino acids, in implicit solvent using the protocol described above, except where noted. T-REMD simulations with 10 replicas were setup using the MELD¹⁴ plugin to OpenMM⁵⁴. Implicit solvent was used and replicas were assigned temperatures between 300 and 425K (exponential spacing of temperatures). Langevin dynamics with a 1ps⁻¹ coupling constant was used. Simulations were run for 1.75 µs, exchanging every 175 ps. At every exchange step 128 swaps were attempted. Each swap consists of attempting to exchange temperature conditions between neighboring replicas and accepting on the basis of the metropolis criteria. After the 128 trials, some replicas that have exchanged successfully several times might have gone up or down several slots in replica index. We used a 3.5 fs time step and hydrogen mass repartitioning⁵⁷. In this scheme hydrogens are three times heavier than usual and the extra mass is removed from the heavy atom to which they are attached. After the runs, secondary structures were derived using Stride⁵⁸ as implemented in VMD⁵⁹ for post-processing by using the Lifson-Roig model (see below).

Lifson-Roig model

Following Best’s work²⁷, we use the Lifson-Roig Model^28,60 to identify the helical propensities of each amino acid. This model measures the equilibrium properties of coil to helix transitions. In particular, three states are defined: coil, start/end of helix and within a helix. Their relative weights are 1, v_i and w_i respectively. A residue (i) is considered helical, if it inside the region: φ ∈ [−100 : −30] and ψ ∈ [−67 : −7]. Everything else is considered random coil within the model. The partition function for a protein of length N is defined as:

$$Z=(\mathrm{0 0 1}){\prod }_{i=1}^N{M}_i\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right),\text{where }{M}_i=\left(\begin{array}{ccc}\hfill w_i\hfill & \hfill v_i\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill v_i\hfill & \hfill v_i\hfill & \hfill 1\hfill \end{array}\right)$$

And the log-likelihood of having a sequence have a specific helical content is given by: lnL = ∑_i N_w,i ln(w_i) + ∑_i N_v,i ln(v_i) − N_k ln(Z). From our simulations we can get the populations of helical and within a helical fragment and then estimate w_i and v_i. We do this with a genetic algorithm to optimize the log-likelihood function. W_i can be understood as the equilibrium constant for a residue in coil conformation to extend an existing helical segment and is related to the free energy of helix extension by: ΔG_ext = −k_BTln(w_i). We can then compare the values of w_i to experimental measurements²⁵. Additionally, we can get estimates for the initial grid correction to apply by noting that $\mathrm{\Delta }G=k_{B}T\mathit{\text{ln}}(\raisebox{1ex}{$w_{\mathit{\text{sim}}}$}\!\left/ \!\raisebox{-1ex}{$w_{\mathit{\text{exp}}}$}\right.)$.

Guided folding simulations of protein G

Guided folding simulations refer to the fact that we use native-like information to make the process of folding faster¹⁴. In particular, we use two kinds of restraints based on secondary structure and contact information. We have selected 12 contacts (see Table 1 and Figure S3) between different SSE elements in the native structure (pdbid 1GB1). We impose those contacts in the simulation with flat bottom potentials in such a way that for Cα-Cα distances between 0 and 6 Å have no penalty, the penalty increases quadratically with a force constant of 0.6 kcal/mol/Ų until 8 Å and linearly after that. These restraints are zero at short distances allowing the force field to guide the details. At the same time, they are strong at far away distances, guiding towards the right kind of topology. Furthermore, for rapid convergence the simulations are simulated using a one-dimensional Hamiltonian and temperature replica exchange (H,T-REMD).

H,T-REMD was setup using the MELD plugin¹⁴ with 20 replicas, in which temperatures were assigned between 300 and 550K increasing exponentially. Exchanges were attempted every 50ps (2304 swap trials between neighboring replicas at each exchange). The strength of the contact restraints was reduced from 0.6 kcal/mol/Ų at low replica index to 0 kcal/mol/Ų at high replica index, using a MELD nonlinear scaler¹⁴ (http://github.com/maccallumlab/meld). In this way, structures at high replicas are unfolded and anneal to folded structures at low temperatures. Simulations were carried out for 500ns starting from an extended state. The lowest replica corresponding to 300K and 0.6kcal/mol/Ų restraints was used for analysis. Input scripts for the exact setup are given in https://github.com/laufercenter/Amap.git.

Testing of ff12SB-cMAP using simulations of small peptides

We validated our runs with a collection of seven peptides that have defined secondary structure (see Table 2). We started each simulation from an extended state as produced by the tleap⁵³ sequence command and ran T-REMD with 8 replicas whose temperatures were exponentially spaced between 270 and 420 K using the gbneck2 implicit solvent⁷ and the protocol described above, exchanging every 175ps (128 swap trials every time an exchange was attempted). Simulation times were at least 1.75µs, with some trajectories being extended to check for convergence. Input scripts for exact setup are given in https://github.com/laufercenter/Amap.git.

Testing of ff12SB-cMAP using simulations of native like proteins

In order to see how the current force field improvement affected simulations around the native state we simulated a small set of 6 proteins for 350 ns each using the different force field modifications. The protocol is the same as described above for tripeptides in implicit solvent simulations, running in OpenMM. Simulated proteins correspond to pdb ids: 1cqg, 1d3z, 1nkl, 1ubq, 3gb1 and 6lyz. Structures where minimized before starting the MD runs, two trajectories were carried out for each system. A sample script is given in https://github.com/laufercenter/Amap.git.

Conclusions

Biomolecular simulation force fields, such as AMBER ff12SB, are usually fairly accurate when used with explicit solvent models. Simulations are subject to greater errors when used with implicit solvent models. Because implicit solvent is useful where computational efficiency is needed, there is value in developing corrections for such force fields used with implicit solvent. Here we develop ff12SB-cMAP, which provides a grid-based correction for AMBER ff12SB when used with the GBneck2 implicit solvent model. Ff12SB-cMAP reduces bias in predicting secondary structures, with the added benefit of introducing correlations between phi and psi dihedrals. Ff12SB-cMAP is easily downloaded, can be readily used within most simulation packages and can be useful where improved agreement is needed between force field simulations and experimental data.