Facial surface morphology predicts variation in internal skeletal shape

Abstract

Introduction

The regular collection of three-dimensional (3D) imaging data is critical to the development and implementation of accurate predictive models of facial skeletal growth. However, repeated exposure to x-ray based modalities such as cone-beam computed tomography (CBCT) have unknown risks that outweigh many potential benefits, especially in pediatric patient populations. One solution is to make inferences about the facial skeleton from external 3D surface morphology captured using safe non-ionizing imaging modalities alone. However, the degree to which external 3D facial shape is an accurate proxy of skeletal morphology has not been previously quantified. As a first step in validating this approach, here we test the hypothesis that population-level variation in the 3D shape of the face and skeleton significantly covary.

Methods

We retrospectively analyzed 3D surface and skeletal morphology from a previously collected cross-sectional CBCT database of non-surgical orthodontics patients, and used geometric morphometrics and multivariate statistics to test the hypothesis that shape variation in external face and internal skeleton covary.

Results

External facial morphology is highly predictive of variation in internal skeletal shape (R_v=0.56, p<0.0001; PLS1-13=98.7% covariance, p<0.001) and asymmetry (R_v=0.34, p<0.0001; PLS1-5=90.2% covariance, p<0.001), while age (r²=0.84, p<0.001) and size-related (r²=0.67, p<0.001) shape variation are also highly correlated.

Conclusions

Surface morphology is a reliable source of proxy data for the characterization of skeletal shape variation, and thus is particularly valuable in research designs where reducing potential long-term risks associated with radiological imaging methods is warranted. We propose that longitudinal surface morphology from early childhood through late adolescence has the potential to be a valuable source of data that will facilitate the development of personalized craniodental planning and treatment plans while reducing exposure levels to “as low as reasonably achievable” (ALARA).

INTRODUCTION

A goal of modern healthcare is to make individual patient care predictive, personalized, preventive, and participatory (“P4”) (1, 2, 3). In dentistry, the ability to accurately predict both how an individual patient’s craniofacial and mandibular skeleton will grow and the likelihood of any future need for clinical intervention would have a transformative effect on orthodontic and surgical practice. However, growth of the skeleton is both idiosyncratic and nonlinear, with individual structures differing in the timing, magnitude, rate, or duration of growth across individuals (4, 5, 6, 7). As a consequence, cross-sectional estimates of age-related changes in shape and size provide only broad generalizations that are insufficient to predict an individual development. This critical limitation suggests that to realize personalized and predictive goals, longitudinal data on skeletal shape and size from the same individuals must be collected. Yet the long-term risks of repeatedly exposing pediatric patients to the ionizing modalities that image the skeleton are unknown and carry significant potential risks (8, 9).

The relationship between internal and external anatomy suggests a possible alternative to ionizing modalities for collecting longitudinal skeletal data. Notably, while the hard tissues are the principal locus of growth and surgical intervention, the soft tissues of the external face mirror this internal bony shape. This suggests that surface features alone, for example those captured from non-ionizing modalities such as 3D photography (10), may be sufficient to infer skeletal shape with high accuracy. However, despite the intuitive appeal of this hypothesis, it has not been directly tested. Moreover, the value of external surface morphology is only as good as the accuracy of its predictive relationship to internal skeletal shape.

Here we test the hypothesis that variation in the shape of the face and skeleton significantly covary using a retrospective analysis of a CBCT database. These data were originally collected in the course of routine orthodontic assessment and patient care. They are appropriate to use here because both surface and skeletal anatomy were captured simultaneously, which both reduces the error associated with registering different time points and facilitates the accurate comparison of covariation. If variation in surface morphology can be shown to significantly covary with internal skeletal shape variation, it would provide quantitative support for the collection of surface shape, and its use as a proxy for measures of skeletal shape. In contrast, a weak or non-significant relationship, for example due to independent soft-tissue variation, would be problematic for the full utilization of resources in which external facial shape is the only regularly collected measure. To address these alternatives, we use methods collectively known as landmark-based geometric morphometrics (GM) to quantify and test for covariation of shape, and enable the direct visualization of results in three-dimensional objects (11, 12, 13).

MATERIALS AND METHODS

Patient Database

This is a retrospective cross-sectional study utilizing a population composed of skeletally normal patients (i.e., non-surgical) previously assessed for orthodontic therapy at UCSF (N=175, Table 1). To be included in this study, subjects must have had a pre-treatment CBCT scan obtained with their IRB-approved consent (UCSF CHR #10-00564 – JCH, JSL). All scans were generated in a period of time between 9/2010 and 1/2011, and were originally collected for the purpose of cephalometric assessment during the course of standard orthodontic planning and treatment. This study included patients with dental crowding and Angle’s classification of Class I (ANB=−0.9–2.5), tendency for Class II or II/2 (ANB>2.5), or Class III (ANB<−1) that was managed with orthodontic therapy only (see Table 1). Patients were excluded from this study if they had a congenital anomaly or other known syndrome that affects craniofacial growth and development. Demographic information (age, gender) was linked to the CBCT data, with all personal identifiers removed (UCSF CHR #11-06996 – NMY). The dataset was stratified according to age (range = 7.5–57.6 years) and gender. Because growth of the facial skeleton is largely complete by early adulthood (14, 15), all patients >21 years were coded as 21.

Table 1.

	Angle Class (ANB)				Sex (N)
Age	I (−0.9– 2.5)	II (>2.5 )	II/II (>2.5)	III (<−1)	Female	Male	All
7–10	2	5	2	0	3	6	9
10–12	4	15	2	0	8	13	21
12–14	9	26	5	8	30	18	48
14–16	11	15	1	6	19	14	33
16–18	3	10	1	1	10	5	15
18–21	4	4	1	3	9	3	12
21+	10	20	3	4	21	16	37
Total	43	95	15	22	100	75	175
Mean	1.30	5.35	5.77	−3.64
Min	−0.70	2.60	3.40	−9.40
Max	2.50	10.60	9.70	−1.00
SD	0.88	1.87	1.57	2.21

3D Data

(1) Cone Beam Computed Tomography (CBCT): a Hitachi MercuRay CBCT scanner (Hitachi Medico, Tokyo, Japan) was used to generate images. CBCT utilizes a low-energy, fixed-anode tube, which produces a cone-shaped x-ray beam, a special image intensifier, and a solid-state sensor. The face was scanned only once, with a total radiation exposure estimated at ~200 μSv by the manufacturer. Subjects were seated upright as the x-ray tube and image acquisition screen revolved around the patient’s head. Each patient was instructed to hold still, keep their teeth in occlusion, not swallow, maintain their tongue on the roof of the mouth, and their head in a natural position. Scanner settings were 110 kVp and 10 mA, generating a total of 512 slices in a 10-second scan, with a 19×19×19 cm field of view (FOV). Images were reconstructed in CBWorks 2.1 (Cyber Med, Seoul, Korea) and Avia (Hitachi, Tokyo, Japan), and saved in the Digital Imaging and Communications in Medicine (DICOM) format. (2) 3D model reconstruction: For each patient, we reconstructed a 3D model in Amira 5.4 (Visage Imaging) using threshold values that best maximized either bone and tooth signal (e.g., 0±100) or external morphology (e.g., −660±30). (3) 3D landmarks: For each object we applied homologous landmarks (external face (N=9 midline, N=10 bilateral, 29 total), internal facial skeleton and mandible (N=10 midline, N=52 bilateral, 114 total)) in Landmark Editor 3.6 (UC Davis) (Figure S1, Table S1). (4) Measurement Error: Potential sources of measurement error include: (1) thresholding values, altering the reconstructed shape of 3D objects, and (2) location of landmarks, both within and between observers. We assessed these factors by thresholding and landmarking a subset of subjects (N=30) on three separate occasions. Following Starbuck et al. 2011 (16), we calculated mean measurement error as the standard deviations of landmark coordinates, which we considered to be sufficiently low as long as error was smaller than voxel size (i.e., <0.38mm) along the x, y, and z dimensions.

Geometric Morphometrics (GM)

GM describes a mathematical approach to the quantification, statistical multivariate analysis, and visualization of 3D shape variation (17, 18, 19), including the modeling of the effects of covariates (e.g., age, size, etc.) (7). (2) Procrustes Superimposition: Raw coordinate (x, y, z) configurations were aligned to the group centroid, scaled to a common centroid size of one, and rotated to minimize squared-deviation in the software MorphoJ 1.05f (20). Because the purpose of these analyses is to test covariation under the null hypothesis of independence, external and internal datasets were treated as individual blocks in different shape spaces. (3) Asymmetry: Procrustes superimposition was modified to estimate the asymmetric component of shape, which is the deviation from the expectation of perfect right-left symmetry of paired landmarks across midline landmarks.

Statistical Analysis

(1) Partial Least Squares (PLS): To assess whether shape variation significantly covaries between external and internal datasets, we analyzed both Procrustes and asymmetric component data with PLS. PLS examines patterns of covariation between two or more sets of variables. We performed a two-block PLS analysis, a widely used method in GM that is based on the singular value decomposition of the matrix of covariances between two sets of variables, here the face and skeleton. Pairs of new axes are derived as linear combinations of the original variables. As with ordination methods, PLS axes are uncorrelated, with the first pair accounting for the largest amount of inter-block covariation, the second pair for the next largest amount, and so on (21). The amount of covariation between the two blocks of variables is measured by the R_V coefficient, which is a multivariate analogue of the squared correlation (22). Statistical significance was tested via permutation (10,000 replicates) under the null hypothesis of complete independence between the two blocks of variables. (2) Multivariate Regression: To assess the correspondence of changes in shape associated with age/size-related changes for each dataset we performed an independent multivariate regression on both centroid size (the average of the summed distances of each landmark from configuration centroid) and age measured in years. Multivariate regression is a technique for predicting the values of one or more dependent variables from the values of one or more independent variables. To compare similarity of growth between datasets, we modeled internal shape scores as a function of external shape scores using a generalized linear model, and tested these against the null hypothesis of no correlation. Since both measures are estimated with error, we performed regressions using reduced major axis (RMA) and evaluated 95% confidence intervals in the smatr3 package (23) implemented in R 3.0.2 (24).

RESULTS

Shape

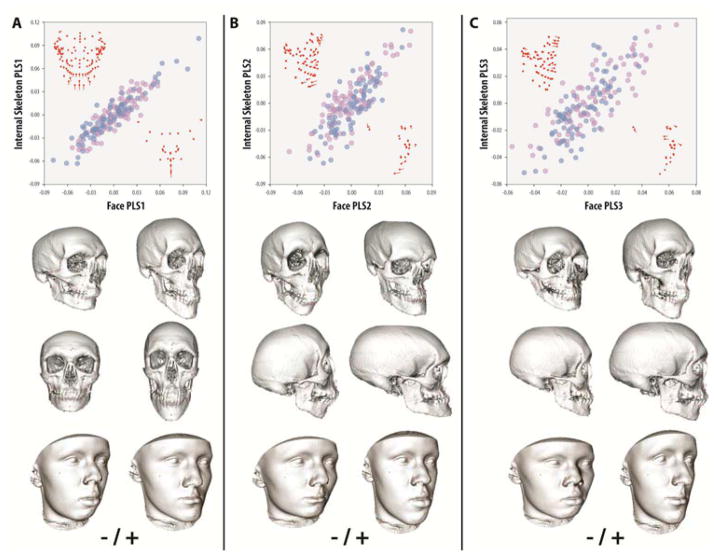
Mean measurement error due to thresholding or landmarking was low relative to voxel size (dimensions: x=0.33mm, y=0.29mm, z=0.34mm). Analysis of internal and external shape covariation indicated a highly significant relationship overall (R_v=0.560, p<0.0001), comparable to previous 2D studies (25), and independent of sex. Individual PLS axes showed a similarly high correlation (Table S2). PLS1-13 accounted for 98.7% of total covariation between datasets and all had singular values with high significance (p<0.0001) and correlations that ranged from 0.92–0.64 (p<0.0001). Based on a scree analysis, it is likely that axes beyond PLS6 (>2% total covariation) are indistinguishable from background or error variation at this sample size. Examination of PLS1-3 demonstrated coordinated shape changes between internal and external datasets (i.e., regional landmark displacements had a similar direction and magnitude), supporting the hypothesis that surface morphology accurately predicts skeletal shape (FIG 1. A–D).

FIGURE 1. Partial Least Squares (PLS) analysis of external surface and internal skeletal shape covariation.

Variation in facial morphology and internal skeletal shape exhibit significant covariation (PLS [Face-Skeleton]: R_v=0.56, p<0.0001; PLS1-13=98.7% covariance, p<0.001). (A) PLS1 (45.7% covariance, r=0.92, p<0.0001) describes depth and anterior projection of the lower jaw, which tracks size and forward location of the mandible as well as location of the zygomatics in the skeleton. (B) PLS2 (25.3% covariance, r=0.83, p<0.0001) describes relative coordination of prognathism of the upper and lower jaw, which in the skeleton is associated with a more convex or concave facial profile. (C) PLS3 (13.1% covariance, p=0.82, p<0.0001) describes location of the eyes as a proportion of the upper jaw plus width of the face, which in the skeleton manifests as orbital location and robusticity of the jaws. Facial and skeletal transformations show shapes associated with the extremes of each PLS applied to a representative cranium or face (note: the shape of the cranial vault is unconstrained by landmarks). Purple = female, blue = male. Red points represent the mean landmark configurations of skeleton and face, lines represent the direction and magnitude of a positive vector displacement along each associated axis.

Asymmetry

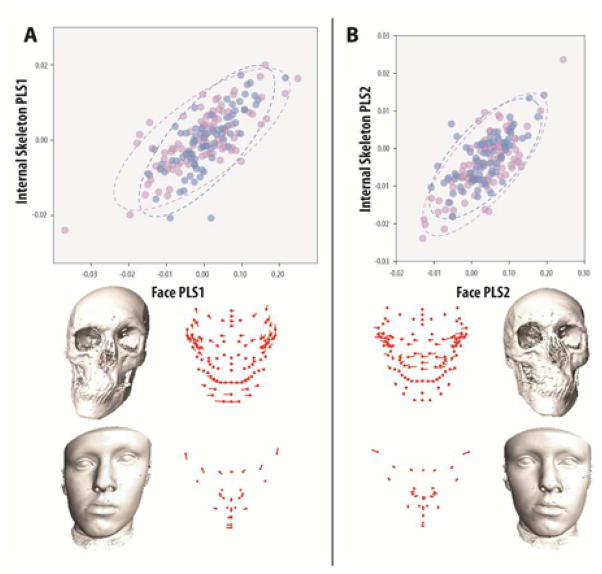
Analysis of internal and external covariation between the asymmetric components likewise indicated a highly significant overall relationship, although not as strong as with shape (R_v=0.340, p<0.0001), and both independent of sex. Individual PLS axes were significantly correlated (p<0.0001) from PLS1-5 (90.2% total covariance), and likely explain the major components of dataset covariation (Table S3). As in the shape based analyses of Procrustes data, these results indicate that asymmetries in the face are correlated with similar underlying skeletal asymmetries, many of which show the same coordinated regional changes in shape. Moreover, because individual PLS axes are independent, it suggests that asymmetries can be subdivided into regionally based etiologies (e.g., mandibular versus maxillary) and identified on the basis of external shape alone (FIG 2. A–C, Supplemental Movies S1–4).

FIGURE 2. Partial Least Squares (PLS) analysis of external surface and internal skeletal asymmetry covariation.

Variation in facial asymmetry and internal skeletal asymmetry exhibit significant covariation (PLS [Face-Skeleton]: R_v=0.34, p<0.0001; PLS1-5=90.2% covariance, p<0.001). (A) PLS1 (52.4% covariance, r=0.73, p<0.0001) describes left-right asymmetries of the anterior lower jaw and height of the eyes, which in the skeleton manifests as a corresponding deviation of the anterior mandible and clockwise-counterclockwise rotation of the orbits, all independent of the upper jaw. (B) PLS2 (24.3% covariance, r=0.73, p<0.0001) describes asymmetry of the mouth and nose, which corresponds to asymmetry in the anterior upper jaw and zygomatics, in this case independent of the lower jaw and orbits. Color coding and landmark descriptions as in Figure 1.

Age/Size-Related Changes in Shape

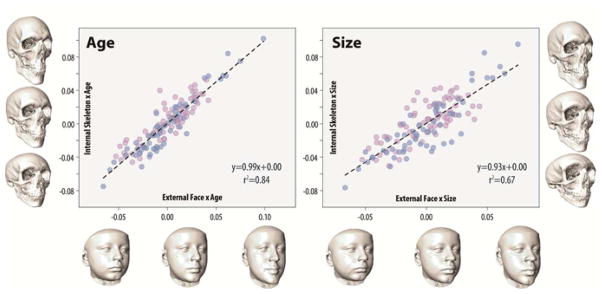
Comparison of individual scores derived from the multivariate regressions of shape on age and size for external and internal morphology indicated a significant (p<0.001) (FIG 3. A–B, Supplemental Movies S5–6). Age-related shape changes in the face explained a greater proportion of skeletal morphology (r²=0.84) than size (r²=0.67). In all cases the variance explained was a small proportion of total shape variance of the dataset (Age x Skeleton = 6.3%, Age x Face = 3.9%, Size x Skeleton = 5.5%, Size x Face = 4.3%).

FIGURE 3. Comparison of external surface and internal skeletal shape covariation associated with population-level age/size related changes.

Size and age-associated shape variation from late childhood to adult (age=7–21+ years) is correlated between internal and external datasets. Internal shape scores from multivariate regressions of shape on age (A) and size (B) predict the majority of variation in external shape scores (84% and 67% total variation, respectively). External faces and internal skeletons reflect shape changes at early, middle and late ages or sizes calculated by applying associated growth vectors to the mean configuration and visualized on a representative face or cranium. Color coding and landmark descriptions as in Figure 1.

DISCUSSION

These results provide quantitative statistical support for the intuitive idea that the shape of the facial skeleton is predictable from external facial morphology. Notably, the variation in shape and asymmetry of external surface morphology significantly covaried with internal skeletal variation. Previous analyses have focused more on how changes in skeletal shape affect external facial morphology, either as a result of surgical or orthodontic manipulations (25, 26, 27), or for forensic reconstruction (28, 29). Our results demonstrate that the external face can also be used as an accurate window into underlying skeletal shape and asymmetry, increasing their clinical value.

Shape variation exhibits the strongest covariation between datasets, extending well into low level PLS axes. This result suggests that not only do the major components of facial shape track internal skeletal variations, such as length, width, height, and prognathism, but also the more subtle aspects of shape that contribute to making each individual’s face recognizably unique. While such a result is encouraging, it is worth noting that the utility of these results is limited by both relatively small sample sizes and averaging across important contributing factors such as sex, ethnicity, or genetic background. Future research that increases the current sample size would likely help to improve the statistical power to associate low level skeletal shape axes with facial shape axes, as would consideration of other levels of population sub-structuring not assessed here.

Variation in asymmetry also significantly co-varied between external and internal datasets, although the association is not as strong as found in the shape comparison. This fact may be due to there being fewer identified independent axes of left-right asymmetry in the skull and mandible, or the fact that there are only two dominant types of asymmetry. As with shape, a larger sample size may help to both distinguish these alternatives and identify potentially less frequent patterns of asymmetry. Regardless, it is notable that even at this level of generalization, asymmetry can be divided into separate anatomical components, one in which the anterior mandible shows significant deviations from symmetry, and one in which the upper jaw does. This independence is consistent with the hypothesis that the etiology of asymmetry depends on the location of growth disruption. For example, upper and lower jaw asymmetries may result from inappropriate or poorly coordinated growth at distinct growth centers. Moreover, because both internal and external datasets identified similar components of asymmetry, analysis of external surface data alone may enable the early identification of individual changes in each of these locations.

Although we cannot address individual trajectories from our population-level data, we found that when estimated in aggregate, age/size-related changes can be identified and are significantly correlated between external and internal datasets. Combined with the general correspondence of shape and asymmetry variation between data types, this result suggests that analyses focused on longitudinal data from individual surface morphology may be able to estimate growth “vectors” corresponding to skeletal growth. Such “individualized” growth vectors would have greater predictive power then the population-level vectors estimated here, but such a hypothesis must be verified directly from longitudinal data.

One caveat is that absolute age was a better predictor of shape than was size. This suggests that size-related changes may be more affected by differences in the amount or location of soft tissue, which may be more variable compared to hard-tissue (e.g., as a result of age-related changes in adults). It is also notable that both age and size explained only a small proportion of total shape variation. A possible reason for this result is that population-level estimates of growth average multiple non-linear growth profiles over individuals, thus averaging across sex and age-specific growth spurts, and linearizing outcomes. Such a deficiency argues in favor of the idea that growth trajectories must be performed on an individual basis to be a predictive tool.

Another potential caveat is that in our study external shape was obtained from CBCT data, whereas quantification of facial shape in clinical settings would likely rely on 3D white light scanners or similar technology (30). There is the possibility that surface data collected at different time points or with other methods may not be as comparable to skeletal measures. However, we argue that this concern is only valid if one were comparing a surface and skeletal measure at different time points, which is not relevant here.

In conclusion, this study demonstrates that variation in 3D surface morphology has a significant predictive relationship with variation in underlying skeletal shape, size, and asymmetry. This result is significant because 3D surface scans can be performed repeatedly without harm to patients, and thus has the potential to fill in critical information about individualized growth in pediatric patients for which repeated CBCT is unacceptable. 3D surface scanners are increasingly accurate and inexpensive, with full facial images obtainable and reconstructed in a few minutes for each patient, with accuracy comparable to the CBCT data used here (10, 32). With these benefits in mind, we argue that in the short term, 3D surface morphology should become an integral part of a patient’s medical record. In the long term, the combination of larger databases that also include familial phenotypes (e.g., parents, siblings) and genomic information may ultimately help to build models that fulfill longstanding goals of predictive dental medicine (e.g., 6, 7, 17, 30)

Highlights.

• We test the relationship between variation in external facial surface morphology and internal skeletal shape in a mixed-age human population

• The face predicts variation in shape, asymmetry, and associated growth parameters of the underlying skeleton

• We speculate that standardized collection of facial surface morphology will contribute to generating accurate predictive models