Maintaining ocular safety with light exposure, focusing on devices for optogenetic stimulation

Abstract

Optogenetics methods are rapidly being developed as therapeutic tools for treating neurological diseases, in particular, retinal degenerative diseases. A critical component of the development is testing the safety of the light stimulation used to activate the optogenetic proteins. While the stimulation needs to be sufficient to produce neural responses in the targeted retinal cell class, it also needs to be below photochemical and photothermal limits known to cause ocular damage. The maximal permissible exposure is determined by a variety of factors, including wavelength, exposure duration, visual angle, pupil size, pulse width, pulse pattern, and repetition frequency. In this paper, we develop utilities to systematically and efficiently assess the contributions of these parameters in relation to the limits, following directly from the 2014 American National Standards Institute (ANSI). We also provide an array of stimulus protocols that fall within the bounds of both safety and effectiveness. Additional verification of safety is provided with a case study in rats using one of these protocols.

1. Introduction

Optogenetics offers a powerful new approach for controlling neural activity. It has numerous applications in both basic and clinical science. For basic science, it provides a method for teasing apart circuit operations, since it allows circuit components to be turned on or off with very high spatial (single cell) and temporal (millisecond) resolution. For clinical applications, it opens the door to new kinds of selective treatments, because it provides a way to activate or inactivate specific components in a damaged or malfunctioning circuit and re-engage them into normal activity (Gradinaru et al., 2009; Nirenberg & Pandarinath, 2012; Paz et al., 2013).

A major clinical goal is the development of a treatment for retinal degenerative diseases, which affect 20–25 million people worldwide (Chopdar, Chakravarthy, & Verma, 2003; Gordois, Pezzullo, & Cutler, 2010; Resnikoff et al., 2008). These diseases trigger a degeneration of the retina’s light-sensing cells (the photoreceptors) which leads to partial or total blindness. Though the photoreceptors degenerate, several of the other retinal cell classes, most significantly, the retina’s output cells (the ganglion cells), remain largely intact. The optogenetic strategy makes use of this. It bypasses the damaged photoreceptors and provides direct stimulation to surviving cells, driving them to send visual signals to the brain.

A key consideration for using optogenetics to treat retinal degenerative diseases is safety: determining the range of stimulation parameters that can be used to effectively drive the optogenetic proteins without damaging the eye. This is a critical issue because the field of optogenetic therapeutics is rapidly evolving.

For example, in the last few years, several new optogenetic proteins, both channelrhodopsins (ChR) and halorhodopsins (HR), have been identified or developed (Govorunova et al., 2011; Govorunova et al., 2013; Klapoetke et al., 2014; Kleinlogel et al., 2011; Lin et al., 2013; Mattis et al., 2011; Yizhar et al., 2011; Zhang et al., 2007, 2008), and many of them differ in their spectral sensitivities, conductances and kinetics. As a result, they require different stimulation parameters, including excitation wavelengths, pulse intensities, and pulse durations.

Along the same lines, new gene delivery systems have also been developed, and this, too, triggers the need for adjustments to stimulus parameters. For example, adeno-associated viral (AAV) vectors, which are the likely vectors for transferring these genes to the retina, since they have already been used successfully in other ocular gene therapies (Cideciyan et al., 2009; MacLaren et al., 2014; Maguire et al., 2008), are limited by the amount of DNA they can carry: this constrains the size of the regulatory sequences that can be used to control ChR or HR gene expression. Since there is a relationship between the amount of ChR and HR protein expressed and the intensity of the light needed to drive a cell to firing threshold, stimulus intensities for a given protein will likely need to be shifted upward, as compared to the intensities that have been effective in transgenic animals, where the complete regulatory sequence can be used. Moreover, it is not possible to predict expression levels in humans with retinal degenerative diseases, since there are no, or very limited, non-human primate models for these conditions. Thus, flexibility in stimulus parameters is, again, critical (e.g., if the expression in a given patient is low, then information concerning the extent to which stimulus intensity, pulse duration, etc., can be increased without exceeding exposure limits, given the patient’s pupil size and the visual angle of the stimulus, becomes truly essential).

Lastly, new neural coding methods have been developed for activating optogenetic proteins to trigger natural neural responses (Nirenberg & Pandarinath, 2012); this, too, alters stimulus parameters that pertain to safety. For example, Nirenberg and Pandarinath developed a device that produces normally-patterned neural responses in ChR-expressing retinal ganglion cells. Briefly, it consists of a camera, an encoder, and a stimulator. The camera takes images in. The encoder converts the images into patterns of electrical pulses, analogous to the patterns of action potentials that would be produced by the normal retina in response to the images. Finally, the electrical pulses are then converted into light pulses to drive ChR in the ganglion cells. The result, shown in mice, is that the ganglion cells produce firing patterns that are very close to the patterns produced by the normal retina, even to complex natural scenes (Nirenberg & Pandarinath, 2012). This method has the potential to significantly improve vision restoration, but, as with other optogentic treatments, the safety of the light delivered needs to be assured before the method can be brought to patients. It is worth noting, though, that the neural coding strategy is able to use less light that other optogenetic treatments (Bi et al., 2006; Doroudch et al., 2011; Lagali et al., 2008) because the amount of time the light is on is determined by neuronal firing patterns: i.e., since neuronal firing is sparse (Olshausen & Field, 2004; Simoncelli & Olshausen, 2001) - cells typically fire only 5–10% of the time (Berry, Warland, & Meister, 1997; Pitkow & Meister, 2012) - this means that stimulation time is also low. However, on occasion, neuronal firing can include bursts of action potentials, and the safety of reproducing these bursts optogenetically needs to be checked.

In sum, there have been, and continue to be, numerous developments in the field of optogenetics for treating eye diseases. The developments have focused largely on improving efficacy - on finding the right combination of factors (ChR/HR genes, delivery systems, promoter/enhancer sequences, and stimulation patterns) that produce reliable neural responses - but ensuring safety is also a critical issue. Because of the potential for eye damage with different stimulus protocols, and, because of the nonlinear interactions among the stimulus parameters as well as the nonlinear interactions in the mechanisms that produce eye damage (photothermal and photochemical), an accessible study of the range of permissible protocols for optogenetic stimulation is needed. Here we provide this based on the 2014 ANSI standards (ANSI, 2014) and building on Delori et al.’s (Delori, Webb, & Sliney, 2007) seminal work in this area. We also provide software to assess exposure limits, given a set of conditions (e.g., pulse width, pulse duration, pulse patterns, wavelength, visual angle, pupil size, etc.). The paper proceeds through, in a step-by step manner, the rationale for all calculations to allow those working in optogenetics to readily utilize the work performed in the Standards to bring safe and effective optogenetic treatments to patients.

The paper is organized as follows: we start, in Section 2, with the exposure limits for single pulse stimulation, as all calculations build from this. Section 3 provides exposure limits for repetitive pulses; this section also includes the formula for our computer implementation, which is provided in Appendix I. Section 4 shows how the implementation is modified to account for cases in which eye and head movements and pupil constriction are reduced. The ANSI Standards assume eye and head movements, a protection that may not necessarily apply to optogenetic therapies, and this section provides the ability to assess exposure limits with and without them. This section also includes a description of a new “interim precaution” that has been added to the Standard for exposures that occur within a 48 h window. Section 5 provides the conversion from corneal exposure limits to retinal irradiances; this is necessary to allow translation between the ANSI Standards, which provide information on safety and are expressed in terms of corneal exposure, and the optogenetic literature, which provides information on efficacy, and typically reports numbers in terms of retinal irradiance. At the end of Section 5, we provide a summary figure that lays out all the relationships among the parameters and the limits discussed in Sections 2–5.

In Section 6, we calculate the safety of an array of stimulus protocols, focusing on parameters most likely to be used in a clinical trial, and we provide a series of tables with the results. We emphasize, though, that the computer implementation attached to this paper explores a much larger range; our aim in the tables was just to provide immediately accessible data on the most likely parameter values. In addition, since the method of light delivery may vary from clinic to clinic, we focus on parameters that can be measured with standard equipment, such as a light meter, at the level of the cornea and thus are independent of the method of light delivery. Briefly, for wavelength, we used 505 nm, as this corresponds to the peak excitation wavelength, or close to it, for several channelrhodopsins with clinical potential (Klapoetke et al., 2014; Kleinlogel et al., 2011). For visual angle, we explored both 10 and 20 degrees, as current AAV vectors deliver the gene largely to central retina. For pupil size, we followed the assumptions of the Standard: for short exposure times (shorter than pupil reflex duration), we used a size of 0.7 cm in diameter; for longer exposures, we used 0.31 cm in diameter; we also include in the Discussion a strategy for conditions of abnormal pupillary response. For total stimulating time, we used the maximum given in the Standard: 8.3 h. For pulse width and pulse pattern, we explored a range: widths ranged from 1.4 to 5.6 ms, chosen to bracket the time needed to produce individual action potentials in ganglion cells, allowing neurally-coded stimulation methods (Nirenberg & Pandarinath, 2012) to be used; patterns included periodic (6–50 Hz) and neurally-coded (e.g., neurally-coded drifting gratings and natural scenes), as these are relevant for recreating normal retinal responses (Nirenberg & Pandarinath, 2012).

What the tables show are the peak light intensities that can be used for each condition without exceeding the ANSI recommendations. Importantly, what the results show is that there exist protocols that are both in the effective range for optogenetic stimulation and also fall below ANSI exposure limits. We emphasize again that the tables just provide examples, focusing on clinically relevant parameters: the computer implementation allows a much broader range to be explored.

Finally, as further confirmation of safety, we show in Section 6.2 a test case we performed with one of these protocols on animals (rats). We used an intensity level that exceeds the maximum likely to be needed for optogenetic therapies (see Klapoetke et al., 2014; Kleinlogel et al., 2011), and treated the animals in sessions over a period of weeks (12 2.5 h sessions over 6 weeks), a regimen likely to be employed in clinical trails. According to the implementation, the intensity used was 5 times lower than the ANSI recommended exposure limit. Consistent with this, no damage to photoreceptors, as measured via outer nuclear layer cell counts, was observed (Fig. 3).

Fig. 3.

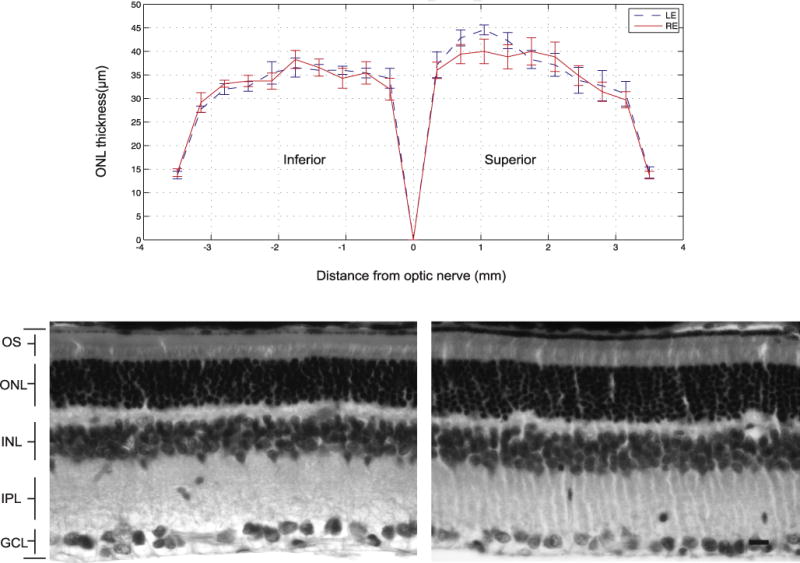
No loss of photoreceptors was observed following 6 weeks of treatment. Top: the thickness of the outer nuclear layer (ONL) of untreated eyes (left eye, LE) and treated eyes (right eye, RE). Values are mean ± SEM (n = 7). The mean ONL thickness across the retina was analyzed at equal intervals from the optic nerve; at each interval, the number of cells was counted and then multiplied by 4 μm (mean ONL cell diameter) to obtain a measure of ONL thickness. Statistical significance was determined using the Student’s t-test. Bottom left: retinal cross-section from an untreated eye. Bottom right: retinal cross-section from a treated eye. Scale bar = 10 μm.

2. Single pulse exposure limit

We now begin the description of the Standard’s limits in the context of optogenetic therapies. We first mention how the Standard refers to the limits. It typically includes a factor of 10 safety margin, that is, a limit that is 10 times lower than what is referred to as the “damage threshold”. The damage threshold is described as the exposure at which there is a 50% probability of a minimum visible lesion. The factor of 10 safety margin cannot be thought of absolute, as shown by Sliney et al. (2002). For example, the factor can be smaller than 10 if the slope of the probability-of-damage curve is steep. Sliney et al. (2002), discusses other potential factors as well. We mention this so that the numbers here are interpreted correctly and safely.

Next, we briefly describe the units used in this section: In the Standard, for visible light (400 nm ≤ λ < 700 nm), retinal irradiances or retinal radiant energies causing threshold damage are converted into “maximum permissible exposure” at the corneal plane, denoted by MPE and expressed in units of W/cm², J/cm², W cm⁻² sr⁻¹, or J cmr⁻² sr⁻¹. In this section, unless otherwise mentioned, we express the limits at the corneal plane as “maximum permissible radiant exposure”, denoted MPH_c, where H is the radiant exposure, and c is the corneal plane, and use units of J/cm². MPE is reserved to denote permissible irradiance in later sections.

With respect to the sources of retinal damage, the Standard focuses primarily on two: thermal (which includes both temperature and thermoacoustic damage) and photochemical. The Standard gives two MPH_c limits, one for each. Together the two limits (thermal and photochemical) are referred to as the “dual limit”. The photochemical limit is only relevant for exposures greater than 0.7 s and for wavelengths between 400 nm and 600 nm. When exposures are in this range, both limits need to be calculated, and the smaller of the two is used. When exposures are out of this range, thermal limits can be depended upon to be sufficient, as indicated by the Standard.

2.1. Thermal

2.1.1. Maximum permissible corneal radiant exposure

As mentioned above, thermal related mechanisms include both temperature-induced and thermoacoustic processes (Delori et al., 2007): the former refers to protein denaturation from temperature increases that result from light absorption by melanin in the retinal pigment epithelium (RPE); the latter refers to nonlinear effects that lead to damage when pulses are shorter than ~1 ns (Rockwell et al., 1999).

Table 1 lists the thermal limits in terms of the MPH_c for wavelengths from 400 nm to 700 nm and different exposure durations. This table was taken from the corresponding thermal limitsin ANSI (2014) Table 5e. The only difference is that the limits for exposure duration T₂ ≤ t < 3 × 10⁴ (expressed in W/cm² in the Standard) are converted, for convenience, to J/cm², by explicitly including the exposure time t as a multiplier. The parameters used in Table 1, C_E, t_min, and T₂, are described in the next section.

Table 1. MPH_c.

for thermal limits (combined temperature-induced and thermoacoustic) for 400 nm ≤ λ < 700 nm.

Exposure duration t (s)	MPHc (J/cm2)
10−13 ≤ t < 10−11	1.0 × 10−7CE
10−11 ≤ t < tmin	2.0 × 10−7CE
tmin ≤ t < T2	1.8 × 10−3CEt0.75
T2 ≤ t ≤ 3 × 104	1.8 × 10−3CET2−0.25t

Table 5. MPH_c.

for photochemical limits for 400 nm ≤ λ < 600 nm.

Exposure duration t (s)	MPHc (J/cm2)
	α ≤ 11 mrad	α > 11 mrad
0.7 ≤ t < 100	1 × 10−2CB	7.85 × 10−5CBmax(α,γ)2
100 ≤ t < 104	1 × 10−4CBt
104 ≤ t ≤ 3 × 104		7.85 × 10−9CBmax(α,γ)2t

2.1.2. Parameters

2.1.2.1. Parameter C_E, α_min, and α_max

The parameter C_E allows limits for extended sources to be obtained from the limits for point sources. For point sources (in the ANSI standard, a source smaller than 1.5 mrad, or about 5 arc-min), C_E = 1; for extended sources, which is the range relevant for optogenetic applications (e.g., 10 degrees of visual angle = 175 mrad), C_E > 1. With respect to the source’s shape, the ANSI covers both circular and non-circular. Table 2 provides the C_E just for the circular case, again, as this is the most relevant for optogenetic studies (e.g., a light source with a circular aperture).

Table 2.

Parameter C_E for circular sources, where α_min = 1.5 mrad, and α_max is given in Table 3 below.

Visual angle α (mrad)	CE
α < αmin	1
αmin ≤ α < αmax	α/αmin
αmax ≤ α	α2/(αminαmax)

The dependence of C_E on visual angle is shown in Table 2. There are two parameters involved. The first is the minimal visual angle, α_min, which is 1.5 mrad (as mentioned above, a source is considered a point source if it subtends an angle less than 1.5 mrad). The second parameter is α_max; as shown in Table 3, α_max is dependent on exposure duration. Both α_min and α_max are given in ANSI (2014) Table 6b.

Table 3.

Parameter α_max.

Exposure duration t (s)	αmax (mrad)
t < 625 × 10−6	5
625 × 10−6 ≤ t < 0.25	200 t0.5
0.25 ≤ t	100

Table 6.

Parameter γ.

Exposure duration t (s)	γ (mrad)
0.7 ≤ t < 100	11
100 ≤ t < 104	1.1 × t0.5
104 ≤ t ≤ 3 × 104	110

2.1.2.2. Parameters t_min and T₂

The parameter t_min reflects the effects of heat dissipation. It specifies a duration during which heat flow away from the irradiated tissue is small enough to be neglected. Thus, for t < t_min, the energy needed to produce retinal damage is not dependent on exposure duration. For t > t_min, heat can dissipate out of the irradiated area, and the energy needed to produce retinal damage increases accordingly; specifically, MPH_c increases as t⁰⁷⁵. Note that t_min has a wavelength dependence, as discussed in the Standard, but in the range of visible light, the value is fixed (t_min = 5 × 10⁻⁶ s).

For exposures longer than T₂ (T₂ in the range of 10–100 s), the Standard assumes that eye and head movements will spread the beam over larger areas of the retina. As a result, when t > T₂, the limit is higher, specifically, MPH_c increases as t instead of t⁰.⁷⁵ (shown in Table 1). Note that the parameter T₂ is dependent on visual angle α and is given in Table 4.

Table 4.

Parameter T₂, where α_min = 1.5 mrad.

Visual Angle α (mrad)	T2 (s)
α < αmin	10
αmin ≤ α ≤ 100	10(1+(α−1.5)/98.5)
100 < α	100

2.2. Photochemical

2.2.1. Maximum permissible corneal radiant exposure

Photochemical damage is thought to be the result of a photooxidative insult to the photoreceptors and to lipofuscin pigments in the RPE (Ham & Mueller, 1989; Stuck, 1998), which occur at short visible wavelengths (400 nm ≤ λ < 600 nm) and for exposure durations longer than 0.7 s.

The photochemical MPH_c in Table 5 was taken from ANSI (2014) Table 5e. Note, though, that the limits are expressed in one form, corneal radiant exposure, H_c in our table, while in the ANSI, they are expressed in multiple forms (e.g., the limits for α ≤ 11 mrad are expressed as radiant exposure for durations 0.7 ≤ t < 100 s, and as irradiance for durations 100 s ≤ t < 3 × 10⁴ s; for α >11 mrad, the limits are expressed as integrated radiance for. durations 0.7 s ≤ t < 10⁴ s and as radiance for durations 10⁴ s ≤ t < 3 × 10⁴ s). In this paper, we first convert irradiance (W/cm²) to radiant exposure (J/cm²), and convert radiance (W cm⁻² sr⁻¹) to integrated radiance (J cm⁻² sr⁻¹) by explicitly including the exposure time t as a multiplier. Then, we convert integrated radiance L_s into radiant exposure H_c using equation H_c ≈ (π/4)L_sα² (L_s is assumed to be constant over a solid angle of πα²/4). Another difference is that we express the limits in terms of the limiting cone angle γ, which is defined in a footnote of ANSI (2014) Table 5e.

2.2.2. Parameters

2.2.2.1. Parameters γ and C_B

Two parameters, γ and C_B, set the photochemical MPH_c. γ is the limiting cone angle, and C_B is a wavelength-dependent correction factor. Table 6 provides the Standard’s values for γ: the minimum γ is 11 mrad for an exposure duration from 0.7 s to 100 s, and then γ increases gradually to 110 mrad for an exposure longer than 10⁴ s. As with the thermal limits, the Standard assumes eye and head movements: longer exposures produce greater movements, which means the exposure is spread over a larger area. γ is the parameter that takes this into account. When calculating the photochemical limits, then, the subtended angle of the source α should be compared with γ, and the larger of the two should be used to calculate the limit.

As shown in Table 7, C_B is dependent on wavelength in a way that mimics the inverse of the action spectrum of photochemical damage (the spectrum shows increasing damage with shorter wavelengths - Ham’s action spectrum (Ham & Mueller, 1989).

Table 7.

Parameters C_B.

Wavelength λ (nm)	CB
400 ≤ λ < 450	1
450 ≤ λ < 600	100.020(λ−450)

3. Repetitive pulses exposure limit

In addition to the limits for single pulses, the Standard also addresses the limits for repetitive pulses in a train, which can include pulses of different widths as well as different inter-pulse intervals.

Note that the exposure limit for a pulse of duration t in a train can be different from the exposure limit of the same pulse when it is alone. To avoid confusion, we use MPH_c[t] to denote the limit for a single pulse alone, and MPH_c,tr[t] to denote the limit for a pulse in a train.

3.1. Three rules for general repetitive pulses

The Standard applies three rules that define three separate exposure limits; safety requires that all are followed. To determine the applicable exposure limits for repetitive pulses in a train, we need to know the duration t of a single pulse in the train, the duration T over which a group of pulses occurs in the train (see Rule 2 below), and the duration of the complete exposure T_max, i.e., the duration of the complete train.

Rule 1. Single-pulse limit

Given a train of pulses, the exposure from any individual pulse must be below the thermal MPH_c for a single pulse with that pulse’s duration. This provides protection against thermal injury from any single pulse in the train.

Rule 2. Average-power limit

Given a train of pulses, the exposure from any subgroup of pulses, must not exceed the MPH_c of a single pulse whose duration equals T, where T is the duration of the subgroup. This rule protects against thermal injury from heat buildup and cumulative injury from the mechanisms that underlie photochemical damage.

Rule 3. Repetitive-pulse limit

The exposure of any single pulse within a group of pulses must not exceed the single-pulse thermal MPH_c multiplied by a multiple-pulse correction factor C_p. In addition, this rule specifies that the pulses in the group must be separated by at least t_min. This rule protects against thermal injury from cumulative effects of sub-threshold pulses.

The Standard provides some information about applying Rule 3. Basically, it specifies that pulses delivered in a short period of time (<t_min) should be merged into a single pulse. After the merging, the total number of pulses in the train may, therefore, be reduced. For each remaining pulse, the exposure must not exceed the MPH_c of that pulse multiplied by a multiple-pulse correction factor C_p.

This correction factor C_p, is shown in Table 8. It is equal to 1.0 unless the following conditions are met: 5 mrad < α ≤ 100 mrad; 400 nm ≤ λ < 1400 nm; and t > t_min. If C_P has to be calculated, the Standard provides information for doing so. Two scenarios are considered: (a) when the duration of the pulse train is short (i.e., when T ≤ T₂); in this case, C_P depends on the total number of pulses in the train, and (b) when the duration of the pulse train is long, i.e., when T > T₂; in this case, a window of length T₂ is placed around the pulse being considered and slid systematically to find the position that contains the largest number of pulses. The number of pulses in this region of length T₂ is then used to calculate C_P. This ensures the most conservative C_P. Note that C_P has to be calculated for each pulse individually.

Table 8.

Parameter C_p. for t > t_min, 5 mrad < α ≤ 100 mrad, and 400 nm ≤ λ < 1400 nm (if these conditions are not met, then, C_p = 1.0).

Visual angle α (mrad)	Cp
	n ≤ 40	40 < n ≤ 625	625 < n
5 < α ≤ αmax	n−0.25	0.4
αmax < α ≤ 100	n−0.25		0.2

3.2. Three rules for evenly spaced identical pulses

While the three rules are general, the examples in the ANSI focus on a single case: evenly spaced identical pulses. Here we go through this case and also expand to others that will likely be used in optogenetic treatments (i.e., patterned stimuli).

We start with the simple case: given a total duration T_max, an evenly spaced identical pulse train is described by its pulse frequency F, the number of identical pulses N, and the duration of each pulse t. For such a pulse train, the calculations of the three rules can be significantly simplified. Since all the pulses are identical, the limits are conveniently expressed as the maximum permissible corneal radiant exposure per pulse. We introduce new notation to keep it simple: MPH_c,tr1[t], MPH_c,tr2[t], and MPH_c,tr3[t] to denote the exposure limits yielded by the three rules, respectively.

3.2.1. Calculation of single-pulse limit (Rule 1)

In general, for a train of uneven pulses, the first rule tests the safety of the pulse with the greatest energy. In the case of evenly-spaced identical pulses, the first rule just reduces to the single pulse case:

$$MP{H}_{c,tr1}[t]=MP{H}_c[t].$$ (1)

Only the thermal limit needs to be tested.

3.2.2. Calculation of average-power limit (Rule 2)

Now we evaluate Rule 2. Given a pulse train of duration T_max, the exposure from any subgroup of pulses in the train delivered in time interval T, where T ≤ T_max, cannot exceed the MPH_c for a single pulse of duration T; thus, none of the individual pulses can exceed (1/n) MPH_c[T]. The MPH_ctr2[t] from Rule 2 is defined as the minimum corneal radiant exposure per pulse over all possible subgroups delivered in any interval T:

$${\mathit{MPH}}_{c,\mathit{tr}2}[t]={\min }_T(\frac{{\mathit{MPH}}_c[T]}{n(T)}).$$ (2)

For evenly spaced identical pulses, the number of pulses in a pulse train is proportional to the duration of the train, that is, n (T) = FT, where F is the pulse frequency. In this case, we have the following relationship

$$\begin{array}{l}{\min }_T\left(\frac{{\mathit{MPH}}_c[T]}{n(T)}\right)={\min }_T\left(\frac{1}{F}\frac{{\mathit{MPH}}_c[T]}{T}\right)=\frac{1}{F}\frac{{\mathit{MPH}}_c\left[T_{\mathit{max}}\right]}{T_{\mathit{max}}}\\ =\frac{{\mathit{MPH}}_c\left[T_{\max }\right]}{N},\end{array}$$ (3)

where the second equality holds because MPH_c[T]/T, is a non-increasing function of T for both thermal and photochemical limits. Therefore, in the case of evenly spaced identical pulses, the maximum permissible corneal radiant exposure per pulse from Rule 2, MPH_c,tr2[t], is always limited by the limit that applies for the total duration T_max

$${\mathit{MPH}}_{c,\mathit{tr}2}[t]=\frac{{\mathit{MPH}}_c[T_{\mathit{max}}]}{N}.$$ (4)

Among the three rules, Rule 2 is the only case where the dual limit (thermal and photochemical) applies.

3.2.3. Calculation of repetitive-pulse limit (Rule 3)

To evaluate Rule 3 for evenly-spaced identical pulses, we define a critical pulse frequency, F_cr = 1/t_min, which equals 200 kHz in the visible range (t_min = 5 × 10⁻⁶ s, for 400 nm ≤ λ < 700 nm). The problem is then divided into two cases: when F ≥ F_cr, and when F < F_cr. When F ≥ F_cr, there are no inter-pulse spaces > t_min. In this case, Rule 3 does not need to be applied; Rule 2 provides the lower limit.

The relevant regime for Rule 3 is therefore when F < F_cr. Here, the inter-pulse spaces are longer, i.e., there are no pulse pairs delivered in t_min or less. So MPH_c,tr3[t] is given by C_pMPH_c[t], where C_p is a multiple-pulse correction factor, dependent on n, as summarized in Table 8. Determination of n in turn breaks down into two cases. For exposure durations ≤ T₂, n is the total number of pulses delivered. For exposure durations > T₂, only those pulses contained within a time equal to T₂ are considered. Therefore, the duration used to determine n is min(T_max,T₂), and n = F × min(T_max,T₂). As a result, MPH_c,tr3[t], can be expressed as

$${\mathit{MPH}}_{c,\mathit{tr}3}[t]=C_p(F\times \min (T_{\max }{T}_2)){\mathit{MPH}}_c[t].$$ (5)

Only the thermal limit needs to be tested for Rule 3.

3.2.4. The lowest limit yielded by three rules

In sum, for evenly-spaced identical pulses, the maximum permissible corneal radiant exposure per pulse MPH_c,tr[t] is the lowest maximum permissible corneal radiant exposure per pulse yielded by the three rules

$$MP{H}_{c,tr}[t]=\mathit{min}(MP{H}_{c,tr1}[t],MP{H}_{c,tr2}[t],MP{H}_{c,tr3}{[t]}^{\ast }),$$ (6)

where the limits for the three rules are given by Eqs. (1), (4), and (5), and * denotes that MPH_ctr3[t] only needs to be calculated when F < F_cr.

In addition to MPH_ctr[t], the limit can also be expressed in terms of the maximum permissible peak irradiance of the pulse MPE_c,tr, which is defined by

$${\mathit{MPE}}_{c,\mathit{tr}}=\frac{{\mathit{MPH}}_{c,\mathit{tr}}[t]}{t},$$ (7)

where t is the width of the pulses.

3.3. Three rules for non-evenly spaced unequal pulse

For many optogenetic applications, the pulses delivered will be non-evenly spaced (e.g., patterned stimuli). In this section, we describe our implementation for non-evenly spaced unequal pulses, where “unequal” refers to pulse width.

For pulses with unequal widths but the same amplitude, the radiant exposures are proportional to pulse width. Note that since pulse amplitude is the same, the peak irradiance of the pulses is the same, but the radiant exposures are different because of the differences in pulse width. Therefore, instead of expressing the limits yielded by the three rules in terms of radiant exposure per pulse, we can express them in terms of peak irradiance, i.e., MPE_c,tr, as defined in Eq. (7).

In this paper, given a pulse train with N non-evenly spaced pulses with different pulse durations, we describe each pulse by its starting time tStart(i) and its width tWid(i), where i = 1, 2,…, N is the pulse index. The ending time is given by tEnd(i) = tStart (i) + tWid(i).

3.3.1. Calculation of single-pulse limit (Rule 1)

The first rule tests the safety of the brightest pulse (pulse with the largest energy) in a train of pulses. Since all the pulses have the same amplitude, the brightest pulse is the one with the longest duration. The implementation of the first rule is straightforward. Assuming the longest duration is t_max, the MPH_c for the brightest pulse is MPH_c[t_max], and the corresponding MPE_c,tr1 is MPH_c[t_max]/t_max. Again, only the thermal limit needs to be tested for the first rule.

3.3.2. Calculation of average-power limit (Rule 2)

Given a pulse train of duration T_max, the corneal exposure from any subgroup of pulses in the train delivered in time interval T cannot exceed the maximum permissible corneal exposure calculated for a single pulse of duration T, which is MPH_c[T]. In other words, the total corneal radiant exposure of pulses within any interval T should be limited by MPH_c[T].

For evenly spaced identical pulses (identical in both amplitude and width), the maximum permissible corneal radiant exposures from Rule 2 can always be determined by just knowing the total duration T_max. The situation becomes challenging when the pulses are non-evenly spaced, because MPH_c[T] and MPH_c[T]/n are determined by different features in the pulse train. For example, since MPH_c[T] may decrease as T gets smaller, the lowest value of MPH_c[T] may be determined by a brief burst of pulses that are unusually closely spaced. However, MPH_c[T]/n, may be limited by another subgroup of pulses, one that has a longer T and a larger n.

In general, for non-evenly spaced pulses, there is no way to find the subgroup that yields the lowest limit unless the limits from all possible subgroups are calculated. In our implementation the limits from all the subgroups are calculated in a bottom-up way (from subgroups, composed of two consecutive pulses up to the subgroup composed of all the pulses in the train). Given a subgroup of n consecutive pulses (i = k, k + 1,…, k + n − 1), the duration of the subgroup is chosen as the minimum duration enclosing all the pulses in the subgroup, which is the ending time of the last pulse minus the starting time of the first pulse T_min = tEnd(k + n − 1) − tStart(k). Note that the choice of minimum duration T_min is guaranteed to generate the lowest limit for the subgroup (i.e., the most conservative). This is because, for any duration T larger than T_min (meaning a duration T that would cover some inter-pulse space before/after the subgroup), MPH_c[T] is PMPH_c[T_min]. This occurs because MPH_c[T] is a non-decreasing function of T.

The maximum permissible peak corneal irradiance for the subgroup is MPH_c[T_min] divided by the sum of pulse widths of all the pulses in the subgroup. This calculation is then repeated for all values of n, the number of consecutive pulses in a subgroup. The maximum permissible peak corneal irradiance from Rule 2, MPE_ctr2, is the lowest value yielded from all subgroups (i.e., all values of n).

3.3.3. Calculation of repetitive-pulse limit (Rule 3)

The third rule protects against sub-threshold pulse cumulative injury and applies only to the thermal limits. As mentioned previously, when applying this rule, some preprocessing has to be done: given a train of N pulses, all pulses delivered in less than t_min are merged into a single pulse. In our implementation, all the pulses in a train are processed sequentially. For each pulse, we check if there are additional pulses delivered in less than t_min. If so, all those pulses will be merged into one single pulse of the same amplitude, and the width of the merged pulse equals the sum of the widths of those pulses. After the merging, the preprocessing will continue from the next pulse in the train that has not been merged. After the preprocessing, the pulses are separated by at least t_min (the difference between the starting times of consecutive pulses is at least t_min)

According to Rule 3, the exposure of any single pulse within a group of pulses must not exceed the single-pulse MPH_c multiplied by C_p; here C_p is calculated using the number of pulses in the group. Since C_p is a non-increasing function of the number of pulses, as shown in Table 8, for any single pulse, the safety limit can always be determined from the maximum duration of the train T_max (which contains the total number of pulses in the train). However, there is a limit on the exposure duration. According to the Standard, when applying Rule 3, for exposure durations exceeding T₂, only those pulses contained within a time equal to T₂ are considered.

Therefore, in the implementation, we go through all the pulses in the preprocessed train. For each pulse, we search all possible windows of length T₂ around the pulse to find the window that has the maximum number of pulses n_max, and then use that number to calculate C_P, as described in Section 3.1. The maximum permissible peak corneal irradiance for that pulse is obtained by dividing the maximum permissible corneal radiant exposure of the pulse by the pulse width, that is, dividing C_p(n_max)MPH_c[t] by t. The maximum permissible peak corneal irradiance from Rule 3, MPE_c,tr3, is the lowest value yielded from all the pulses in the train.

3.3.4. The lowest limit yielded by three rules

In sum, for non-evenly spaced pulses with unequal widths but the same amplitude, the maximum permissible corneal peak irradiance MPE_c,tr is the lowest value yielded by the three rules

$${\mathit{MPE}}_{c,\mathit{tr}}=\min ({\mathit{MPE}}_{c,\mathit{tr}1},{\mathit{MPE}}_{c,\mathit{tr}2},{\mathit{MPE}}_{c,\mathit{tr}3}).$$ (8)

4. Eye movements, head movements, pupil dilation, and the added luminance dose restrictions in Section 8.3 of the new ANSI (2014)

In this section, we consider what the Standard refers to as the “special considerations” for ocular exposures; they include eye and head movements, pupil dilation, and the added luminance dose restrictions in Section 8.3 of 2014 ANSI. The protective effects of eye movements, head movements, and pupil responses may be reduced in optogenetic treatments, where a patient is expected to look toward the stimulation. In this section, we modify the implementation to assess the effects of eliminating this extra protection. Note that this is a conservative approach, since typically the altered viewing conditions only result in a reduction, not a complete elimination, of eye or head movements.

4.1. Eye And Head Movements

4.1.1. Thermal limit correction

For the thermal limit, the protective effects from eye and head movements are incorporated with the parameter T₂. With the eye and head movement assumption, T₂ is in the range of 10–100 s as shown in Table 4. With the movements restricted, however, T₂ = 10⁴ s should be used to calculate MPH_c, as mentioned in ANSI Section 8.3.2.b.

4.1.2. Photochemical limit correction

For the photochemical limit, the protective effects from eye and head movements are incorporated with the limiting cone angle γ (γ increases as exposure duration increases, reflecting the increased spread of light over a larger retinal area that comes with these movements). Following the approach in Delori et al. (2007), the MPH_c can be obtained by reducing γ to the minimal visual angle α_min =1.5 mrad for all exposure durations (see Table 5). The resulting limits are then given in Table 9.

Table 9.

MPH_c for photochemical limits (400 nm ≤ λ < 600 nm) without eye and head movements.

Exposure duration t (s)	MPHc (J/cm2)
0.7 ≤ t < 104	7.85 × 10−5CBmax(α,αmin)2
104 ≤ t ≤ 3 × 104	7.85 × 10−9CBmax(α,αmin)2t

Note that according to Table 9, with α = α_min, the corneal radiant exposure limit for 0.7 s ≤ t < 10⁴ s can be calculated as H_c = 7.85 × 10⁻⁵C_Bα_min² = 1.766 × 10⁻⁴C_B. Using Eq. (9) to convert corneal exposure to retinal exposure, assuming a pupil diameter of 3.1 mm, a retinal circular area with a diameter of 25 μm (1.5 mrad), and an ocular media transmission of 1.0, we obtain a retinal exposure limit, H_r, of 2.72C_B.

4.1.3. Repetitive pulses limit correction

When computing C_p for the repetitive-pulse limit (Rule 3), it should be calculated with T₂ = 10⁴ s when head and eye movements are restricted. In addition, according to ANSI Section 8.3.5, when calculating the limits for Rule 3, there is an additional reduction factor of 0.5 applied to the single pulse MPH_c when the following three conditions are met: (1) C_p = 1.0, (2) the pupil is large and/or the eye is immobilized, and (3) the number of pulses is 600 or greater.

4.2. Pupil dilation

According to Section 8.3.1 in the ANSI, when the exposure duration exceeds 0.7 s, and pupil constriction is inhibited by drugs or other means, the exposure limits must be reduced as follows: for wavelengths between 400 and 600 nm, exposure limits (both thermal and photochemical) should be reduced by a factor of 5; for wavelengths from 600 to 700 nm, the thermal limits (photochemical limits do not apply in this range) should be reduced by a factor of 10^{0.0074(700−λ)}. The reduction factor, termed “pupil factor”, is summarized in Table 10 (see Section 5, the table is given there, as it is also used to convert corneal limits to retinal limits). Also, we mention that for repetitive pulses, the reduction factor of 0.5 (mentioned in Section 4.1.3) may also apply when calculating the limits for Rule 3.

Table 10.

Pupil factor.

Wavelength λ (nm)	P
	t* ≤ 0.7	0.7 < t*
400 ≤ λ < 600	1	5
600 ≤ λ < 700	1	100.0074(700−λ)

4.3. An interim precaution: luminance dose restrictions from Section 8.3 in the 2014 ANSI

A new limit termed “Luminance Dose Restriction” has been added to the Standard as an interim precaution (Morgan et al., 2008). Basically, for exposures that occur within a 48 h window and exceed 100 s, the cumulative retinal radiant exposure should be below 5/V(λ), where V(λ) is the photopic luminous efficiency function, and the units for 5/V(λ) are in J/cm². We include the values for wavelengths from 400 to 700 nm (relevant for optogenetic studies) in Appendix II of this paper.

5. Conversion back to retinal irradiance

In the Standard, retinal irradiances or retinal radiant energies causing threshold retinal damage were determined at the retina, and then converted into exposure limits that are generally expressed as maximum permissible corneal radiant exposure. Here we do the reverse: given the maximum permissible corneal radiant exposure, we determine the corresponding maximum permissible retinal irradiances or retinal radiant energies. This is useful because in the optogenetics field, the light intensities required to produce neural responses are generally given in terms of retinal irradiance. In this section, we go through the procedure to convert between the two.

The Standard was developed in the condition of free or Newtonian illumination, in which a distant source irradiates an area larger than the pupil of the eye. In this condition, given the corneal radiant exposure H_c, the retinal radiant exposure H_r is

$$H_r=\tau H_c\frac{A_p}{A_r},$$ (9)

where A_p is the area of the pupil, A_r is the area of retinal exposure, and τ is the transmission of the ocular media. Basically, this means the energy landing on the retina H_rA_r should be equal to the energy through the pupil H_cA_p multiplied by the transmission of the ocular media τ. Dividing both sides of Eq. (9) by t, the relationship between retinal irradiance E_r and corneal irradiance E_c is

$$E_r=\tau E_c\frac{A_p}{A_r},$$ (10)

Therefore, in order to convert radiant exposures or irradiances between cornea and retina, we need to know both the area of the pupil and the area of the retina that is exposed. Note that τ varies with wavelength and age. With respect to wavelength, our computer implementation allows τ to be adjusted (Geeraets & Berry, 1968). With respect to age, the Standard assumes the ocular transmission of young adults (Delori et al., 2007), and, for the purposes of this paper, we do the same, as, from a safety perspective, this is conservative.

5.1. The area of retinal exposure

Assuming that the exposed retinal field is circular, the diameter of the retinal exposure area, is approximately given by

$$d_r\approx f_e\alpha ,$$ (11)

where α is the visual angle, and f_e is the eye’s effective focal length (f_e = 1.7cm, Emsley’s reduced eye (Smith & Atchison, 1997). The visual angle α can be measured from the pupil, roughly at the first nodal point of the eye, which is given by

$$\alpha =2\mathit{arctan}\frac{d_s}{2s},$$ (12)

where d_s is the diameter of the source, and s is the distance between the source and the eye. Given the diameter d_r in Eq. (11), a circular area of retinal exposure can be approximately calculated as

$$A_r\approx \frac{\pi }{4}{\left(f_e\alpha \right)}^2.$$ (13)

5.2. The area of pupil

In the Standard, the pupil is assumed to constrict in response to bright light in the visible spectrum. The area of the pupil A_p is dependent on exposure duration: the area is assumed to be maximal (0.7 cm in diameter) for very short exposures and constrict as exposures get longer. To model the change in pupil area with light, a pupil factor P was introduced (Delori et al., 2007):

$$A_p=\frac{A_{p,\mathit{max}}}{P(\lambda ,t^{\ast })},$$ (14)

where A_p,max is the area, assuming a pupil diameter of 0.7 cm (A_p,max = 0.385 cm²), and P is the pupil factor that simulates the pupil’s response to light, which varies with both wavelength and exposure duration t*. Pupil dilation numbers are given in Table 10 following ANSI Section 8.3.1. For example, as shown in the table, when t* > 0.7 s, and λ is < 600 nm, the pupil factor is 5, and thus A_p = 0.077 cm², which is the area of a ~0.31 cm diameter pupil. Note that under conditions with dilated pupil, P should be set to 1 when converting corneal irradiance back to retinal irradiance.

For single-pulse exposures, the duration of the pulse itself, t, is used to calculate the pupil factor, that is, t* = t. For repetitive pulses, the exposure limit is the lowest limit yielded by the three rules. In our implementation, if the single-pulse rule (Rule 1) yields the lowest limit, the duration of a single pulse is used to calculate the pupil factor (t* = t); if the average-power rule (Rule 2) yields the lowest limit, the total duration of the pulse train is used (t* = T_max); if the repetitive-pulse rule (Rule 3) yields the lowest limit, then t* = min(T_max,T₂) is used.

Fig. 1 provides a summary of all the calculations in Sections 2–5. As shown on the upper-left-hand side, the essential limit, the retinal limit, is dependent on the corneal limit, and the repetitive pulse limit is dependent on the single pulse limit. Each step, though, has many dependencies (e.g., the single pulse limit includes both the photochemical and thermal limits, with the former in turn dependent on C_B, γ, and α_min, and the latter on T₂, t_min, and C_E; C_E is then dependent on α_min and α_max, etc.). Several parameters, such as T₂, t_min, α_min, α_max, P, are relevant in multiple places. It is because of all the dependencies that we provide the computer implementation (see Appendix I). The implementation makes it possible to readily obtain maximum permissible exposure levels for different stimulus conditions, and the paper and figure provide an understanding of all the underlying calculations.

Fig. 1.

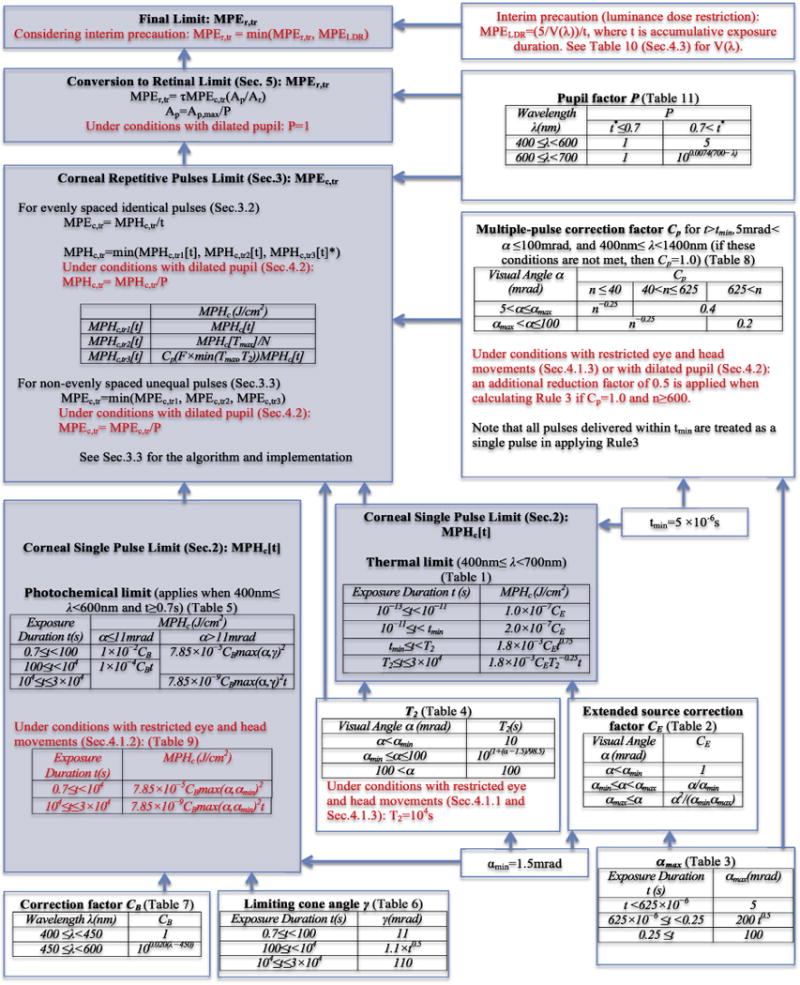
Summary of calculation dependencies (assuming 400nm ≤ λ < 700 nm): the parameters in Sections 2–5 are shown, along with their dependencies on other parameters. Steps involving factors that may or may not be needed to be taken into consideration, or are adjustable, such as eye and head movements, pupil dilation, and the new interim precaution (all described in Section 4) are marked in red. Note that the gray-colored steps are the main steps for exposure limit calculations. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

6. Assessing safety of stimulus protocols

6.1. Clinically relevant stimulus protocols

We set up stimulus protocols that use parameters relevant to humans in, for example, a clinical trial, including wavelength, visual angle of the stimulus, pupil size, total stimulating time, pulse width, and pulse pattern. We then used the computer implementation (given in Appendix I) to determine maximum permissible exposures for these protocols. As described in the Introduction, for wavelength, we used 505 nm, as this covers a reasonable range of clinically relevant channelrhodopsins (Klapoetke et al., 2014; Kleinlogel et al., 2011) and is the peak emission wavelength of a commonly used LED in digital light projectors that drive the proteins. For visual angle, we used 10 degrees, as current AAV vectors deliver the gene largely to central retina; we also show calculations for 20 degrees of visual angle. For pupil size, it is assumed to be maximal (0.7 cm in diameter) for short exposures (shorter than pupil reflex duration), and to constrict to a diameter of 0.31 cm for longer exposures, following the assumption of the Standard. For total stimulating time, we used 8.3 h (3 × 10⁴ s), also following the Standard; this is the maximum duration provided. For pulse width, we explored a range: widths ranged from 1.4 to 5.6 ms (chosen to bracket the time needed to trigger individual action potentials in retinal ganglion cells, allowing neurally-coded stimulation to be used). Finally, for pulse patterns, we used two conditions: pulses that were presented periodically (using a range from 6 to 50 Hz) and pulses that were presented using a neural code generator. For the latter, we used the neural code to drifting square wave gratings and a natural scene stimulus; for a description of neurally coded stimuli, see Nirenberg and Pandarinath (2012).

Given these conditions, we asked whether the intensities needed to drive channelrhdopsin would fall below damage levels. The results are shown in the next sections and Tables 11–15. They show for each condition the peak light intensities that can be used without exceeding the ANSI (2014) limits. They also make clear that there exist protocols that are both effective for driving optogenetic proteins and safe, where “safe” is defined here as falling below ANSI limits. Note that in this section we switch from units of W/cm² to mW/mm² to be consistent with the common usage in optogenetics.

Table 11.

Maximum permissible corneal peak irradiance MPE_c,tr (mW/mm²). As indicated in Section 6.1, the calculations assume parameters relevant to a clinical trial: peak wavelength λ = 505 nm, visual angle = 10 degrees (diameter of exposed retinal area d_r = 3.0 mm), total exposure time T_max = 8.3h (the maximum provided in the Standard). Given this wavelength, visual angle, duration, and assuming evenly spaced identical pulses, the recommended ANSI safety limit is determined by the pulse width t, and the repetition frequency F. Note that, both results remain the same whether or not head and eye movements are included (see text in Section 6.1.1). Briefly, the assumption of eye and head movements only affects the exposure limit when the visual angle α is smaller than the limiting cone angle γ. Since the visual angle here (α = 10° = 174.5 mrad) is larger than the limiting cone angle (γ = 110mrad), no protective effect occurs with eye and head movements.

Frequency (Hz)	Pulse width (ms)
	1.4	2.8	4.2	5.6
6	3.58	1.79	1.19	0.90
10	2.15	1.08	0.72	0.54
14	1.54	0.77	0.51	0.38
18	1.19	0.60	0.40	0.30
22	0.98	0.49	0.33	0.24
26	0.83	0.41	0.28	0.21
30	0.72	0.36	0.24	0.18
34	0.63	0.32	0.21	0.16
38	0.57	0.28	0.19	0.14
42	0.51	0.26	0.17	0.13
46	0.47	0.23	0.16	0.12
50	0.43	0.22	0.14	0.11

Table 15.

Maximum permissible corneal and retinal peak irradiance (mW/mm²) for the neurally coded natural scene stimulus. Conditions are the same as for Table 14.

	Pulse Width (ms)
	1.4	2.8	4.2	5.6
MPEc,tr	2.88	1.44	0.96	0.72
MPEr,tr	2.66	1.33	0.89	0.67
MPEr,tr(with interim precaution)	0.39	0.20	0.13	0.10

6.1.1. Examples of stimuli with evenly spaced identical pulses

Tables 11 and 12 give the corneal and retinal exposure limits for the conditions described above, focusing on periodic stimuli. Specifically, they show the peak intensities that can be used without exceeding the limits. As mentioned above, they also indicate that there are an array of protocols that are both sufficient for driving optogenetic proteins and fall within ANSI recommendations. For example, for a peak irradiance of 0.1 mW/mm² at the level of the retina - an intensity that exceeds the maximum likely to be needed for optogenetic therapies (see Klapoetke et al., 2014; Kleinlogel et al., 2011) - there are numerous stimulus protocols that would satisfy the conditions: e.g., as shown in Table 12, the peak irradiance exposure limit, MPE_r,tr for a stimulus with a frequency of 18 Hz and a pulse width of 2.8 ms or one with a frequency of 10 Hz and a pulse width of 5.6 ms, is about 0.5 mW/mm². Thus, an exposure with a retinal irradiance of 0.1 mW/mm² at the level of the retina is 5 times lower than the ANSI recommended limit. We mention again that the ANSI recommendations generally include a safety margin: the recommended limits can be as much as 10-fold lower than the damage threshold, if the slope of the probability-of-damage curve is not steep; see Sliney et al. (2002) for discussion, including caveats.

Table 12.

Maximum permissible retinal peak irradiance MPE_r,tr (mW/mm²), calculated from Table 10 using Eqs. (10), (13), and (14). Conditions are the same as in Table 11.

Frequency (Hz)	Pulse Width (ms)
	1.4	2.8	4.2	5.6
6	3.31	1.66	1.10	0.83
10	1.99	0.99	0.66	0.50
14	1.42	0.71	0.47	0.35
18	1.10	0.55	0.37	0.28
22	0.90	0.45	0.30	0.23
26	0.76	0.38	0.25	0.19
30	0.66	0.33	0.22	0.17
34	0.58	0.29	0.19	0.15
38	0.52	0.26	0.17	0.13
42	0.47	0.24	0.16	0.12
46	0.43	0.22	0.14	0.11
50	0.40	0.20	0.13	0.10

We now go through the tables. Table 11 shows the exposure limits for peak irradiances at the corneal plane, MPE_c,tr; the table shows the limits for different pulse widths (1.4 ms, 2.8 ms, 4.2 ms, 5.6 ms) and different repetition frequencies up to 50 Hz. The MPE_c,tr is obtained from maximum permissible corneal exposures per pulse MPH_c,tr[t] divided by the pulse duration t, according to Eq. (7). The MPH_c,tr[t] is calculated with our computer implementation of the Standard. Clearly, the MPE_ctr decreases as the pulse width and frequency increases. Among the three rules, the photochemical average-power limit (Rule 2) yields the lowest value in all cases in Table 11.

In Table 12, the values from Table 11, which give maximum permissible peak corneal irradiance limits, are converted to maximum permissible peak retinal irradiance limits via Eqs. (10), (13), and (14). As mentioned above, the peak intensity needed to drive many channelrhodopsins (Klapoetke et al., 2014; Kleinlogel et al., 2011), 0.1 mW/mm² is less than or equal to the recommended exposure limits up to a frequency of 50 Hz and pulse width of 5.6 ms.

Comparing the results in Tables 11 and 12, the retinal irradiance is similar to the corresponding corneal irradiance. The relationship between corneal and retinal irradiance is given in Eq. (10), which is dependent on the area of pupil A_p the area of retinal exposure A_r, and the transmission of the ocular media τ. In the Standard, the pupil is assumed to constrict in response to bright light to a diameter of 3.1 mm for longer exposures. Given a visual angle of 10 degrees, the diameter of the retinal exposure area is also close to 3 mm (slightly smaller than the pupil size 3.1 mm). Given these areas and the transmission of the ocular media (τ ≈ 0.83 for λ = 505 nm), τA_p/A_r in Eq. (10) is 0.9 (i.e., close to 1), which leads to similar values for corneal and retinal irradiances.

We also calculate the exposure limits based on the implementation in Section 4 to account for potential clinical tests with restricted eye and head movements, and the results remain the same. The lowest exposure limits are all yielded by the photochemical limit of Rule 2, which do not decrease, because the assumption of eye and head movements only affects the rule when the visual angle α is smaller than the limiting cone angle γ. In the current application, the visual angle (α = 10° = 174.5 mrad) is larger than the limiting cone angle (γ = 110 mrad), so there is no protective effect of eye and head movements.

We also calculate the exposure limits corresponding to a visual field of 20 degrees. The retinal irradiance limits are the same as for a visual angle of 10 degrees (Table 12). But the corneal irradiance limits are four times larger than for a 10-degree field (Table 11), since the light incident on the cornea is now spread over a retinal area that is four times larger.

In Table 13, we take it a step further and include the recently added interim precaution ‘Luminance Dose Restrictions’, which focus on the effects of long stimulus durations in a relatively short window (48 h). The table shows the effects of the limits for several durations: 2 h, 4 h, and the maximum 8.3 h. Briefly the calculation is as follows: For λ = 505 nm, the photopic luminous efficiency function, V(λ), is 0.4073 (shown in Appendix II). According to the new restriction, which at this stage is still an interim precaution, the cumulative retinal radiant exposure should be kept below 5 (J/cm²) divided by V(λ), which equals 12.276 (J/cm²). To find the quantity we need, the peak irradiance at the level of the retina, MPE_r,tr, we take the cumulative retinal radiant exposure and divide it by the exposure time (giving us units of power per unit area (i.e., irradiance)). As shown in Table 13, while the interim precaution lowers the limits for MPE_r,tr, many viable stimulus protocols remain - that is, protocols that drive optogenetic proteins to trigger neural responses yet stay below ANSI recommended limits. As a rule of thumb, given a train of pulses with equal amplitude, the maximum permissible retinal peak irradiance given the interim precaution is inversely proportional to the cumulative exposure duration within the 48 h period, regardless of the patterns of the pulses.

Table 13.

Maximum permissible retinal peak irradiance MPE_r,tr (mW/mm²) taking into consideration the recently added interim precaution, referred to as the “Luminance dose restriction”. The results are shown for different durations: 2 h, 4 h, and the maximum 8.3 h. All other conditions are the same as in Table 12. Note that the calculated limit for a frequency of 6 Hz, a pulse width 1.4 ms, and a duration of 2 h is much higher (top left value) than the other values in the table, because the accumulated exposure in this case is small enough (less than 100 s) that it doesn’t fall in the range relevant for the interim precaution.

Frequency (Hz)	Pulse Width (ms)
	1.4			2.8			4.2			5.6
	Durations (h)
	2	4	8.3	2	4	8.3	2	4	8.3	2	4	8.3
6	4.60	1.01	0.49	1.01	0.51	0.24	0.68	0.34	0.16	0.51	0.25	0.12
10	1.22	0.61	0.29	0.61	0.30	0.15	0.41	0.20	0.10	0.30	0.15	0.07
14	0.87	0.43	0.21	0.43	0.22	0.10	0.29	0.15	0.07	0.22	0.11	0.05
18	0.68	0.34	0.16	0.34	0.17	0.08	0.23	0.11	0.05	0.17	0.08	0.04
22	0.55	0.28	0.13	0.28	0.14	0.07	0.18	0.09	0.04	0.14	0.07	0.03
26	0.47	0.23	0.11	0.23	0.12	0.06	0.16	0.08	0.04	0.12	0.06	0.03
30	0.41	0.20	0.10	0.20	0.10	0.05	0.14	0.07	0.03	0.10	0.05	0.02
34	0.36	0.18	0.09	0.18	0.09	0.04	0.12	0.06	0.03	0.09	0.04	0.02
38	0.32	0.16	0.08	0.16	0.08	0.04	0.11	0.05	0.03	0.08	0.04	0.02
42	0.29	0.15	0.07	0.15	0.07	0.03	0.10	0.05	0.02	0.07	0.04	0.02
46	0.26	0.13	0.06	0.13	0.07	0.03	0.09	0.04	0.02	0.07	0.03	0.02
50	0.24	0.12	0.06	0.12	0.06	0.03	0.08	0.04	0.02	0.06	0.03	0.01

6.1.2. Examples of stimuli with non-evenly spaced identical pulses

This section focuses on the exposure limits for two neurally-coded stimuli, both of which are composed of non-evenly spaced identical pulses (Fig. 2). The first one is a neurally-coded drifting grating stimulus, i.e., it is generated from the neuronal response of a retinal ganglion cell to a drifting grating (temporal frequency 1 Hz, spatial frequency 1/6 cycle/degree). The second one is a neurally-coded natural scene stimulus, generated from the neuronal response to a natural scene movie (as seen walking through a park) (Nirenberg & Pandarinath, 2012). The average pulse rate (defined as the total number of pulses divided by the total duration) is ~10.5 Hz and ~7.5 Hz, respectively, for the two stimuli, with the natural scene stimulus having transient periods of rapid firing. In each case, the stimulus is repeated so that the total duration for each one reaches the maximum duration available in the Standard (8.3 h).

Fig. 2.

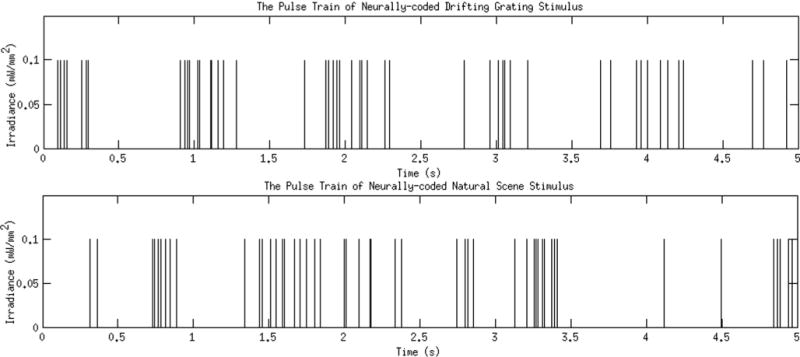
Example pulse train patterns for two neurally-coded stimuli. Top: a stretch of a neurally-coded drifting grating stimulus. The stimulus is a pattern of light pulses that mimics the pattern of action potentials that would be produced by a retinal ganglion cell in response to a drifting grating. Bottom: a stretch of a neurally-coded natural scene stimulus. The stimulus is a pattern of light pulses that mimics the pattern of action potentials that would be produced by a retinal ganglion cell in response to a movie of natural scenes, as in Nirenberg and Pandarinath (2012). Note that the stimuli are only on ~3–6% of the time on average for a typical pulse width of 2.8 or 5.6 ms.

The exposure limits for the neurally-coded grating stimulus and the neurally-coded natural scene stimulus are shown in Tables 14 and 15 respectively. In each table, the limits are expressed in terms of both peak corneal and peak retinal irradiance. In the first step, we calculate corneal and retinal limits without the interim precaution: the peak corneal irradiance limits MPE_c,tr are converted to the peak retinal irradiance limits MPE_r,tr, via Eqs. (10), (13) and (14). The exposure limits are assessed at different pulse widths (1.4 ms, 2.8 ms, 4.2 ms, 5.6 ms). The photochemical average-power limit (Rule 2) yields the lowest value in all cases. We also calculate the exposure limits assuming minimal eye and head movements, and the results remain the same (see Table 14 caption). As shown in both tables, many conclusions drawn from the periodic stimuli also hold true for the neurally-coded cases. In particular, the peak intensity used to drive many channelrhodopsins (Klapoetke et al., 2014; Kleinlogel et al., 2011), 0.1 mW/mm² is still about 5 times lower than the recommended exposure limits - up to a pulse width of 5.6 ms. If one further includes the interim precaution, as shown in the last row of Tables 14 and 15, 0.1 mW/mm² does not exceed the recommended exposure limits up to a pulse width of 2.8 ms for the neurally-coded grating stimulus, and up to a pulse width of 5.6 ms for the neurally-coded natural scene stimulus.

Table 14.

Maximum permissible corneal and retinal peak irradiance (mW/mm²) for the neurally coded grating stimulus. As indicated in Section 6.1, the calculations assume parameters relevant to a clinical trial: peak wavelength λ = 505 nm, visual angle = 10 degrees (diameter of exposed retinal area d_r = 3.0 mm), total exposure time T_max = 8.3 h (the maximum provided in the Standard). Given this wavelength, visual angle, duration, and assuming non-evenly spaced identical pulses, the recommended ANSI limit is determined by the pulse width t, and the pulse train pattern as described in Section 3.3. Note that the results remain the same whether or not head and eye movements are included: as discussed above in Section 6.1.1, eye and head movements only affect exposure limits when the visual angle is smaller than the limiting cone angle. Since the visual angle here is larger than the limiting cone angle, there is no protective effect of eye and head movements.

	Pulse width (ms)
	1.4	2.8	4.2	5.6
MPEc,tr	2.05	1.02	0.68	0.51
MPEr,tr	1.89	0.95	0.63	0.47
MPEr,tr (with interim precaution)	0.28	0.14	0.09	0.07

6.2. Safety study using retinal irradiance of 0.1 mW/mm² in rat model

In the previous subsection, we described example protocols that could be used in a human clinical trial, i.e., protocols that are expected to be both effective for driving optogenetic proteins (Klapoetke et al., 2014; Kleinlogel et al., 2011) and safe according to our implementation of the ANSI Standards. Here we further test for safety using a rat model. To approximate conditions relevant for a clinical trial, we (1) used the same peak irradiance described in the previous section (0.1 mW/mm² at the level of the retina, an intensity greater than or equal to what is necessary to drive most ChRs; note that since the rat eye has higher refractive power than the human eye, the intensity at the cornea has to be reduced so as to achieve 0.1 mW/mm² at the level of the retina), and (2) provided the stimuli in sessions over the course of several weeks (2.5 h sessions for 6 weeks, totaling 12 sessions) to mimic exposure in a human trial. Note that because the animals had to be anesthetized for each session, the total time was limited to 6 weeks, in order to be humane. The work was carried out in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

6.2.1. Experimental setup

The experimental set up was as follows:

6.2.1.1. Light source

The light source was composed of a mounted high-power LED (505 nm peak), a collimation adapter for collimating the output from the LED, and a ground glass diffuser placed in front of the collimation adapter. The extent of the light source was 20 mm in diameter, which was controlled by a ring-shaped cover on top of the glass diffuser. The LED was controlled with an LED driver (DC2100, Thorlab) with pulse modulation. Using this set up, we delivered a periodic stimulus with the following features for 2.5 h (the length of time of each session): frequency = 10 Hz, pulse duration = 5 ms, and wavelength = 505 nm. Note the stimulation was pulsed light, so the light was not on continuously, but the pulsing was steadily occurring for the duration of the 2.5 h.

6.2.1.2. Retinal exposure area

To determine the exposed area, we assumed a homogeneous model of the rat eye, following Ref. Chaudhuri, Hallett, and Parker (1983). The diameter of the exposed area is determined by the visual angle and the effective focal length in Eq. (11). The rat eye is one-third the size of the human eye and has significantly greater total optical power. At a wavelength of 500 nm, the total optical power is 296.53 diopters (Chaudhuri, Hallett, and Parker, 1983), and thus the effective focal length is 3.37 mm, which is much shorter than the effective focal length of the human eye (17 mm). Correspondingly, given a visual angle of 10 degrees, the diameter of the retinal exposure area d_r in rats is 0.59 mm, which is much smaller than the diameter would be in humans (3 mm). To increase the exposed area for the experiment so that potential damage would be more easily assessed, we used a larger stimulus, one that covers an area of 4 mm diameter on the retina, and we targeted the stimulus to central retina.

6.2.1.3. Light intensity delivered at the corneal plane

According to the ANSI recommended exposure limits calculated in Section 6.1, a retinal irradiance of 0.1 mW/mm² is less than or equal to the maximum permissible up to a repetition frequency of 50 Hz. In order to experimentally test the safety of the retinal irradiance, the light intensity to be delivered to the corneal plane needs to be determined.

Given a retinal irradiance E_r and an area of retinal exposure A_r, the corneal irradiance E_c can be calculated from the area of pupil A_p, following Eq. (10). For ocular transmission at 505 nm, we used 0.9, following Ref. Dillon et al. (2000), which shows that ocular transmission for the rat eye is 0.9 or greater. In the experiment, atropine was used to dilate the pupil of the rats. After dilation, pupil size ranges from 4 to 5 mm in diameter. If 4 mm is used, A_p is 12.57 mm², and E_c is 0.11 mW/mm². Note that it is conservative to choose 4 mm as the pupil diameter to calculate the light intensity to be delivered. If the diameter is larger than 4 mm, the retinal irradiance would be larger than 0.1 mW/mm². This means the actual retinal irradiance in the experiment would be greater than 0.1 mW/mm². Thus, if there is no damage to the retina after the experiment, the retinal irradiance E_r = 0.1 mW/mm² should be sufficiently safe.

6.2.2. Experimental results

Seven wild-type Long-Evans rats were anesthetized with Isoflurane (99.9%) to a depth that minimized eye movements. Each animal was placed on its right side, with its right eye illuminated by the stimulus. The pupil was dilated with an atropine sulfate ophthalmic solution (1%) and the eye was kept wet with artificial tears applied regularly (every 7 min). The left eye was left untreated. Each animal was presented with a stimulus of the same wavelength (505 nm) and peak retinal irradiance (0.1 mW/mm²), as given in Section 6.1. The stimulus, as mentioned above, was a pulse of 5 ms in width, presented periodically at 10 Hz for 2.5 h per session. 12 sessions were given over a period 6 weeks. Two animals had one session of 2 h.

Two weeks after completion of the last session (8 weeks after treatment began), the retinas were prepared for sectioning and histological analysis by fixing whole eyes in 10% formalin, processing for paraffin embedding, sectioning at a thickness of 4 μm, and staining with hematoxylin and eosin (H&E). The thickness of the outer nuclear layer was determined by counting the number of cell bodies present as a function of distance from the optic nerve head, following Ref. Faktorovich et al. (1990). Briefly, at 0.35 mm intervals on a vertical axis from periphery to periphery and through the optic nerve head, the number of outer nuclear layer cells was counted in triplicate. Thus, there were a total of 60 counts (samples) at 20 equally spaced intervals in each of the 14 eyes examined, 7 with light exposure and the partner 7 without light exposure.

As shown in Fig. 3, there was no loss of photoreceptors as a result of this treatment, consistent with the expectation from the ANSI Standards. Statistical significance was measured using a one-tailed paired t-test covering each of the 20 retinal locations, and no difference was found (p > 0.1). Unpaired t-tests at each location, comparing the 7 treated and untreated groups, also showed no significance either by the Bonferroni method or the false-discovery-rate method (p > 0.25) for multiple comparison correction; the lowest raw p-value of the 20 comparisons was 0.065. With respect to assessing power, ~3500 cells were counted for each condition (3538 in the treated eye, 3483 in the untreated), so by Poisson statistics, our confidence limits (2 SD) on each overall cell count is <3.5% of its total. Thus, changes of 5% in the number of cells would be readily detected. This indicates that we counted enough cells to detect changes as small as 5% and, as mentioned above, no such change was found. As an added measure to ensure the validity of the study, a large area was used for the exposure (a 4 mm diameter area, as mentioned above, in an 8 mm diameter retina) so damage would be unmistakable and not misattributed to a tissue processing artifact.

Note that this paper focuses largely on data from the ANSI Standards, which focuses significantly on monkey data, as this is the most relevant to human patients. We included this rat study because it allowed us to explore a stimulus protocol different from those mentioned in the Standard, but similar to what might be employed in a clinical trial focused on optogenetic therapy, i.e., stimuli presented in 2.5 h sessions over a period of weeks, and, as discussed above, no photoreceptor loss was observed.

7. Discussion

There has been rapid growth in the field of optogenetics for the treatment of eye diseases. Much of the work has focused on improving effectiveness, specifically, finding the right combination of factors, such as the choice of ChR/HR genes, gene regulatory elements, gene delivery systems, and stimulation strategies that produce effective and neurally-coded retinal responses. Ensuring safety, though, is also a critical issue. Because of the potential for retinal damage with different stimulus protocols, and the nonlinear interactions both among stimulus parameters and the mechanisms that produce damage (photothermal and photochemical), an accessible study of the range of permissible protocols for optogenetic stimulation was needed, and it was our aim to provide it here. The work follows directly from the recently updated ANSI Standards (2014), using the visible light range (400–700 nm). In addition to the calculations and tables presented, a computer implementation is also provided in Appendix I.

To summarize the work: Section 2 describes the calculation used for determining exposure limits for single pulses and the description and rationale for all parameters, building on ANSI (2014) and Delori et al. (2007). Section 3 provides the exposure limits for repetitive pulses and the underlying calculations for the computer implementation. Section 4 shows how the limits need to be modified in cases where eye movements, head movements, and pupil constriction are considered. It also includes the potential risks specified by the new interim precaution in the 2014 ANSI. Section 5 provides the conversion from limits at the cornea to limits at the retina and a summary figure that shows all the relationships among the parameters discussed in the previous sections. Finally, Section 6 shows the safety of an array of stimulus protocols relevant for clinical trials and a case study using one of the protocols and the rat as a model system.

The ANSI Standards employ a large number of parameters, equations, and tables: using them to determine the safety of a stimulation paradigm is nontrivial (see Fig. 1). The complexity is further increased when Standard assumptions, such as eye movements, head movements, and pupil constriction, have to be removed. In addition, when designing equipment, such as optogenetic stimulators, it is often necessary to evaluate multiple parameters multiple times until all the design requirements are satisfied, and optimality is achieved; manual testing for this would be onerous. It is for this reason that we provide a computer utility.

Note that in the case of non-equally spaced pulses, a computer implementation of the Standard becomes irreplaceable. While the three rules in the Standard are general, the examples in the ANSI Standard (2014) and in Delori et al. (2007) only focus on a single case: evenly spaced identical pulses. In this special case, the limit can be obtained with a relatively small number of calculations and look-up tables. However, this is not the case for non-equally spaced pulses (such as patterned stimuli in optogenetic applications). For example, to evaluate the limit from Rule 2 for non-evenly spaced pulses, there is no way to find which subgroup yields the lowest limit unless the limits from all possible subgroups are calculated. In our implementation, the limits from all the subgroups are calculated in a bottom-up way (from subgroups composed of two consecutive pulses up to the subgroup composed of all the pulses in the train), a search that would be impossible or prohibitively expensive to proceed through manually.

7.1. Cell types most susceptible to damage from light

As discussed in Hunter et al. (2012), the cell types most vulnerable to damage from light are the cells with specializations to absorb light (e.g., photopigments). These include rods, cones, and retinal pigment epithelial cells. The intrinsically photosensitive ganglion cells might also be expected to be vulnerable, but evidence for this is not available. La Morgia et al. (2011) suggest that it may be less than expected, as melonopsin, the pigment in these cells, may have some neuroprotective effects. Note that when we make cells light-sensitive, as we do when we introduce an optogenetic protein, we create a new potential susceptibility. Several studies suggest that light exposure of optogenetic proteins is not phototoxic (Diester et al., 2011; Han et al., 2009; Ivanova & Pan, 2009; Lignani et al., 2013; Mehdi Doroudchi et al., 2011); however, these studies were in areas outside the eye (Diester et al., 2011; Han et al., 2009; Lignani et al., 2013) or performed in freely-moving animas (mice) exposed to a 12-h background light-dark cycle (Ivanova & Pan, 2009; Mehdi Doroudchi et al., 2011), where light exposures at the corneal plane were not able to be well-controlled; thus, new studies with ChR- or HR-expressing cells in the retina will be needed before advancing to clinical trials for ocular therapy.

7.2. Potential differences in susceptibility to damage between normal subjects and patients with retinal degenerative disease

The ANSI Standards provide a critical first step in evaluating the safety of optogenetic treatments, but evaluation in patients with retinal degenerative diseases is also necessary, as susceptibility to damage may be different (reviewed in Hunter et al. (2012)), either via increased photopigment absorption due to disruption of the visual cycle (the postulated Noell mechanism (Noell et al., 1966), increased amounts of lipofuchsin in retinal pigment epilthelial (RPE) cells (the postulated Ham mechanism (Ham et al., 1978), or both. In Stargardt’s macular dystrophy, for example, both are relevant: there is impaired removal of all-trans-retinal from the photoreceptor discs, and also increased accumulation of RPE lipofucsin (Travis et al., 2007). In Best’s disease, there is an increased accumulation of RPE lipofuchsin (Frangieh, Green, & Fine, 1982; Weingeist, Kobrin, & Watzke, 1982). In fundus albipunctatus and some forms of retinitis pigmentosa, there are disruptions of the visual cycle (Cideciyan et al., 2005; Travis et al., 2007; Wang et al., 1997; White et al., 2007). Some forms of Leber’s congenital amaurosis are associated with increased generation of retinoids, which is anticipated to lead to increased susceptibility to light (Maeda et al., 2006).

With respect to age-related macular degeneration (AMD), there is still a lack of strong epidemiologic evidence for phototoxicity as a causative factor, despite several epidemiological studies (Hunter et al., 2012; Yooussef, Sheibani, & Albert, 2011). The lack of evidence may be due to difficulties in determining the relevant light exposure, which can occur over a lifetime, and may be wavelength-dependent; see Hunter et al. review for further discussion (Hunter et al., 2012). There is also some concern that affected individuals have larger-than-average pupils and may be more susceptible to light damage on that basis (Hunter et al., 2012). But with respect to optogenetic therapy, the increased pupil size can be accommodated by delivering less light during the treatment, as described below. Because of these considerations for patients with retinal degenerative diseases, clinical trials assessing safety will be needed in addition to the ANSI Standards recommendations.

7.3. Pupil size in blind patients

The relevant measurement for driving optogenetic proteins is the amount of light on the retina. But in the clinic, we can only measure light intensity at the corneal plane. The conversion from corneal intensity to retinal intensity depends, of course, on pupil size. While pupil size is reasonably predictable for normal subjects, for patients with retinal degenerative diseases, it can be highly variable (for discussion, see Newsome, Milton, and Gass (1981)). Thus, it is necessary to measure pupil size in patients individually, so that corneal exposures can be adjusted to allow appropriate stimulation to reach the retina. E.g., if the pupil response is weaker, and pupil diameter is larger, then one can use less light at the level of the cornea to achieve successful activation of the optogenetic protein at the retina. Note, though, that if the optogenetic treatment is successful, and the pupil response recovers, the light intensity will need to be adjusted in the other direction.

7.4. Comparing the stimulation required for optogenetic therapies to intensities normally encountered in the everyday world

Sliney (2005) shows retinal irradiances from common light sources (a tungsten filament in a clear light bulb, which has an absorbed retinal irradiance of ~10⁻²–10⁻¹ W/cm², a candle, which has an absorbed retinal irradiance of ~10⁻⁵–10⁻⁴ W/cm², and a TV, which has an absorbed retinal irradiance of ~10⁻⁶ W/cm²). We can use the irradiances from these common sources to gain perspective on the retinal irradiances produced by the stimulus protocols one might use for optogenetic therapy. For example, using the neurally-coded stimulus protocol in Section 6, the peak retinal irradiance is 0.1 mW/mm² (i.e., 10⁻² W/cm²) and the time-averaged is 10–20-fold lower. So the peak irradiance is at the lower end of the tungsten filament range, and the time-averaged irradiance is about 5–10 times brighter than a candle.

Highlights.

• Optogenetics-based treatments are being rapidly developed for visual diseases.

• A key issue is the safety of the light exposure needed for optogenetic stimulation.

• The limiting factors, based on the ANSI (2014) Standards, are presented.

Appendix A. Supplementary data

Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.visres.2016.01.006.