Elastic Stability of Concentric Tube Robots: A Stability Measure and Design Test

Abstract

Concentric tube robots are needle-sized manipulators which have been investigated for use in minimally invasive surgeries. It was noted early in the development of these devices that elastic energy storage can lead to rapid snapping motion for designs with moderate to high tube curvatures. Substantial progress has recently been made in the concentric tube robot community in designing snap-free robots, planning stable paths, and characterizing conditions that result in snapping for specific classes of concentric tube robots. However, a general measure for how stable a given robot configuration is has yet to be proposed. In this paper, we use bifurcation and elastic stability theory to provide such a measure, as well as to produce a test for determining whether a given design is snap-free (i.e. whether snapping can occur anywhere in the unloaded robot’s workspace). These results are useful in designing, planning motions for, and controlling concentric tube robots with high curvatures.

I. Introduction

Concentric tube robots appear promising in many kinds of minimally invasive surgical interventions that require small diameter robots with articulation inside the body. Examples include surgery in the eye [2], heart [3], sinuses [4], lungs [5], prostate [6], brain [7], and other areas. For a review of concentric robot development and applications, see [8]. In most of these applications, higher curvature is generally desirable to enable the robot to turn “tighter corners” inside the human body and work dexterously at the surgical site.

However, it was noted early in the development of concentric tube robots that unless gradual tube curvatures are used or minimal overlap of curved tube sections is ensured, tubes can exhibit elastic instabilities [9] (also previously referred to as “snaps” and “bifurcations”). Elastic instabilities occur due to torsional elastic energy storage in the tubes that make up a concentric tube robot. An instability occurs when this energy is rapidly released, and the robot “snaps” to a new configuration. Unforeseen snapping is clearly not desirable and could be dangerous in surgical applications.

The snapping problem has been approached from design, modeling, and planning perspectives. With the exception of the early work in [9], these studies have used the mechanics based model of concentric tube robots found in [10], [11]. For example, it has recently been shown that tubes can be laser machined to reduce the ratio of bending to torsional stiffness, which improves stability [12], [13]. However, even using this approach, snaps will still occur if high curvatures are employed, so methods for design and snap prediction will still be needed. Another approach is to use non-constant precurvature tubes to enhance the elastic stability, as shown by Ha et al. [14]. In that work, analytical stability conditions for a two-tube robot with planar precurvatures are presented, and an optimal control problem is used to design tube precurvatures which result in a completely stable actuation space. Our work complements theirs by analyzing the stability of robots which possess unstable configurations in their actuation space. We also consider designs of an arbitrary number of tubes with more general precurvature.

It is also possible to plan stable paths for robots that do have the potential to snap, as shown by Bergeles et al. [7], by examining the relative axial angle between the base of a tube and its tip for all possible rotations for a given set of tubes. While this work provides a method to design and use high-curvature robots, the stability condition chosen by the authors was stated as a definition. One of the contributions of our paper is to derive a stability criterion from first principles. Another model-based approach is that of Xu et al. [15], who sought design parameter bounds for constant curvature robots to ensure a snap-free unloaded robot workspace. Xu et al. provided exact design bounds for a two-tube robot and non-exact, conservative bounds for robots with more than two tubes. In addition, the solutions in [15] for more than two tubes only apply to robot configurations where the precurved portions of tubes are precisely aligned in arc length.

In this paper, we characterize the solution multiplicity and elastic stability of unloaded concentric tube robots with any number of tubes, each of which may be preshaped as a general space curve. We do this by analyzing the stability properties predicted by the accepted model which has been experimentally validated in the literature [10], [11]. We connect concentric tube robot stability analysis to the analysis of post-buckled Euler beams from the mechanics literature [16], [17], [18]. Based on this analysis, we also propose a measure for relative stability, which can be used to inform real-time controllers, planners, and automated designers to safely design and operate a robot that would otherwise snap. We also show that from the perspective of bifurcation theory [19], one can derive an exact, analytic method which predicts stability properties throughout the entire actuation space of a concentric tube robot with constant precurvature tubes.

II. The Beam Buckling Analogy

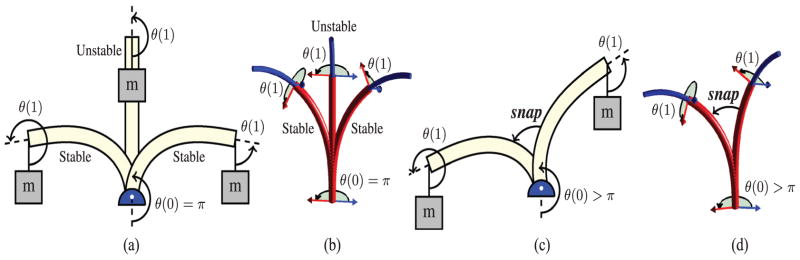
A two-tube concentric tube robot and a loaded beam are analogous systems, and both systems exhibit buckling and snapping. To build intuition, we begin by describing these analogous behaviors. Concentric tube robots are controlled by prescribing relative translations and rotations at the proximal ends of the tubes. The tubes twist and bend one another along their arc length s. When there are two circularly precurved tubes the twist angle between them, θ(s), is governed by the same differential equation as a beam under a dead load as shown in Figure 1. The configuration of both systems is determined by the nonlinear boundary value problem

Fig. 1.

The analogy between an Euler beam and a two-tube concentric tube robot for λ greater than its critical value. For the beam, θ (s) denotes the angle of the beam, while for the robot it denotes the angle between precurvature vectors. (a) There are three solutions when the base has been rotated to θ (0) = π. The straight solution is unstable and the two buckled solutions are stable. (b) When the tube precurvatures are anti-aligned at the base there exists one torsionless unstable solution and two stable buckled solutions. (c) As the base angle approaches some value θ (0) > π, the beam snaps into a new, stable configuration. (d) As the relative angle between the tubes approaches some value θ (0) > π the tubes snap into a new, stable configuration. Note that the value of θ (0) when the snap occurs depends on λ.

$$\begin{array}{ll}\hfill f[\lambda ,\theta (s)]& ={\theta }^{″}-\lambda sin(\theta )=0\hfill \\ \hfill \theta (0)& ={\theta }_0\hfill \\ \hfill {\theta }^{\prime }(1)& =0,\hfill \end{array}$$ (1)

where the equations have been normalized to unit length, so that 0 ≤ s ≤ 1. For both the beam and the concentric tube robot, it is known that increasing values of the parameter λ can lead to buckling and instability. For the beam, this parameter is controlled by the material properties, the geometry, and the magnitude of the dead load. Likewise, for the robot, λ involves the material properties and geometry of the tubes, but the dead load is replaced by the influence of the tube precurvatures.

In the set of solutions to (1), two straight beam configurations exist: θ (s) = 0 and θ (s) = π, which represent the beam in pure tension and compression, respectively. Similarly, for concentric tubes, two torsionless solutions exist in which the tube precurvatures are aligned and anti-aligned, respectively. Just as a beam in tension cannot buckle, a robot configuration with aligned precurvatures is stable. In contrast, when the beam is compressed (Figure 1a) or when the concentric tube robot has anti-aligned precurvatures (Figure 1b), the configurations which are straight for the beam and torsionless for the robot can buckle if λ exceeds a critical value. Buckling occurs because the solution to (1) becomes non-unique when λ is large enough, and two new, energetically favorable solutions arise in a process known as bifurcation (see Figure 1a and 1b). The two new solutions are stable, and the original solution becomes unstable at the point of bifurcation.

For many applications of beam theory, like column buckling, the instability of the trivial, straight configuration is all that is important, but concentric tube robots typically operate far from these areas and may exhibit instability at other configurations and snap across their workspace as shown in Figure 1d. The equivalent phenomenon for a beam is shown in Figure 1c. Consider an active counter-clockwise rotation of θ (0) starting from θ (0) = 0. If λ is small enough, we expect that the beam will pass stably through a straight configuration when θ (0) = π, and the concentric tube robot will pass stably through the configuration with anti-aligned precurvatures. On the other hand, when λ exceeds the critical value, even when θ (0) = π, the beam will never straighten out and will instead settle into a buckled configuration, and the concentric tube robot will settle into a high-torsion configuration. Eventually, as θ (0) increases to some value beyond π, the buckled configuration becomes unstable and some of the stored energy is released as each system snaps to a new configuration.

In our stability analysis, since we control θ (0) for concentric tube robots, we seek the value of θ (0) at which a concentric tube robot will snap. In the beam buckling literature, this problem is referred to as the stability of postbuckled equilibrium states, and important results have emerged in this area in recent years [16], [17], [18]. There has also been recent interest in robotics in the stable quasistatic manipulation of rods [20]. Before applying these results to concentric tube robots, we first present the mechanics-based kinematic model.

We provide a self-contained description of the kinematic model which is derived from energy. The kinematic model presented here was first derived in [11] and [21]. We present the model in a concise form suitable for implementation, and discuss the simplification of the multi-point boundary value problem to a two-point boundary value problem, which was also mentioned in [11]. We choose the angle of twist and the torsional moment as the model states, which results in continuous solutions even across discontinuities caused by precurvature functions or tube endpoints.

Table I provides a list of variable definitions, and Figure 2 shows the frame definitions for each tube. Each tube has a predefined shape which is described with a material-attached coordinate frame assignment ${\mathit{g}}_i^{\ast }(s_i)=({\mathbf{R}}_i^{\ast },{\mathit{p}}_i^{\ast }):ℝ\to SE(3)$, where ${\mathit{p}}_i^{\ast }(s_i)$ is the origin of the frame and ${\mathbf{R}}_i^{\ast }(s_i)$ is the orientation of the frame. The frame propagates along the tube with its z-axis tangent to the tube centerline and with unit velocity so that the variable s_i is arc length along the i^th tube, and 0 ≤ s_i ≤ L_i, where L_i is the length of the tube. Without loss of generality, the frames ${\mathit{g}}_i^{\ast }$ are chosen as Bishop frames and obey the differential relationship

TABLE I.

Nomenclature

a	Bold typeface for vectors
A	Bold, upright typeface for matrices
n	Number of tubes in concentric tube robot
pB	Position of backbone Bishop frame
RB	Rotation matrix of backbone Bishop frame
ψi	Angle between the material frame of tube i and RB
Rψ	Canonical rotation about z-axis of angle ψ
uB	Bishop frame curvature
·̂	The conversion from ℝ3 to the cross product matrix
(·)∨	Inverse function of ·̂, i.e. (x̂)∨ = x
(·)*	Denotes variable in undeformed state
${\mathit{u}}_i^{\ast }$	Precurvature of the ith tube in the local material frame
kib	Bending stiffness of tube i
kit	Torsional stiffness of tube i
Ki	Linear elastic constitutive map
βi	Arc length where tube i is held
αi	Absolute rotational actuation of tube i
Li	Total length of tube i
β	mini {βi}
L	maxi {βi + Li}
(·)′	Derivative with respect to arc length/dimensionless length
ei	ith standard basis vector
ui	Curvature of the ith tube in the local material frame
θi	Relative angle ψi − ψ1
h, h, hi	Allowable variation function(s)
𝓢	Linear second variation operator
σ	Dimensionless arc length
Fα	Partial derivative of a function F with respect to a
λ	Bifurcation parameter

Fig. 2.

A depiction of a concentric tube robot which has been straightened for clarity, with arc lengths β_i and β_i + L_i located at the proximal and distal ends of the tubes, respectively. The section view A-A depicts the centerline Bishop frame and the material-attached frames of tubes 1 and 2, with angles ψ₁ and ψ₂ labeled.

$$\frac{\partial }{\partial s_i}{\mathit{g}}_i^{\ast }(s_i)={\mathit{g}}_i^{\ast }(s_i)\widehat{{\mathit{\xi }}_i^{\ast }}(s_i)$$

for $\widehat{{\mathit{\xi }}_i^{\ast }}(s_i)\in \mathfrak{s}\mathfrak{e}(3)$. In this case, the “hat” denotes the conversion $\widehat{(·)}:R^6\to \mathfrak{s}\mathfrak{e}(3)$ as defined in [22]. By the preceding definitions, ${\mathit{\xi }}_i^{\ast }(s_i)={[\begin{array}{ll}{({\mathbf{v}}^{\ast })}^T\hfill & {({\mathit{u}}_i^{\ast }(s_i))}^T\hfill \end{array}]}^T$, with v^* = e₃ and ${\mathit{u}}_i^{\ast }(s_i)={[\begin{array}{lll}{u}_{ix}^{\ast }(s_i)\hfill & u_{iy}^{\ast }(s_i)\hfill & 0\hfill \end{array}]}^T$.

The model assumes that the combined tubes follow a common centerline, which we define as another Bishop frame (R_B, p_B). After the conformation of the tubes, we define the resulting material-attached frame of each tube as g_i = (R_i, p_i). While the z-axes of the frames g_i must lie tangent to the z-axis of R_B, the physical constraint does not require the other axes to match because the tubes are free to rotate axially with respect to one another. Thus we have, by definition, that R_i = R_B R_ψi where R_ψi is shorthand for the standard z-axis rotation about the angle ψ_i. The curvature of the i^th tube is ${\mathit{u}}_i={({\mathbf{R}}_i^T{\mathbf{R}}_i^{\prime })}^{\vee }$. Since the predefined frame assignment ${\mathit{g}}_i^{\ast }$ is chosen in the Bishop convention, ${\psi }_i^{\prime }$ is proportional to the axial moment carried by the i^th tube.

The energy of each tube is given according to the Kirchhoff kinetic analogy, in which the stored elastic energy is that of a slender rod that undergoes bending and torsion, but not elongation or shear, according to an arc-length parameterized linear elastic constitutive map K_i (s_i) : ℝ³ → ℝ³ from curvature to moment. When expressed in the frame R_i, the constitutive map is diagonal for annular tubes,

$${\mathbf{K}}_i(s_i)=\left[\begin{array}{ccc}{k}_{ib}(s_i)& 0& 0\\ 0& k_{ib}(s_i)& 0\\ 0& 0& k_{it}(s_i)\end{array}\right],$$

where k_ib represents the bending stiffness, and k_it represents the torsional stiffness. Then, the total energy for n tubes is given by

$$E[{\mathit{u}}_1,\dots ,{\mathit{u}}_n]=\sum _{i=1}^n{\int }_0^{L_i}\mathrm{\Delta }{\mathit{u}}_i^T{\mathbf{K}}_i\mathrm{\Delta }{\mathit{u}}_i{ds}_i,$$ (2)

where $\mathrm{\Delta }{\mathit{u}}_i={\mathit{u}}_i-{\mathit{u}}_i^{\ast }$. The robot arc length s is defined so that s = 0 occurs at the constrained point where the tubes exit the actuation unit. The tubes are actuated at robot arc lengths β_i ≤ 0 so that we have n functions

$$s_i(s)=s-{\beta }_i$$

which relate the robot arc length to the tube arc length. The robot arc length s is then defined on the interval β ≤ s ≤ L where

$$\begin{array}{l}\beta =\underset{i}{min}\{{\beta }_i\}\\ L=\underset{i}{max}\{{\beta }_i+L_i\}\end{array}$$

The actuators also impose rotational actuation of the tubes, modeled as the algebraic conditions ψ_i (β_i) = α_i. The various functions of interest, u_i, ψ_i, K_i, etc. may thus be considered functions of either s_i or of s. From here forward, when an expression explicitly includes any function with the robot arc length s as an argument, all other functions in the expression are assumed, unless otherwise noted, to be evaluated at s as well.

Define the operator [·]_xy as the orthogonal projection onto the first two coordinate axes, i.e. ${[\mathit{x}]}_{xy}=\left(\mathbf{I}-{\mathit{e}}_3{\mathit{e}}_3^T\right)\mathit{x}$. It has been previously shown in the literature by Rucker et al. [21] and Dupont et al. [11] that under these assumptions, extremals of the energy functional require that the backbone curvature ${\mathit{u}}_B={({\mathbf{R}}_B^T{\mathbf{R}}_B^{\prime })}^{\vee }$ satisfy

$${[{\mathit{u}}_B(s)]}_{xy}={\left[{\mathbf{K}}^{-1}\sum _{i\in P(s)}{\mathbf{K}}_i{\mathbf{R}}_{{\psi }_i}{\mathit{u}}_i^{\ast }\right]}_{xy},$$ (3)

with

$$\mathbf{K}(s)=\sum _{i\in P(s)}{\mathbf{K}}_i(s),$$

and the set P (s) = {i ∈ ℕ : 1 ≤ i ≤ n ∧ 0 ≤ s_i (s) ≤ L_i} is the set of indices of tubes which are present at the arc length s. Note that by definition, u_B · e₃ = 0.

Since the unknowns u_i in (2) are related algebraically to u_B through ψ_i, the energy functional may be written in the form

$$E[\mathit{\psi }]={\int }_{\beta }^{L}F(\mathit{\psi },{\mathit{\psi }}^{\prime },s)ds$$

where $\mathit{\psi }={[\begin{array}{ccc}{\psi }_1& \dots & {\psi }_n\end{array}]}^T$. After substituting the relation ${\mathit{u}}_i={\mathbf{R}}_{{\psi }_i}^T{\mathit{u}}_B+{\psi }_i^{\prime }{\mathit{e}}_3$ into Δu_i and the resulting expression into the energy functional, the Euler-Lagrange equations can be applied directly to this functional for each pair of variables ψ_i, ${\psi }_i^{\prime }$. After some simplifications arising from the equal principal bending stiffnesses and the choice of precurvature frames, the kinematic equations are found.

Concentric Tube Robot Kinematics

The spatial configuration of a concentric tube robot is determined by the solution to a boundary value problem with first order states ψ_i,( $k_{it}{\psi }_i^{\prime }$), p_B, and R_B. The solution is governed by the differential equations

$${\psi }_i^{\prime }=\{\begin{array}{ll}{k}_{it}^{-1}(k_{it}{\psi }_i^{\prime })\hfill & 0\le s_i(s)\le L_i\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (4a)

$${(k_{it}{\psi }_i^{\prime })}^{\prime }=\{\begin{array}{ll}-{\mathit{u}}_B^T{\mathbf{K}}_i\frac{\partial {\mathbf{R}}_{{\psi }_i}}{\partial {\psi }_i}{\mathit{u}}_i^{\ast }\hfill & 0\le s_i(s)\le L_i\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (4b)

$${\mathit{p}}_B^{\prime }={\mathbf{R}}_B{\mathit{e}}_3$$ (4c)

$${\mathbf{R}}_B^{\prime }={\mathbf{R}}_B\widehat{{\mathit{u}}_B}$$ (4d)

with boundary conditions

$${\mathit{p}}_B(0)=\mathbf{0},{\mathbf{R}}_B(0)=\mathbf{I}$$ (5a)

$${\psi }_i(\beta )={\alpha }_i,(k_{it}{\psi }_i^{\prime })(L)=0$$ (5b)

Equations (4a) and (4b) are the equations which determine the angle of twist and torsional moment carried by each tube along its arc length. For the elastic stability analysis, we will focus on the second-order form of (4a) and (4b) taken together, along with the boundary conditions of (5b). The elastic stability is independent of (4c), (4d), and (5a).

The boundary conditions (5a) assume that the tubes are constrained at the location chosen as s = 0. If, additionally, some physical constraint is present which straightens the tubes when s < 0, then u_B = 0 trivially over that region. We assume that there is an arc length s^* > β_max such that

$${\mathit{u}}_B(s)=0,\forall s<s^{\ast },$$ (6)

which implies that tubes have no curvature between where the tubes are physically held. Where the i^th tube does not physically exist, it is extended by a non-physical entity that has infinite torsional stiffness (i.e. $k_{it}^{-1}\to 0$), but zero bending stiffness (i.e. k_ib = 0). Intuitively, this must contribute no energy, since neither an infinite nor zero-stiffness element stores energy, and therefore this modification will not change the solution to the energy minimization problem. This extension converts the multi-point boundary value problem uniquely into a two-point boundary value problem at β and L for the states ψ_i and ( $k_{it}{\psi }_i^{\prime }$).

Although the most general results will apply to equations (4a) and (4b), we utilize the following simplification in the bifurcation analysis for the sake of finding closed form expressions. In the case that all tubes have planar precurvature, which is a common design, the precurvature functions can be expressed as ${\mathit{u}}_i^{\ast }={\kappa }_i(s){\mathit{e}}_1$, and the torsional evolution equation (4b) simplifies to

$${(k_{it}{\psi }_i^{\prime })}^{\prime }=\{\begin{array}{ll}\frac{k_{ib}}{k_b}\sum _{j=1}^n{k}_{jb}{\kappa }_i{\kappa }_{j}sin({\psi }_i-{\psi }_j)\hfill & 0\le s_i(s)\le L_i\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (7)

where $k_b={\sum }_{i=1}^n{k}_{ib}$. Due to the difference of angles in the expression sin(ψ_i − ψ_j) on the right hand side, the evolution of torsion is invariant under a constant rotational offset of all angles. Equation (7) may thus be expressed in terms of relative angles θ_i = ψ_i − ψ₁, which we will use for the analysis of two tubes and for plotting results for three tubes.

IV. Bifurcation and Elastic Stability of Two-Tube Robots

Before proceeding to the analysis of many-tube robots, for clarity we first present the analysis of both bifurcation and stability for two-tubes. Where applicable, we introduce the necessary concepts from the literature.

A. Local Bifurcation Analysis

Consider a problem defined by an operator f which takes two arguments, λ ∈ ℝⁿ and x ∈ V. The space V is the configuration space. For the concentric tube robots this is a space of real-valued functions of a single argument, together with the boundary conditions that must be satisfied. The operator f defines a problem f [λ, x] = 0. An equilibrium x(s) = x_e is a fixed point (i.e. it does not change in arc length s) that solves f [λ, x_e] = 0. Note that an equilibrium in this sense is not the same concept as static equilibrium of a mechanical system. A point (λ₀, x_e) on the trivial branch of an equilibrium is called a bifurcation point on this branch if and only if in every neighborhood of this point there is a solution pair (λ, x) with x ≠ x_e [19, p. 149].

The strategy of the local bifurcation analysis is to linearize f about x_e and search for nontrivial solutions x ≠ x_e to the linearized problem. The presence of a nontrivial solution is equivalent to the linearized operator failing to have a bounded inverse, which is a necessary condition for a bifurcation point [19, Theorem 5.4.1].

For two-tube robots with constant precurvature, equation (7) simplifies to

$$f[\lambda ,\theta (\sigma )]={\theta }^{″}-\lambda sin(\theta )=0$$ (8a)

$$\theta (0)=\theta ({\beta }_{\sigma })-{\beta }_{\sigma }{\theta }^{\prime }(0)$$ (8b)

$${\theta }^{\prime }(1)=0,$$ (8c)

where we have nondimensionalized the problem, moved the proximal boundary condition to s = 0, and assumed the tubes have equal transmission length β. Arc length has been nondimensionalized as σ = s/L_c and the dimensionless transmission length β_σ = β/L_c, where L_c is the length over which both tubes are present and precurved. The parameter

$$\lambda =L_c^2{\kappa }_1{\kappa }_2\frac{k_{1b}}{k_{1t}}\frac{k_{2b}}{k_{2t}}\frac{k_{1t}+k_{2t}}{k_{1b}+k_{2b}}.$$

Result 1 (Bifurcation of Two-Tube Robots)

A bifurcation point exists at the point (λ, π) where λ obeys

$${\beta }_{\sigma }=\frac{-cot(\sqrt{\lambda })}{\sqrt{\lambda }}.$$ (9)

We can prove this result by linearizing (8a) at the trivial anti-aligned solution θ (σ) = π and finding a non-trivial solution. The linearization is given by

$${\theta }^{″}+\lambda (\theta -\pi )=0,$$ (10)

which has the general solution

$$\theta (\sigma )=C_{1}cos(\sqrt{\lambda }\sigma )+C_{2}sin(\sqrt{\lambda }\sigma )+\pi .$$

Enforcing the proximal boundary (8b) requires

$$C_1=-{\beta }_{\sigma }\sqrt{\lambda }{C}_2,$$

and substituting this relation into the distal boundary (8c) condition gives

$$\sqrt{\lambda }{C}_2\left[{\beta }_{\sigma }\sqrt{\lambda }sin(\sqrt{\lambda })+cos(\sqrt{\lambda })\right]=0.$$

C₂ = 0 results in the trivial solution θ(σ) = π, but C₂ can take any value if the bracketed quantity goes to zero, which recovers (9) from Result 1.

When β_σ = 0, this simplifies to λ = π²/4, the well-known result for two tubes with no transmission lengths [10], [11]. This result is found in a different form in [15] as an inequality that, if satisfied, guarantees a unique solution to the state-linearized model. A bifurcation diagram which plots the solutions of the nonlinear boundary value problem at θ (1) against the parameter λ for several values of β_σ is shown in Figure 3. The transmission length β_σ can be visualized as “pushing” the bifurcation point towards λ = 0, reducing the bifurcation-free design space.

Fig. 3.

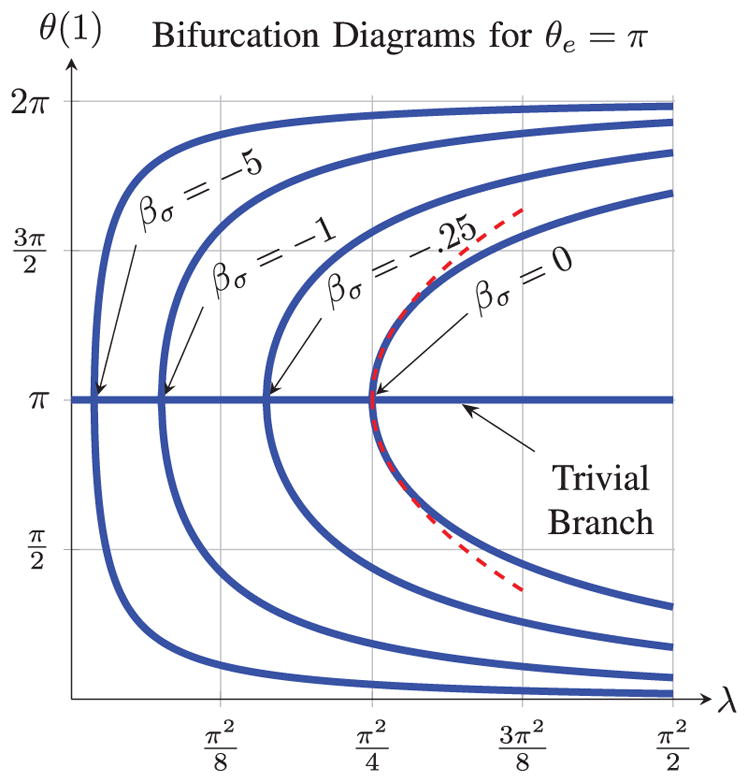
Bifurcation diagrams are shown for various transmission lengths. As the transmission length grows, the bifurcation points, indicated by the arrowheads, are pushed closer to λ = 0. The red dashed line shows equation (11), which describes the behavior near the bifurcation point λ₀ = π²/4.

This type of bifurcation is known as a supercritical pitchfork bifurcation because the bifurcation only occurs for values equal to or exceeding the critical bifurcation parameter. Using perturbation methods, an algebraic relationship between θ(1) and λ near λ₀ = π²/4 can be found as

$$\theta (1)=\pi \pm 2\sqrt{2}\sqrt{\frac{\lambda -{\lambda }_0}{{\lambda }_0}},\lambda \ge \frac{{\pi }^2}{4},$$ (11)

which is derived in [19] for the beam buckling problem. From equation (11) and Figure 3, we see that the non-trivial branches intersect the trivial branch with infinite slope, which explains why snaps may occur when the bifurcation parameter is only slightly greater than the critical value.

In a physical manifestation of a concentric tube robot, the straight transmission lengths will not be equal since each tube must be exposed to be held in the actuation unit. However, it is possible to remedy this such that (9) still applies by finding an equivalent transmission length.

Result 2 (Two-Tube Equivalent Transmission Length)

Any two-tube robot can be equivalently represented as two tubes with equal transmission lengths given by

$${\beta }_{eq,\sigma }=\frac{{\beta }_{1,\sigma }{k}_{2t}+{\beta }_{2,\sigma }{k}_{1t}}{k_{1t}+k_{2t}}.$$ (12)

We can prove this result by first giving the proximal boundary condition with differing transmission lengths

$$\theta (0)={\alpha }_2-{\alpha }_1-{\beta }_{2,\sigma }{\psi }_2^{\prime }(0)+{\beta }_{1,\sigma }{\psi }_1^{\prime }(0).$$ (13)

Next, we give the torsional equilibrium equations, which must be satisfied at every arc length

$$k_{1t}{\psi }_1^{\prime }(0)+k_{2t}{\psi }_2^{\prime }(0)=0.$$ (14)

The last equation necessary to prove (12) is the definition of θ′ (0)

$${\theta }^{\prime }(0)={\psi }_2^{\prime }(0)-{\psi }_1^{\prime }(0).$$ (15)

Combining (14) and (15) defines a relationship for both ${\psi }_1^{\prime }(0)$ and ${\psi }_2^{\prime }(0)$ in terms of θ′(0). This can be substituted into (13) to allow re-expression of the proximal boundary in the same form as (8b) (note that θ (β_σ) = α₂ − α₁ ) where β_σ is given by (12) from Result 2.

B. Local Stability Analysis

The bifurcation analysis gives information on what parameters give rise to multiple kinematic solutions and insight into the local behavior of the system near equilibria, but it does not reveal information about stability away from the equilibria. To obtain this information, we look to the energy landscape of the system. Specifically, when are solutions to Euler’s equations local minima of the energy functional? The answer to this question will also provide a relative measure of stability, which gives an indication of which solutions are closer to instability.

We begin by constructing the energy functional which corresponds to the simplified, non-dimensional boundary value problem of (8). The functional

$$\begin{array}{l}E[\theta ]={\int }_{{\beta }_{\sigma }}^0\frac{1}{2}{({\theta }^{\prime })}^{2}d\sigma +{\int }_0^1\left(\frac{1}{2}{({\theta }^{\prime })}^2-\lambda cos(\theta )\right)d\sigma \\ ={\int }_{{\beta }_{\sigma }}^{1}F(\sigma ,\theta ,{\theta }^{\prime })d\sigma \end{array}$$ (16)

will give the desired result after application of the Euler-Lagrange equation on each interval [β_σ, 0] and [0, 1],

$${(F_{{\theta }^{\prime }})}^{\prime }-F_{\theta }=0.$$ (17)

The energy functional (16) in terms of θ is related to the functional (2) by a scaling and constant offset, and therefore defines an equivalent minimization problem.

Much like the finite dimensional case where the eigenvalues of the Hessian matrix classify stationary points of functions into minima, maxima, and saddle points, we use the second order information about solutions to determine elastic stability. The second variation operator 𝒮 takes the place of the Hessian matrix, and, in the case where the mixed partial derivatives F_θθ′ = 0, it is given by

$$\mathcal{S}h=-{(F_{{\theta }^{\prime }{\theta }^{\prime }}{h}^{\prime })}^{\prime }+F_{\theta \theta }h,$$ (18)

where h is a variation of θ which satisfies the necessary boundary conditions, i.e. (θ + h)(β_σ) = θ(β_σ) and (θ + h)′ (1) = 0. The elastic stability is determined by the eigenvalues of the operator 𝒮, which is in this case a Sturm-Liouville operator. Some further details connecting the eigenvalues of 𝒮 with the energy functional are provided in Appendix A.

From the energy functional (16), the second variation operator 𝒮 is defined from (18) as

$$\mathcal{S}h=-h^{″}+\lambda u(\sigma )cos(\theta )h,$$ (19)

together with its domain, where u(σ) is the unit step function introduced for conciseness. The domain of 𝒮 includes the boundary conditions h(β_σ) = 0 and h′ (1) = 0, which are necessary for θ + h to satisfy the boundary values of the original problem. The second variation of the energy δ² E[h] > 0 if and only if all eigenvalues of 𝒮 are positive. This condition can be ensured by solving the following initial value problem.

Result 3 (Stability of Two-Tube Robots)

A solution θ to the boundary value problem

$${\theta }^{″}-\lambda sin(\theta )=0,\theta (0)=\theta ({\beta }_{\sigma })-{\beta }_{\sigma }{\theta }^{\prime }(0),{\theta }^{\prime }(1)=0$$

is stable if the solution to the initial value problem defined by

$$\mathcal{S}h=0,h({\beta }_{\sigma })=0,h^{\prime }({\beta }_{\sigma })=1$$ (20)

satisfies h′ (σ) > 0 for β_σ ≤ σ ≤ 1.

See Appendix B for a proof of this result.

This result indicates that a sufficient condition for determining the stability of a solution entails only an integration of an initial value problem, which can be performed numerically. Importantly, the exact same reasoning which produced Result 3 can be repeated in reverse in arc length, which produces the following corollary.

Corollary 1

The stability of a solution θ can also be determined by solution of the initial value problem defined by

$$\mathcal{S}h=0,h^{\prime }(1)=0,h(1)=1$$ (21)

The solution is stable if h(σ) > 0 for β_σ ≤ σ ≤ 1.

Due to the choice of the boundary conditions of the Corollary, and noting that 𝒮h = 0 is equivalent to what we obtain if (8) is differentiated by θ(1), the solution h of Corollary 1 can be interpreted as the slope h(s) = ∂θ (s)/∂θ (1). The equations and boundary conditions of Corollary 1 were previously derived in [14], but the result in terms of local stability was not stated and the result was not derived in the context of examining the system energy. We also have the following corollary due to the continuity of h′ (1) and h(β_σ) with respect to changes in λ and rotational actuation and the symmetry of the two stability problems.

Corollary 2

The value h′ (1) in Result 3, or the value of h(β_σ) in Corollary 1, may be used as a measure of relative stability when the conditions of Result 3 and Corollary 1 are met, where larger positive values indicate greater stability. Moreover, the values h′ (1) and h(β_σ) in the two tests are the same.

The results of the stability test for a two-tube robot with different values of λ and nonzero transmission length are shown in Figure 4 on an S-curve, which plots solutions to (8) at the proximal and distal endpoints. The S-curve was previously used to visualize the stability of two tubes by Dupont et al. [11]. The test clearly reproduces the known result that the negative slope region of the S-Curve is unstable and thus these configurations are not physically possible in concentric tube robots. Note especially that the relative stability measure varies continuously with respect to θ(1).

Fig. 4.

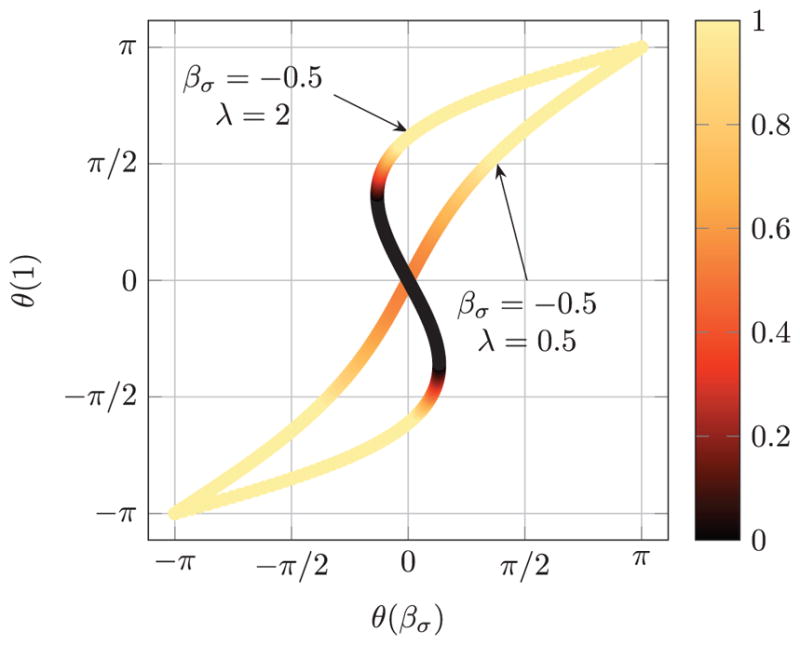
An S-Curve is shown for two different choices of parameters β_σ and λ. The curve is colored based on the relative stability measure h′(1), with the color axis truncated at 0 and 1.

The elastic stability test of Result 3 also implicitly contains the bifurcation results of Section IV-A, despite being derived from different perspectives. This is illustrated in Figure 5 where the bifurcation result from (9) plots β_σ against λ at the equilibrium θ_e = π, while the entire space is colored according to relative stability. Equation (9) occurs exactly at the points where the relative stability is zero. This means that when the solution under test is the equilibrium θ(σ) = π, the appearance of a conjugate point exactly at the end of the domain is the same as the appearance of a non-trivial solution to the linearized problem, since the second variation operator and the linearization of (8) are equivalent at equilibria.

Fig. 5.

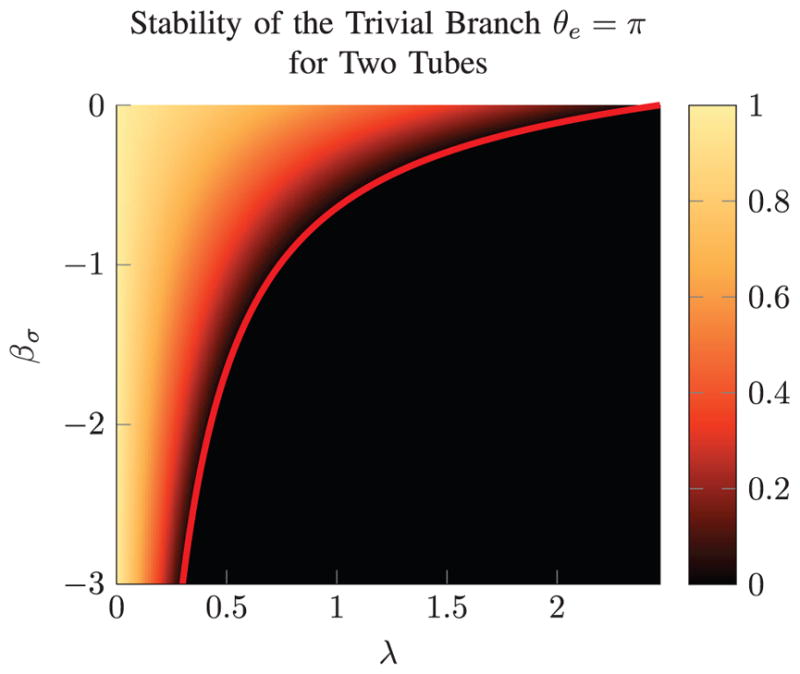
This plot shows the relative stability of the θ_e = π trivial branch. The red curve gives the bifurcation result from (9). A point above this curve guarantees stability for two tubes across all rotational actuation, while a point below indicates a bifurcation, and a snap will be seen for some rotational actuation. Relative stability values less than 0 have been truncated to 0.

From Figure 5 it is also clear that transmission lengths are very important to consider for guaranteed elastic stability. The designer should consider ways to reduce these lengths, if possible. Alternatively, if the transmission sections do not need to be superelastic, replacing these sections with stiffer sections can dramatically improve the stability of the design.

The stability analysis also reveals why the instability always appears first at equilibrium solutions. Compare a solution h_π(σ) to the initial value problem of Result 3, where θ(σ) = π, to a second solution h₂(σ), with θ(σ) ≠ π. Note that θ = π maximizes the coefficient of h in (19). If the function $h_{\pi }^{\prime }(\sigma )$ does not cross zero on its domain, then neither does $h_2^{\prime }(\sigma )$, because everywhere $h_{\pi }^{″}\le h_2^{″}$. This proves that if the equilibrium θ(s) = π has not bifurcated for a given λ, all tube rotations are elastically stable. This fact was formerly given by Ha et al. in [14].

V. Bifurcation and Elastic Stability of Many-Tube Robots

A. Local Bifurcation Analysis

Consider the simplified model of a many-tube concentric tube robot given by equation (7) where the boundaries are

$$\begin{array}{l}{\psi }_i(0)={\alpha }_i-{\beta }_i{\psi }_i^{\prime }(0)\\ (k_{it}{\psi }_i^{\prime })(L)=0.\end{array}$$ (22)

For our initial analysis, we assume the transmission lengths of the tubes are equal such that β_i = β (we will relax this constraint later). We define ψ_e ∈ ℝⁿ as an equilibrium point of (7), and linearizing (7) at the equilibrium gives

$${({\mathbf{K}}_t{\mathit{\psi }}^{\prime })}^{\prime }={\mathbf{A}}_e(\mathit{\psi }-{\mathit{\psi }}_{\mathit{e}}),{\mathbf{A}}_e={\frac{\partial {({\mathbf{K}}_t{\mathit{\psi }}^{\prime })}^{\prime }}{\partial \mathit{\psi }}|}_{\mathit{\psi }={\mathit{\psi }}_e},$$ (23)

where K_t = diag(k_1t, …, k_nt). The entries of the symmetric matrix A_e are given by

$${\mathbf{A}}_e(i,j)=\{\begin{array}{ll}\sum _{\begin{array}{l}k=1\\ k\ne j\end{array}}^n{\mathrm{\Phi }}_{ik}{c}_{ik}\hfill & i=j\hfill \\ -{\mathrm{\Phi }}_{ij}{c}_{ij}\hfill & i\ne j\hfill \end{array}$$ (24)

where c_ij = cos(ψ_i − ψ_j) and

$${\mathrm{\Phi }}_{ij}=\frac{k_{ib}{k}_{jb}{\kappa }_i{\kappa }_j}{k_b}.$$ (25)

Result 4 (Bifurcation of n Tube Robots)

The equilibrium ψ_e bifurcates when

$$\frac{\beta }{L}={\beta }_{\sigma }=\frac{-cot(\sqrt{{\gamma }_i})}{\sqrt{{\gamma }_i}},$$ (26)

where γ_i = −L² λ_i and λ_i is any of the eigenvalues of ${\mathbf{K}}_t^{-1}{\mathbf{A}}_e$.

We begin the proof of this result by re-expressing (23) as a first order system. We define the state vector

$$\mathit{x}=\left[\begin{array}{c}\mathit{\psi }-{\mathit{\psi }}_e\\ {\mathbf{K}}_t{\mathit{\psi }}^{\prime }\end{array}\right],$$ (27)

such that (23) becomes

$${\mathit{x}}^{\prime }=\underset{{\mathbf{\Gamma }}_e}{\underbrace{\left[\begin{array}{cc}\mathbf{0}& {\mathbf{K}}_t^{-1}\\ {\mathbf{A}}_e& \mathbf{0}\end{array}\right]}}\mathit{x}.$$ (28)

Consider a section of the robot (s₁, s₂) of length ℓ_s where both the precurvature of each tube and the number of tubes is constant, (28) can be solved in closed form as

$$\mathit{x}(s_2)=e^{{\ell }_s{\mathbf{\Gamma }}_e}\mathit{x}(s_1).$$ (29)

For intuition, consider the most simple several tube case where Γ_e is constant for s ≥ 0. This corresponds to a fully overlapped configuration where the precurved portion of each tube begins at s = 0 and terminates at s = L. The linearized twist and moment at s = L is

$$\mathit{x}(L)=e^{L{\mathbf{\Gamma }}_e}\mathit{x}(0),$$ (30)

which can be simplified further by decomposing ${\mathbf{K}}_t^{-1}{\mathbf{A}}_e$ into its eigendecomposition¹ as ${\mathbf{K}}_t^{-1}{\mathbf{A}}_e=\mathbf{V}\mathbf{\Lambda }{\mathbf{V}}^{-1}$. With this simplification, (30) becomes

$$\mathit{x}(L)={\mathbf{TGT}}^{-1}\mathit{x}(0),$$

where

$$\mathbf{G}=\left[\begin{array}{cc}cosh(L\sqrt{\mathbf{\Lambda }})& {\sqrt{\mathbf{\Lambda }}}^{-1}sinh(L\sqrt{\mathbf{\Lambda }})\\ \sqrt{\mathbf{\Lambda }}sinh(L\sqrt{\mathbf{\Lambda }})& cosh(L\sqrt{\mathbf{\Lambda }})\end{array}\right],$$

and

$$\mathbf{T}=\left[\begin{array}{cc}\mathbf{V}& \mathbf{0}\\ \mathbf{0}& {\mathbf{K}}_t\mathbf{V}\end{array}\right].$$

More details of this computation can be found in Appendix D. Note that the hyperbolic trigonometric functions only operate on the diagonal elements of the matrix argument, such that the four resulting blocks of G are diagonal. Also note that one of the eigenvalues of ${\mathbf{K}}_t^{-1}{\mathbf{A}}_e$ will always be zero since (7) is invariant under a rotational shift of all angles ψ_i → ψ_i + δ. Note that the function $sinh(L\sqrt{\lambda })/\sqrt{\lambda }$ takes the value L at λ = 0.

We can express the proximal and distal bounds from (22) in state form as

$$\begin{array}{ll}\hfill \left[\begin{array}{cc}\mathbf{I}& \beta {\mathbf{K}}_t^{-1}\end{array}\right]\mathit{x}(0)& =\mathbf{0}\hfill \\ \hfill \left[\begin{array}{cc}\mathbf{0}& \mathbf{I}\end{array}\right]\mathit{x}(L)& =\mathbf{0},\hfill \end{array}$$ (31)

and substituting (30) into the distal bound of (31) gives

$$\left[\begin{array}{cc}\mathbf{0}& \mathbf{I}\end{array}\right]e^{{\mathbf{\Gamma }}_{e}L}\mathit{x}(0)=\mathbf{0}.$$

Combining the boundary conditions into a single matrix equation, we have

$$\mathbf{M}\mathit{x}(0)=\mathbf{0},$$

where

$$\mathbf{M}=\left[\begin{array}{cc}\mathbf{I}& \beta {\mathbf{K}}_t^{-1}\\ {\mathbf{M}}_{21}& {\mathbf{M}}_{22}\end{array}\right],$$

and

$$\begin{array}{l}{\mathbf{M}}_{21}={\mathbf{K}}_t\mathbf{V}\sqrt{\mathbf{\Lambda }}sinh(L\sqrt{\mathbf{\Lambda }}){\mathbf{V}}^{-1}\\ {\mathbf{M}}_{22}={\mathbf{K}}_t\mathbf{V}cosh(L\sqrt{\mathbf{\Lambda }}){\mathbf{V}}^{-1}{\mathbf{K}}_t^{-1}.\end{array}$$

For a given equilibrium point, when M drops rank, a nontrivial solution exists that solves (7) with the boundaries from (22), which indicates the equilibrium point has bifurcated. The matrix M will drop rank when its determinant is zero, which, because V is full rank, simplifies to

$$\mid cosh(L\sqrt{\mathbf{\Lambda }})-\sqrt{\mathbf{\Lambda }}sinh(L\sqrt{\mathbf{\Lambda }})\beta \mid =0.$$

Since Λ is diagonal, this determinant evaluates to zero when

$$\beta =\frac{coth(L\sqrt{{\lambda }_i})}{\sqrt{{\lambda }_i}}$$ (32)

for any λ_i, where λ_i is the i^th eigenvalue of ${\mathbf{K}}_t^{-1}{\mathbf{A}}_e$. This equation is only solvable for −π²/4 ≤ λ_i < 0 since β ≤ 0. If we let γ_i = −L²λ_i, then equation (32) may be rewritten as (26) from Result 4, which is exactly analogous to equation (9) for two tubes. For β = 0, the value of λ_j which solves this equation is L²λ_j = −π²/4, which is a generalization of the design condition shown in the literature for snap-free two-tube robots.

B. Local Stability Analysis

The local stability analysis of solutions for n tubes is analogous to the procedure for two tubes. Just as for two tubes, the condition δ² E > 0 is simplified to requiring all eigenvalues of the second variation operator 𝓢 to be positive. Fortunately, the eigenvectors of 𝓢 still form an orthonormal basis for the underlying space of allowable variations, but each eigenvector now consists of n functions rather than a single function. The extension of the scalar Sturm-Liouville problem to a matrix Sturm-Liouville problem is considered in depth in [23].

It is a standard result in the calculus of variations that the generalization of the conjugate point test to n unknown functions involves a condition on the determinant of the fundamental solution matrix of the Jacobi equations, which are the equations 𝓢h = 0 [24]. As before, the result is usually only derived for Dirichlet boundary conditions, but again we apply the modified test proposed by Manning [17]. Reference [16, Section II] provides an excellent high level overview of the arguments necessary to conclude that the following result is a sufficient condition. A straightforward generalization of the argument in the proof of Result 3 for why the eigenvalues are positive on a small interval for the two-tube problem results in the conclusion that this also holds in the case of n tubes. The following result provides the stability test for n tubes at an arbitrary solution ψ(s) of Euler’s equations.

Result 5 (Stability of Solutions for n Tubes)

A solution ψ(s) to (4), with boundary conditions (5), is stable if the 2n × 2n fundamental solution matrix H for the differential equations

$$\begin{array}{l}{\mathbf{H}}^{\prime }=\mathbf{\Gamma }\mathbf{H},\\ \mathbf{H}(\beta )=\mathbf{I},\end{array}$$

where the matrix

$$\mathbf{\Gamma }(s)=\left[\begin{array}{cc}\mathbf{0}& {\mathbf{\Gamma }}_{{\mathit{\psi }}^{\prime }{\mathit{\psi }}^{\prime }}^{-1}\\ {\mathbf{F}}_{\mathit{\psi }\mathit{\psi }}& \mathbf{0}\end{array}\right],$$

satisfies the condition det H₂₂ (s) > 0, where H₂₂ is the n×n lower-right sub-matrix of H, for all s ∈ [β, L]. The matrices ${\mathbf{F}}_{{\mathit{\psi }}^{\prime }{\mathit{\psi }}^{\prime }}^{-1}$ and F_ψψ are defined element-wise, and as functions of arc length, as

$$\begin{array}{c}{\mathbf{F}}_{{\mathit{\psi }}^{\prime }{\mathit{\psi }}^{\prime }}^{-1}(i,j)=\{\begin{array}{ll}{k}_{it}^{-1}\hfill & i=j\mathit{and}s\in [{\beta }_i,{\beta }_i+L_i]\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\\ {\mathbf{F}}_{\mathit{\psi }\mathit{\psi }}(i,j)=\{\begin{array}{ll}0\hfill & s\notin [{\beta }_i,{\beta }_i+L_i]\cap [{\beta }_j,{\beta }_j+L_j]\hfill \\ F_{ii}\hfill & i=j\wedge s\in [{\beta }_i,{\beta }_i+L_i]\cap [{\beta }_j,{\beta }_j+L_j]\hfill \\ F_{ij}\hfill & i\ne j\wedge s\in [{\beta }_i,{\beta }_i+L_i]\cap [{\beta }_j,{\beta }_j+L_j]\hfill \end{array}\end{array}$$

where

$$\begin{array}{l}{F}_{ii}=-{\frac{\partial {\mathit{u}}_B}{\partial {\psi }_i}}^T\frac{\partial {\mathbf{R}}_{{\psi }_i}}{\partial {\psi }_i}{\mathbf{K}}_i{\mathit{u}}_i^{\ast }-{\mathit{u}}_B^T\frac{{\partial }^2{\mathbf{R}}_{{\psi }_i}}{\partial {\psi }_i^2}{\mathbf{K}}_i{\mathit{u}}_i^{\ast }\\ F_{ij}=-{\frac{\partial {\mathit{u}}_B}{\partial {\psi }_j}}^T\frac{\partial {\mathbf{R}}_{{\psi }_i}}{\partial {\psi }_i}{\mathbf{K}}_i{\mathit{u}}_i^{\ast }\end{array}$$

See Appendix C for a proof of this result.

Corollary 3

The stability of a solution ψ(s) may also be determined by solution of the differential system of equations in Result 5 with initial condition H(L) = I, with the stability condition now replaced by det H₁₁ (s) > 0.

Corollary 4

The value of det H₂₂(L) in Result 5, or the value of det H₁₁(β) in Corollary 3, may be used as a measure of relative stability when the solution is stable, where larger positive values indicate greater stability. Furthermore, the values det H₂₂(L) and det H₁₁(β) for the two tests are the same.

Once again, the stability results capture the bifurcation results when applied to equilibrium solutions. In fact, the matrix Γ is equal to the matrix Γ_e of equation (28) when ψ(σ) = s_e is chosen as the solution under test. Thus, the equations of Result 5 can be used to provide all of the results in this paper.

VI. Preventing Snap for All Actuation: Implementation

To this point, our bifurcation results for robots composed of n tubes has been limited to the case when the tubes start and end at the same arc length and have equal straight transmission lengths. This case is very useful for gaining intuition and seeing the relationship between two-tube robots and many-tube robots but is a rarely-seen configuration for physical prototypes. A general many-tube robot configuration will have several distinct sections with differing numbers of tubes and tube precurvatures as well as differing transmission lengths. The purpose of this section is to provide an algorithm which is capable of testing for bifurcation of equilibria for this case.

A. Finding Equilibria

For this section, we will assume that the ends of each tube are not precisely aligned in arc length, which is a standard requirement for concentric tube robot prototypes. This requirement means we will have distinct sections where 1, 2, 3, …, n tubes are present. Enforcing this requirement ensures that the only equilibria present in the system are when the tubes are aligned or anti-aligned. This can be easily understood as follows: in the two-tube section of the robot, there are only two equilibria (i.e. tubes aligned and anti-aligned), and as you move back towards the base of the robot, the three tube section must have the third tube in the same plane as the two tubes within it (i.e. it must be aligned/anti-aligned relative to the tubes within it) so that the two-tube section remains at an equilibrium. This argument propagates backwards from the tip of the robot to the section with n tubes, and guarantees that the only equilibria are those where the tubes are aligned/anti-aligned.

When the ends of tubes exactly overlap, additional equilibria arise. In fact, when there are more than three tubes which are exactly overlapped, there are infinite equilibria. In simulations, we have found that these special-case equilibria bifurcate after the anti-aligned equilibria, but because we have not proven this, we limit our algorithm to tube configurations where the tubes ends are not precisely at the same arc length. Because the designer only needs to consider aligned/anti-aligned equilibria, the only θ_e that needs to be considered is composed of only zero and π elements. Therefore, for an n tube robot, the designer needs to only consider 2ⁿ⁻¹ equilibria.

B. Checking Equilibria for Bifurcation

For each section (which we identify with the index q) of the robot, where the number of tubes present and the precurvature of each tube is constant, there will be a different Γ_q,e from (28). We assume that the most proximal section corresponds to q = 1 and that there are m total sections. The state x in each section is given by (28). For the first section of the robot, s ∈ [0, s₁]; the twist and moment at s₁ are x(s₁) = e^{s₁Γ_{1, e}}x(0). Similarly, for the second section of the robot, s ∈ [s₁, s₂], the twist and moment at s₂ are x(s₂) = e^{(s₂;−s₁)Γ_{2, e}} x(s₁). By propagating the proximal boundary through the sections to the most distal arc length of the robot, s = L, we have that

$$\mathit{x}(L)=\mathbf{P}\mathit{x}(0),$$ (33)

where

$$\mathbf{P}=e^{{\ell }_m{\mathrm{\Gamma }}_{m,e}}{e}^{{\ell }_{m-1}{\mathrm{\Gamma }}_{m-1,e}}\dots e^{{\ell }_1{\mathrm{\Gamma }}_{1,e}},$$ (34)

and ℓ_i is the length of section i. In matrix form, the proximal boundary condition from (22) can be written as

$$\mathit{x}(0)=\left[\begin{array}{c}-{\mathbf{BK}}_t^{-1}\\ \mathbf{I}\end{array}\right]({\mathbf{K}}_t{\mathit{\psi }}^{\prime })(0)$$

where B is diag(β_i, …, β_n). This can be substituted into (33) to produce

$$\mathit{x}(L)=\underset{\mathbf{W}}{\underbrace{\mathbf{P}\left[\begin{array}{c}-\mathbf{B}{\mathbf{K}}_t^{-1}\\ \mathbf{I}\end{array}\right]}}({\mathbf{K}}_t{\mathit{\psi }}^{\prime })(0).$$ (35)

In the bottom half of this system, the distal, moment-free boundary condition at s = L, from equation (5b), is embedded and must be equal to zero.

Algorithm 1.

Determining a Bifurcation-Free Actuation Space

Input: Tube parameters (geometry, material, lengths): p
	Translational actuation: B
	All equilibria: {e1,...,en} ∈ e
Output: Bifurcation: true/false
1	define m sections ← using B,p
2	for k = 1 to m do
3	Φk ← Eq. (25) using p
4	end for
5	for all e do
6	for k = 1 to m do
7	Γk,e ← Eq. (28), (24) using Φk, e
8	end for
9	P ← Eq. (34) using Γ1,e,...,Γm,e.
10	W2 ← Eq. (35) using P, B.
11	if det(W2) ≤ 0 then
12	return true
13	end if
14	end for
15	return false

If the bottom half of W, denoted W₂, is singular, then a non-trivial solution can be found (i.e. a non-equilibrium solution can be found that solves the linearized boundary value problem) and this indicates that the equilibrium is at a bifurcation point. Since a bifurcation indicates that our system has lost its uniqueness, we know that the robot could snap between configurations.

As tube parameters and translational actuation values are smoothly varied, the determinant will vary in a smooth way, even across a bifurcation point. We know that |W₂ | > 0 for non-bifurcated configurations (this can easily be shown with straight tubes, for example), so any configuration with |W₂ | ≤ 0 indicates the equilibrium configuration assessed has previously bifurcated. We note that |W₂ | = 0 at every mode of bifurcation, similar to how a beam has additional buckling modes, and therefore it is good practice to initialize a simulation in a known stable configuration and vary parameters from this configuration, checking each step for a zero crossing of the determinant.

Algorithm 1 gives a test to determine if a circularly pre-curved robot in any configuration (where the ends of tubes are not exactly overlapped), composed of any number of tubes with varying transmission lengths has any bifurcated equilibria. We believe, and have tested in simulation, that if no equilibria has bifurcated, then the entire actuation space is elastically stable (this is proven only for two tubes). Therefore, we believe that Algorithm 1 can be used to determine if the entire actuation space is elastically stable. However, because we have not proven for more than two tubes that instability is guaranteed to arise at an equilibrium, we title the algorithm “Determining a bifurcation-free actuation space.” We also note that to be certain a design which results from Algorithm 1 contains no elastic instabilities, Result 5 can be used. To see an example application of this algorithm for a three tube robot, see [1].

VII. Experimental Validation

To validate the bifurcation and stability analysis, we performed experiments with two circularly precurved tubes. The tubes were designed so that they would snap or pass stably through the anti-aligned configuration depending on the choice of base location where the inner tube is grasped.

A. Materials & Methods

The physical data for the two tubes used are shown in Table II. The experimental setup is shown in Figure 6. The outer tube is grasped and held fixed at the front plate of the actuation unit, while the inner tube is grasped at varied distances proximal to this point. For each transmission length tested, one of four straight, rigid sheaths may be added to the front of the robot which physically straightens the tubes over that length. It can be shown that the model predicts that this situation is equivalent to the tubes simply not having any precurvature over the length where the sheath is present, thus allowing us to test model predictions which vary over both dimensionless parameters λ and β_σ with a single set of tubes.

TABLE II.

Data for Snapping and Bifurcation Experiments

	Tube 1	Tube 2
Outer Dia.	1.02 mm	1.78 mm
Inner Dia.	0.86 mm	1.27 mm
Precurvature	10.78 m−1	9.96 m−1
Curved Length	100 mm	100 mm

Fig. 6.

The experimental setup for the bifurcation/elastic stability experiments.

The lengths of the sheaths, denoted by L_sheath, were 0, 10, 20, 30, and 40 mm, and the grasp locations for tube 1, denoted by β_*, were −23, −30, −40, −50, −60, −70, −80, −90, and −100 mm. Since the point s = 0 is defined at the most distal point on the sheath, the values of β₁ and β₂ are given by

$${\beta }_1={\beta }_{\ast }-L_{\mathit{sheath}}{\beta }_2=-L_{\mathit{sheath}}.$$ (36)

Let L_c be the overlapped length given by L_c = 100 mm – L_sheath. Then, λ is calculated as $\lambda =L_c^2{u}_{1x}^{\ast }{u}_{2x}^{\ast }(1+\nu )$ For Poisson’s ratio ν we assume a value of 0.33 as quoted by Nitinol manufacturers. The equivalent transmission length β_eq,σ is calculated using equation (12).

For each pair L_sheath and β_* which were tested, the tubes were first checked for a bifurcation. Bifurcation was determined by attaching a flag to the end of the inner tube and observing whether all tip rotations were achievable and stable through rotations of the base. If some tip rotations were not achievable, then the snap angle was determined by rotating the tubes through four snaps. First, the snap was approached by rotating the inner tube base counter-clockwise as viewed from behind. When a snap was visibly or audibly observed, the angle was recorded. Second, the inner tube was rotated clockwise through a snap at the same speed, and the angle recorded. The third and fourth observations were made by repeating the two previous steps. All rotations through the snaps were performed at a speed of approximately 1 degree/s.

Denote the four recorded angles θ_ccw,1, θ_cw,1, θ_ccw,2, and θ_cw,2. Because of the symmetry in the graph of Figure 4, the snap angle (in radians) is given by π plus half of the average distance between the snaps,

$${\theta }_{\mathit{snap}}=\pi +\left|\frac{{\theta }_{cw,1}-{\theta }_{\mathit{ccw},1}+{\theta }_{cw,2}-{\theta }_{\mathit{ccw},2}}{4}\right|.$$ (37)

For each experimental trial, the conditions of Corollary 3 were solved via a bisection routine to find the relative tip angle at which the condition det H₁₁ (β) = 0 is met. The modeled relative base angle corresponding to the tip angle is then used as the modeled snap angle prediction for comparison against θ_snap.

B. Results & Discussion

The results of the experiment are shown in Figures 7 and 8, which assess the accuracy of the model predictions for bifurcation and stability, respectively. Figure 7 plots the observation of whether the anti-aligned equilibrium is stable versus the λ and β_σ pairs for each experimental trial. Configurations above the bifurcation boundary do not exhibit snapping, while those below do exhibit snapping. The model correctly predicted 42 of the 45 data points. The model predicted that three of the configurations would not snap when in fact they did, and all of these erroneous predictions were near the bifurcation boundary.

Fig. 7.

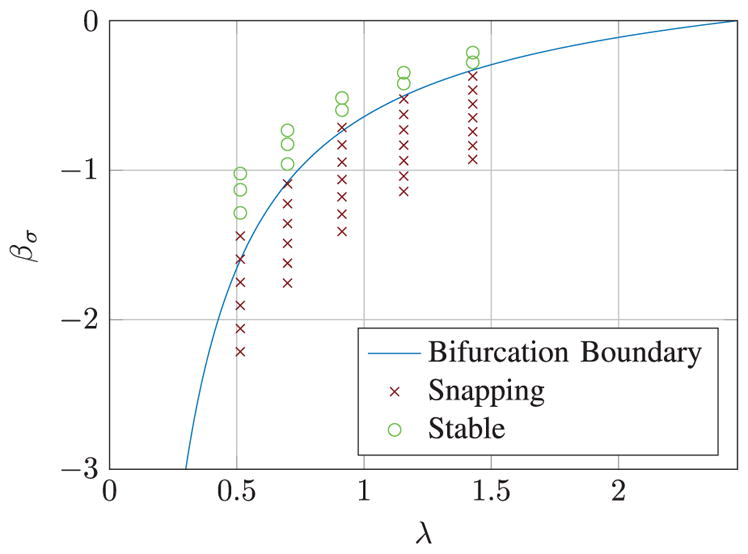
Graph of bifurcated and non-bifurcated configurations. Bifurcation was predicted correctly in all but three configurations, with all three of the incorrect predictions near the bifurcation boundary. These results are an experimental validation of Figure 5.

Fig. 8.

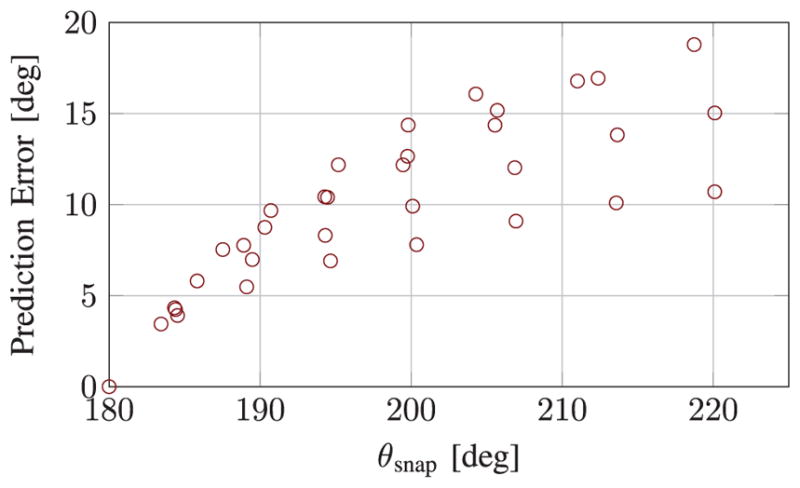
Graph of snap angle prediction error vs. the measured snap angle. Generally, as the snap angle increases the prediction becomes increasingly conservative. All model data predicts the snap at a lesser angle than was observed experimentally.

Figure 8 shows the error in the modeled snap angle as a function of the observed snap angle. All errors were less than 20 °, and the general trend is for the error to increase as the snap angle does. All model data predicts the snap at a lesser angle than was observed experimentally.

Sources of error in these predictions include both unmodeled effects such as friction and nonlinear material behavior, and measurement errors in the tube design parameters such as the curved length and precurvature. In addition, there is a small amount of uncertainty (±1 mm) in the value of β_* since these lengths were measured by ruler.

The predictions of snap angle can be made significantly more accurate by altering the assumed ratio of bending stiffness to torsional stiffness. It was previously noted by Lock and Dupont that a value of ν = 0.6 yielded a good fit for the experimentally measured torsional relationship between tip and base angles [25]. Although this value of Poisson’s ratio is not physically realistic, the material behavior of Nitinol under bending and torsion is known to differ from traditional strength of materials formulas due to tension/compression asymmetry, and thus the simplification k_ib/k_it = 1 + ν may not be valid even for small strains [26]. We used a nonlinear least-squares regression to fit the snap angle data and found a best fit of k_ib/k_it = 1.605, which resulted in a mean absolute prediction error of 2.06°. This also corroborates the previous finding that ν ≈ 0.6. Although a more in-depth analysis of nonlinear material effects is outside the scope of this article, it is possible that future work will be able to make better model predictions by taking into account the nonlinear elastic behavior of Nitinol.

VIII. Discussion

The preceding analysis reveals insights about the stability of concentric tube robots and enables prevention of snaps in high curvature robots. For example, the addition of a third tube may allow actuators to steer around instabilities. In addition, path planners and controllers can take advantage of the smooth relative stability measure to plan stable paths and to avoid instability during teleoperation.

The following example shows how the stability theory outlined above has ramifications for motion planners and controllers. Existing approaches for dealing with solution stability in motion planning methods have relied on the fact that the kinematic solutions are almost everywhere locally continuous with respect to the set of variables ${\mathit{q}}_0=\left[\begin{array}{cccccc}{\beta }_1& \dots & {\beta }_n& {\alpha }_1({\beta }_1)& \dots & {\alpha }_n({\beta }_n)\end{array}\right]$. However, from the standpoint of the topology of the solutions, a much better choice for planning purposes is the distal angles α₁(L), …, α_n(L), since this makes all components of the kinematic solution continuous with respect to the set of configuration variables ${\mathit{q}}_L=\left[\begin{array}{cccccc}{\beta }_1& \dots & {\beta }_n& {\alpha }_1(L)& \dots & {\alpha }_n(L)\end{array}\right]$. Then, the motion planning problem can be considered as finding continuous, admissible paths in both the physical space occupied by the robot and the configuration variable space.

Previously, without a test which could accurately determine the stability of an arbitrarily chosen configuration q_L, sampling based planning methods could not guarantee that the resulting planned trajectory is everywhere elastically stable. Figure 9 shows for a three-tube robot how a continuous path in the distal angle space remains continuous in the proximal angles, but the shape of the trajectory becomes distorted when the relative stability measure approaches zero. If these distortions are allowed to become too large, then very small changes in the proximal relative angles of the tubes can result in large but stable angular displacements at the distal end. Near these points of ill-conditioning, modeling errors or unpredictable external loads may make it possible for the physical robot to snap.

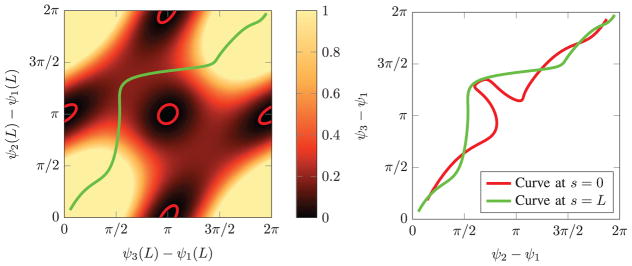
Fig. 9.

Here the stability metric det H₁₁ of Corollary 3 is shown on the left for a system of three tubes of equal stiffness and circular precurvature which subtend a total arc of 78.2 degrees in the undeformed state. Each tube is assumed to be actuated rotationally at s = 0, and is precurved over the entire length of the tube. If there were only two tubes, no continuous path would exist for the tubes to be rotated fully 360 degrees with respect to one another. With three tubes, however, a continuous path can be found which allows tubes 2 and 3 to be rotated 360 degrees with respect to tube 1. The green line drawn on the left chart shows a chosen stable path in the distal angle space, and the right chart shows how that path transforms to the proximal angles which are actuated. The amount of distortion in the curve is related to the stability measure, with lower stability measures indicating greater distortion.

At present, the relative stability measure is a heuristic that indicates which solutions are closer to instability, hence the use of the word “relative.” It is important to note that we have not associated this measure with energetic units, and also have not proven bounds on how rapidly the measure can change across the actuation space. In principle, the smallest eigenvalue of 𝓢 could give a more direct measurement of stability, but in practice this quantity is much more difficult to compute.

One important consequence of the step from two tubes to three tubes is that the third tube can actually provide paths in actuation space for the tubes to make complete rotations with respect to one another without snapping, which would not be possible with only two tubes. This effect exists for designs that are beyond the bifurcation of the anti-aligned equilibria, but for which the regions of instability in the rotational actuation space have not yet connected. For circularly precurved tubes, we suspect the growth of instability from the bifurcating equilibria is a fundamental property regardless of the number of tubes, but we leave proof of this to future work. For complex, non-planar tube designs, there may not exist any equilibria, so it is less clear where instability will first arise; however, Result 5 still predicts the instability.

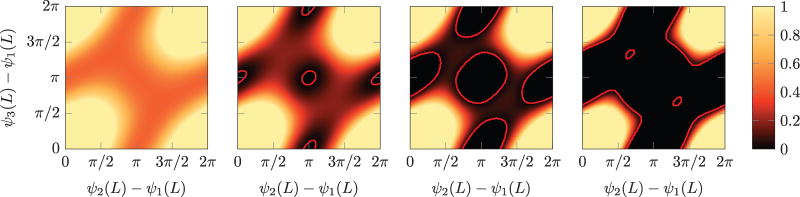
Note that the true rotational actuator space is of each angle modulo 2π, so that the opposite edges of the graphs in Figure 10 are equivalent to one another. In the last plot of Figure 10, the connection between the unstable regions has prevented all paths which traverse complete relative rotations of any tube with respect to any other tube. In some cases such a full rotation is possible between one pair of tubes but not another pair.

Fig. 10.

In these plots we show the effect of increasing component tube curvature on the relative stability metric. We simulated three fully overlapping tubes with zero transmission length and an overlapped length of 50 mm and equal curvature and stiffness. The curvatures, from left to right, are 21 m⁻¹, 27.5 m⁻¹, 31 m⁻¹, and 36 m⁻¹. As the curvature increases, the regions of instability grow from the bifurcated equilibria until they disconnect the stable equilibria. In the last figure it can be seen that very small contours surround the special case equilibria at (2π/3, 4π/3) and (4π/3, 2π/3), where the precurvatures are offset by 120°, which are remarkably still stable despite the entire area surrounding them being unstable.

Resolved-rate style control methods can also take advantage of the stability metric for redundancy resolution or for a secondary weighted objective optimization. By computing or precomputing the gradient of the stability metric, ∇_q det(H₁₁(β)), resolved-rate methods can locally enforce a minimum stability measure to ensure that a relative margin of stability is maintained from snapping configurations.

In terms of stability over the entire rotational actuation space, increasing transmission lengths and tube precurvatures tend to continuously destabilize the system. We show this effect by plotting the relative stability metric for every relative angle ψ_i − ψ₁ at the distal tip L. This space contains all possible configurations up to a rigid body rotation. Figure 10 shows how increases of the tube precurvature in a three tube robot cause instability to arise at the equilibria with curvatures anti-aligned, and the regions of instability eventually grow until the space of stable tip rotations becomes disconnected and traversing the full relative rotation of any tube can only occur through a snap.

IX. Conclusions and Future Work

In this paper we have provided an analysis of bifurcation and elastic stability of unloaded concentric tube robots. This paper proposes an energy-based stability computation which assigns a relative measure of stability to each configuration of the robot, which we believe will be useful for future work in control and motion planning. We have also connected existing frameworks from the mechanics literature on Euler beams to concentric tube robots. The bifurcation analysis enables a systematic, computationally inexpensive, and closed form algorithm for designers to create snap-free robots.

One important future advancement to the stability theory will be the inclusion of externally applied loads, so that motion planning and control can incorporate stability information when the environmental interaction forces are large. Our results in this paper provide an approach to understanding concentric tube robot stability, and it is our hope that this work will facilitate the use of high curvature concentric tube robot designs that were previously avoided.

Biographies

Hunter B. Gilbert (S’10) received the B.S. degree in mechanical engineering from Rice University in Houston, TX in 2010. Since then he is a pursuing a Ph.D. in mechanical engineering at Vanderbilt University in Nashville, TN, in the Medical Engineering and Discovery lab. He is currently researching medical robotics and continuum robotics. He received the NSF Graduate Research Fellowship in 2012.

Richard J. Hendrick (S’12) received his B.S. degree in biomedical engineering from Texas A&M University in College Station, TX in 2011. He now is pursuing his Ph.D. in mechanical engineering at Vanderbilt University and is interested in hand-held robotics, continuum robot design and control, and robotic endoscopic surgery. He currently works in the Medical Engineering and Discovery lab. He received the NSF Graduate Research Fellowship in 2013.

Robert J. Webster III (S’97-M’08–SM’14) received the B.S. degree in electrical engineering from Clemson University in 2002 and the M.S. and Ph.D. degrees in mechanical engineering from the Johns Hopkins University in 2004 and 2007, respectively.

In 2008, he joined the Faculty of Vanderbilt University. He is currently an Associate Professor of Mechanical Engineering, Electrical Engineering, Otolaryngology, Neurological Surgery, and Urologic Surgery and directs the Medical Engineering and Discovery Laboratory. He serves on the steering committee for the Vanderbilt Institute in Surgery and Engineering, which brings together physicians and engineers to solve challenging clinical problems. He chairs the SPIE Image-Guided Procedures, Robotic Interventions, and Modeling Conference, and serves as an associate Editor for IEEE Transactions on Robotics.

Dr. Websters research interests include surgical robotics, image-guided surgery, and continuum robotics. He is a recipient of the IEEE Robotics & Automation Society Early Career Award, the National Science Foundation CAREER award, the Robotics Science and Systems Early Career Spotlight Award, and the IEEE Volz Award.

Appendix A. The Second Variation

In the calculus of variations, it is well known that Euler’s equation is a necessary but not sufficient condition for a minimum, and it is equivalent to the first variation functional being equal to zero,

$$\delta E[\mathit{h}]={\int }_{\mathcal{D}}[F_{\mathit{x}}\mathit{h}+F_{{\mathit{x}}^{\prime }}{\mathit{h}}^{\prime }]d\sigma =0$$

for all admissible variations h for which x₀ + h satisfies the boundary conditions of the problem. The quantities F_x and F_x′ are evaluated along the extremal curve x₀ for which Euler’s equation is satisfied. The expression F_xh is interpreted as a row vector multiplied by a column vector.

It is also well known that for x₀ to be a weak minimum of the energy functional, the second variation δ² E[h] must be strictly positive for all nonzero admissible variations h. The second variation is given by

$${\delta }^{2}E[\mathit{h}]=\frac{1}{2}{\int }_{\mathcal{D}}(F_{\mathit{x}\mathit{x}}\mathit{h},\mathit{h})+2(F_{\mathit{x}{\mathit{x}}^{\prime }}{\mathit{h}}^{\prime },\mathit{h})+(F_{{\mathit{x}}^{\prime }{\mathit{x}}^{\prime }}{\mathit{h}}^{\prime },{\mathit{h}}^{\prime })d\sigma$$ (A.1)

where F_xx, F_xx′, and F_x′x′ are the matrices of second partial derivatives, evaluated as before along the extremal curve x₀, and the parentheses denote the scalar product (a, b) = Σ a_ib_i.

For the problems generated by the concentric tube robot problem, we have that the mixed partial derivatives F_xx′ = 0. An integration by parts reveals that (A.1) is equivalent to

$${\delta }^{2}E[\mathit{h}]=\langle \mathcal{S}\mathit{h},\mathit{h}\rangle ={\int }_{\mathcal{D}}(\mathcal{S}\mathit{h},\mathit{h})d\sigma$$ (A.2)

which is an inner product on the underlying Hilbert space of admissible variations. Then, the spectral theorem for self-adjoint operators on Hilbert spaces shows that the second variation is strictly positive only when all eigenvalues of the second variation operator 𝓢, defined by

$$\mathcal{S}\mathit{h}=-{(F_{{\mathit{x}}^{\prime }{\mathit{x}}^{\prime }}{\mathit{h}}^{\prime })}^{\prime }+F_{\mathit{x}\mathit{x}}\mathit{h},$$

are positive.² It is a prerequisite for the condition δ² E[h] > 0 to be transformed into the condition on the eigenvalues of 𝓢 that the eigenvectors of 𝓢 form a complete orthonormal set for the underlying Hilbert space. For the operators generated by the concentric tube robot model, the eigenvectors of 𝓢 do form such a basis, as guaranteed by Theorem 1 of Dwyer and Zettl, which says that 𝓢 is a self-adjoint operator [23]. The eigenvalue equation 𝓢ψ = ρψ is a Sturm-Liouville eigenvalue problem, which has a countably infinite number of orthonormal eigenvectors with eigenvalues that are all real and bounded below. Because there are an infinite number of eigenvalues, a direct computation will not suffice for a feasible numerical test of stability.

Fortunately, continuous changes in F_xx, F_x′x′ and the endpoints of the interval 𝓓 cause continuous changes in the spectrum of 𝓢 [27]. The basic idea for a numerical test is the following: if one can show that 𝓢 has positive eigenvalues on some shortened domain which is a subset J ⊂ 𝓓, then the endpoints of J can be continuously varied to the endpoints of 𝓓 while watching for zero-crossings in the eigenvalues of 𝓢 [17]. If 𝓢 has a zero eigenvalue for some choice of J, then we have an equation 𝓢h = 0 on that domain with boundary conditions on h also satisfied at the endpoints of J.

If the problem has Dirichlet boundary conditions, it is well known that stability is determined by looking for conjugate points [24], and the conjugate point formulation and the eigenvalue characterization have been shown to be equivalent [17], [28]. For concentric tube robots, the boundary conditions are not Dirichlet, and therefore the conjugate point condition must be modified. We must first verify that all eigenvalues of 𝓢 are positive when the operator is taken to act on a shorter domain. For concentric tube robots, this means a shorter robot. Second, we look for conjugate points, which occur when 𝓢h = 0 is solved for an admissible variation h, which is precisely when 𝓢 has an eigenvalue at zero. This two-part modification is explained in detail by Hoffman et al. [16].

We are no longer guaranteed that a conjugate point results in an increase in the number of negative eigenvalues [17], because the Neumann boundary condition, in general, prevents the eigenvalues from being strictly decreasing functions of the domain length. Nevertheless, we can still conclude that the absence of a conjugate point implies positive eigenvalues, making it a sufficient condition.

Appendix B. Proof Of Result 3

We define the family of related eigenvalue problems

$$\mathcal{S}\varphi =\rho \varphi ,\varphi (\beta )=0,{\varphi }^{\prime }(a)=0$$ (B.1)

for the variable endpoint a, with β < a ≤ 1. It is known that the eigenvalues ρ_i, i = 1, 2, …, move continuously with respect to continuous changes in a [17], [27]. The basic idea of the test is that if there is a small enough a where all eigenvalues are positive, then for an eigenvalue of the problem (B.1), with a = 1, to be negative, it must cross zero as a varies between β and 1. This condition can be checked with a simple test.

To look for an eigenvalue at zero in any of the related problems (B.1), we assume that zero is an eigenvalue, with eigenvector h, by setting 𝓢h = 0, i.e. we set −h″+ λcos(θ)h = 0. It follows that there exists a length σ for which 𝓢h = 0, h(β) = 0, and h′(σ) = 0. Since we do not know σ, we begin at the proximal boundary, where we know that h(β) = 0. Because 𝓢 is linear, the eigenvectors have arbitrary scale, so that if h is an eigenvector, h′(β) may be arbitrarily chosen by scaling (h must be non-trivial). We choose h′(β) = 1, and integrate the differential equation forward. In doing this, we have enforced both the differential form and the proximal boundary of the entire family of operators (B.1). If the distal boundary condition h′(σ) = 0 is not satisfied for any σ, then zero is not an eigenvalue for any of the operators of the family (B.1), contradicting the assumption of an eigenvalue at zero.

Since zero is not an eigenvalue for any of the problems, and if the problem has no negative eigenvalues for a sufficiently small value of a, it is not possible that the boundary value problem on the whole interval has a negative eigenvalue by continuity of the spectrum with changes in the interval endpoint a.

To see that no eigenvalues are negative for small a, note that 𝓢 can be decomposed into 𝓢 = 𝒯 + 𝒬, with 𝒯 h = −h″ and 𝒬h = λcos(θ)h. As a becomes smaller, it is known that the eigenvalues of T become larger. The operator 𝒬 can be seen as a perturbation of 𝒯, and when the eigenvalues of 𝒯 are made sufficiently large by choosing a sufficiently small, the perturbation 𝒬, being bounded in magnitude, is incapable of moving an eigenvalue negative. The argument of this paragraph is made rigorously by Hoffman and Manning in [16].

Appendix C. Proof Of Result 5

We begin by showing that the eigenvalues of the problem are positive when the boundary conditions at L are moved to be close to the boundary conditions at β. Here the allowable variation h_i belongs to the space 𝓓_i ([β_i, a_i]) = {f, (k_it f′) ∈ AC([β_i, a_i]) : f(β_i) = 0, (k_it f′)(a_i) = 0}, and the collection h belongs to the Cartesian product 𝓓(𝓢) = 𝓓₁ × … × 𝓓_n. Consider the eigenvalue problem in which a_i = β_i + ε for some small ε. Then, we still have the decomposition of 𝓢 as in the proof of Result 3 as 𝓢 = 𝒯 + 𝒬. The operator 𝒯 acts diagonally on the h_i, and so the eigenvalues γ of 𝒯h = γh may be found as the eigenvalues of n independent problems. The eigenvalues are positive and the smallest eigenvalue can be made arbitrarily large by the choice of ε. Consider the extension of h_i to the whole interval [β, L], where it must be that h(β) = h(β_i) and h′(L) = h′(β_i +L_i) since the two-point extension of (4) simulates the tubes as having infinite torsional stiffness and zero bending stiffness in the regions [β, β_i] and [β_i + L_i, L]. The operator 𝒬 is identically the zero operator over the interval [β, β_max] due to the restriction of equation (6) and the form of F_ψψ. The extended domain of the operator will be called 𝓓_[β,L] (𝓢). We will refer to h as the extension, since any solution on the domain 𝓓(𝓢) can be extended to a solution on the domain 𝓓_[β,L] (𝓢). The eigenvalues of 𝓢 do not change during the extension to the left when all β_i are moved to the left to β. The eigenvalues may change as all a_i which are less than β_max are increased to β_max, but all remain strictly greater than zero since the equations are decoupled and still of the form 𝒯h = γh. Finally, the eigenvalues may change by a bounded amount as the a_i are increased to β_max + ε, but by choice of ε we can guarantee that this change will not cause the eigenvalues to become negative. Thus, there is some domain for which the eigenvalues are all positive. As a_i are then increased together, a_i = a → L, if an eigenvalue crosses zero we have a sub-problem on the interval [β, a] for which 𝓢h = 0 has a non-trivial solution h, which is to say that there is a choice of constants c with c ≠ 0 so that H₂₂(a)c = 0, and therefore h(σ) = H₁₂c is an eigenvector with eigenvalue zero. If, on the other hand, we do not have det H₂₂(a) = 0 for any a, then it must be that if zero is not an eigenvalue of 𝓢h = 0 on any interval [β, a], and since the spectrum changes continuously with a, det H₂₂ > 0 on the whole interval thus guarantees that 𝓢 has only positive eigenvalues on the whole domain [β, L].

The proof tacitly assumes that the eigenvalues move continuously with changes in the endpoint of the interval on which 𝓢 is defined, which is known to be true for the scalar Sturm-Liouville problem [27]. It is reasonable to assume this remains true for the matrix problem due to the fact that the resolvent operators of 𝓢 on different domains with “close” endpoints are close in precise sense. For a discussion of resolvent convergence in the context of Sturm-Liouville problems, see for example [29].

Appendix D. Computation of the State Transition Matrix e^LΓ_e

First, assume that Γ_e is constant over some length L. Additionally, assume that all tubes are present in this section. Then, use the change of coordinates y = T⁻¹ x, to yield

$${\mathit{y}}^{\prime }={\mathbf{T}}^{-1}{\mathbf{\Gamma }}_e\mathbf{T}\mathit{y}=\mathbf{Q}\mathbf{y}$$ (D.1)

where

$$\mathbf{Q}=\left[\begin{array}{cc}\mathbf{0}& {\mathbf{V}}^{-1}{\mathbf{K}}_t^{-1}{\mathbf{K}}_t\mathbf{V}\\ {\mathbf{V}}^{-1}{\mathbf{K}}_t^{-1}{\mathbf{A}}_e\mathbf{V}& \mathbf{0}\end{array}\right]=\left[\begin{array}{cc}\mathbf{0}& \mathbf{I}\\ \mathbf{\Lambda }& \mathbf{0}\end{array}\right]$$ (D.2)

Compute the flow of the differential equation (D.1) over a length L as

$$\mathit{y}(L)=e^{L\mathbf{Q}}\mathit{y}(0)$$ (D.3)

The matrix exponential e^LQ is given by

$$e^{L\mathbf{Q}}=\mathbf{G}=\left[\begin{array}{cc}cosh(L\sqrt{\mathbf{\Lambda }})& {\sqrt{\mathbf{\Lambda }}}^{-1}sinh(L\sqrt{\mathbf{\Lambda }})\\ \sqrt{\mathbf{\Lambda }}sinh(L\sqrt{\mathbf{\Lambda }})& cosh(L\sqrt{\mathbf{\Lambda }})\end{array}\right],$$ (D.4)

where we define the hyperbolic trigonometric functions and the square roots to operate only on the diagonal elements of the matrix arguments. This equivalence can be shown by comparing the Taylor series expansions of e^LQ and the Taylor series expansions of the entries in G. Then, in the original coordinates we have

$$\mathit{x}(L)={\mathbf{TGT}}^{-1}\mathit{x}(0)$$ (D.5)

as claimed.