A Longitudinal Support Vector Regression for Prediction of ALS Score

Abstract

Longitudinal studies play a key role in various fields, including epidemiology, clinical research, and genomic analysis. Currently, the most popular methods in longitudinal data analysis are model-driven regression approaches, which impose strong prior assumptions and are unable to scale to large problems in the manner of machine learning algorithms. In this work, we propose a novel longitudinal support vector regression (LSVR) algorithm that not only takes the advantage of one of the most popular machine learning methods, but also is able to model the temporal nature of longitudinal data by taking into account observational dependence within subjects. We test LSVR on publicly available data from the DREAM-Phil Bowen ALS Prediction Prize4Life challenge. Results suggest that LSVR is at a minimum competitive with favored machine learning methods and is able to outperform those methods in predicting ALS score one month in advance.

I. Introduction

Longitudinal analyses are common in clinical research, particularly in longitudinal studies. These analyses are typically conducted via model-driven regression approaches such as linear regression models, mixed-effects models, or the generalized estimating equations [1,2]. These approaches assume a specific form of model (e.g., linear) and therefore require strong prior assumptions regarding the data. Furthermore, these methods require a primal-space implementation and are therefore not scalable to high-dimensionality data due to high computational demands.

The potential for machine learning techniques to make a contribution to longitudinal clinical studies was recently highlighted in a crowdsourcing competition known as the DREAM-Phil Bowen ALS Prediction Prize4Life challenge [3]. The goal of this challenge was to develop algorithms that can improve the prediction of Amyotrophic lateral sclerosis (ALS) (also known as Lou Gehrig’s disease) progression as measured by the ALS Functional Rating Scale (ALSFRS). ALS is a fatal neurodegenerative disease with substantial heterogeneity in its clinical presentation. This makes diagnosis and effective treatment difficult. Surprisingly, none of the contestants explicitly modeled the temporal nature of the data in their training methods. Time-resolved features generally could not be incorporated into the machine-learning algorithms employed. Rather, participants performed linear regression on the time-varying features and represented those features by a slope and intercept [3]. (Other data reduction techniques were used as well, e.g., maximum/minimum representations.)

In another recent development, Chen and Bowman proposed a longitudinal support vector classifier (LSVC) as an approach that is scalable to classify high-dimensional longitudinal data such as neuroimaging data [4,5]. LSVC extends the well-known support vector machine (SVM) to longitudinal data by simultaneously estimating the traditional SVM separating hyperplane parameters with proposed temporal trend parameters. The authors provided only a limited test result on two time points of fMRI imaging data. To our knowledge, further extensive tests of LSVC have not been published.

We have hypothesized that Chen and Bowman’s longitudinal extensions to the SVM could be further generalized as a longitudinal support vector regression (LSVR) and that the LSVR method may be applicable to longitudinal studies such as the ALS challenge. In this work, we present an evaluation of the LSVR on anonymized public data provided by the organizers of the DREAM-Phil Bowen ALS Prediction Prize4Life challenge. We did not seek to repeat the challenge itself. However, we did compare the performance of LSVR with an implementation of traditional linear support vector regression (SVR) [6] as well as a random forest approach, similar to the approach used by many of the challenge contestants. (e.g., [7]).

II. Methods

As LSVR is an extension of SVR, we first review the primal formulation of SVR and its dual form for quadratic programming (QP) optimization. Then we show how SVR is generalized to LSVR and describe the QP formulation of LSVR. Our derivation of LSVR closely follows Chen and Bowman’s derivation of LSVM [4,5], including use of similar notation. The reader should be cautioned that implementation of LSVR requires a QP solver such as found in Matlab (The Mathworks, Natick, MA) or an original implementation of a QP solver. Standard SVM libraries such as libSVM [8] cannot be used with LSVR.

A. SVR and dual problem

Suppose we are given clinical training data x_s ∈ ℛ^p corresponding to N subjects, i.e., s = 1,…,N as well as N corresponding ALSFRS scores y_s. In ε-SVR, the goal is to find a function f(x) that has at most ε deviation from the assessed scores y for all the training data, and at the same time is as flat as possible (equivalent to minimizing the gap in SVM) [9]. Then we have

$$f(\mathbf{x})={\mathbf{w}}^T\mathrm{\Phi }(\mathbf{x})+b.$$

We can write this problem as a convex optimization problem:

$$\mathrm{min\hspace{1em}\hspace{1em}}\frac{1}{2}{\Vert \mathbf{w}\Vert }^2$$

$$\mathrm{s.t.\hspace{1em}\hspace{1em}}\{\begin{array}{c}\hfill y_i-{\mathbf{w}}^{\mathit{T}}\mathrm{\Phi }({\mathbf{x}}_i)-b\le \epsilon \hfill \\ \hfill {\mathbf{w}}^{\mathit{T}}\mathrm{\Phi }({\mathbf{x}}_i)+b-y_i\le \epsilon \hfill \end{array}$$

where Φ is a function mapping x to the feature space. Analogously to the soft margin loss function that was adapted to SVM by Cortes and Vapnik [10], one can introduce slack variables ξ_i, ${\mathrm{\xi }}_{\mathrm{i}}^{*}$ to the optimization problem. Hence we arrive at the formulation:

$$\text{min\hspace{1em}\hspace{1em}}\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C{\sum }_{i=1}^N({\xi }_i+{\xi }_i^{*})$$

$$\text{s.t.\hspace{1em}\hspace{1em}}\{\begin{array}{cc}\hfill y_i-{\mathbf{w}}^{\mathit{T}}\mathrm{\Phi }({\mathbf{x}}_i)-b\hfill & \hfill \le \epsilon +{\xi }_i\hfill \\ \hfill {\mathbf{w}}^{\mathit{T}}\mathrm{\Phi }({\mathbf{x}}_i)+b-y_i\hfill & \hfill \le \epsilon +{\xi }_i^{*}\hfill \\ \hfill {\xi }_i,{\xi }_i^{*}\hfill & \hfill \ge 0\hfill \end{array}$$

The constant C > 0 determines the trade-off between the flatness of f (which corresponds to the magnitude of ‖w‖²) and the amount up to which deviations larger than ε are tolerated.

In most cases, it is computationally advantageous to solve the optimization problem in its dual formulation as described by:

$${\text{min}}_{\gamma ,\gamma *}\frac{1}{2}\sum _{i,j=1}^N({\gamma }_i-{\gamma }_i^{*})({\gamma }_j-{\gamma }_j^{*})\mathbf{G}({\mathbf{x}}_i,{\mathbf{x}}_j)-\sum _{i=1}^N{y}_i({\gamma }_i-{\gamma }_i^{*})+\epsilon \sum _{i=1}^N({\gamma }_i-{\gamma }_i^{*})$$

$$\mathrm{s}.\mathrm{t}.{\sum }_{i=1}^N{y}_i({\gamma }_i-{\gamma }_i^{*})=0\text{and}{\gamma }_i,{\gamma }_i^{*}\in [0,C]$$

where G(x_i, x_j) =< Φ(x_i), Φ(x_j) > acts as inner product that represents an entry in kernel matrix G. Then the above dual problem can be rewritten as

$${\text{min}}_{\gamma ,\gamma *}\frac{1}{2}[{({\mathbf{\gamma }}^{*})}^T,{\mathbf{\gamma }}^T]\left[\begin{array}{cc}\hfill \mathbf{G}\hfill & \hfill -\mathbf{G}\hfill \\ \hfill -\mathbf{G}\hfill & \hfill \mathbf{G}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathbf{\gamma }}^{*}\hfill \\ \hfill \mathbf{\gamma }\hfill \end{array}\right]+[\epsilon {\mathbf{e}}^T-{\mathbf{y}}^T,\epsilon {\mathbf{e}}^T+{\mathbf{y}}^T]\left[\begin{array}{c}\hfill {\mathbf{\gamma }}^{*}\hfill \\ \hfill \mathbf{\gamma }\hfill \end{array}\right]$$

$$\mathrm{s}.\mathrm{t}.{\mathbf{z}}^T\left[\begin{array}{c}{\mathbf{\gamma }}^{*}\hfill \\ \mathbf{\gamma }\hfill \end{array}\right]=0,{\gamma }_i,{\gamma }_i^{*}\in [0,C],i=1,2,\dots ,N$$

where $\mathbf{z}={[\underset{N}{\underbrace{1,\dots ,1}},\underset{N}{\underbrace{-1,\dots ,-1}}]}^T$.

Once the separating hyperplane has been determined through QP optimization, the estimated regression value of a new observation x_i can be obtained as

$${ŷ}_i=\sum _i{\alpha }_i\mathbf{G}({\mathbf{x}}_i,\mathbf{x})+\hat{b}$$

where α is calculated by γ^* − γ and nonzero α are considered as support vectors.

B. Longitudinal SVR

Consider longitudinal data collected from N subjects at T measurement occasion or visits, with p features quantified during each visit. The expanded feature matrix is then TN by p. Let ${\mathbf{x}}_s^{(t)}$ represent the features collected for subject s at time t. Hence, our aim is to assign each individual, a T-by-p matrix ${\tilde{\mathbf{x}}}_s={[{\mathbf{x}}_s^{(1)},{\mathbf{x}}_s^{(2)},\dots ,{\mathbf{x}}_s^{(T)}]}^T$, a T-by-1 vector ${\mathbf{ỹ}}_s={[y_s^{(1)},y_s^{(2)},\dots ,y_s^{(T)}]}^T$. We predict linear trends of change

$${\mathbf{x}}_s^{(1)}+{\beta }_1{\mathbf{x}}_s^{(2)}+\dots +{\beta }_{T-1}{\mathbf{x}}_s^{(T)}={\tilde{\mathbf{x}}}_s^T\mathit{\beta }$$

$$y_s^{(1)}+{\beta }_1{y}_s^{(2)}+\dots +{\beta }_{T-1}{y}_s^{(T)}={\mathbf{ỹ}}_s^T\mathit{\beta }$$

where unknown parameter vector β = [1, β₁, β₂, …, β_{T − 1}]^T is a T-by-1 vector. The trend information takes into account observational dependence within subjects. We intend to jointly estimate the parameter vector β and α in a LSVR model.

The Lagrangian function incorporating longitudinal parameter is as follows:

$$ℒ≔\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C{\sum }_{i=1}^N({\xi }_i+{\xi }_i^{*})-{\sum }_{i=1}^N({\eta }_i{\xi }_i+{\eta }_i^{*}{\xi }_i^{*})-\sum _{i=1}^N{\gamma }_i(\epsilon +{\xi }_i-y_i+<\mathbf{w},{\mathbf{x}}_{\mathit{i}}>+b)-\sum _{i=1}^N{\gamma }_i^{*}(\epsilon +{\xi }_i^{*}+y_i-<\mathbf{w},{\mathbf{x}}_{\mathit{i}}>-b)=\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^N({\xi }_i+{\xi }_i^{*})-{\sum }_{i=1}^N({\eta }_i{\xi }_i+{\eta }_i^{*}{\xi }_i^{*})-\sum _{i=1}^N{\gamma }_i(\epsilon +{\xi }_i-{ỹ}_i^T\beta +<\mathbf{w},{\tilde{\mathbf{x}}}_i^T\beta >+b)-\sum _{i=1}^N{\gamma }_i^{*}(\epsilon +{\xi }_i^{*}+{ỹ}_i^T\beta -<\mathbf{w},{\tilde{\mathbf{x}}}_i^T\beta >-b)$$ (1)

Here ℒ is the Lagrangian and η_i, ${\eta }_i^{*}$, γ_i, ${\gamma }_i^{*}$ are the Lagrange multipliers. It follows from the saddle point condition that the partial derivatives of ℒ with respect to the primal variables (w, b, ξ_i, ${\xi }_i^{*}$) have to vanish to optimize the Lagrangian function. Thus we are left with

$$\frac{\partial ℒ}{\partial b}=\sum _{i=1}^N({\gamma }_i^{*}-{\gamma }_i)=0$$ (2)

$$\frac{\partial ℒ}{\partial \mathbf{w}}=\mathbf{w}-\sum _{i=1}^N({\gamma }_i-{\gamma }_i^{*}){\tilde{\mathbf{x}}}_i^T\beta =0$$ (3)

$$\frac{\partial ℒ}{\partial {\xi }_i}=c-{\gamma }_i-{\eta }_i=0$$ (4)

$$\frac{\partial ℒ}{\partial {\xi }_i^{*}}=c-{\gamma }_i^{*}-{\eta }_i^{*}=0$$ (5)

Substituting equations (2) through (5) into (1) yields the dual-space quadratic programming problem:

$$\text{max\hspace{1em}\hspace{1em}}-\frac{1}{2}{\sum }_{i,j=1}^N({\gamma }_i-{\gamma }_i^{*})({\gamma }_j-{\gamma }_j^{*}){\mathit{\beta }}^{\mathit{T}}{\tilde{\mathbf{x}}}_{\mathit{i}}{\tilde{\mathbf{x}}}_j^T\mathit{\beta }+{\sum }_{i=1}^N{ỹ}_i^T\mathit{\beta }({\gamma }_i-{\gamma }_i^{*})-\epsilon {\sum }_{i=1}^N({\gamma }_i-{\gamma }_i^{*})$$

$$\text{s.t.\hspace{1em}\hspace{1em}}{\sum }_{i=1}^N({\gamma }_i^{*}-{\gamma }_i)=0\text{and}{\gamma }_i,{\gamma }_i^{*}\in [0,C]$$

Similarly, the above dual problem can be rewritten as

$${\text{min}}_{{\mathbf{\alpha }}_m}\frac{1}{2}{\mathbf{\alpha }}_m\left[\begin{array}{cc}\hfill {\mathbf{G}}_m\hfill & \hfill -{\mathbf{G}}_m\hfill \\ \hfill -{\mathbf{G}}_m\hfill & \hfill {\mathbf{G}}_m\hfill \end{array}\right]{\mathbf{\alpha }}_m+{\mathbf{y}}_m^T{\mathbf{\alpha }}_m$$

where α_m = [γ^*T β₁γ^*T … β_{T − 1}γ^*T γ^T β₁γ^T ⋯ β_{T − 1}γ^T]^T, y_m = [εe^T −y^(1)T −y^(2)T … −y^(T)T εe^T + y^(1)T y^(2)T ⋯ y^(T)T]^T and

$${\mathbf{G}}_m=\left[\begin{array}{ccc}\hfill {\mathbf{G}}^{(1,1)}\hfill & \hfill \dots \hfill & \hfill {\mathbf{G}}^{(1,T)}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{G}}^{(T,1)}\hfill & \hfill \dots \hfill & \hfill {\mathbf{G}}^{(T,T)}\hfill \end{array}\right],$$

subject to

$${\mathbf{z}}^T\left[\begin{array}{c}\hfill {\gamma }^{*}\hfill \\ \hfill \gamma \hfill \end{array}\right]=0,{\gamma }_i{\gamma }_i^{*}\in [0,C],i=1,2,\dots ,N$$

and there is no constraint on β.

Parameters α_m can be determined using QP and then β can be estimated from α_m to obtain the relationship among responses of different time points.

III. Experimental Results

We investigated the performance of the proposed method by applying it to public ALS challenge data and comparing the results with that of two popular machine-learning methods, specifically LibLinear SVR [11] and the Random Forest (RF) implementation function TreeBagger in Matlab.

A. Data set

Experimental data were downloaded from The DREAM-Phil Bowen ALS Prediction Prize4Life challenge website. This large data set comprises 1824 anonymized patients from phase 2 and 3 clinical trials. Although the original challenge segmented the data into training, validation, and holdout sets, we rather followed a cross-validation protocol. Up to twelve months of longitudinal data as well as the corresponding ALSFRS are included in the feature space. There are about 44 time varying features, including protein biomarkers, urine pH, calcium, etc., as well as 34 constant features, including age, race, sex, etc. In our tests, instead of estimating the slope between months 3 and 12 (as was done in the original challenge), we predict the next month’s ALSFR based on the clinical data up to and including the current month.

B. Experimental design

Let $y_s^{(t)}$ represents the ALSFRS of month t for subject s. When predicting ${ŷ}_s^{(t+k)}$, the training features include clinical data up to month t as well as $y_s^{(1)},y_s^{(2)},\dots ,y_s^{(t)}$. Then we predict ${ŷ}_s^{(t+k)}$ by training obtained static features for another LibLinear and RF, renamed as LibLinear-M and RF-M. In this paper, we predict ALSFRS one, two, and three months ahead, e.g., ${ŷ}_s^{(t+k)}$, k = 1,2,3, using data up to month t. When k = 1, we investigate the prediction performance of using month 1 to t (t = 3,4, … 11), respectively. When k = 2 and k = 3, we evaluate the performance of up to month 10 and 9, respectively.

We perform the same experiments using LSVR, LibLinear SVR and RF. LibLinear SVR and RF were each implemented with two treatments of the data in the feature vectors. For those algorithms, in order to provide versions of the tests comparable with the ALS challenge addition, we convert each type of time-resolved features per patient into static features by calculating their mean across t months. These reduced-data implementations are referred to as LibLinear-M and RF-M in the results. We also implement LibLinear and RF feature vectors which were constructed by concatenating the features from each time point; these implementations are simply referred to as LibLinear and RF.

During the cross-validation, we randomly select training and testing subjects from the available data set, and calculate the root-mean square error (RMSE) for each algorithm. This procedure repeats 100 times, where each run is an independent trial, to obtain the average RMSE. The algorithm parameters used in LSVR and LibLinear are the same, namely linear kernel with box constrain as 10. RF is implemented as an ensemble of 50 trees.

C. Results

We vary the number of training data from 50 to 150 subjects, incrementing upward by 25 subjects per test. The number of testing data is fixed at 50 subjects. In general, we find that both LSVR and RF respond to increased training data through better regression performance all the way up to 150 subjects and likely beyond. LibLinear SVM performance, however, improves little beyond 100 subjects in training.

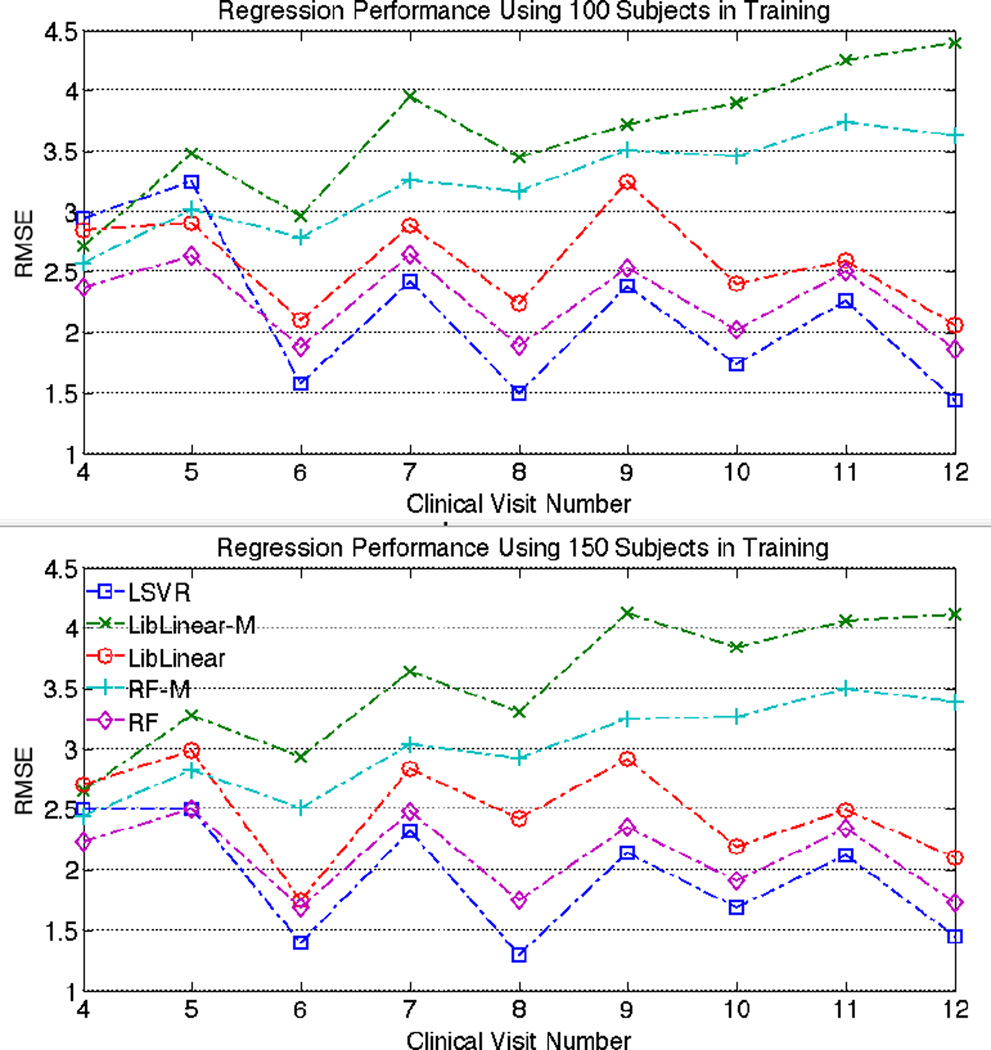
Fig. 1 shows the prediction error of the various algorithms trained with 100 and 150 training subjects to predict ALSFRS for the next month. It indicates that LSVR yields the best performance of the various algorithms when predicting ALSFRS at 6 months and beyond. Using more time points to predict the next one leads to slightly better results for the three algorithms. The mean-feature implementations of LibLinear-M and RF-M are not competitive after month 5. The incorporation of additional data points seems to deteriorate the performance of LibLinear-M and RF-M. Like LSVR, the “stacked feature” implementations LibLinear and RF display a similar oscillatory pattern after month 5.

Fig. 1.

Performance comparison when predicting ALSFRS of the next month. The numbers of subjects in training are 100 and 150. The x-asis represents which month’s ALSFRS is predicted. The y-axis denotes the average RMSE. Smaller RMSE indicates better regression performance. LSVR yields the best performance amongst the algorithms when estimating ALSFRS after month 5th.

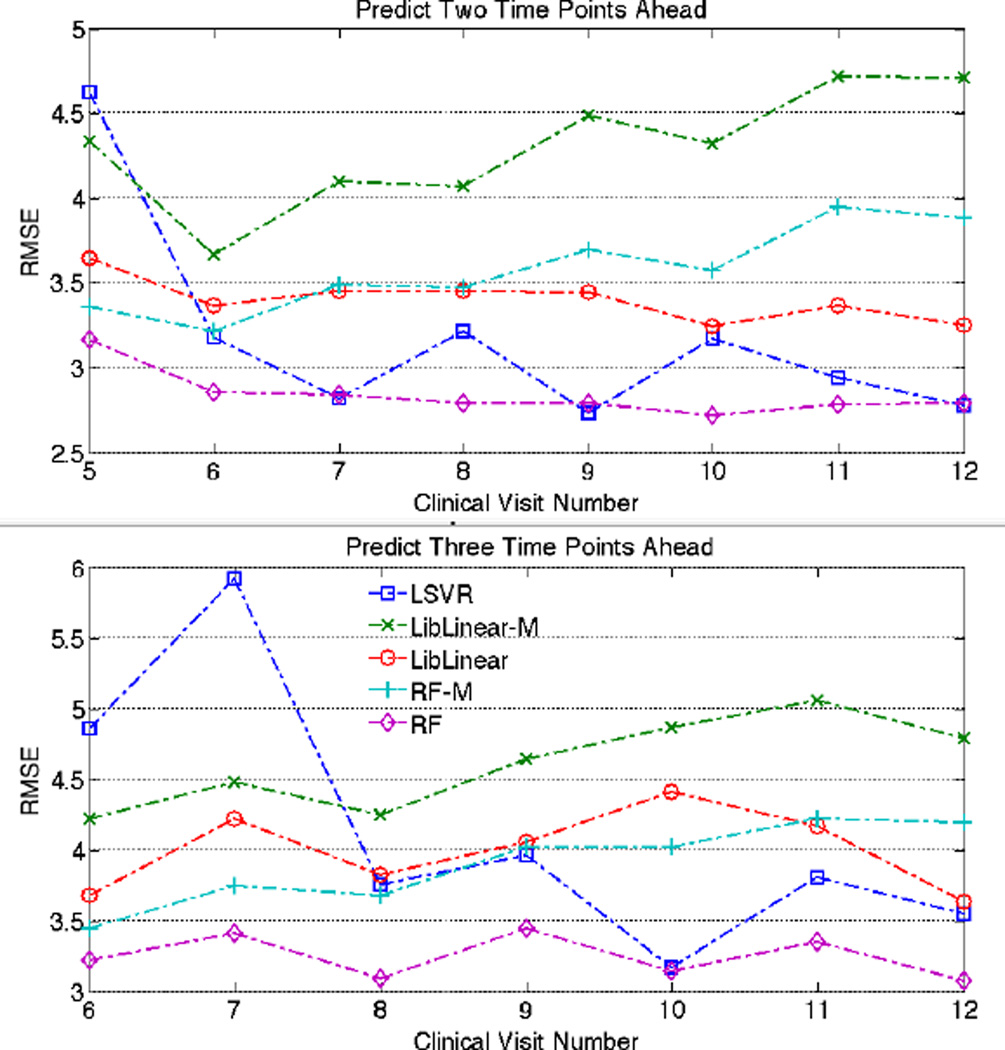
Results of predicting ALSFRS two and three months ahead are shown in Fig. 2. We can observe that the performance of all algorithms worsens as the prediction interval increases. RF appears to have gained the advantage predicting three months with LSVR remaining competitive. The trend of the curve suggests that LSVR’s performance in predicting beyond one month ahead improves with additional temporal data.

Fig. 2.

Performance comparison between LSVR and the other algorithms when prediction ALSFRS two and three months ahead. The horizontal axis indicates number of monthly clinical visit.

IV. Discussion and Conculusions

In this paper, we propose a novel longitudinal machine learning algorithm that takes into account observation dependence within subjects through estimation of additional weighted parameters corresponding to the different time points. It allows simultaneous estimation of the SVR hyperplane parameters and the temporal trend parameters. Our derivation of LSVR was motivated by the apparent need for methods that fuse longitudinal modeling and machine learning paradigms. We drew heavily from the work of Chen and Bowman [4,5], extending their longitudinal SVM classifier to perform regression. While Chen and Bowman’s work was foundational and influential, their testing of their longitudinal classifier was rather restricted to two samples. In addition to extending the longitudinal support vector classifier to regression, we sought to gain a more thorough understanding of the performance of LSVR by testing it under various conditions and by training and testing it with different amounts of data.

The publicly available ALS challenge data on which we tested LSVR serve as a surrogate for a wide class of clinical longitudinal data in which both temporal data (including blood biomarkers) and constant data (e.g., demographic) data are available. Our results suggest that LSVR is indeed competitive with currently favored machine-learning methods. In testing LSVR against implementations of a random forest and a conventional SVR, LSVR seems to find its forte in predicting ALS score one time-point (one month) ahead. LSVR also appears to respond favorably to increased training data and, to a lesser extent, to multiple time points tested.

At this point, we are unable stipulate on the extent to which the comparative performance of LSVR with the other algorithms is a function of the nature of the ALS data, or whether we can expect to see similar trends in other data. Quite simply, more testing is required on additional data sets. However, the results do suggest that LSVR is worthy of such further tests. A common problem in longitudinal clinical data is missing data. Unfortunately, LSVR does not model missing data, although the effect of estimating missing data appears to be no more severe than in other algorithms. We postulate that LSVR may find its most suitable application in prediction of high-dimensional time-series genomic data, since LSVR is amenable to parallel implementation and the computational performance of LSVR is certainly scalable.