The statistical power and validity of Ebola vaccine trials in Sierra Leone: A simulation study of trial design and analysis

Abstract

Background

Safe and effective vaccines may help end the ongoing Ebola virus disease (EVD) epidemic in West Africa, and mitigate future outbreaks. We evaluate the statistical validity and power of randomized controlled (RCT) and stepped-wedge cluster trial (SWCT) designs in Sierra Leone, where EVD incidence is spatiotemporally heterogeneous, and rapidly declining.

Methods

We forecasted district-level EVD incidence over the next six months using a stochastic model fit to data from Sierra Leone. We then simulated RCT and SWCT designs in trial populations comprising geographically distinct clusters of high risk, taking into account realistic logistical constraints, as well as both individual-level and cluster-level variation in risk. We assessed false positive rates and power for parametric and nonparametric analyses of simulated trial data, across a range of vaccine efficacies and trial start dates.

Findings

For an SWCT, regional variation in EVD incidence trends produced inflated false positive rates (up to 0.11 at α=0.05) under standard statistical models, but not when analyzed by a permutation test, whereas all analyses of RCTs remained valid. Assuming a six-month trial starting February 18, 2015, we estimate the power to detect a 90% efficacious vaccine to be between 48% and 89% for an RCT, and between 6.4% and 26% for an SWCT, depending on incidence within the trial population. We estimate that a one-month delay in implementation will reduce the power of the RCT and SWCT by 20% and 49%, respectively.

Interpretation

Spatiotemporal variation in infection risk undermines the SWCT's statistical power. This variation also undercuts the SWCT's expected ethical advantages over the RCT, because the latter but not the former can prioritize high-risk clusters.

Funding

US National Institutes of Health, US National Science Foundation, Canadian Institutes of Health Research

Introduction

At the peak of the devastating 2014-15 Ebola outbreak in West Africa, international public health agencies and pharmaceutical companies committed to assessing the efficacy of several candidate vaccines. Even with the outbreaks in apparent decline, vaccine trials may prove important to minimize future outbreaks. Alternative vaccine trial designs were proposed, each striking a different balance between ethical, logistical and statistical concerns. In February 2015 an individually randomized controlled trial (RCT) was initiated in Liberia and a ring vaccination trial (RVT) began in Guinea in March 2015.¹ A stepped wedge cluster trial (SWCT) was originally proposed for Sierra Leone, but has been revised to a phased-rollout RCT with implementation imminent.² In an RCT, trial participants are randomized at the individual level to a vaccine or control arm. In an SWCT, all trial participants are vaccinated, but in a random sequence of geographically distinct clusters of individuals. In the newly proposed RVT design, contacts of incident EVD cases are randomized to be vaccinated either immediately (as in traditional ring-vaccination strategies) or after some delay.³ Although the SWCT is no longer planned, we evaluate the tradeoffs between SWCT and RCT designs in Sierra Leone to inform decisions during similarly challenging circumstances that may arise in future epidemics. We do not consider the RVT, which was never proposed for Sierra Leone, and which would require a different modeling framework to assess than that used here.

When EVD risk remains high, testing candidate vaccines with an RCT--particularly, assigning trial participants to a control arm--can present an ethical problem. Phase I/II trial results suggest that candidate vaccines are safe and have a strong promise of efficacy. If the medical community believes that--given the high case fatality rate of Ebola--trial participants at significant infection risk are likely to fare better in the vaccinated arm than the control arm, then an RCT may lack clinical equipoise.^4,5However, an uncontrolled trial would be susceptible to confounding bias, eroding reliability of resulting vaccine efficacy estimates.

In October 2014, when EVD incidence was still increasing in West Africa, the United States Centers for Disease Control and Prevention (CDC) proposed an SWCT in light of these concerns. In theory, SWCTs allow comparison between randomized treatment assignments without delaying vaccination to any participants.^6,7 If practical constraints, such as limited availability of vaccines or trained personnel, restrict the delivery of vaccines, then vaccinating groups as quickly as possible while randomizing their order could avoid the ethical dilemma of withholding vaccines while allowing not-yet-vaccinated participants to serve as an unbiased control population. However, there are two plausible scenarios under which an SWCT loses its ethical advantage over an RCT: (1) if vaccine delivery is delayed deliberately in order to improve trial power, and (2) if there is predictable heterogeneity in risk between clusters such that prioritizing vaccination of high risk clusters is anticipated to be more effective than vaccinating clusters in random order.

While ethics and logistics govern the acceptability of trial designs, the size and structure of a trial determines its speed and success in evaluating vaccine efficacy. Randomization protects against confounding because, on average, randomized intervention assignment distributes known and unknown confounders equally among trial arms. However, randomization alone does not ensure statistical validity. Another important concern is whether a study maintains its pre-specified target false positive rate, usually set to 0.05, which is the probability that--in the absence of any effect--the study will, by chance alone, erroneously conclude that an effect is present. False positive rates include spurious conclusions that the intervention decreases or increases risk. Studies whose design produces a false positive rate elevated above this target value are invalid.⁸ While other study characteristics can also invalidate a study, we assess validity with respect to the pre-specified false positive rate only. Inflation of the false positive rate can arise from an inappropriate statistical model that overestimates the precision of the effect estimate. Importantly, this can happen even when estimates of an intervention effect remain unbiased, for instance, when the clustered nature of data is not properly accounted for.⁸

Finally, even valid trial designs may have insufficient statistical power to ascertain that a protective vaccine is indeed effective (a high Type II error rate) and thus waste valuable resources. Assuming identical trial populations, cluster-randomized designs (including SWCT) typically have lower power than individual-randomized designs (like RCT) because cluster-randomization leaves similarities between individuals within groups, reducing the effective sample size.^9,10

Here, we compare the statistical validity and power for SWCT and RCT designs in Sierra Leone, where declining trends in EVD incidence vary regionally.

Methods

We compare the false positive rates and power of SWCT and RCT designs through four steps. First, we fit a stochastic exponential decay model to recent EVD incidence trends in Sierra Leone and use the model to project district-level incidence. Second, we simulate a trial population comprising several clusters, each a geographically distinct high-risk subpopulation that experiences a temporally varying hazard based on our district-level incidence projections. Third, across a range of assumed vaccine efficacies and for 600,000 synthetic trial populations, we simulate both RCT and SWCT designs. Finally, we analyze the simulation data using parametric and nonparametric tests to estimate vaccine efficacy, assessing the false positive rates and statistical power of trial designs and corresponding analyses.

Projecting District-level Incidence in Sierra Leone

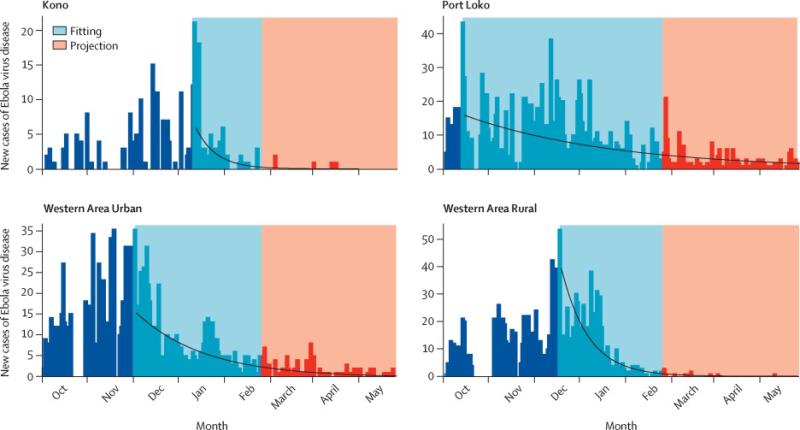
EVD infection risk is spatiotemporally heterogeneous; that is, both the current risk and the rate of decline vary regionally. To capture this variation, we used maximum likelihood to fit exponential decay functions to district-level incidence in Sierra Leone¹¹ from each district's peak incidence to the most recent data.¹² To project district-level incidence over the next six months, we sampled negative binomial random deviates around these decay curves that replicate the overdispersion in the observed incidence data (Figure 1).

Figure 1. Fitted incidence projection models.

Exponential decay functions (blue) fit to EVD incidence (black) within four Sierra Leone districts, with example stochastic incidence projections (red). The models were fit to district-level incidence data from the local peak until February 9, 2015 with negative binomial distributions. We estimated an average negative binomial overdispersion parameter of 1.2 across districts and used this estimate in projections.

Simulating Trial Populations

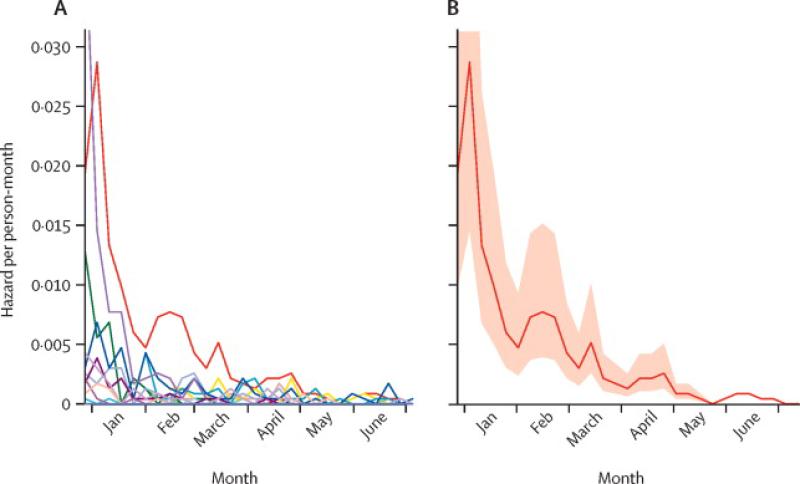
Each simulated trial population included 6000 individuals distributed into 20 clusters of 300 individuals as considered for Sierra Leone.¹³ Clusters represented high-risk subpopulations at distinct locations, such as personnel working in an Ebola treatment unit (ETU) or a group of front-line caregivers within a district (e.g., health care workers, laboratory personnel, burial team staff).¹⁴ We allowed for both cluster- and individual-level variation in EVD risk. Cluster-level variation and declines in infection risk were based on our district-level projections. Specifically, we assumed that each cluster resided in one of the districts in Sierra Leone and created cluster-level hazard trajectories by resampling district-level projections. We then assumed that, without effective vaccination, a proportion of the forecasted cases would occur in the trial population. Given that an estimated 5.2% of EVD cases in Sierra Leone were healthcare workers,¹⁵ we considered scenarios with this proportion set at 2.5%, 5%, 7.5%, and 10% (Figure 2A). Individual-level variation in risk within clusters was modeled using a relative hazard that was lognormally distributed around one with standard deviation of one, simulating biological or occupation-related differences in risk (Figure 2B).

Figure 2. Ebola risk projections in simulated trial populations.

(A) Cluster-level projections. An example of simulated weekly Ebola infection hazards for 20 clusters based on district-level forecasts from Sierra Leone under the assumption that, in the absence of vaccination, 5% of district-level cases would occur in trial clusters within each district. (B) Individual-level variation. Mean and interquartile range of infection risk across individuals in one example cluster.

Simulating Trial Designs

We simulated both RCT and SWCT designs within trial populations experiencing hazards as described above, with a trial start date of February 18, 2015 and duration of six months. In a sensitivity analysis, we varied the start dates from January 15 until April 1.

Because an SWCT is only ethically justified when logistical delays impede simultaneous vaccination of all individuals, comparisons between SWCT and RCT designs should assume the same logistical constraints apply to an RCT (i.e. an RCT with phased vaccine rollout). We assumed that only one cluster could be vaccinated each week.¹³ However, because an RCT would vaccinate half the individuals in each cluster, this rate of rollout would accomplish half the rate of vaccination (150 people / week) in an RCT compared to a SWCT (300 people / week). If the limiting factor is the number of individuals rather than the number of clusters vaccinated per week, then an RCT could vaccinate the same number of people as an SWCT. To address this scenario, we also simulate a “fast” RCT (denoted FRCT), where half of each of two clusters get vaccinated per week (Figures 3, S1).

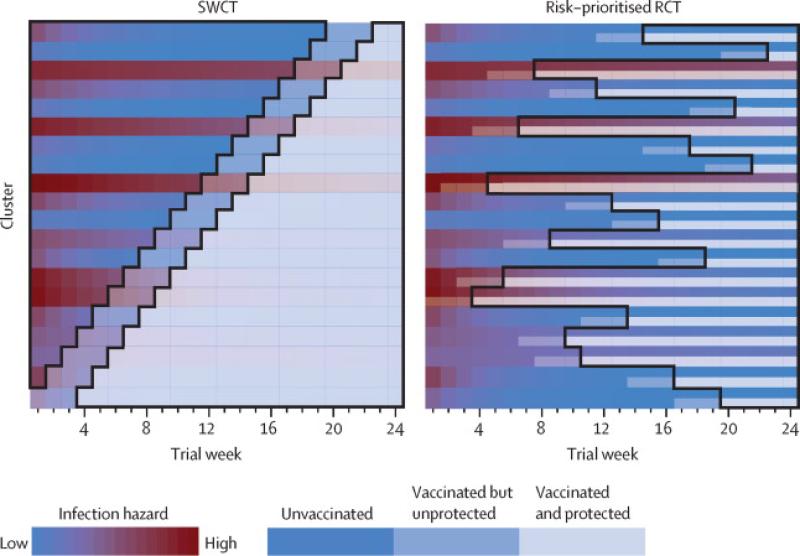
Figure 3. Schematic diagram of trial designs.

A diagrammatic representation of the stepped wedge cluster trial (SWCT) and the risk-prioritized randomized controlled trial (RCT) on the same trial population, assuming that only one cluster can receive vaccination per week. Each row corresponds to a single cluster over the 24 weeks of the trial, with color indicating the level of infection risk within the cluster (ranging from red to blue for high to low risk) and transparency indicating vaccination status (opaque, intermediate and transparent corresponding to unvaccinated, vaccinated but not yet protected, and vaccinated and protected, respectively). Areas outlined in black indicate the person-time at risk analyzed in either design, with both analyses excluding the 21-day delay between vaccination and protection. In the SWCT, entire clusters are vaccinated in random order to allow unbiased comparison between vaccinated and not-yet-vaccinated clusters. In the RCT, half of the individuals in each cluster are chosen at random to be vaccinated, and cluster order can be nonrandom. Here, we assume that clusters are prioritized in order of recently estimated risk (the reddest cluster two weeks preceding each round of vaccination). When risk varies both in time and across clusters, the RCT allows more direct and sustained comparison of vaccinated and unvaccinated individuals in similar high-risk settings. The RCT also maintains a balanced ratio of person-time in vaccinated and control arms, in contrast to the SWCT, in which this ratio changes throughout the trial. For these reasons and because of the greater power achieved by individual randomization, the risk-prioritized RCT achieves greater statistical power to detect vaccine efficacy. For diagrams of the random-ordered and simultaneous instant RCT and the FRCT in the same trial population and alternative analyses of the SWCT, see Figures S1-S2.

In the SWCT, clusters are vaccinated in random order by definition, whereas, in an RCT, we assume that clusters are either vaccinated in a random order or prioritized according to risk. In the latter case, each week the cluster (or two clusters for an FRCT) with the highest incidence two weeks prior is added to the trial. For comparison with these phased-rollout RCTs, we also considered an ideal scenario, free from logistical constraints, in which an RCT could immediately vaccinate half the trial population (simultaneous instant RCT). Note that this cannot be fairly compared to an SWCT, which is predicated on the necessity of delayed rollout.

We assumed a 21-day delay between vaccination and development of protective immunity (hereafter, denoted ‘protective delay’) but conducted a sensitivity analysis considering shorter delays.^2,16,17 We then simulated individual infections based on the hazard models described above and individual immune status. We considered scenarios with vaccine efficacies of 0, 0.5, 0.7 or 0.9, and did not include the indirect benefits of vaccination (i.e., herd immunity) within a cluster, based on the evidence that HCW, while at high infection risk, rarely infect each other.¹⁸

Trial Analysis

Analyses of RCTs only included person-time within a cluster following the development of protective immunity among vaccinated individuals therein. Analyses of SWCTs included all person-time except for the protective delay, with other options explored in a sensitivity analysis (Figures 3, S2-S4). We analyzed simulated trial data using three types of approaches: (1) parametric or semiparametric regression (i.e. the Cox proportional hazards mixed effect frailty model (CoxPH) and a Poisson regression model with cluster-level effects), and two non-parametric methods based on estimates from these same regressions: (2) bootstrap tests and (3) permutation (randomization) tests. For all tests, statistical significance was determined using a target two-tailed false positive rate of α = 0.05, yielding a one-tailed cutoff of 0.025 for vaccine efficacy. For each combination of assumed vaccine efficacy, protective delay, trial design, start date, and hazard levels, we simulated 2,000 trials (totaling 600,000), with each trial based on a unique set of stochastically generated district-level EVD projections for Sierra Leone. All code necessary to replicate these analyses and a more detailed discussion of the methods are provided in the Supplementary Appendix.

Role of the Funding Source

The funding sources had no role in study design, data collection, data analysis, data interpretation, or writing of the report. The authors were not paid by any pharmaceutical company or other agency to write this article. The corresponding author had full access to all the data in the study and had final responsibility for the decision to submit for publication.

Results

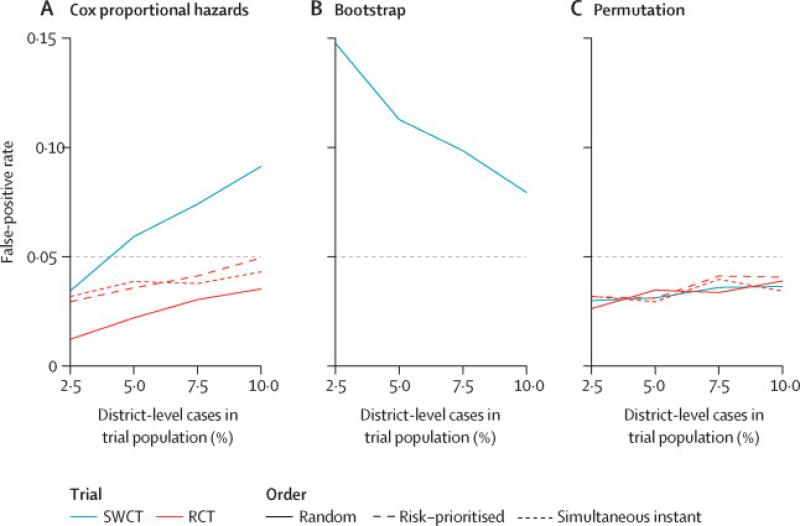
First, we consider trials of a vaccine with no effect on infection risk and examine the false positive rate, i.e. frequency with which trials erroneously conclude that the vaccine affects risk. All RCT scenarios yielded false positive rates below the target α= 0.05. In contrast, SWCTs exhibited inflated false positive rates as high as 0.09, 0.11, and .08 when analyzed with CoxPH, Poisson regression, or bootstrap methods, respectively (Figure 4, S5). This was due to Type I errors in both directions (i.e. erroneous conclusions that the vaccine either decreases or increases risk when it does not affect risk). The false positive rate of CoxPH increased with Ebola incidence in the trial population (Figure 4) and arose from cluster-level variation in hazardtrends(Figure S6-S7). The false positive rate of the bootstrap approach, in contrast, decreased with increasing incidence (Figure 4) and was unrelated to hazard trends or variation therein (Figure S7). Permutation test analyses of SWCTs maintained the targeted false positive rate.

Figure 4. False positive rates by trial design and analysis.

False positive rates shown by trial design, analytical method, proportion of district-level cases occurring among trial participants, and order of cluster vaccination (for RCT). Elevation above the target false positive rate of 0.05 (horizontal gray line) indicates an invalid study for SWCT when analyzed with a Cox proportional hazards frailty model (A) or with cluster-level bootstrap confidence intervals (B), while all analyses of RCTs or of an SWCT with a permutation test (C) maintain pre-specified false positive rates. Line types indicate whether RCT clusters are vaccinated in random order (random), in order of highest risk (risk-prioritized), or all simultaneously at the start of the trial (simultaneous instant). Underlying hazards are based on district-level incidence forecasts (Figure 2). We did not apply cluster-level bootstrapping to the RCT designs because they rely on individual-level randomization. FRCT results are not shown here but were qualitatively similar to those of the RCT.The simultaneous instant design is a hypothetical idealized design and is presented here for comparative purposes but is not considered a feasible trial design in this context.

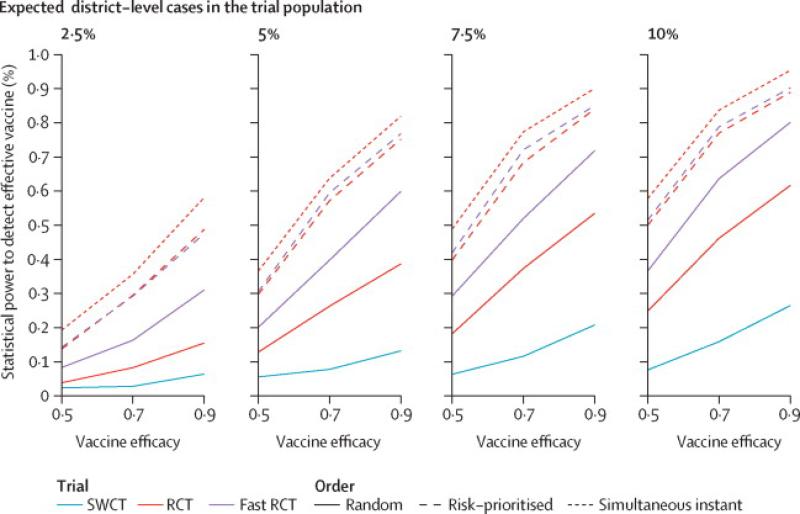
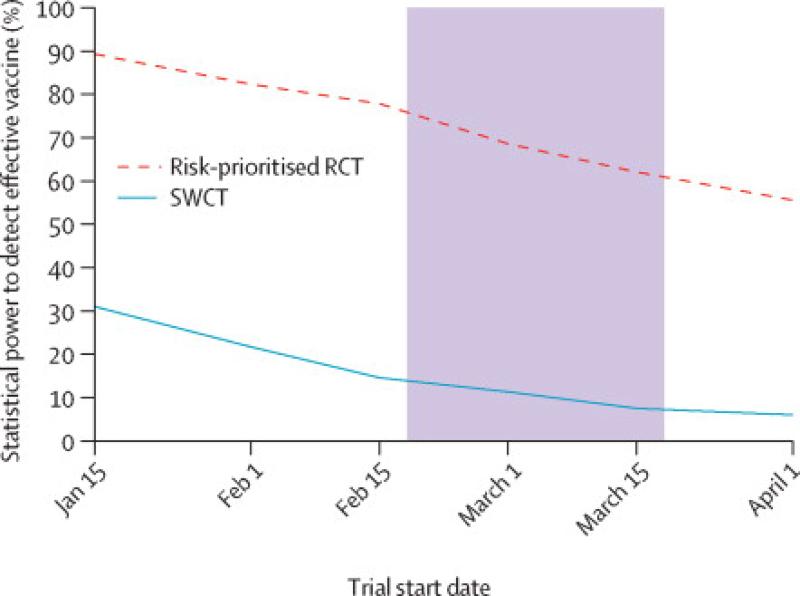
We focused our subsequent analysis of statistical power on two methods that retained the target false positive rate, specifically CoxPH for RCT and permutation tests for SWCT (Figure 5). Power is largely determined by the number of cases observed in the trial (Figure S8-S9). An RCT that rolls out vaccination to clusters in random order provides modest gains in statistical power over an SWCT despite accumulating vaccinated person-time at half the rate of an SWCT, in which the full cluster is vaccinated. An FRCT, in which vaccinated person-time accumulates at the same rate as the SWCT, has even greater power. For RCT designs, prioritizing high-risk clusters for vaccination increases power; risk-prioritized RCT and FRCT designs achieve similarly high power--substantially higher than either random-order design. Assuming a trial start date of February 18, 2015 and duration of six months, we estimate the power to detect a 90% efficacious vaccine to be between 49% and 89% for a risk-prioritized RCT, and between 6.4% and 26% for a SWCT, depending on the proportion of incidence that occurs within the trial population. Assuming 5% of district-level cases occur in the trial population, we estimate that a month long delay in trial start date will decrease the power of RCT and SWCT designs from 75% to 62% and from 13% to 7.5%, respectively (Figure 6). Under this same assumption, evaluation of a vaccine with a 5- versus 21-day protective delay would increase the power of RCT and SWCT designs from 75% to 81% and from 13% to 22%, respectively (Figure S10).

Figure 5. Statistical power by trial design and expected hazard to trial participants.

Panels differ by proportion of district-level cases occurring among trial participants in the absence of vaccination. Line types indicate whether RCT clusters are vaccinated in random order (random), in order of highest risk (risk-prioritized), or all simultaneously at the start of the trial (simultaneous instant). RCT/FRCT data are analyzed with a Cox proportional hazards frailty model; SWCT data are analyzed with a permutation test over estimates from the Cox proportional hazards frailty model. The simultaneous instant design is a hypothetical idealized design and is presented here for comparative purposes but is not considered a feasible trial design in this context.

Figure 6. Statistical power by trial design and start date.

Estimated power by trial start date, assuming that, in the absence of vaccination, 5% of district-level cases occur in the trial, the candidate vaccine is 90% efficacious, and the vaccine protective delay is 21 days. The shaded area highlights the effect of a one-month delay in the start date.

Discussion

The spatiotemporal variation of infection risk in Sierra Leone's EVD epidemic profoundly impacts both the validity and power of vaccine trial designs. Cluster-level variation in Ebola incidence trends inflates false positive rates when applying standard statistical methods to SWCTs. Inflation above the pre-specified target false positive rate indicates that study results are less conservative than intended, though we show that a permutation test can remedy this issue. Nevertheless, in such spatiotemporally variable settings, the power of an SWCT to detect an effective vaccine is 3-10 times less than that of a risk-prioritized RCT in the same trial population, given identical logistical constraints.

While an SWCT, by design, must vaccinate clusters in random order, an RCT can vaccinate clusters in order of the highest to lowest risk, thereby providing the most information on vaccine efficacy. In fact, prioritization of high-risk clusters increased power far more than rolling out vaccines at double the speed (FRCT). Thus, a risk-prioritized RCT may still have sufficient power to definitively identify an efficacious vaccine, though power will continue to decline rapidly if incidence declines continue at current rates. The imminent CDC-led phased-rollout design compares closely to the risk-prioritized RCTs simulated here and will include several geographically distinct clusters of front-line caregivers in areas of ongoing Ebola transmission.²Individuals within clusters will be randomized to immediate vaccination or delayed vaccination after six months (without placebo), with vaccine rolled out to clusters sequentially at the maximum logistically feasible speed. The design allows flexible addition of clusters to improve power and vaccine distribution as transmission patterns shift, which would not be possible in an SWCT, which requires random apriori specification of the vaccination rollout sequence.

Despite the statistical advantages of an RCT, there may be scenarios in which the SWCT would remain preferable. In weighing practical and ethical considerations at the height of the Ebola epidemic, policy makers proposed an SWCT for Sierra Leone in response to the concern that an RCT would withhold lifesaving interventions from the control arm (lacking equipoise). The ethical linchpin of the SWCT is that it delivers vaccines as quickly as possible to maximize public health benefits, while monitoring vaccine efficacy as a noncompeting secondary objective. Any delays or modifications to vaccine deployment for the sake of improving statistical power would undermine its ethical foundation. We argue that the ongoing decline and spatial variation in risk in Sierra Leone presents not only statistical hurdles, but also an ethical challenge for the SWCT design. If the goal is to maximize public health impact, then clusters and/or individuals should be prioritized by risk of infection, which is not allowed in an SWCT. This would not, however, pose a problem in scenarios where infection risk is homogeneous or unpredictable across clusters. We conclude that the RCT is the more promising design for Sierra Leone, given its greater statistical power and the lack of ethical advantage for the SWCT.

Still, permissibility of an RCT relies on its own equipoise considerations. We note that RCT equipoise is a function of anticipated protective or adverse effects of vaccination, combined with infection risk, which modulates their relative importance.¹⁹For instance, equipoise is more achievable in low risk settings because the potential risks and benefits of vaccination are more balanced. Thus, given Sierra Leone's substantial declines in EVD incidence, the imminent phased-rollout RCT may now be ethically viable. Finally, we reiterate our claim¹⁹that, for fatal diseases like Ebola, equipoise is easier to achieve when other lifesaving resources are dedicated to caring for trial participants who become infected.

Assumptions and limitations

Our power estimates are based on epidemic projections from a simple model that assumes EVD incidence is exponentially decaying in all regions, albeit at different rates. These projections should not be taken out of context, as they simply extrapolate recent trends, which may change. We did not aim to forecast incidence accurately, rather to assess vaccine trial power and validity in the context of realistic spatiotemporal variation. An increase in EVD incidence or a sudden end to the epidemic would increase or decrease, respectively, the power of any trial. Our simple model captures realistic variation in infection risk at both the individual and cluster level, but does not consider underlying stochastic dynamics in the transmission process, movement of EVD cases among districts, or the indirect benefits of vaccination within a cluster.

The most important determinant of power is the expected number of cases that would occur in the trial population (in the absence of vaccination), which is determined both by the trial population size and by the infection hazard experienced by individuals in the trial. We have considered a single trial population size, and conducted a sensitivity analysis varying infection hazard. In our analysis, the hazard of infection among trial participants was determined by both district-level incidence projections and the proportion of cases assumed to occur within the trial population. To account for variation in the former, we implemented stochastic projections and assumed random distribution of trial clusters across districts. For the latter, we considered a range of values, based on the proportion of total cases occurring within healthcare worker populations to date.

There are a number of other important design considerations not included in our models. For example, RCT, but not SWCT, designs can use placebo or comparator vaccines to avoid bias induced by participant behavioral change upon knowing their vaccination status. On the other hand, an SWCT may be more palatable for high-risk communities, where vaccinating only half of trial participants may be unacceptable. The greater power of an RCT could also increase the speed with which a vaccine is definitively identified as efficacious and subsequently rolled out to the greater population.

Generalizing results to other epidemics

Cross-over cluster-randomized designs (i.e. those in which each cluster is observed both pre and post-intervention), such as the SWCT, are based on the ability to make comparisons between clusters that control for underlying time trends. We show that, when trends differ between clusters, the statistical validity of this approach is at least partially compromised due to confounding between the timing of intervention and time-dependent changes in risk to clusters. In particular, classical regression approaches, including Cox proportional hazards or generalized linear mixed models, that ignore this time dependency within clusters have inflated false positive rates. This problem may be more common than has been recognized, particularly during acute infectious disease epidemics or outbreaks, in which risk is highly variable in space and time.^20,21 For instance, this issue could be a concern for the ring vaccination trial planned in Guinea, which is another crossover cluster-randomized design. Other non-parametric approaches have also been suggested to handle complex, and potentially unknown, spatiotemporal dependencies in risk.²²

Our findings demonstrate the utility of simulation approaches for evaluating trial designs and analyses under realistic and variable scenarios. Classical power analyses rely on analytic calculations that make strong assumptions, such as the absence of spatiotemporal dependency in infection risk. Evaluation of estimates from simulated data, where the underlying true parameters are known, provides a powerful tool with which to discover biases and evaluate the robustness of estimators when not all assumptions are met. Here, we have leveraged modern computational approaches to identify problems with conventional methods and new analytic approaches to resolve them.

Conclusion

Given observed temporal and geographical variation in infection risk, an SWCT design to evaluate candidate Ebola vaccines in Sierra Leone would have little power to detect efficacy and may not retain anticipated ethical advantages over other designs. An RCT, in contrast, may have sufficient power to detect efficacy but must start soon to avoid substantial reductions in power as the epidemic declines. Adapting the basic RCT design to prioritize high-risk clusters substantially increases statistical power and ensures more rapid distribution of a potentially effective vaccine to the groups that would benefit most.

Research in Context

Evidence before this study

We searched PubMed for articles published after January 1, 1990 and before March 3, 2015 using the following search terms: “(Ebola vaccine trial) OR (stepped wedge AND (statistic* OR power analysis OR Ebola OR infectious disease OR HIV OR dengue OR emerging OR outbreak OR epidemic OR pathogen)),” excluding studies of non-infectious diseases and also identifying relevant citations within selected articles. We did not identify any studies evaluating Ebola vaccine efficacy trial design. We found methodological papers describing power analyses for stepped-wedge trials (SWCT) and randomized controlled trials (RCTs), and studies assessing trial design for evaluation of candidate vaccine efficacy for other infectious diseases. Amongst these, only two studies discussed the potential effects of spatiotemporal variation in infection risk on trial design; however, they did not assess the resulting effects on trial validity or power.

Added value of this study

We provide the first evaluation of Ebola candidate vaccine efficacy trial design and the first comparison of RCT and SWCT designs in the context of spatiotemporally variable infection risk and realistic logistical constraints. We show that spatiotemporal variation in infection risk invalidates traditional statistical analyses of SWCT designs and develop a permutation test that allows valid analysis. We found that, under identical logistical constraints and within the current epidemiological context of Sierra Leone, an RCT has 3-10 times the power of an SWCT to detect an effective vaccine, largely due to an RCT's ability to prioritize high-risk clusters for earlier enrollment. Finally, we argue that the SWCT loses its ethical advantages over the RCT if there is predictable heterogeneity in risk between clusters such that rolling out vaccination first to high risk clusters is anticipated to be more effective than vaccinating clusters in random order.

Implications of all the available evidence

An SWCT design to evaluate candidate Ebola vaccines in Sierra Leone will have little power to detect efficacy and may not have its anticipated ethical advantages over other randomized designs. An RCT, in contrast, may have sufficient power to detect efficacy but must start soon to avoid substantial reductions in power as the epidemic declines. More generally, we note that researchers should be cautious when using SWCT or other cross-over designs to evaluate interventions in the context of emerging infectious disease epidemics, or in other contexts with spatiotemporally variable infection risk.