Influence of diffusion on the kinetics of multisite phosphorylation

Abstract

When an enzyme modifies multiple sites on a substrate, the influence of the relative diffusive motion of the reactants cannot be described by simply altering the rate constants in the rate equations of chemical kinetics. We have recently shown that, even as a first approximation, new transitions between the appropriate species must also be introduced. The physical reason for this is that a kinase, after phosphorylating one site, can rebind and modify another site instead of diffusing away. The corresponding new rate constants depend on the capture or rebinding probabilities that an enzyme‐substrate pair, which is formed after dissociation from one site, reacts at the other site rather than diffusing apart. Here we generalize our previous work to describe both random and sequential phosphorylation by considering inequivalent modification sites. In addition, anisotropic reactive sites (instead of uniformly reactive spheres) are explicitly treated by using localized sink and source terms in the reaction‐diffusion equations for the enzyme‐substrate pair distribution function. Finally, we show that our results can be rederived using a phenomenological approach based on introducing transient encounter complexes into the standard kinetic scheme and then eliminating them using the steady‐state approximation.

Introduction

Posttranslational modification of proteins plays an important role in signal transduction. Using the rate equation of chemical kinetics, it has been shown that phosphorylation–dephosphorylation cycles exhibit remarkable behavior1 such as ultrasensitive response to small changes in the relative kinase and phosphatase concentrations2 and the existence of multiple steady states when the substrates have multiple modification sites.3, 4 A few years ago, it was found from simulations of the diffusive dynamics of hundreds of reactants that when diffusion is sufficiently slow, the kinetics can be dramatically altered due to the natural emergence of processive phosphorylation.5 After modifying one site, the enzyme–substrate pair do not always diffuse apart allowing the enzyme to phosphorylate another site. The importance of such processive phosphorylation is greater, slower the diffusion. Because processivity can lead to the loss of bistability6 in phosphorylation‐dephosphorylation cycles and a crowded environment slows down diffusion, the same system can be bistable in vitro but not in vivo.5, 7, 8

Recently we have shown that all the key results obtained from many‐particle simulations5 can be reproduced in the framework of chemical kinetics by not only using diffusion‐influenced rates, but by also introducing new transitions between certain species.9 The rates of these new reaction channels turned out to have a physically transparent interpretation. They are proportional to the probability that an isolated enzyme–substrate pair, just formed by dissociation or catalysis at one site, will react at the other site rather than diffuse apart (escape). These escape/capture (also called splitting or commitment) probabilities appear to have been introduced in chemical physics by Onsager10, 11 to describe ion recombination. In the context of diffusion‐influenced rates, they have been used12 to give a physical interpretation to the Collins–Kimball association rates13 for spherical reactants interacting via a potential of mean force. These probabilities also play a key role in modern transition‐path theories of unimolecular reactions.14, 15, 16 In the context of protein folding, they are called p‐fold, which is the probability that a configuration in the transition state region folds rather than unfolds.17

In this article we generalize our previous work by obtaining diffusion‐modified rate equations that describe the double phosphorylation of a substrate with inequivalent sites. We assume that the binding and catalytic sites of the enzyme are the same and the substrate cannot bind more than one enzyme. Let S denote the unphosphorylated substrate with binding sites labeled by 1 and 2. Let SE_i denote the species where the enzyme is bound to site i, i = 1, 2. Let P_i denote substrates where only site i is phosphorylated and P ₁₂ denote substrates where both sites are phosphorylated. Finally, let $P_i{E}_j$ be the species in which the site i is phosphorylated and the enzyme is bound to site j. In summary, the index on P denotes which substrate site is phosphorylated, the index on E denotes the site on the substrate to which the enzyme is bound.

For the Michaelis–Menten mechanism, the chemical kinetic scheme that describes these reactions is

$$S+E\underset{d_1}{\overset{a_1}{\rightleftharpoons }}S{E}_1\stackrel{c_1}{\to }{P}_1+E$$

$$S+E\underset{d_2}{\overset{a_2}{\rightleftharpoons }}S{E}_2\stackrel{c_2^{}}{\to }{P}_2+E$$

$$P_1+E\underset{d_2^{\prime }}{\overset{a_2^{\prime }}{\rightleftharpoons }}{P}_1{E}_2\stackrel{c_2^{\prime }}{\to }{P}_{12}+E$$

$$P_2+E\underset{d_1^{\prime }}{\overset{a_1^{\prime }}{\rightleftharpoons }}{P}_2{E}_1\stackrel{c_1^{\prime }}{\to }{P}_{12}+E$$ (1)

Here a _i, d _i, and c _i (i = 1, 2) are the association (binding), dissociation, and catalytic rate constants for the ith site of the unmodified substrate. The corresponding rate constants for the substrate P _j phosphorylated at site $j\ne i$ are $a_{\mathrm{i}}^{\prime },\hspace{0.17em}{d}_{\mathrm{i}}^{\prime }$ and $c_{\mathrm{i}}^{\prime }$. Note that in this kinetic scheme [see also Fig. 1(a)] the enzyme acts distributively (i.e., at most one site can be modified before the enzyme‐substrate complex dissociates).18, 19 Processivity will arise naturally when diffusion is accounted for.

Figure 1.

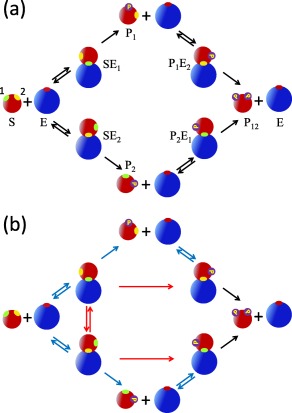
(a) Standard Michaelis–Menten kinetic scheme for the double phosphorylation of a substrate with two inequivalent sites: 1(green) and 2 (yellow). The rate constants are specified in Eq. (1). In this mechanism, the dissociation of the product is assumed to be much faster than catalysis. The subscript on E indicates the site that is bound to the enzyme. The subscript on P indicates the site that is phosphorylated. For example, $P_1{E}_2$ indicates that the first (green) site is phosphorylated and the enzyme is bound to the second (yellow) site. (b) The diffusion‐modified kinetic scheme with the rate constants specified in Eqs. (2) and (3). The blue arrows indicate that the corresponding chemical rate constants have been scaled by the appropriate escape probabilities. The red arrows correspond to new reaction channels with rate constants obtained by multiplying the chemical ones by the appropriate capture probabilities.

The kinetic scheme in Eq. (1) can describe both random and sequential phosphorylation.18 For example, by setting the rate constants in the lower pathway in Figure 1(a) to zero, we obtain the kinetic scheme for sequential phosphorylation, where site 1 is always modified first. By setting the rates in the upper pathway equal to those in the lower one, we recover the scheme that describes random binding to equivalent sites. In this limit, since for example SE ₁ and SE ₂ are indistinguishable, we can simply add the concentrations of the upper and lower species and recover the model that was explicitly analyzed in our previous paper.9

Results

The kinetic scheme in Eq. (1) [and in Fig. 1(a)] corresponds to the reaction‐controlled limit when diffusion is much faster than reaction and therefore does not affect the kinetics of phosphorylation. We will account for the effect of diffusion by deriving new diffusion‐modified rate equations using two different approaches (see Methods). The first starts with the exact rate equations for a microscopic model where an enzyme and a substrate must diffuse together and reorient before reaction can occur. These equations contain enzyme‐substrate pair distribution functions for which no closed set of equations exists. The time dependence of these pair distribution functions can be approximated in increasingly sophisticated ways20, 21, 22, 23, 24 but here we use the simplest one that is valid only for sufficiently low reactant concentrations and long (but not asymptotically so25) times. Specifically, we assume that the position‐dependent pair distribution functions have reached steady state and can be found by balancing the changes due to diffusion and reaction (i.e., binding, dissociation, and catalysis). The resulting formalism is rather complicated but we have been able to express all rate constants of our diffusion‐modified rate equations in terms of the chemical (intrinsic) rates and the escape and capture probabilities of a variety of isolated enzyme–substrate pairs that can react irreversibly.

The second approach is a phenomenological one based on Eigen's concept of an encounter complex,26 which is a transient kinetic species formed by the reactants diffusing together. Basically, one first adds encounter complexes to the standard kinetic scheme and then eliminates them using the steady‐state approximation. In this way new transitions can occur between the original species that were connected to directly interconverting encounter complexes. The expressions for the resulting rate constants are rather messy since they depend on all the new phenomenological rate constants that govern the encounter complex concentrations. However, if one calculates the escape and capture probabilities in the framework of the encounter complex model by solving the appropriate rate equations, then the new rate constants can be rewritten in a form identical to that obtained using the microscopic approach discussed previously. It is not obvious that the phenomenological and microscopic approaches lead to the same results.27 This was proved previously12 only for the rates and escape probabilities of the Collins–Kimball model13 for diffusion‐influenced reactions between two spherical molecules interacting via a potential of mean force.

The resulting diffusion‐modified kinetic scheme for double phosphorylation with inequivalent sites is shown in Figure 1(b). The renormalized rates for the transitions that exist in the conventional kinetic scheme (the blue and black arrows) are

$$S+E\underset{d_1{ϵ}_1^{}}{\overset{a_1{ϵ}_1^{}}{\rightleftharpoons }}S{E}_1\stackrel{(1-q_{1\to 2}^{\prime })c_1}{\to }{P}_1+E$$

$$S+E\underset{d_2^{}{ϵ}_2^{}}{\overset{a_2^{}{ϵ}_2}{\rightleftharpoons }}S{E}_2\stackrel{(1-q_{2\to 1}^{\prime })c_2^{}}{\to }{P}_2+E$$

$$P_1+E\underset{d_2^{\prime }{ϵ}_2^{\prime }}{\overset{a_2^{\prime }{ϵ}_2^{\prime }}{\rightleftharpoons }}{P}_1{E}_2\stackrel{c_2^{\prime }}{\to }{P}_{12}+E$$

$$P_2+E\underset{d_1^{\prime }{ϵ}_1^{\prime }}{\overset{a_1^{\prime }{ϵ}_1^{\prime }}{\rightleftharpoons }}{P}_2{E}_1\stackrel{c_1^{\prime }}{\to }{P}_{12}+E$$ (2)

The corresponding differential equations are given in Eq. (14). Here ϵ_i and ${ϵ}_i^{\prime }$ are the escape probabilities corresponding to unphosphorylated and singly phosphorylated substrates, respectively, and $q_{\mathrm{i}\to \mathrm{j}}^{\prime }$ are the corresponding capture or rebinding probabilities. They are defined and explained in detail in the caption of Figure 2. Note that the chemical association (a _i, $a_{\mathrm{i}}^{\prime }$) and dissociation (d _i, $d_{\mathrm{i}}^{\prime }$) rate constants have been scaled by the diffusion‐dependent escape probabilities in such a way that the binding equilibrium constants do not depend on the ϵ's and hence on diffusion. The catalytic rate constants of the first phosphorylation steps (c_i, i = 1, 2) are scaled by $1-q_{\mathrm{i}\to \mathrm{j}}^{\prime }$. These scaling factors are the probabilities that an enzyme–substrate pair, where initially the enzyme is close to the phosphorylated site i, diffuses apart (escapes) rather than binds at site j. When diffusion is fast, the escape probabilities are close to unity and hence conventional kinetics becomes an excellent approximation.

Figure 2.

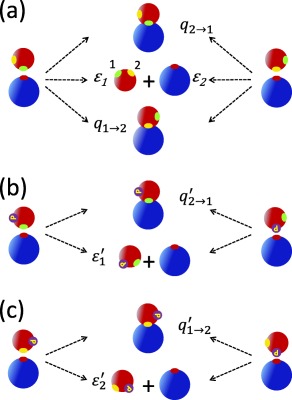
Definition of the escape and capture probabilities that determine the rate constants in the diffusion‐modified kinetic scheme shown in Figure 1(b). (a) The fate of unphosphorylated substrate–enzyme pairs that can either irreversibly react or diffuse apart. Initially, the active site of the enzyme is near site 1 (green, left) or site 2 (yellow, right) of the substrate. These transient states can be produced by the enzyme and substrate diffusing together or by dissociation of the bound complex. The escape probability ϵ_i, i = 1, 2, is the probability that a pair, with the substrate site i initially near the active site of the enzyme, diffuses apart rather than binds at either the first or second site. The capture probability $q_{\mathrm{i}\to \mathrm{j}}$ is the probability that the enzyme initially near site i of the substrate will bind to site j rather than diffuse away or bind to site i. (b) and (c) The fate of singly phosphorylated substrate‐enzyme pairs. The escape probability ${\epsilon }_{\mathrm{i}}^{\prime }$ (the prime indicates that the substrate is singly phosphorylated) is the probability that an enzyme, initially near the unphosphorylated site i of the substrate, will not bind. The capture probability $q_{\mathrm{i}\to \mathrm{j}}^{\prime }$ ($i\ne j$) is the probability that the enzyme binds to site j given that initially the phosphorylated site i of the substrate was near the active site of the enzyme. Thus $1-q_{\mathrm{i}\to \mathrm{j}}^{\prime }$ is the escape probability of such a pair.

The rate constants for the transitions that did not exist in the conventional kinetics scheme [shown in red in Fig. 1(b)] are

$$S{E}_1 \underset{d_2{q}_{2\to 1}}{\overset{d_1{q}_{1\to 2}}{\rightleftharpoons }}S{E}_2$$

$$S{E}_1\stackrel{c_1{q}_{1\to 2}^{\prime }}{\to }{P}_1{E}_2$$

$$S{E}_2\stackrel{c_2{q}_{2\to 1}^{\prime }}{\to }{P}_2{E}_1$$ (3)

All these rate constants have simple physical interpretations. The rate constants for the direct transition $S{E}_1\to S{E}_2$ is the product of the dissociation rate constant of SE ₁ (d ₁) and the probability ($q_{1\to 2}$) that the configuration generated immediately after dissociation (i.e., the binding site of the enzyme and the first site of the substrate are close together), reacts to form the complex in which the enzyme is bound to site 2 rather than diffusing apart or rebinding to site 1 [see Fig. 2(a)]. Similarly, the rate constant for the direct catalytic transition $S{E}_1\to P_1{E}_2$ is the product of the rate of phosphorylating site 1 (c ₁) and the probability ($q_{1\to 2}^{\prime }$) that the enzyme initially near the phosphorylated site binds to the unphosphorylated one rather than diffusing away.

Discussion

The attractive feature of the above formalism is that the influence of diffusion is completely described by the appropriate escape and capture (rebinding) probabilities. The expressions for the diffusion‐influenced rate constants in retrospect seem so obvious that the mathematical derivations presented in the next section appear to be hardly necessary. But this transparency is the very reason that the approach presented here is so powerful. In application, the escape and capture probabilities can be treated as adjustable but physically meaningful parameters. Alternately one can adopt a microscopic model where even for realistic geometries (anisotropic sites, rotational and translational diffusion of arbitrary shaped proteins) these probabilities can be obtained from simulations of just pairs of reactants rather than hundreds that would be required to directly calculate concentrations.

The magnitude of the capture (or rebinding) probabilities, and hence the flux that flows through the new reaction channels, depends on a variety of factors. For example, the capture probability increases as the relative diffusion coefficient decreases. This is why the crowded environment of the cell can induce processivity.5, 7, 8 Another factor is the relative proximity of the two phosphorylation sites. The capture probability and hence the likelihood that the same enzyme phosphorylates both sites increases with their proximity. This is illustrated in Figure 3, which was obtained by numerically solving the coupled differential equations [see Eq. (14)] that correspond to the diffusion‐modified kinetic scheme [see Fig. 1(b) and Eqs. (2) and (3)]. We considered sequential phosphorylation (the upper pathway in Fig. 1 with the rates for the binding in the lower pathway set to zero). We first assumed that the two sites are so far apart that $q_{1\to 2}^{\prime }=0$. In this case we recover the “naive” diffusion‐modified scheme, in which only the rate constants of the existing transitions have been scaled by the escape probabilities. The resulting progress curves are dashed. When the two sites are close together, the capture probability is assumed to be $q_{1\to 2}^{\prime }=0.5$, so the bound states SE ₁ and $P_1{E}_2$ are now directly connected [see the upper part of Fig. 1(b)]. Consequently the relative concentrations of doubly phosphorylated substrate (solid red line) increases faster than when the sites are far apart (dashed red line).

Figure 3.

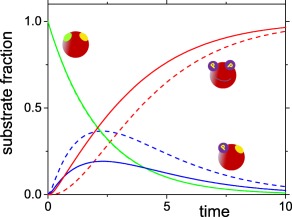
The relative concentrations of the unphosphorylated substrates ($[S]/{[S]}_{\text{tot}}$, green), the singly phosphorylated substrates ($[P_1]/{[S]}_{\text{tot}}$, blue) and the doubly phosphorylated substrates ($[P_{12}]/{[S]}_{\text{tot}}$, red) as a function of time for diffusion‐modified sequential phosphorylation. The solid lines correspond to sites close together ($q_{1\to 2}^{\prime }=0.5$), whereas the dashed lines correspond to sites that are so far from each other that $q_{1\to 2}^{\prime }=0$. The curves were obtained by numerically solving Eq. (14). Initially, the substrate is unbound and unphosphorylated. All other parameters are $a_1{[S]}_{\text{tot}}=a_2^{\prime }{[S]}_{\text{tot}}=d_1=d_2^{\prime }=1,\hspace{0.17em}{c}_1=c_2^{\prime }=10,\hspace{0.17em}{a}_2=a_1^{\prime }=0,\hspace{0.17em}{\epsilon }_1={\epsilon }_2^{\prime }=0.5,\hspace{0.17em}{[S]}_{\text{tot}}={[E]}_{\text{tot}}$.

This work can be extended in a number of directions. It can immediately be applied to dephosphorylation, so the influence of diffusion on the properties of phosphorylation–dephosphorylation cycles can be obtained by solving the same number of ordinary differential equations as in chemical kinetics. One can readily construct diffusion‐modified kinetic schemes when multiple phosphorylation sites are present. This can be done by analogy without recourse to mathematical derivations. It can be readily shown that our expressions for the rate constants in the diffusion‐modified kinetic scheme are valid when the enzyme and substrate interact. An attractive potential would increase the capture probabilities and thus magnify the contributions of the new reaction channels.

Generalization to more complex mechanisms is less straightforward. For example, suppose that the enzyme is inactivated after phosphorylating a site and needs time to become active again.5 Previously we considered only the limit when the reactivation time is very fast9 and the resulting diffusion‐modified rate equations did not exactly reduce to those of chemical kinetics in the fast diffusion limit. Preliminary results show that the correct diffusion‐modified kinetic scheme contains negative rate constants but fortunately lead to positive steady‐state concentrations. This is a result of a Markovian approximation implicit in our treatment and its full implications remain to be explored.

Methods

In this section we derive the diffusion‐modified kinetic equations for double phosphorylation occurring via the Michaelis–Menten mechanism. In the reaction‐controlled limit (reaction slow compared to diffusion), it is described by the scheme shown Figure 1(a) with the rate constants given in Eq. (1). We begin by describing a microscopic model, which considers diffusing molecules explicitly. Then we obtain the diffusion‐modified kinetic schemes in Eqs. (2) and (3) by extending our previous derivation9 to the case where only small regions on protein surfaces are reactive. Finally, we rederive these results in the framework of a phenomenological model involving transient encounter complexes, in which the interconversions are described by ordinary rate equations.

Microscopic model

Let us specify our microscopic model of binding, dissociation and catalytic conversion. Binding of the substrate and enzyme can occur only when they are in close proximity and oriented so that their reactive sites are in contact. The binding rate depends on the relative position, r, and on the orientation of the enzyme and substrate, Ω_E and Ω_S. This dependence is described by functions ${\sigma }_1(\mathrm{x})$ and ${\sigma }_2(\mathrm{x})$ for the binding to the first and second site, respectively, where $\mathrm{x}=\{\mathrm{r},{\Omega }_{\mathrm{E}},{\Omega }_{\mathrm{S}}\}$ denotes a collective coordinate, which specifies the relative location and orientation of the enzyme and substrate. The space‐dependent factor ${\sigma }_{\mathrm{i}}(\mathrm{x})$ differs from zero in a small region near the ith site. It is defined such that ${\displaystyle \int {\sigma }_{\mathrm{i}}}(\mathrm{x})\hspace{0.17em}d\mathrm{x}\equiv {\displaystyle \int {\sigma }_{\mathrm{i}}}\hspace{0.17em}d\mathrm{r}d{\Omega }_{\mathrm{E}}d{\Omega }_{\mathrm{S}}=1$. Let a _i be the bimolecular rate constant of binding (association) to site i in the reaction‐controlled limit. Then $a_{\mathrm{i}}{\sigma }_{\mathrm{i}}(\mathrm{x})$ is a unimolecular rate constant, which equals to the reciprocal of the mean time required for the enzyme and substrate pair fixed at x to bind at site i.

After binding, the enzyme E and substrate S form the bound states SE ₁ and SE ₂, where the subscript indicates the site where binding has occurred. The bound state can then dissociate and form an unbound enzyme‐substrate pair located at x. Microscopic reversibility requires that the spatial and angular distribution for binding and dissociation must be the same, so the unimolecular rate constant to form an unbound pair at x via dissociation is $d_{\mathrm{i}}{\sigma }_{\mathrm{i}}(\mathrm{x})$ (i = 1, 2). We also assume that the rate constant to form an unbound pair at x via catalysis is $c_{\mathrm{i}}{\sigma }_{\mathrm{i}}(\mathrm{x})$.

The site that has been phosphorylated becomes unreactive. The substrate with the first site modified, P ₁, can bind to the enzyme via its second site and form a bound state $P_1{E}_2$. The unimolecular binding rate constant for the pair of P ₁ and E is $a_2^{\prime }{\sigma }_2(\mathrm{x})$, where the prime indicate that these quantities are for the singly phosphorylated substrate. The bound state $P_1{E}_2$ can dissociate and form a P ₁ and E pair at x with unimolecular rate constant $d_2^{\prime }{\sigma }_2(\mathrm{x})$. The enzyme can also phosphorylate the second site and form a P ₁₂ and E pair at x with the unimolecular rate constant $c_2^{\prime }{\sigma }_2(\mathrm{x})$. The rate constant for the binding of P ₂ and E is $a_1^{\prime }{\sigma }_1(\mathrm{x})$. The corresponding dissociation and catalytic rate constants are $d_2^{\prime }{\sigma }_2(\mathrm{x})$ and $c_2^{\prime }{\sigma }_2(\mathrm{x})$.

To obtain the diffusion‐modified rate equations, we start with the conventional rate equations that correspond to the kinetic scheme shown in Figure 1(a) with the rate constants defined in Eq. (1)

$$\frac{d[S]}{dt}=-{\displaystyle \sum _{n=1}^2 }(a_n[S][E]-d_n[S{E}_n])$$

$$\frac{d[S{E}_{\mathrm{i}}]}{dt}=a_{\mathrm{i}}[S][E]-(d_{\mathrm{i}}+c_{\mathrm{i}})[S{E}_{\mathrm{i}}]$$

$$\frac{d[P_{\mathrm{j}}]}{dt}=-a_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}][E]+d_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}{E}_{\mathrm{i}}]+c_{\mathrm{j}}[S{E}_{\mathrm{j}}]$$

$$\frac{d[P_{\mathrm{j}}{E}_{\mathrm{i}}]}{dt}=a_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}][E]-(d_{\mathrm{i}}^{\prime }+c_{\mathrm{i}}^{\prime })[P_{\mathrm{j}}{E}_{\mathrm{i}}]$$ (4)

Here $i,j=1,2$ and $i\ne j$. The equations for $[P_{12}]$ and $[E]$ are similar. The total concentration is conserved, therefore

$$[S]+[P_1]+[P_2]+[P_{12}]+[S{E}_1]+[S{E}_2]+[P_1{E}_2]+[P_2{E}_1]={[S]}_{\text{tot}}$$

$$[E]+[S{E}_1]+[S{E}_2]+[P_1{E}_2]+[P_2{E}_1]={[E]}_{\text{tot}}$$ (5)

To account for the influence of enzyme and substrate diffusion, we use the fact that the binding rates are in general related to the pair distribution functions, which depend on the relative location and orientations of the reactants. Let the pair distribution function of the enzyme and unphosphorylated sub strate be denoted by $\rho (\mathrm{x},t)$. The pair distribution of an enzyme and a substrate that has been phosphorylated at site i is ${\rho }_{\mathrm{i}}(\mathrm{x},t)$. When $\left|\mathrm{r}\right|\to \infty$, the reactants are uncorrelated, so $\rho \to [E][S]$ and ${\rho }_{\mathrm{j}}\to [E][P_{\mathrm{j}}]$. The binding rate for the unphosphorylated substrate is found by summing over all possible configurations that can bind, so the binding rate in Eq. (4), $a_{\mathrm{i}}[S][E]$, is replaced by $a_{\mathrm{i}}{\displaystyle \int {\sigma }_{\mathrm{i}}}(\mathrm{x})\rho (\mathrm{x},t)\hspace{0.17em}d\mathrm{x}$. Similarly, the binding rate of the singly phosphorylated substrate is obtained by replacing $a_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}][E]\to a_{\mathrm{i}}^{\prime }{\displaystyle \int {\sigma }_{\mathrm{i}}}(\mathrm{x}){\rho }_{\mathrm{j}}(\mathrm{x},t)\hspace{0.17em}d\mathrm{x},\hspace{0.17em}i\ne j$. In this way we get:

$$\frac{d[S]}{dt}=-{\displaystyle \sum _{n=1}^2(a_n{\displaystyle \int {\sigma }_n}(\mathrm{x})\rho (\mathrm{x},t)\hspace{0.17em}d\mathrm{x}-d_n[S{E}_n])}$$

$$\frac{d[S{E}_{\mathrm{i}}]}{dt}=a_{\mathrm{i}}{\displaystyle \int {\sigma }_{\mathrm{i}}}(\mathrm{x})\rho (\mathrm{x},t)\hspace{0.17em}d\mathrm{x}-(d_{\mathrm{i}}+c_{\mathrm{i}})[S{E}_{\mathrm{i}}]$$

$$\frac{d[P_{\mathrm{j}}]}{dt}=-a_{\mathrm{i}}^{\prime }{\displaystyle \int {\sigma }_{\mathrm{i}}}(\mathrm{x}){\rho }_{\mathrm{j}}(\mathrm{x},t)\hspace{0.17em}d\mathrm{x}+d_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}{E}_{\mathrm{i}}]+c_{\mathrm{j}}[S{E}_{\mathrm{j}}]$$

$$\frac{d[P_{\mathrm{j}}{E}_{\mathrm{i}}]}{dt}=a_{\mathrm{i}}^{\prime }{\displaystyle \int {\sigma }_{\mathrm{i}}}(\mathrm{x}){\rho }_{\mathrm{j}}(\mathrm{x},t)\hspace{0.17em}d\mathrm{x}-(d_{\mathrm{i}}^{\prime }+c_{\mathrm{i}}^{\prime })[P_{\mathrm{j}}{E}_{\mathrm{i}}]$$ (6)

The dissociation and catalytic terms are the same as in Eq. (4). When diffusion is sufficiently fast, the pair distribution functions are well approximated by the product of the appropriate bulk concentrations and Eq. (6) reduces to Eq. (4).

The above equations are exact for our model. The pair distribution functions ρ and ρ _j are now assumed to satisfy the following approximate equations, which equate steady‐state fluxes due to diffusion and reaction

$$\mathcal{L}\rho -{\displaystyle \sum _{n=1}^2{\sigma }_n}(\mathrm{x})\left(a_n\rho -d_n[S{E}_n]\right)=0$$

$$\mathcal{L}{\rho }_{\mathrm{j}}-{\sigma }_{\mathrm{i}}(\mathrm{x})\left(a_{\mathrm{i}}^{\prime }{\rho }_{\mathrm{j}}-d_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}{E}_{\mathrm{i}}]\right)+{\sigma }_{\mathrm{j}}(\mathrm{x})c_{\mathrm{j}}[S{E}_{\mathrm{j}}]=0$$ (7)

where $i,j=1,2$ and $j\ne i$ in the last equation. Here $\mathcal{L}$ is the operator describing translational and rotational motion of the enzyme and substrate. For the sake of simplicity we assume that phosphorylation does not alter the dynamics of the substrate. When the reactants are uniformly reacting spheres and their relative motion is described by diffusion, then $\mathcal{L}=D{\nabla }^2$, where D is the sum of the enzyme and substrate diffusion coefficients. The terms with a _i and $a_{\mathrm{i}}^{\prime }$ describe depletion in the distribution functions ρ and ρ _j due to binding to site i; the terms with d _i and $d_{\mathrm{i}}^{\prime }$ describe the influence of the pairs that appear at x due to the dissociation of the bound complexes SE _i and $P_{\mathrm{j}}{E}_{\mathrm{i}}$; the term proportional to c_j describes the effect of the pairs that are formed after phosphorylation of site j. The reactants are treated as impenetrable bodies, so the ρ's satisfy reflecting boundary conditions when the enzyme and substrate are in contact. When $\left|\mathrm{r}\right|\to \infty ,\hspace{0.17em}\rho \to [E][S]$ and ${\rho }_{\mathrm{j}}\to [E][P_{\mathrm{j}}]$. Equation (7) is approximate because we neglected the influence of the distribution functions that involve three molecules. In addition, we assumed that the pair distributions depend on time only through the time‐dependent concentrations.

Equations (6) and (7) completely specify our theory. To solve them, we first rewrite Eq. (7) in terms of the deviations of the pair distribution functions from their chemical kinetics (bulk) values, $\delta \rho (\mathrm{x})=\rho (\mathrm{x})-[S][E]$ and $\delta {\rho }_{\mathrm{j}}(\mathrm{x})={\rho }_{\mathrm{j}}(\mathrm{x})-[P_{\mathrm{j}}][E]$, j = 1, 2:

$$\mathcal{L}\delta \rho -{\displaystyle \sum _{n=1}^2{a}_n}{\sigma }_n(\mathrm{x})\delta \rho ={\displaystyle \sum _{n=1}^2{\sigma }_n}(\mathrm{x})\left(a_n[S][E]-d_n[S{E}_n]\right)$$

$$\mathcal{L}\delta {\rho }_{\mathrm{j}}-a_{\mathrm{i}}^{\prime }{\sigma }_{\mathrm{i}}(\mathrm{x})\delta {\rho }_{\mathrm{j}}=-{\psi }_{\text{ij}}(\mathrm{x})$$ (8)

where we have defined

$${\psi }_{\text{ij}}(\mathrm{x})={\sigma }_{\mathrm{j}}(\mathrm{x})c_{\mathrm{j}}[S{E}_{\mathrm{j}}]+{\sigma }_{\mathrm{i}}(\mathrm{x})(d_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}{E}_{\mathrm{i}}]-a_{\mathrm{i}}^{\prime }[E][P_{\mathrm{j}}])$$ (9)

and used $\mathcal{L}[S][E]=0$ and $\mathcal{L}[P_j][E]=0$. Then we introduce the Green's functions $g(\mathrm{x},{\mathrm{x}}^{\prime })$ and $g_{\mathrm{i}}(\mathrm{x},{\mathrm{x}}^{\prime })$ (i = 1, 2), which satisfy

$$\mathcal{L}g-{\displaystyle \sum _{n=1}^2{a}_n}{\sigma }_n(\mathrm{x})g=-\delta (\mathrm{x}-{\mathrm{x}}^{\prime })$$ (10a)

$$\mathcal{L}{g}_{\mathrm{i}}-a_{\mathrm{i}}^{\prime }{\sigma }_{\mathrm{i}}(\mathrm{x})g_{\mathrm{i}}=-\delta (\mathrm{x}-{\mathrm{x}}^{\prime })$$ (10b)

subject to reflecting boundary conditions at contact. They are required to vanish as $\left|\mathrm{r}\right|\to \infty$. These time‐independent Green's functions describe irreversible binding to both sites of the unphosphorylated substrate (g) and to the ith site of the singly phosphorylated one (g _i). They are time integrals of the time‐dependent Green's functions or propagators, i.e., $g(\mathrm{x},{\mathrm{x}}^{\prime })={\displaystyle {\int }_0^{\infty }G}(\mathrm{x},t\hspace{0.17em}|\hspace{0.17em}{\mathrm{x}}^{\prime },0)dt$ and $g_{\mathrm{i}}(\mathrm{x},{\mathrm{x}}^{\prime })={\displaystyle {\int }_0^{\infty }{G}_{\mathrm{i}}}(\mathrm{x},t\hspace{0.17em}|\hspace{0.17em}{\mathrm{x}}^{\prime },0)dt$, where $G(\mathrm{x},t\hspace{0.17em}|\hspace{0.17em}{\mathrm{x}}^{\prime },0)$ and $G_i(\mathrm{x},t\hspace{0.17em}|\hspace{0.17em}{\mathrm{x}}^{\prime },0)$ are the probabilities to be in x at time t provided initially the system was in ${\mathrm{x}}^{\prime }$ in the presence of two and one (ith) absorbing sinks, respectively. Both $\delta \rho$'s, Eq. (8), and g's, Eq. (10), satisfy the same boundary condition at the contact and when the enzyme‐substrate separation tends to infinity.

As can be verified by direct substitution, the solution of Eq. (8) can be written in terms of the above Green's functions as

$$\delta \rho (\mathrm{x})={\displaystyle \sum _{n=1}^2{\displaystyle \int g}}(\mathrm{x},{\mathrm{x}}^{\prime }){\sigma }_n(\mathrm{x}) (d_n[S{E}_n]-a_n[E][S])\hspace{0.17em}d{\mathrm{x}}^{\prime }$$

$$\delta {\rho }_{\mathrm{j}}(\mathrm{x})={\displaystyle \int g_{\mathrm{i}}}(\mathrm{x},{\mathrm{x}}^{\prime }){\psi }_{\text{ij}}({\mathrm{x}}^{\prime })\hspace{0.17em}d{\mathrm{x}}^{\prime }$$ (11)

where $i,j=1,2,\hspace{0.17em}i\ne j$. Using these we find after some algebra that the binding terms in Eq. (6) can be written as

$${\displaystyle \int a_{\mathrm{i}}}{\sigma }_{\mathrm{i}}(\mathrm{x})\rho (\mathrm{x}) d\mathrm{x}=a_{\mathrm{i}}{ϵ}_{\mathrm{i}}[S][E]+{\displaystyle \sum _{n=1}^2{d}_n}{q}_{n\to i}[S{E}_n]$$ (12a)

$${\displaystyle \int a}{\prime }_{\mathrm{i}}{\sigma }_{\mathrm{i}}(\mathrm{x}){\rho }_{\mathrm{j}}(\mathrm{x}) d\mathrm{x}=a_{\mathrm{i}}^{\prime }{ϵ}_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}][E]+d_{\mathrm{i}}^{\prime }(1-{ϵ}_{\mathrm{i}}^{\prime })[P_{\mathrm{j}}{E}_{\mathrm{i}}]+c_{\mathrm{j}}{q}_{\mathrm{j}\to \mathrm{i}}^{\prime }[S{E}_{\mathrm{j}}]$$ (12b)

where we have introduced the notation ($i,j=1,2$)

$$q_{\mathrm{i}\to \mathrm{j}}=a_{\mathrm{j}}{\displaystyle \int {\sigma }_{\mathrm{j}}}(\mathrm{x})g(\mathrm{x},{\mathrm{x}}^{\prime }){\sigma }_{\mathrm{i}}({\mathrm{x}}^{\prime }) d\mathrm{x}d{\mathrm{x}}^{\prime }$$ (13a)

$${ϵ}_{\mathrm{i}}=1-q_{\mathrm{i}\to 1}-q_{\mathrm{i}\to 2}$$ (13b)

$$q_{\mathrm{i}\to \mathrm{j}}^{\prime }=a_{\mathrm{j}}^{\prime }{\displaystyle \int {\sigma }_{\mathrm{j}}}(\mathrm{x})g_{\mathrm{j}}(\mathrm{x},{\mathrm{x}}^{\prime }){\sigma }_{\mathrm{i}}({\mathrm{x}}^{\prime }) d\mathrm{x}d{\mathrm{x}}^{\prime }$$ (13c)

$${ϵ}_{\mathrm{i}}^{\prime }=1-q_{\mathrm{i}\to \mathrm{i}}^{\prime }$$ (13d)

In the derivation of Eq. (12a), we used the detailed balance condition $a_{\mathrm{i}}{q}_{\mathrm{i}\to \mathrm{j}}=a_{\mathrm{j}}{q}_{\mathrm{j}\to \mathrm{i}}$ (which follows from the definition of $q_{\mathrm{i}\to \mathrm{j}}$ and $g(\mathrm{x},{\mathrm{x}}^{\prime })=g({\mathrm{x}}^{\prime },\mathrm{x})$). We have chosen our notation well because, as explained below, ϵ_i, ${ϵ}_{\mathrm{i}}^{\prime },\hspace{0.17em}{q}_{\mathrm{i}\to \mathrm{j}}$, and $q_{\mathrm{i}\to \mathrm{j}}^{\prime }$ are indeed the escape and capture probabilities depicted in Figure 2.

Finally, using Eq. (12) in Eq. (6), we find that the diffusion‐modified rate equations are

$$\frac{d[S]}{dt}=-{\displaystyle \sum _{n=1}^2(a_n{ϵ}_n[S][E]-d_n{ϵ}_n[S{E}_n])}$$

$$\frac{d[S{E}_{\mathrm{i}}]}{dt}=a_{\mathrm{i}}{ϵ}_{\mathrm{i}}[S][E]-(d_{\mathrm{i}}{ϵ}_{\mathrm{i}}+c_{\mathrm{i}})[S{E}_{\mathrm{i}}]$$

$$\frac{d[P_{\mathrm{j}}]}{dt}=-a_{\mathrm{i}}^{\prime }{ϵ}_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}][E]+d_{\mathrm{i}}^{\prime }{ϵ}_{\mathrm{i}}^{\prime }[S_{\mathrm{j}}^p{E}_{\mathrm{i}}]+c_{\mathrm{j}}(1-q_{\mathrm{j}\to \mathrm{i}}^{\prime })[S{E}_{\mathrm{j}}]$$

$$+d_{\mathrm{j}}{q}_{\mathrm{j}\to \mathrm{i}}[S{E}_{\mathrm{j}}]-d_{\mathrm{i}}{q}_{\mathrm{i}\to \mathrm{j}}[S{E}_{\mathrm{i}}]$$

$$\frac{d[P_{\mathrm{j}}{E}_{\mathrm{i}}]}{dt}=a_{\mathrm{i}}^{\prime }{ϵ}_{\mathrm{i}}^{\prime }[P_{\mathrm{j}}][E]-(d_{\mathrm{i}}^{\prime }{ϵ}_{\mathrm{i}}^{\prime }+c_{\mathrm{i}}^{\prime })[P_{\mathrm{j}}{E}_{\mathrm{i}}]+c_{\mathrm{j}}{q}_{\mathrm{j}\to \mathrm{i}}^{\prime }[P_{\mathrm{i}}{E}_{\mathrm{j}}]$$ (14)

where $i,j=1,2$ and $i\ne j$. These equations correspond to the kinetic scheme in Figure 1(b) with rate constants defined in Eqs. (2) and (3). Comparing these equations with the conventional rate equations, Eq. (4), one can see that the “old” binding and dissociation rates have been multiplied by the corresponding escape probabilities (ϵ's). The terms proportional to the capture or rebinding probabilities $q_{\mathrm{i}\to \mathrm{j}}$ and $q_{\mathrm{j}\to \mathrm{i}}^{\prime }$ correspond to the new reaction channels.

The scaling coefficients $q_{\mathrm{i}\to \mathrm{j}},\hspace{0.17em}{q}_{\mathrm{j}\to \mathrm{i}}^{\prime }$, ϵ _i, and ${ϵ}_{\mathrm{i}}^{\prime }$ are defined in Eq. (13). Reading Eq. (13a) from the right to the left, it can be seen that the coefficient $q_{\mathrm{i}\to \mathrm{j}}$ is the probability that an enzyme and unphosphorylated substrate with configuration ${\mathrm{x}}^{\prime }$ chosen from the distribution ${\sigma }_{\mathrm{i}}({\mathrm{x}}^{\prime })$ will eventually bind to (be captured by) the reactive site j with the unimolecular rate constant $a_{\mathrm{j}}{\sigma }_{\mathrm{j}}(\mathrm{x})$. The Green's function g in the definition of $q_{\mathrm{i}\to \mathrm{j}}$ implies that both sites are reactive and the enzyme‐substrate pair binds irreversibly and cannot dissociate [see Eq. (10a))]. The coefficient ϵ _i in Eq. (13b) is the probability that an enzyme and unphosphorylated substrate pair initially near the site i will eventually diffuse apart (escape). $q_{\mathrm{j}\to \mathrm{i}}^{\prime }$ and ${ϵ}_{\mathrm{i}}^{\prime }$ are the capture and escape probabilities that involve the singly phosphorylated substrate. $q_{\mathrm{i}\to \mathrm{j}}^{\prime }$ in Eq. (13c) is the probability to be captured by the only reactive site j starting out near the inactive (phosphorylated) site i (see the definition of the Green's function g_i in Eq. (10b)). The escape probability ${ϵ}_{\mathrm{i}}^{\prime }$ in Eq. (13d) is the probability to diffuse apart rather than to bind to site i having started near the active site i. In general, the capture and escape probabilities in Eq. (13) must be found numerically. Approximate expressions for these probabilities can be found applying approaches similar to those used to calculate diffusion‐controlled rates involving reactants with two active sites.28, 29, 30, 31

Encounter complex model

The new connections in the diffusion‐modified kinetic scheme in Figure 1(b) can be also obtained in the framework of the encounter complex model of Eigen.26 In this model, the overall diffusion‐influenced binding is considered as a two‐step chemical reaction described by conventional rate equations. First, the reactants diffuse together and form an encounter complex (i.e., the reactants that are in close proximity but not yet bound) and then either diffuse apart or bind. In this way the problem is reduced to solving conventional rate equations with a finite number of states. The advantage of the encounter complex model is that it is simple. Some results, such as Collins–Kimball rate constants for partially absorbing spheres, can be readily obtained using the encounter complex model.12 In the context of multisite phosphorylation, encounter complexes have been used in Refs. 27, and 32. In this section we show how the encounter complex model can be adapted to get our results in Results section.

The encounter complex model for double phosphorylation with two inequivalent sites is given in Figure 4. There are two different encounter complexes involving the unphosphorylated substrate, $S\dots E_1$ and $S\dots E_2$, which correspond to the enzyme being near the first and the second site of the substrate, respectively. Just after the first site is phosphorylated, the encounter complex $P_1\dots E_1$ is formed, in which the enzyme is near the site of the substrate that has been phosphorylated. This complex can be transformed into the encounter complex $P_1\dots E_2$ where the enzyme is near the unphosphorylated site of the singly phosphorylated substrate. The encounter complexes with the second site phosphorylated are $P_2\dots E_2$ and $P_2\dots E_1$.

Figure 4.

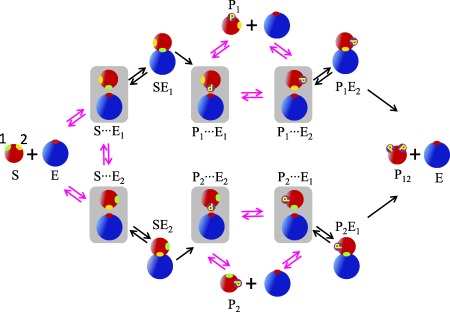
The standard kinetic scheme in Figure 1(a) augmented by six encounter complexes that have been shaded. The transitions not present in the chemical kinetics scheme are magenta colored. The subscript on E denotes the site on the substrate (1, green, or 2, yellow) that is close to the active site of the enzyme. The subscript on P indicates which site is phosphorylated. Thus $P_{\mathrm{i}}\dots E_{\mathrm{j}},\hspace{0.17em}i,j=1,2$ is an encounter complex in which an enzyme is close to site j of a substrate with site i phosphorylated.

We are going to apply the steady‐state approximation and eliminate the encounter complexes from the rate equations. The scheme in Figure 4 has three groups of species, in which an unbound enzyme and a substrate and two encounter complexes are connected by magenta arrows. The generic kinetic scheme for such a group is shown in Figure 5(a), where A stands for a substrate (S, P ₁ or P ₂), B for the enzyme, C ₁ and C ₂ are the bound states, and $A\dots B_1$ and $A\dots B_2$ are the encounter complexes. The bimolecular rate constant $k_{\text{Di}}^{+}$ describes the formation of the encounter complex $A\dots B_{\mathrm{i}}$ due to diffusion. $k_{\text{Di}}^{-}$ is the rate constant for the dissociation of $A\dots B_{\mathrm{i}}$. The β's describe the interconversion of the encounter complexes. These rate constants are restricted by the detailed balance condition:

$${\beta }_1{k}_{D1}^{+}{k}_{D2}^{-}={\beta }_2{k}_{D2}^{+}{k}_{D1}^{-}$$ (15)

Figure 5.

(a) Definition of a generic three‐state motif involving two encounter complexes. Species A has two sites, $A\dots B_{\mathrm{i}}$ denotes an encounter complex where B is close to the ith site of A. The association (dissociation) constants $k_{\text{Di}}^{+}$ ($k_{\text{Di}}^{-}$) depend on diffusion but the unimolecular rate constants α_i and d_i do not. (b). The irreversible kinetic scheme used to calculate the capture and escape probabilities of the encounter complexes. The capture probability ϵ_i is the probability that the encounter complex $A\dots B_{\mathrm{i}}$ eventually diffusively separates. The capture probability $q_{\mathrm{i}\to \mathrm{j}}$ ($i,j=1,2$) is the probability that the encounter complex $A\dots B_{\mathrm{i}}$ eventually reacts to form C_j. (c) The diffusion‐modified scheme obtained using the steady‐state approximation for $A\dots B_{\mathrm{i}}$ in panel (a) and rewriting the rates in terms of the escape and capture probabilities calculated from the kinetic scheme in panel (b). The new transitions are shown in red, the transitions with the modified rate constants are in blue.

The rate equations corresponding to the scheme in Figure 5(a) involve concentrations of A, B, $A\dots B_1,\hspace{0.17em}A\dots B_2$, C ₁, and C ₂. We use the steady‐state approximation, $d[A\dots B_{\mathrm{i}}]/dt=0$, to find the concentrations of the two encounter complexes, and then eliminate them from the rate equations. The rate constants in the resulting rate equations for the concentrations of A, B, C ₁, and C ₂ are complicated when expressed in terms of the rates in the scheme in Figure 5(a). For example, the rate constant of the transition $C_1\to C_2$ is equal to

$$\frac{d_1{\beta }_1{\alpha }_2}{(k_{D1}^{-}+{\alpha }_1+{\beta }_1)(k_{D2}^{-}+{\alpha }_2+{\beta }_2)-{\beta }_1{\beta }_2}$$ (16)

However, we will now show that this and all other rate constants can be simplified if expressed in terms of the capture and escape probabilities.

Let us now define the capture probabilities in the framework of the encounter complex model. Consider two interconverting encounter complexes, which decay irreversibly [see Fig. 5(b)]. In this kinetic scheme, an encounter complex $A\dots B_{\mathrm{i}}$ can either bind (through the first or second binding channel) or separate (through the escape channel). The probabilities to eventually exit through the two binding channels are $q_{i\to 1}$ and $q_{i\to 2}$. The probability to exit through the escape channel is ϵ_i. These probabilities must add up to 1 (i = 1, 2):

$$q_{i\to 1}+q_{i\to 2}+{ϵ}_i=1$$ (17)

The capture and escape probabilities can be expressed in terms of the total flux through the corresponding channels:

$$q_{\mathrm{i}\to \mathrm{j}}={\alpha }_{\mathrm{j}}{\displaystyle {\int }_0^{\infty }G}(j,t\hspace{0.17em}|\hspace{0.17em}i,0)\hspace{0.17em}dt$$

$${ϵ}_{\mathrm{i}}={\displaystyle {\int }_0^{\infty }\left(k_{D1}^{-}G(1,t\hspace{0.17em}|\hspace{0.17em}i,0)+k_{D2}^{-}G(2,t\hspace{0.17em}|\hspace{0.17em}i,0)\right)} dt$$ (18)

where $G(j,t\hspace{0.17em}|\hspace{0.17em}i,0)$ ($i,j=1,2$) is the probability to be in state $A\dots B_j$ at time t given that initially the system was in state $A\dots B_i$. These are the discrete analogues of the expressions in Eqs. (13a) and (13b).

The probabilities $G(j,t\hspace{0.17em}|\hspace{0.17em}i,0)$ satisfy the kinetic equations corresponding to the scheme in Figure 5(b):

$$\begin{array}{c}\frac{dG(1,t\hspace{0.17em}|\hspace{0.17em}i,0)}{dt}=-({\alpha }_1+k_{\mathrm{D}1}^{-}+{\beta }_1)G(1,t\hspace{0.17em}|\hspace{0.17em}i,0)+{\beta }_{2}G(2,t\hspace{0.17em}|\hspace{0.17em}i,0)\\ \frac{dG(2,t\hspace{0.17em}|\hspace{0.17em}i,0)}{dt}=-({\alpha }_2+k_{\mathrm{D}2}^{-}+{\beta }_2)G(2,t\hspace{0.17em}|\hspace{0.17em}i,0)+{\beta }_{1}G(1,t\hspace{0.17em}|\hspace{0.17em}i,0)\end{array}$$ (19)

with the initial condition $G(j,0\hspace{0.17em}|\hspace{0.17em}i,0)={\delta }_{\text{ji}}$. This equation can be written in matrix form for the matrix G with the elements $G(j,t\hspace{0.17em}|\hspace{0.17em}i,0)$:

$$\frac{d\mathit{G}(t)}{dt}=-\mathit{M}\mathit{G}$$ (20)

where M is the 2 × 2 matrix:

$$\mathit{M}=\left(\begin{array}{cc}{k}_{D1}^{-}+{\alpha }_1+{\beta }_1& -{\beta }_2\\ -{\beta }_1& k_{D2}^{-}+{\alpha }_2+{\beta }_2\end{array}\right)$$ (21)

with the initial condition $\mathit{G}(t=0)=\mathit{I}$, where I is the unit matrix. To find the splitting probabilities $q_{\mathrm{i}\to \mathrm{j}}$ and ϵ_i we only need the time integrals of G [see Eq. (18)]. Integrating both sides of Eq. (20) with respect to t and using $\mathit{G}(t=\infty )=0$, we have

$$\mathit{I}=\mathit{Mg}$$ (22)

where $\mathit{g}\equiv {\displaystyle {\int }_0^{\infty }\mathit{G}}(t)\hspace{0.17em}dt$. This is the discrete analogue of Eq. (10a).

Thus the capture and escape probabilities in Eq. (18) are

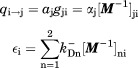(23)

Using these expressions, one can verify that the rate constant of $C_1\to C_2$ in Eq. (16) can be simply expressed as $d_1{q}_{1\to 2}$. The same procedure for all transitions leads to the kinetic scheme shown in Figure 5(c). In this scheme, the bimolecular chemical binding constants are defined as $a_{\mathrm{i}}={\alpha }_{\mathrm{i}}{k}_{\text{Di}}^{+}/k_{\text{Di}}^{-}$ and the capture and escape probabilities are given by Eq. (23). The chemical rate constants a_i do not depend on diffusion because $k_{\text{Di}}^{+}/k_{\text{Di}}^{-}$ is an equilibrium constant. The new rates in Figure 5(c) (shown in red) have a transparent physical interpretation. For example, the rate from C ₁ to C ₂ is equal to the product of the dissociation rate from site 1 (d ₁) and the probability that the enzyme binds to site 2 before escaping to infinity. The capture probabilities $q_{1\to 2}$ and $q_{2\to 1}$ are not independent because the cycle shown in Figure 5(c) obeys detailed balance (i.e., the product of the clockwise rates is equal to the product of the counterclockwise ones). The rate constants in the kinetic scheme shown in Figure 5(c) depend on the phenomenological rate constants $k_{\text{Di}}^{\pm }$, β _i, α _i only through the chemical rate constants a _i and d _i, the escape probabilities, ϵ _i, and the capture probability, $q_{1\to 2}$ (or equivalently $q_{2\to 1}$).

Now we are ready to eliminate the encounter complexes in the scheme in Figure 4 using the steady‐state approximation and exploiting the results in Figure 5. To treat the triangular motif on the left side of Figure 4, we make the following correspondence: $A\to S,\hspace{0.17em}B\to E,\hspace{0.17em}{C}_{\mathrm{i}}\to S{E}_{\mathrm{i}}$. For the motif on the top, $A\to P_1,\hspace{0.17em}B\to E,\hspace{0.17em}{C}_1\to S{E}_1$ and $C_2\to P_1{E}_1$, and similarly for the one at the bottom. The resulting kinetic scheme has the same structure as that in Figure 1(b) with the new reaction channels shown by red arrows. Because the transitions $S{E}_1\to P_1\dots E_1$ and $S{E}_2\to P_2\dots E_2$ in Figure 4 are irreversible, they lead to the one‐way connections $S{E}_1\to P_1{E}_2$ and $S{E}_2\to P_2{E}_1$. The rate constants are the same as in Eqs. (2) and (3), but with the capture and escape probabilities defined in the framework of the encounter complex model. Thus, in this case, the phenomenological encounter complex model reproduces the diffusion‐modified kinetic scheme obtained using the microscopic model, even though the kinetic scheme in Figure 5(b) yields a poor description of the irreversible diffusive geminate recombination of an isolated contact pair in solution, whose time course is not exponential, but a power law.