Computational study of the W260A activating mutant of Src tyrosine kinase

Abstract

Tyrosine kinases are enzymes playing a critical role in cellular signaling. Mutations causing increased in kinase activity are often associated with cancer and various pathologies. One example in Src tyrosine kinases is offered by the substitution of the highly conserved tryptophan 260 by an alanine (W260A), which has been shown to cause an increase in activity. Here, molecular dynamics simulations based on atomic models are carried out to characterize the conformational changes in the linker region and the catalytic (kinase) domain of Src kinase to elucidate the impact of the W260A mutation. Umbrella sampling calculations show that the conformation of the linker observed in the assembled down‐regulated state of the kinase is most favored when the kinase domain is in the inactive state, whereas the conformation of the linker observed in the re‐assembled up‐regulated state of the kinase is favored when the kinase domain is in the unphosphorylated active‐like state. The calculations further indicate that there are only small differences between the WT and W260A mutant. In both cases, the intermediates states are very similar and the down‐regulated inactive conformation is the most stable state. However, the calculations also show that the free energy cost to reach the unphosphorylated active‐like conformation is slightly smaller for the W260A mutant compared with WT. A simple kinetic model is developed and submitted to a Bayesian Monte Carlo analysis to illustrate how such small differences can contribute to accelerate the trans‐autophosphorylation reaction and yield a large increase in the activity of the mutant as observed experimentally.

Abbreviations

WT

wild‐type

ATP

adenosine triphosphate

US

umbrella sampling

MD

molecular dynamics

PMF

potential of mean force

SH

Src‐homology

SFK

Src‐family kinase

A‐loop

activation loop

Introduction

The c‐Src kinase, which belongs to the family of Src‐related nonreceptor tyrosine kinases (Src, Yes, Fyn, Lyn, Lck, Blk, Hck, Fgr, and Yrk),1 plays vital roles in regulating cell growth, proliferation, metabolism, differentiation, adhesion, and migration.2, 3, 4 It has been discovered that overactivation of Src is often at the origin of tumorigenesis, tumor metastasis, and obesity.5, 6, 7 Recent studies suggest that protein kinases are not optimized to function as efficient enzymes. Rather, they are dynamical allosteric structures designed to serve as highly sensitive molecular switches, regulating cellular signaling by toggling between inactive and active states.8 Therefore, studying the intramolecular motions associated with Src activation may lead to a better functional understanding of protein kinases, and identify metastable intermediate states that could be targeted to design pharmaceutical inhibitors.

Src comprises of an N‐terminal myristoylation site, a SH3 and SH2 regulatory domains, followed by a catalytic/kinase domain (see Supporting Information Fig. S1). The activity of Src is regulated through post‐translational modifications and allosteric conformational changes in multiple domains.1, 9, 10, 11, 12 The inactive state (down‐regulated state) of Src adopts an autoinhibitory conformation [Supporting Information Fig. S1(A)] in which the SH2 domain binds to the phosphorylated Y527 (pY527, chicken c‐Src numbering is used throughout this article) and the SH3 domain binds to the linker connecting the SH2 and kinase domains. The binding of the SH3 domain to the linker is associated with the formation of a β‐turn motif in the linker region (residues 256 to 259). This β‐turn is also observed in the crystal structure of the autoinhibited Hck kinase.13, 14 Disruption of either SH2‐pY527 or SH3‐linker interaction disassembles the autoinhibitory conformations and eventually leads to the activation of Src kinases.15, 16, 17

Phosphorylation of the activation‐loop (A‐loop) is ultimately required to lock the catalytic domain into the fully active conformation and is a general mechanism to activate a kinase.18 In Src, this process is carried out by a second Src kinase during a bimolecular encounter event, according to a classical enzyme‐substrate reaction (n.b., it is a trans‐autophosphorylation process because the reaction involves two Src kinases).19, 20, 21 The linker region around W260 also displays conformational changes upon activation of Src, accompanying the conformational transition in the kinase domain: the β‐turn which consists of residues 256 to 259 in the assembled state is shifted to residues 258 to 261. Figure 1 illustrates the conformational change in the truncated linker region. This new β‐turn can be observed in the crystal structure of active Lck kinase as well.22 A representative structure of the activated conformation is shown in Supporting Information Figure S1(B). The importance of the conformational change in the linker region can be reflected by Supporting Information Figure S2 as well: superimposing the regulatory domains of the inactive and the active structures show great structural similarity (RMSD of Cα atoms from residue 84 to 244 is 2.02 Å). No significant conformational change within the regulatory domains occurs during activation. However, a large conformational difference appears when aligning only the kinase domain. This conformational change is associated with the shift of β turns.

Figure 1.

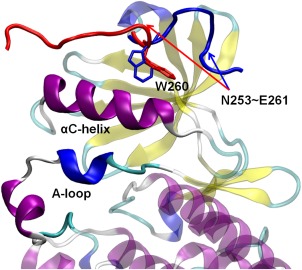
A cartoon representation of the truncated linker and the kinase domain of Src in inactive and active conformations. Only the inactive kinase domain is shown as a background. Residues 253 to 261 in the inactive kinase are colored in blue, whereas the counterparts in the active kinase are colored in red.

A number of Src point mutations identified experimentally are known to cause various levels of increase in kinase activity. Specific mutations that are of functional importance include T338I, T338M,23 W260A,24, 25 and L255V.26 Mutation of the threonine at position 338, called the “gatekeeper” residue because it controls the accessibility to a hydrophobic region deep in the ATP binding pocket, can have important consequences on the specificity of kinase inhibitors.27 Mutations of the medium‐size threonine to amino acids with a bulkier side chain can lead to drug resistance, such as the resistance to imatinib and dasatinib in the treatment of chronic myeloid leukemia (CML).28 Also of particular interest is the activating mutant W260A. This highly conserved tryptophan is located near the N‐terminal of the kinase domain and is believed to play an important role in the coupling of the regulatory domains to the kinase domain and in exogenous ligand binding.14, 22 W260 appears to stabilize the αC‐helix pointing outward, a structural feature associated with the down‐regulated inactive state. In vitro functional assays showed that the W260A mutation increased the basal activity, accelerated the rate of autophosphorylation, lowered the sensitivity to regulatory domain ligands, and modified the accessibility of ligand binding surfaces for the regulatory domains.24, 25 However, the detailed molecular mechanism underlying these experimental observations is still elusive. For example, it is unclear whether W260A acts by locking the kinase domain into an active conformation, or by destabilizing the inactive state. Furthermore, it has been suggested that disruption of the SH3 domain binding to the linker would destabilize the interaction of W260 with the outward αC‐helix.21 As W260 is located at the boundary of the kinase domain and the linker region, it is also unclear which of the two structural features is most responsible for the increased activity caused by the mutation.

Molecular dynamics (MD) simulations offer an attractive approach to help such issues by providing atomic‐level information about the conformational dynamics of biological molecules that is not easily accessible from experiments. Several MD simulation studies have focused on the role of the linker29, 30 and the conformational changes and phosphorylations of the isolated kinase domain.31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41 US calculations and MSMs have been proved to be effective in understanding the conformational changes in SFKs. The picture that emerges from these computational studies—whereby the catalytic domain makes dynamical transient visits to an “active‐like” conformation—provides a broad framework for understanding the sequence of events leading to full kinase activation. These transient visits increase the availability of Y416 in the A‐loop for the trans‐transphosphorylation bio‐molecular process, which ultimately locks the enzyme in the catalytically competent state.

In the present study, the conformational equilibrium of Src kinase domain is investigated using MD simulations and US calculations to elucidate the impact of the W260A mutation. The calculated free energy landscapes are used to determine the mechanism by which the W260A mutation yields a constitutively active kinase according to experiments. The computations include only the kinase domain, without the SH2 and SH3 regulatory domains. While it is clear that the latter play an important role in shaping the free‐energy landscape governing kinase activation, computations with a truncated kinase are expected to be meaningful because a previous study based on a similar construct showed that the kinase domain without the regulatory domains is predominantly in the inactive state.38 The present results will show that this remains true for the W260A mutation. We also investigate how phosphorylation of the A‐loop affects the time‐dependence for the activation of a population of kinases in solution as monitored experimentally in functional assays. To this end, we develop a kinetic model that explicitly addresses the formation of the enzyme‐substrate dimer in order to gain more insight into the functional impact of the W260A mutant on the rate of trans‐autophosphorylation reaction of the Src kinase.

Results

Free energy landscape and stability of the linker region

Crystal structures of near full‐length Hck and Src kinases show that a β‐turn motif from residues 256 to 259 is formed in the autoinhibited state.13, 14, 42 In contrast, a β‐turn going from residues 258 to 261 is observed in the active Lck and Src crystal structures.22, 43 According to an earlier umbrella sampling simulation of Hck kinase by Banavali and Roux,29 the formation of such β‐turns is mutual exclusive and is conditioned on the conformational state of the catalytic kinase domain. However, one limitation of this study was the reliance on a homology model for the active state of Hck built from Lck as template. Here, we revisit this issue using c‐Src as the model system so that both conformational states of linker region and the corresponding conformations of the kinase domain are taken from crystallographic structures. In the umbrella sampling simulations, the distance between the Cα atoms of A256 and A259 and the distance between the Cα atoms of D258 and E261 are used to describe the formation and deformation of the β‐turns (Supporting Information Figure S4 displays the two β‐turns and the order parameters). Following the definition in the paper of Banavali and Roux,29 the configuration of the linker is referred to as the “restricted conformation” when the β‐turn from A256 to A259 is formed and the β‐turn from D258 to E261 is not, whereas it is labeled as the “released conformation” when the formation of β turns is swapped. The restricted conformation of the linker can represent the SH3 domain is engaged with the linker, and the released conformation represents the opposite.

Figure 2(A,B) show the two‐dimensional potential of mean force free energy surfaces (2D‐PMFs) of the WT construct, which describe the conformational equilibrium of the linker region for the inactive and the unphosphorylated active‐like kinase domain, respectively. In the crystal structure of the autoinhibited Src, the distances d _{256CA‐259CA} and d _{258CA‐261CA} are approximately 5 and 9 Å, respectively. The values are swapped in the crystal structure of an active Src. Therefore, a free energy basin located at the upper left corner of the PMF corresponds to the restricted conformation of the linker, and that at the lower right corner corresponds to the released conformation. A common feature of both free energy landscapes is that the free energy basins are shallow. The barriers separating basins are smaller than 3 kcal/mol, indicating that the truncated linker is quite flexible, possibly because the SH3 and SH2 domains are not attached in our constructs. This flexibility can also be reflected in the projection of 100 ns unbiased MD onto the 2D‐PMF (Supporting Information Fig. S5).

Figure 2.

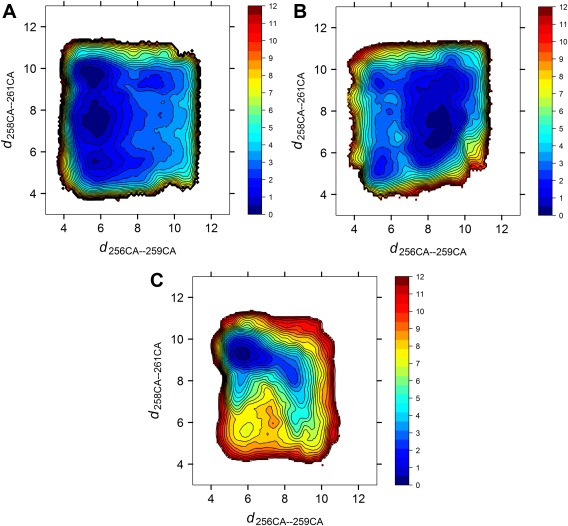
Free energy landscape of the conformational changes in the truncated linker region. All free energies are in the unit of kcal/mol. (A) Wild‐type Src, the kinase domain is in the inactive conformation. (B) Wild‐type Src, the kinase domain is in the active conformation. (C) The W260A mutant, the kinase domain is in the inactive conformation.

When the kinase domain adopts the inactive conformation, only the restricted conformation, rather than the released conformation, is stable. This suggests that the spontaneous disengagement of the SH3 domain with the linker is difficult: the inactive kinase domain couples with a configuration of the regulatory apparatus that negatively controls the activity. On the other hand, both the restricted and the released conformations are stable when the kinase domain adopts the unphosphorylated active‐like conformation. However, the released conformation is much more favorable than the restricted one in this case. Since the released conformation of the linker is unfavorable for binding to the SH3 domain, our modeling yields that activating the kinase domain is able to hijack the regulatory mechanisms.

W260 is located at the boundary of the linker and the kinase domain. The W260A mutation could influence both the conformational equilibrium of the linker and the kinase domain. Two possible hypothetical mechanisms can be proposed to explain the functional impact of the mutation: (1) W260A stabilizes the released conformation of the linker, which in turn, disrupts the regulatory mechanism (SH3•Linker binding) and activates the kinase, and (2) W260A stabilizes the unphosphorylated active‐like conformation of the kinase domain directly. We first examine the conformational equilibrium of the linker in the mutant. One piece of evidence supporting the first hypothesis is that the basin of released conformation can appear in the free energy landscape when the kinase domain is in the inactive conformation. The resulting free energy landscape from umbrella sampling simulation of the W260A construct is illustrated in Figure 2(C). According to this figure, there is only one free energy basin in the landscape that corresponds to the restricted conformation. Furthermore, the conformational flexibility of the linker region is reduced in the W260A construct. The W260A mutation will generate more restricted conformation of the linker, and hence possibly strengthens the SH3•Linker interaction, which contradicts to the first hypothesis.

Free energy landscape and stability of the catalytic domain

To examine the second hypothesis, we carried out 2D umbrella sampling simulations on the conformational equilibrium of the kinase domain for both the WT and the W260A constructs. We have studied the activating conformational changes in the unphosphorylated WT Src kinase domain previously.41 A three‐state conformational equilibrium has been observed and the inactive conformation is found to be the most stable state. The unphosphorylated active‐like conformation is approximately 3.9 kcal/mol higher in free energy than the inactive conformation (ΔG _{inactive→active} = 3.9 kcal/mol). In the current work, we kept all those umbrella windows and extended the MD propagation for another 10 ns per window. The resulting PMF is displayed in Figure 3(A). The new free energy landscape demonstrates the same features as what we observed previously and yields a ΔG _{inactive→active} of 3.7 kcal/mol. The convergence in our 2D‐PMFs can be partially reflected in the quantitative agreement between the two ΔG values.

Figure 3.

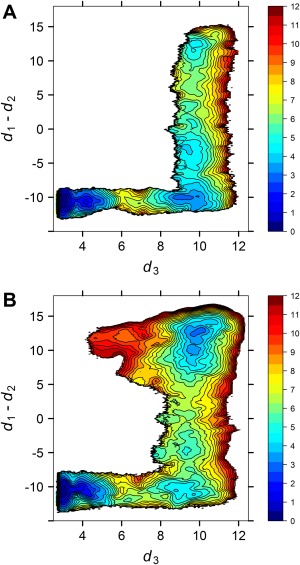
Free energy landscape of the kinase domain activation. All free energies are in the unit of kcal/mol. (A) Wild‐type Src. (B) The W260A mutant.

Figure 3(B) displays the free energy landscape underlying the activation pathway in the kinase domain of the unphosphorylated W260A construct. The three‐state conformational equilibrium is still preserved. The conformation of the intermediate state (lower right corner of the free energy landscape) resembles that of the WT construct. The inactive conformation still has the lowest free energy, even though the free energy of the active conformation is lowered. The ΔG _{inactive→active} becomes 2.0 kcal/mol. The mutation is not able to eliminate the inactive conformation of the kinase domain. It could not turn over the relative stability between the inactive and the active‐like species either. However, lowering the free energy by 1.7 kcal/mol corresponds to a drastic increase in the population of the unphosphorylated active‐like conformation which can accelerate the trans‐autophosphorylation reaction. The US calculations of the kinase domain further supports the hypothesis that the main impact of the W260A mutation is to enhance the probability of the unphosphorylated active‐like state relative to that of the inactive state. The relative shift in equilibrium has the consequence to facilitate the trans‐autophosphorylation process, leading to an accelerated activation of a population of kinases in solution.

To determine the impact of Y416 phosphorylation on the conformational equilibrium of the W260A construct, a set of one‐dimensional (1D) US calculations, which monitors the movement of the αC‐helix, was carried out. The A‐loop of the W260A construct in each umbrella window adopts an open and extended conformation. The resulting free energy profile is shown in Figure 4 (the blue dash line). To compare with it, projection of 2D‐PMFs onto the y‐axis was performed for the WT unphosphorylated A‐loop, WT phosphorylated A‐loop, and W260A unphosphorylated A‐loop and the 1D‐PMFs are also displayed in Figure 4. Likewise to the WT construct, phosphorylation of Y416 in the mutant is able to eliminate the “αC‐helix‐out” conformation and locks the kinase domain of the mutant in the active state. A full activation of the mutant can thus be achieved. To avoid any confusion, however, we emphasize that the free energy landscapes for the WT and mutant shown in Figures 3 and 4 contain only information about the relative probability of the conformations; they do not provide information about the absolute stabilization or destabilization of the protein for any of the states.

Figure 4.

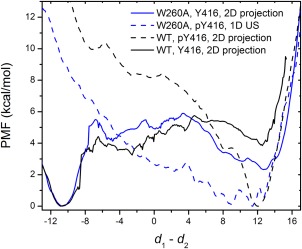
Free energy profile of the movement of the αC‐helix.

Kinetic model of src autophosphorylation

Results from the present US calculations indicate that the W260A mutation gives rise to a small thermodynamic perturbation of the free energy landscape of the unphosphorylated kinase domain compared to the WT. The major impact of this mutation appears to slightly reduce the free energy difference between the inactive and the unphosphorylated active‐like conformations of the kinase domain. At first glance, the results from US calculations seem to indicate that only minuscule effects arise from this mutation, which seems to be in contradiction with the increased rate of autophosphorylation of the W260A mutant relative to the WT kinase observed in experiments.25 A critical question is whether such a small shift in the ΔG _{inactive→active} is consistent with experimental observations regarding the rate of autophosphorylation. The time‐dependence for the activation of a population of kinases in solution mainly reflects the rate of trans‐autophosphorylation of Y416 in the A‐loop, which takes place through a bimolecular encounter. In this bimolecular encounter, one kinase acts as an enzyme (to catalyze the reaction) while the other kinase acts as a substrate (to be phosphorylated). The latter must be able to present its unphosphorylated Y416 as a substrate, which means that it must be able to adopt an open A‐loop conformation. Furthermore, because all the kinases are initially all unphosphorylated, a small fraction of kinases with unphosphorylated Y416 in a catalytically competent conformation must exist to catalyze the phosphorylation of a substrate in the early stage of the activation.

As no direct experimental thermodynamic measurements about the conformational equilibrium population of the kinase domain are available, it is necessary to rely on a more complete framework model which enables to establish a direct connection to the experimental kinase activity assays in order to assess the results from the US calculations. To this end, we designed a simple kinetic state model as follows:

$$I\stackrel{ K_{\text{eq} }}{\leftrightarrow }A$$

$$A\hspace{0.17em}+\hspace{0.17em}A\begin{array}{c}\stackrel{ k_{\text{on}} }{\to }\\ \underset{ k_{\text{off} }}{\overset{}{\leftarrow }}\end{array}A•A \hspace{0.17em}\stackrel{ k_{\text{phos}} }{\to }\hspace{0.17em}A\hspace{0.17em}+\hspace{0.17em}A{}^{*}$$

$$A\hspace{0.17em}+\hspace{0.17em}A{}^{*} \begin{array}{c}\stackrel{ k_{\text{on}} }{\to }\\ \underset{ k_{\text{off} }}{\overset{}{\leftarrow }}\end{array}A•A^{*}\hspace{0.17em}\stackrel{ k_{\text{phos} }}{\to } A^{*}+\hspace{0.17em}{A}^{*}$$

In this kinetic scheme, the state I represents the inactive kinase domain identified in US and MSM studies,35, 37, 38, 39, 40 the state A represents the unphosphorylated active‐like conformation of the kinase domain, the state A* represents the fully activated kinase domain in which Y416 is phosphorylated, the state A•A represents the bimolecular enzyme‐substrate encounter complex of two kinase domains in an open active‐like conformation with Y416 unphosphorylated, and the state A•A* represents the enzyme‐substrate complex in which the enzyme domain is phosphorylated at Y416 but the substrate domain is not. Of critical importance, both the phosphorylated state A^* as well as the unphosphorylated state A are catalytically competent. The equilibrium constant K _eq reflects the relative population of the I and A states and is the main focus of the US calculations. The rate constant k _on and k _off are used to describe the formation and dissociation of the dimer (A•A and A•A*), and k _phos is the rate constant for the phosphorylation reaction. To further simplify our calculation of the concentration of each species in solution, it is assumed that the rates k _on and k _off of dimerization and k _phos are the same for two last reactions. Therefore, the time‐evolution of the concentration of each species can be obtained by solving the rate equations numerically. Additional details of the kinetic model are given in Methods and Materials.

The kinetic model presented here has a similar structure as that of an earlier model designed to consider the autophosphorylation process in kinase activation,38 but goes further by explicitly taking the formation of enzyme‐substrate bimolecular complex into account. Using this expanded model, information regarding the binding affinity can be inferred by estimating the k _on and k _off parameters of the model from the experimental data.

We first apply this kinetic model to the WT kinase domain and generate an estimate of the k _on and k _off using a Bayesian Monte Carlo (BMC) procedure (see the section of Methods and Materials for details of the BMC). We further assume the k _on and k _off have the same value for the W260A construct and estimate the ΔG _{inactive→active} with the same BMC procedure. With such analysis, we are able to estimate the binding affinity of the enzyme‐substrate complex, and also compare the ΔG _{inactive→active} obtained from different approaches. One million BMC steps were carried out to estimate k _on and k _off (see Supporting Information Fig. S6 for the joint probability distribution of the parameters k _on and k _off). The time series of the squared error between the calculated and the experimental t _1/2 values (χ ²) is illustrated in Supporting Information Figure S7(A). The k _on and k _off is estimated to be 4500 ± 860 M⁻¹ s⁻¹ and 0.35 ± 0.27 s⁻¹, respectively. Supporting Information Figure S7(B) illustrates the time evolution of the fraction of the fully activated Src (phosphorylated in the A‐loop, A ^*) when the mean of k _on and k _off are utilized. The statistics of the k _on and k _off also yields the dissociation constant (K _d) of the enzyme‐substrate complex to be approximately 77 ± 60 μM. The joint probability distribution of k _on and k _off (Supporting Information Fig. S6) indicates that the two values are linearly correlated, suggesting that their ratio, i.e., the dissociation constant K _d = k _off/k _on, is well constrained by the analysis. While there remains considerable uncertainty with these BMC estimates, the analysis suggests a fairly weak association for the enzyme‐substrate complex. This may partly explain why such a dimeric structure is difficult to observe experimentally, or captured by X‐ray crystallography.

In the next stage, the mean of the k _on and the k _off deduced for the WT kinase are used as input parameters for the kinetic model for the W260A mutant. The ΔG _{inactive→active} (ΔG _{inactive→active} ≡ −k _B T· ln(K _eq)) is estimated via the same BMC process. Supporting Information Figure S8(A) displays the time series of χ ² and Figure 5(A) displays that of the K _eq, respectively. The K _eq for the W260A construct yielded from our kinetic model is 127 ± 30, which corresponds to a ΔG _{inactive→active} of 2.9 ± 0.2 kcal/mol. This free energy difference agrees well with the US calculations, and give more confidence to our perspective on the impact of the W260A mutation. The time‐courses of the fraction of the fully activated W260A mutant at different initial concentrations are illustrated in Supporting Information Figure S8(B). The t _1/2 values of both the WT and the W260A constructs are displayed in Figure 5(B).

Figure 5.

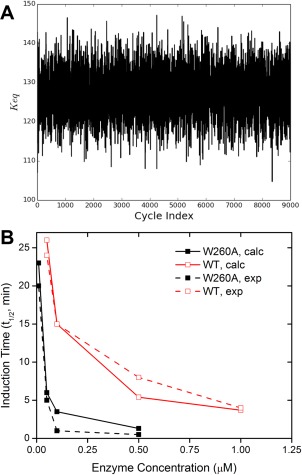
Outputs from out kinetic model. (A) Time series of K _eq (between the inactive and the active species) for the W260A kinase domain from the BMC estimation. (B) The calculated t _1/2 with respect to initial concentration of the kinase. The experimental data extracted from Ref. 25 are also displayed for comparison.

W260 conformational flexibility and the linker‐kinase domain interactions

W260 plays an important role in down‐regulating the activity of SFKs. It is believed that disruption of the SH3 domain binding to the linker will destabilize the interaction of W260 with the “outward” αC‐helix.21 Here, we analyze the conformational flexibility of W260 in the inactive and the active‐like state based on our 100 ns MD equilibrations. The backbone conformations of W260 in the inactive and the active‐like constructs resemble each other [Supporting Information Fig. S9(A,B)]. However, the side chain of W260 is more flexible in the active construct than that in the inactive one. In addition, the side chain conformation that is observed in the inactive kinase is rarely visited by W260 in the active kinase. The local conformational state at W260 correlates with specific global conformation of the kinase domain. We also analyze the interaction between W260 and the other residues in the kinase domain in order to elucidate the role of W260 in Src activation. To achieve this, we utilize the pairwise nonbonded interaction energy (sum of the Coulomb and the Lennard‐Jones potentials); a negative value indicates a mutual stabilizing effect, whereas a positive one indicates the opposite. Supporting Information Figure S10 summarizes the pairwise interaction energy involving W260 and focuses on regions showing most of the nonzero values (residues in the vicinity of W260 also produce nonzero values and are not shown). Analysis of the pairwise interaction energy demonstrates that W260 mainly interacts with the αC/β4 region in both types of the kinase domain. The side chain conformational change at W260 concerts with the movement of the αC‐helix. This conformational change enables W260 to stabilize the αC‐helix in both conformational states. The MD simulation suggests that W260 is not only crucial for keeping the kinase domain inactive but also able to stabilize the active conformation. The W260A mutation substitutes the large indole side chain by a small methyl group. This eliminates a number of favorable interactions that contribute to stabilize both the inactive and the active‐like conformations. However, as revealed by calculated PMFs, the net effect of the mutation is to shift the relative equilibrium between these states, decreasing the probability of the inactive state and increasing the probability of the active‐like state. The truncated linker interacts with the β2/β3 and the αC/β4 regions regardless of the conformations of the kinase domain (see Supporting Information Fig. S11). The overall interaction between the truncated linker region and the kinase domain is always favorable no matter the conformational state of the kinase domain. When a point mutation happens in the linker region, e.g. L255V, it tends to influence the inactive and the active kinase domain in the same direction but may differ in the amplitude. This competition will cause subtle change in the conformational equilibrium.

Discussion

In this study, molecular dynamics (MD) simulations and umbrella sampling (US) calculations were used to characterize the impact of the W260A mutation on the catalytic domain of Src kinase. First, the conformational equilibrium of the linker region for both the WT and the W260A constructs were examined. When the kinase domain is in the inactive conformation, the linker favors the restricted conformation in which the linker is suitable for binding to the SH3 domain. No free energy basin corresponding to the released conformation is seen in the PMF. When the kinase domain is in the unphosphorylated active‐like conformation, both the restricted and the released conformations appear in the free energy landscape and the released conformation is much more favorable. Our observations agree with the earlier study on Hck kinase and confirm the coupling between the kinase domain and the linker region.29 Since the released conformation of the linker is unfavorable for binding to the SH3 domain, our umbrella sampling simulation also demonstrates that activation of the kinase domain is able to hijack the regulatory mechanisms. Our results are consistent with the experimental observation that phosphorylation of the A‐loop of Src is able to relieve the autoinhibition and to make the SH3 domain more accessible to exogenous ligands.44 According to our model, autophosphorylation on the A‐loop first locks the kinase domain in the active conformation, and the activated kinase domain stabilizes the linker in the released form which disturbs the SH3•Linker binding and promotes the SH3 domain binding to exogenous ligands. Furthermore, an active kinase domain with a linker in the restricted conformation could represent an intermediate step in the activation of Src via activating its kinase domain (e.g. phosphorylation of the A‐loop). Unexpectedly, when the kinase domain is inactive, the population of the restricted conformation is increased in the W260A construct, compared with WT. Consequently, the SH3‐linker interaction is strengthened which makes it more difficult to be activated. Our calculations suggest it is unlikely that W260A activates Src via disrupting the binding of the SH3 domain to the linker directly. The domain effect from the mutation seems to find its origin in the free energy landscape of the kinase domain itself.

Previous US simulations established a three‐state conformational equilibrium for the isolated WT kinase domain:41 the inactive state, the intermediate state, and the unphosphorylated active‐like state. The present US calculation of the mutant kinase domain displays the same three states, with the inactive conformation being the most stable. But the ΔG _{inactive→active} relative free energy is lowered in the mutant, dropping 1.7 kcal/mol from the 3.7 kcal/mol for the WT kinase domain. Lowering the free energy by 1.7 kcal/mol corresponds to a drastic increase in the population of the unphosphorylated active‐like conformation. This change will lead to an increased rate of the trans‐autophosphorylation reaction for the mutant. When the initial concentrations of the WT and the mutant are equal, an increased population of the unphosphorylated active‐like conformation in the mutant system will result in faster completion of the trans‐autophosphorylation, which agrees with experimental observations.25 On the other hand, a significant amount of the kinase domain being in the inactive state suggests that phosphorylation of Y416 in the A‐loop can further shift the conformational equilibrium toward the active state which is also consistent with the experimental observation that the W260A mutant is still subject to autophosphorylation to reach maximal activity.25 This view is confirmed by 1D US calculations to characterize the effect of Y416 phosphorylation in W260A.

To correlate the free energy results from our US calculation with the experimental rate of autophosphorylation quantitatively and to gain more insights into the trans‐autophosphorylation of Src kinase, we use a classical kinetic model describing the activation of a population of kinases in solution. The simple model provides a cogent framework to explain how small differences in conformational equilibrium of the isolated kinase domain as revealed by the US computations can contribute to accelerate the trans‐autophosphorylation reaction of Y416 in the A‐loop and yield a large increase in the activity. The parameters of the model were optimized, via a BMC procedure, to fit the experimental rate of autophosphorylation on the A‐loop. The main advantage of the BMC procedure is to provide sound and robust estimates of the parameters of the model, together with their uncertainty. This analysis yields a relative free energy ΔG _{inactive→active} that is in excellent agreement with the value obtained from the US calculations for the W260A mutant. This result demonstrates that a small shift in conformational equilibrium can lead to a sizable acceleration of the trans‐autophosphorylation reaction. The kinetic model also gives a rough estimation of the binding affinity of the enzyme‐substrate dimeric complex, a quantity that is difficult to measure directly. The weak binding affinity (∼100 μM) deduced from the model is consistent with the difficulty in obtaining a crystal structure of Src/Hck enzyme‐substrate dimeric complex. The present analysis demonstrates that combining classical kinetic models together with the results from all‐atom MD computations offers a powerful avenue to gain insight into the function of these complex signaling systems.

Materials and Methods

Umbrella sampling simulations of the conformational change in the linker

Three sets of 2D‐US calculations were performed to characterize the conformational change in the truncated linker region and correspond to the top three rows of Table 1. Figure 1 shows a cartoon representation of the conformational transition that is used in this section. The preparation of the simulation systems and the parameters utilized in propagating MD are given in Ref. 35. The unphosphorylated active‐like kinase domain used in all US calculations was based on the crystallographic structure 1Y57 of Src. The concept of a Src kinase domain with Y416 unphosphorylated that is catalytically competent and able to phosphorylate an incoming substrate is required mechanistically to explain the time‐course of activation of a population of kinases (see Kinetic model of Src activation section below). The present study is based on the assumption that the X‐ray structure 1Y57 is representative of such the unphosphorylated active‐like state. The conformation of the kinase domain in each one of the three sets was not subject to any restraining potential. The two order parameters are the distance between CA‐A256 and CA‐A259 (describes the formation/deformation of the β‐turn consisting of residues 256–259) and the distance between CA‐D258 and CA‐E261 (describes the formation/deformation of the β‐turn consisting of residues 258–261). The self‐learning adaptive umbrella sampling method45 was used to compute the 2D‐PMFs and a free energy threshold of 6.0 kcal/mol is utilized in these sets of US simulations. The weighted histogram analysis method (WHAM)46 was employed to combine time series from US calculations and to generate PMFs; 100 ns of unbiased MD equilibration was carried out before launching the US calculations for each construct.

Table 1.

Computational Details of the 2D‐US Simulations

	Residues	Linker conformation	Kinase domain conformation	# Windows	ns/window	k kcal/(mol·Å2)	d w (Å)
WT	253‐523	Restricted↔released	Inactive	245	30	10	0.5
WT	253‐523	Restricted↔released	Active	238	30	10	0.5
W260A	253‐523	Restricted↔released	Inactive	245	40	10	0.5
WT	260‐521	n/a	Inactive↔active	1101	15	20	0.25
W260A	260‐521	n/a	Inactive↔active	681	16	20	0.5

Supporting Information Fig. S3 shows the sequence and the structural motifs of Src which are utilized in the present work. The conformation of the kinase domain in each one of the top three constructs was not subject to any restraining potential and was found to be stable during umbrella sampling calculations of the linker region. Y416 in the A‐loop is not phosphorylated in all five sets of umbrella sampling calculations. “n/a” stands for not applicable.

Umbrella sampling simulations of the conformational change in the kinase domain

Two sets of 2D‐US calculations were performed to characterize the conformational change in the kinase domain and correspond to the bottom two rows of Table 1. The difference between the distances of the E310–R409 salt‐bridge (d ₁) and E310–K295 salt‐bridge (d ₂) is used to characterize the rotation of αC‐helix during the activation process, while the average distances between O‐D413 and N‐T417, O‐N414 and N‐A418, and O‐E415 and N‐R419 is used to reflect the opening of the A‐loop in the process. Graphical representations of the two order parameters and the conformational change in the kinase domain can be found in Ref. 35.

The activating conformational change in the WT kinase domain has been subjected to 2D US calculations previously. The umbrella windows determined from the previous run were kept in this study. Another 10 ns of MD propagation was continued per umbrella window in order to increase the sampling and evaluate the convergence in the 2D‐PMF, resulting in 15 ns of sampling per window.

The self‐learning adaptive strategy was also employed to compute the 2D‐PMF of the W260A construct. However, the initial windows were collected from the WT simulations. W260 in each of the selected umbrella window was mutated into an alanine residue. Each umbrella window in the first cycle of the self‐learning adaptive procedure was given extra 5 ns of MD propagation in order to relax A260. A free energy threshold of 9.0 kcal/mol was utilized in the self‐learning adaptive procedure.

Umbrella sampling simulations of the W260A construct with pY416

1D‐US simulations were performed in order to investigate the impact of Y416 phosphorylation on the conformational equilibrium of the W260A kinase domain. 1D umbrella sampling simulations were employed so that the computational cost can be reduced. The order parameter utilized in this set of umbrella sampling calculations was (d ₁ – d ₂) where d ₁ and d ₂ were defined in the previous section. A harmonic biasing potential with a force constant of 20 kcal/(mol·Å²) and a uniform spacing of 0.5 Å were applied to the order parameter. A total of 63 umbrella windows were utilized in this set of simulations and each window was subjected to 10 ns of MD propagation. The A‐loop in this set of umbrella sampling simulation was in the extended conformation.

Kinetic model of src activation

To link the free energy information obtained from umbrella sampling simulations to the experimentally observed time‐course for the activation of a population of kinases in solution, we propose the following kinetic model in which a dimerization step forming the enzyme‐substrate complex is also incorporated:

$$\frac{d\left[A^{*}\right]}{dt}\hspace{0.17em}=\hspace{0.17em}{k}_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{s}}\left[A•A\right]\hspace{0.17em}+\hspace{0.17em}{k}_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{s}}\left[A•A^{*}\right]$$

$$\frac{d[A•A]}{dt}\hspace{0.17em}=\hspace{0.17em}{k}_{\mathrm{o}\mathrm{n}}\left[A\right]\left[A\right]\hspace{0.17em}-\hspace{0.17em}{k}_{\mathrm{o}\mathrm{f}\mathrm{f}}\left[A•A\right]\hspace{0.17em}-\hspace{0.17em}{k}_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{s}}[A•A]$$

$$\frac{d[A•A^{*}]}{dt}\hspace{0.17em}=\hspace{0.17em}{k}_{\mathrm{o}\mathrm{n}}\left[A\right]\left[A^{*}\right]\hspace{0.17em}-\hspace{0.17em}{k}_{\mathrm{o}\mathrm{f}\mathrm{f}}\left[A•A^{*}\right]\hspace{0.17em}-\hspace{0.17em}{k}_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{s}}[A•A^{*}]$$

$$\left[I\right]\hspace{0.17em}+\hspace{0.17em}\left[A\right] + \left[A^{*}\right]\hspace{0.17em}+\hspace{0.17em}2\left[A•A\right]\hspace{0.17em}+\hspace{0.17em}2\left[A•A^{*}\right]\hspace{0.17em}=\hspace{0.17em}{C}_0$$

$$\left[I\right]\hspace{0.17em}=\hspace{0.17em}{K}_{\text{eq}}\left[A\right]$$

Here, C ₀ is the initial concentration of the kinase and K _eq is the equilibrium constant between the inactive and the active species. Note that the first term in the first equation represents the trans‐autophosphorylation process catalyzed by a kinase in an active‐like conformation with Y416 unphosphorylated. After further manipulation, the above rate equations can be reduced to the following ones:

$$\frac{d\left[A^{*}\right]}{dt}\hspace{0.17em}=\hspace{0.17em}{k}_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{s}}\left[D\right]$$

$$\frac{d\left[D\right]}{dt}=k_{\mathrm{o}\mathrm{n}}\left[A\right]\left(\left[A\right]+\left[A^{*}\right]\right)\hspace{0.17em}-\hspace{0.17em}\left(k_{\mathrm{o}\mathrm{f}\mathrm{f}}\hspace{0.17em}+\hspace{0.17em}{k}_{\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{s}}\right)\left[D\right]$$

$$\left(1\hspace{0.17em}+\hspace{0.17em}{K}_{\mathrm{e}\mathrm{q}}\right)\left[A\right]\hspace{0.17em}+\hspace{0.17em}\left[A^{*}\right]\hspace{0.17em}+\hspace{0.17em}2\left[D\right]\hspace{0.17em}=\hspace{0.17em}{C}_0$$

The D stands for the enzyme‐substrate complex (a protein dimer) which consists of A•A and A•A*. The k _phos of 0.8 and 1.7 s⁻¹ is used in this work for the WT and the W260A construct respectively.25 K _eq is the equilibrium constant determining the population of the inactive and the active species. The K _eq of the WT construct is calculated using the free energy difference yielded by integrating the 2D‐PMF, i.e., ΔG = 3.7 kcal/mol. Therefore, the K _eq is set to be 477. k _on and k _off are unknown parameters. However, once the k _on and k _off are assigned, the above differential equations can be solved numerically and the K _d and the t _1/2 can be acquired. To obtain the distributions of k _on and k _off, a procedure utilizing Bayesian Monte Carlo (BMC) strategy is proposed as follows:

$$P\left(k_{\mathrm{o}\mathrm{n}},k_{\mathrm{o}\mathrm{f}\mathrm{f}}\right|\left\{t_{1/2}\right\})=\frac{P\left(\right\{t_{1/2}\left\}\right|k_{\mathrm{o}\mathrm{n}},k_{\mathrm{o}\mathrm{f}\mathrm{f}})\cdot P(k_{\mathrm{o}\mathrm{n}},k_{\mathrm{o}\mathrm{f}\mathrm{f}})}{P\left(\right\{t_{1/2}\left\}\right)}$$

In the above equation, P(k _on, k _off | {t _1/2}) is the posterior probability. The prior probability P(k _on, k _off) is assumed to be the uniform probability distribution and the likelihood function is defined to have the following form:

$$P\left(\left\{t_{1/2}\right\}|k_{\mathrm{o}\mathrm{n}},k_{\mathrm{o}\mathrm{f}\mathrm{f}}\right)\propto \mathrm{e}\mathrm{x}\mathrm{p}(-{\chi }^2)$$

$${\chi }^2={\sum }_{i=1}^N{\left[\frac{t_{1/2,i}\left(\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}\right)\hspace{0.17em}-\hspace{0.17em}{t}_{1/2,i}\left(\mathrm{e}\mathrm{x}\mathrm{p}\right)}{{\sigma }_i}\right]}^2$$

The σ ² is the experimental error on t _1/2(exp). Essentially, the likelihood function assumes the normal distribution of the fitting errors. Unfortunately, the values of t _1/2(exp) and σ ² are not explicitly given in the literature. Thus, the experimental t _1/2s were estimated values, and the σ ² represents the range in which we believe the actual experimental value lies. In our BMC estimation of k _on and k _off, one million steps of MC moves were performed and the Metropolis criteria were utilized to accept/reject the move. The first 10% of the time series was designated as the burn‐in time, and was not included in computing the mean and the variance of k _on and k _off. The binding affinity of the enzyme‐substrate complex is represented by K _d ≡ k _off/k _on. The same BMC procedure was employed in the estimation of the ΔG for the W260A system with the assumption that k _on and k _off are the same as those in the WT construct.

Supporting information

Supporting Information