Estimating first‐passage time distributions from weighted ensemble simulations and non‐Markovian analyses

Abstract

First‐passage times (FPTs) are widely used to characterize stochastic processes such as chemical reactions, protein folding, diffusion processes or triggering a stock option. In previous work (Suarez et al., JCTC 2014;10:2658‐2667), we demonstrated a non‐Markovian analysis approach that, with a sufficient subset of history information, yields unbiased mean first‐passage times from weighted‐ensemble (WE) simulations. The estimation of the distribution of the first‐passage times is, however, a more ambitious goal since it cannot be obtained by direct observation in WE trajectories. Likewise, a large number of events would be required to make a good estimation of the distribution from a regular “brute force” simulation. Here, we show how the previously developed non‐Markovian analysis can generate approximate, but highly accurate, FPT distributions from WE data. The analysis can also be applied to any other unbiased trajectories, such as from standard molecular dynamics simulations. The present study employs a range of systems with independent verification of the distributions to demonstrate the success and limitations of the approach. By comparison to a standard Markov analysis, the non‐Markovian approach is less sensitive to the user‐defined discretization of configuration space.

Introduction

The first‐passage problem occupies a prominent place in the natural sciences, as the first‐passage time (FPT) is a key characterization of the kinetics of any process. The FPT has received attention in many areas of physics and applied mathematics,1, 2, 3, 4, 5 chemistry,6, 7, 8 protein folding,9, 10, 11, 12 and even credit‐risk modeling.3

In the study of protein folding, the timescales accessible by molecular dynamics (MD) simulations are still in the hundreds of microseconds, and in the better cases, in the millisecond range,13 while the experimentally observed protein‐folding timescales often lie between a few milliseconds to minutes.14 In this scenario, the computation of the FPTs is a real challenge, as even the mean FPT (MFPT) requires at least 10 events to be statistically robust. The FPT distribution (FPTD), which provides a key description of the fluctuations in kinetic behavior, could require hundreds of events, and is clearly prohibitive for many biological systems of interest using standard simulations.

The challenge of simulating sufficiently long timescales in molecular systems has motivated a wide range of approaches.15, 16, 17, 18 One prominent approach is Markov state modeling,19, 20, 21, 22, 23 where the phase space is divided into regions or states which are kinetically and/or structurally related. The trajectory is then mapped every τ (the lag time) onto those regions and the sequence of states generated is considered as a discrete‐time Markov chain. The model is characterized by its transition matrix $K(\tau )$ from which equilibrium and non‐equilibrium properties can be calculated analytically once a suitable lag time is estimated.

Path‐sampling approaches also attempt to extract long‐timescale information without bias. Transition path sampling (TPS) methods sample directly the path ensemble between two states using a Monte Carlo procedure.24, 25, 26, 27 A variation of TPS, transition interface sampling, divides the transition region into subregions using interfaces, and the transition probabilities between neighboring interfaces is used to evaluate the rate constant.28, 29 A similar approach is followed by the forward flux sampling method.30, 31 The milestoning method typically partitions the space into smaller regions (in this case, cells) by dividing hypersurfaces to extract kinetic observables based on short trajectories,32, 33 as does nonequilibrium umbrella sampling.34

The weighted ensemble (WE) path‐sampling approach35, 36, 37, 38, 39, 40, 41, 42, 43 is the primary focus of the present work. WE divides configuration space into regions called bins and attempts to sample an ensemble of trajectories that is relatively uniform among bins. WE is statistically rigorous,35, 36 and any average property can be estimated in a straightforward manner, in analogy to averaging behavior in ordinary simulations.37 Nevertheless, the distribution of the FPTs cannot be obtained by direct observation in WE trajectories.

Here, we show that a non‐Markovian analysis we previously proposed37 can also be used to estimate distributions of the FPT from WE simulations. This analysis maps continuous trajectories onto discrete states (bins) with history information and is not limited to WE simulations. It can also be applied to postanalyze any other unbiased trajectories generated in other approaches including regular single‐trajectory simulations.

A potential advantage of non‐Markovian analysis compared with standard Markov modeling is that states (bins) can be more coarsely defined. True Markovian behavior requires, in general, fairly small states such that intrastate relaxation is extremely fast,44 in turn requiring a substantial trajectory set for accurate estimation of interbin transition rates.44, 45, 46 When the Markovian assumption is relaxed, larger states can be used so long as sufficient history is retained.37, 47 Put another way, with finite trajectory data necessitating larger states in rate‐estimation schemes, there appears to be great potential in using the additional history information that typically is present in trajectory segments, but discarded in standard Markov analysis.

It is important to note that a first‐passage process, by definition, is unidirectional (from initial to target state) and hence does not reflect equilibrium behavior (see Fig. 1). A focus on the subset of pertinent trajectories is equivalent to using non‐Markovian history information regarding whether a trajectory originated from the chosen initial state.

Figure 1.

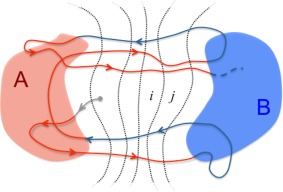
First‐passage processes are unidirectional. This schematic shows a long “equilibrium” trajectory transitioning between arbitrary states A and B, with red A‐to‐B segments representing the first‐passage process of interest. Importantly, the kinetics of transitions between substates or bins (e.g., i and j) relevant to the FPT differ from what would be inferred if all trajectories (both red and blue) were included. In the subset of red trajectories, trajectories in bin i are more likely to have originated from the left, compared with the full set of trajectories. Modified from Ref. [ 66].

In this work, we calculate the FPTD for several models. We start with a simple toy model that can be exhaustively sampled, and next study alanine tetrapeptide (Ala4) in GB/SA implicit solvent, which is also amenable to good sampling. We then focus on both the molecular association and dissociation processes in explicit solvent of two systems: methane/methane and Na ${}^{+}$/Cl ${}^{-}$. Finally, we explore the conditions under which the non‐Markovian analysis can be performed.

Theoretical Formulation

WE simulation

As background, consider a regular “brute force” (BF) simulation of a single trajectory where the observables that we want to estimate are time averaged. In this case, every single “observation” (snapshot) has the same statistical weight. A similar approach would be to perform n independent BF simulations, with each simulation having a weight $1/n$. Both strategies will yield the same results with sufficient simulation time.

A WE simulation uses multiple weighted simultaneous trajectories,35, 36 with weights that sum to one. In WE, however, the number of trajectories and their weights are dynamically and rigorously changed on the fly, following two rules:

• A single trajectory can be “split”—i.e., replicated—into two or or more trajectories as long as the sum of the weights is conserved. Each “child” trajectory inherits an equal share of the parent's weight.

• Two or more trajectories can be “merged” into a single trajectory in such a way that the current state and history of the resulting “child” trajectory will be chosen stochastically from one of the original trajectories in proportion to their weights. In other words, one or more parent trajectories is pruned. The surviving “child” trajectory inherits the sum of the weight of the parents, which conserves probability.

The above two rules, by themselves, do not enhance sampling. The key advantage of WE comes when the phase space is divided in regions or bins and the trajectories are examined every τ (lag time): when one or more trajectories enters an unoccupied bin, those trajectories are replicated so that their count conforms to a (typically) preset value, M. In this manner, the sampling of new regions of the phase space is enhanced (see Fig. 2). Alternatively, if more than M trajectories are found to occupy a bin, trajectories are combined statistically following the second rule; in this way, the amount of sampling is controlled. The procedures of replication and/or combination are followed every τ, and their statistical nature as a resampling procedure ensures the dynamics remain unbiased.36

Figure 2.

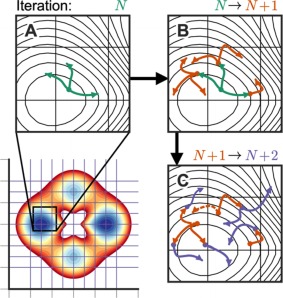
Basic WE protocol 42. The two‐dimensional configurational space is divided into bins (lower left panel), with a target of M = 3 trajectories per bin. During each iteration, the trajectories are propagated for a time τ as shown for iteration N in (A). After iteration N, the trajectories are examined and replicated to keep 3 trajectories in every occupied bin, then the trajectories are propagated again for an interval τ in iteration N + 1 (orange paths in B). After iteration N + 1, one of the bins contains more than the target number of trajectories. In this case, one of the trajectories is terminated (dashed path in C), and its weight is assigned statistically to the remaining trajectories in the bin. Reprinted (adapted) with permission from Ref. [42]. Copyright 2015, American Chemical Society.

In this study, WE simulations employ static bins (see below). However, dynamic binning strategies are also possible, such as using Voronoi cells48 or a “string” approach.49

Post analysis of WE simulation data

Although WE simulations can directly generate estimates of observables by calculating sums of weights and flows of weights37, 38, 39, here we estimate observables indirectly using a “post analysis” of simulation data.37 Conditional transition probabilities are obtained and processed via the Markovian and non‐Markovian analyses described below.

Markovian calculation of FPTs

A regular Markov analysis will be performed for reference in all of the systems. Here, by construction, there is no history information and the rates k_ij between two bins are defined by the single‐step conditional probability

$$k_{ij}=P\{X_{t+\tau }=j|X_t=i\},$$ (1)

where X_t is the random variable representing the state of the system at time t, and τ is the lag‐time used for the Markov model. In practice, the rates among bins are estimated as in Ref. 37 using

$${\widehat{k}}_{ij}={〈{\omega }_{ij}〉}_2/〈{\omega }_i〉,$$ (2)

where ω_ij is the probability flux transferred after the lag‐time τ from bin i to bin j, and ω_i the population in i before τ. The subscript “2” indicates that the rate is considered nonzero only when at least two transitions are observed, to reduce noise.37 Notice that for a BF trajectory Eq. (2) is equivalent to ${\widehat{k}}_{ij}={〈c_{ij}〉}_2/〈c_i〉$, where $\left\{c_{ij}\right\}$ is the count matrix, i.e., the number of transitions observed from i to j, and $c_i={\displaystyle {\sum }_j{c}_{ij}}$.

The FPT is a random variable and the probability distribution associated with it in the discrete bin space is derived from the transition matrix of the process $K=\left\{k_{ij}\right\}$. Let $f_{ij}^{(n)}$ denote the probability that the FPT from state i to j is equal to $n\tau$. Then $f_{ij}^{(1)}=k_{ij}$ since by definition, k_ij is the probability that the transition $i\to j$ occurs in one τ. The $f_{ij}^{(2)}$ values can be derived from $f_{ij}^{(1)}$, since the “path” has to go through a third bin $m\ne j$ (otherwise n would be 1), and the transitions to m take place with probability k_im, so $f_{ij}^{(2)}={\displaystyle {\sum }_{m\ne j}{k}_{im}{f}_{ij}^{(1)}}$. Similarly, for any n > 1, we can derive $f_{ij}^{(n)}$ from $f_{ij}^{(n-1)}$, and in general, the following recursive formula is satisfied50

$$f_{ij}^{(n)}=\{\begin{array}{lll}{k}_{ij}& \text{for}& n=1\\ {\displaystyle \sum _{m\ne j}{k}_{im}}{f}_{mj}^{(n-1)}& \text{for}& n=2,3,\mathrm{...}\end{array}$$ (3)

Non‐Markovian calculation of FPTs

A first‐passage process, by definition, is unidirectional (e.g., from state A to state B), which has important consequences for estimating FPTs without bias. Most notably, as illustrated in Figure 1, the bin‐to‐bin transition probabilities should be based only on the pertinent subset of trajectories (e.g., A to B) rather than the full equilibrium set. Using such a subset of trajectories in the analysis is implicitly a non‐Markovian analysis37, 39 because it depends on the last state visited (A or B).

The mathematical formalism in the non‐Markovian analysis is similar to the regular Markov analysis shown in the previous section, but the history‐labeling requires generalized expressions for populations and rates. Assume we have defined two nonoverlapping “macroscopic” states A and B, which may encompass only a small portion of the full phase space. Every segment of a sufficiently long trajectory is given a label μ according to whether the system was last in state A (the label α) or state B (label β). Then the total bin population p_i is decomposed into two parts,

$$p_i=p_i^{\alpha }+p_i^{\beta }.$$ (4)

For rates, the main difference from the Markov formulation is that there are two additional labels μ and ν in the transition rates $k_{ij}^{\mu \nu }$.37 After a transition, the label can change if that transition implies an “event”, i.e., a trajectory which was most recently in A (α trajectory) enters B or vice versa; thus, we use a second label ν to specify which label applies (α or β) after τ. Formally, the labeled rate definition is given by

$$k_{ij}^{\mu \nu }=P\{X_{t+\tau }=j,L_{t+\tau }=\nu |X_t=i, L_t=\mu \}\hspace{1em}\mu ,\nu =\alpha ,\beta$$ (5)

where L_t and $L_{t+\tau }$ account for the label of the trajectory (α or β) before and after τ, respectively.

Figure 3 shows the transformation that a regular Markov model with three bins would undergo to include the relevant history information. For each unlabeled rate k_ij, four history labeled elements $k_{ij}^{\mu \nu }$ have to be considered.37 Without loss of generality, we consider that the states A and B are defined by single bins, since it is always possible to adapt the bin boundaries to the definition of the states. Note that, even though the labels μ and ν are not completely independent of the bin indexes, they only store history‐related information, and each of them can only have two possible values (α or β), in contrast to the bin index $i\in \{1,\mathrm{...},N\}$, where N is the number of bins.

Figure 3.

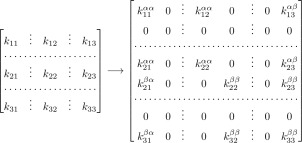
Modified from Ref. [37]. Constructing a history‐labeled rate matrix for a system with three bins. Here, state A consists solely of bin 1 and state B solely of bin 3. Left: A traditional rate matrix without history information. Right: The labeled rate matrix accounting for which state was visited most recently. The element $k_{ij}^{\mu \nu }$ is the conditional probability for the i to j transition for trajectories initially in the μ subensemble (either α or β) and ending in the ν (α or β) subensemble.

More than half of the elements of the matrix are zero by construction: an α trajectory cannot be transformed into a β trajectory outside B, for instance. We can also see “forbidden bins” in the extended scheme: the labeled bin i is forbidden when a column and a row with the same index i are both zero, since we cannot have an α trajectory inside B or vice versa. All the unnecessary rows and columns are suppressed before any algebraic manipulation.

If N is the number of bins, the $2N\times 2N$ matrix $\mathcal{K}$ (see Fig. 3 right) has all the necessary information to estimate any property of interest. For example, under the steady state condition

$${\mathcal{K}}^T{p}^{\mu }=p^{\mu }$$ (6)

the unlabeled (p_i) and labeled ( $p_i^{\mu }$) bin populations can be obtained: see Eq. (4). The matrix $\mathcal{K}$ also permits calculation of the MFPTs, and the distribution of the FPTs.

If we are only interested in FPTs, it is easier to manipulate two smaller matrices $K^{\alpha }$ and $K^{\beta }$ where we store the relevant rates for the $A\to B$ and $B\to A$ FPTs, respectively. In our 3‐bin example in Figure 3 these matrices are

$$K^{\alpha }=\left[\begin{array}{ccc}{k}_{11}^{\alpha \alpha }& k_{12}^{\alpha \alpha }& k_{13}^{\alpha \beta }\\ k_{21}^{\alpha \alpha }& k_{22}^{\alpha \alpha }& k_{23}^{\alpha \beta }\\ 0& 0& 1\end{array}\right]\hspace{1em}\text{and}\hspace{1em}{K}^{\beta }=\left[\begin{array}{ccc}1& 0& 0\\ k_{21}^{\beta \alpha }& k_{22}^{\beta \beta }& k_{23}^{\beta \beta }\\ k_{31}^{\beta \alpha }& k_{32}^{\beta \beta }& k_{33}^{\beta \beta }\end{array}\right],$$ (7)

which preserves the same kinetics represented by the full $\mathcal{K}$ matrix. The distributions are obtained from $K^{\alpha }$ and $K^{\beta }$ using the same recursive approach of Eq. (3) except with labeled rates:

$$f_{ij}^{(n)}=\{\begin{array}{lll}{k}_{ij}^{\mu \nu }& \text{for}& n=1\\ {\displaystyle \sum _{m\ne j}{k}_{im}^{\mu \nu }}{f}_{mj}^{(n-1)}& \text{for}& n=2,3,\mathrm{...}\end{array}\hspace{1em}\mu ,\nu =\alpha ,\beta$$ (8)

All non‐Markovian FPTDs are calculated from this approach, with rates defined in Eq. (5).

States defined by multiple bins

The recursion formula in Eq. (8) is defined only for the case when the initial and target states are single bins, but that is not a generally applicable formulation. Here, we consider the more general case, when the states A or B are defined by more than one bin and the recursion formula can not be applied directly. To calculate the FPTs, e.g., from A to B (α trajectories), we can “merge”, for simplicity, all the bins in B without affecting the FPT. The rates to that single bin with index b from any other bin $i\notin B$ are computed as the sum

$$k_{ib}^{\alpha \beta }={\displaystyle \sum _{j\in B}{k}_{ij}^{\alpha \beta }}.$$ (9)

Furthermore, in $K^{\alpha }$ the rows with index $i\in B$, are all eliminated except for one, and since B is defined as absorbing in $K^{\alpha }$, then k_bb = 1 and the rest of the elements in the same row will be zero.

The FPTs depend not only on the definitions of A and B, but also on how the trajectories are started in A. As in Figure 1, consider a single, long trajectory BF simulation where multiple events from A to B and from B to A are observed and from which we want to estimate the FPTs. When the trajectory coming from B enters A, the chronometer is restarted and we start counting the time that the trajectory spends before it hits B again, and the time measured will be the FPT (A → B). That is, with time‐continuous trajectories, we would have to restart the chronometer at the surface of A –just when the β trajectory hits A for first time. With sufficient sampling, we would be able to “see” the distribution of the trajectories coming from B on the surface of A. Using the incoming distribution of trajectories reaching the A surface to start simulations in A, we would obtain, on average, the same FPTs ( $A\to B$) observed in the continuous BF trajectory.51

The description of space/time‐continuous trajectories coming from A that hit the surfaces of B and vice versa (Fig. 1) has to be “translated” to the case of discrete trajectories, since in practice, we have time‐ and space‐discrete trajectories, and there is no explicit notion of the surface of A. To replicate the same results observed in BF after mapping the trajectory into the discrete bin space, it is sufficient to start the α trajectories following the discretized distribution of entry points, i.e., the trajectories are started in every bin $j\in A$ with probability equal to

$$P^{\alpha }(j)=\frac{{\displaystyle {\sum }_{i\notin A}{p}_i^{\beta }{k}_{ij}^{\beta \alpha }}}{{\displaystyle {\sum }_{j\in A}{\displaystyle {\sum }_{i\notin A}{p}_i^{\beta }{k}_{ij}^{\beta \alpha }}}},$$ (10)

where $p_i^{\beta }$ are the β populations obtained from solving the steady‐state condition for the labeled matrix $\mathcal{K}$ [Eq. (6)]. Then, the MFPT( $A\to B$) can be computed as the weighted average

$$\text{MFPT}(A\to B)={\displaystyle \sum _{j\in A}{P}^{\alpha }(j) \text{MFPT}\hspace{0.17em}(j\to B)},$$ (11)

and the FPT distribution is obtained based on the probability $f_{AB}^{(n)}$ of observing FPT( $A\to B$) $=n\tau$ evaluated as

$$f_{AB}^{(n)}={\displaystyle {\sum }_{j\in A}{P}^{\alpha }(j) f_{jB}^{(n)}}.$$ (12)

Since B has been redefined as a single bin, $f_{jB}^{(n)}$ is calculated from Eq. (8). Analogously, $f_{BA}^{(n)}$ can be obtained following the same protocol.

Model Systems and Simulation Details

In this section, we describe the simulation protocols used for each model system. All simulations were carried out using the open‐source highly scalable WESTPA software package (https://westpa.github.io/westpa),42 an implementation of the WE algorithm. WESTPA has been designed to conveniently interface with any stochastic dynamics engine, such as GROMACS,52 OpenMM,53 AMBER,54 or with Monte Carlo software.37, 38, 39

Toy model

We examined a one‐dimensional toy model first to enable exhaustive reference sampling. The landscape of Figure 4 was sampled using Monte Carlo (MC) as the effective dynamics. The energy function is given by

$$E_{1D}(x)/k_{B}T=\{\begin{array}{ll}\sin (x)+2.5\cos (4x)+0.0008x^4-0.11{(x-0.5)}^2& \text{if}\hspace{0.17em}-14<x<14\\ \infty & \text{otherwise}\end{array}$$ (13)

Figure 4.

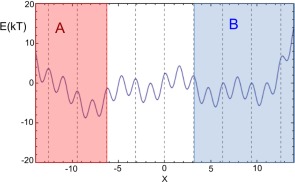
One‐dimensional toy model. The figure shows the definition of the states A and B and the partition of the space in bins is indicated with dashed lines.

The trial move δx was chosen randomly in the interval $[-\pi /2,\pi /2]$ with uniform probability distribution.

For the WE simulation, the space is divided into 10 bins, most of them of width π, except for the first and last bin that are formally infinite–defined by the intervals $(-\infty ,-4\pi )$ and $[4\pi ,+\infty )$. Two states A and B were defined as shown in Figure 4, the state A is constituted by the first three bins $(x<2\pi )$ while state B by the last four bins $(x\ge \pi )$. The WE simulation was run for a total of $3\times {10}^4$ iterations with a maximum of 10 trajectory walkers per bin. The lag‐time used was $\tau =$ 5 MC steps for both WE and the postanalysis.

Alanine tetrapeptide (Ala4)

For Ala4, the WE simulation was performed using the WESTPA software interfaced with the AMBER 11 software package,54 all‐atom AMBER ff99SB force‐field,55 and GB/SA implicit solvent. No cutoff was used for the evaluation of nonbonded interactions. The Hawkins, Cramer, Truhlar56, 57 pairwise generalized Born model is used, with parameters described by Tsui and Case58 (option igb = 1 in AMBER 11 input file). To maintain the temperature at 300 K, a Langevin thermostat59 was applied throughout the simulations with a collision frequency of $5.0p{s}^{‐1}$.

To run the WE simulation, a two‐dimensional progress coordinate was “binned” using 10 × 10 partitions following our previous work.37 A dihedral distance $D=\sqrt{\frac{1}{N}{\displaystyle {\sum }_i{d}_i^2}}$ $\in [0,180]$ with respect to a reference set of torsions is used in the first dimension, where N is the number of torsional angles considered and d_i is the circular distance between the current value of the i‐th angle and our reference, i.e., the smaller of the two arc lengths along the circumference. This dimension was divided every ${14}^{°}$ from 0 to ${126}^{°}$ and then a final partition covering the interval $({126}^{°},{180}^{°}]$. In the second dimension, we used the heavy‐atom RMSD with respect to an α‐helical structure.37 In this case, the space was divided every 0.4 Å from 0 to 3.6 Å and then a final partition covering the space $[3.6,+\infty )$. The same partition of the space used for the WE simulation was used for the postanalysis. In the two‐dimensional space A is defined by the set $\{{56}^{°}\le D<{84}^{°}\}\cap \{0\le RMSD<0.8\}$ and $B=\{{56}^{°}\le D<{84}^{°}\}\cap \{3.2\le RMSD<+\infty \}$. The WE simulation was run for a total of 4600 iterations with a maximum of 5 trajectory walkers per bin. A lag‐time of $\tau =5\text{ps}$ was used for both WE and the postanalysis.

Methane/methane and Na ${}^{+}$/Cl ${}^{-}$

We simulated both the molecular association and dissociation processes of the methane/methane and Na ${}^{+}$/Cl ${}^{-}$ systems in explicit solvent. For both systems, dynamics were propagated using the GROMACS 4.6.3 software package52 as in previous work.60 Briefly, the solute molecules, which were represented using the united‐atom GROMOS 45a3 force field,61 were immersed in dodecahedral boxes of SPC/E62 explicit water molecules that accommodate the unbound states (see below) with a minimum solute‐wall distance of 12 Å. Simulations were run in the NVT ensemble maintaining the temperature at 300 K using a weak Langevin thermostat59 (coupling time of 1.0 ps). Van der Waals interactions were switched off smoothly between 8 and 9 Å. Real‐space electrostatic interactions were truncated at 10Å; long range electrostatic interactions were calculated using particle mesh Ewald summation63 and periodic boundary conditions. To enable a 2 fs timestep, bonds to hydrogen atoms were constrained to their equilibrium values using the LINCS algorithm.64

WE simulations were performed following established protocols.37 For both methane/methane and Na+/Cl− systems, the simulations were started from 50 well‐equilibrated, bound‐state conformations (state A), which were defined as having center‐to‐center distances of < 4.0 (methane/methane) Å and < 2.80 Å (Na+/Cl−). The unbound state (state B) was defined as having center‐to‐center distances of $\ge$ 11.0 Å (methane/methane) and $\ge$ 14.98 Å (Na+/Cl−). For each system, the 50 starting conformations in the bound state were selected according to their statistical weights from the final iteration of a separate WE simulation in which the ensemble of bound‐state conformations, including solvent configurations, was extensively sampled. All WE parameters are the same as those used in Ref. 60 (e.g., τ values, progress coordinates, bin spacings, etc.) with the exception that once the target state was reached, the trajectories were not “recycled” as new simulations starting from the initial state. Thus, instead of maintaining steady state conditions, as done in the original WE algorithm,35 an equilibrium set of trajectories was generated that could be decomposed into two steady states.37 The τ values were set to 0.5 and 5 ps for the methane/methane and Na ${}^{+}$/Cl ${}^{-}$ systems, respectively. Both systems were run for a total of 2000 τ intervals (or “iterations”) using a progress coordinate consisting of the center‐to‐center distance between the solute molecules; this progress coordinate was divided up into bins with 50 trajectory walkers per bin. For the methane/methane system, the progress coordinate was divided into 10 bins, resulting in a maximum of 500 trajectory walkers per bin. For the Na ${}^{+}$/Cl ${}^{-}$ system, the progress coordinate was divided into 21 bins, resulting in a maximum of 1050 trajectory walkers. The total wall‐clock time invested for the WE simulations of the methane/methane and Na ${}^{+}$/Cl ${}^{-}$ systems was 33 hours using 250 CPU cores and 4 days using 320 CPU cores, respectively, on 2.3 GHz AMD Interlagos processors.

Results

We present our data with two primary goals in mind: (i) to show that the FPT distribution (FPTD) can be obtained from WE simulation; and (ii) to determine whether non‐Markovian analysis improves estimation of the FPTD compared with standard Markov analysis for the types of bins typically used in WE simulation. We also wish to show (iii) that the non‐Markovian analysis can be applied directly to standard (e.g., ordinary MD) simulation and (iv) to demonstrate the conditions under which the approach breaks down.

Non‐Markovian analysis of WE simulations

In every case, the FPT distribution estimated from postanalysis of WE simulation is compared with reference data from extensive, brute‐force MDs simulations, generated under the same conditions as the trajectory segments employed for WE. See Methods section for details. To generate the reference distribution and confidence intervals, a histogram was constructed and the bin counts were analyzed via multinomial statistics to yield error bars for a 95% confidence interval. The histograms were rescaled for comparison with the FPT probability densities generated via WE and matrix analysis.

The primary results are presented in Figures 5 (toy model), 6 (Ala4), 7 (methane/methane), and 8 (Na+/Cl−). The plots show the reference (Long MD) data compared with WE results postanalyzed using either a standard Markov approach (Markov) or the non‐Markovian matrix (Non‐Markovian). In all of the systems, the non‐Markovian analysis agrees with the reference confidence interval and generally performs better than a standard Markov analysis.

Figure 5.

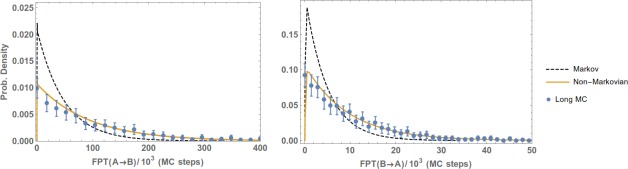
Non‐Markovian estimation of the the FPT distribution in a toy model from WE data. FPT distributions of the one‐dimensional toy model from A to B (left plot) and from B to A (right) are obtained by post‐analyzing a WE simulation using a regular first‐order Markov analysis (Markov) and non‐Markovian analysis (Non‐Markovian). The results are compared with a reference long MC simulation and error bars indicating a 95% confidence interval.

Figure 6.

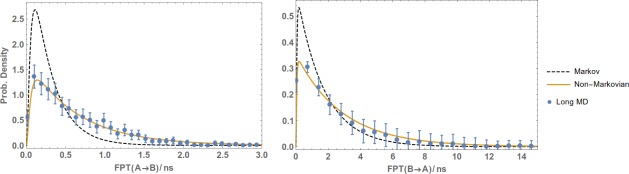
Non‐Markovian estimation of the the FPT distribution in the Ala4 peptide from WE data. FPTDs of the Ala4 system from A to B (left plot) and from B to A (right) were obtained by postanalyzing a WE simulation using a regular first‐order Markov analysis (Markov) and non‐Markovian analysis (Non‐Markovian). The results are compared with a reference long MD simulation and error bars indicating a 95% confidence interval.

Figure 7.

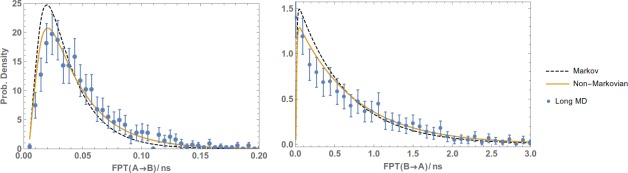
Non‐Markovian estimation of the the FPT distribution of the methane/methane system from WE data. FPTDs of the methane/methane system from A to B (left plot) and from B to A (right) were obtained by post‐analysing a WE simulation using a regular first‐order Markov analysis (Markov) and non‐Markovian analysis (Non‐Markovian). The results are compared with a reference long MD simulation and error bars indicating a 95% confidence interval.

Figure 8.

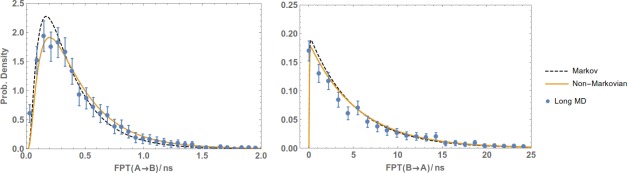
Non‐Markovian estimation of the the FPT distribution of the Na ${}^{+}$/Cl ${}^{-}$ system from WE data. FPTDs of the Na ${}^{+}$/Cl ${}^{-}$ system from A to B (left plot) and from B to A (right) were obtained by postanalyzing a WE simulation using a regular first‐order Markov analysis (Markov) and non‐Markovian analysis (Non‐Markovian). The results are compared with a reference long MD simulation and error bars indicating a 95% confidence interval.

Reference data were provided by independent long simulations. For the toy system, 10⁸ steps of Monte Carlo simulation were used. For Ala4, the reference simulation was about $3\hspace{0.17em}\mu s$ of MD, in which 1038 events (i.e., $A\to B$ and $B\to A$ transitions) were observed. For methane/methane and Na ${}^{+}$/Cl ${}^{-},\hspace{0.17em}1.0\hspace{0.17em}\mu s$ of MD simulation was performed which yielded around 1200 and 1600 events, respectively.

Non‐Markovian analysis of standard MD simulations

Although our non‐Markovian approach was developed for WE simulations, the theory underpinning the analysis is very general and not specific to WE. We therefore sought to confirm that the non‐Markovian analysis could be useful for analyzing ordinary “BF” (e.g., standard MD) trajectories.

Figures 9 and 10 show that the FPT distribution can be obtained to good accuracy by post‐analyzing standard MD trajectories. In each case, the figure compares matrix estimates from both Markovian and non‐Markovian analysis obtained from a very long MD trajectory exhibiting more than 1000 events, as well as the direct measurement obtained by histogramming the FPTs (Long MD). In addition, and perhaps of greater interest, the figures also show that non‐Markovian analysis can produce a good estimate for the full FPT distribution even from a fraction of the original MD trajectory using only 30 events [Non‐Markovian/(30 events)]. Note that generating a distribution by histogramming a standard trajectory would require many counts in each bin for statistical reliability.

Figure 9.

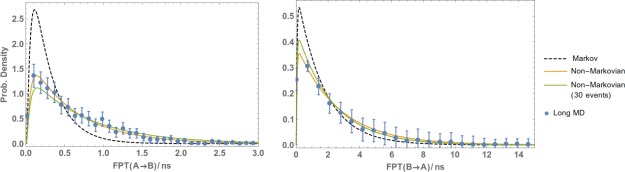
Non‐Markovian analysis of standard MD data. FPTDs of the Ala4 system from A to B (left plot) and from B to A (right) were obtained by postanalyzing a very long MD simulation. Also shown is the non‐Markovian analysis of a much shorter trajectory where only 30 events ( $A\to B$ and $B\to A$) are observed. The results are compared with a reference long MD simulation and error bars indicating a 95% confidence interval.

Figure 10.

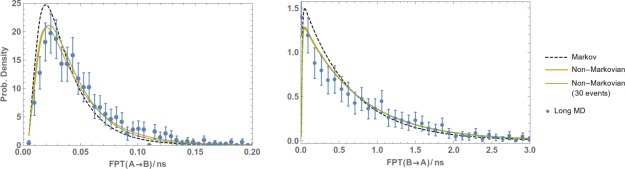
Non‐Markovian analysis of standard MD data. FPTDs of the methane/methane system from A to B (left plot) and from B to A (right) were obtained by postanalyzing a very long MD simulation. Also shown is the non‐Markovian analysis of a much shorter trajectory where only 30 events ( $A\to B$ and $B\to A$) are observed. The results are compared with a reference long MD simulation and error bars indicating a 95% confidence interval.

Limitations of the approximation

Although the non‐Markovian analysis is unbiased for the mean FPT, it is not constructed to yield the exact distribution. We empirically examined the conditions under which the approach would fail for characterizing the full distribution, and found that in general the approach breaks down in the limit when $A\cup B$ covers the whole space or nearly so, when the intermediate region is very small. This is not totally unexpected since, despite the remarkable fact that the MFPT can be estimated without bias with even a single intermediate bin, the description given by the non‐Markovian model of the dynamics inside the states (A and B) is still purely Markovian.

Figure 11 is an example of that situation for our one‐dimensional toy model where $A=\{x<-\pi \}$ and $B=\{x\ge 0\}$; the intermediate region is a single bin and there is no appreciable difference between “Markov” and “Non‐Markovian.” In this limit of a single‐bin intermediate, both Markovian and non‐Markovian analyses tend to fail and yield similar results, since in effect the non‐Markovian approach embodies little additional history information compared with the Markov model: see Figure 1.

Figure 11.

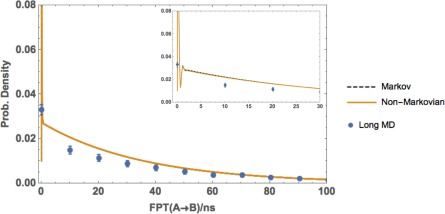
Breakdown of the non‐Markovian analysis for a minimal intermediate region. FPTDs of the one‐dimesional toy model from A to B with a small intermediate region, see text, were obtained by postanalyzing a WE simulation using a regular first‐order Markov analysis (Markov) and non‐Markovian analysis (Non‐Markovian). The results are compared with a reference long MD simulation and error bars indicating a 95% confidence interval. The inset shows the same distribution in the interval $[0,30\times {10}^3]$ MC steps.

Discussion

The results presented above indicate that our previously developed non‐Markovian analysis37 can usefully be applied to estimating FPT distributions based on weighted‐ensemble (WE) and even ordinary MD simulations. WE simulations do not directly yield the FPT distribution, and straightforward MD would require an impractical amount of simulation to allow the distribution to be resolved, so our approach may have significant utility in the analysis of simulations. The method is fairly successful even when rather crude bins or states are used.

The FPT distribution can provide insights into kinetic behavior not available from the mean FPT. Most obviously, as seen in some of the distributions, significant deviations from simple exponential behavior reveal the complexity of true molecular landscapes in contrast to idealized pictures. For example, the finite event duration—i.e., the time for a transition even excluding the dwell time in the initial state A 65—essentially forces the FPT distribution to have a low‐probability transient at small values of the FPT. In systems, more complex than those examined here, such as with multiple significant metastable intermediates, the FPT distribution could exhibit further features of interest.

This work was motivated by the observation that a non‐Markovian analysis based solely on the most‐recent‐state history yields the mean FPT without bias.37, 66 Although the extension of the approach to estimating the FPT distribution is approximate, it seems reasonable that the inclusion of history information could significantly improve calculation of the distribution. By definition, all trajectory generating methods (such as MD simulations) include at least some history information—although that history does not seem to be exploited in common analyses.

We emphasize that in projections of continuum behavior to finite states, kinetic behavior is generally expected to be non‐Markovian for the simple reason that relaxation within a finite state is never infinitely fast—nor will there generally be a clean separation of fast and slow timescales. For example, in the projection of a continuous process to quasi‐one‐dimensional discrete states (see Fig. 1), the probability to transition from one finite state to the neighboring state on the left, say, will depend on whether the (continuous) trajectory arrived from the left or right. This is a non‐Markovian history effect.

In principle, a standard Markov analysis can also yield the FPT distribution, but that approach requires carefully chosen and relatively small states. Our goal, by contrast, was to examine larger, non‐Markovian states by construction. The advantage of the non‐Markovian approach employed here seems to be its relative insensitivity to the division of configuration space into states (or “bins”) and its evident accuracy in cases where states are relatively large and non‐Markovian, as they were in our study. The motivation for the non‐Markovian approach is the expectation that computing‐power limitations will prevent the collection of trajectory data sufficient for truly Markovian (i.e., small) states in many highly complex systems of interest. Nevertheless, we emphasize that Markov modeling has been shown to yield good results for long timescales in cases where sufficient trajectory data is available.19, 67

The FPT distribution estimates here are approximate. We find, fortunately, that the approach is quite accurate for reasonable definitions of states and intermediate regions. Our data suggest that the approximation breaks down when a small intermediate region is used, i.e., when the whole space is substantially covered by the states A and B. In that limit, the dynamics inside the states A and B essentially determines the FPTD, and our non‐Markovian model, which remains equivalent to the Markov model inside A and B by construction in our analysis (see Fig. 1), cannot improve our estimates.

Because the non‐Markovian analysis is capable of yielding accurate FPT distributions based on fairly crude divisions of configuration space, we anticipate it could be a very useful tool in analyzing not only WE simulations, but also much more common ordinary MD trajectory data. The initial data presented here analyzing standard MD trajectories support this. The approach should be applicable so long as unbiased raw trajectory data is used to generate the non‐Markovian transition matrix elements. That is, as with standard Markov state modeling, trajectories should not be subject to artificial forces, but they may be distributed in configuration space using a variety of creative algorithms.

Conclusions

We showed that a non‐Markov analysis previously developed for unbiased estimation of the mean FPT37 could be extended to provide good, but approximate, characterizations of the full distribution of FPTs in WE simulation. Standard WE simulations and analysis were not able to provide estimates for the FPT distribution before now, to our knowledge. The non‐Markovian approach could prove valuable in characterizing fluctuations in kinetics and mechanisms generated not only by WE simulation, but also by other methods: the analysis is fully applicable to unbiased trajectories generated by any means.

The non‐Markovian analysis appears capable of providing good results even when the partitioning of configuration space is fairly crude and the states are highly non‐Markovian. In future work, we hope to explore whether the use of such bins will enable estimation of kinetic and mechanistic properties using less trajectory data than is required using finer bins.