Evaluating the dynamics and electrostatic interactions of folded proteins in implicit solvents

Abstract

Three implicit solvent models, namely GBMVII, FACTS, and SCPISM, were evaluated for their abilities to emulate an explicit solvent environment by comparing the simulated conformational ensembles, dynamics, and electrostatic interactions of the Src SH2 domain and the Lyn kinase domain. This assessment in terms of structural features in folded proteins expands upon the use of hydration energy as a metric for comparison. All‐against‐all rms coordinate deviation, average positional fluctuations, and ion‐pair distance distribution were used to compare the implicit solvent models with the TIP3P explicit solvent model. Our study shows that the Src SH2 domains solvated with TIP3P, GBMVII, and FACTS sample similar global conformations. Additionally, the Src SH2 ion‐pair distance distributions of solvent‐exposed side chains corresponding to TIP3P, GBMVII, and FACTS do not differ substantially, indicating that GBMVII and FACTS are capable of modeling these electrostatic interactions. The ion‐pair distance distributions of SCPISM are distinct from others, demonstrating that these electrostatic interactions are not adequately reproduced with the SCPISM model. On the other hand, for the Lyn kinase domain, a non‐globular protein with bilobal structure and a large concavity on the surface, implicit solvent does not accurately model solvation to faithfully reproduce partially buried electrostatic interactions and lobe‐lobe conformations. Our work reveals that local structure and dynamics of small, globular proteins are modeled well using FACTS and GBMVII. Nonetheless, global conformations and electrostatic interactions in concavities of multi‐lobal proteins resulting from simulations with implicit solvent models do not match those obtained from explicit water simulations.

Introduction

The solvent environment plays a crucial role in determining the structure, dynamics, and function of a biomolecule. In order to utilize molecular dynamics simulations to examine the conformational equilibrium of biomolecules, it is imperative that the solvent environment be accurately modeled. The most accurate approach is to explicitly include the water molecules in a biomolecular simulation. Although this approach offers a high level of detail and accuracy, it greatly reduces the computational efficiency due to the substantial increase in system size from the addition of explicit water molecules. Because computing resources are often rate‐limiting for large‐scale studies of proteins in explicit waters, many strategies and methods to facilitate efficient sampling of the protein configurational space have been developed, including coarse‐grained modeling,1 adaptive biased dynamics,2, 3, 4 and implicit solvation.5, 6, 7, 8, 9 The technical details as well as advantages and disadvantages of these strategies have been discussed elsewhere.1, 2, 3, 4, 5, 6, 7, 8, 9 Here, we focus on the implicit solvation strategy, and compare selected implicit solvent models (ISMs) with the TIP3P explicit solvation model in conformational sampling of a small, single domain protein, Src SH2, and a larger protein with bilobal structure, the kinase domain (KD) of Lyn, a Src‐family tyrosine kinase.

Implicit solvation, in comparison to the atomistic representation of water molecules, is a computationally simplified approach to describe the solvent environment in molecular dynamics (MD) simulations. The solvent effect is computed using an effective free energy function that depends solely on the coordinates of the solute atoms. The solute‐solvent interactions, and subsequently, the solvent effect on structural and dynamical characteristics of the solute, are estimated from the change in the solute energy landscape due to the addition of solvation energy. Because water molecules are not present, the system size is substantially reduced; the implicit solvation approach, therefore, provides a significant gain in computational efficiency.

Various implicit solvent models are implemented in popular MD programs. In particular, models developed from Generalized‐Born formalism are widely available in IMPACT,10, 11 AMBER,12, 13 GROMACS,14 and TINKER.15 In the CHARMM MD program, ACE2,16 ASPENR,17 EEF1,18 GBORN,19 SASA20 models are used with CHARMM19FF21 and FACTS,22 GBMVII,23, 24 GBSW,25 SCPISM,26 and RUSH27 with CHARMM22FF/CMAP.28, 29 Here we examine ISMs parameterized with CHARMM22FF/CMAP.

In ISMs based on the continuum electrostatic theory, the solute is taken to be a low dielectric region with a charge distribution while the solvent is treated as a uniformly high‐dielectric environment. The nonpolar and the electrostatic components of the solvation free energy of the simulation system are separately approximated. While the treatment of the nonpolar contribution is common and taken to be proportional to the solvent‐accessible‐surface area (SASA),30, 31 calculations of the electrostatic contribution to the solvation energy vary among ISMs. The Poisson‐Boltzmann (PB) equation provides a continuum solvation model with an accurate description of the solute‐solvent electrostatic interactions. Yet, this solvation model suffers from too expensive of a computational cost due to the lack of analytical solutions. Even when numerical solvers are utilized to calculate the solvation energy, the difficulties in computing the derivatives prompt the PB solvent model to be unsuitable for simulations of large biomolecules. As a result, Generalized Born ISMs, some of which are GBSW,25 GBMVII,23, 24 FACTS,22 AGBNP2,10 and GB‐Neck2,12 were developed as robust and efficient means to approximate the solution to the Poisson‐Boltzmann equation. The effective Born radii, which quantify the extent of burial for individual charges in a biomolecule, are crucial quantities for a reasonable estimate of the electrostatic component of the solvation free energy. Thus, various GB‐based solvent models essentially differ in strategies to calculate the effective Born radii and to define the boundary separating the low and high dielectric regions. Some other non‐GB solvent models, one of which is the Screened Coulomb Potential ISM (SCPISM)26, were also developed with similar objectives: to accurately describe the solvent environment and its effect in a computationally efficient manner. In contrast to the GB‐based models, a SCPISM simulation box is not separated into two regions of high and low dielectric constants. The implemented dielectric profile is distance‐dependent: the variation in dielectric permittivity is continuous and follows a sigmoidal curve, indicating that it is no longer necessary to define the boundary for dielectric discontinuity.

Although the accuracy of conformational ensembles produced with ISMs is compromised as a trade‐off for improved speed, the results of previous studies show excellent progress of ISMs towards correctly reproducing the hydration energies and solvation effects. Knight and Brooks32 and others^12, 33, 34 demonstrated that many ISMs can reasonably estimate the hydration free energy for small molecules. Juneja et al.35 evaluated implicit solvation methods parameterized for CHARMM force fields for their accuracy to depict the unfolding process of a small peptide and describe the effect of mutations or substrate binding on its stability. Their work showed that GBORN, GBMVII, and SCPISM are indeed capable of reproducing the peptide's structural characteristics as observed in explicit solvent. Formaneck and Cui found the structures and relaxation properties from a conformational ensemble of a small single‐domain protein produced with GBSW were in good agreement with those obtained for the explicit solvent ensemble;36 however, they also observed that the hydrogen bond interactions were overstabilized with GBSW. Recently, Bottaro et al.37 demonstrated that FACTS, GBSW and SCPISM can maintain the native structures and are capable of reproducing the experimental NMR scalar couplings of small proteins (GB3 and ubiquitin) with reasonable accurary. Nevertheless, the performance of implicit solvation methods in capturing the equilibrium conformational ensembles, dynamics, and in particular, the solvent‐exposed charge‐charge interactions in folded proteins including those with non‐globular, bilobal structures, needs further evaluation.

Work by Juneja et al. indicated that FACTS is the most efficient GB‐based solvent model, and GBMVII and SCPISM performed better than other CHARMM22FF implicit solvent models, namely RUSH and GBSW. Thus, we selected these implicit solvent models, namely GBMVII, FACTS, and SCPISM, for a comparative study on equilibrium structures, dynamics and electrostatic interactions of the single‐domain Src SH2 and the non‐globular Lyn KD from simulations in TIP3P and in the three ISMs. Our results show the Src SH2 domains solvated in TIP3P, GBMVII and FACTS have similar amplitude of positional fluctuations, charge‐charge interactions, and sample similar conformations. The SCPISM solvent, however, does not adequately model the solvent‐accessible electrostatic interactions. Moreover, our results suggest that in simulations of the non‐globular Lyn KD with a bilobal structure, charge‐charge interactions of residues located in a surface concavity and lobe‐lobe structure vary considerably between ISM and explicit water ensembles.

Results and Discussion

Backbone structural and dynamic characteristics of the SH2 domain

One measure often used to examine the quality of solvent models is their ability to reproduce backbone structure. Distributions of $\varphi$, ψ dihedral angles (Supporting Information Fig. S1) and time profiles of rms differences in backbone coordinates (Supporting Information Fig. S2) were used to compare the conformational ensembles generated with the ISMs and TIP3P. Consistent with previous observations that secondary structures of folded protein are stable with ISMs,12, 37 the equilibrium MD trajectories at 300 K of folded SH2 domain have minimal differences in $\varphi$, ψ distributions between the three ISMs and TIP3P [Supporting Information Fig. S1(E–G)]. The conformations sampled with TIP3P, GBMVII, and FACTS do not differ substantially from the energy‐minimized structure [average rmsd ≈1.4 Å, Supporting Information Fig. S2(A,B,D)] while those sampled with SCPISM are more dissimilar [average rmsd >2 Å, Supporting Information Fig. S2(C)].

The dynamics and flexible nature of the backbone structures generated with various solvents is considered through the time‐development and magnitude of N, C_α, and C positional fluctuations. The time‐development of the fluctuations not only illustrates the flexibility of the backbone but also shows the convergence behavior of atomic fluctuations, which reflects the nature of the sampled potential energy landscape.38 Figure 1(A) displays the time‐development of backbone positional fluctuations from simulations of the Src SH2 domain in various solvent models. For simulations in TIP3P, GBMVII, and FACTS, a rapid build‐up in fluctuations is observed within 500 ps, followed by a slower increase. At the 5 ns time interval, the fluctuations have reached approximately 95% of the total value. At long time limit, the time‐development curves for these ISMs have nearly plateaued and show similar convergence. At shorter timescale [see inset of Fig. 1(A)], the fluctuation amplitudes for simulations with FACTS and GBMVII increase more rapidly than that for simulations with TIP3P, consistent with the expectation of more rapid sampling of atomic fluctuations in ISM.

Figure 1.

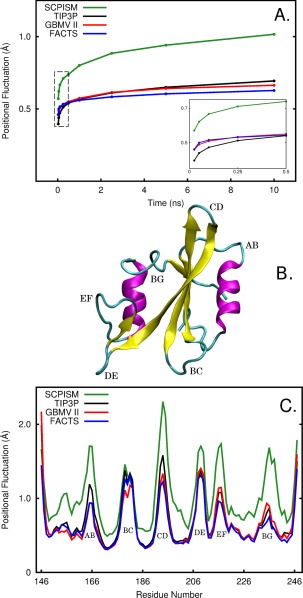
A: The time‐development of the backbone (N, C, C_α atoms) positional fluctuations of the unbound Src SH2 domain simulated in TIP3P (black), GBMVII (red), FACTS (blue), and SCPISM (green) solvent models. For an indicated time interval, backbone positional fluctuations were calculated, and then ensemble‐averaged over 102 residues and forty 10‐ns trajectories. The inset corresponds to the section bounded by dashed lines and shows the time‐development of backbone positional fluctuations at short timescale. B: Ribbon structure of Src SH2 domain with α‐helices in magenta, β‐sheets in yellow, loops and turns in cyan. The flexible loops are labeled according to their topological nomenclature. C: Residue averages of the backbone (N, C, C_α atoms) positional fluctuations of the unbound Src SH2 domain obtained from forty 10‐ns simulations in TIP3P (black), GBMVII (red), FACTS (blue), and SCPISM (green) solvent models.

The time‐development curve for SCPISM, however, is distinct from the other three curves: the fluctuation amplitudes are greater over the full time course and continue to increase over the 10 ns period. For a protein sampling the conformational space corresponding to a single energy minimum, the time‐development curve is expected to rise sharply at shorter time intervals and approach a limiting value as the time intervals increase. If the protein is sampling a small region in the configurational space, the time‐development curve will reach the plateau stage more quickly than that of a protein sampling a broad region in the configurational space. This analysis reveals that solvation with SCPISM results in dynamics of longer timescale and greater amplitude, indicative of enhanced backbone flexibility and access to a larger conformational space.

It is of interest to discern whether the large positional fluctuation of Src SH2 domain in SCPISM is limited to a particular region of the structure. Thus, the averages of the backbone positional fluctuations were used to compare and contrast the backbone flexibility for various structural elements [colored coded in Fig. 1(B)]. The residue profile of the backbone positional fluctuations averaged over a 10 ns window [Fig. 1(C)] shows that the Src SH2 domain solvated in SCPISM has larger backbone fluctuations while TIP3P, GBVMVII, and FACTS solvation produces nearly identical fluctuation amplitudes. SH2 domains solvated with GB‐based models, albeit considered reduced systems, exhibit remarkably similar dynamical behavior in comparison with that solvated with TIP3P explicit water, demonstrating that GB‐based models can efficiently reproduce the solvent effect on protein motion. The pattern of fluctuation with respect to the residue number, is similar for all solvent models and in agreement with the fluctuation profile determined from the crystallographic temperature factors39, 40 (B‐factors) (see Supporting Information Fig. S2) and from a previous MD study of a peptide‐Src SH2 complex in explicit solvent.41 The fluctuation profile of the unbound Src SH2 domain solvated with TIP3P waters and ISMs follows the expected trend of the relative fluctuations among loops, α‐helices and β‐sheets. The residue profile indicates that the large fluctuations observed in the time‐development curve for SCPISM is largely the result of a general increase in backbone flexibility, although fluctuations of the flexible loops, excluding the BC loop, are relatively enhanced and thus largely responsible for dissimilar convergence in the time‐development curve of SCPISM in comparison to those of TIP3P, GBMVII, and FACTS. Together with the time‐development of backbone positional fluctuations, it is concluded that the Src SH2 domain solvated using TIP3P, GBMVII, and FACTS have highly similar equilibrium backbone dynamics, while solvation with SCPISM leads to considerably higher fluctuation amplitudes, particularly in loop regions.

Solvent‐accessible electrostatic interactions of the SH2 domain

Electrostatic interactions are responsible for variations in enthalpy of unfolding among proteins42, 43 and therefore, are important for protein structure and function44, 45 and have been used to parameterize improvements in GB models.^10, 12 Src SH2 domain has 26 charged amino acids out of 102 residues; thus, a large number of electrostatic interactions exist and contribute to maintaining the structural integrity of the protein. Because the strength and stability of the electrostatic interactions depend not only on the separation of the charged residues but also their local environments,46 we have examined the distance distributions of eight solvent‐exposed ion pairs (see ribbon structures in Fig. 2), two of which contribute to the binding of substrate, as a measure for assessing ISMs effect on charge‐charge interactions.

Figure 2.

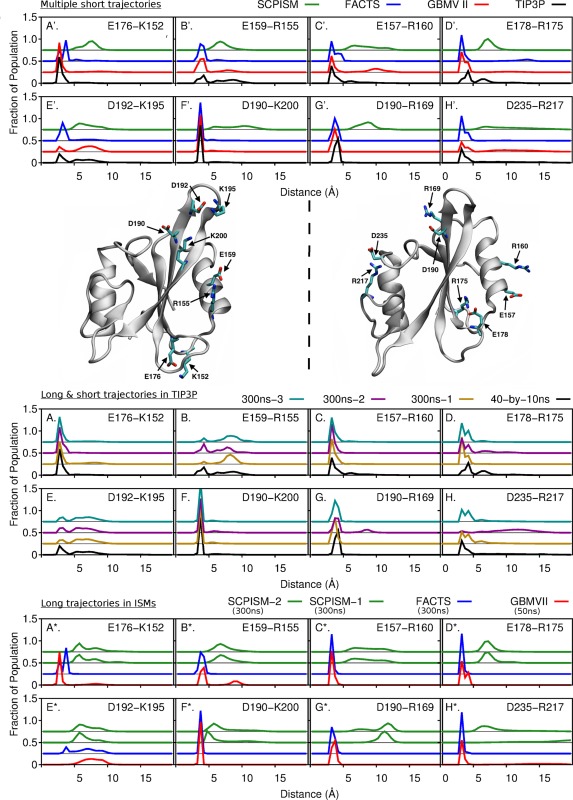
A’ to H’: Distance distributions of eight ion pairs (as labeled) from forty 10‐ns simulations of the unbound Src SH2 domain in TIP3P (black), GBMVII (red), FACTS (blue) and SCPISM (green) solvent models. Protein structure: Ribbon representations of the unbound Src SH2 domain with ion pairs shown in sticks. A to H: Distance distributions of eight ion pairs (as labeled) from forty 10‐ns simulations (black) and three of 300‐ns simulations (gold, purple, and cyan) of the unbound Src SH2 domain in TIP3P solvent model. A* to H*: Distance distributions of eight ion pairs (as labeled) from longer trajectories of the unbound Src SH2 domain in GBMVII (red, 50‐ns simulation), FACTS (blue, 300‐ns simulation) and SCPISM (green, 300‐ns simulations) solvent models. For every ion pair, the distributions are shifted along the y‐axis to give a gap of 0.25 unit between two distributions. The distance between two charged residues is between C_ζ atom of Arg, the N_ζ atom of Lys, the midpoint of O_δ1 and O_δ2 atoms of Asp, and the midpoint of O_ϵ1 and O_ϵ2 atoms of Glu.

A variety of distance distributions are observed for the eight ion pairs calculated from the combined forty 10‐ns trajectories [Fig. 2(A’–H’)]. That is, certain interactions are very stable based on narrow distributions peaked at short distance. By contrast, the D192‐K195 interaction flanking a β‐turn is less stable and the distributions are broad.

In general, for proteins simulated with GBMVII and FACTS, the peak positions and distribution profile compare well with those of TIP3P. For example, D190 is sandwiched between K200 and R169, and the distributions for both interactions [see Fig. 2(F’,G’)] are nearly identical for GBMVII, FACTS, and TIP3P. Nonetheless, disparities are observed for the E178‐R175 salt bridge; the peak positioned at 6 Å in TIP3P is a solvent‐mediated interaction (seen in trajectory) and was sampled with neither FACTS nor GBMVII solvents. This behavior was previously pointed out by Nguyen et al.12 and indicates an overstabilization of charge‐charge interactions with ISM as observed by Formaneck and Cui.36

In contrast to overstabilization of short‐range charge‐charge interactions, there are cases (shown in panel D’ and H’ of Fig. 2) in which the sampling of ion pair distances in TIP3P does not include the noninteracting long distance separation observed with FACTS, GBMVII, or SCPISM. For the D235‐R217 pair [Fig. 2(H’)], side‐chain dihedral rotations lead to a distance of approximately 10 Å being populated in GBMVII but not in TIP3P. Similarly, for the E178‐R175 ion pair [Fig. 2(D’)], a distance of 13 Å was only sampled in FACTS. To query whether these differences are results of more extensive sampling with ISMs, we compared the distance distributions obtained from multiple 300‐ns TIP3P‐trajectories and the forty 10‐ns TIP3P‐trajectories [see Fig. 2(A–H)]. Overall, these distributions do not vary appreciably, indicating that the distributions calculated over 400 ns total simulation from multiple short TIP3P trajectories are representative of the longer‐time behavior of a single 300‐ns trajectory. Nevertheless, a low population of noninteracting distance is observed for the D235‐R217 pair in TIP3P [Fig. 2(H)] but not for the E178‐R175 pair [Fig. 2(D)]. Together, the results suggest that these fully solvated forms of ion pairs may be lowly populated, but their probabilities may differ with TIP3P and GB‐based ISMs [Fig. 2(D’)].

We also examined results for sampling of electrostatic interactions with ISMs over a longer trajectory. The distance distributions of the eight ion pairs were calculated with longer trajectories of the unbound Src SH2 domain solvated with GBMVII (one 50‐ns trajectory), FACTS (one 300‐ns trajectory) and SCPISM (two 300‐ns trajectories) [see Fig. 2(A*–H*)]. For all implicit solvents, the sampling of electrostatic interactions at long time [Fig. 2(A*–H*)] do not differ substantially from that seen with shorter trajectories [Fig. 2(A’–H’)]. For GBMVII and FACTS solvents, the ion‐pair distance distributions calculated from longer trajectories [Fig. 2(A*–H*)] are similar to those from TIP3P trajectories [Fig. 2(A–H)].

GBMVII and FACTS, therefore, can model with reasonable accuracy the solvent‐exposed electrostatic interactions; however, SCPISM solvent failed to capture the energetically favorable electrostatic interactions seen with TIP3P. With SCPISM, the most probable distances for interactions between charged side chains of the eight ion pairs are greater than 5 Å. Electrostatic interactions between solvent‐exposed charged amino acids of Src SH2 domain are, therefore, weak and overly screened with SCPISM, resulting in long distance separation between charged residues as shown in Figure 2(A’–H’).

Sampling of the SH2 domain global conformations

For a small, well‐folded protein such as the Src SH2 domain, the global conformations sampled with ISMs and those with TIP3P are expected to be similar. Here, we examined the nearness of trajectories in conformational space by an all‐against‐all pairwise comparison of structures; the rms deviation in backbone coordinates was calculated between snapshots taken from ISM trajectories and snapshots taken from TIP3P trajectories. We utilized the all‐against‐all rms deviation analysis, as opposed to the rms deviation against a single reference structure, because such analysis eliminated the bias of the reference structure selected to represent the sampled conformations. Furthermore, the distribution of rms deviation from all possible pairwise comparisons is a more accurate indicator of the similarity of sampled conformations and thus the nearness of one trajectory to another in conformational space.

Figure 3 displays the distributions for the all‐against‐all rms deviations between snapshots taken from the TIP3P trajectories and snapshots taken from the trajectories generated with GBMVII, FACTS, and SCPISM solvents, as well as an all‐against‐all distribution for pairs within TIP3P trajectories. The distributions are unimodal, indicating that the ISM‐trajectories sample from one energy superbasin and solvation with ISMs does not promote the sampling of either multiple energy basins or conformational transitions. The remarkable overlaps in the all‐against‐all rms deviation distributions for TIP3P, GBMVII, and FACTS imply that the accessible conformational spaces to Src SH2 domain with these solvents are nearly identical. The difference in the mean values is only 0.1 Å.

Figure 3.

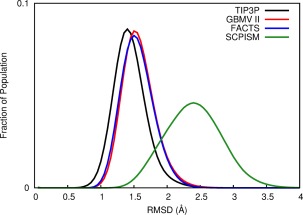
The distributions of pairwise rms deviation (rmsd) values calculated using all pairs of snapshots between the combined forty 10‐ns trajectories of the unbound Src SH2 domain simulated with TIP3P and GBMVII (red), FACTS (blue) or SCPISM (green) solvent models, as well as all pairs within the TIP3P trajectories (black). For every pair of snapshots, the rmsd value was computed over all backbone heavy atoms (N, C, C_α atoms) following the superposition of the two protein structures.

The distribution corresponding to SCPISM shows considerably less overlap with that of TIP3P, and is shifted to a larger rms deviation value. Thus, the conformations sampled with SCPISM are largely different from those with TIP3P.

Electrostatic interactions of the Lyn kinase domain

Our above analysis of the SH2 simulations suggests that GBMVII and FACTS models reproduce the solvent environment equally well in terms of stabilizing the well‐folded structure and fluctuations of Src SH2 domain. Because FACTS and SCPISM are more computationally efficient than GBMVII (see Table 1), in this and the next sections, we compare conformational ensembles of Lyn KD from trajectories calculated with FACTS, SCPISM and TIP3P solvents. Lyn KD is nonglobular with a bilobal structure: a smaller N‐terminal lobe and a larger C‐terminal lobe that enable conformational activation to regulate enzymatic activity [see Fig. 4(G)]. The Lyn KD provides a test case for how well FACTS and SCPISM can model implicitly the solvation of a protein with an extensive concave surface area between the two lobes [see Fig. 4(H)].

Table 1.

Approximate Computational Cost Associated With Each Solvent Model Relative to the Cost of a Vacuum Calculation for Simulations of Src SH2 Domain

Solvent model	ns/daya	Cost relative to vacuuma
Vacuum	91.1	1
TIP3P	3.82	∼23.8b
GBMV II	13.93	∼6.5
FACTS	26.44	∼3.4
SCPISM	60.75	∼1.5

^aCalculated using two 8‐core Intel Xeon‐E5 processors, totaling 16 cores.

^bSimulation box contains the SH2 domain and 6840 water molecules.

Figure 4.

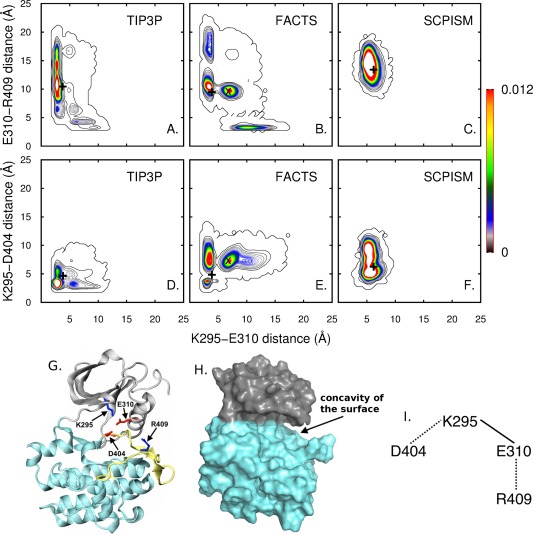
A to F: Maps showing the distance distributions of two sets of ion pairs in the Src Kinase switch electrostatic network. The distances were calculated from trajectories of Lyn Kinase domain in TIP3P (A and D), FACTS (B and E) and SCPISM (D and F) solvents. Residues are numbered according to the convention for the Src Kinase domain. The black X marks in B and D indicate the regions of the map that are highly populated with FACTS while being lowly populated with TIP3P solvent. The initial distances between K295‐E310, K295‐D404, and E310‐R409 ion pairs are 3.51 Å, 5.88 Å, and 10 Å, respectively. The black + marks indicate the distances between various ion pairs after equilibration. The distance between two charged residues was calculated as described for Fig. 2. G: Ribbon representation of the Lyn KD with the N‐lobe, A‐loop, and C‐lobe colored in gray, yellow, and cyan, respectively. The positively charged residues (K295 and R409) are shown in blue sticks. The negatively charged residues (E310 and D404) are shown in red sticks. H: Surface representation of the Lyn KD with the N‐ and C‐lobes colored in gray and cyan. The cleft between the N‐ and C‐lobes results in a concavity of the protein surface. I: A schematic showing the electrostatic interactions in the inactive (dashed lines) and active states (solid line) of the Src KD.

In this section, we compared the interactions of three ion pairs that are in the cleft region between the two lobes, namely K295‐D404, K295‐E310, and E310‐R409, from simulations of Lyn KD with TIP3P, FACTS, and SCPISM. These ion pairs partially make up the switched electrostatic network (SEN) in which charged residues switch between the most favored salt‐bridge partners in the active and inactive states of the protein47 [see Fig. 4(I)]. Specifically, for these four residues, in the crystal structure of the Src KD active conformation (PDB ID: 1Y5748), K295‐E310 is the energetically favored interacting ion pair while in the Src KD inactive conformation (PDB ID: 2SRC49), K295‐D404 and E310‐R409 are the stabilized interactions. The SEN has been proposed to be important for the transition between active and inactive conformations by reducing the free‐energy barrier between these two states.47 In this work, ion pairs in the active conformation of the Lyn KD were characterized using equilibrium MD. Therefore, transient excursions to sample the inactive interactions with the other charged residues might be anticipated based on the SEN.

Presented in Figure 4(A–F) are contour plots for the distance distributions of the two sets of ion pairs in the SEN from simulations with TIP3P [Fig. 4(A,D)], FACTS [Fig. 4(B,E)], and SCPISM [Fig. 4(C,F)]. The top panel [Fig. 4(A–C)] illustrates the switch of E310 between K295 and R409 while the bottom panel [Fig. 4(D–F)] displays the switch of K295 between E310 and D404. The black + mark in each plot indicates the distances between the ion pairs after equilibration. Because the simulations are started from the active conformation of Lyn KD, the K295‐E310 interaction is expected to be strongly favored over the other two interactions, and the K295‐E310 distances less than 4 Å should be highly populated. This is the case observed with TIP3P solvent [Fig. 4(A,D)]. The switched interactions of K295 and E310 with their partners in the inactive forms and K295‐E310 distance being greater than 5 Å are also seen with TIP3P solvent but with smaller population [Fig. 4(A,D)]. Moreover, both Figure 4(A,D) show the transition between the salt‐bridge partners of the active and inactive conformations in TIP3P solvent to be a ‘hand‐off’ between the pairs47, 50 corresponding to density at approximately (4 Å, 4 Å) in the lower left corner of the panels. To the contrary, the plots corresponding to simulations in FACTS solvent show a highly populated intermediate state, labeled with black X marks in Figure 4(B,E), which is not observed for simulations with TIP3P. A single contour in Figure 4(A,D) indicates that this region is visited but not highly populated in TIP3P solvent. That these conformations are relatively favored in FACTS demonstrates a clear difference in the energetics between FACTS and TIP3P, and reveals a shortcoming of FACTS solvent in modeling electrostatic interactions in this concave region of the protein surface. From a 25‐ns trajectory calculated with GBMVII solvent, contour plots for the ion‐pair distance distributions [Supporting Information Fig. S4(A,A’)] indicate that the highly populated intermediate states seen with FACTS solvent [black X marks in Fig. 4(B,E) and Supporting Information Fig. S4(B–J,B’–J’)] may not exist for simulations of Lyn KD solvated with GBMVII.

In contrast to the sampling of electrostatic interactions with FACTS solvent, in which the regions visited on the conformational landscape were similar to those of TIP3P, the conformational landscape sampled with SCPISM solvent showed little overlap with the TIP3P landscape. The plots corresponding to simulations with SCPISM [Fig. 4(C,F)] showed unimodal distance distributions, indicating that with SCPISM, the conformational landscape is less rugged and the energetics of solute‐solvent interactions in SCPISM solvent are distinct from those in TIP3P explicit waters. In addition, favorable electrostatic interactions seen with TIP3P [<4 Å distances for K295‐E310 and K295‐D404 ion pairs in Fig. 4(A,D)] were hardly sampled with SCPISM solvent, consistent with earlier analysis (see Solvent‐accessible electrostatic interactions of the SH2 domain subsection).

Sampling of the lyn kinase domain global conformations

The KD of Lyn has a lobe‐lobe structure related to its function of an activated enzyme; the concave cleft region described above lies between the two lobes and forms the enzyme active site [see Fig. 4(H)]. To query whether the choice of solvent affects the lobe‐lobe structure, we calculated the distances between the N‐ and C‐lobes’ center of mass (COM) from simulations with FACTS, SCPISM, and TIP3P. Average distances calculated from each of the nine simulations with TIP3P and FACTS are shown in Table 2 and in Figure 5(A) as red and blue filled circles, respectively. Average distances calculated from each of the three simulations with SCPISM are shown in Figure 5(A) as green filled circles. The standard deviations from the average distances are displayed as error bars, and the ensemble average of lobe‐lobe distances over all trajectories as a solid line in Figure 5(A). Our analysis on the Lyn kinase domain finds that for a bilobal protein with concave regions on the surface, the lobe‐lobe conformations sampled with FACTS and SCPISM differ from those with TIP3P. With SCPISM, smaller average COM distances were sampled. Simulations with FACTS generally resulted in a larger average COM distance than TIP3P by approximately 2 Å; the ensemble averages are 29.8 Å and 28.1 Å, respectively. Only three trajectories with FACTS have COM distances that substantially overlap with those of TIP3P.

Table 2.

Average Distances Between the N‐Lobe and C‐Lobe’ Center of Mass Calculated From Nine 50‐ns Trajectories of Lyn Kinase Domain in TIP3P and FACTS Solvent Models

	Average interlobal distancesa (Å)
Trajectory ID	TIP3P	FACTS	FACTS to TIP3Pb
1	27.8 ± 0.4	30.0 ± 0.6	29.0 ± 0.5
2	27.8 ± 0.3	28.9 ± 0.4	28.7 ± 0.4
3	27.7 ± 0.6	29.2 ± 0.4	26.8 ± 0.4
4	28.9 ± 0.5	30.4 ± 0.6	31.3 ± 0.3
5	28.0 ± 0.5	30.3 ± 0.5	28.3 ± 0.3
6	28.1 ± 0.3	30.3 ± 0.6	28.8 ± 0.4
7	28.0 ± 0.4	30.7 ± 0.6	29.0 ± 0.4
8	28.1 ± 0.5	28.5 ± 0.4	28.1 ± 0.3
9	28.4 ± 0.6	29.9 ± 0.4	28.9 ± 0.4
Ensemble averagec	28.1	29.8	28.4

^aIndividual averages are reported with the standard deviations.

^bStructure from each trajectory generated with FACTS solvent model was re‐solvated in a TIP3P water box.

^cFor TIP3P and FACTS columns, the ensemble average is the mean of the nine individual averages. For FACTS‐to‐TIP3P column, the ensemble average is the mean of the eight individual averages, excluding the average value corresponding to the fourth trajectory.

Figure 5.

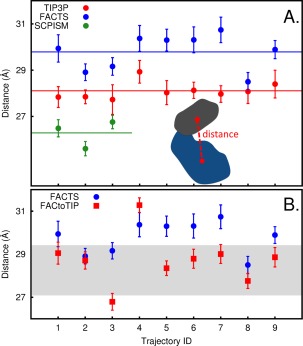
A: Average distances between the center of mass (COM) corresponding to the N‐lobe (residues 233 to 322) and C‐lobe (residues 323 to 384 and 411 to 504) of Lyn kinase domain calculated from simulations with TIP3P (red filled circles), FACTS (blue filled circles), and SCPISM (green filled circles). The standard deviations from the averages are shown as error bars. The red, blue and green solid lines indicate the mean of the average distances corresponding to TIP3P, FACTS, and SCPISM, respectively. A, inset: A schematic of the Lyn KD to illustrate the COM (red circles) distance (red dashed line) between the N‐lobe (gray) and C‐lobe (blue). B: Average COM distances for FACtoTIP trajectories initiated with coordinates from FACTS trajectories and solvated with TIP3P water molecules (red filled squares). The starting structure of each TIP3P simulation was extracted from a FACTS simulation of the same Trajectory ID. The COM distances from these FACTS trajectories are shown for comparison (blue filled circles). The standard deviations from the averages are shown as error bars. The shaded region displays the range of the lobe‐lobe distance calculated from the original set of trajectories with TIP3P.

The structural difference measured by the lobe‐lobe COM distance of Lyn KD generated with FACTS solvent compared to TIP3P could arise either from chance sampling of alternative regions of conformational space that have comparable energies or because FACTS does not reproduce the TIP3P solvation energy surface. To test if the increase in COM distance is a result of alternative sampling, conformations from the ensemble generated with FACTS were resolvated with TIP3P water molecules and an additional nine 50‐ns trajectories calculated (see Methods section), which from now on will be referred to as FACtoTIP trajectories. The distances between the N‐ and C‐lobes’ COM calculated from the FACtoTIP trajectories are plotted in Figure 5(B) as red filled squares. The COM distances from trajectories generated with FACTS are shown for comparison in the same plot as blue filled circles. The shaded box displays the range of the lobe‐lobe distance calculated from the original set of trajectories with TIP3P. Except for one case where the lobe‐lobe distance remains relatively large, resolvating conformations from eight of the nine FACTS trajectories with TIP3P water molecules produces structures with COM distances reduced by as much as 2 Å. Further, the range of these COM distances overlaps that of the original TIP3P simulations. Excluding the one trajectory (ID 4) where the COM distance remains relatively large (ID 4), the new global average is 28.4 Å, comparable to the original global average of 28.1 Å (see Table 2). The results indicate that the larger COM distance obtained in FACTS solvent is not the result of alternative sampling, but is the failure of FACTS solvent to reproduce the TIP3P solvation energy surface and the lobe‐lobe structure of Lyn KD.

Conclusion

Three implicit solvent models, namely GBMVII, FACTS, and SCPISM, were evaluated for their abilities to emulate the solvent environment of TIP3P explicit solvent as measured by the structures, dynamics and electrostatic interactions of the Src SH2 domain and the Lyn KD. We note in particular that for the small, globular protein Src SH2 domain, GBMVII and FACTS satisfactorily model the solvent‐exposed electrostatic interactions (Fig. 2). Given the reduced computational cost to carry out simulations with FACTS (Table 1), and the substantial overlap in sampling of global conformations, FACTS can be a reliable alternative solvent model for the simulation of small, globular proteins. Measures of the average positional fluctuations, ion pair distance distributions, and all‐against‐all rms coordinate deviations (Figs. 1, 2, 3) reveal that with SCPISM, specific electrostatic interactions were poorly modeled and conformations sampled were largely different from those with TIP3P. The reasons are not completely clear, particularly in view of the ability of SCPISM to model the temperature‐dependent folding of a helical peptide where many other ISMs in CHARMM failed.35

Considering the increasing use of MD simulations to investigate structure‐function relationships of large, nonglobular proteins,69 we examined whether FACTS remains a suitable solvent model for these MD studies. Using the Lyn KD as the test case having a set of ion pairs proposed to function in switching between the active and inactive conformations,47 we compared the sampling of local electrostatic interactions between charged residues in the cleft between the N‐ and C‐lobes. Discrepancies between the distance distribution maps corresponding to TIP3P and FACTS [Fig. 4(A)] demonstrate that key electrostatic interactions such as those involved in the electrostatic switch network were not properly sampled and represented with the FACTS solvent model. These ion pairs are partially buried in the active site and less solvent exposed than those in Src SH2 domain, which likely accounts for the poorer agreement with the distributions generated for the explicit solvent ensemble. Additionally, the average lobe‐lobe COM distances, which are measurements relevant to the global conformations, varied by approximately 2 Å, with proteins in FACTS solvent having larger lobe‐lobe distances [Fig. 5(A)]. A solvent‐swapping study [Fig. 5(B)] showed that the larger lobe‐lobe distances, observed for proteins solvated with FACTS, were not likely caused by more extensive conformational sampling and could be attributed to the absence of explicit water molecules in FACTS. Although FACTS can be reliably utilized to simulate small, globular proteins at lower computational cost, explicit water remains the more accurate, recommended solvation method for MD studies of nonglobular proteins due to the difficulty in reproducing the hydration effects on complex surfaces.

Our assessment of ISMs in terms of structural features in folded proteins expands previous studies that have utilized hydration energy as the primary metric for comparison. Our work reveals that although ISMs show poor performance for non‐sphrerical, multilobal proteins, ISMs are well‐suited for small, globular proteins. In order to substitute explicit solvent with ISMs to study a broad range of macromolecules, further development and parameterization are needed for accurate description of hydration effects on proteins with large concavities in their surfaces.

Theory and Methods

Implicit solvent models

The GBMVII,23, 24 FACTS,22 and SCPISM26 solvation methods are discussed in detail in the original articles. Here, we briefly describe some key features of each approach and recent applications.

The free energy of solvation calculated using GBMVII, FACTS, and SCPISM is decomposed into two components: electrostatic and nonpolar, $\Delta G_{\text{solvation}}=\Delta G_{\text{elec}}+\Delta G_{\text{nonpol}}$. The nonpolar component is usually estimated in terms of the total molecular SASA. For GBMVII and SCPISM, the nonpolar component of the solvation free energy can be written as: $\Delta G_{\text{nonpol}}=\alpha \left(\text{SASA}\right)+\beta$, where α and β are parameters obtained from fitting the solvation free energy of hydrocarbon molecules, and SASA is the usual molecular surface calculated with a spherical probe of 1.4 Å radius. For FACTS, $\Delta G_{\text{nonpol}}=\alpha \left(\text{SASA}\right)$ where α is an empirically fitted parameter and SASA is determined from the spatial arrangement and volumes of the solute atoms surrounding an atom i.

The three solvation methods differ substantially regarding the calculation of the electrostatic component of the solvation free energy. Both GBMVII and FACTS are GB‐based models; hence, the electrostatic component is defined using the formulation proposed by Still et al.51

$$\Delta G_{\text{elec}}^{\text{GB}}=-\frac{1}{2}(\frac{1}{{ϵ}_{\text{mol}}}-\frac{1}{{ϵ}_{\text{solv}}}){\displaystyle \sum _{i,j}\frac{q_i{q}_j}{\sqrt{r_{ij}^2+{\alpha }_i{\alpha }_j\hspace{0.17em}\text{exp}(-r_{ij}^2/4{\alpha }_i{\alpha }_j)}}}$$ (1)

where ${\in }_{\text{mol}}$ and ${\in }_{\text{solv}}$ are the assigned dielectric constants of the solute molecule and the solvent, respectively, N is the total number of solute atoms, q_i and q_j are the charges of atom i and atom j, r_ij is the distance between the two charges, and α_i and α_j are the effective Born radii of atom i and atom j. The effective Born radius of atom i is calculated from the atomic self‐solvation energy

$${\alpha }_i=-\frac{1}{2}(\frac{1}{{ϵ}_{\text{mol}}}-\frac{1}{{ϵ}_{\text{solv}}})\frac{q_i^2}{\Delta G_{\text{elec},i}{}^{\text{GB}}}$$ (2)

The strategies for computing the effective Born radii and defining the dielectric boundary differ between the GBMVII and FACTS solvation methods. The GBMVII solvation method evaluates a volume integral inside a defined molecular surface to estimate the atomic self‐solvation energies and Born radii. The results of structural and dynamical studies of biomolecules52, 53, 54 with GBMVII show agreement with experimental data. Using metrics such as RMSD, hydrogen bond count, and helicity, recent comparison by Juneja et al. shows35 that GBMVII was better than other ISMs in capturing characteristics of an unfolding peptide as well as disruptions to protein stability due to mutations or ligand binding.

Unlike GBMVII, FACTS utilizes an empirically parameterized formula to estimate the atomic self‐solvation energies and Born radii. In particular, the formulation of FACTS model only requires the calculation of interatomic distances to determine the volume and arrangement of solute atoms surrounding any atom i, which indicate the extent of desolvation for atom i. FACTS solvent model is validated by its applications in recent studies of biomolecules, some of which include studies of α‐helix $\rightleftharpoons$ β‐sheet transition pathways in a miniprotein,55 and self‐assembly of aspartate‐rich short peptides.56

In contrast to the GB‐based ISMs, in which there is a discrete boundary between the low and high dielectric regions, with the classic Lorentz‐Debye‐Sack (LDS) theory of polar liquids,57, 58, 59, 60 the dielectric profile is sigmoidal. Because the SCPISM model derives from the LDS theory, the variation between solute and solvent in dielectric is continuous. The formulation of SCPISM, therefore, does not require the separation of the simulation system into two regions of high and low dielectric constants, as in the case of GB‐based implicit solvent models. Because the shape of the dielectric permittivity profile changes depending on the solvent environment as well as the charge of the solute atom, a parameter controlling the shape of the profile (see Ref. 26) is parameterized for each atom type. Afterwards, the electrostatic component of the solvation free energy is a straightforward calculation using the inter‐atomic distances and partial charges. SCPISM is the most computationally efficient model among the three ISMs. Our benchmarking shows that simulations in SCPISM are merely 1.5 times more costly than simulations in vacuum (see Table 1). The validity of the SCPISM solvation method has been established in studies of biomolecules such as dynorphin, protein G and BPTI.61, 62

Model Systems and Simulation Details

Simulations of Src SH2 domain

Results from MD simulations of the unbound 102‐residue Src SH2 domain with various solvent models were compared. Src SH2 domain is a small, globular, well‐folded single‐domain protein (Fig. 1). Simulations of the unbound Src SH2 were carried out with CHARMM63 version c37b1 for GBMVII, FACTS, and SCPISM solvent models, and with NAMD64 version 2.9 for TIP3P solvent model using the CHARMM22 all‐atom force fields with CMAP dihedral angle correction. For each solvent model, a set of forty 10‐ns simulations was generated. The use of multiple trajectories benefits from the paralellization of computing resources while increases sampling efficiency with disparate initial configurations.65 In addition, a 50‐ns trajectory of Src SH2 domain solvated with GBMVII solvent model and 300‐ns trajectories of the protein in TIP3P (three trajectories), SCPISM (two trajectories), and FACTS (one trajectory) solvent models were calculated to compare with results obtained from multiple short trajectories.

Five coordinate sets for the Src SH2 domain were obtained from independent models in the asymmetric unit of the crystals (PDB codes: 1IS066 and 1SPS67) and used to initiate simulations using each solvent model. For TIP3P simulations, each of the five initial sets of coordinates was solvated with 6840 explicit water molecules in octahedral boxes so that the box edges were at least 14 Å from the protein. The energy of SH2 domains solvated with TIP3P was minimized first with the position of protein atoms fixed, followed by harmonic constraints on protein main chain atoms, and lastly without constraints. The energy was minimized with 500 steps of the steepest descent algorithm and 1000 steps of the adopted basis Newton‐Raphson algorithm, or until the energy difference between steps was less than 1 kcal/mol. For each of the five starting coordinate sets, eight sets of velocities were specified using random seeds, ultimately yielding 40 unique initial conditions for simulations of unbound Src SH2 in each solvent model.

The leapfrog integrator was used to calculate the trajectories with a 2 fs timestep for simulations in all solvent models. The SHAKE constraint algorithm was applied to fix the length of bonds involving hydrogen atoms. Constant temperature and pressure (CPT) dynamics in TIP3P solvent was performed using the Langevin thermo‐ and baro‐stat with a friction coefficient of 1 ps⁻¹, a reference temperature of 298 K and a reference pressure of 1 atm. For simulations in GBMVII, FACTS, and SCPISM, a Langevin heatbath with a friction coefficient of 2 ps⁻¹ was used for constant temperature dynamics at 298 K. The protein systems were equilibrated for 2500 ps before production runs began. Coordinates were saved every 1000 steps for all simulations.

With TIP3P solvent, the non‐bonded list was generated using a 14 Å cutoff. Nonbonded interactions were calculated with a switching function applied to the van der Waals potential energy from 10 Å to 12 Å. Electrostatic interactions were computed using the Particle Mesh Ewald (PME) method. With FACTS and SCPISM solvent, the nonbonded list was generated using a 14 Å cutoff. Electrostatic interactions were calculated with a shifting function applied to the potential energy at 12 Å, and van der Waals interactions were calculated with a switching function applied to the potential energy from 10 Å to 12 Å. With GBMVII solvent, the nonbonded list was generated using a 21 Å cutoff. Electrostatic and van der Waals interactions were calculated with switching functions applied to the potential energies from 16 Å to 18 Å.

Simulations of Lyn kinase domain

The active structure of the 272‐residue catalytic domain of the Lyn kinase, a member of the Src kinase family, was simulated with TIP3P, FACTS, and SCPISM water models using the CHARMM22/CMAP force field. For TIP3P and FACTS solvents, nine independent 50‐ns trajectories with different initial velocites were calculated. For SCPISM solvent, three 50‐ns trajectories were calculated. The initial structure was homology‐modeled as previously described.68

For simulations with explicit solvent, the initial structure was solvated in a 76 Å cubic box filled with 14,299 TIP3P water molecules as well as 39 Na⁺ and 36 Cl^– ions so that the salt concentration is 0.15M. For simulations with FACTS and SCPISM, the initial structure was energy minimized with the adopted basis Newton‐Raphson method for 1000 steps.

Simulation conditions and non‐bonded parameters were the same as those used for Src SH2 domain simulations. Combining the independent trajectories yielded a total simulation time of 450 ns for the Lyn catalytic domain in TIP3P and FACTS solvent models, and 150 ns for the protein in SCPISM solvent model. Coordinates were saved every 1 ps for all simulations.

Solvent‐swapping simulations of Lyn kinase domain

The response of Lyn kinase in a conformational state generated with FACTS to solvation by TIP3P was examined. The average structure was calculated from each 50‐ns trajectory of Lyn kinase domain generated with FACTS and the snapshot with the lowest rms deviation to this average structure was used for a trajectory calculated with explicit water. Each starting structure was re‐solvated in a cubic box filled with TIP3P water molecules as well as Na⁺ and Cl^– ions so that the salt concentration is 0.15M. A production trajectory of 50 ns was calculated for each starting structure, yielding a total of nine 50‐ns trajectories with TIP3P using simulation conditions given in the Simulations of Lyn kinase domain subsection.

Computational cost relative to vacuum simulations

Benchmarkings of simulation time obtained per day were carried out for simulations of the Src SH2 domain in vacuum, TIP3P, GBMVII, FACTS, and SCPISM (see Table 1) using two 8‐core Intel Xeon‐E5 processors, totaling 16 cores. As expected, simulations with TIP3P are most computationally expensive. For FACTS and SCPISM, the costs relative to vacuum are comparable to previously calculated costs35, 37 with SCPISM being the most computationally efficient ISM. Compared with previous benchmarking35 in which a peptide was the model system, an improvement in computational efficiency is seen for GBMVII, consistent with the observation23, 24 that the cost relative to vacuum decreases as the system size increases.

Analysis

Positional fluctuations

For simulations of Src SH2 domain, residue averages of the root mean squared (rms) displacement of the N, C, and C_α atoms from their average positions were calculated using the COOR DYNA module in CHARMM and then averaged over forty 10 ns trajectories for each solvent model. For simulations of Lyn KD, residue averages of the backbone rms displacement were averaged over nine 50 ns trajectories.

The time development of backbone positional fluctuations was also determined for the Src SH2 domains solvated in various solvent models. Backbone positional fluctuations were calculated at different time intervals, and then ensemble‐averaged over all residues and all blocks of corresponding lengths from forty 10 ns trajectories. For example, at the 5‐ns interval, the backbone positional fluctuations were calculated and averaged over 102 residues and eighty blocks. The time intervals were 25, 50, 100, 250, 500 ps and 1, 2.5, 5, 10 ns.

All‐against‐all rmsd

An all‐against‐all analysis of rms difference (rmsd) in coordinates was done by comparing the backbone (N, C, and C_α atoms) coordinates of the Src SH2 domain between snapshots taken from trajectories corresponding to an ISM and snapshots taken from TIP3P trajectories. For every pair of snapshots, the protein structures were superimposed prior to calculating the coordinate difference. For each solvent, the distribution of all‐against‐all rmsd was plotted using 0.1 Å bins of rms deviation values ranging from 0 Å to 4 Å.

Ion pair distance distribution

For simulations of the Src SH2 domain, electrostatic interactions were characterized for the ion pairs E157‐R160, E159‐R155, E176‐K152, E178‐R175, D190‐R169, D190‐K200, D192‐K195, and D235‐R217, and for Lyn KD, the ion pairs E310‐K295, E310‐R409, and D404‐K295. Residues from the Lyn KD are numbered to the convention for the Src KD. Distance distributions of ion pairs were generated from positions of the side chains of two charged residues. For amino acid ARG, LYS, ASP, and GLU, side chain positions are defined by the coordinates of the C_ζ atom, the N_ζ atom, the midpoint of O_δ1 and O_δ2 atoms, and the midpoint of O_ϵ1 and O_ϵ2 atoms, respectively.

Relative motion of Lyn kinase N‐ and C‐lobes

The distance between the center of masses (COMs) corresponding to the N‐ and C‐lobes of the Lyn kinase was used to characterize the relative lobe‐lobe motion. The COM was calculated from the masses and coordinates of residues 233 to 322 for the N‐lobe, and residues 323 to 384 and 411 to 504 for the C‐lobe. The flexible A‐loop was excluded from all lobe‐lobe distance analyses. Before the distance calculation, the lobe‐lobe motion was separated from the protein local fluctuation using an algorithm developed and implemented in CHARMM by Roy, Hua and Post (scripts available in Resources at http://post.bio.purdue.edu).

Supporting information

Supporting Information