Successful application of the DBLOC method to the hydroxylation of camphor by cytochrome p450

Abstract

The activation barrier for the hydroxylation of camphor by cytochrome P450 was computed using a mixed quantum mechanics/molecular mechanics (QM/MM) model of the full protein‐ligand system and a fully QM calculation using a cluster model of the active site at the B3LYP/LACVP*/LACV3P** level of theory, which consisted of B3LYP/LACV3P** single point energies computed at B3LYP/LACVP* optimized geometries. From the QM/MM calculation, a barrier height of 17.5 kcal/mol was obtained, while the experimental value was known to be less than or equal to 10 kcal/mol. This process was repeated using the D3 correction for hybrid DFT in order to investigate whether the inadequate treatment of dispersion interaction was responsible for the overestimation of the barrier. While the D3 correction does reduce the computed barrier to 13.3 kcal/mol, it was still in disagreement with experiment. After application of a series of transition metal optimized localized orbital corrections (DBLOC) and without any refitting of parameters, the barrier was further reduced to 10.0 kcal/mol, which was consistent with the experimental results. The DBLOC method to C—H bond activation in methane monooxygenase (MMO) was also applied, as a second, independent test. The barrier in MMO was known, by experiment, to be 15.4 kcal/mol.1 After application of the DBLOC corrections to the MMO barrier compute by B3LYP, in a previous study, and accounting for dispersion with Grimme's D3 method, the unsigned deviation from experiment was improved from 3.2 to 2.3 kcal/mol. These results suggested that the combination of dispersion plus localized orbital corrections could yield significant quantitative improvements in modeling the catalytic chemistry of transition‐metal containing enzymes, within the limitations of the statistical errors of the model, which appear to be on the order of approximately 2 kcal/mole.

Introduction

Cytochrome p450 is an important enzyme superfamily that plays a vital role in drug metabolism, biosynthesis of hormones, and detoxification of xenobiotic compounds, among other biological processes. In a recent article,2 it was estimated that p450 enzymes catalyze the metabolism of well over 75% of drugs; often the toxicity of the drug candidate can be directly linked to the unintended inhibition of a p450. The p450 enzymes catalyze the oxidation of organic substrates and are found in many classes of organisms from bacteria to mammals. The most common reaction facilitated by p450 is the insertion of a single oxygen atom into a C—H bond. This is normally a challenging task in organic synthesis owing to the high energetic costs associated with cleaving such bonds2, 3, 4 and typically requires a catalytic agent to proceed on a measurable timescale under room temperature and pressure conditions.

Experimental efforts to elucidate the mechanism of p450‐catalyzed reactions have been limited by the relatively short lifetimes of many of the oxygenic intermediates produced,2, 3, 4 as well as possible conformational changes in the active site which can be significant for some P450 isoforms and substrates. Computational methods present an attractive approach, complementary to experiment, in this situation. A significant number of density‐functional theory (DFT)‐based studies using both cluster models and full protein‐ligand systems with quantum mechanics/molecular mechanics (QM/MM) have been carried out over the last decade,5, 6, 7, 8, 9, 10, 11, 12 primarily focused on P450cam, a bacterial P450 variant adapted to bind and hydroxylate camphor, for which substantial high resolution structural information is available. As the mechanism of action of p450s is remarkably well conserved across different organisms, conclusions drawn from investigation of P450cam are highly relevant to other P450 enzymes such as those involved in human metabolism.

Computational studies, primarily using DFT methods, have provided a great deal of insight into catalytic chemistry of p450 enzymes, but these investigations have also encountered problems in quantitatively reproducing experimental data. In the rate limiting step of the P450cam catalytic cycle, the catalytically competent compound I (CPD I) species [believed to be in an Fe(IV) oxidation state, with the iron atom bound to a ferryl oxygen] abstracts a hydrogen atom from the C5 position of camphor (as depicted in Fig. 1). The DFT calculations to date (using both cluster and QM/MM models) have systematically overestimated barrier of the cleavage of the C—H bond in this reaction by approximately 5–10 kcal/mol.3, 9, 10 Various improvements in the model, such as inclusion of a key structural water in the active site, reduce the barrier height,9 but not to the point where it is consistent with current experimental estimates. Recently, Harvey and coworkers12 have attributed this discrepancy between theory and experiment to the inadequate treatment of dispersion interactions in hybrid DFT methods such as B3LYP.12 In order to evaluate this hypothesis, they performed a computational study comparing standard B3LYP with B3LYP‐D3, the later referring to an empirically based correction scheme for incorporating dispersion interactions into the B3LYP functional.13 The barrier height computed with B3LYP‐D3 using B3LYP‐D3 optimized geometries was reduced from 14.1 (B3LYP/B3LYP) to 12.1 kcal/mol (B3LYP‐D3/B3LYP‐D3). These calculations show that the inclusion of dispersion effects is clearly relevant to accurate computation of the barrier height, and move the results in the right direction compared with the experimental data. However, the use of a truncated cluster model limits the overall accuracy of the barrier height determination.

Figure 1.

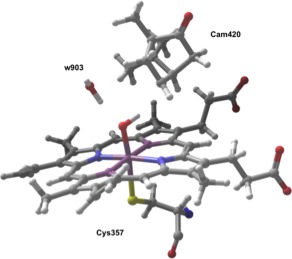
Composition of QM Region for QM/MM investigation. Included in this region are the heme, camphor, the catalytic water (w903), and the coordinated cysteine residue (cys357).

A second possible source of error is intrinsic inaccuracy in the B3LYP functional due to deficiencies other than inadequate treatment of dispersion. Over the past decade, our group has developed a model using localized orbitals corrections, which we have termed DFT‐LOC,14, 15 to address fundamental problems with the treatment of nondynamical correlation in DFT approaches. This method requires a valence bond description of the system, as the corrections themselves are simple additive parameters based on bond type and atomic hybridization states, among other properties from valence bond theory. After evaluating a series of DFT functionals, the performance was found to be optimized when used in conjunction with the B3LYP functional. The LOC method was originally tested against the Pople G2 and G3 sets of atomization energies,16, 17 but has since been successfully extended to a variety of properties including reaction barriers,18 ionization potentials,15 and the thermochemistry of a variety of molecular reactions,19 and provides substantial improvements in accuracy at essential no additional computational cost. For example, the B3LYP mean unsigned error (MUE) in atomization energy in the G3 data set was reduced from 4.8 to 0.8 kcal/mol, while the MUE for ionization potentials and electron affinities in the G2 data set was reduced from 0.137 to 0.039 eV.15 A description of the LOC model including its theoretical basis and current implementation is presented in detail in Refs. 14 and 15.

We have since extended the scope of the LOC method to transition metals, using localized 3d orbital corrections. This new model has been termed B3LYP‐DBLOC.20, 21, 22 The parameters in the DBLOC model are assigned based on a ligand field description of the system. DBLOC parameters have been developed for redox reactions,20 spin splittings,22 and ligand removal enthalpies.21 Typical MUEs for the model are in the range of approximately 0.1 eV; for example, the MUE in redox potentials across 95 organometallic complexes were reduced from 0.4 to 0.12 eV, via the use of seven fitting parameters in the DBLOC model. More recently,23 we successfully applied the LOC/DBLOC method to the challenging problem of predicting first‐row, hexaaqua transition metal pKas. Without any refitting of the previously determined B3LYP‐DBLOC parameters, the MUE over a series of 10 such complexes is reduced from 4.8 to 0.9 pKa units.

In previous work, we estimated DBLOC corrections for the P450 hydrogen atom abstraction, and determined that (as in the case of dispersion as noted above), the DBLOC model moves the P450 barrier height toward the experimental results. However, these calculations did not incorporate dispersion effects. In the present article, we carry out a full scale QM/MM modeling of P450, incorporating both DBLOC corrections and dispersion into the model, in an effort to provide a benchmark result for the hydrogen atom abstraction reaction that can be fairly compared with experimental data. We also investigate a second system, methane monooxygenase (MMO), which has a similar hydrogen atom abstraction reaction as a key step, although the non‐heme iron core of MMO is chemically quite different from the porphyrin at the heart of P450 catalysis. MMO has also attracted a number of computational studies in recent years.24, 25, 26, 27, 28, 29 The process is very similar to that of p450cam, involving a single reduction of a Fe(IV) center.30 By examining the effects of dispersion and DBLOC corrections on MMO hydrogen atom abstraction, we provide a second data point to calibrate whether these more sophisticated DFT models improve agreement between theory and experiment in a consistent fashion.

Results

P450cam barrier calculations

For our QM/MM study, we utilized a previously prepared protein‐ligand system for p450cam taken from our earlier work on p450cam, which was based on an x‐ray crystal structure from the PDB (PDB ID: 1DZ9). A detailed image of the active site is shown in Figure 2. For consistency, we construct a similar QM region from this earlier work, which consists of the heme porphyrin, camphor, catalytic water w903, and the entire cys357 residue. The importance of this water was demonstrated in a previous study.12 We encountered some technical issues when this water was not included in the QM region, so it is included here; there is an implicit assumption in this treatment (as in previous work) that the water is a structural water which would have a high occupation probability in the location used in our model. In this work, we limit our investigation to the doublet reaction surface, as the doublet and quartet barriers have been shown to be very similar. The QM/MM interface is handled using a frozen orbital approach with a total of two frozen orbital cuts. The total QM region consisted of 136 atoms. We believe that this QM region is of sufficient size to yield useful results.

Figure 2.

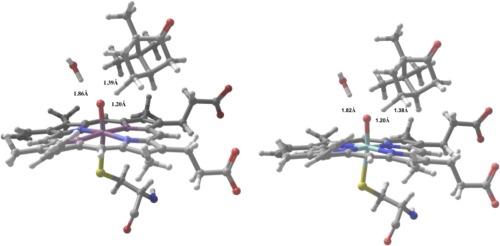
(a,b) Computed TS structures for camphor C—H activation showing B3LYP/LACVP* (2a, left) and B3LYP‐D3/LACVP* (2b, right).

The transition state (TS) of the hydrogen atom abstraction was located by performing an adiabatic potential energy scan along the hydrogen abstraction pathway, starting from an initial guess based on previous work of 1.2 Å for the O—H distance. At each point, we performed a constrained geometry optimization where the O—H distance was frozen. Using the latest version of the Qsite31 software at the time that the calculations were performed, it was not possible to perform vibrational frequency calculations in order to determine the zero point energy (ZPE) contribution to the reaction barrier when the QM/MM partitioning is handled using frozen orbitals. In our previous study,7 the ZPE was estimated by making the assumption that it would be dominated by the reaction coordinate. In this way, a value of −3.5 kcal/mol was determined. We use the same value in our QM/MM study, and are thus able to estimate the free energies of hydroxylation. However, in the cluster model, we are able to compute vibrational frequencies directly and report free energies in the results and we are able to show that the ZPE is well estimated in the QM/MM model.

In addition to our QM/MM study, we performed a parallel investigation of the p450cam barrier using a cluster model and a fully QM treatment of the enzyme active site. The cluster model was taken from our QM region in the QM/MM study where the cys357 coordinating residue has been replaced with a —SH group (Fig. 3).

Figure 3.

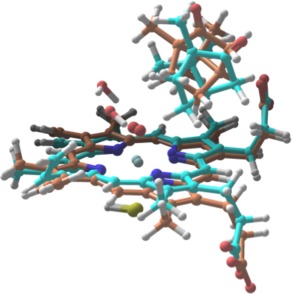
Computed TS structures with full QM based on cluster model of p450cam active site. The orange structure shows the TS structure computed with B3LYP, while the TS structure obtained with B3LYP‐D3 is shown in cyan.

The complete list of computed barriers for both the QM/MM model and the cluster model of P450cam, with and without dispersion and DBLOC corrections, are presented in Table(s) I and II. As can be seen in Tables 1 and 2, the barrier is lowered for both the QM/MM and cluster models by the use of the larger basis set. The larger basis set may be more necessary to fully describe the wavefunction at the strained transition state geometry than as opposed to the reactants and products. The discrepancy with regard to the amount that the barrier is lowered for the two models (1.9 kcal/mol for the QM/MM model vs. 3.2 kcal/mol for the cluster model) is less obviously rationalized, although significant enough that there likely is a systematic explanation.

Table 1.

QM/MM Computed Barrier Heights for C—H Bond Activation in Camphor Comparing B3LYP and B3LYP‐D3 Along With DBLOC Correction

Method	ΔE TS	ΔE TS + ZPE	ΔE TS + ZPE + DBLOC
B3LYP/LACVP*/LACV3P**	21.0	17.5	15.2
B3LYP‐D3/LACVP*/LACV3P**	16.8	13.3	10.0
B3LYP/LACVP*	22.9	19.4	16.1
B3LYP‐D3/LACVP*	18.8	15.3	12.0

All energies in kcal/mol.

Table 2.

QM Computed Barrier Heights for C—H bond Activation in Camphor Comparing B3LYP and B3LYP‐D3 With and Without DBLOC Corrections Using the Cluster Model

Method	ΔG TS	ΔG TS + DBLOC
B3LYP/LACVP*/LACV3P**	17.6	15.3
B3LYP‐D3/LACVP*/LACV3P**	10.4	8.2
B3LYP/LACVP*	20.8	18.6
B3LYP‐D3/LACVP*	13.9	10.6

All energies in kcal/mol.

As can also be seen in Tables 1 and 2, dispersion lowers both barriers as well, although in this case the effect is much larger in the cluster model than in the QM/MM model. There are a number of potential reasons for this difference. Dispersion stabilizes the transition state relative to the reactants because it packs the atoms of the substrate and porphyrin ring in the TS geometry more tightly; the average distance between neighboring non‐bonded atoms is significantly diminished in the TS geometry (which is very similar in both the B3LYP and B3LYP‐D3 calculations). However, the effect is diminished in the QM/MM model, because the atoms of the substrate move further away from other atoms of the protein with which they were initially in van der Waals contact in the reactant geometry. The total change in van der Waals energy is therefore smaller in the QM/MM environment, because interactions with atoms not present in the cluster model decrease as the TS is formed, and thus oppose the additional stabilization provided by the TS packing with the porphyrin ring. This behavior is quantified in Table 3, which decomposes the dispersion interaction into components representing interactions between different groups of atoms (atoms in the porphyrins, atoms in the camphor, and other atoms exclusive to the QM/MM model). The difference in the extent of the barrier lowering for the cluster model and the QM/MM model is 2.9 kcal/mol. The sum of the contributions of those atoms not included in the cluster model with that of the full QM/MM model is 1.9 kcal/mol. The change in the interactions between the camphor, porphyrin, and other atoms exclusive to the QM/MM model, when the QM/MM representation is used as opposed to the cluster model, accounts for most of the difference in the change in the barrier height. This suggests that the discrepancy concerning the impact of dispersion corrections on the two models is likely due to the loss of these interactions involving atoms not included in the cluster model.

Table 3.

Contribution of Dispersion Interactions Involving Additional Receptor Atoms Not Included in the QM Cluster Model and the Camphor and HEM Groups, to the Barrier Height (B3LYP‐D3/LACVP*/LACV3P**)

	Receptor atoms only in QM/MM model	HEM	CAM
Receptor atoms only in QM/MM model	−0.06	−0.85	−0.98
HEM	−0.85	−0.40	−0.84
CAM	−0.98	−0.84	0.01

Finally, a more detailed analysis of the cluster model reveals significant changes in structure with and without the van der Waals term. In contrast with our QM/MM study, where the computed TS structures for both B3LYP and B3LYP‐D3 were nearly identical, in the cluster model there are large differences in the positions of the heme side chains, the catalytic water, and the orientation of the camphor. These structural changes result from a lack of environmental constraints in the cluster model, which are present in the full enzyme active site.

MMO barrier calculations

Gherman and Friesner29 investigated the hydroxylation of a series of substrates by the hydroxyl part of a MMO in a QM/MM study. For hydrogen atom abstraction from methane, they reported an MUE from experiment of 3.2 kcal/mol. It should be noted that the estimation of an experimental barrier height in this system requires some processing of the experimental data, as is discussed in detail in Ref. 28. The hydrogen atom abstraction reaction is similar to that carried out by p450cam (including the PCET aspect of the reaction), however, the ligands of the Fe atom are different, enabling a straightforward test of the impact of the DBLOC corrections, and the incorporation of a dispersion model into the DFT, discussed above.

MMO is a non‐heme, diiron enzyme. The catalytically competent species responsible for activating the substrate C—H bond is a diiron(IV) intermediate, referred to as Q in this work. A model of Q, taken from Ref. 26, is shown in Figure 4. The total DBLOC correction for this system was −3.05 kcal/mol. When this correction is added to the barrier reported in Ref. 29, the predicted free energy barrier becomes 15.6 kcal/mol, which is very close to the experimental value. The authors of the study in Ref. 29 do not include any dispersion corrections. We incorporated those corrections to the predicted barrier, but did not perform a full QM/MM investigation of the barrier as was done in p450, as this had been well documented in Ref. 29. Instead, for the purposes of computing the dispersion correction, we simply re‐optimized the transition state and reactant geometries at the level of theory used in this work. The system was partitioned similarly to Ref. 29, and included the methane group, diiron center, and other nearby residues for a total of 220 atoms. The total dispersion correction is small in this case (as the methyl group is much smaller than camphor) and lowers the barrier by a further 1.2 kcal/mol. If this correction is added to the DBLOC corrected barrier, we obtain a result of 13.2 kcal/mol, as compared with the experimental value of 15.4 kcal/mol. The absolute deviation against experiment is reduced to 2.2 kcal/mol. Agreement with experiment that is this close is fortuitous; however, we again observe that the DBLOC and dispersion corrections improve the result as compared with a standard B3LYP calculation.

Figure 4.

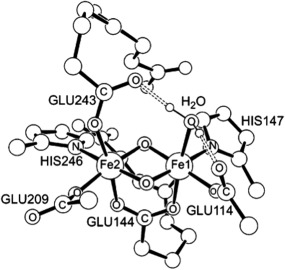
A model of the catalytically competent species in methane hydroxylation by MMO. Taken from Ref. 26. Hydrogens atoms are omitted for clarity.

Discussion

With the application of both the dispersion and DBLOC corrections at the B3LYP‐D3/LACVP*/LACV3P** level of theory, we arrive at a barrier height of 8.8 kcal/mol for the hydrogen atom abstraction reaction in the P450cam catalytic cycle. A kinetic investigation conducted by Rittle and Green4 establish a lower limit on the rate constant of C—H activation of k less than or equal to 210 per second, which corresponds to a barrier height less than or equal to 10 kcal/mol.4

The results presented above demonstrate that the identification of CPD(I) as the reactive intermediate for hydrogen atom abstraction and hydroxylation in the P450 catalytic cycle is consistent with the experimental data for the reaction rate. Previous DFT models overestimated the barrier height, due to both errors in the energetics of the reduction of the heme iron atom by the electron from hydrogen, which is completed at the transition state and to neglect of dispersion interactions in the QM region of the QM/MM calculation. The combined magnitude of these effects, estimated here to be 7.5 kcal/mol, is significant. Similarly, the results for MMO yield an overall 5.6 kcal/mol correction, which brings theory into quantitatively better agreement with experiment.

These results were obtained without the use of any new adjustable parameters; all of the parameter values were taken from prior work on the LOC and DBLOC models, and used as is. There are choices that have to be made regarding atom type assignment, most importantly for the porphyrin ring nitrogens. Such assignments are the most challenging aspect of applying the LOC and DBLOC models to new systems. However, they usually can be addressed by a detailed investigation of the electronic structure, as was done in this case by performing the Mulliken population analysis. There may be some anionic nitrogen character in the wavefunction; this would increase the correction term, and thus lower the predicted barrier, but by a relatively modest amount, which would not lead to inconsistency with experiment. For MMO, there are no such ambiguities, and the results can be regarded as a well‐defined test of the methodology, one that yielded a quite successful outcome. While many more such tests will be required to fully validate the LOC/DBLOC correction scheme, these results, in combination with a similarly successful application to TiO₂ nanoparticles32 provide an encouraging starting point.

Materials and Methods

Overview of computational methodology

All QM/MM calculations in this work were performed with the Qsite31 electronic structure program of Schrodinger, Inc. Qsite is a general‐purposed QM/MM program combining the Jaguar electronic structure program with Impact, a molecular mechanics program. All QM calculations were performed using Jaguar v.8.0. We estimate dispersion effects within the QM region using a modified version of the B3LYP‐D3 model of Grimme and coworkers.13 The modification involves damping the dispersion term for 1–2 and 1–3 interactions where the atoms are very close together. This is in line with standard molecular mechanics treatments of dispersion. Finally, localized orbital corrections are assigned using the B3LYP‐LOC and DBLOC models described in previous work.14, 19, 20, 21, 22 Details of the parameter assignments for both p450cam and MMO are given in this section below.

Assignment of DBLOC parameters

The B3LYP‐DBLOC method provides localized corrections to account for changes to the electronic structure of the metal‐ligand system. In this work, C—H bond activations in Cytochrome p450 and MMO were discussed. The DBLOC method provides corrections for redox potentials which have been fit to a database of 95 model organometallic complexes containing first row transition metals. Determining the total DBLOC correction in each case is simply a matter of summing the individual DBLOC corrections, which are assigned based on a ligand‐field theory description of each system. The individual corrections, themselves, are determined both by the nature of the redox process and the relative position of each ligand on the spectrochemical series. In both systems, an Fe center undergoes a single redox process from Fe(IV) to Fe(III). A key point is that this electron transfer is completed by the time the hydrogen to be abstracted reaches the transition state; thus, what appears at first glance to be an H atom abstraction is actually a proton‐coupled electron transfer (PCET) reaction, in which electron transfer is followed by completion of proton transfer. In order to characterize changes to the electronic structure of the iron center, we must understand the process in terms of ligand field theory. As the relative position on the spectrochemical series of the ligands coordinated to the Fe center that undergoes reduction are different in p450 and MMO, the parameter assignment is also different. We discuss the specific assignment of DBLOC parameters in both systems below.

Assignment of DBLOC parameters to cytochrome p450

For P450, the lone iron center of the heme molecule undergoes a single‐electron reduction from Fe(IV) to Fe(III). Within the context of ligand‐field theory, this is equivalent to bringing an additional electron from infinite separation to the d‐manifold of the iron center. The current DBLOC corrections are independent of whether the electron goes into a t_2g or an e_g orbital, and whether that orbital is empty or half filled. A more accurate parametrization could likely be produced by taking the final orbital the electron arrives at into account, however, this would necessitate the introduction of a significant number of additional parameters, which in turn would require more training set data to avoid overfitting.

The appropriate parameters for this process are taken from the DBLOC redox paper20 and describe an infinity ‐> metal d orbital transfer of a single electron from the perspective of a ligand on the left (relss), middle (remss), or right(rerss) of the spectrochemical series. In order to determine which of the three corrections are appropriate for each ligand, it is necessary to make individual qualitative assignments to the left, middle, and right of the spectrochemical series. The assignments are straightforward with the exception of the four nitrogen atoms in the porphyrin. The cys357 residue, which is coordinated through an anionic sulfur, is determined to be on the left of the spectrochemical series, and therefore the relss parameter is applied. In a similar fashion, the ferryl oxygen atom is determined to be in the middle of the spectrochemical series, and the rmss parameter is applied. These assignments are in agreement with those discussed in Hughes and Friesner.22

Assignment of the ring nitrogens coordinated to the Fe is more complex. In previous work,20 we employed two aromatic nitrogen parameters and two anionic nitrogen parameters, based on the −2 charge that is formally assigned to the porphyrin ring in Compound I. Note that this assignment is qualitative and is equivalent to that of a single nitrogen in a resonant state with an average of such parameters. However, it is not clear what fraction of that charge is actually on the ring as opposed to associated with the Fe atom; furthermore, the charge that is on the ring is likely to be distributed throughout the macrocycle rather than residing primarily on the nitrogen atoms. To provide further insight, we performed a Mulliken population analysis on our QM cluster model of p450cam and compared the charges on the nitrogens with that of a reference system, free base porphyrin. Porphine has no metal atom and is charge neutral. Table 4 shows the charges on each ring nitrogen in our system and in porphine. The maximum deviation of the partial charges from their average value among the ring nitrogens in the p450 cluster model is only 0.01 units, suggesting that the state of the nitrogen atoms with regard to charge is similar in both structures. Based on this result, we have assigned all four of the nitrogens as aromatic, leading to the use of the remss correction parameter as an aromatic nitrogen is in the middle of the spectrochemical series. This represents a revision of the parameters used in previous work20 discussed above. Use of the anionic nitrogen parameters would result in a lower value of the barrier than what we report below, and thus would not be inconsistent with experiment; however, we believe that in view of the Mulliken population results, treating the four nitrogens as aromatic represents our best estimation of the appropriate DBLOC correction parameters at present.

Table 4.

Mulliken Partial Charges on Aromatic Nitrogens in the p450cam Cluster Model and Porphine Computed at the B3LYP‐D3/LACVP*/LACV3P** Level of Theory

	p450cam (cluster)	Porphine
N(1)	−0.43	−0.44
N(2)	−0.45	−0.49
N(3)	−0.44	−0.49
N(4)	−0.43	−0.44

Summarizing the above discussion, and further assigning parameters for the hydrogen abstraction itself based on B3LYP‐LOC, we make the following parameter assignments. For the oxygen atom (1) we apply the remss parameter 0.08 V For the cys357 (2) residue, we apply the relss parameter (−0.04 V) for an anionic sulfur (left spectrochemical series). The corrections for these atoms agree with those used in our previous work to describe part of the p450cam correction. We make the approximation that the ligand field created by each of the four coordinated nitrogens is the same. Furthermore, we identify an aromatic nitrogen atom as being in the middle of the spectrochemical series. Thus, we stipulate that the correct DBLOC parameter assignment for these four nitrogen atoms involves the remss parameter (4 * 0.08).

Next, we apply an LOC correction to properly account for radical formation at C5, based on the parametrization described in Ref. 14. The LOC radical delocalization parameters are applied on a per bonded atom basis. For the lone hydrogen bonded to C5 after hydrogen abstraction, we apply the RH parameter of 0.52 kcal/mol, and for the two carbons bonded to C5 (C4 and C6), we apply the RA parameter for bonded atoms in the first and second period, which is 1.65 kcal/mol.

Finally, we apply the parallel spin correction described in Ref. 20. We used a low spin model for our P450 calculation, so the additional electron from the hydrogen goes into a half filled t_2g orbital, and diminishes the number of interacting parallel spin pairs by one. The value of the correction is −0.05 eV, or 1.4 kcal/mole. The total DBLOC correction (obtained by adding all of these terms together) then becomes 0.25 V or 3.3 kcal/mol.

Assignment of DBLOC parameters to MMO

The reaction in MMO is identical to that of p450cam and features an Fe(IV) ‐> Fe(III) reduction of Fe2. From a ligand field perspective, Fe2 undergoes a ∞ ‐> t_2g reduction. Hence, the application of the relss, remss, and rerss DBLOC parameters as correction terms are appropriate. In order to apply the DBLOC method to this process, it is first necessary to properly characterize each ligand. The ligands coordinated to the iron that is reduced are three glutamic acid residues (GLU209, GLU144, and GLU243), one histidine (HIS246), and a pair of bridging oxygens. The three glutamic acid residues are coordinated through the carboxylate groups. A carboxylate is identified in the DBLOC model as a ligand on the left side of the spectrochemical series. Thus, the correction for each of these ligands is −0.04V. The lone histidine ligand is coordinated through a nitrogen atom, which is identified as a ligand in the middle of the spectrochemical series, so the remss parameter of 0.08 V is used. Finally, for the two bridging anionic oxygen atoms, which are located on the right of spectrochemical series, the rerss parameter of 0.12 V is applied. Thus, the total DBLOC correction becomes 3 * (−0.04) + 0.08 + 2 * 0.12 = 0.20 eV or −4.6 kcal/mol, where the change in sign arises from G = −nFE. Finally, we also add an LOC radical delocalization correction for methane. This radical is delocalized over the three hydrogens on the methyl radical. The correction for each hydrogen is 0.52 kcal/mol yielding a total of 1.56 kcal/mol.

As in the case of the cytochrome P450 hydrogen atom abstraction reaction, we need to calculate corrections due to changes in parallel spin interactions. In this case, we used a high spin model for the initial Fe(IV) MMO state (see Ref. 29 and references therein for further discussion). There are four electrons in the ligand field diagram of the initial state, three in the t_2g manifold and one in an e_g orbital. The additional electron goes into the e_g state, creating one additional parallel spin pair (we do not consider pairings between electrons in different manifolds). This leads to a correction of the opposite sign as compared with P450, lowering the computed barrier by 1.4 kcal/mol.

We also compute the dispersion correction for the methyl group to the barrier with Grimme's DFT‐D3 model. In our experience in developing our own correction scheme for dispersion interactions in DFT, B3LYP‐MM, we found it necessary to exclude 1,3 atom interactions as they are already well described by the DFT. As the hydrogen abstraction process in MMO features a late transition state, the distance between the hydrogen and the acceptor oxygen atom is near‐covalent in length in our computed transition state. We explicitly subtract the contribution from 1,3‐interactions involving the abstracted hydrogen atom and the heme molecule. When this is done, the total dispersion correction to the barrier is small, as expected, lowering the barrier by 1.2 kcal/mol. If this correction is added to the LOC corrected barrier, we obtain a result of 13.2 kcal/mol. The absolute deviation against experiment obtained is 2.3 kcal/mol. This represents a modest improvement on the original, uncorrected B3LYP result, but does demonstrate that application of DBLOC again produces a physically reasonable result, on the order of the statistical errors estimated for the method in the model system studies (on the order of 2 kcal/mol). We also note that the impact of 1–3 interactions involving the abstracted hydrogen in p450‐cam to the total dispersion correction to the barrier were negligible.

Supporting information

Supplementary Filenames: Coordinates and Jaguar/QSite input parameters for calculations in this work (support_info_pka_paper_formatted.pdf)