Molecular dynamics simulation of triclinic lysozyme in a crystal lattice

Abstract

Molecular dynamics simulations of crystals can enlighten interpretation of experimental X‐ray crystallography data and elucidate structural dynamics and heterogeneity in biomolecular crystals. Furthermore, because of the direct comparison against experimental data, they can inform assessment of molecular dynamics methods and force fields. We present microsecond scale results for triclinic hen egg‐white lysozyme in a supercell consisting of 12 independent unit cells using four contemporary force fields (Amber ff99SB, ff14ipq, ff14SB, and CHARMM 36) in crystalline and solvated states (for ff14SB only). We find the crystal simulations consistent across multiple runs of the same force field and robust to various solvent equilibration schemes. However, convergence is slow compared with solvent simulations. All the tested force fields reproduce experimental structural and dynamic properties well, but Amber ff14SB maintains structure and reproduces fluctuations closest to the experimental model: its average backbone structure differs from the deposited structure by 0.37Å; by contrast, the average backbone structure in solution differs from the deposited by 0.65Å. All the simulations are affected by a small progressive deterioration of the crystal lattice, presumably due to imperfect modeling of hydrogen bonding and other crystal contact interactions; this artifact is smallest in ff14SB, with average lattice positions deviating by 0.20Å from ideal. Side‐chain disorder is surprisingly low with fewer than 30% of the nonglycine or alanine residues exhibiting significantly populated alternate rotamers. Our results provide helpful insight into the methodology of biomolecular crystal simulations and indicate directions for future work to obtain more accurate energy models for molecular dynamics.

Introduction

Molecular dynamics (MD) simulations of protein and nucleic acid crystals are poised to offer significant contributions to two fields: experimental crystallography and computational chemistry. Crystallographic methods have played an immense role in providing detailed biomolecular structural information and have been fundamental in the development of our understanding of the structure‐function relationship. At the same time, crystallographic models can display an overreliance on static representations of biomolecular structure, despite the fact that biomolecules are both dynamic and heterogeneous.1, 2, 3, 4, 5, 6, 7 Current models for protein function increasingly rely on an ensemble‐based view where a statistical distribution of conformations exhibiting fluctuations around energy minima is modified upon binding events. This ensemble‐based heterogeneity and dynamic behavior is also present in biomolecular crystals.8, 9 Efforts in recent years have sought to elucidate and account for these aspects of crystals that are often hidden in the time and space averaged diffraction data.10, 11, 12, 13, 14, 15, 16 Molecular dynamics simulations of crystals can contribute to this effort. Past work has shown that MD is in principle capable of accurately reproducing experimental diffraction data while offering a time resolved glimpse of the hidden inner life of crystals.17

Simulations of biomolecular crystals also provide an excellent arena for validation of the procedures and force fields used in such simulations.18, 19 Crystal simulations have a long history,20, 21, 22, 23, 24, 25, 26 but convergence is slow (as we illustrate below), it can be difficult to model disordered solvent, and modeling lattice disorder requires simulations that encompass many unit cells. We have developed a methodology for all‐atom molecular dynamics of biomolecular crystals employing modern force fields (with explicit solvent and ions) to represent the interactions within crystals.17, 18, 27, 28, 29 To help guide future work we have undertaken an evaluation of four modern force fields on the molecular dynamics of a protein crystal. HEWL, an enzyme of 129 amino acids, was chosen as the host crystal, since it is one of the most commonly studied proteins. A number of experimental studies have been carried out to investigate HEWL crystal packing and flexibility via structural and dynamic properties.30, 31, 32, 33, 34 Several earlier computational studies focused on conformational differences in solution and in the crystalline environment35, 36, 37 as well as solvent and ion mobility in crystals.38, 39 We constructed a supercell composed of 12 unit cells of triclinic hen egg‐white lysozyme (HEWL, PDB:4LZT)40 with explicit solvent. In total we performed more than 9 μs of molecular dynamics sampling of the crystal lattice equivalent to more than 100 μs sampling of the lysozyme monomer. The results offer insight into both the strong and weak points of the current force fields and more generally into the accuracy of results that can be expected from crystal simulations using popular current force fields.

Results

The crystal supercell was set up as shown in Figure 1 and described in detail in Methods. In all we performed the set of simulations shown in Table 1. Whenever not specifically identified below, ff99SB and ff14SB refer to the first μs of each simulation (for consistency with the other 1 μs simulations).

Figure 1.

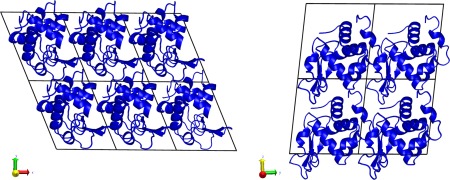
Simulation setup of the HEWL supercell. The P1 space group unit cell was extended three times along the crystallographic a axis and two times each along the b and c axes. Addition of solvent is described in Table I.

Table 1.

Molecular Composition and Basic Statistics of the Simulated Systems

	Exp.	ff99SB	ff14SB	ff14ipq	C36	ff14SB_solv
Protein molecule	—	12	12	12	12	1
Force field		Amber ff99SB	Amber ff14SB	Amber ff14ipq	Charmm 36	Amber ff14SB
Solvent model	—	tip3p	tip4p‐ew	tip4p‐ew	tip3p	tip4p‐ew
Water (H2O)	55.5M	3358	3358	3278	3268	9375
Acetate (CH3COO−)	100 mM	39	39	39	39	‐
Nitrate ( ${\text{NO}}_3^{-}$)	250 mM	91	91	91	91	‐
Sodium (Na+)	250 mM	22	22	22	22	8(Cl‐)
Total atoms	—	34,265	34,265	34,025	33,995	39,468
Density (g/cm3)		1.281	1.281	1.274	1.273	1.019
Equilib. length (ns)	—	176	176	196	196	28
Production length (ns)	—	3000	3000	1000	1000	1000
Mean press. (bar)	1	129 ± 323	−25 ±322	−22 ± 304	82 ± 310	0.8 ± 141
Mean trajectory RMSD (Å)	—	0.75/1.27	0.65/1.15	0.76/1.25	0.78/1.37	0.95/1.47

Last line provides the mean instantaneous backbone atom/all heavy atom RMSD after optimal alignment to the deposited model as a reference over the course of each trajectory.

Structure

The root mean square deviation (RMSD) is a measure of structural similarity between two sets of atomic coordinates (Fig. 2). Following previous work,17, 18 two types of RMSD metric were calculated. “Best‐fit” RMSD is calculated by rotating and translating each monomer snapshot to optimize agreement with the experimental structure. “Lattice” RMSD is calculated by using the crystal symmetry and translation operations to move all snapshots to the same unit cell, but without rotational‐translational optimization for a best fit. Thus, best‐fit RMSD only includes contributions from intramolecular fluctuations, whereas lattice RMSD includes both intramolecular fluctuations and also contributions from the intermolecular motion of protein monomers relative to each other within the crystal lattice. As expected, crystal simulations give lower RMSD values vs. experiment compared with the solvated molecular dynamics simulation (Table 1, Fig. 2). The closest agreement to the experimental model is obtained with ff14SB.

Figure 2.

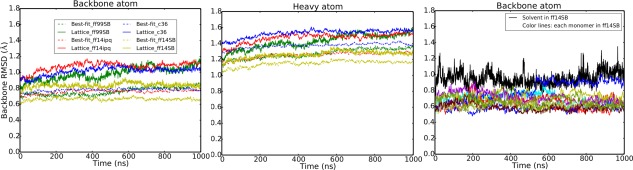
RMSD for four different force field simulations and comparison with solution simulation. Left hand panel shows backbone atom RMSD; middle panel shows all heavy atom RMSD. Dotted lines show best‐fit and solid lines show lattice RMSD (see text and Ref. 17 for more details). Black line in right panel represents the best‐fit backbone RMSD of the liquid state simulation (ff14SB_solv). Colored lines show the best‐fit backbone RMSD of each monomer in the ff14SB crystal simulation. The final 1000 ns of each simulation are shown (first 160–180 ns of each simulation were discarded to allow the systems to equilibrate).

Furthermore, the RMSD results indicate that convergence towards equilibrium in crystal simulations is slower than in typical solvated simulations. Results of several additional microseconds of simulation to test equilibration times and reproducibility of results are presented in the Supporting Information. In particular, we find that the ff99SB crystal simulation does not reach convergence until more than 1 μs of simulation (Supporting Information Fig. 2). On the other hand ff14SB RMSD converges after about 250 ns.

For each simulation we also calculated the average protein structure and its RMSD to the experimental model. Results are shown in Table 2. Consistent with previous crystal simulations, RMSDs of the average structures are significantly lower than those from a similar solution simulation and are also lower than the average instantaneous RMSD discussed above. This is not surprising, as the RMSD of an ensemble average must be smaller than the average of the corresponding instantaneous RMSDs;41 both sorts of statistic are commonly used (here and elsewhere) in characterizing ensembles of structures. The instantaneous RMSD in the solution simulation also deviates more, sometimes making short‐lived excursions of about 0.3 Å above the mean value. By comparison (Fig. 2, third panel) crystal simulations have lower and more stable RMSD without the excursions seen in solution. Among the force fields, ff14SB and ff14ipq simulations most closely reproduce experimental data (0.37/0.79 backbone/heavy atom best‐fit RMSD for ff14SB and 0.40/0.77, respectively for ff14ipq). Interestingly, ff14ipq average structure heavy atom RMSD is the lowest of the four simulations even though the instantaneous heavy atom RMSD for ff14ipq (Fig. 2) was consistently higher. As in previous studies17, 29 a larger degree of conformational variation is sampled by the molecules at any given moment in the simulation (instantaneous backbone RMSD 0.65–0.78, Table 1) even though the average coordinates are much closer to the experimental values (average backbone RMSD 0.37–0.47, Table 2).

Table 2.

Average Structure and Average Electron Density Statistics Calculated Directly from Simulation and After Refinement of the Experimental Model into the Simulation Average Electron Density

	Simulation				Refinement
	Backbone RMSa	Heavy atom RMSDb	Elec. density R‐factorc	MapCCd	R‐worke	R‐freee	Backbone RMSDf	Heavy atom RMSDg
ff99SB	0.41	0.84	46.4	0.547	18.5	19.9	0.39	0.56
ff14ipq	0.40	0.77	86.3	0.511	22.5	26.0	0.37	0.67
C36	0.47	1.00	83.7	0.515	18.3	19.7	0.46	0.79
ff14SB	0.37	0.79	46.6	0.588	15.1	16.0	0.38	0.79

^aBackbone atom RMSD of the average simulated structure compared with the experimental model.

^bHeavy atom RMSD of the average simulated structure compared with the experimental model.

^cR‐factor of the amplitudes from the simulation average electron density and the experimental model.

^dMap correlation coefficient of the simulation average electron density map and the experimental model map after optimal translation using phenix.get_cc_mtz_pdb and phenix.get_cc_mtz_mtz.

^eR‐work and R‐free statistics after fifteen macrocycles of standard refinement and one round of manual rebuilding of the experimental model into the simulation average electron density.

^fBackbone atom RMSD of the model refined into the simulation average electron density and the experimental model.

^gHeavy atom RMSD of the model refined into the simulation average electron density and the experimental model.

Simulations of crystals permit comparison directly against observed experimental data. We calculated the average electron density and corresponding structure factors from each simulation (using the asymmetric unit alignment and electron density averaging methods outlined in Ref. 17). Comparison against the experimental model (Table 2) is consistent with RMSD conclusions: ff14SB agrees more closely with experiment. We furthermore refined the experimental model against the average electron density from each simulation by a limited procedure of 10 automated macrocyles of reciprocal space coordinate and isotropic B‐factor refinement in phenix.refine,42 followed by a limited manual rebuilding in COOT43 aimed at removing the most flagrant disagreements with electron density, and followed by a further five macrocyles of standard automated refinement. The resulting models are arguably the most representative structures of each simulation17 and avoid the structural artifacts of direct coordinate averaging. RMSDs of the resulting structures (Table 2) are consistent with those of the average simulation structures, with backbone atom RMSD varying between 0.37Å and 0.46Å. R _free values for the refinements against simulation density vary from 16.0% for ff14SB to 26.0% for ff14ipq. Interestingly, the R _free statistic obtained for the ff14SB simulation is close to the experimental R _free for PDB:4LZT which was 14.7%. It should be noted that the refinements performed here were limited and without refinement of anisotropic atomic displacement parameters. This was done for consistency in order to place the refinements against the density obtained with each of the four force fields on comparable footing. A more exact refinement approach with the use of anisotropic atomic displacement parameters and ordered solvent would likely bring the ff14SB R _free very close to the experimental value.

The secondary structure of lysozyme (shown in Fig. 3) has three β‐strands (β1, β2, β3), four α‐helices (α1, α2, α3, α4), and four 3₁₀ helices (G1, G2, G3, G4). Figure 3 shows mean stability of these secondary structure elements during the simulations. All the force fields consistently maintain the α‐helical structures, although there is a uniform tendency to unravel the helix termini, particularly the C‐terminus, in favor of turn or 3₁₀ helical conformations. The situation is markedly different for the 3₁₀ helices. Helix G1 is poorly maintained by all of the force fields, from about 25% of the time with ff14SB to about 10% of the time with C36. Helix G3 is well maintained by all the Amber force fields but unravels about 50% of the time with C36 in favor of a turn conformation. A similar situation occurs with Helix G4, although here there is also a tendency of all force fields to lose the N‐terminus (maintained 80% of the time with ff14SB but only 10% of the time with C36). β‐sheet structures are well maintained by all of the force fields but most strongly by C36. In summary, α‐helices tend to be understabilized at termini (ff99SB and ff14ipq understabilize the most; ff14SB and C36 the least) and all force fields tend to understabilize 3₁₀ helices (C36 and ff99SB the most, ff14ipq and ff14SB the least). These results may provide helpful insights into future development of the respective force fields.

Figure 3.

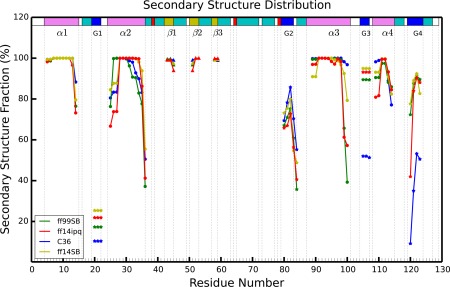
Comparison of secondary structure elements during each of four different force field simulations. Residue numbers are on the x‐axis and percentage of simulation time spent in a particular type of secondary structure is on the y‐axis. Each simulation is represented by a different color and each type of secondary structure is shown by a different geometric figure (α, β, and G are alpha helix, beta sheet, 3₁₀ helix, respectively).

Fluctuations

In addition to structural accuracy of the average atomic coordinates in the simulation, it is important to consider the fluctuations around those mean positions. Furthermore, atomic root mean square fluctuations (RMSF) can be directly compared with the atomic B‐factors determined during the crystallographic structural refinement. As in previous work17, 18 we calculated two sets of fluctuations, “best‐fit” which account for intramolecular fluctuations in the atomic positions and “lattice” which also include contributions from intermolecular fluctuations in the crystal lattice. “Best‐fit” fluctuations are calculated by first rotationally and translationally fitting all monomer snapshots to a reference structure to minimize RMSD, finding the average coordinates of that set of fitted snapshots and then calculating fluctuations around that average; this monitors intramolecular atomic movement around a mean position. “Lattice” fluctuations are calculated by first aligning each supercell snapshot by center of mass and then applying the crystal symmetry and lattice translation operations to bring all monomers into the space of a common asymmetric unit. No RMSD‐minimizing rotational translational fitting is applied, thus preserving the contribution of lattice distortion during the simulation.

These two sets of fluctuations are presented in the two top panels of Figure 4, and fluctuations derived from refinement of the model against the average electron density derived from the simulation is presented in the bottom panel. Experimental root mean squared fluctuations have been calculated from the deposited B‐factors using the relation: $B= \frac{8}{3}{\pi }^2\times {\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{F}}^2$. Backbone and per‐residue RMSF values from all of the simulations correlate modestly (Pearson correlation 0.76–0.85) with the experimental set (Supporting Information Table II), above the typical range of 0.5 to 0.7 previously reported in MD simulations.44, 45, 46, 47, 48, 49, 50, 51 Correlations with ff14SB and ff14ipq are slightly higher than with C36 and ff99SB. For example, ff14SB and ff14ipq exhibit all heavy atom correlations of 0.79 and 0.78 while C36 and ff99SB have correlations of 0.71 and 0.70, respectively.

Figure 4.

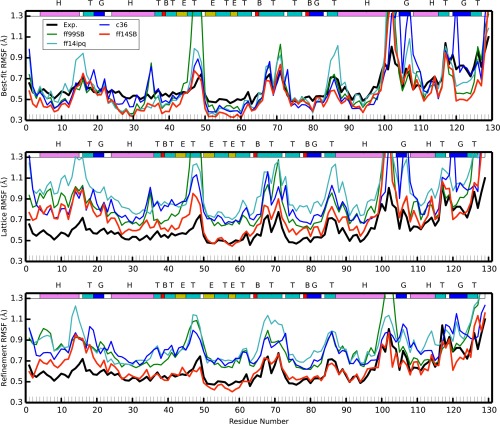
Best‐fit (top) and lattice (middle) and refined (bottom) C_α carbon RMSF for the four crystal simulations and compared with experiment. Colored lines correspond to each of the four simulations (red: ff14SB, blue: C36, cyan: ff14ipq, green: ff99SB); black shows the experimental results. The colored band across the top describes the secondary structure (T: turn, E: β‐sheet, H: α‐helix, G:3₁₀ helix, B:isolated bridge).

The best‐fit RMSF underestimates the baseline of the experimental fluctuations. This is to be expected as the experimental fluctuations contain contributions from various sources, both static and dynamic disorders, which are eliminated when naively performing the best‐fit RMSF calculations. On the other hand, lattice fluctuations for all simulations overestimate the experimental fluctuations. We suggest that this is due to the lattice distortion effect described in the next section of this article. The ff14SB RMSF are closest to experiment, followed by ff99SB, C36, and ff14ipq. Interestingly, when we calculate lattice fluctuations for each monomer individually (Supporting Information Fig. 10) and average the resulting fluctuations, we obtain results that match experiment very closely (Fig. 5). It remains to be seen whether this is a coincidental result for this system only or if this will be a consistent result across other crystal simulations as well.

Figure 5.

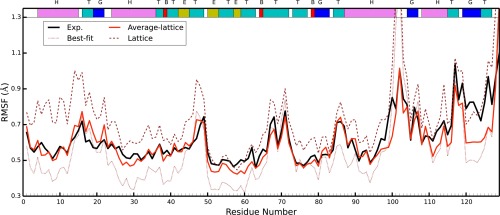
The averaged lattice fluctuations from each individual monomer in the ff14SB simulation (shown in red). Lattice RMSF were calculated for each of the 12 monomers and then averaged. Experimental results are shown in black. The best‐fit (brown dots) and lattice(brown dashes) fluctuations are those of ff14SB found in Figure 4 and are shown here for reference.

Experimental RMSF peaks (regions of high fluctuation) are recapitulated in the simulations, but the RMSF peaks derived from simulation are significantly higher. In part this may be because refined B‐factors are known to underestimate atomic fluctuations52, 53 while the simulations may be revealing the true extent of the fluctuations in the physical crystal. On the other hand, force field inaccuracies can lead to structural molecular and lattice instability producing higher than experimental fluctuations. Thus, it may be posited that the true fluctuations in these regions are to be found somewhere between the refined and the simulation‐derived values. Fluctuations obtained from refinement against the simulation electron density (Fig. 4, bottom panel) appear to confirm this conjecture: the ff14SB refined fluctuations are generally lower than the ff14SB lattice fluctuations and in excellent agreement with experimental results, whereas refined fluctuations from the other three force fields, while lower than the corresponding lattice fluctuations, are still higher than the experimental result. Because we find ff14SB to preserve the crystal lattice and structure of the protein with higher integrity than the other force fields (see next section), this does indicate that the higher than refined “real” fluctuations are due to both a limitation of the refinement algorithm52, 53 and excessive fluctuations resulting from inaccurate force fields. This insight will be treated in more detail in an upcoming publication. Furthermore, we see that all of the fluctuation peaks occur at helix termini (regions around residues 88, 100, 105) or at extended turn loops (around residues 16, 49, 70, 115). As discussed previously, our simulations tend to under‐stabilize helix termini; this could lead to the higher fluctuations we observe.

Side‐chain disorder

An analysis of side chain disorder (cf. Supporting Information Table III) reveals that χ ₁ angle distributions behave similarly across the four crystal simulations as well as the solution simulation. For each residue we computed the percentage of trans, gauche minus, and gauche plus (t, g−, g+, respectively) conformers. About half of the residues display at least some disorder (major χ ₁ rotamer population <99%), but we focused on residues where the major χ ₁ conformation was sampled less than 80% of the time (Fig. 6). The number of these “multimeric” residues was ff14SB: 24, ff99SB: 31, ff14ipq: 28, C36: 26, and ff14SB_solv: 28. While there is a common set of 56 residues that are not multimeric in any simulation, there are only nine residues that are consistently multimeric across all four simulations. This could be indicative of insufficient sampling. In all there are 50 unique residues that are multimeric in at least one simulation. Out of these 35 have polar or charged side chains. The share of polar/charged multimeric side chains varies in the simulations and is 66% in ff14SB, 71% in ff99SB, 79% in ff14ipq, 88% in C36, and 75% in ff14SB_solv. Thus, while the number of total multimeric residues is approximately the same, C36 (and to a lesser extent ff14ipq,) tend toward more frequent heterogeneity in charged and polar side chains than in hydrophobic side chains. Only two of the 50 distinct multimeric residues are buried residues (solvent accessible surface area is 0 Ų) and only 11 have an accessible surface area of less than 50 Ų. Thus the great majority of the multimeric residues are surface residues and all but the buried two are involved in contacts at crystal interfaces.

Figure 6.

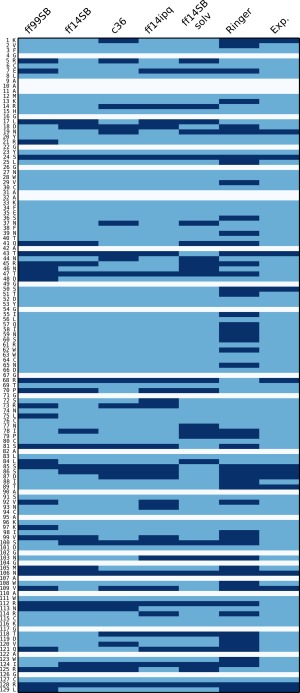
χ ₁ angle side chain disorder in each of the simulations. In each simulation (first five columns), each residue (rows) is classified as either multimeric (dark blue) or nonmultimeric (light blue). White rows indicate alanine or glycine residues. See text for explanation on the classification method. For the Ringer column, dark blue means Ringer predicted more than one χ ₁ rotamer, light blue if Ringer predicted only one. Experimental column is dark blue if the side chain was modeled with an alternate conformer in the 4LZT deposition, light blue otherwise.

Among the crystal simulations, the force fields disagree on the most populated rotamer of a given residue in 22 instances out of a possible 106. However, between ff14SB and ff14SB_solv, we find only seven residues where major rotamer preferences differ, suggesting that force field differences play a stronger role in rotamer disorder than solvent/crystal environment. We also performed a Ringer analysis54 of the experimental electron density and model and found weak correlation between the simulation multimeric residues and those identified as containing alternate conformations by Ringer. Out of the 50 multimeric residues, Ringer identifies 26 as having secondary χ ₁ peaks. However, of the 56 nonmultimeric simulation residues, Ringer finds 19 residues with secondary χ ₁ peaks. In other words, in some cases our simulations find side chain disorder that is not supported by experimental evidence and in other cases we fail to find disorder that can be predicted from the experimental data. Again, this could be due to insufficient sampling or force field deficiency.

In summary, a significant amount of side chain rotamer disorder is sampled by the simulations. The χ ₁ rotamer disorder is consistent among the crystal simulations, although C36 and ff14ipq tend to sample rotamer disorder of polar/charged residues more frequently. The amount of disorder in the solution simulation does not appear to be higher than in the crystal simulations. Most disordered side chains are charged or polar and almost all lie on the surface of the protein and are involved in crystal contacts within the lattice.

Crystal lattice disorder

We next attempted to characterize the disorder in the crystal lattice. An analysis of monomer movement (Fig. 7) indicates that all of our simulations exhibit a small progressive deterioration of the ideal crystal lattice. The centers of mass (COM) of the independent unit cells (each containing a single lysozyme molecule) explore regions close to but slightly away from the location of the COM in an ideal crystal lattice (Fig. 7, top‐left). The mean instantaneous distance (in Å) from the ideal position in the crystal lattice, averaged over all the monomers and all snapshots, is 0.31 for ff14SB, 0.42 for ff99SB, 0.53 for ff14ipq, and 0.43 for C36. The mean distance from the ideal crystal position of each monomer's average center of mass position is 0.20 for ff14SB, 0.31 for ff99SB, 0.47 for ff14ipq, and 0.35 for C36. The degree of lattice deterioration appears to be force field dependent (Fig. 7, top‐right), with ff14SB showing the least deterioration and ff14ipq the greatest. Deterioration appears to increase with simulation time and then level off: a comparison of the three microseconds of the ff14SB simulation shows that the mean ASU distance from ideal is 0.20 during the first microsecond, 0.24 during the second microsecond, and 0.23 during the third microsecond (Fig. 7, bottom left and bottom right). In ff99SB, the mean ASU distance from ideal is 0.31 during the first microsecond, 0.38 during the second microsecond and 0.36 during the third microsecond. The movement of the ASU centers of mass within the lattice appears to be stochastic and does not appear to follow any specific pattern, such as a monotonic movement away from the ideal crystal lattice position. Some ASU's (e.g. #5 and #6 in Fig. 7 bottom panels) do progressively move away from the crystal ideal, whereas others (e.g. #4) move away and then return during the first and second microsecond of the simulation respectively; still others (e.g. #2) move away first along in one direction and then “swing around” to move away in a different direction.

Figure 7.

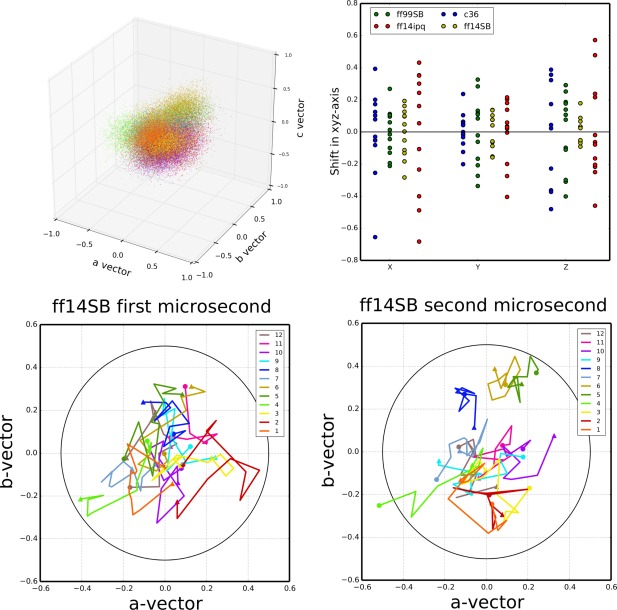
ASU center of mass movement relative to ideal crystal lattice positions. Upper‐left: cumulative plot of the center of mass of each ASU relative to the ideal lattice position at each time point in the simulation. Points are colored by each independent copy of the ASU in the system (12 independent ASUs). ff14SB is shown, data for the other simulations can be found in the Supporting Information. Upper‐right: mean distance of each independent ASU relative to the ideal crystal position along each of the crystal system axes (a–c). Lower‐left: mean position of each ASUs center of mass plotted over intervals of 100 ns over the course of the first microsecond of simulation. Starting position (<t = 0–100 ns>) indicated by a circle and ending position (<t = 900–1000 ns>) indicated by a triangle. Data shown for the ff14SB simulation; similar plots for the other simulations available in the Supporting Information. Lower‐right: similar plot for the second microsecond of the ff14SB simulation. A circle is drawn at 0.5 Å from the ideal center of mass in both plots.

To further characterize the changes in the crystal lattice during the simulation, we investigated the behavior of the crystal interfaces. Triclinic lysozyme contains six unique crystal interfaces {x + 1,y,z}, {x,y + 1,z}, {x,y,z + 1}, {x + 1,y + 1,z}, {x + 1,y,z + 1}, and {x,y + 1,z − 1} which we will refer to here as X, Y, Z, XY, XZ, and YZ, respectively. There are 12 independent copies of each interface in the simulated supercell. We calculated the relative distance between the centers of mass of lysozyme monomers across crystal interfaces (see Table 3 below and Fig. 7 in Supporting Information). Behavior across the interfaces is variable. In particular, the distance between interfaces X, XY, and XZ is on average very close to experiment, whereas interfaces Y, Z, and YZ tend to come slightly closer together (by about 0.25Å). These results are consistent for all simulations. However, maintaining the interface distance close to the experimental value may be artificially imposed by the periodic boundary conditions: when one set of monomers move apart, another set must necessarily move closer together. Therefore, it may be more informative to look at the deviations from experiment of individual ASUs (Supporting Information Fig. 7). Here we observe a variety of behaviors between simulations. For example, across the XZ interface, the greatest interface distance change for ff14SB is 0.5 Å while for ff14ipq most of the monomers spend most of the time at interface distance changes greater than 0.5 Å and the largest deviations are of more than 1.5 Å. In general, the greatest fluctuations are observed for interfaces XY and XZ. ff14SB exhibits the smallest fluctuations of all the force fields.

Table 3.

Interface Behavior Relative to Deposited Model for each of four Different Simulations

Interface		X	Y	Z	XY	XZ	YZ	Total
Avg. Δdist of monomer COM across interface	ff14SB	0.01	−0.1	−0.08	0.01	0	−0.13	0.33
	ff14ipq	0.01	−0.14	−0.16	0.01	0	−0.33	0.65
	C36	0.01	−0.03	−0.06	0.01	0	−0.16	0.27
	ff99SB	0.01	−0.09	−0.10	0.01	0.01	−0.19	0.41
Avg. no. contacts	Exp	9	15	14	11	5	4	58
	ff14SB	10.69	14.45	15.69	11.14	7.54	5.10	64.61
	ff14ipq	11.87	18.39	13.76	12.33	6.01	4.61	66.97
	C36	11.02	16.13	13.43	12.31	6.54	4.57	64.00
	ff99SB	11.69	14.74	13.90	11.51	7.69	4.79	64.32
Crystal contacts maintained (strong/weak)	ff14SB	7 (6/1)	9(4/5)	11(5/6)	10(7/3)	5(3/2)	4(4/0)	46
	ff14ipq	8(7/1)	14(7/7)	8(3/5)	9(8/1)	2(1/1)	3(2/1)	44
	C36	9(4/5)	9(6/3)	7(3/4)	8(6/2)	3(2/1)	3(2/1)	39
	ff99SB	9(4/5)	10(5/5)	11(4/7)	9(8/1)	5(3/2)	4(2/2)	48
Crystal contacts lost	ff14SB	2	6	3	1	0	0	12
	ff14ipq	1	1	6	2	3	1	14
	C36	0	6	7	3	2	1	19
	ff99SB	0	5	3	2	0	0	10
New contacts	ff14SB	1	4	3	0	3	1	12
	ff14ipq	4	7	4	0	3	1	19
	C36	2	7	4	3	2	1	19
	ff99SB	2	2	1	0	1	1	7
Interface area	Exp	268	394	379	239	168	113
	ff14SB	319	347	348	252	248	112
	ff14ipq	326	396	298	277	196	109
	C36	314	399	337	266	227	112
	ff99SB	303	374	323	264	243	109
Avg. no. H‐bonds (crystal/newly formed)	Exp	5	2	3	2	1	0	13
	ff14SB	2.14/0.81	0.14/0.91	0.74/1.65	1.03/0	0.61/0	0	4.66/3.37
	ff14ipq	2.34/1.71	0.29/1.85	0.34/2.68	1.02/0	0.14/0.25	0	4.13/6.49
	C36	1.77/0	0.63/1.35	0.70/1.99	0.84/0	0.36/0.16	0	4.30/3.50
	ff99SB	2.40/0.88	0.78/0.69	0.73/0.93	1.08/0	0.47/0.15	0	5.46/2.65

Six columns correspond to each of the six unique crystal interfaces in the model. Each simulation contained 12 independent copies of each interface. The top block shows the relative change in distance between the centers of mass of the interfacing residues. The second block shows the average number of contacts made between unique residues across interface. The third block shows the number of residue contacts from the experimental models that were maintained in each simulation. This number is further subdivided (in parentheses) into strong contacts (on average found in 10 or more unit cells at a time) and weak contacts (on average found in more than 6 but less than 10 unit cells at a time). The fourth block shows the number of residue contacts from the experimental model that were lost in each simulation (found in less than six unit cells at a time). The fifth block shows the number of new interface residue contacts formed in each simulation that were not present in the experimental model (“formed” means that they were present on average in more than seven unit cells at a time). The sixth block shows the average surface area in each simulation. The last block shows the average number of hydrogen bonds across each interface. The first number corresponds to hydrogen bonds that exist also in the experimental model and the second number to new hydrogens bond formed in the simulation.

Another factor that could account for lattice disintegration could be the inaccurate modeling of crystal contacts and hydrogen bonds across the crystal interfaces. To further characterize the relocation of monomers inside the crystal lattice, we performed a detailed analysis of crystal interface contact residues and hydrogen bonds (Table 3; see also Supporting Information for detailed presentation of all bonds and contacts: Tables IV–VII). Use of various cut‐off values for assigning contacts yielded similar conclusions. For the results printed here a “contact” is defined as two residues belonging to different ASUs with at least two heavy atoms within 3.2 Å of each other. We note that the average number of contacts per interface, compared with the number of contacts in the experimental structure, is slightly higher in all four force fields, ranging from 64 to 67 compared with 58 in the experimental structure. This includes both contacts found in the experimental structure and new contacts formed during the simulations, indicating that a rearrangement of contacts takes place. We classified the contacts found in the experimental structure into strong (found on average in more than 10 of the 12 independent interface copies during the course of the simulation), weak (found on average in more than 6 of the 12 interfaces), or broken (found on average in less than 6 of the 12 interfaces). We also identified new contacts, not present in the experimental structure, if a contact occurred on average in 7 or more of the 12 interfaces during the simulation. We see that ff99SB maintains more crystal contacts than the other simulations (48 vs. 46, 44, and 39 for ff14SB, ff14ipq, and C36, respectively). ff99SB and ff14SB also create fewer new contacts (7 and 12, respectively) than ff14ipq and C36 (19 in both cases). This indicates that ff99SB and ff14SB result in less rearrangement of interface contacts.

On a perinterface basis, results vary and patterns are less clear. For example, ff14SB loses more crystal contacts than the other force fields do at the X and Y interfaces but fewer than the other force fields at the Z, XY, XZ, and YZ interfaces. C36 does well at the X interface but loses many contacts at the Y and Z interfaces. In general, all interfaces average more contacts per interface in all simulations than the number of contacts found in the crystal structure. The exception to this is interface Z. In three of the simulations this interface has slightly fewer contacts on average (13.90 for ff99SB, 13.76 for ff14ipq, 13.43 for C36) than the crystal, which has 14 contacts. Only ff14SB has more, with 15.69 Z interface contacts. Of the contacts that are maintained by the simulations, the most stable contacts tend to be hydrophobic interactions, whereas polar and electrostatic interactions tend to be less stable. This could indicate that the force fields model hydrophobicity well, but that some electrostatic‐based effects are too weak compared with alternative interactions with waters.

A “hydrogen bond” is defined here as a nitrogen or oxygen with a covalent hydrogen on one of the atoms and a distance between the two heavy atoms of less than 3.2 Å (no angle cut‐off was used). For ff14SB, we first analyzed hydrogen bonds within the active site and compared them to those identified from an analysis of the experimental electron density by Held and van Smaalen.³¹ We found that the simulation reproduces the same set of hydrogen bonds and with similar relative strengths as those reported in the cited work: reported strong bonds between Ala31 and Glu35, between Asn44 and Asp52 and between the side chain of Asp52 and one of the side chains of either Asn44, Asn46 or Asn59 are all consistently maintained (>75%). A reported weaker bond between Glu35 and Ala110 is also less common in the simulations (<30%). This shows that intramolecular hydrogen bonds (at least in the active site) are maintained by the force field in a manner that is consistent with experimental density.

On the other hand, crystal interface hydrogen bonds are not stably maintained in the simulation: there are 13 interface H‐bonds in the deposited model: two across the Y interface, three across Z, five across X, two across XY, and one across XZ. In general, H‐bond occupancy statistics are remarkably similar across all of the force fields, with the same bonds being the most strongly maintained or most likely to be broken across all simulations (see Tables 4–7 in Supporting Information for stabilities of specific hydrogen bonds in the simulations). Of the five hydrogen bond interactions across the X interface, only three in ff14SB and ff99SB (45@O–77@ND2; 114@NH2–18@O; 114@NH1–16@O), two in ff14ipq (45@O–77@ND2; 114@NH2–18@O), and one in C36 (45@O–77@ND2) are preserved more than 50% of the time. In all simulations, the crystal hydrogen bond 45@O–77@ND2 is maintained more than 50% of the time. The other crystal hydrogen bonds across interface Y and Z are not preserved well: all the crystallographic hydrogen bonds are preserved less than 50% of the time. For interface XZ and XY there are fewer crystal hydrogen bonds compared with that in interfaces X, Y, and Z. However, the crystal hydrogen bond 116@NZ–77@OD1 across interface XY is generally maintained in all simulations. Furthermore, the same rearrangements of hydrogen bonding are seen to occur in all cases, such as the Y interface Arg21@NH2‐Asp66@O breaking in preference of Arg21@O‐Arg68@NH1/NH2 with Arg21 switching roles from H‐bond donor to acceptor and Asn19@ND2–Ser81@O breaking in preference of Asn19@ND2–Leu84@O and Asn19@OD1–Gln41@NE2. However, this particular rearrangement occurs more frequently in ff14ipq, C36, and ff14SB than in ff99SB. Across the Z interface, all four force fields completely break the H‐bond Ser100@OG‐Leu128@NH1 found in the experimental model but involving the terminal Leu128. However, Phe3@O‐Arg73@NH1, is almost completely broken in ff14ipq and C36, but is more strongly maintained in ff99SB and ff14SB (respectively 35% and 37% of the time). On average ff14SB and ff99SB tend to maintain more of the hydrogen bonds found in the experimental model (on average 4.66 and 5.46 experimental H‐bonds vs. 4.13 and 4.30 for ff14ipq and C36, respectively), and to create fewer new H‐bonds not found in the experimental model (on average 3.37 and 2.65 new bonds vs. 6.49 and 3.50 new bonds for ff14ipq and C36, respectively; Table 3). Nevertheless, the results do not allow us to draw definite conclusions about H‐bond behavior that could explain the varying degrees of crystal lattice degradation observed in the different force fields.

Discussion

Our simulations of a triclinic lysozyme crystal with explicit solvent reproduce experimental structural results well, both in regards to atomic mean positions and fluctuations. In terms of atomic RMSD, ff14SB performs particularly well (0.37/0.79 Å backbone/heavy atom RMSD), but none of the crystal simulations produce RMSD deviations of more than 0.50/1.00 Å backbone/heavy atom. These results are encouraging considering that this degree of structural divergence is on par within the deviations seen between independent crystal structures of triclinic lysozyme. For example, the backbone RMSD between PDB:3LZT/4LZT is 0.28 Å40 and between PDB:1V7T/4LZT it is 0.37 Å.55 These results are maintained even for simulations up to 3 μs in length. Thus, even if one were to possess a “perfect” force field, it might not necessarily produce smaller structural deviations. Atomic fluctuations are also generally consistent with experiment, with Pearson correlations ranging from 0.77 to 0.85 for backbone atoms. Correlations are slightly better when including the effect of both dynamic (intramolecular) and static (lattice) disorder. Direct comparison of average electron density against experimental measurements and refinement reinforces these conclusions: ff14SB and ff99SB perform slightly better than the other two force fields and refinement results produce similar RMSD results (e.g. 0.37/0.67 Å backbone/heavy atom for ff14SB). Fluctuation obtained from refinement against the simulation electron density are lower than the “true” lattice fluctuations in all force fields, but in particular show excellent agreement in the case of ff14SB, possibly indicating a lower degree of artifactual disorder in this simulation. The improved performance of the newer ff14SB is encouraging in that is implies that force field development is progressing in the right direction. The ff14SB force field differs from earlier Amber force fields (such as ff99SB) in terms of torsion preferences of certain side chains. It is likely that these side chain torsional preferences are important in yielding structures that more consistent with the crystal density. Studies on a wider variety of proteins would be needed to establish this is a general trend. Lastly, a slight unraveling of helix termini is common to all of the force fields. It is possible this is a physical phenomenon that is masked in the electron density by experimental error or averaging effects, but the systematic nature of the small differences that we see, which extend to almost all 3₁₀ and α‐helical segments, suggests limitations in the force fields used here as a more likely contributor.

We noted above that crystal simulations of proteins are not new. In 2000, Stocker et al. compared simulations of lysozyme in solution and in an orthorhombic crystal.37 It is representative of improvements in computer speed and dynamics algorithms that the earlier results (which had four monomers in a single unit cell) were carried out for 2 ns, compared with 3 μs in the present study. The differences between solution and crystal are remarkably similar to those seen here (compare Fig. 1 of Ref. 37 with Fig. 2 here), but improvements in force fields are also evident: the instantaneous Cα atom deviation of the earlier crystal simulation from experiment was about 1.3 Å, compared with 0.7 Å here for ff14SB. A 20 ns study of tetragonal lysozyme38 showed Cα atom deviations ranging from 1.1 Å for Amber ff03, to 1.6 Å for OPLS‐AA, to 4.0 Å for GROMOS96 and most likely would have been higher had those simulation been extended to sample time scales on par with the current results. It remains to be seen how much of the difference between those studies and this one stems from differences in the packing of the crystal space group (previous studies used tetragonal; we use triclinic). Nevertheless, in this sort of structural comparison, there is a clear trend in going from GROMOS96 (43A1)56 [developed in 1996], to ff99SB57 [developed in 2006] to ff14SB [developed in 2014]. The ff14SB results for fluctuations are also in remarkably good agreement with B‐factors refined from a room‐temperature crystal study, as shown in Figures 4 and 5.

Our results also provide information on limitations of current MD force fields. First, some atomic fluctuations are too high compared with experimental results. These fluctuations correspond to regions of the structure that are solvent exposed and involved in crystal contacts. It is known that refined B‐factors tend to underestimate the true atomic fluctuations,52, 53 but large differences between individual asymmetric units, deterioration of secondary structure and changes in the crystal lattice indicate that structural instability during the simulation also contributes. Second, secondary structure analysis also indicates that fluctuation and structural differences can be attributed to inaccurate modeling of hydrogen bonds. In particular it may be that 3₁₀ helices are understabilized by C36 and ff14ipq. Third, we observe a slight but progressive distortion of the crystal lattice that grows as the simulations progress, but that is actually quite small, especially for the best performing force field (ff14SB average ASU center of mass 0.20 Å from ideal lattice position). This deterioration is not affected by system pressure or small variations in the amount of solvent. A rearrangement of contacts and bonding networks across the crystal interfaces occurs during the simulations, but no clear correlation between that and the degree of lattice deterioration was discovered. Further analysis of the factors contributing to this lattice distortion, such as the implications of the size of explicit supercell, as well as a potential implementation of crystal molecular dynamics that restrains monomer center of mass to idealized crystal positions are two possible future areas of investigation. Such an approach would complement recent efforts at obtaining accurate MD trajectories by means of electron density based restraints.58

As we noted above, times required to reach equilibrium are longer than those typically required for solution simulations. This is not surprising considering the somewhat constrained nature of the crystal lattice that hinders solvent rearrangement. On the other hand, it does not appear that more conservative equilibration schemes (Supporting Information Fig. 1) using longer (up to 500 ns) heating and restraint protocols lead to different results. However, crystal simulations allow for independent sampling of multiple unit cells, which enhances the sampling of protein configurations. In the past computational resources often restricted crystal simulation studies to single unit cells.35, 36 The current approach can help re‐examine those findings and identify possible artifacts resulting from periodic boundary conditions imposed on a single unit cell. Further methodological investigation is needed to find the best way to harness and consolidate this information.

One of the most exciting potential contributions of crystalline MD is that it provides a detailed synthetic data set for probing crystal refinement applications. Refinement of the lysozyme structure against the observed simulation electron density yields an R‐free factor that is on par with experimental results (16.7% ff14SB refinement without alternate conformations vs. 14.7% experimental result), but it remains to be seen whether the same factors are responsible for that similar level of disagreement. A more detailed analysis of this "R‐factor gap"59 will be presented in a separate publication.

Methods

Preparation of the simulation supercell

Atomic coordinates were taken from Protein Data Bank60 entry 4LZT.⁴⁰ This structure of hen egg‐white lysozyme was solved in a triclinic P1 space group at 295 K. Alternate conformations were removed, in each case keeping only the major conformer. His15 was set to the protonated state consistent with its experimental pK _a of 4.5 to 4.6.⁴⁰ A “supercell” of 3 × 2 × 2 unit cells measuring 81.72 × 63.74 × 68.46 Å and containing 12 copies of the lysozyme molecule was created by using the PropPDB module of the AmberTools61 package (Fig. 1). Solvent conditions followed the strategy described earlier:27, 28 we retained all of the experimentally determined solvent positions (except for minor alternate conformers) which included 134 water, 7 nitrate, and 3 acetate molecules. We used the AmberTools AddToBox program to add additional acetate, nitrate, and sodium ions to both neutralize the system and replicate crystal liquor concentrations. Three of the additional acetates and one nitrate were placed in the positions identified in the cryogenic structure (PDB:3LZT ⁴⁰). Test simulations of about 10 ns in the NPT ensemble after equilibration were performed in order to find the amount of solvent that best matched the experimental volume of the crystal. Details of the simulations are given in Table 1.

Molecular dynamics simulations

Protonation of the protein and construction of molecular topology and coordinate files for the crystal supercell were done using the tleap module of AmberTools and Reduce.62 Acetate ions were modeled with parameters derived using the IPOLQ method.63 Nitrate ion parameters were taken from Ref. 64. All other parameters were taken from the corresponding force field's standard parameters. The force fields used were ff99SB,⁵⁷ ff14SB, ff14ipq,65 and CHARMM 3666 (C36). The TIP4P‐Ew parameters67, 68 were used for the water model with the corresponding Joung/Cheatham parameters set for Na⁺ ions.69

System optimization, equilibration, and production dynamics were performed using the PMEMD module of Amber14.70 When the system volume was allowed to vary (during equilibration only), constant pressure was maintained by a Berendsen barostat71 with isotropic pressure scaling and a time constant of 1.0 ps. Constant temperature was maintained with a Langevin thermostat72 (collision frequency of 1/ps) at the experimental crystal diffraction temperature of 295 K. Force calculations were performed with a 9.0 Å real space cutoff in the context of periodic boundary conditions, smooth particle‐mesh Ewald electrostatics73, 74 and a homogeneity assumption for long‐range van der Waals contributions. The SHAKE75 and SETTLE76 algorithms were used to constrain the lengths of bonds to hydrogen and the internal geometry of rigid water molecules, respectively. A 2 fs timestep was used.

To test the amount of solvent necessary to replicate experimental volume, the equilibration scheme of Ref. 17 was used, followed by approximately 10 ns of unrestrained dynamics propagated in the isothermal/isobaric ensemble. Volumes over the trajectory were compared with experimental volume and the systems shown in Table 1 were chosen for production.

For equilibration, noncrystallographic solvent positions were relaxed via 100 steps of steepest descent optimization followed by 900 steps of conjugate gradient optimization with 256 kcal/(mol Å²) position restraints applied to protein and crystallographic solvent molecules. Next the conformations of protein residues, including added hydrogens, were relaxed using the same minimization algorithm and with restraints applied to all solvent molecules. A third round of coordinate optimization followed in the same manner but with no restraints. Next, initial restrained dynamics were performed at constant volume for 1 ns with 10 kcal/(mol Å²) restraints on all protein, acetate, and nitrate atoms, as the system was heated to the experimental temperature of 295 K. Restraints were then relaxed with 4 ns of 10 kcal/(mol Å²) restraints on the same atoms, 6 ns of 1 kcal/(mol Å²) and 12 ns of 0.1 kcal/(mol Å²) restraints. Unrestrained dynamics were then propagated in the NVT ensemble with a two femtosecond timestep for 1140 to 1160 ns. Only the final 1000 ns of each simulation were used for the analysis presented here.

A parallel solution simulation placed a single monomer in a box of 9375 TIP4P‐EW water and 8 Cl⁻ ions in a rectangular box of dimension 60 × 67 × 74 Å. We performed 28 ns of equilibration, with gradually decreasing constraints on the protein atoms, followed by 1 μs of production simulation, using a 1 fs time step, a Langevin thermostat with a collision time of 1 ps⁻¹, and a weak‐coupling barostat with a time constant of 5 ps.

Analysis of data

Data analysis was carried out using a combination of in‐house scripts and the AmberTools cpptraj 77 module. Two root mean square deviation (RMSD) metrics referred to here as “best‐fit superposition RMSD” and “lattice‐fit RMSD” were calculated using the Kabsch algorithm,78 and two B‐factor metrics were calculated as described below and in greater detail in Ref. 17. Secondary structure was determined using the DSSP79 algorithm. Simulation average electron density was calculated as described in detail in Ref. 17 using md2map, part of the crystal simulation analysis toolkit in AmberTools and making use of CCP4 programs.80 The maps were truncated at a resolution of 0.95 Å, corresponding to the experimental result. The Visual Molecular Dynamics (VMD) program81, PyMOL,82 and matplotlib83 were used for visualization and image generation.

Refinements against the simulation average electron density were carried out via 10 automated macrocyles of reciprocal space coordinate and isotropic B‐factor refinement in phenix.refine,42 followed by a limited manual rebuilding in COOT,⁴³ followed by a further five macrocyles of standard automated refinement. To ensure consistency of results and eliminate possible contributions stemming from differences in refinement protocols and software, we repeated a refinement of the lysozyme model against the original experimental structure factor amplitudes (deposited in the PDB) using a similar protocol. Results were in very close agreement to the deposited model (backbone RMSD 0.04, B‐factor Pearson correlation 0.97, Rfree difference .003, see also Supporting Information Fig. 15). Thus details of the refinement protocol play a minor role, and we have chosen to make all comparisons below against the deposited model.

Supporting information

Supporting Information