Assessment of the utility of contact‐based restraints in accelerating the prediction of protein structure using molecular dynamics simulations

Abstract

Molecular dynamics (MD) simulation is a well‐established tool for the computational study of protein structure and dynamics, but its application to the important problem of protein structure prediction remains challenging, in part because extremely long timescales can be required to reach the native structure. Here, we examine the extent to which the use of low‐resolution information in the form of residue–residue contacts, which can often be inferred from bioinformatics or experimental studies, can accelerate the determination of protein structure in simulation. We incorporated sets of 62, 31, or 15 contact‐based restraints in MD simulations of ubiquitin, a benchmark system known to fold to the native state on the millisecond timescale in unrestrained simulations. One‐third of the restrained simulations folded to the native state within a few tens of microseconds—a speedup of over an order of magnitude compared with unrestrained simulations and a demonstration of the potential for limited amounts of structural information to accelerate structure determination. Almost all of the remaining ubiquitin simulations reached near‐native conformations within a few tens of microseconds, but remained trapped there, apparently due to the restraints. We discuss potential methodological improvements that would facilitate escape from these near‐native traps and allow more simulations to quickly reach the native state. Finally, using a target from the Critical Assessment of protein Structure Prediction (CASP) experiment, we show that distance restraints can improve simulation accuracy: In our simulations, restraints stabilized the native state of the protein, enabling a reasonable structural model to be inferred.

Introduction

Molecular dynamics (MD) simulations with physics‐based, all‐atom force fields have been used successfully for decades1 to study the structural dynamics of proteins, including complex conformational changes like the folding/unfolding transition of small, fast‐folding proteins.2, 3 In principle, MD simulations also offer a straightforward approach to the important problem of ab initio protein structure prediction: that is, the determination of the three‐dimensional structure of a protein using only its primary sequence as input information. Many unstructured protein chains spontaneously fold to their native conformations in vitro and in vivo, and physics‐based computer simulations started from an unstructured chain of amino acids should similarly be able to spontaneously reach the protein's native conformation. While coarse‐grained or knowledge‐based methods can be successful in ab initio protein structure prediction,4, 5, 6, 7, 8, 9, 10, 11, 12 atomistic physics‐based approaches may have greater potential for discovering novel folds and new loop conformations.

In general, however, physics‐based MD simulations, despite some recent progress in the area of structural refinement,13, 14, 15, 16 have had limited success in ab initio structure prediction,17, 18, 19, 20, 21, 22, 23 in part because the simulation time required to reach the native state can be prohibitively long, and also because errors in the force field can result in discrepancies between the calculated global free energy minimum and the true native state.24 The utility of MD simulations for protein structure prediction would be greatly enhanced by the introduction of protocol modifications that reduce the simulation time required to observe the native state, and that also prevent deviations from the native state due to force field inaccuracies.

An approach that has the potential to achieve both of these goals is the incorporation of additional information, in the form of structural restraints,25 to bias simulations toward native conformations—an avenue explored by Ron Levy more than two decades ago.26 Structural restraints can be inferred from a variety of experimental techniques,27 such as low‐resolution cryo‐EM,28 FRET,29, 30 NMR,31, 32, 33, 34, 35, 36 or chemical cross‐linking.37 Restraints can even be inferred for proteins for which no experimental structural information is available, if residue–residue native contacts can be identified from bioinformatics methods that make use of sequence alignments of large numbers of homologous proteins.38, 39, 40, 41

Here we investigate the extent to which incorporating residue–residue contact information can speed up convergence to the native state in all‐atom MD simulations starting from extended conformations. We carried out folding simulations of ubiquitin biased by different numbers of restraints based on randomly chosen native contacts. The choice of ubiquitin as a benchmark system for this study is motivated by its small size (76 residues), its complex topology, the stability of its native state when simulated with a modern all‐atom, physics‐based force field42 (CHARMM22*43), and its relatively long millisecond folding timescale, as determined by experiment.44, 45, 46, 47 Most importantly, folding of ubiquitin can also be achieved in unbiased MD simulations42—albeit with a considerable computational effort. The folding timescale of ubiquitin as measured in unbiased MD simulations (∼3 ms) provides an appropriate reference for assessing the speedup that can be obtained by introducing contact restraints.

We find that ubiquitin simulations biased by even a relatively small number of restraints can reach native or near‐native structures within a few tens of microseconds of simulation time, a speedup of more than an order of magnitude compared to unbiased simulations. Structural restraints, however, appear to slow down relaxation from near‐native conformations to the fully native structure. We discuss potential remedies for this problem.

We also examine, in a more limited manner, the extent to which incorporating contact information into simulations can improve the accuracy of protein structure predictions. To do so, we carried out simulations of a protein whose native state is unstable in unrestrained simulation with the CHARMM22* force field. This protein was supplied as a contact‐assisted structure prediction target in the 10th Critical Assessment of protein Structure Prediction (CASP) experiment.25, 48 At least for the CASP target investigated here, structural restraints help stabilize the native structure in simulation to the extent that MD can be used to infer a reasonable structural model.

Materials and Methods

All MD simulations of ubiquitin were started from a completely extended conformation, prepared using Maestro.49 Native contacts in ubiquitin were defined as pairs of Cα atoms that are within a distance of 10 Å. These contacts were identified using the first conformer of the NMR structure of ubiquitin (PDB ID: 1D3Z).50 A set of contacts was selected using our implementation of the “cone‐peeling” algorithm.51 The cone‐peeling algorithm removes contacts that have a contact order of less than four (short‐range contacts) and a subset of the redundant contacts (two contacts are deemed redundant if they share one residue and if the other residues have a sequence separation of less than four residues) in a systematic manner, resulting in a set of non‐redundant contacts. In the case of ubiquitin, this procedure resulted in a set of 205 non‐redundant native contacts. Subsets of 62 non‐redundant contacts were generated by random selection from the full set of 205, subsets of 31 contacts were randomly selected from these 62‐contact subsets, and subsets of 15 contacts were randomly selected from the 31‐contact sets. The specific contact sets used in the simulations are illustrated in Supporting Information Figure S5. Contacts were implemented in simulation as distance restraints on pairs of Cα atoms using a weak flat‐bottomed harmonic potential with a “flat” range of 10 Å and a spring constant of 0.05 kcal (mol Å⁻²)⁻¹. Extended conformations were initially simulated in vacuo for 50 ns in the presence of restraints using replica‐exchange molecular dynamics52 (REMD) with a 16‐rung temperature ladder ranging from 300 to 700 K and with the CHARMM22* force field,43 which is a modification of the CHARMM22/CMAP force field.53, 54 A term was introduced to prevent backbone cis–trans isomerization (see Supporting Information). These simulations were carried out in order to generate compact structures that respect the majority of restraints. The 300‐K trajectory was filtered to select structures that satisfied the largest number of restraints.

The most compact structure among the structures that satisfied the largest number of restraints was solvated and relaxed by way of a simulated annealing simulation55, 56 with the CHARMM22* force field for 40 ns with a linear ramp‐up in temperature from 300 to 350 K over the first 10 ns, followed by constant‐temperature simulation at 350 K for the next 10 ns, followed by a linear ramp‐down to 300 K over the next 10 ns, followed by constant temperature simulation at 300 K for the final 10 ns. The replica‐exchange and annealing simulations were carried out using Desmond.57 Finally, the last snapshot from each annealing simulation was used as a starting structure in all‐atom, explicit‐solvent simulated tempering MD simulations, using the CHARMM22* force field, which were performed on Anton.58, 59

We used a 20‐rung temperature ladder ranging from 300 to 420 K for all simulated tempering simulations. Weights for individual temperature rungs were computed using the energy averaging method as described in Park and Pande,60 although they had to be frequently re‐estimated over the course of a simulation, especially after the occurrence of large conformational changes in the protein. Exchanges between temperature rungs were attempted every 10 ps.

In cases in which predicted secondary‐structure information was incorporated into the simulation,26 we used a consensus‐based method, Concord,61 for secondary‐structure predictions. Concord has a low false‐positive rate, so residues not present in secondary‐structure elements are very likely to remain unrestrained in simulation. Secondary‐structure restraints were implemented as torsional terms in the force field that restrain the ϕ and ψ backbone dihedral angles in helices to −57° and −47°, respectively, and those in β strands to −110° and 130°, respectively, with a maximum torsional force constant of 1.0 kcal mol⁻¹. The actual force constant used was scaled down from this maximum by the degree of confidence in the quality of secondary‐structure prediction (see Supporting Information). In the one simulation in which exact secondary structure was used to restrain dihedral angles, secondary structure was calculated using STRIDE,62 and dihedral angles in all residues within calculated secondary‐structure elements were restrained with a torsional force constant of 1.0 kcal mol⁻¹.

The sequence for CASP target Tc684 (domain 1: residues 24 to 96) was downloaded from the CASP website. Preparations of the extended state and preprocessing of the structure (replica exchange in vacuo followed by annealing of the solvated structure) were performed as described for ubiquitin. The eight contacts between Cβ atoms provided by CASP were implemented as distance restraints during simulation. Because relatively few contacts were provided, we used a distance restraint potential that was twice as strong as the one used for ubiquitin, with a spring constant of 0.1 kcal (mol Å⁻²)⁻¹ and a flat region of 8 Å (corresponding to the Cβ contact definition used by CASP). The starting structure for the native‐state simulation was also downloaded from the CASP website.

Further details of the simulations and the analyses are described in the Supporting Information.

Results and Discussion

Simulations restrained by a complete set of nonredundant native contacts: The utility of simulated tempering

We identified a set of native contacts between ubiquitin residues by selecting pairs of Cα atoms that are within 10 Å of each other in the first conformer of the NMR structure of ubiquitin (PDB ID: 1D3Z).50 We used the cone‐peeling algorithm51 to remove redundant contacts as well as contacts with a sequence separation of less than four residues (see Methods). This procedure resulted in a set of 205 nonredundant native contacts. We then ran three simulations of ubiquitin at 300 K with the full set of 205 restraints. Each simulation started from a different conformation generated during the equilibration phase (see Methods). We found that the second hairpin and the helix were already mostly formed during the equilibration stage (see Supporting Information). In two of the simulations, shown in Figure 1(A,C), ubiquitin reached its native state within a few microseconds: most conformations sampled within the native ensemble had Cα root‐mean‐square deviations (RMSD) of about 1 Å or less from the NMR structure, the same RMSD that is obtained for unrestrained simulations started from the native state.42 In the third simulation, ubiquitin adopted a native‐like state in a similar timeframe [Fig. 1(B)]. Native‐like conformations, which we define as conformations not found in the native ensemble but with Cα RMSD from native <3 Å, closely resemble the native structure but contain small regions of non‐native structure. The simulation shown in Figure 1(B) was trapped for several microseconds in a native‐like state in which the 3–10 helix (part of loop 2) had not formed, and thus a small fraction of the restraints were not satisfied. Other examples of such near‐native kinetic traps are discussed below.

Figure 1.

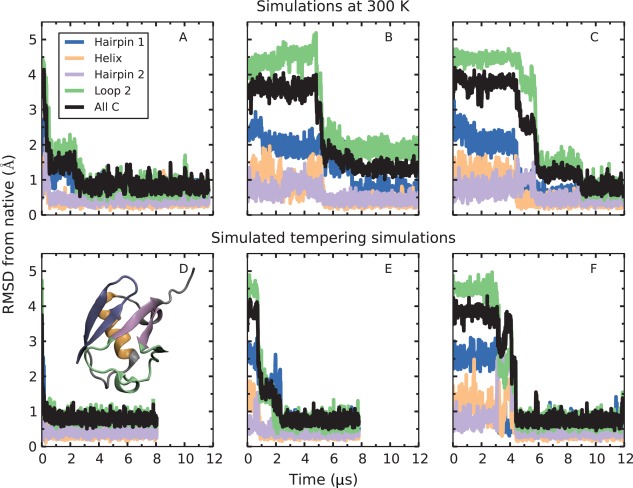
Comparison of 300‐K and simulated tempering simulations with all 205 nonredundant restraints applied. The top three simulations (A–C) were conducted at a temperature of 300 K. Each of these simulations started from different initial snapshots taken from the annealing phase. The bottom three simulations (D–F) are simulated tempering simulations that started from the same initial snapshots as A, B, and C, respectively. Although a native or native‐like state was adopted within a few microseconds in each case, the simulated tempering simulations did so more rapidly. Furthermore, constant‐temperature simulation B was trapped in a state in which the 3–10 helix (part of loop 2) was not formed; the corresponding simulated tempering simulation (E) escaped from this kinetic trap and found the native state in less than three microseconds. Here, “Hairpin 1” refers to residues 2–16, “Helix” to residues 25–35, “Hairpin 2” to residues 40–45 and 67–71, “Loop 2” to residues 46–66, and “all Cα” to all but the last five residues (72–76), which form a floppy tail. The native structure of ubiquitin with secondary structure elements colored according to their corresponding RMSD time series is shown in the inset of panel D.

We reasoned that allowing the protein access to higher temperatures might help it escape entrapment in near‐native states. Starting from the same three structures as the constant‐temperature runs, we ran simulated tempering MD simulations with the full set of 205 restraints and a 20‐rung temperature ladder ranging from 300 to 420 K (see Methods). We found that for every starting structure, the time to find the native state was less with simulated tempering than with constant‐temperature simulation [Fig. 1(D–F)]; notably, the kinetic trap observed in simulation B was also encountered in simulation E, but the protein quickly escaped this trap and found the native state [Fig. 1(E)], presumably because the system had access to higher temperatures. The combination of simulated tempering and distance restraints appears to speed up finding the native state. Simulated tempering without distance restraints is unable to reach the native state within a comparable timescale (see Supporting Information).

Simulated tempering simulations with varying numbers of randomly selected contacts

In many cases, only a limited number of contacts might be available for the protein of interest. We assessed whether the speedup in reaching native conformations is dependent on the number of contacts used in simulation. We performed nine simulated tempering simulations of ubiquitin; these simulations used either 62, 31, or 15 distance restraints chosen at random from the original set of 205 nonredundant restraints. At each of these three restraint levels, we performed three simulations, each with a different set of randomly chosen contacts, except for the 62‐restraint level, where two of the three simulations used the same set of restraints. As shown in Figure 2, as few as 15 randomly chosen restraints appear to be sufficient, in most cases, to drive the system to a native or native‐like state within tens of microseconds. In eight of the nine simulations, the protein either adopted the native conformation [Fig. 2(A,D,G)] or native‐like conformations in which one of the structural motifs was slightly misfolded. Examples of these misfolded regions are a register shift between the two strands that form hairpin 2 [Fig. 2(B,C)], a complete disruption of the hydrogen bond network of hairpin 2 [Fig. 2(H)], a register shift in hairpin 1 [Fig. 2(I)], and a conformational change in loop 2 [Fig. 2(E)] (see Supporting Information for details). Only the simulation shown in Figure 2(F) failed to fold into a native or native‐like state—in this case, the simulation remained stuck in a non‐native structure rich in β‐sheet content that satisfied 25–29 out of 31 restraints, and hairpin 1 was the only native structural motif formed even after 120 µs of simulation time.

Figure 2.

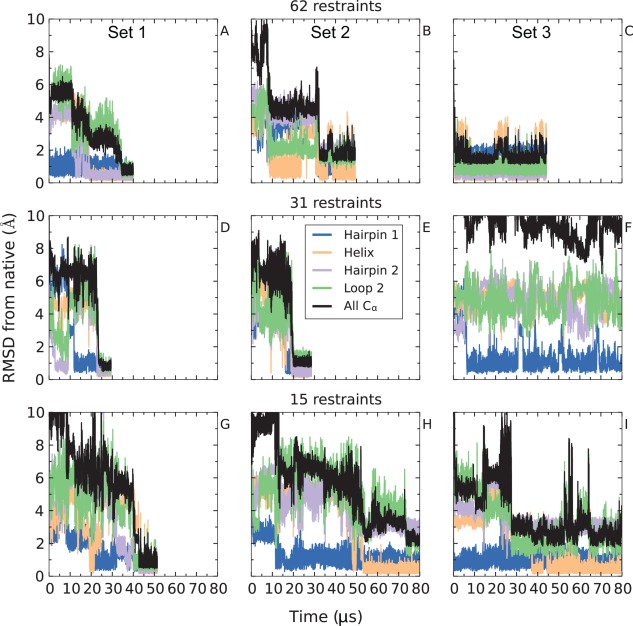
Varying the number of restraints. In 8 of 9 simulations with 15 or more random restraints, ubiquitin found a conformation that is within 3 Å of the native state within tens of microseconds. In three of nine simulations (A, D, and G), the true native state was found. In one simulation, the system did not converge to the native conformation within 130 µs of simulation time (F). In the five remaining simulations (B, C, E, H, and I), the system was trapped in native‐like conformations that ranged in RMSD from 1.5 to 3 Å from the native state. In general, increasing the number of contacts tends to decrease the time to convergence to a native or native‐like conformation. Atom selections are defined in the caption of Figure 1.

The observation that the native state was reached rapidly in only three cases [Fig. 2(A,D,G)] suggests that not all combinations of restraints are equally helpful. Comparison of the different sets of restraints shows that the simulations that successfully reached the native state contain a larger number of restraints in the flexible loop 2 (Supporting Information Fig. S5), possibly directing the correct formation of loop 2 and hairpin 2, which are often misfolded in the near‐native kinetic traps.

In summary, at each of the three restraint levels studied, one simulation converged to the exact native conformation, and two simulations (one in the case of 31 restraints) reached conformations very close to the native state within tens of microseconds but remained trapped in these conformations despite the use of simulated tempering (see Supporting Information). The average time to reach a native or native‐like conformation for these eight simulations was 33 µs, an ∼50‐fold speedup with respect to unbiased simulations.42 Although we do not have enough independent simulations to robustly estimate the rate of convergence as a function of the number of contact restraints applied, the results reported in Figure 2 suggest that native or native‐like conformations are reached somewhat faster as the number of contact restraints increases.

Inclusion of backbone torsion‐angle restraints can speed up convergence to native or native‐like conformations

We also examined, to a more limited extent, whether there is a further speedup in convergence to native or native‐like conformations upon addition of restraints to the backbone dihedral angles that enhance the formation of local secondary structure (see Methods). As a first test, we performed one simulation with 15 contact restraints in which the backbone torsion angles of residues that in the native structure are in helices or sheets were restrained to the α_h or β regions of the Ramachandran plot. Figure 3(A) shows the effect of adding dihedral‐angle restraints corresponding to the actual secondary structure of ubiquitin [the corresponding simulation with distance restraints only is shown in Fig. 2(G)]. Convergence to the native state was achieved in about 15 µs, roughly a third of the time‐to‐convergence compared to when dihedral‐angle restraints were absent. We also examined the effect of dihedral‐angle restraints when predicted, rather than experimentally determined, secondary structure is used to define the restraints (see Methods). Here we also found some speedup in the time required to reach native‐like conformations for two out of three simulations [cf., Fig. 3(B–D) with Fig. 2(G–I)].

Figure 3.

Introduction of backbone dihedral‐angle restraints based on exact (A) and predicted (B, C, D) secondary structure (see Methods) resulting in faster convergence to a native‐like state. Atom selections are defined in the caption of Figure 1.

We conclude that the inclusion of dihedral‐angle restraints corresponding to actual or predicted secondary structure appears to reduce the time to reach a native or native‐like conformation. Dihedral‐angle restraints do not appear to affect the chance of simulations becoming trapped in native‐like conformations; indeed, in simulations both with and without the dihedral restraints we observe essentially the same non‐native conformation in which hairpin 2 is register shifted (see Supporting Information).

Escape from near‐native kinetic traps upon removal of distance restraints

We performed unrestrained simulated tempering simulations starting from the trapped conformations, and found in all cases that the unrestrained system escaped from near‐native kinetic traps (Fig. 4), confirming that the near‐native traps observed in restrained simulations are very likely to be an artifact of the presence of restraints. We examined whether escape from traps was to native or to unfolded states. In simulations starting from the most prevalent kinetic trap—the one in which hairpin 2 has a register shift [Fig. 4(A–D)]—the protein unfolded in <15 μs in three cases [Fig. 4(A,B,D)] and, in one case, adopted the native conformation in about 27 µs [Fig. 4(C)]. In the case of the trap in which hairpin 2 is completely disrupted [Fig. 4(E)], the protein also unfolded in <10 µs. With the third trap, in which hairpin 1 suffers a register shift, the system folded to the native conformation about 5 µs after release of the restraints (before eventually unfolding due to transitions to higher rungs of the simulated tempering ladder) [Fig. 4(F)]. In the case of the fourth trap, in which loop 2 is stuck in a non‐native conformation, the system quickly unfolded after restraint removal [Fig. 4(G)]. The protein thus mostly escaped traps to a completely unfolded state rather than to the native state. Notably, however, in a minority of cases, hairpin register shifts were corrected without complete unfolding.

Figure 4.

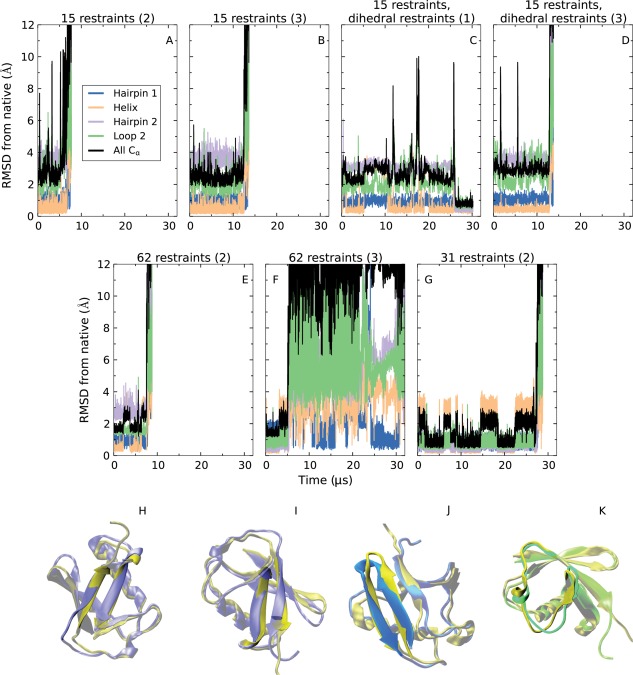
Behavior of kinetically trapped systems after removal of distance restraints. The above RMSD plots correspond to unrestrained simulations of systems that were stuck in four different kinetic traps: one in which hairpin 2 suffered a register shift (A–D; initial conformation shown in H), another in which hairpin 2 was disrupted (E; initial conformation shown in I), another in which hairpin 1 suffered a register shift (F; initial conformation shown in J), and another in which loop 2 adopted a non‐native conformation (G; initial conformation shown in K). The simulations are labeled by the number of distance restraints in the kinetically trapped conformation and by whether or not dihedral restraints corresponding to predicted secondary structure were present. As an example, D is a simulation starting from a conformation in which the third set of 15 restraints was imposed and dihedral restraints were present. Note that in two cases, C and G, the system visited the native conformation after removal of restraints. Atom selections are defined in the caption of Figure 1, and in H–J the gold‐colored structure is the native conformation of ubiquitin.

Contact restraints can help mitigate force field inaccuracies

We also simulated a protein whose native state is not well described by physics‐based simulations, to assess the extent to which distance restraints derived from contact information can help alleviate the effects of force field errors. Domain 1 of Tc684, which is a target protein from the CASP10 experiment48 (PDB ID: 4GL6, residues 24 to 96), has about the same number of residues as ubiquitin and comprises a helix and four β strands. In unrestrained simulations at 300 K, the protein drifted away from the native state after about 10 µs [Fig. 5(A)]. The major deformations occurred in loop 1, loop 3, and the helix, which was displaced with respect to the rest of the structure, although the helix and the β strands were well‐formed and stable by themselves. In the presence of distance restraints corresponding to the eight contacts supplied by CASP, the protein was stable for 25 µs at 300 K and fluctuated within <4 Å Cα RMSD from the native state [Fig. 5(B)].

Figure 5.

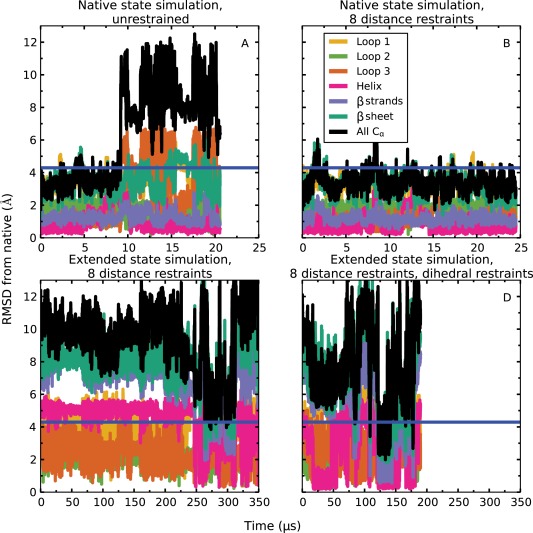
Simulations of domain 1 of CASP target Tc684 (PDB ID: 4GL6). Unrestrained simulations starting from the native state (A) drifted away from the starting conformation, but the native state was stable if the eight native contacts supplied by CASP were enforced using distance restraints (B). A simulation starting from an extended conformation with the distance restraints imposed did not converge to native‐like conformations within 360 µs (C). When dihedral restraints based on predicted secondary structure were also applied (and subsequently released, after formation of the helix, at about 46 µs), a simulation starting from the same extended conformation as in (C) adopted the ensemble realized in (B) between about 120 µs and 140 µs. The blue horizontal line in all plots corresponds to an RMSD of 4.3 Å, which is the lowest RMSD among CASP submissions. Here, “Loop 1” (residues 51–60) is the loop between strand 1 and strand 2, “Loop 2” (residues 70–75) is the loop between strand 2 and strand 3, and “Loop 3” (residues 83–91) is the loop between strand 3 and strand 4. The “β sheet” (residues 44–83) refers to the three major β strands and the two loops between them, whereas “β strands” (all residues in the “β sheet” other than the residues in “Loop 1” and “Loop 2”) refers to just the three major β strands.

We also started simulations from extended structures and were able to reach the ensemble sampled by the native‐state simulations (see Supporting Information Fig. S9) within 140 µs by applying both distance restraints and dihedral restraints corresponding to predicted secondary structure [Fig. 5(D)]. The same structural ensemble was not reached within 400 µs of simulated time when only distance restraints were applied but dihedral restraints were not enforced [Fig. 5(C)]. This suggests that dihedral restraints also allow this protein to reach the native state faster, but more simulation would be required to quantify the speedup. Native‐like states can be readily identified from the simulation trajectory of Figure 5(D) by clustering trajectory snapshots that satisfy all eight distance restraints (see Supporting Information). We find that, depending on the number of clusters chosen, the snapshot at the centroid of the largest cluster has an RMSD of between 2.69 Å and 4.07 Å from the native state, with a median RMSD of 3.73 Å (for reference, the RMSD from the native state of the best CASP submission for this target was 4.29 Å).

Conclusion

The main purpose of this work was to assess the extent to which the inclusion of native contact information can increase the rate of convergence to the native state in long, atomistic MD simulations. We found that the inclusion of a small number of contact‐based restraints, selected randomly from the entire set, can indeed speed up the folding of the millisecond‐scale folder ubiquitin by over an order of magnitude.

We found a weak dependence of the folding timescale on the number of restraints: Although distance restraints based on the entire set of 205 essential native contacts led to adoption of the native state in a few microseconds of simulation, the timescales for convergence to the native state with 62, 31, and 15 restraints were comparable, on the order of tens of microseconds. Deliberate selection of contacts that are important in the folding process seems likely to lead to much faster folding, although the use of such key contacts would require additional information about the folding transition. We also found that the addition of dihedral restraints based on predicted secondary structure further increases the speed of folding, although this speedup is not nearly as dramatic as the one obtained by adding a few distance restraints to unrestrained MD simulations.

A recurring feature of our simulations is that they often converged to one of several native‐like conformations (<3 Å away from the true native state) in which the system was kinetically trapped by the presence of the distance restraints. These native‐like conformations are very similar to the native state, but they typically feature distortions in some regions of the protein, and may not be accurate enough for some applications. These kinetic traps are clearly an artifact of restrained simulations, as they were not observed in previous unbiased MD simulations.42 Indeed, simulated tempering was not sufficient to facilitate escape from these trapped conformations unless the restraints were also removed. In some cases, removal of restraints resulted in folding to the native state, suggesting that although native‐like states sit on the unfolded side of the folding free energy barrier, they could be a useful starting point for further refinement.

To address the issue of near‐native traps, we carried out preliminary experiments with two additional simulated tempering protocols (see Supporting Information). In one protocol, we carried out simultaneous tempering of temperature and the restraint potential, using low values of the spring constant at high temperatures and high values at low temperatures. We found that weights for simulated tempering ladder rungs in this scenario had to be re‐estimated too often over the course of the simulation for the method to be practically useful. In another protocol, we replaced the flat‐bottomed harmonic restraint potential with a flat‐bottomed linear restraint potential that is much weaker than the harmonic potential at large distances. Although employing a linear potential did not completely prevent trapping in near‐native states, it appears to be a promising approach (see Supporting Information), and the further development of methods along these lines in the future might be sufficient to alleviate this problem.

Simulations with distance restraints can also be useful for preventing drift away from the native structure that may be caused by force field errors. We find, for example, that although the native state of CASP target Tc684 drifted away in unrestrained simulation, it was stable for tens of microseconds when the eight restraints supplied by CASP were applied. More importantly, these eight restraints were sufficient (along with predicted secondary structure but no additional homology‐based information) to drive the protein from an extended conformation to the stable native ensemble in about 140 µs. This example suggests promise for distance‐restrained MD simulations in ab initio structure prediction, even for cases in which the folded state is not accurately described by the force field.

Supporting information

Supporting Information