A 3D‐RISM/RISM study of the oseltamivir binding efficiency with the wild‐type and resistance‐associated mutant forms of the viral influenza B neuraminidase

Abstract

The binding affinity of oseltamivir to the influenza B neuraminidase and to its variants with three single substitutions, E119G, R152K, and D198N, is investigated by the MM/3D‐RISM method. The binding affinity or the binding free energy of ligand to receptor was found to be determined by a subtle balance of two major contributions that largely cancel out each other: the ligand‐receptor interactions and the dehydration free energy. The theoretical results of the binding affinity of the drug to the mutants reproduced the observed trend in the resistivity, measured by IC₅₀; the high‐level resistance of E119G and R152K, and the low‐level resistance of D198N. For E119G and R152K, reduction of the direct drug‐target interaction, especially at the mutated residue, is the main source of high‐level oseltamivir resistance. This phenomenon, however, is not found in the D198N strain, which is located in the framework of the active‐site.

Abbreviations

3D‐RISM

three‐dimensional reference interaction site model

MM/3D‐RISM

molecular mechanics/three‐dimensional reference interaction site model

RDF

radial distribution function

Introduction

Influenza B virus is one of the three distinct influenza virus (Orthomyxoviridae) types which coincides every few years1, 2 with two lineages circulating (Victoria and Yamagata). Influenza B viruses do not have the pandemic potentials like influenza A virus that causes significant morbidity and mortality in humans, but always associate with acute respiratory illness leading to the death in children and adults.3 Hence, this virus, A/H1N1 and A/H3N2 have been included in the seasonal influenza vaccine for the upcoming season as the primary strategy to prevent influenza infection.4 Both experimental and theoretical studies of influenza B virus are considerably less well developed than those for influenza A virus.2, 3

Although all three types of virus share many features and viral activities, influenza B virus harbors unique genetics and can only infect humans.5, 6 Its surface membrane has two glycoproteins: hemagglutinin and neuraminidase, which recognize the terminal sialic acid on host cell membrane components. Neuraminidase plays a role for virus replication by cleaving the sialic acid residues and then releasing the new virions from the infected cell in order to infect new cells. Currently, neuraminidase inhibitors have been employed as anti‐influenza agents either influenza A or B strains7, 8 in which the structure of their active‐site and framework site are almost identical and conserved (Supporting Information Table S1). Hence, we can propose that the effective drug of anti‐influenza B virus could be applicable against influenza A virus. Note that the relationships between influenza A and B strains in terms of amino acid homology and similarity, and RMSD (Supporting Information Table S2) are relatively low (these relationships among the influenza A strains themselves which can be found elsewhere are rather high).

To date, the FDA‐approved neuraminidase inhibitors are zanamivir (Relenza® marketed by GlaxoSmithKline), oseltamivir (Tamiflu® from Roche) and recent peramivir (Rapivab® from BioCryst Pharmaceuticals). The orally administered drug oseltamivir has been widely used and stockpiled for the treatment both of influenza A and B viruses more often than zanamivir,9, 10 although it is less effective for treatment of influenza B and its resistance is commonly reported in both influenza types. The high level of oseltamivir treatment worldwide has led to the rapid spread of mutations of the viral neuraminidase gene that produces drug resistance. The neuraminidase mutations, which lead to oseltamivir resistance in both in vitro and in vivo experiments and/or isolation from patients with resistance, are listed as follows. The seasonal influenza H1N1 and avian influenza H5N1 viruses carry single substitutions in neuraminidase at H274Y or N294S, whereas the pandemic H1N1‐2009 neuraminidases have three single mutations, H274Y, I223R, and S246N, plus the S246N and H274Y double mutation that confer resistance to oseltamivir. In H3N2, the oseltamivir‐resistant variants contain the single mutations of E119V, R292K, and N294S. For influenza B virus, the emergence of the reduced neuraminidase inhibitor sensitivities imparted by the E119G, R152K, and D198N single mutations has been isolated from patients after drug treatment.11, 12, 13 From an in vivo study, the R152K and D198N neuraminidase mutants have resulted a 100‐ and 9‐fold lower susceptibility to oseltamivir inhibition (in terms of IC₅₀ values), respectively, compared to the wild‐type strain.14 Using reverse genetics, oseltamivir was found to have a 31‐ and 252‐fold lowered efficiency against influenza B viruses with the E119G and R152K neuraminidase mutants, respectively, compared with that for the wild‐type.15

The extensively previous studies of oseltamivir‐resistance are the mutated framework residues H274Y and N294S mutations of influenza A H5N1 neuraminidase16, 17, 18 and the important mutations found in N1 and N2 as well as N9 subtypes of influenza A H1N1‐200919, 20, 21 including the R292K mutation of novel H7N9 neuraminidases.22 From the long time dynamics simulations, the results suggest that the loss of major hydrogen bond between drug and residues in the 150‐loop induces the flexibility of this loop which eventually causes the unbinding of oseltamivir from the active‐site pocket.21, 23 In addition, the susceptibility of all neuraminidase inhibitors against E119G of H1N1‐2009 neuraminidase was recently discovered.24 In the present study, we try to ascertain theoretically how oseltamivir inhibits influenza B neuraminidase, and to investigate the source of oseltamivir resistance that is ascribed to the three influenza B neuraminidase single substitutions, which are R152K at the catalytic site and E119G and D198N at the framework site (Fig. 1).

Figure 1.

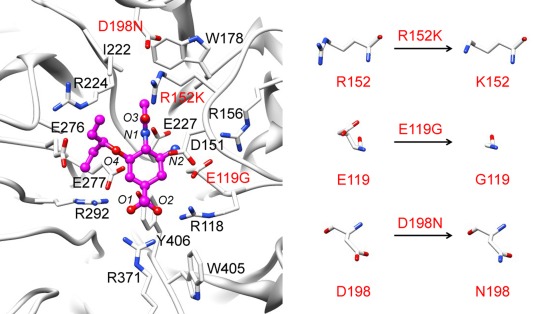
Oseltamivir (bond and stick model) and the bound residues of influenza B neuraminidase wild‐type (black) showing also the three residues in red that were singly mutated for study on the source of discussion oseltamivir resistance (E119G, R152K, and D198N). The oseltamivir heteroatoms are labeled for later discussion.

Two aspects of information should be provided for clarifying the mechanism of a drug to inhibit a receptor: one of those is structural information of the receptor, and the other is the binding affinity of a ligand to the receptor. A structure of a receptor in the wild type is available in many cases from the protein data bank. However, it is not necessarily the case for mutants, since it takes considerable amount of time to determine the structure of a protein from the X‐ray or NMR measurement. Fortunately, the structural change due to a mutation should not be so large in nature that the receptor is still able to keep its intrinsic function. We believe that molecular dynamics (MD) simulation can produce the protein structure perturbed by mutation, starting from the structure of wild type as a template.

On the other hand, it is quite difficult for MD to evaluate the binding affinity of a ligand to the target protein directly. The binding affinity is determined by difference in the free energy between the bound and unbound states of the molecules in which the free energy of a molecule or a molecular complex consists of the intramolecular interactions and the solvation free energy. The difficulty of properly sampling water configurations in MD, especially at the internal cavity of protein, limits its ability to predict the solvation free energy. We employ the 3D‐RISM/RISM method to evaluate the solvation free energy, which is free from the sampling problem inherent to the molecular simulation.25, 26, 27 The theory of 3D‐RISM has been briefly described elsewhere.28, 29, 30 The combination of molecular mechanics and 3D‐RISM solvation approach is known as MM/3D‐RISM calculation.31, 32 This approach directly includes solvent finite‐size effects and explicit water interaction potentials. The previous study shows that MM/3D‐RISM with KH closure can predict the binding of biotin analogues to avidin33 and binding free energy of DNA double stranded oligonucleotides, which are in good agreement with the experimental data.34 Last, this is an honor for us to be a part of the special issue of the journal, which tributes Prof. Ronald Levy for his great accomplishments in biophysics and chemistry. One of the authors (F.H.) especially is gratefull to Prof. Levy for guiding him to the bioscience. The paper presented in the special issue is one of the fluites of his guidance.

Results and Discussion

Factors to determine the binding affinity

The result for the binding free energy of the wild type neuraminidase is shown in the Table 1 along with its components. There is a general trend in which the binding energy and entropy without solvent make large negative contribution to the binding free energy, which is mostly compensated by the large positive contribution from the change in the solvation free energy. The large negative value in $\Delta G_{\text{bind}}^{\text{MM}}$ is dominated by the electrostatic interaction of opposite charges between atoms in the receptor and ligand.

Table 1.

The Free Energy Change Associated with Oseltamivir Binding to the Wild‐Type of Influenza B Neuraminidase and Its Energy Components in kcal/mol

Energetics		Structural components
		Complex	Receptor	Ligand
$\Delta E_{\text{ele}}^{\text{MM}}$	−175.1 ± 4.2	−26,870.5 ± 75.3	−26,417.4 ± 75.2	−278.1 ± 0.6
$\Delta E_{\text{vdW}}^{\text{MM}}$	−28.0 ± 1.1	−3,198.3 ± 8.1	−3,165.4 ± 7.8	−4.8 ± 0.1
$\Delta E_{}^{\text{MM}}$	−203.1 ± 4.7	−30,068.8 ± 80.4	−29,582.8 ± 79.7	−282.9 ± 0.7
$T\Delta S_{}^{\text{MM}}$	−21.9 ± 10.6	3,986.0 ± 11.6	3,962.6 ± 11.6	45.3 ± 1.6
$\Delta G_{\text{bind}}^{\text{MM}}$	−181.2 ± 5.6	−34,054.8 ± 77.9	−33,545.4 ± 77.0	−328.2 ± 0.9
$\Delta \Delta G_{\text{ele}}^{\text{solv}}$	168.9 ± 3.8	−4,365.2 ± 75.3	−4,447.2 ± 74.7	−86.9 ± 0.9
$\Delta \Delta G_{\text{cav}}^{\text{solv}}$	12.0 ± 0.8	9,851.5 ± 8.4	9,776.7 ± 8.1	62.8 ± 0.1
$\Delta \Delta G_{\text{bind}}^{\text{solv}}$	180.9 ± 4.6	5,486.3 ± 67.0	5,329.5 ± 66.7	−24.1 ± 0.9
$\Delta G_{\text{bind}}^{}$	−0.3 ± 1.1	−28,568.5 ± 12.8	−28,215.9 ± 12.1	−352.2 ± 0.2

On the other hand, the large positive contribution to $\Delta \Delta G_{\text{bind}}^{\text{solv}}$ originated from the dehydration free energy of both the receptor and ligand. It is worthwhile to look at the dehydration free energy more closely. $\Delta \Delta G_{\text{bind}}^{\text{solv}}$ is further decomposed into two contributions; the electrostatic contribution $\Delta \Delta G_{\text{ele}}^{\text{solv}}$, and the free energy due to the cavity formation $\Delta \Delta G_{\text{cav}}^{\text{solv}}$ which is calculated by removing all the charges from the protein and the ligand. $\Delta \Delta G_{\text{cav}}^{\text{solv}}$ is positive for both the receptor and the ligand, while $\Delta \Delta G_{\text{ele}}^{\text{solv}}$ makes negative contribution. Apparently, $\Delta \Delta G_{\text{cav}}^{\text{solv}}$ gives a minor contribution to the binding free energy in this particular case. This is because the exclusion volume is dominated essentially by the receptor. Such a situation may be quite different in the case where the active‐site is composed of mainly hydrophobic residues. So, let us concentrate our attention to the electrostatic contribution to the binding free energy, or $\Delta \Delta G_{\text{ele}}^{\text{solv}}$. $\Delta \Delta G_{\text{ele}}^{\text{solv}}$ depends sensitively on the charges of atoms in a receptor and a ligand. The contribution should be always positive, because solvent molecules accessible to the complex become less upon binding compared to the free forms, in particular, at the active‐site. As exhibited in Figure 2(a), there are five amino acid residues in the active‐site of the receptor, which potentially make hydrogen‐bonds with either water or the ligand. Correspondingly, there are three moieties, ‐COO^‐, ‐NHAc, and ‐ ${\text{NH}}_3^{+}$ in the ligand, which can form hydrogen‐bonds with either the amino acid residues or water molecules, while the ‐OCHEt₂ side chain was accommodated in hydrophobic pocket between E267 and R224 residues with van der Waals interaction [Fig. 3(a)]. The conformational change of this bulky group during the complexation is shown in terms of the dihedral angles (see Supporting Information Fig. S3). The dihedral angles of oseltamivir are basically conserved between free form and complex form, although there are some changes in the angular distribution depending on the type of mutations. Interestingly, the less susceptibility of oseltamivir against influenza B than influenza A virus8, 9, 14, 35 may be relevant to the existence of glycine (G) at residue 347 instead asparagine (N), tyrosine (Y), and or glutamine (Q) of influenza A neuraminidase (Supporting Information Table S1), which cannot stabilize the ‐COO^‐ group of oseltamivir. When an oseltamivir molecule is in free form, the residues and the moieties are making hydrogen‐bonds with solvent water molecules. Some or all the hydrogen‐bonds with water molecules will be lost upon the complexation. But, the loss of hydrogen‐bonds between the solutes and solvent is largely compensated by the gain of hydrogen‐bonds between the receptor and the ligand.

Figure 2.

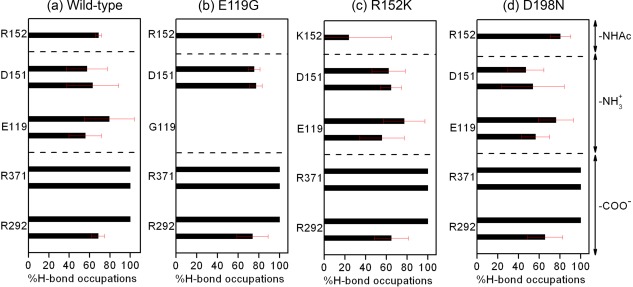
Percentage occupation of hydrogen bonds averaged over three MDs with different velocities for the oseltamivir‐neuraminidase interactions (mean ± SD) of the (a) wild‐type and the (b) E119G, (c) R152K and (d) D198N neuraminidase mutations.

Figure 3.

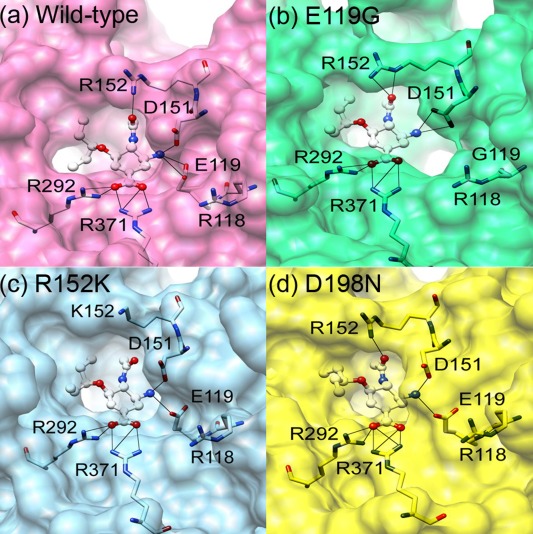
Close up of oseltamivir (bond and stick model) in the neuraminidase binding pocket (surface) from the representative structure of each system. The likely hydrogen bonds between the five amino acid residues and ligand are shown as a black line.

In this respect, it is very important to determine how the desolvation penalty gets involved and which water molecules are removed from the active‐site of protein and ligand upon binding. In following subsection, we focus our attention on the distribution of water molecules before and after the ligand binding takes place.

Our results concerning the binding affinity for the wild‐type of neuraminidase show a correct trend qualitatively, but significantly underestimate the binding affinity compared to the experimental values, −11.91, −11.45, and −10.20 kcal/mol, converted from the IC₅₀ values 1.83, 4, and 33 nM, respectively.14, 15 There are three sources conceivable for the errors: (1) improper evaluation of the structural entropy, (2) not including salt effect, and (3) the free energy calculation due to 3D‐RISM. In the following, we briefly discuss about the source of errors.

Our calculation includes the contributions from the structural entropies of the protein, ligand, and their complex, which are making non‐negligible contributions to the binding free energy. However, the results may not be conclusive quantitatively, because the entropy was evaluated based on the normal mode analysis in vacuum,36 that does not properly account for the structural fluctuation of molecules in solution. The structural entropy of a molecule in solution is originated essentially from the structural fluctuation which is affected by the detailed distribution of solvent molecules around and inside the molecule.37, 38 The normal mode analysis does not include such a solvent effect on the structural fluctuation.

The protein contains many charged residues in its active‐site, while the ligand also includes several charged moieties, as is shown in Figure 1. So, their binding affinity may be influenced significantly by the electrolytes included in the solution. We did not take the electrolytes into consideration due to the lack of information for the solution condition in the experiment. It is our future plan to include the salt effect into the calculation.

It is well documented that the 3D‐RISM calculation overestimates the free energy concerning hydrophobic hydration or the cavity formation, and that magnitude of the error is proportional to the partial molar volume of solute.39 So, it is likely that the solvation free energy of each species in the thermodynamic cycle (Fig. 7) suffers from a significant error. However, the errors will be largely canceled out along the thermodynamic cycle to get the binding free energy, since the partial molar volume of the protein‐ligand complex is expected to be similar to the sum of the quantities for each molecule. In the case of evaluating the effect of mutation, which will be discussed in binding affinity topic, the problem will become even less, because the errors will be mostly canceled out by taking difference of the binding free energy between the two variants. Therefore, we suppose that the errors from the free energy calculation due to 3D‐RISM are minor.

Figure 7.

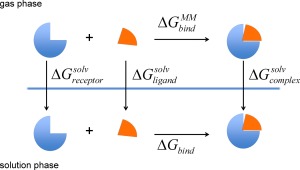
The thermodynamic cycle for calculating the binding free energy.

Distribution of water molecules around the ligand and active‐site of wild‐type receptor

As depicted in Figure 4, the 3D‐distribution function of water oxygen and hydrogen atoms around the ligand before and after the complexation of wild‐type, as well as the corresponding radial distribution functions (RDF) from particular atoms in the moieties is shown. It is quite obvious from the figure that the hydrogen bonds between ligand and water molecules are disappeared or largely reduced upon the complexation. Those reductions of the hydrogen‐bond with water molecules upon complexation are obviously the origin of the dehydration penalty concerning the ligand.

Figure 4.

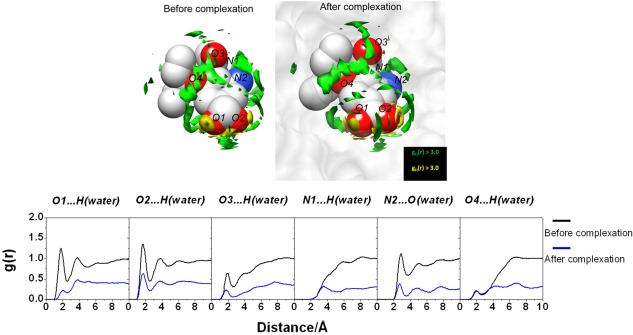
(Upper) 3D‐distribution function of water O‐atom and H‐atom around oseltamivir via 3D‐RISM calculation with g(r) > 3.0 before and after the complexation. (Lower) 3D‐RISM RDF of hydrogen‐bonded pairs between oseltamivir heteroatoms and water molecules before and after the complexation calculated from the free oseltamivir and oseltamivir in complex with wild‐type neuraminidase.

Similar phenomena can be observed in the receptor side as depicted in Figure 5, the 3D‐distribution function and RDF of water molecules around the residues in the active‐site of the wild‐type receptor before and after the complexation. It is distinctive that in most of the cases water molecules hydrogen‐bonded to the amino acid residues in the bulk solution are either disappeared or largely reduced after the complexation, in particular the distribution around the residues of R292 and R371. So, it is again obvious that the change in the hydrogen‐bond with water molecules upon the complexation is the important source of the dehydration penalty concerning the receptor.

Figure 5.

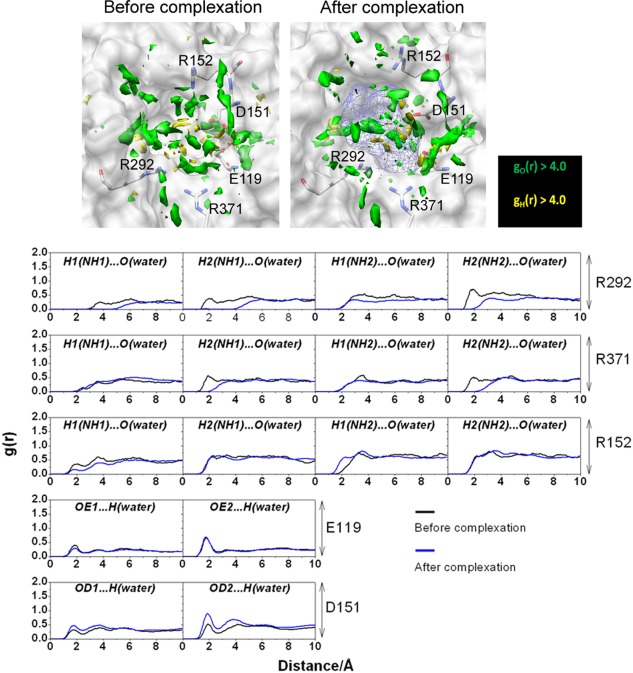
(Upper) 3D‐distribution function of O‐water (green) and H‐atoms (yellow) with g(r) > 4.0 within 7.0 Å of oseltamivir (depicted as blue mesh sphere). (Lower) 3D‐RISM RDF of hydrogen‐bonded pairs between water molecules and five amino acid residues before and after complexation

The change in the water distribution upon the ligand binding shows more complexity depending on the position in the binding site: some are virtually intact, and some are even increased. In free form, oseltamivir and neuraminidase protein are stabilized through the water solvationg. After complexation, the removing of water molecules from neuraminidase binding pocket was placed by ligand molecule evidenced from the decreased water distribution of both ligand and receptor. However, the some water molecules remain in the pocket as the bridging water formed interaction with the residue and the ligand, which can be observed from the sharp and high probability of water distribution around the O2 and N2 ligand atoms (Fig. 4) and the carboxylate group of the D151 residue (Fig. 5).

Binding affinity of oseltamivir to the mutants

The energetics related to the binding affinity of oseltamivir to the different mutants of neuraminidase are listed in Table 2 along with the experimental binding free energy ( $\Delta G_{}^{IC50}$) converted from IC₅₀ data. The MM/3D‐RISM binding free energy is the summation of the contribution from solute molecules ( $\Delta G_{\text{bind}}^{\text{MM}}$) and solvation free energy ( $\Delta \Delta G_{\text{bind}}^{\text{solv}}$), where $\Delta G_{\text{bind}}^{\text{MM}}$ is a combination of molecular mechanics energy ( $\Delta E_{}^{\text{MM}}$) and structural entropy of protein ( $T\Delta S_{}^{\text{MM}}$) as is defined in the MM/3D‐RISM calculation. The relative energy $\delta \Delta G_{\text{bind}}$ of mutant strains is the difference of binding free energy in comparison with that of the wild type. Although the statistical errors of the binding free energies are relatively large, all mutation systems show the same trend compared to those of wild‐type. This implies that the error from MM/3D‐RISM calculation was similar to all mutation systems, hence, we will focus the trend of the binding affinities.

Table 2.

The Average MM/3D‐RISM Binding Free Energies and Their Components of Four Influenza B Neuraminidase Complexes Are in kcal/mol

Energetics	Wild‐type	E119G	R152K	D198N
$\Delta E_{}^{\text{MM}}$	−203.1 ± 4.7	−171.0 ± 3.0	−199.0 ± 11.6	−200.2 ± 2.2
$T\Delta S_{}^{\text{MM}}$	−21.9 ± 10.6	−22.1 ± 13.8	−21.4 ± 9.2	−22.0 ± 9.6
$\Delta G_{\text{bind}}^{\text{MM}}$	−181.2 ± 5.6	−148.8 ± 2.7	−177.6 ± 9.3	−178.2 ± 1.9
$\Delta \Delta G_{\text{bind}}^{\text{solv}}$	180.9 ± 4.6	151.8 ± 2.5	178.6 ± 7.4	178.3 ± 2.5
$\Delta G_{\text{bind}}^{}$	−0.3 ± 1.0	2.9 ± 2.5	0.9 ± 2.0	0.1 ± 2.1
$\delta \Delta G_{\text{bind}}$	−	3.2	1.3	0.4
$\delta \Delta G_{}^{IC50}$	−	2.0a	3.4a/2.7b	1.3b

The relative binding free energy from the prediction ( $\delta \Delta G_{\text{bind}}^{}$) and experiment converted from IC₅₀ ( $\delta \Delta G_{}^{IC50}$) was compared for mutated systems.

^aRef. 15.

^bRef. 14.

The computational results are roughly in accordance with the experimental trend, but for the D198N mutant the affinity is relatively close to the wild type. In the following, let us look closely at the change of water distribution around the mutated residues in each mutant.

(1) E119G mutant

In the mutant, one of the hydrogen‐bonding sites is lost entirely [Fig. 2(b)] due to the mutation from the negatively charged and long side chain of glutamate (E) to the nonpolar and short side chain of glycine (G) [Fig. 3(b)]. This is the same as that found previously for E119V19, E119A40, and E119G24 substitution of influenza A H1N1‐2009 and neuraminidase inhibitor complexes. The loss of the hydrogen‐bond site brings two effects into the binding affinity. First, the hydrogen‐bonding between the residue and the ligand is lost, which shifts the binding‐free energy toward the positive side. Second, the hydrogen‐bond between the residue and water molecules is lost, which makes the dehydration penalty of the receptor less. The substitution of the large residue (E) by a small residue (G) introduces another effect into the binding affinity, which is concerned with the dehydration penalty of the ligand. Shown in Figure 6(b) is the RDF of O‐water atoms and heteroatoms of the drug in the E119G‐drug complex, compared with that of the wild type [Fig. 6(a)]. The figure clearly indicates that the RDF around the ‐ ${\text{NH}}_3^{+}$ group in this mutant is not reduced upon binding as much as that in the wild type. It is because the substitution created a cavity for a water molecule hydrating the ligand to be accommodated in the binding site without dehydrating. The effect will lead to the reduction of the dehydration penalty of the ligand. The reduction in the binding affinity due to the mutation is determined by loss of the hydrogen bonding between the receptor and the ligand, which exceeds the reduction of the dehydration penalty both in the receptor and the ligand.

Figure 6.

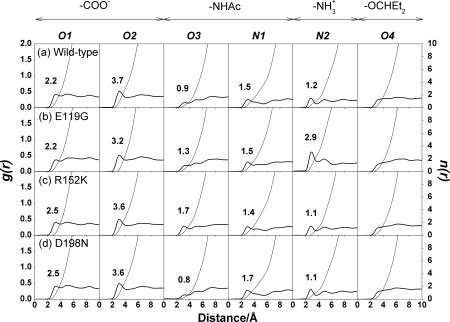
3D‐RISM radial distribution function (g(r)) between the heteroatoms of oseltamivir (O1‐O4, N1 and N2; see Fig. 1) and O‐water atoms is illustrated. The occupation numbers of water molecules (n(r))

integrated up to the first minimum are also given.

(2) R152K mutant

In the mutant, one of the basic residues, arginine (R), is replaced by the other basic residue lysine (K). The mutation causes a mild effect on the electrostatic interactions of solute free energy, because both residues bear charges with the same positive sign. The interaction depends apparently on the geometry of the residues. Arginine is slightly bigger in size than lysine. The smaller size of lysine makes the receptor‐ligand interaction unfavorable due to the increased separation to the hydrogen‐bond partner in the drug Figure 3(c). The situation is reflected in the frequency of the hydrogen‐bonds between the residues and drug as shown in Figure 2(c). The frequency is greater for arginine than for lysine, which is different to the entire loss of the K152 interaction in zanamivir and R152K H1N1‐2009 complex from single simulation.40 On the other hand, the dehydration penalty for lysine is less than that for arginine (Table 2). The results can be understood from the RDF of water around the ‐NHAc group in the drug molecule [Fig. 6(c)]. The hydrogen‐bond peak around the O3 atom of the ‐NHAc group in the R152K mutant is not reduced as much as that in the wild type. This indicates that some portion of water molecules around the residue and the drug can remain upon binding without dehydration.

(3) D198N mutant

This is the mutation of a charged residue to a polar residue. The effect of the mutation on the structure should be significant, because a net charge is removed from the protein. Nonetheless, the effect on the binding affinity is minor, because the location of the substitution is at framework of the active‐site, which has no direct interaction with oseltamivir [Fig. 1]. The crystal structure of oseltamivir and D198E influenza B neuraminidase complex discovers that the carboxylate group of E276 does not rotate sufficiently to interact with R224 forming the hydrophobic pocket for oseltamivir binding,41 however, this is not found in wild‐type or mutant system. In fact, the frequency of hydrogen‐bond between the drug and the receptor, exhibited in Figure 2(d) and Fig. 3(d), hardly changes for all the hydrogen‐bond pairs. Accordingly, the RDFs of water around the drug and the residues do not suffer at all from the mutation [in Fig. 6(d)]. This might be the reason why the affinity of the drug to the mutant does not change much compared to the wild type.

Conclusions

The aim of this research is to understand the oseltamivir efficiency toward wild‐type as well as the three single mutations E119G, R152K, and D198N in terms of molecular recognition. The MM/3D‐RISM approach was employed to explore the binding affinity of oseltamivir to the receptors, and the change in water distribution upon the binding.

The results show the binding affinity or the binding free energy of ligand to receptor is determined by a subtle balance of two major contributions, which largely cancel out each other: the ligand‐receptor interactions and the dehydration free energy. It was found that the dehydration free energy is determined by change in the detailed distribution of solvent at the active‐site before and after the ligand binding. The findings suggested that the detailed description of solvent distributions at the active‐site of receptor and its complex with ligand is required to evaluate the binding affinity accurately.

The theoretical results of the binding affinity of the drug to the mutants reproduced the observed trend in the resistivity, which is measured by IC₅₀; the high‐level resistance of E119G and R152K, and the low‐level resistance of D198N. Both the direct drug‐target interactions and the dehydration penalty are reduced due to the mutation, compared to those of the wild type, which make compensatory effects on the binding affinity. The former effect exceeds the latter, causing the reduction of the binding affinity of the drug to the neuraminidase variants. It is the main source of high‐level resistance of the virus mutants to oseltamivir. The resistivity of the D198N variant is not high since substitution is located at framework of the active‐site.

The theoretical analysis made in the present paper remains to be qualitative, since several elements of physics are not properly taken into consideration, especially the structural entropy and solution condition including electrolytes. The study to include those elements of physics in the analysis is in progress in our group.

Materials and Methods

Preparation of systems

All preparations for MDs were performed using the AMBER 10 software package.42 The crystal structure of B/Beijing/1/87 wild‐type neuraminidase in complex with sialic acid, Protein Data Bank (PDB) code 1NSC43 was chosen as the starting structure for structure of the receptor. To construct the complex between the wild‐type neuraminidase and oseltamivir, the sialic acid was replaced by the oseltamivir structure taken from the PDB code 2HU444 without any modification. The crystallographic calcium ions and water molecules were kept. The resultant wild‐type neuraminidase‐oseltamivir complex is shown in Figure 1. Then, this system was used as the template for preparing the three variants, E119G, R152K and D198N, by single residue mutation to the residue of interest (Fig. 1) using the LEaP module in AMBER 10. The ionizable residues (K, R, D, E, and H) were considered to be in their protonated state at pH 7.0. All missing hydrogen atoms of the protein and ligand were added using the LEaP module and were then minimized in order to remove the bad contacts. Each system was neutralized by chloride ion (Cl^‐) and immersed in a TIP3P45 water box that extended at least 13 Å from the protein surface. The AMBERff03 force field was employed for all protein atoms,46 while the force field and RESP charge of oseltamivir were retrieved from previous work.47

Protocol for MDs

All MD calculations were performed using the SANDER module implemented in AMBER. The solvent molecules (only) were first optimized, and subsequently the whole system was minimized with 1000 steps of steepest descent and 2000 steps of conjugate gradient. For the thermalization step, the temperature applied for each system was gradually increased from 10 K to 310 K with 2 fs of time step for 100 ps. After the target temperature was reached, the simulated system was maintained at that temperature for 100 ps using a weak‐coupling algorithm for the barostat and thermostat constants. All atomistic MDs were run at 310 K and 1 atm using the periodic boundary condition and the NPT ensemble. The SHAKE algorithm was applied to constrain the bond length involving the hydrogen atoms, while the Particle mesh Ewald (PME) was used to treat the long‐range electrostatic interactions.48 The nonbonded interaction cutoff was set at 12 Å and the time step at 2 fs. An unrestrained simulation was performed for 20 ns. Then to obtain precision for the drug‐target interaction calculation, two more MDs with different starting velocities were performed for each system. The global RMSD of all the neuraminidase protein atoms relative to the starting structure and the plots of the distance measured from the oseltamivir atom to its neuraminidase binding‐residue atom versus the simulation time were monitored to verify the stability of the simulated system (see Supporting Information Fig. S1 and S2).

3D‐RISM calculations

The protein was placed at the center of a 729,000 ų box (90 × 90 × 90 Å) with a grid spacing of 0.5 Å. The TIP3P model was chosen for the water‐water, water‐protein, and water‐ligand interactions, while the AMBER force field was adopted for the interactions among atoms in the protein and ligand. The TIP3P solvent susceptibility function was obtained using the rism1d module with a grid size of 0.025 Å and a tolerance of 1e‐12 for the convergence criteria. The 3D‐RISM equation was closed using the KH‐closure with a grid size of 0.5 Å and a tolerance of 1e‐5.49

MM/3D‐RISM calculation

The binding free energy is calculated according to the standard thermodynamic cycle illustrated in Figure 7, and the suffix "MM" indicates that those quantities are calculated with the molecular mechanics (MM) method for the molecules in "vacuum". The binding free energy is defined by the free energy change due to the ligand binding:

$$\begin{array}{c}\Delta G_{\text{bind}}=G_{\text{complex}}^{}-(G_{\text{receptor}}^{}+G_{\text{ligand}}^{})\\ =\Delta G_{\text{bind}}^{\text{MM}}+\Delta \Delta G_{\text{bind}}^{\text{solv}}\end{array}$$

where $G_{\mathrm{x}}^{}$ denotes the total free energy of the spices x in solution, which is sum of the MM energy, $G_{\mathrm{x}}^{\text{MM}}$, and the solvation free energy, $\Delta G_x^{\text{solv}}$. (x is the "complex," "receptor," or "ligand.") $\Delta G_{\text{bind}}^{\text{MM}}$ is the free energy change upon ligand binding in "vacuum".

$$\begin{array}{c}\Delta G_{\text{bind}}^{\text{MM}}=G_{\text{complex}}^{\text{MM}}-(G_{\text{receptor}}^{\text{MM}}+G_{\text{ligand}}^{\text{MM}})\\ =E_{\text{complex}}^{\text{MM}}-(E_{\text{receptor}}^{\text{MM}}+E_{\text{ligand}}^{\text{MM}})-T{S}_{\text{complex}}^{\text{MM}}+(T{S}_{\text{receptor}}^{\text{MM}}+T{S}_{\text{ligand}}^{\text{MM}})\\ =\Delta E^{\text{MM}}-T\Delta S^{\text{MM}}\end{array}$$

where ΔE ^MM and ΔS ^MM denote the changes in the interaction energy and entropy, respectively, upon ligand binding. The structural entropy is obtained from the normal mode analysis (NMA). ΔE ^MM is further decomposed into two contributions, the electrostatic and van der Waals interactions as follows.

$$\Delta E_{}^{\text{MM}}=\Delta E_{\text{ele}}^{\text{MM}}+\Delta E_{\text{vdW}}^{\text{MM}}$$

The change in the solvation free energy upon ligand binding, $\Delta \Delta G_{\text{bind}}^{\text{solv}}$, is defined by,

$$\Delta \Delta G_{\text{bind}}^{\text{solv}}=\Delta G_{\text{complex}}^{\text{solv}}-\left(\Delta G_{\text{receptor}}^{\text{solv}}+\Delta G_{\text{ligand}}^{\text{solv}}\right)$$

where $\Delta G_{\text{receptor}}^{\text{solv}}$, $\Delta G_{\text{ligand}}^{\text{solv}}$, and $\Delta G_{\text{complex}}^{\text{solv}}$ denote the solvation free energies of receptor, ligand, and their complex, respectively.

Three different 20 ns simulations with different starting velocity were performed on the oseltamivir‐neuraminidase complexes concerning the wild‐type, E119G, R152K, and D198N strains of influenza B. The production phase of each simulation contains 7500 snapshots. The binding free energy was calculated based on the 3D‐RISM, MM, and NMA by taking an ensemble average over the three trajectories with different initial conditions, each having 100 snapshots extracted from the trajectories at every 0.2 ps. The MM/3D‐RISM calculations were performed using the MMPBSA.py50 program, while NMA was carried out using the AMBER 12 program36. The MM/3D‐RISM binding free energy will be compared with the experiment binding free energy ( $\Delta G_{}^{IC50}$) estimated from the IC₅₀ values using $\Delta G_{}^{IC50}\approx \mathrm{RT}\text{ln}$ IC₅₀.

Supporting information

Supporting Information