AB‐Bind: Antibody binding mutational database for computational affinity predictions

Abstract

Antibodies (Abs) are a crucial component of the immune system and are often used as diagnostic and therapeutic agents. The need for high‐affinity and high‐specificity antibodies in research and medicine is driving the development of computational tools for accelerating antibody design and discovery. We report a diverse set of antibody binding data with accompanying structures that can be used to evaluate methods for modeling antibody interactions. Our Antibody‐Bind (AB‐Bind) database includes 1101 mutants with experimentally determined changes in binding free energies (ΔΔG) across 32 complexes. Using the AB‐Bind data set, we evaluated the performance of protein scoring potentials in their ability to predict changes in binding free energies upon mutagenesis. Numerical correlations between computed and observed ΔΔG values were low (r = 0.16–0.45), but the potentials exhibited predictive power for classifying variants as improved vs weakened binders. Performance was evaluated using the area under the curve (AUC) for receiver operator characteristic (ROC) curves; the highest AUC values for 527 mutants with |ΔΔG| > 1.0 kcal/mol were 0.81, 0.87, and 0.88 using STATIUM, FoldX, and Discovery Studio scoring potentials, respectively. Some methods could also enrich for variants with improved binding affinity; FoldX and Discovery Studio were able to correctly rank 42% and 30%, respectively, of the 80 most improved binders (those with ΔΔG < −1.0 kcal/mol) in the top 5% of the database. This modest predictive performance has value but demonstrates the continuing need to develop and improve protein energy functions for affinity prediction.

Abbreviation and Symbols

ΔΔG

change in free energy of binding

Ab

antibody

mAbs

monoclonal antibodies

Fab

fragment antigen binding

CDR

complementarity determining region

MD

molecular dynamics

KIC

kinematic closure

ROC

receiver operator characteristic

AUC

area under the curve

SPM

single point mutation

SPR

surface plasmon resonance

Yeast Disp. Flow Cyt

yeast surface display analyzed using flow cytometry

ELISA

enzyme‐linked immunosorbent assay

phage ELISA

phage display ELISA

KinExA

kinetic exclusion assay

ITC

isothermal titration calorimetry

ASA

accessible surface area

SASA

solvent‐accessible surface area

bASA

buried accessible surface area

VdW

van der Waals

CI

confidence interval

D. Studio

Discovery Studio

Introduction

Antibodies (Abs) are an important class of molecules used in research and increasingly as therapeutic agents to treat human diseases. Currently, 46 monoclonal antibodies (mAbs) are marketed for therapeutic use in the United States or Europe, and an increasing number of mAbs are entering late‐stage clinical studies or receiving first approvals.1, 2, 3, 4 Therapeutic antibodies have certain advantages over small molecules or other protein therapeutics, such as longer serum half‐lives, higher avidity and selectivity, and the ability to invoke desired immune responses.5, 6, 7, 8 Antibody paratopes—the parts of antibodies that interact with the target antigen—can recognize almost any biomolecular target, with a large range of specificities and affinities. This binding flexibility is due to the antibody complementarity determining regions (CDRs), 6 loop regions that are parts of the fragment antigen‐binding (Fab) heavy and light chains. The CDRs are supported on a β‐sheet framework and can adopt a number of canonical conformations, although CDR3 of the heavy chain exhibits more conformational diversity.9 The high mutational tolerance of CDRs enables optimization of properties necessary for the development of effective antibody‐based therapeutics, including the critical properties of high affinity and specific binding. Fab domains isolated from phage/yeast display screens on the basis of binding must frequently be further engineered to improve drug‐like properties such as stability, solubility, and reduced immunogenicity.5, 10, 11 Constant regions of Ab heavy chains are also optimized to enhance or reduce effector‐mediated immune response and/or half‐life.12 Antibody engineering is typically accomplished using high‐throughput screening of combinatorial libraries, most typically by phage display,13, 14 but the enormous candidate sequence space makes it very challenging to identify optimal molecules that meet specifications.

Knowledge of the structure of an antibody–antigen or antibody–receptor complex provides insight into how the antibody recognizes its binding partner and can guide the process of antibody design. But structures alone do not directly reveal the influence of specific amino‐acid mutations on binding affinity. Molecular modeling can in theory be used to predict specific favorable contacts, and this information can direct the design of high‐throughput experimental screens. However, the predictive performance of computational tools must be established before these can be effectively used in prospective antibody paratope design projects.

Accurate prediction of the effect of a mutation on protein binding energy is a challenging task,15 requiring knowledge of the interface structure and the relative energies of other possible states, including conformational variants of the bound state as well as unbound states.16, 17, 18 The role of solvent is a particular challenge, whether modeling water‐mediated interface contacts or correctly accounting for tradeoffs in protein–solvent and protein–protein interactions.19, 20 Methods such as free‐energy perturbation or thermodynamic integration, which model these complexities in detail, are computationally expensive and are not always accurate.21, 22, 23 Empirical methods that use implicit solvation models are computationally more tractable, but accuracy is often further reduced.24 Even faster and less accurate methods used to model protein interactions often ignore complex physics and use potentials based on the statistics of known structures. Combinations of these approaches are also available.

Computational methods have been used to design antibodies with improved binding properties, particularly when combined with input from expert designers.8, 18 Lippow et al. generated higher affinity variants for 3 antibody targets by computationally selecting mutations that improved antibody–antigen interaction energy, focusing on binding electrostatics.25 Similarly, Clark et al. searched for affinity improving mutations by evaluating electrostatics and van der Waals (VdW) energies, and these authors were able to generate an eightfold improvement in binding affinity for anti‐VLA1 antibody Fab domain.26 Farady et al. designed a human serine protease MT‐SP1 inhibitor antibody (E2) to recognize murine MT‐SP1 using a molecular mechanics‐based binding energy evaluation with an implicit solvation model. In that work, eight computationally identified mutations were tested experimentally, and one showed a 14‐fold improvement in binding specifically to the mouse antigen.27

Computational method development and evaluation rely on experimental data for benchmarking. A recent community collaboration project retrospectively analyzed the ability of different computational methods to predict the effects of 20 possible substitutions at approximately 50 positions on two (non‐antibody) influenza hemagglutinin binders. High‐throughput yeast display enrichment data were used as an experimental measure of binding; it is not clear how closely these values reflect binding affinities.20 Independent research groups computed protein stability and binding affinity using a range of scoring functions that accounted for packing, electrostatics, and/or solvation terms. The best methods were able to identify about a third of the mutations that improved binding. Successful methods considered the effects of mutations on both protein stability and binding affinity and carried out side‐chain sampling and backbone relaxation during mutant structure prediction. In a separate project, ensembles of protein conformations generated using a variety of tools that sample backbone structures such as molecular dynamics (MD), kinematic closure (KIC), or backrub sampling were used to predict the effect of mutations in Herceptin antibody–Her2 complexes.28 This study showed that sampling backbone space using KIC or the backrub approach was superior to using MD to identify amino acids that were well tolerated at interface positions in a phage display study. Most recently, binding energy calculations that combined molecular mechanics with Poisson–Boltzmann electrostatics and an evaluation of solvent‐accessible surface area (SASA) were benchmarked against 173 mutations across 7 protein complexes that included anti‐VLA1, anti‐lysozyme, anti‐EGFR, anti‐HER2 antibodies, and the Barnase–Barstar complex. The predictor successfully identified 89% of hot spot alanine mutations, where a hot spot is a residue that results in at least 1 kcal/mol loss in affinity.29

Several large experimental datasets have been compiled that facilitate testing of modeling methods. Kortemme and Baker compiled 773 protein interface single‐point mutations across 19 systems that were subsequently used to evaluate an interaction model for hotspot identification.30 The Kortemme and Baker dataset was subsequently used to benchmark the performance of several other computational models, including some based on a molecular mechanics description of interactions.31, 32, 33 Similar to the Kortemme and Baker dataset, the Binding Interface Database (BID) includes over 1300 mutational measurements across 170 different proteins complexes.34 Most recently, the SKEMPI database compiled binding free energy data for more than 3000 mutant variants of heterodimeric protein–protein interactions involving 159 different complexes, along with some data reporting Δk _on, Δk _off, ΔΔH, and ΔΔS.35 These databases contain primarily single‐point alanine substitutions at protein–protein interfaces, and include a relatively small number of mutations in antibodies. For example, the SKEMPI database includes around 300 antibody–antigen mutants, of which more than 75% are single‐residue mutations to alanine.

To increase the amount of relevant binding data available for computational method validation—with a specific emphasis on improving antibody engineering—we compiled mutational data from antibody–antigen, antibody–effector, and antibody‐like protein complexes with known structures. Our AB‐Bind database complements existing data compilations by including many nonalanine mutations. The database enables computational benchmarking studies of existing methods and can thereby be used to drive improvements in modeling methodology. In this article, we present the database and its characteristics along with the results of different computational methods tested on the task of predicting the effects of mutations on binding.

Results

AB‐Bind database

To construct the AB‐Bind database, we curated a diverse set of binding data for parent and mutant antibody complexes. Antibody–antigen interfaces differ from other protein interfaces in that they are mediated by 6 CDR loops, where 5 of the loops have a definable set of canonical conformations.36, 37 We focused on antibody interactions with large globular antigens and also included Fc‐receptor, nanobody–antigen, and antibody–antigen‐like complexes to increase the amount of data for analysis. Although additional binding data are available for antibody complexes with haptens and peptidic antigens, these data were not included in this version of AB‐Bind due to the small contact areas of these complexes38 and the greater conformational flexibility of unbound peptidic ligands, which increases the uncertainty in molecular modeling.39, 40, 41, 42, 43 AB‐Bind includes 1101 mutational data points with experimentally determined binding affinities. The protein complexes and experimental assays used to generate the data are summarized in Supporting Information, Table S1. To minimize the uncertainty introduced when experimental observations from various projects are aggregated, we prioritized inclusion of complexes for which numerous mutations have been made and measured by the same laboratory, with the same techniques. Consequently, AB‐Bind data points are derived from studies of just 32 complexes; between 7 and 246 variants are included for each complex. The data come from complexes with crystal structures either of the parent complex or of a homologous complex with high sequence identity. Thus, AB‐Bind enables structure‐based computational modeling of all mutants. More than 700 interactions in the AB‐Bind database are not included in BID, SKEMPI, or the Kortemme et al. datasets mentioned above.

Figure 1 summarizes the content of AB‐Bind using violin plots, where the distribution of experimentally measured changes in binding free energies are illustrated using kernel estimated probability density, and the minimum, median, and maximum values are indicated using red lines. Overall, the data feature a large range of experimentally measured changes in binding energies (Supporting Information, Fig. S1). Although most mutations weaken binding, 26% of variant sequences show an improvement in measured binding affinity relative to the parent complex (ΔΔG < 0 kcal/mol). In Figure 1(A), mutations are divided into subgroups by the experimental technique used to measure binding affinity. AB‐Bind includes binding affinities measured by many methods: surface plasmon resonance (SPR), AlphaScreen, enzyme‐linked immunosorbent assay (ELISA), kinetic exclusion assay (KinExA), phage display ELISA (phage ELISA), yeast surface display analyzed using flow cytometry (Yeast Display Flow Cyt.), and enzymatic assays. Brief descriptions of all experimental techniques used for affinity measurements are provided as part of the Supporting Information. Analysis of the database by experimental technique is useful because not all methods are equally accurate or precise.30 Biophysical techniques such as SPR and isothermal titration calorimetry (ITC) provide quantitative measurements, whereas quantitative accuracy is sacrificed for throughput in some studies, e.g., using ELISA or phage ELISA assays to generate large datasets.

Figure 1.

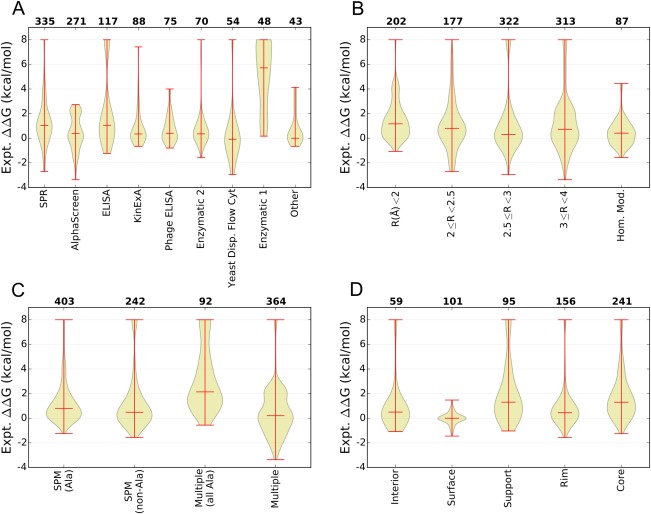
Analysis of the content of the AB‐Bind Database. (A–D) Violin plots illustrating the median, range, and distribution of experimentally observed changes in free energies of binding (ΔΔG) in kcal/mol over subsets of the database, where the vertical axis gives the observed ΔΔG, the bottom horizontal axis describes a subset of the database, and the top horizontal axis lists the number of variants found within the specified subset. The data are grouped based on (A) the experimental technique used, (B) the X‐ray structure resolution, (C) the mutation type, or (D) the location of the mutation site for single point mutations. Location definitions are given in the Materials and Methods section.

Mutations reported in the AB‐Bind database come from 27 protein complexes with experimentally determined structures (Supporting Information, Table S2) and 5 complexes for which it was possible to build a homology model based on a template with 76–90% sequence identity, as described in Supporting Information, Table S3 (see Methods for details). Figure 1(B) divides the database into exclusive categories using the parent PDB resolution, which ranges from 1.50 to 3.79 Å, and the homology modeled structures. Not all structures were solved at high resolution: 701 variants correspond to PDB structures with good resolution (<3 Å), 313 correspond to structures with resolution >3 Å, and for 87 variants the complex structures analyzed here were derived from homology models. However, the quality of most structures was high according to the MolProbity server, when judged by an all‐atom clash score that is defined as the number of unfavorable all‐atom steric overlaps per 1000 atoms.44, 45 Twenty‐one out of 27 crystal structures has clash scores <20, and only two structures had a clash score in the mid‐40s. Statistics for the crystal structures, including the templates used for homology modeling, are reported in Supporting Information, Table S2 and the homology models are listed in Supporting Information, Table S3. Also, the accessible surface area buried upon complex formation (bASA) for each parent PDB structure is plotted in Supporting Information, Figure S2. On average, 56% ± 5% (std dev) of bASA in AB‐Bind parent complexes is nonpolar.

Mutations can be classified by the type of substitution and by the surface exposure of the parent residue at the mutated site. Figure 1(C) summarizes the types of mutations in the database, with protein variants grouped into those with only single‐point mutations (SPM) and non‐SPM (multiple mutations per variant) categories, made up of 645 and 466 variants, respectively. Many published databases are composed primarily of alanine SPMs.30, 46 In the AB‐Bind data set, 403 variants are alanine SPMs and an additional 242 variants include nonalanine SPMs. There are 92 variants with multiple alanine substitutions and 364 variants with multiple substitutions that include nonalanine mutations. Many database variants with multiple substitutions are made up of SPMs characterized individually; 119 variants with multiple substitutions were exclusively composed of SPMs with known ΔΔGs and 25 variants with multiple substitutions had at least one SPM with a known ΔΔG. The binding affinity distributions for alanine and nonalanine SPMs are similar. Within the AB‐Bind dataset, multiple alanine mutations tend to be associated with weakened binding more than SPMs, but multiple nonalanine mutations in this database are frequently associated with improved binding affinities. This is because many variants with multiple nonalanine mutations resulted from combining individual mutations already known to increase binding affinity. The SPM mutation types were also grouped based on the substitution types into non‐exclusive groups such as alanine to nonalanine, polar to nonpolar, and so on. These mutation types were further mapped into exclusive subsets based on whether they came from antibody–antigen, antibody–Fc receptor, nanobody or antibody‐like complexes (Supporting Information, Figure S3). Although there are many nonalanine to alanine (nA2A) mutations, other types of substitutions involving polarity changes or charge changes are also represented in the database.

SPM locations in relation to the protein–protein interface were characterized as interface or noninterface positions; see Methods for details. The noninterface residues (ΔASA = 0) were further grouped as interior or surface, whereas interface residues (ΔASA > 0) were further grouped as support, rim, or core; see Figure 1(D) for residue distributions across sites and the binding energy changes associated with each class. Out of the 160 SPMs designated as noninterface, 59 positions were classified as interior and the remaining 101 positions were grouped as surface; surface mutants show the least variation in binding affinity. Out of 492 protein–protein interface positions, 95 were classified as support, 156 as rim, and 241 as core. Most surface mutations show less deleterious effect on binding than interface mutations. Also, mutations in the rim region are slightly more likely than surface or core mutations to improve binding relative to the parent. Similar to findings from other analyses of protein interface mutations,47 free energies of binding associated with interface mutations in the AB‐Bind database are highly variable.

Scoring potentials

We used the curated experimental binding data to benchmark a variety of scoring potentials and evaluate their ability to predict changes in binding free energies (ΔΔG) upon mutation. The general structure‐based workflow is described in the Methods and is summarized in Supporting Information, Figure S4. In addition, complete protocols and command lines are given in Supporting information. We only evaluated methods that can score mutants in a timeframe appropriate for pharmaceutical discovery, i.e., those fast enough to evaluate thousands of mutations in less than a few days when using a computing cluster of several hundred processors. This ruled out approaches such as free‐energy perturbation, which may become more commonly accessible as the computational algorithms become more robust and graphics processor units become widely used.48, 49, 50, 51

To evaluate different methods, binary classifications of variants as improved vs weakened binders were calculated using each computational method and reported as the area under the curve (AUC) of receiver operator characteristic (ROC) curves such as those shown in Figure 2 and Supporting Information, Figure S5. The details of the binding energy calculations are described in the section titled Methods. In most binding energy calculations, the protein partners were assumed to interact as rigid bodies. For most of the AB‐Bind complexes, unbound structures are not available. Thus, to assess the validity of this rigid body binding assumption, the average root‐mean‐square displacements of interface residue Cα atoms between the bound and unbound conformations (iRMSD)52 of 17 antibody–antigen complexes not in AB‐Bind were analyzed.53 The average iRMSD for these antibody–antigen X‐ray crystal structures was 0.64 Å (range: 0.17–1.24 Å, median: 0.51 Å), indicating available antibody–antigen interfaces do not undergo large structural changes upon complex formation. Nevertheless, assuming rigid‐body binding is clearly a severe approximation.

Figure 2.

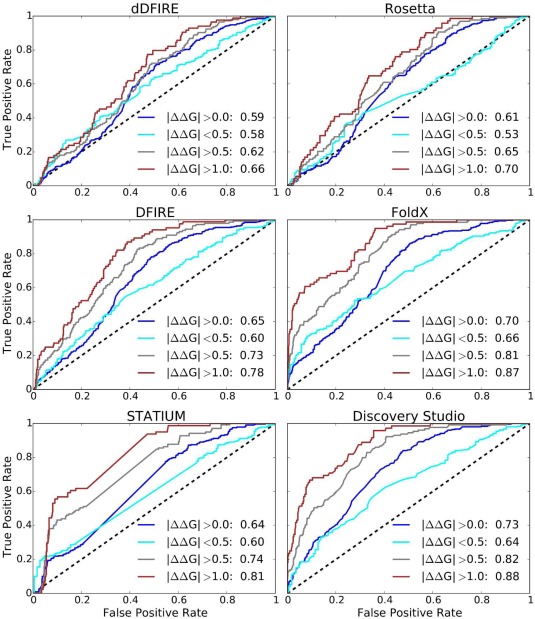
Performance of interaction predictors. ROC curves illustrate performance in classifying mutations as improved vs weakened binders, relative to a parent complex, for the whole data set (blue), or low confidence (|ΔΔG| < 0.5 kcal/mol—cyan), medium confidence (|ΔΔG| > 0.5 kcal/mol—gray), and high confidence (|ΔΔG| > 1 kcal/mol—red) subsets.

As a simple reference model for predicting changes in binding energy, we used the buried accessible surface area (bASA). NACCESS54 was used to determine accessible surface area (ASA) for the complex and unbound structures, and the buried interface was computed for each variant and the parent complex (see Methods for details). In this model, greater buried surface predicted improved binding. For comparison with this naïve approach, we evaluated the performance of various statistical potentials for predicting changes in free energies of binding, specifically benchmarking the DFIRE,55 dipolar DFIRE (dDFIRE),56 and STATIUM57, 58 potentials. DFIRE is an all‐atom, distance scaled, pairwise potential derived using a database of about 1000 nonhomologous protein structures with resolution <2 Å. dDFIRE is a modified version of DFIRE that accounts for dipole–dipole interactions. STATIUM is a pairwise statistical potential that scores how well a protein complex can accommodate different pairs of residues in the parent complex geometry; our implementation considers only interface positions. STATIUM is the only computational method that did not require generation of mutant structures; only the structures of the parent complexes and the identities of the mutated residues were necessary for the calculation.

All‐atom protein force fields from FoldX (FOLDEF),59, 60 Discovery Studio (CHARMMPLR),61, 62 and Rosetta63, 64, 65 were also evaluated for their predictive performance. In general, these force fields describe van der Waals (VdW), hydrophobic packing, electrostatic, and desolvation forces using either semiphysical or statistical terms. The scoring functions are parameterized using empirical/theoretical data to reproduce experimentally observed structures, folding stabilities, and/or binding hot spots. In FoldX, terms representing interactions such as VdW, electrostatics, solvation effects, hydrogen bonds, water bridges, and entropy effects for the backbone and side‐chain atoms are weighted to reproduce experimentally measured effects of single‐point mutations on protein folding stability. In Rosetta, terms representing physical interactions are weighted and combined into a single energy function to predict binding energy hot spots in protein interfaces.30 VdW and solvation energies are evaluated using approximate physical expressions, whereas statistically derived terms describe pairwise electrostatics and orientation‐dependent hydrogen bonds, as well as side‐chain and backbone conformational preferences. In Discovery Studio, binding affinities are calculated as a sum of physical terms including VdW, generalized Born electrostatics, an entropy term based upon side‐chain mobility, and structure‐based SASA nonpolar terms. The method uses the CHARMPLR force field. The relative weighting of these four terms is optimized to reproduce experimentally determined protein stability data.

Computational performance

Changes in binding free energies upon mutation (ΔΔG) were predicted using the bASA, Rosetta, dDFIRE, DFIRE, STATIUM, FoldX, and Discovery Studio scoring functions. The quantitative correlations between experimental and computed free energy changes were low (Supporting Information, Table S4): Pearson correlation coefficients ranged from 0.16 (Rosetta) to 0.45 (Discovery Studio). Figure 2 shows the ROC curves for correctly binning variants into increased or decreased binding affinity categories for statistical and force‐field‐based energy potentials, while the ROC curve for the reference bASA approach is shown in Supporting Information, Figure S5. We looked at performance over the whole dataset (blue), and for low‐, medium‐, and high‐confidence subsets (in, cyan, gray, and brown, respectively). The medium‐ and high‐confidence subsets include only variants with |ΔΔG| > 0.5 or 1.0 kcal/mol, respectively, while the low‐confidence subset includes those variants with |ΔΔG| < 0.5 kcal/mol. Supporting Information, Table S5 lists the computed AUC values and associated 95% confidence intervals (CI) after bootstrap sampling for all scoring potentials. All methods, including the simple surface area‐based method, showed some ability to distinguish mutations that increase binding affinity from those that decrease binding affinity. However, performance was close to random for the low‐confidence mutants, for which experimental ΔΔG values are subject to measurement errors close to the magnitude of the observed energy changes.

In accordance with the assumptions of our bASA model, we found that burial of additional surface area at the interface is correlated with an increase in binding affinity. Using ΔbASA as predictor of binding affinity gave an AUC of 0.63 (0.59–0.66) for correctly binning variants as higher or lower affinity than the parent (95% confidence intervals are given in parentheses). When variants with small changes in binding affinities were excluded, average performance improved slightly; AUC values were 0.67 (0.63–0.73) and 0.68 (0.63–0.75) for correctly binning medium‐ or high‐confidence variants, respectively. Rosetta and dDFIRE performance was comparable to that of the simple bASA model. DFIRE and STATIUM performed better, giving AUC values of 0.78 (0.74–0.83) and 0.81 (0.76–0.85), respectively, for high‐confidence variants. FoldX and Discovery Studio predictions gave the best AUC values of 0.87 (0.83–0.91) and 0.88 (0.85–0.92) for binning high‐confidence variants, respectively. FoldX and Discovery Studio predictive performance over the whole dataset was significantly better than other scoring functions studied in this work (Supporting Information, Table S6).

The FoldX energy function was among the best performing potentials studied in this project. In addition to providing good AUC values for classifying variants, FoldX also gave one of the best correlations between predicted and observed ΔΔG values, although this correlation was very weak (r = 0.34). We analyzed individual FoldX components to determine if any were predictive when used alone. Interestingly, the electrostatic, VdW, and hydrophobic and polar components of the solvation terms all gave very similar AUC values, although they did not perform as well as the complete scoring function (Supporting Information, Fig. S6). Greater differences were apparent when examining the correlation coefficients between the observed ΔΔG values and FoldX electrostatics, VdW, polar, or nonpolar solvation terms. Pearson r values were 0.52, 0.27, −0.33, and 0.23 for these energy terms, respectively, compared to 0.34 for the complete FoldX scoring function. The magnitude of experimental correlations with VdW, polar, and nonpolar solvation terms are similar. The sign for the polar solvation term is negative because burial of polar atoms disfavors, rather than favors stability.

The AB‐Bind dataset combines information from multiple sources. Protein‐binding affinities were measured using a range of experimental techniques in a number of research laboratories. In addition, the crystal structures used in model generation differed in quality. Thus, we grouped the data into categories based on experimental technique, structure quality, mutation type, and mutation location for SPMs, and looked at the prediction performance for subsets of mutations. Figure 3 shows the AUC values calculated for each category over all subsets of the dataset, and Supporting Information, Tables S7–S13 list p‐values for comparing the ROC curves for these subsets for bASA, Rosetta, dDFIRE, DFIRE, STATIUM, FoldX, and Discovery Studio predictions. When the predictions of different scoring functions were compared across experimental approaches, we found that performance predicting SPR data was significantly better than performance predicting ELISA‐generated data (significance was defined as a p‐value of 0.05 or less). Predictive performance over the homology‐modeled subset of structures was similar to the performance of methods run on crystal structure subsets for FoldX and STATIUM approaches.

Figure 3.

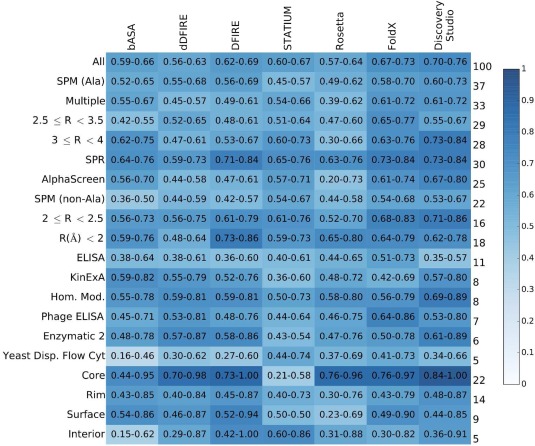
Breakdown of predictor performance over database subsets. Each cell is colored according to AUC value, see heatmap key at right, and lists 95% confidence intervals. Row labels on the left indicate database subgroup names, and labels on the right give the percentage of the database within the named subgroup. The column headings indicate the computational method used.

Enrichment

In antibody engineering, a real‐world challenge is to minimize the number of experiments required to identify mutations that lead to improved affinity. We evaluated the ability of different methods—and combinations of methods—to prioritize candidate mutations for experimental testing. To do this, all variants or only the SPM variants were separately ranked by each method. Then, the percentage of mutants that improve binding affinity was calculated for a given top fraction of the ranked lists.

Figure 4(A) illustrates the percentage of variants with ΔΔG < −1.0 kcal/mol that could be identified as a function of the percentage of the database screened. Over the whole dataset, the top‐performing methods, FoldX and Discovery Studio, provided slightly more than 10‐fold enrichment in the top 1% of the database (enrichment = % of tight binders discovered/% of dataset considered, see Table 1 for values). The naïve bASA and DFIRE models provided around fivefold and twofold enrichment, respectively, in this interval while other methods did not result in any enrichment. To illustrate the extent to which DFIRE, FoldX, and Discovery Studio identified the same or different mutations that enhance binding, Figure 4(B) shows the Venn diagram of the number of improved‐affinity variants (ΔΔG < −1.0 kcal/mol) within the top 5, 10, or 15% of the computationally ranked database. In the top 5% of the entire 1101‐variant database, DFIRE, FoldX, and Discovery Studio identified different stabilized variants; only 11 out of 89 total variants with ΔΔG < −1.0 kcal/mol were found by all three methods. Combining the predictions of the different methods, it was possible to identify 45 stabilized variants in the top 5% of the three ranked lists (discovering these would require testing 115 unique variants). The overlap of predictions made by different methods increased as we probed deeper into the list; 28 and 39 high‐affinity binders were identified by all three methods by sampling the top 10 or 15% of each list, respectively, out of a maximum of 56 or 57 that could be identified using any method (discovering these would require testing 200 or 298 variants, respectively, to evaluate the top 10 or 15% of each list).

Figure 4.

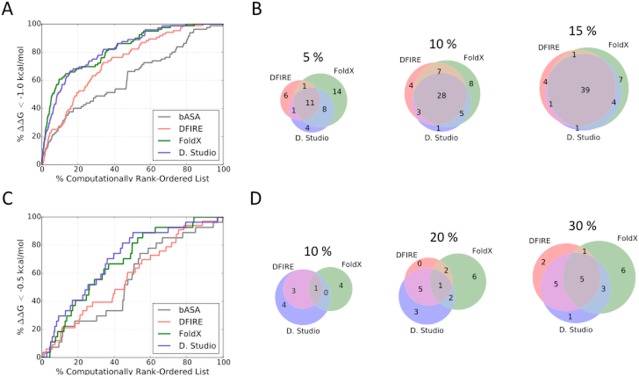
Enrichment of improved‐affinity binders. (A) Plot illustrating the percentage of all variants with ΔΔG < −1.0 kcal/mol found in the indicated top percentage of the computationally rank‐ordered list. (B) Venn diagrams comparing the number of variants with ΔΔG < −1.0 kcal/mol that were identified within the top 5%, 10%, or 15% of the computationally ranked database. (C) Plot illustrating the percentage of SPM variants with ΔΔG < −0.5 kcal/mol found in the indicated top percentage of the computationally rank‐ordered SPM list. (D) Venn diagrams comparing the number of SPMs with ΔΔG < −0.5 kcal/mol that were found within 10%, 20%, or 30% of the computationally ranked database.

Table 1.

Enrichment of Improved‐Affinity Variants (ΔΔG < −1 kcal/mol) in the Rank‐Ordered Dataset (Enrichment = Percentage of Tight Binders Discovered/Percentage of Dataset Considered)

% Database	bASA	DFIRE	dDFIRE	STATIUM	Rosetta	FoldX	Discovery Studio
1	6.8	2.2	0.0	0.0	0.0	12.7	11.4
5	3.4	4.4	2.6	4.8	2.5	8.9	6.5
10	2.6	2.7	2.0	5.3	2.2	6.0	5.1
15	2.5	2.6	1.7	3.8	2.3	4.3	4.2
20	2.0	2.5	1.7	3.1	2.1	3.4	3.4
30	1.6	2.1	1.6	2.1	1.7	2.4	2.5
40	1.3	1.9	1.5	1.6	1.5	2.1	2.1
50	1.3	1.6	1.3	1.8	1.3	1.7	1.8

We also examined the ability of the computational methods to enrich SPMs for variants with improved affinity. This is more difficult as the observed range in affinity changes for SPMs is smaller (Supporting Information, Fig. S1B), and computational performance on small ΔΔG variants is generally poor (Fig 2 and Supporting Information Fig. S5). However, enrichment of stabilizing SPMs is an important test because in silico affinity maturation approaches often rely on mutating residues individually and then combining the favored substitutions to generate variants with further improved binding. Figure 4(C) plots the percentage of improved‐affinity SPMs with observed ΔΔG < −0.5 kcal/mol versus the fraction of all SPMs (645 in total) that would have to be screened to discover them; Table 2 reports the enrichment rates for all scoring functions considered. For SPMs, the enrichment performance is poor relative to enrichment over the whole dataset. In the top 10% of the database, Discovery Studio identified just 8 improved‐affinity SPMs, whereas DFIRE and FoldX identified only 4 and 5 out of 27 total improved‐affinity SPMs [Figure 4(D)]. Only 1 variant was identified by all three methods in the top 10% of the database. In the top 30% of the SPM subset, DFIRE identified 13 improved‐affinity SPMs, while FoldX identified 15 and Discovery Studio identified 14 examples. The number of improved‐affinity SPM variants predicted in the top 30% by all methods considered here remained small (5 variants), indicating that an approach that only considers those mutations identified by all scoring schemes would miss many SPMs that improve binding. In total, 23 out of 27 improved‐affinity SPM variants were identified in the top 30% of the database by any of the methods considered; discovering these would require testing of 344 SPM variants.

Table 2.

Enrichment of Improved‐Affinity SPM Variants (ΔΔG < −0.5 kcal/mol) in Rank‐Ordered SPM Subsets (Enrichment = Percentage of Tight Binders Discovered/Percentage of Dataset Considered)

% Database	bASA	DFIRE	dDFIRE	STATIUM	Rosetta	FoldX	Discovery Studio
1	3.4	0.0	0.0	0.0	0.0	0.0	0.0
5	1.5	1.2	1.2	0.7	0.0	2.2	2.2
10	1.1	1.2	1.2	1.5	0.4	1.8	2.9
15	1.5	1.4	0.8	1.2	0.5	2.0	2.2
20	1.3	1.2	0.8	0.9	1.3	2.0	2.0
30	1.0	1.3	0.9	1.0	1.1	1.8	1.8
40	0.8	1.1	0.9	0.7	0.9	1.7	1.8
50	1.2	1.2	1.0	0.7	1.0	1.6	1.7

Next, we investigated whether a combination of predictions made by different scoring methods could improve the enrichment rates for the whole dataset or the SPM subset. We used rank‐by‐number, rank‐by‐rank, and rank‐by‐best consensus scoring schemes (see Methods) to evaluate enrichment of improved‐affinity binders (ΔΔG < −1.0 kcal/mol for all mutants and ΔΔG < −0.5 kcal/mol for SPM subset only).66 Figure 5 plots the consensus enrichment rates using FoldX and Discovery Studio predictions only, where panels A and B illustrate performance over the whole dataset and SPM subset, respectively. Table 3 lists the enrichment values. The consensus schemes provide very little improvement over the performance using Discovery Studio or FoldX alone. The rank‐by‐rank and rank‐by‐number schemes provide some early enrichment advantage for analyzing the whole dataset. However, this advantage disappears when sampling 15% or more of the database. There are no detectable early improvements of a consensus method over Discovery Studio when evaluating the more challenging SPM subset of the database. The consensus approaches provide a slight enrichment around 20–30% of the SPM dataset. To further evaluate whether increasing the number of computational predictions incorporated into the consensus scheme could improve enrichment, we computed consensus scores using DFIRE, STATIUM, Rosetta, FoldX, and Discovery Studio predictions, with the results reported in Supporting Information Figure S7 and Table S14. Combining additional predictors in the consensus calculations did not provide any additional enrichment advantage.

Figure 5.

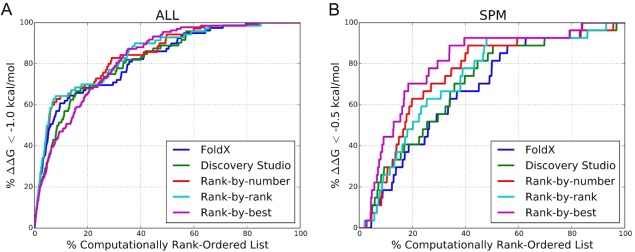
Enrichment of improved‐affinity binders with consensus scoring. Plot showing the percentage of (A) all variants with observed ΔΔG < −1.0 kcal/mol or (B) SPM variants with observed ΔΔG < −0.5 kcal/mol found in the computationally rank‐ordered lists using rank‐by‐number, rank‐by‐rank, and rank‐by‐best consensus methods computed using FoldX and Discovery Studio predictions.

Table 3.

Enrichment of Variants With Improved Binding Affinity (ΔΔG < −1.0 kcal/mol for All‐Variant Analysis or ΔΔG < −0.5 kcal/mol for SPM) Using Rank‐by‐Number, Rank‐by‐Rank, and Rank‐by‐Best Consensus Schemes Computed Using FoldX and Discovery Studio Predictions Only

	All					SPM
% Database	FoldX	Discovery Studio	Rank‐by‐number	Rank‐by‐rank	Rank‐by‐best	FoldX	Discovery Studio	Rank‐by‐number	Rank‐by‐rank	Rank‐by‐best
1	12.7	11.4	14.3	14.3	9.5	0.0	0.0	0.0	0.0	0.0
5	8.9	6.5	9.8	9.8	6.4	2.2	2.2	1.5	0.7	3.6
10	6.0	5.1	6.4	6.4	4.7	1.8	2.9	2.2	2.6	4.4
15	4.3	4.2	4.4	4.4	3.7	2.0	2.2	2.9	2.5	3.4
20	3.4	3.4	3.5	3.5	3.3	2.0	2.0	3.1	2.4	3.5
30	2.4	2.5	2.8	2.6	2.6	1.8	1.8	2.3	2.1	2.7
40	2.1	2.1	2.1	2.2	2.2	1.7	1.8	2.1	1.9	2.3
50	1.7	1.8	1.9	1.9	1.9	1.6	1.7	1.8	1.8	1.8

Discussion

In this article, we describe the AB‐Bind mutational database, which contains protein–protein interaction affinity data with an emphasis on antibody–antigen complexes. We report binding data compiled from the literature for mutations made in complexes with known structures, including data for mutations that improve binding relative to a parent antibody complex. AB‐Bind consists of approximately 45% alanine‐only mutants, and 55% mutants with at least one non‐Ala substitution, thus providing a resource that enables computational analysis of the effects of chemically diverse mutations. Although these data are useful for identifying and diagnosing limitations in prediction and scoring protocols, the data are biased toward mutations that reduce binding affinity. Often, practical applications will require identification of mutations that improve binding affinity by more than a trivial amount and, because these are hard to discover, such examples are rare in AB‐Bind. When compared to a parent, only 7% of all variants improve affinity by more than 1 kcal/mol (ΔΔG < −1 kcal/mol); only 4% of SPM variants improve affinity by more than 0.5 kcal/mol (ΔΔG < −0.5 kcal/mol). However, an ability to identify mutations that are deleterious for binding would also be beneficial in narrowing the amino‐acid search space and for reducing the risk of disrupting binding when making mutations to optimize other physical–chemical properties of the antibody.

We used AB‐Bind to benchmark a representative subset of computational scoring functions for their ability to predict binding affinity changes and to enrich a set of candidate mutations in those that improve binding. Performance distinguishing improved‐affinity from nonimproved mutations was modest, particularly when predicting small binding affinity changes. The higher experimental uncertainty for such measurements may limit the maximum performance that can be expected on this task.35, 53 Computational performance was better for correctly classifying medium‐ and high‐confidence variants (those with |ΔΔG| > 0.5 and 1.0 kcal/mol, respectively) as improved or weakened binders. Modest success on this task suggests that these types of approaches, although not highly reliable, nevertheless have potential to guide experimental studies. Performance is limited by the numerous approximations and assumptions made to reduce computation time and render the modeling problem tractable. Here, these included (1) the assumption that the crystal structure is an appropriate representation of the protein complex structure in the binding experiments, despite differences in experimental conditions such as pH, (2) the assumption of minimal conformational change upon complex dissociation, (3) the extremely limited conformational sampling of the structures of the bound and unbound states, (4) neglect of explicit solvent and ion molecules, and (5) use of approximate energy functions, including statistical potentials that do not explicitly treat atomic interactions.

One strategy to improve computational binding affinity predictions could be to decompose existing scoring function into their components, and reweight these components to better predict experimental data in AB‐Bind. Although this could improve performance on our benchmarks, the risk is that any such energy function could be over‐fit to a biased dataset and consequently not be useful for new prediction tasks.67 FoldX was developed by optimizing the fit of predicted energies to stability data for more than 1000 single‐point protein mutants. Despite the use of stability data for parameterization, FoldX has been previously applied to predict changes in binding affinity,59, 68 and we observed good performance relative to other scoring functions in a large‐scale test of this application. Kortemme and Baker also used protein‐binding data to parameterize Rosetta for predicting binding free energies.30 Our efforts to improve prediction by reweighting FoldX terms using regression techniques to fit AB‐Bind data did not lead to significant improvements in performance (data not shown). However, we did not perform an exhaustive test of parameter reweighting for multiple energy functions as part of this work.

Another strategy that can potentially improve prediction performance is to combine results from multiple scoring functions. This approach, known as consensus scoring, has seen widespread use in small‐molecule drug discovery over the past 15 years.69, 70, 71 The quality of the results can depend on the chosen scoring functions and their specific weaknesses, as well as the specific method used to combine individual functions' scores into an overall consensus score. Although there are many reports of success, in other cases, individual functions outperform consensus methods.66, 72, 73 Our results do not argue strongly for a consensus approach to discovering mutations that improve affinity, but we did observe slight improvement in enrichment both for all mutations and for SPMs at certain cut‐offs. It is of course possible that consensus scoring methods that incorporate functions beyond those considered here may provide additional improvements.

Current practice in antibody optimization involves not only designing small numbers of individual point mutants but also screening large protein libraries using display technologies. Notably, the complete sequence space of an antibody interface is too large to sample comprehensively. A common solution is to sample sequences randomly, but this may be nonoptimal for identifying the best mutants. Despite the limited capacity of current computational methods to predict specific binding energies, these methods can enrich a set of protein variants in those that improve binding, relative to random sampling, and can also help identify destabilizing mutations [Figs. 4(A,C) and 5]. Therefore, current methods should be useful for focusing protein libraries so that they sample more promising regions of sequence space. A further application of binding energy prediction methods is to identify CDR residues that are predicted not to make significant contributions to binding. Such residues would become available for mutation to optimize properties such as stability, immunogenicity, aggregation, and post‐translational modification.74 The ability to accurately determine which residues do or do not contribute to differentiated behavior of closely related sequences may also be relevant during analysis of intellectual property claims.

In summary, we constructed AB‐Bind, a database of antibody‐focused binding affinity measurements with significant contribution of non‐Ala mutations, as well as mutations that increase binding affinity. We hope the limitations of this dataset will motivate publication of additional antibody optimization experiments that will expand the data available for testing new modeling methods. We used AB‐Bind to identify differences in performance among several published scoring protocols, and these results can guide further improvement in scoring function design. Finally, some of the methods tested showed slight enrichment relative to random sampling of an SPM dataset with diverse mutation types (Table 2), indicating their potential to improve the efficiency of library screening experiments in a real‐world setting.

Materials and Methods

Datasets

The database entries were manually curated and organized. Experimentally observed binding affinities are reported as the change in free energy of binding upon mutagenesis (ΔΔG = ΔG _mutant − ΔG _parent) in kcal/mol. Experimental ΔΔG data are reported in an Excel worksheet (see Supporting Information), where related PDB IDs are also provided. The individual datasets are summarized in Supporting Information, Table S1.

Parent complex structures

The curated crystal structures of parent complexes are summarized in Supporting Information, Table S2. When more than one biological unit existed in the crystal structure, the first unit was selected and used in subsequent modeling. For antibody–antigen systems where the heavy and light chains had different chain names in the PDB, the chain IDs were changed to their canonical H and L naming representation. For each crystal structure, quality metrics such as the resolution, R_work, R_free, and MolProbity scores, and experimental conditions such as pH and temperature were included in the database.

For datasets without accompanying crystal structures, template structures with high sequence identity were used to generate homology models of the parent complex using default parameters in BioLuminate.75, 76 The homology model sequence was aligned to the target using Clustal W.77 Loop models were generated using an automated workflow in BioLuminate. Briefly, loop models required as part of this process were obtained by searching the PDB for templates of the appropriate length‐and‐stem geometry. Once a feasible template was identified, the loop side chains were mutated and repacked to give the desired sequence, and the resulting structures were minimized. Supporting Information, Table S3 summarizes the templates and the sequence identity to the target for all homology models.

For each parent complex, the accessible surface area (ASA) buried by complex formation (bASA) was computed using Eq. (1), where ASA_AB represents the ASA of the protein–protein complex and ASA_A, ASA_B represent the ASA of the individual protein components of the complex. For ASA calculations, the protein surface was scanned using a probe radius of 1.4 Å using NACCESS and values were compared to references values for each amino acid that correspond to that residue in ALA–XXX–ALA tripeptide, giving relative ASA values.54 Residue locations were classified into exclusive interface and noninterface groups. Interface residues were further classified as rim, support, and core, and noninterface residues were also further classified as surface or interior, based on the classification approach described by Levy.78 Briefly, interface residues had ΔASA > 0 and were further grouped as support, rim, and core depending on the computed ASA in the unbound and bound states. Support residues had <25% side‐chain ASA in the unbound configuration, indicating that these amino acids are mostly buried prior to complex formation. The rim residues had >25% side‐chain ASA in the bound configuration, indicating that they are partially solvent exposed even after complex formation. Core residues had ASA >25% in the unbound state, but <25% in the bound state, indicating burial upon complex formation. Noninterface residues exhibited no change in ASA between the bound and unbound configurations (ΔASA = 0) and were further grouped as interior or surface depending on the computed ASA in the unbound state. Interior residues had <25% of the side‐chain surface exposed, whereas surface residues had >25% ASA in the unbound state.

$$bASA=\Delta AS{A}_{Interface}=(AS{A}_A+AS{A}_B)-AS{A}_{AB}$$ (1)

PyMOL scripts

A PyMOL79 function was developed to enable users to better visualize mutated residue positions and interacting residues in the parent complex, where hydrogen bonds between the position and the rest of the protein are also highlighted. We provide the PyMOL function and an example script to generate a sample PyMOL session as part of the Supporting Information. The “show_ interactions” command requires the PDB name and a mutant residue selection as STDIN, for example $pymol  show_interactions_example.pml – 1MPH.pdb “H:T50V” “H:K64E,L:S28Q” “reads in a PDB file named 1MPH.pdb and illustrates two space separated mutants specified within the quotation marks. Mutants are formatted as following: < chain name >: < parent residue name > < residue number > < mutant residue name >.

Structure generation

Mutant structures for computational analysis were generated using FoldX (release 3.0),59 Discovery Studio (release 4.0),61 or Rosetta (release 3.1).63 The scripts used to generate structures are provided as part of the Supporting Information. Briefly, the parent and mutant complex models were generated based on their corresponding crystal‐ or homology‐modeled parent structure. In FoldX, missing side chains were filled, hydrogen atoms were added, side‐chain rotamers were optimized, and the structure was relaxed to remove any VdW clashes in the parent complex. In the mutant generation step, the mutated side chains were built and repacked using a rotamer library; this was followed by side‐chain minimization of mutant residues to relieve VdW clashes. When using Rosetta, parent and mutant structures were optimized using the following protocol: all residues within 8 Å of mutated positions in the parent conformation were repacked using either the mutant or the wild‐type amino acid at the design site. This was the only workflow that considered conformational flexibility of bound and unbound states, thus the only non‐rigid‐body calculation. This was repeated 20 times for the bound and unbound conformations and the minimum energy of each was used in binding energy calculations. In Discovery Studio, the parent structures were prepared by correcting nonstandard atom names, selecting single conformations for sites with alternative conformations by taking the position with highest occupancy, and adding missing side‐chain atoms. Subsequently, side chains for residues with missing atoms were optimized, waters removed, missing loops modeled, and protonation states of titratable side chains were predicted using a pH of 7.4. In mutant generation, new side chains were built and optimized in the unbound state. The computational models of the parent and mutant complexes were used for the binding energy calculation.

Scoring

For the bASA model, the accessible surface area (ASA) buried upon complex formation for a parent vs mutant structure was computed, using structures generated with FoldX. For each structure, the buried ASA (bASA) was computed using eq. (1) and changes in bASA (ΔbASA) after in silico mutagenesis were calculated using eq. (2).

$$\Delta bASA=\Delta \Delta ASA=\Delta AS{A}_{Interface}^{MUT}-\Delta AS{A}_{Interface}^{WT}$$ (2)

For Rosetta, DFIRE, dDFIRE, FoldX, and Discovery Studio, the binding interaction energies for mutant and wild‐type protein complexes (ΔE_Interaction) were computed using eq. (3), where E_AB is the energy of the complex, and E_A and E_B are the energies of the interaction units in the unbound states. The change in interaction energy after mutagenesis was computed using eq. (4), where $\Delta E_{Interaction}^{MUT}$and $\Delta E_{Interaction}^{WT}$ represent the binding energies computed for mutant and parent complexes. For DFIRE and dDFIRE, FoldX‐generated structures were used in scoring. For Rosetta, Discovery Studio, and FoldX, structures were generated using the same method with which they were evaluated.

$$\Delta E_{Interaction}=E_{AB}-(E_A+E_B)$$ (3)

$$\Delta \Delta E_{Interaction}=\Delta E_{Interaction}^{MUT}-\Delta E_{Interaction}^{WT}$$ (4)

STATIUM estimates binding affinities using eq. (5) and is the only scoring potential that did not require input structures of the mutant complexes. The STATIUM potential has been described by DeBartolo et al.58 Briefly, STATIUM takes as input the structure of a parent complex. The method then identifies pairs of interacting residues at the complex interface and calculates the effects of substitutions on complex stability by examining the statistics of pairwise residue–residue interactions with the same geometry in a nonredundant PDB database. After complex‐specific residue pair frequencies are tabulated, STATIUM can score millions of sequences in a matter of seconds.

$$\Delta E=E_{MUT}-E_{WT}$$ (5)

Evaluation of predictive performance

The area under the curve (AUC) of the receiver operator characteristic (ROC) was used to assess the ability of each computational method to correctly group variants as improved or weakened binders. A mutant variant that was both computationally predicted and experimentally shown to have improved binding relative to the parent scaffold was a true‐positive (TP) and a false‐positive (FP) prediction corresponded to a variant that was computationally predicted to have improved binding but experimentally shown to have weakened binding. Similarly, a true‐negative (TN) prediction was a mutant variant both computationally predicted and experimentally shown to have decreased binding relative to the parent scaffold, and a false‐negative (FN) prediction arose if a variant was computationally predicted to have decreased binding but was experimentally shown to have improved binding. The true‐positive rate (TPR) and false‐positive rate (FPR) are given as TPR = TP/(TP + FN) and FPR = FP/(FP + TN). To generate ROC curves, the TPR was plotted as a function of the FPR, and the AUC was calculated as the integral under the curve using Python 2.7 (Anaconda); see Supporting Information for code snippets. Using this evaluation scheme, a random predictor would result in an AUC of 0.5 and a perfect predictive model would give an AUC of 1. The AUCs were determined over the whole dataset, the low‐confidence subset (|ΔΔG| < 0.5 kcal/mol), the medium‐confidence subset (|ΔΔG| > 0.5 kcal/mol), and the high‐confidence subset (|ΔΔG| > 1 kcal/mol). The 95% confidence intervals for the AUCs were calculated using 100,000 bootstrap samples. Briefly, 100,000 data points were chosen using sampling with replacement and the AUCs associated with data subsets were calculated as described above. List of AUCs were sorted and the 95% CI was determined. The bootstrap sampling simulation and AUC calculations were carried out using Python. For the p‐value calculation, the ROC curves were compared using a two‐sided test for difference using R.80

Enrichment and consensus scoring

The ability of each scoring function to enrich a set of predictions in improved binders was evaluated by plotting the percentage of high‐affinity binders found versus depth in the ordered list of computational predictions going from the highest affinity binder to the nonbinder(s). An improved‐affinity binder was defined as a variant with ΔΔG < −1 kcal/mol, when determining enrichment over the whole dataset. For the SPM subset, an improved‐affinity SPM variant was defined to have ΔΔG < −0.5 kcal/mol. Enrichment was also calculated using consensus scoring approaches, namely, rank‐by‐number, rank‐by‐rank, and rank‐by‐best. The rank‐by‐number and rank‐by‐rank approaches are adopted from the descriptions by Verdonk et al.66 In the rank‐by‐number approach, computational scores from different methods are normalized by converting them to Z‐scores (Z score function was used as implemented in Python.spicy.stats library) and then averaged; proteins are subsequently reranked using this new averaged score. In the rank‐by‐rank approach, proteins are first ranked by the computational scores for each individual scoring function, their ranks are then averaged, and this averaged rank is used for the final ranking of the protein variants. If variants had the same predicted ΔΔG, then they were given the same rank. In the rank‐by‐best approach, we progressively probed into the top X% of each computational list and for each value of X, we (1) counted the total number of positive predictions—allowing any prediction made by any method to count as a positive, (2) converted the total number of predictions considered to a percentage of the database (generating an x‐axis value), and (3) converted total number of positives found to a percentage of database positives (generating a y‐axis value). Enrichment for consensus scoring approaches was determined as described above.

Supporting information

Supporting Information

Supporting Information