High‐throughput identification of protein mutant stability computed from a double mutant fitness landscape

Abstract

The effect of a mutation on protein stability is traditionally measured by genetic construction, expression, purification, and physical analysis using low‐throughput methods. This process is tedious and limits the number of mutants able to be examined in a single study. In contrast, functional fitness effects can be measured in a high‐throughput manner by various deep mutational scanning tools. Using protein GB 1, we have recently demonstrated the feasibility of estimating the mutational stability effect ( $\Delta \Delta$ G) of single‐substitution based on the functional fitness profile of all double‐substitutions. The principle is to identify genetic backgrounds that have an exhausted stability margin. The functional effect of an additional substitution on these genetic backgrounds can then be used to compute the mutational $\Delta \Delta$ G based on the biophysical relationship between functional fitness and thermodynamic stability. However, to identify such genetic backgrounds, the approach described in our previous study required a benchmark dataset, which is a set of known mutational $\Delta \Delta$ G. In this study, a benchmark‐independent approach is developed. The genetic backgrounds of interest are identified using k‐means clustering with the integration of structural information. We further demonstrated that a reasonable approximation of $\Delta \Delta$ G can also be obtained without taking structural information into account. In summary, this study describes a novel method for computing $\Delta \Delta$ G from double‐substitution functional fitness profiles alone, without relying on any known mutational $\Delta \Delta$ G as a benchmark.

Introduction

Traditionally, mutational stability is measured using spectroscopy‐based methods, or thermal denaturation and calorimetry. Although these techniques allow precise determination of protein stability, the experimental process is tedious. These low‐throughput methods limit the number of mutations able to be examined in a single study. In light of the importance and challenge of measuring mutational stability, several high‐throughput strategies have been explored (reviewed in [1]). They have been successfully applied to aid enzyme design,2 and to increase protein stability.3 Nonetheless, these existing approaches lack the power to accurately quantify mutational stability. As a result, there is a demand for an alternative high‐throughput approach to quantify mutational stability.

In contrast to protein stability, protein function can often be simply and directly assayed. In addition, the advancement of next‐generation sequencing (NGS) permits quantification of functional fitness for a large number of mutants in parallel using deep mutational scanning techniques (reviewed in [4]). However, according to the threshold robustness model, the relationship between functional fitness and stability is not straightforward.5 Many destabilizing mutations will not appreciably reduce the amount of native protein at room temperature. This is because the deleterious effect of destabilizing mutations can be buffered by the excess stability margin and may not be reflected in the functional fitness of the protein mutant.6, 7, 8, 9 Consequently, although functional fitness data can be readily obtained using deep mutational scanning, computing mutational stability effects from such data is a nontrivial process.

Recently, we have measured the affinity of all double‐substitutions on protein G using mRNA display.10 This dataset can be viewed as a set of functional fitness profiles of single‐substitutions in different genetic backgrounds that are one substitution away from wild type (WT). It opens up the opportunity to identify genetic backgrounds with an exhausted stability margin, which permit the quantification of $\Delta \Delta$ G for individual substitutions across protein G. We have previously demonstrated the feasibility of using the fitness dataset of all double‐substitutions to compute $\Delta \Delta$ G for individual single‐substitutions across the entire protein domain.10 However, the approach described previously requires a benchmark dataset, which is a set of mutations with known $\Delta \Delta$ G. This prerequisite limited the application of our previously described $\Delta \Delta$ G approximation approach to well‐characterized protein, in which mutational $\Delta \Delta$ G is readily available in the literature. In this study, we were able to overcome this limitation by applying k‐means clustering approach to analyze the functional fitness profiling data. We demonstrated the feasibility of quantifying mutational stability effect from functional fitness profiling data alone, without any prior knowledge of the mutational $\Delta \Delta$ G of the protein.

Results

Conceptual basis of transforming mutational fitness to $\Delta \Delta$ G

Several studies have shown that naturally occurring proteins can tolerate one to a few destabilizing mutations without significantly affecting their folding and function.6, 7, 8, 9 It is best described by the threshold robustness model,5 in which the deleterious effect of destabilizing mutations can be buffered by the excess stability margin and would not result in a reduction of native protein [Fig. 1(A, B)]. However, if this stability margin is exhausted, addition of a destabilizing mutation will partially unfold the protein and lead to a decrease in observed functional fitness. The same principle can be applied to stabilizing mutations. When protein stability is above the threshold, a further increase in stability would not detectably increase the amount of native protein and would not improve functional fitness. Whereas if this stability margin is exhausted such that the protein is partially unfolded, addition of a stabilizing mutation will lead to an improvement in fraction folded and an increase in functional fitness. Consequently, under threshold robustness model, an additive effect in stability can lead to a nonadditive effect in functional fitness, hence epistasis.

Figure 1.

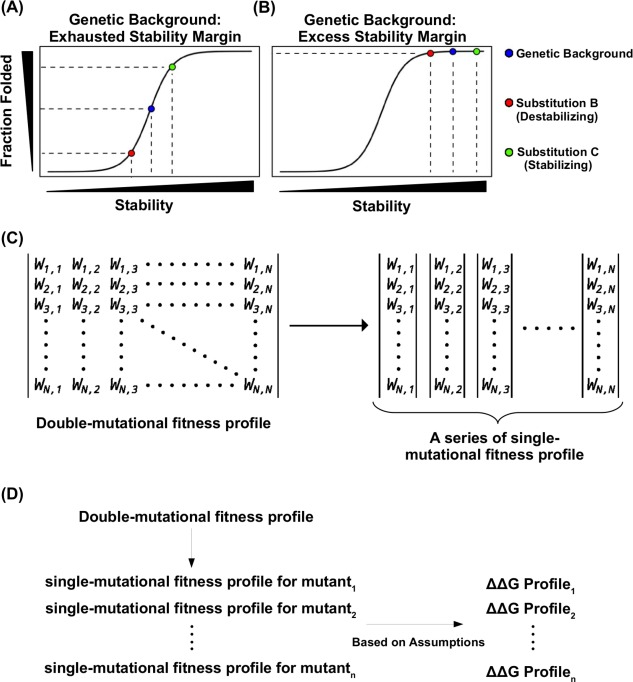
Conceptual basis for studying protein stability from functional measurement. (A, B) A schematic representation of the nonlinear relationship between mutant stability and protein folding under genetic backgrounds with different stabilities is shown for (A) a destabilizing genetic background, in which the protein is partially unfolded, and (B) a stable genetic background, in which the protein is fully folded (native state). Blue represents the genetic background, red represents a destabilizing substitution on the genetic background, green represents a stabilizing substitution on the genetic background. (C) A double‐substitution functional profile can be partitioned into individual single‐substitution functional profile for different genetic backgrounds. The double‐substitution functional profile is shown as a symmetric matrix. The fitness value of each mutant was indicated by $W_{i,j}$, where i and j indicates the substitution. When i equals j, it represents a single substitution. (D) A diagram shows the logical flow of computing $\Delta \Delta$ G from a double‐substitution functional profile. $\Delta \Delta$ G for individual single substitution can be computed from the functional profile of a given genetic background. Nonetheless, several assumptions are involved in the computing of $\Delta \Delta$ G from functional profile. As a result, only those genetic backgrounds that satisfy the assumptions would allow accurate calculation of $\Delta \Delta$ G from the functional profile.

We have recently described a deep mutational scanning dataset, in which the functional fitness of all single‐substitutions and double‐substitutions across protein G was measured in a high‐throughput manner.10 This dataset can be partitioned into different single‐substitution functional fitness profiles in all genetic backgrounds that are one substitution away from wild type (WT) [Fig. 1(C, D)]. Each functional fitness profile can then be converted to a $\Delta \Delta$ G profile based on the biophysical relationship between fitness, protein folding, and stability (see Materials and Methods section). Nonetheless, accurate measurement of $\Delta \Delta$ G from functional fitness requires a genetic background which has an exhausted stability margin, and therefore, be partially unfolded. If the stability margin of the genetic background is not exhausted (i.e., the protein is fully folded), the bona fide $\Delta \Delta$ G value cannot be inferred from the corresponding functional fitness profile. Here, we refer to single‐substitutions that distinguish individual genetic backgrounds from WT as S _BG.

Previously, we have shown the feasibility of identifying S _BG of interest (genetic backgrounds with an exhausted stability margin) using the double‐substitution fitness dataset and a set of known mutational $\Delta \Delta$ G.10 Briefly, we did an iterative comparison between the $\Delta \Delta$ G profiles for individual S _BG and a set of $\Delta \Delta$ G for 82 single‐substitutions found in the literature. The correlation between the $\Delta \Delta$ G profile and the benchmark is termed as R _Literature. A range of R _Literature (range: −0.40 to 0.90, mean: 0.21, standard deviation: 0.25) is observed for different S _BG (Supporting Information, Fig. S1). In our previous study, those S _BG that gave a high R _Literature would be identified as the S _BG of interest. Subsequently, the $\Delta \Delta$ G of all the other substitutions across the protein can be extrapolated based on the S _BG of interest. If the benchmark set was not available, we would not be able to identify the S _BG of interest, hence compute the $\Delta \Delta$ G for individual single‐substitutions. Unfortunately, such a benchmark dataset is not usually available for most naturally occurring proteins. Here, we aimed to develop a general approach, that is independent of any benchmark dataset, for identifying those S _BG of interest to accurately compute $\Delta \Delta$ G for individual single‐substitutions from functional fitness data alone.

Properties of genetic backgrounds of interest

Consequently, we investigated whether there was any intrinsic property for the S _BG to achieve a high R _Literature. This set of parameters, if existing, would help identify those genetic backgrounds that allow accurate computing of $\Delta \Delta$ G when a set of benchmark $\Delta \Delta$ G is not available.

Here, we examined two parameters, namely relative solvent accessibility (RSA) and functional fitness (W). We hypothesized that those S _BG with a high R _Literature would reside in the protein core, and thus, have a low RSA. The reasoning is that substitutions at the protein core are more likely to unfold the protein.11 In addition, we also proposed that S _BG that partially unfolded the protein would acquire an intermediate fitness between the WT protein (W = 1) and completely nonfunctional variants (W = 0.01 is the limit of detection). Indeed, our data are consistent with these notions [Fig. 2(A) and Supporting Information, Fig. S2(A,B)]. Most S _BG with a R _Literature of >0.75 have an intermediate fitness and reside in the core of the protein [Fig. 2(B, C) and Supporting Information, Table S1]. However, although many S _BG with a high R _Literature displayed an intermediate fitness and low RSA, a significant number of S _BG with a low R _Literature also satisfied these selection criteria [Fig. 2(A) and Fig. Supporting Information, S2(C)]. This suggests that additional parameters need to be considered to identify those S _BG of interest.

Figure 2.

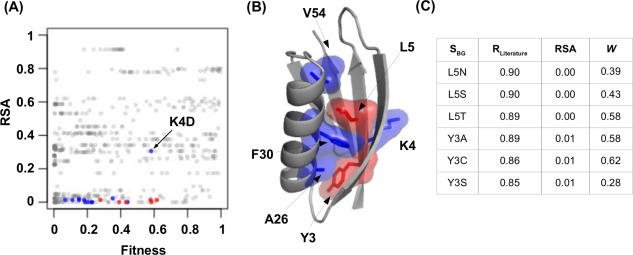
Property of S _BG with a higher R _Literature. (A, B) S _BG with a R _Literature of >0.85 are colored in red and S _BG with a R _Literature of >0.75 are colored in blue. (A) A two dimension scatter plot is shown with each S _BG represented by a data point. The y‐axis represents the RSA and the x‐axis represents the fitness (W). The only nonburied S _BG with high correlation is K4D which is labeled. (B) The spatial locations for those S _BG with a R _Literature of >0.75 are shown on the protein G structure (PDB: 1PGA).12 (C) The R _Literature, RSA, and W are shown for those S _BG with a R _Literature of >0.85.

Grouping genetic backgrounds based on intercorrelation of $\Delta \Delta$ G profiles

Instead of testing more parameters, we turned to explore a more general approach to identify those S _BG of interest based on clustering of the $\Delta \Delta$ G profiles. The underlying rationale is that those S _BG with high R _Literature should have a similar $\Delta \Delta$ G profile, thus being grouped together. Since beneficial S _BG was unlikely to exhaust the stability margin and would give a complex number in the transformation of the fitness profile to the $\Delta \Delta$ G profile [see Eq. (11) in Materials and Methods section], only 678 S _BG, which had a W of 0–1, were included in the subsequent analyses unless otherwise stated.

To test this idea, we first built a correlation matrix based on $\Delta \Delta$ G profiles. This correlation matrix represented all the pairwise correlation among the $\Delta \Delta$ G profiles of individual S _BG. Subsequently, a hierarchical clustering was performed to group S _BG based on the correlation matrix. Interesting, we observed three major groups of S _BG, in which the $\Delta \Delta$ G profiles of the S _BG within the group were intercorrelating [Fig. 3(A)]. According to our rationale, S _BG of interest would fall into the same group. Therefore, the distribution of R _Literature for individual S _BG within each group was examined [Fig. 3(B)]. The R _Literature of S _BG in group II was significantly higher than that of group I and group III (P = 4 $\times {10}^{-11}$, Wilcoxon rank‐sum test). In fact, 8 of the top 10 S _BG with the highest R _Literature were within group II. This suggests that S _BG with high R _Literature would group together.

Figure 3.

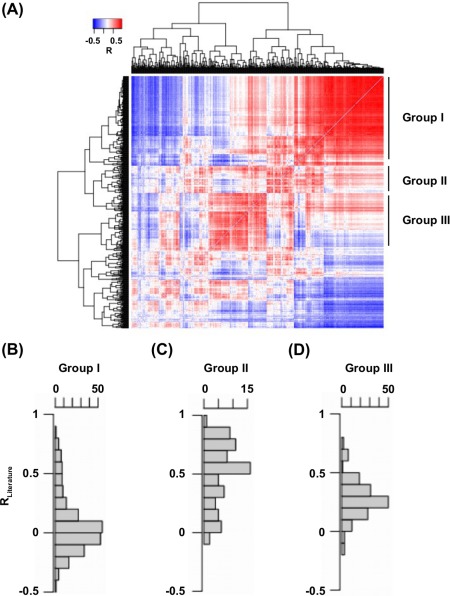
Hierarchical clustering of genetic backgrounds based on the similarity of $\Delta \Delta$ G profile. (A) Hierarchical clustering of individual S _BG based on their pairwise correlation of $\Delta \Delta$ G profile. The pairwise correlation between $\Delta \Delta$ G profiles is color coded as indicated. (B–D) Distribution of R _Literature for individual S _BG within (B) group I, (C) group II, and (D) group III was shown.

We aimed to further understand the biophysical basis of the clustering result for group I (Supporting Information, Table S2), group II (Supporting Information, Table S3) and group III (Supporting Information, Table S4) by examining the fitness and RSA of the S _BG within each group [Fig. S3(A, B)]. Group I was enriched in highly deleterious, and presumably highly destabilizing S _BG. Under these genetic backgrounds, addition of a stabilizing mutation would not improve functional fitness due to the extremely destabilizing effect brought by S _BG. Likewise, addition of a destabilizing mutation would also exert no effect on functional fitness, simply because the protein cannot be further unfolded. Thus, the S _BG in group I produced correlated $\Delta \Delta$ G profiles simply due to lethality common to all S _BG in group I. S _BG in group III possessed a range of functional fitness and RSA. When we looked at the list of S _BG in group III, we found that 92% of S _BG were located within a dynamic region which displays positive epistasis in general.10 This indicates the intercorrelation among S _BG in group III was predominantly driven by a functional epistatic effect. S _BG in group II acquired the best R _Literature among these three groups. Many of the S _BG in group II were at core residues which are predicted to partially unfolded the protein. Consistent with this notion, those S _BG in group II had an attenuated functional fitness and a low RSA.

Overall, these analyses demonstrated the possibility of grouping S _BG with high R _Literature together. Nonetheless, decreasing the size of each group (i.e., increasing the number of groups) was needed to improve the true positive rate in the S _BG group of interest. Since there were only a small number of S _BG of interest, a smaller cluster size would group the S _BG of interest and exclude S_BG that possessed a lower R _Literature.

Identification of genetic backgrounds of interest by k‐means clustering and subsequent group sorting

To further refine the grouping of S _BG, we performed a k‐means clustering based on the correlation matrix. By the definition of k‐means clustering, each run of clustering would generate k S _BG groups. This method would give a fine control of the number of S _BG groups being generated in each clustering run. The remaining challenge was to distinguish the S _BG group of interest (i.e., the S _BG group with an enrichment in S _BG with a high R _Literature) from other S _BG groups.

From our analysis above, we observed that those S _BG with a high R _Literature possessed a low RSA. Therefore, we aimed to design a RSA‐based sorting strategy to identify the S _BG group of interest. First, k‐means clustering were performed 100 times to generate 100 × k S _BG groups (see Materials and Methods section). The mean RSA of all S _BG within each S _BG group was then computed. Subsequently, a mean RSA was obtained for each of the 100 × k S _BG groups. In this approach, the S _BG group with the lowest mean RSA would be identified as the S _BG group of interest. The $\Delta \Delta$ G for each substitution was then calculated using the median $\Delta \Delta$ G among the genetic backgrounds within the group of interest.

We tested this approach with a range of k using those 678 S _BG which carried a functional fitness within 0 to 1. When the k was sufficiently large (k > 10), the S _BG group of interest would carry an R _Literature of ∼0.8 [Fig. 4(A)]. We also tested if the result would improve by only considering a subset of S _BG within a narrower functional fitness range. The underlying rationale is from the analysis above, in which S _BG of interest carried an intermediate functional fitness. Indeed, the result could be slightly improved by filtering out those S _BG with a low functional fitness (W < 0.4). Furthermore, an apparent correlation was observed between the mean RSA and R _Literature for S _BG groups generated from k‐means clustering [Fig. 4(B)]. In contrast, $\Delta \Delta$ G predicted from Rosetta software only achieved an R _Literature of 0.52.13 It highlights the strength of estimating $\Delta \Delta$ G from functional fitness data and reflects the success of our approach. Those S _BG within best hit (R _Literature = 0.91) are indicated in Supporting Information, Table S1. The $\Delta \Delta$ G for all single‐substitutions computed from the best hit are shown in Supporting Information, Table S5.

Figure 4.

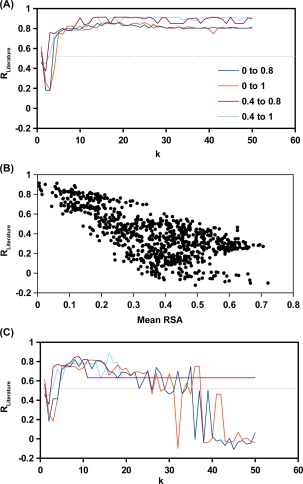
Results from k‐means clustering. k‐means clustering was performed to group S _BG by the similarity of $\Delta \Delta$ G profile. For a given k selection, 100 independently runs of k‐means clustering were performed. Consequently, 100 × k groups of S _BG would be obtained. This analysis was performed for S _BG with a fitness within the indicated range. There were 678 S _BG within a fitness range of 0–1 (orange), 249 S _BG within a fitness range of 0.4–1 (cyan), 153 S _BG within a fitness range of 0.4–0.8 (brown), 582 S _BG within a fitness range of 0–0.8 (blue). (A) The R _Literature was computed for the S _BG group with the lowest mean RSA. (B) The relationship between mean RSA and R _Literature for the S _BG groups produced from 100 runs of k‐means clustering with k = 18 and an S _BG fitness range between 0.4 and 0.8. (C) The R _Literature was computed for the S _BG group with the lowest mean hydrophobic score of the WT amino acids of S _BG. The gray‐dotted line represents the R _Literature from $\Delta \Delta$ G prediction using Rosetta software.13 Parameters were taken from row 16 of Table I in Kellogg et al.14

Since RSA can only be obtained when the structural information is available, another sorting parameter would be needed. Consequently, we tested whether the S _BG group of interest could be identified without using RSA as the sorting parameter. Instead, we used hydrophobicity of the WT residue of each S _BG as the sorting parameter. The rationale is that core residues (low RSA) are in general more hydrophobic. We performed k‐means clustering for 100 times to generate 100 × k S _BG groups. The mean hydrophobicity for each S _BG group was used as the sorting parameter. Here, the Hopp–Woods hydrophilicity scale was used,15 in which the lower the value, the more hydrophobic the residue is. The S _BG group with the lowest mean Hopp–Woods hydrophilicity value would be identified as the S _BG group of interest. The S _BG group of interest carry an R _Literature of ∼0.6 to ∼0.8 for a wide range of k [Fig. 4(C)]. Nonetheless, the result would get worse as k increased above 20, especially when those S _BG with a low functional fitness (W < 0.4) were included in the run. Although the result was not as robust as that of using RSA as the sorting parameter, it showed the possibility of computing $\Delta \Delta$ G from functional fitness data without any prior knowledge in the protein structure.

Discussion

Developing a high‐throughput approach for measuring mutant stability effect is a popular research area in both experimental and computational biology. It is because the stability effect upon mutation is the foundation of various biological processes, ranging from natural evolution to protein engineering. Experimental approaches usually infer the mutant stability effect from an indirect functional readout, which possess a low quantitative potential for computing $\Delta \Delta$ G. Computational approaches estimate the mutant stability effect based on a predefined set of force field parameters and energy functions. It has been demonstrated that in silico mutant stability prediction can achieve a correlation of ∼0.6 to ∼0.7 with experimental data.14, 16 This imperfect correlation indicates more parameters have to be considered during the prediction. In this study, we demonstrated an alternative approach of computing mutational stability effect based on functional profiling of double substitutions. By integrating the structural information as RSA for each residues, we were able to reliably compute the $\Delta \Delta$ G for individual substitutions across the entire protein domain.

The principle of our approach is that mutational $\Delta \Delta$ G and functional fitness follow a defined biophysical relationship when the genetic background has an exhausted stability margin, hence is partially unfolded. Those genetic backgrounds, despite being useful, are presumably rare and difficult to be identified. When k‐means clustering is applied to group the S _BG based on their intercorrelations of $\Delta \Delta$ G profile, those S _BG of interest would be grouped together. Among different S _BG groups produced by the clustering, the S _BG group of interest can be identified by the low mean RSA. One caveat of using mean RSA as the sorting parameter is that other S _BG groups may possess an equally low mean RSA as that of the S _BG group of interest. It would happen if those low RSA S _BG that have a low R _Literature intercorrelated with each other. Of note, S _BG that have a low R _Literature do exist, as evidenced by Figure 3(A). But apparently, these S _BG do not have a tight intercorrelation as evidenced by Figure 4(B), in which S _BG group with low R _Literature and low mean RSA do not exist. This result suggests that correlation of $\Delta \Delta$ G profile between different S _BG is independent of RSA similarity, which is indeed observed in our study (Supporting Information, Fig. S4).

We acknowledge that our approach may not be the optimum method for computing mutational $\Delta \Delta$ G from functional fitness profiling data. While mutations at residues with low RSA are more likely to exhaust the stability margin of the protein,11 certain mutations at residues with high RSA may also achieve the same effect. It is possible that in other proteins, mutations at residues with high RSA provide a better genetic background for computing mutational $\Delta \Delta$ G from functional fitness profiling data. Therefore, alternative approaches should be investigated in the future. For instance, usage of maximum‐entropy probability models, which are efficient at discerning real correlation in biological data with a high signal‐to‐noise ratio,17 may improve the performance in identifying the S _BG group of interest.

Due to the continued development of high‐throughput sequencing technologies, functional fitness profiling has recently become a popular tool. Most studies focuses on the functional effect of single‐substitution, which is not instrumental for computing the mutational stability effect. Our recent study has demonstrated the possibility of studying the fitness effect of all double‐substitution on a protein domain.10 Here, we further showed that such datasets alone can be used to identify the $\Delta \Delta$ G for all single‐substitution without any prior knowledge on mutational $\Delta \Delta$ G of the given protein. In summary, the approach described in this study represents a combination of an advanced experimental techniques and a novel analytical method for $\Delta \Delta$ G profiling. This approach can be applied to other proteins of interest to facilitate protein engineering and study natural evolution from a thermodynamic perspective.

Materials and Methods

Fitness profiling data

Experimental profiling data, which contained the fitness value relative to WT of all single substitutions and all double substitutions across protein G binding domain 1, was obtained from our previous study.10 We only employed the fitness value from mutants (single or double substitutions) with an input count of >10 to minimize the statistical noise in computing the fitness value. All 19 × 55 = 1045 single substitutions and 529,902 (98.8%) out of ${}^{55}{C}_2\times {19}^2$ = 536,085 all possible double substitutions satisfied this cutoff.

RSA measurement

Solvent accessibility surface area (SASA) was measured by DSSP18 using the protein G monomer structure in PDB 1PGA.12 SASA was then normalized with the SASA calculated from an unfolded Gly‐X‐Gly tripeptide structure (X = any amino acid) using PyMOL to obtain the RSA.

Transforming fitness profile to $\Delta \Delta$ G profile

The fitness profile of double substitutions in the WT genetic background was partitioned into 1485 single substitution fitness profiles in a genetic background that was one substitution away from WT. Each fitness profile was then converted to a $\Delta \Delta$ G profile based on the assumptions described in our recent publication.10 In this study, we referred $\Delta \Delta$ G as the $\Delta \Delta$ G of unfolding. Thus, the higher the $\Delta \Delta$ G, the more stability the substitution confers. Here the relative association constant is indicated by ΔK_A, which represents the ratio of association constant (K _A) for a given mutant to K _A of the WT. In addition, subscript N represents native state and subscript U represents unfolding. Here are the assumptions:

1. Assuming mutational effect on affinity is additive, such that the relative association constant (ΔK _A) of the double substitution (AB) is a product of that of the corresponding single substitutions (A and B). Therefore,

   $$\Delta K_{\mathrm{A},\text{AB}}=\Delta K_{\mathrm{A},\mathrm{A}}\times \Delta K_{\mathrm{A},\mathrm{B}}$$ (1)

   where $\Delta K_{\mathrm{A},\text{AB}}$ represents the relative association constant for double substitution AB, $\Delta K_{\mathrm{A},\mathrm{A}}$ represents the relative association constant for single substitution A, and $\Delta K_{\mathrm{A},\mathrm{B}}$ represents the relative association constant for single substitution B.

2. Assuming the fitness (W) of a given substitution i is a product of the fraction of the protein in the native state (f _N) and the fitness of the native state (W _N). Therefore, W _i = f ${}_{\mathrm{N},\mathrm{i}}$ × W ${}_{\mathrm{N},\mathrm{i}}$Here, we set the fitness for WT (W _WT) to 1, the fraction of the protein in the native state for WT (f ${}_{\mathrm{N},\text{WT}}$) to 1 (the amount of unfolded protein for WT is negligible), and the fitness of the native state for WT (W ${}_{\mathrm{N},\text{WT}}$) to 1.

3. Assuming the native state of a given substitution i has the same fitness with that of the WT. Therefore, W ${}_{\mathrm{N},\mathrm{i}}$ = W ${}_{\mathrm{N},\text{WT}}$ = 1. Hence, according to assumption 2, W _i = f ${}_{\mathrm{N},\mathrm{i}}$.Since fitness of the native state (W _N) can be related to the relative association constant (ΔK _A) by a one‐to‐one function as previously described,10 genotypes with the same W _N carry the same ΔK _A. Therefore, the binding constant of a given substitution i is the same as that of the WT (K ${}_{\mathrm{A},\mathrm{i}}$ = K ${}_{\mathrm{A},\text{WT}}$) if the native state of a given substitution i has the same fitness with that of the WT. Hence, Δ $K_{\mathrm{A},\mathrm{i}}$ = 1.

4. Assuming the native state of a given substitution i has the same fraction of protein in the native state as that of the WT. Therefore, $f_{\mathrm{N},\mathrm{i}}=f_{\mathrm{N},\text{WT}}=1$, and hence according to assumption 2, W _i = W ${}_{\mathrm{N},\mathrm{i}}$.

We anticipated that most substitutions would satisfy assumption 4 but not assumption 3. This is reasoned by the fact that most substitutions would not unfold the protein at room temperature. In contrast, only a few substitutions would partially or fully unfold the protein.

In the following, we considered that substitution A satisfied assumption 3 and substitution B satisfied assumption 4, fraction of the protein in the native state for double substitution AB ( $f_{\mathrm{N},\text{AB}}$) would be equal to the ratio of the fitness of double substitution AB to the fitness of substitution B (W _AB/W _B), which is derived as follows:

According to assumption 2, W _AB =  $f_{\mathrm{N},\text{AB}}$ × W ${}_{\mathrm{N},\text{AB}}$, and, therefore:

$$W_{\mathrm{N},\text{AB}}=\frac{W_{\text{AB}}}{{\mathrm{f}}_{\mathrm{N},\text{AB}}}$$ (2)

Since substitution A satisfied assumption 3,

$$\Delta K_{\mathrm{A},\mathrm{A}}=1$$ (3)

Since substitution B satisfied assumption 4,

$$W_{\mathrm{B}}=W_{\mathrm{N},\mathrm{B}}$$ (4)

Substituting Eq. (3) into Eq. (1) states that the relative association constant of double substitution AB equals the relative association constant of substitution B (Δ $K_{\mathrm{A},\text{AB}}$ = Δ $K_{\mathrm{A},\mathrm{B}}$), hence fitness of the native state of double substitution AB ( $W_{\mathrm{N},\text{AB}}$) equals fitness of the native state of substitution B ( $W_{\mathrm{N},\mathrm{B}}$):

$$W_{\mathrm{N},\text{AB}}=W_{\mathrm{N},\mathrm{B}}$$ (5)

Substituting Eq. (4) into Eq. (5) states that the fitness of the native state of double substitution AB equals fitness of substitution B:

$$W_{\mathrm{N},\text{AB}}=W_{\mathrm{B}}$$ (6)

Substituting Eq. (6) into Eq. (2) states that the ratio of the fitness to the fraction of protein in the native state of substitution AB equals the fitness of substitution B (W _AB/ $f_{\mathrm{N},\text{AB}}$ = W _B), and hence:

$$f_{\mathrm{N},\text{AB}}=\frac{W_{\text{AB}}}{W_{\mathrm{B}}}$$ (7)

Assuming stability effect is additive, the change in free energy of unfolding for substitution B can be obtained by subtracting the change in free energy of unfolding for substitution A from the change in free energy of unfolding for double substitution AB ( $\Delta \Delta G_{\mathrm{U},\mathrm{B}}$ = Δ $G_{\mathrm{U},\text{AB}}$ − Δ $G_{\mathrm{U},\mathrm{A}}$). The relationship between an equilibrium constant (K) and change of free energy (ΔG) states that ΔG =  $-RT\times \ln (K)$, where R represents the ideal gas constant and T represents the temperature. Therefore,

$$\Delta \Delta G_{\mathrm{U},\mathrm{B}}=(-RT\times \ln (K_{\mathrm{U},\text{AB}}))-(-RT\times \ln (K_{\mathrm{U},\mathrm{A}}))$$ (8)

where $K_{\mathrm{U},\mathrm{A}}$ represents the equilibrium constant of unfolding of substitution A and $K_{\mathrm{U},\text{AB}}$ represents the equilibrium constant of unfolding of double substitution AB. Since equilibrium constant of unfolding (K _U) is related to fraction of protein in the native state (f _N) by K _U = (1 − f _N)/f _N, Eq. (8) can be rearranged to:

$$\Delta \Delta G_{\mathrm{U},\mathrm{B}}=-RT\times \ln ((1-f_{\mathrm{N},\text{AB}})/f_{\mathrm{N},\text{AB}})+RT\times \ln ((1-f_{\mathrm{N},\mathrm{A}})/f_{\mathrm{N},\mathrm{A}})$$ (9)

Substituting Eq. (7) into Eq. (9):

$$\Delta \Delta G_{\mathrm{U},\mathrm{B}}=-RT\times \ln ((1-W_{\text{AB}}/W_{\mathrm{B}})/(W_{\text{AB}}/W_{\mathrm{B}}))+RT\times \ln ((1-f_{\mathrm{N},\mathrm{A}})/f_{\mathrm{N},\mathrm{A}}))$$ (10)

Since substitution A satisfied assumption 3, W _A =  $f_{\mathrm{N},\mathrm{A}}$:

$$\Delta \Delta G_{\mathrm{U},\mathrm{B}}=-RT\times \ln ((W_{\mathrm{B}}-W_{\text{AB}})/W_{\text{AB}})+RT\times \ln ((1-W_{\mathrm{A}})/W_{\mathrm{A}})$$ (11)

The challenge was to identify those substitutions that satisfy assumption 3 (i.e., substitution A, see above). In this study, this set of substitutions was called (S _BG), which acted as a substitution in the genetic background for accurately estimate of the real $\Delta \Delta$ G of each single substitution across the protein domain (i.e., substitution B, see above). These substitutions would be those S _BG with a high R _Literature. In contrast, when a substitution that did not satisfy assumption 3 was used as a genetic background for computing the $\Delta \Delta$ G of other substitutions, the $\Delta \Delta$ G would be deviate from the real $\Delta \Delta$ G value. These substitutions would be those S _BG with a low R _Literature.

Clustering of background substitutions (S _BG)

A correlation matrix for all genetic background was generated based on the pairwise Pearson's correlation of their single‐substitution $\Delta \Delta$ G profiles. k‐means clustering was performed on the correlation matrix to group the S _BG. k‐means clustering was performed 100 times using random seeding. As a result, 100 × k S _BG groups were obtained. Groups with < 3 S _BG were filtered out. The $\Delta \Delta$ G of each substitution was then calculated by taking the median value of its $\Delta \Delta$ G computed from individual genetic backgrounds with a given S _BG group. Of note, we acknowledge that nonadditive stability would prevent accurate estimation of $\Delta \Delta$ G [Eq. 8]. Therefore, we took the median value instead of mean to prevent $\Delta \Delta$ G estimation being confounded by sporadic nonadditive stability effect. For example, if the S _BG group of interest consists three different genetic backgrounds (e.g., A, B, and C). If we wanted to compute the $\Delta \Delta$ G for mutation Z, which has an estimated $\Delta \Delta$ G = 0 under genetic background A, an estimated $\Delta \Delta$ G = 1 under genetic background B, and an estimated $\Delta \Delta$ G = −1 under genetic background C, the median value (in this case, $\Delta \Delta$ G = 0) would be taken as the final computed $\Delta \Delta$ G for mutation Z in our approach.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information