Characterizing a partially ordered miniprotein through folding molecular dynamics simulations: Comparison with the experimental data

Abstract

The villin headpiece helical subdomain (HP36) is one of the best known model systems for computational studies of fast‐folding all‐α miniproteins. HP21 is a peptide fragment—derived from HP36—comprising only the first and second helices of the full domain. Experimental studies showed that although HP21 is mostly unfolded in solution, it does maintain some persistent native‐like structure as indicated by the analysis of NMR‐derived chemical shifts. Here we compare the experimental data for HP21 with the results obtained from a 15‐μs long folding molecular dynamics simulation performed in explicit water and with full electrostatics. We find that the simulation is in good agreement with the experiment and faithfully reproduces the major experimental findings, namely that (a) HP21 is disordered in solution with <10% of the trajectory corresponding to transiently stable structures, (b) the most highly populated conformer is a native‐like structure with an RMSD from the corresponding portion of the HP36 crystal structure of <1 Å, (c) the simulation‐derived chemical shifts—over the whole length of the trajectory—are in reasonable agreement with the experiment giving reduced χ ² values of 1.6, 1.4, and 0.8 for the Δδ¹³C^α, Δδ¹³CO, and Δδ¹³C^β secondary shifts, respectively (becoming 0.8, 0.7, and 0.3 when only the major peptide conformer is considered), and finally, (d) the secondary structure propensity scores are in very good agreement with the experiment and clearly indicate the higher stability of the first helix. We conclude that folding molecular dynamics simulations can be a useful tool for the structural characterization of even marginally stable peptides.

Introduction

Molecular dynamics simulations of foldable peptides performed with the AMBER99SB family of force fields1, 2, 3, 4 have matured to the point of becoming useful analytical tools for the identification of structurally stable peptide folders. To our knowledge, there is not a single example of a stably folded peptide for which the combination of the AMBER99SB‐ILDN (or AMBER99SB‐STAR‐ILDN) force field with TIP3P water model5 and full electrostatics6 has failed to correctly identify the peptide's native state. To the contrary, the aforementioned combination has been shown to be able to accurately predict the structure and dynamics of peptides ranging from very stable folders,1, 2, 3, 4, 7 to marginally stable peptides,7, 8, 9, 10, 11 and for all structural motifs from mainly helical2, 3, 4, 8 to almost exclusively β‐hairpin like.3, 11, 12, 13 It should be noted, however, that recent studies have indicated the presence of a tendency of these force fields to produce overly compact structures in the case of disordered peptide systems14, 15, 16 which are known to be rather difficult systems to study with empirical force fields.17 In this communication we examine the ability of folding molecular dynamics simulations to reproduce the experimental findings for HP21, a mostly disordered peptide derived from the villin headpiece helical subdomain.

The folding of the villin headpiece helical subdomain (HP36) has extensively been studied both experimentally18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 and computationally.32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47 Two papers from the Raleigh group48, 49 showed using both CD and NMR spectroscopy that HP21, a mostly disordered 21‐residue peptide fragment derived from HP36, maintains a native‐like structure in the unfolded state. The structure and sequence of HP36 with the portion corresponding to HP21 highlighted are shown in Figure 1. The major evidence supporting the presence of a persistent native‐like structure of HP21 was the similarity between the Δδ¹³C^α, Δδ¹³CO, and Δδ¹³C^β secondary shifts recorded from HP21 and HP36.49 We perceived these results as an opportunity to test the ability of folding molecular dynamics simulations to reproduce a situation intermediate between a completely disordered system and a stable peptide folder. In this spirit we performed a 15‐μs long folding molecular dynamics simulation of HP21 in explicit water and with full electrostatics and compared the computational results with the experimental evidence. In the following paragraphs we describe the simulation protocol, the results obtained from its analysis, and attempt to statistically quantify the agreement between experiment and simulation.

Figure 1.

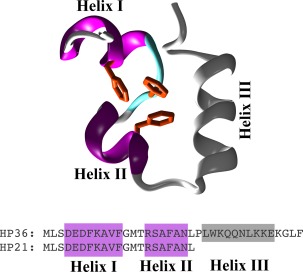
Sequences and structures. The top panel is a schematic (cartoon) representation of the HP36 structure with the HP21 portion highlighted in color (magenta for α‐helices, cyan for turns, white for coil). The lower panel shows the sequences of HP21 and HP36 with the helices' locations marked as filed rectangles.

Methods

System preparation and simulation protocol

The starting peptide structures were in the fully extended state as obtained from the program Ribosome (http://folding.chemistry.msstate.edu/~raj/Manuals/ribosome.html). Addition of missing hydrogen atoms and solvation‐ionization were performed with the program LEAP from the AMBER tools distribution.50 The simulation was performed using periodic boundary conditions and a cubic unit cell sufficiently large to guarantee a minimum separation between the PBC‐related images of the peptide of at least 16 Å. We followed the dynamics of the peptide's folding simulation using the program NAMD51, 52 for a grant total of 15 μs using the TIP3P water model,5 the AMBER99SB‐STAR‐ILDN force field,3, 4 and adaptive tempering53 as implemented in the program NAMD (adaptive tempering is formally equivalent to a single‐copy replica exchange folding simulation with a continuous temperature range. For our simulation this temperature range was 300 K to 400 K inclusive and was applied to the system through the Langevin thermostat, see below).

The simulation protocol was the following. The system was first energy minimized for 1000 conjugate gradient steps followed by a slow heating‐up phase to the final temperature of 300 K (with a temperature step of 20 K) over a period of 32 ps. Subsequently the system was equilibrated for 10 ps under NpT conditions without any restraints, until the volume equilibrated. This was followed by the production NpT run with the temperature and pressure controlled using the Nosè‐Hoover Langevin dynamics and Langevin piston barostat control methods as implemented by the NAMD program, with adaptive tempering applied through the Langevin thermostat, while the pressure was maintained at 1 atm. The Langevin damping coefficient was set to 1 ps⁻¹, and the piston's oscillation period to 200 fs, with a decay time of 100 fs. The production run was performed with the impulse Verlet‐I multiple timestep integration algorithm as implemented by NAMD. The inner timestep was 2 fs, short‐range non‐bonded interactions were calculated every one step, and long‐range electrostatics interactions every two timesteps using the particle mesh Ewald method54 with a grid spacing of ∼1 Å and a tolerance of 10⁻⁶. A cutoff for the van der Waals interactions was applied at 9 Å through a switching function, and SHAKE55 (with a tolerance of 10⁻⁸) was used to restrain all bonds involving hydrogen atoms. Trajectories were obtained by saving the atomic coordinates of the whole system every 0.8 ps.

The initial equilibration of the system was accessed by verifying that the cumulative distribution of the adaptive tempering temperatures was approaching the expected (1/β) distribution.53 The distribution of temperatures approached the expected distribution fast enough that no portion of the trajectory was excluded from any of the subsequent calculations. It should be noted, however, that the distribution of the adaptive tempering temperatures is dynamically dependent on the actual trajectory been followed during the simulation and, thus, cannot be used as a measure of convergence, especially for such a disordered system. This is discussed more fully in the Extent of Sampling section below.

Trajectory analysis

The programs CARMA56 and GRCARMA57 have been used for almost all of the analyses, including removal of overall rotations/translations, calculation of RMSDs from a chosen reference structure, calculation of the radius of gyration, calculation of the average structure (and of the atomic root mean squared fluctuations), production of PDB files from the trajectory, Cartesian space principal component analysis and corresponding cluster analysis, dihedral space principal component analysis and cluster analysis, calculation of the frame‐to‐frame RMSD matrices, calculation of similarity Q values, and so forth. Chemical shifts were calculated using the program SPARTA+.58 Reduced χ ² values were computed using the simulation‐derived variances from the formula χ ² = [Σ (S _Obs − S _Calc)²/σ²]/ν where S _Obs and S _Calc are the experimental and simulation derived secondary shifts, σ is the estimated variance and ν is the number of degrees of freedom. Secondary structure assignments were calculated with the program STRIDE.59 All molecular graphics work and figure preparation were performed with the programs VMD,60 RASTER3D61 and CARMA.

Extent of sampling

HP21—as will be shown in the next section—is mostly disordered in solution. The absence of a well‐defined gradient in its folding energy landscape (toward a would‐be native state) necessarily implies that a folding molecular dynamics simulation will have to face the full complexity of attempting to sample the vast configurational space associated with the unfolded (disordered) state. Although we have used adaptive tempering53 in order to increase the sampling efficiency of the simulation, it is highly unlikely that even a 15‐μs long simulation is anywhere near a meaningful sampling of the unfolded state. To quantify this statement, we apply a recently described probabilistic method based on the application of Good–Turing statistics to molecular dynamics trajectories.62 The method estimates the probability of unobserved species (i.e., thus far unobserved structures) as a function of the RMSD (of those unobserved structures) from the structures that have already been observed in the simulation. The results are shown in Figure 2 and clearly indicate that if we were to continue the simulation significantly different structures would be observed. For an example aiming to clarify this diagram (see the black curve in Fig. 2) we would expect that on average one out of twenty new (previously unobserved) structures (P _unobserved = 0.05) would differ by an RMSD of at least 3.5 Å from the structures already observed. These large RMSDs clearly indicate the less than ideal sampling for highly flexible disordered peptide systems. The lower (red) curve in this same diagram shows the results obtained from the same type of calculation, but this time using only structures whose corresponding adaptive tempering temperature was <320 K, corresponding to more stable (from the simulation's point of view) peptide conformers. The significant differences between the two curves demonstrate the better sampling of the stable peptide conformers, but again show that significantly different peptide structures would be observed if we continued the simulation.

Figure 2.

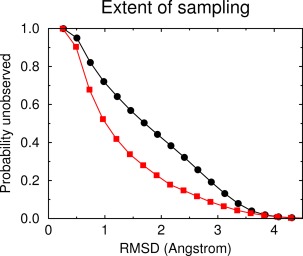
Extent of sampling. Good‐Turing estimates for the probability of unobserved species (thus far unobserved structures) as a function of RMSD. See Extent of Sampling section for details. The black upper curve is the estimate obtained using all structures recorded in the simulation, the lower (red) curve is the estimate using only structures with an associated adapting tempering temperature of less than 320 K (corresponding to structurally more stable peptide conformers).

The implication of the results presented above is clear: the conclusions drawn from the analysis of this 15‐μs trajectory cannot be based solely on quantities derived from the behavior of the peptide in the unfolded state. A much more realistic expectation is that the transiently stable peptide structures observed during the simulation (and their persistences) are a fair representation of the physical reality, that is, that they do represent energetically favorable conformations of the peptide. We should note, however, that even this last statement is probably not true: As Figure 2 shows (lower red curve) even the set of the marginally stable peptide conformers observed during the simulation appears to be incomplete as indicated by the nonnegligible P _unobserved values at high RMSDs.

In summary, the Good‐Turing‐based analysis presented above allows us to define the limits of interpretation for the simulation: it is not possible to directly compare the experimental chemical shifts with those derived from the whole trajectory because the sampling of the disordered structures is nowhere near convergence. The best that can be achieved is to establish that the peptide is indeed mostly disordered, and then (through cluster analysis) identify transiently stable conformers and compare the experimental chemical shifts with those derived from these structures. These analysis steps are outlined in the sections that follow.

Results

The peptide is mostly disordered, but with persistent secondary structure

The top panel of Figure 3 is a graphical representation of the RMSD matrix of the trajectory, which color‐codes an all‐to‐all RMSD‐based comparison of the peptide structures recorded during the simulation. Low RMSD values (denoting highly similar structures) are colored dark blue, dissimilar structures correspond to yellow‐red. Dark blue areas centered on the diagonal of the matrix indicate persistent (in time) peptide structures, off‐diagonal blue areas indicate that the same structure has been visited repeatedly and independently during the simulation. The panel immediately below the RMSD matrix in Figure 3 shows (in a one‐to‐one correspondence with the matrix) the STRIDE‐derived secondary structure assignments for the respective peptide structures (the limits of the two helices in the HP36 structure are also marked). The RMSD matrix clearly indicates that HP21 is mostly disordered, quickly interconverting between numerous conformations with only a handful of transiently stable peptide conformations observed. The major conformer is visited thrice during the simulation, the first time at ∼7.0 μs, the second at ∼13.5 μs, plus a rather short‐lived appearance at ∼10.5 μs (notice the major off‐diagonal blue areas of the diagram connecting these structures). To aid interpretation, these time periods have been marked with the letter “a” in the line immediately below the secondary structure diagram. Comparison of these regions with the secondary structure diagram (second panel in Fig. 3) shows that the major conformer has the helix‐turn‐helix secondary structure motif observed in the native (HP36) structure (Fig. 1). The second major conformer—appearing at ∼1 μs and then again at 12.5 and 14.0 μs—is also mainly helical as indicated by the STRIDE diagram, but its helical regions are shifted with respect to the native HP36 structure (this conformer is marked with the letter “b” in the line below the STRIDE diagram). The third transiently stabilized peptide conformation is observed at ∼2.5 μs and is notable due to the presence of β structure in its C‐terminal region with a mostly disordered N‐terminus (marked as “c”). The three dimensional structures of these prominent peptide conformers will be presented and discussed in the next section.

Figure 3.

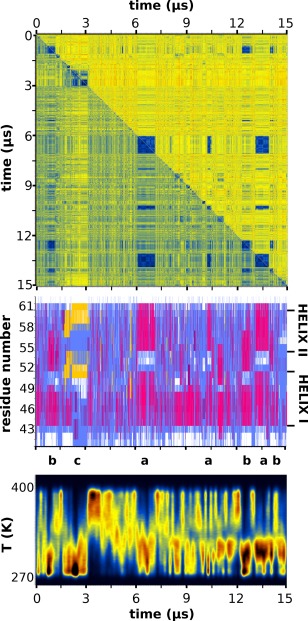
RMSD matrix, secondary structure and temperature distribution. The top panel depicts the RMSD matrix for the whole length of the trajectory in which warm colors (red, yellow) correspond to large RMSD values and cold colors (blue) to low RMSD values (similar structures). The upper half of the matrix was calculated using all non‐hydrogen atoms, the lower half only the peptide's C_α atoms. The middle panel is the STRIDE‐derived per residue secondary structure assignments with magenta depicting helical structure, yellow for β‐structure, cyan for turns, and white for random coil. Immediately below the secondary structure panel, the locations of the three most prominent peptide conformations (denoted as “a,” “b,” and “c”) along the extent of the trajectory have been marked. The lowest panel shows the distribution of the adaptive tempering temperature as a function of simulation time (notice the one‐to‐one correspondence between major conformers and low temperatures). See The Peptide is Mostly Disordered, but with Persistent Secondary Structure section for a detailed discussion of this figure.

Examination of the secondary structure diagram in Figure 3 shows that although HP21 is structurally flexible, there is a consistent conservation of a helical preference throughout the trajectory, especially in the N‐terminal region (corresponding to Helix I in Fig. 1). This conservation persists even at elevated adaptive tempering temperatures as can be deduced by comparing the secondary structure assignments with the simulation's temperature distribution shown in the lowest panel of Figure 3. Notice also how the stable peptide conformations—marked as “a,” “b,” and “c”—correspond to the low temperature regime of adaptive tempering. The higher stability of the first helix is consistent with the NMR‐derived experimental evidence as will be shown later.

To summarize this section, the simulation of HP21—even at this coarse level of analysis—appears to be fully consistent with the experiment: although the peptide is mostly disordered, with only few short‐lived stable conformations, there appears to be a persistent preference for helical structure especially in its N‐terminal region.

The major peptide conformation is a native‐like helix‐turn‐helix structure

The top panel of Figure 4 shows schematic representations of the major peptide conformers recorded from the molecular dynamics trajectory. The structures are marked as “a,” “b,” and “c” in a one‐to‐one correspondence with the peptide conformer identifications discussed in the previous section and shown in Figure 3 (below the secondary structure diagram). The peptide structures were obtained as follows. In the first stage dihedral principal component analysis (dPCA)63, 64, 65 was performed, and an initial set of clusters was identified by five‐dimensional dPCA cluster analysis as performed by the programs CARMA, GRCARMA, and CLUSTER5D (ASB & NMG, unpublished data). In the second stage, these dPCA‐derived clusters were used as input to a five‐dimensional Cartesian PCA clustering but using only the peptides' backbone atoms. The result from these two stages is a set of prominent clusters with distinct backbone conformations but without any differentiation with respect to putative heterogeneity in the side chains' conformations. In the final step, these clusters were further analyzed using another round of five‐dimensional Cartesian PCA, but this time using all of the peptides' nonhydrogen atoms. Representative structures for these final clusters were identified by calculating an average structure for each cluster and then selecting the frame from the trajectory with the lowest RMS deviation from the corresponding average structure.

Figure 4.

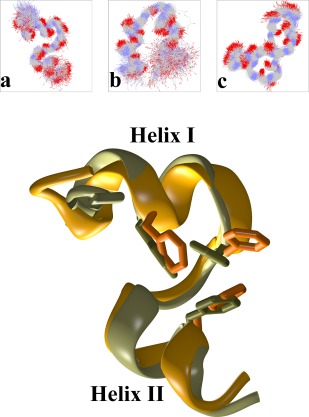
Major peptide conformers and comparison with the experimental structure. The top panel shows schematic diagrams of the three major peptide structures observed during the simulation. Each diagram is a superposition of 500 structures (backbone atoms only) belonging to each conformer (see also Fig. 3). The lower panel compares the major peptide conformer (colored orange, marked as “a” in the top panel and in Fig. 3) with the portion of the experimental structure of HP36 that corresponds to HP21 (PDB entry 1VII, residues 41–61, colored light green).

The major peptide conformation (marked as “a” in both Figs. 3 and 4) is a native‐like parallel helix‐turn‐helix structure as will be discussed below. The second peptide conformation (“b” in Figs. 3 and 4) exhibits an antiparallel helix‐turn‐helix motif with shorter helices and a highly flexible C‐terminus. The last conformer (marked as “c”) is significantly different in structural terms: it contains a stably formed β‐hairpin at its C‐terminus (visible in the upper right portion of the diagram) and a more flexible N‐terminal region that interconverts between helical and turn‐like conformations (most easily seen in the secondary structure diagram of Fig. 3, region marked as “c”).

The lower panel of Figure 4 shows a direct comparison between the three dimensional structures of the major peptide conformation as obtained from the simulation (colored orange) versus the structure of HP21 as observed in the experimentally determined HP36 structure (colored light green, PDB entry 1VII). The agreement between the two structures is excellent down to the level of individual side chains as indicated by the comparison between the three phenylalanines (residues 47, 51, 58) that form a characteristic hydrophobic cluster (shown with an all‐atom representation in Fig. 4). The RMS deviation between the two structures is only 0.9 Å when backbone atoms are considered, becoming 1.9 Å when all non‐hydrogen atoms are used for the calculation. With such a good agreement between the experimental and simulation‐derived structures—and given the similarity between the chemical shifts of HP21 and HP3648, 49—it is not surprising that the simulation‐derived chemical shifts are in good agreement with the experiment as is discussed in the next section.

The simulation‐derived chemical shifts are in reasonable agreement with the experiment

Figure 5 shows results from a quantitative comparison between the experimentally determined Δδ¹³C^α, Δδ¹³CO, and Δδ¹³C^β secondary shifts and those derived from the simulation via the application of the SPARTA+ program.53 Before we continue, we should mention here that for the calculation of reduced χ² values we have ignored the variance arising from the application of the SPARTA+ program53 which implies that our variances—being based on the simulation only—are underestimated, and thus, the derived goodness of fit values are expected to be overestimated (but see the discussion concerning the application of adaptive tempering later in this section).

Figure 5.

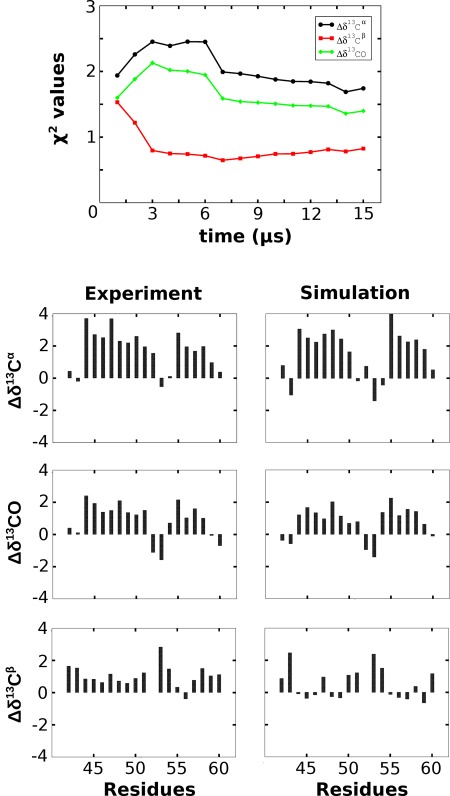
Comparison between chemical shifts. The upper panel shows the evolution of the reduced χ ² values for the Δδ¹³C^α, Δδ¹³CO, and Δδ¹³C^β secondary shifts as a function of simulation time. The lower three panels are a direct per‐residue comparison between the experimental (left row of diagrams) and simulation‐derived (right row) secondary shifts from the major peptide conformer in units of p.p.m. See The Simulation‐derived Chemical Shifts are in Reasonable Agreement with the Experiment section for a detailed discussion of this figure.

The top panel in Figure 5 shows the evolution of the reduced χ ² values for the Δδ¹³C^α, Δδ¹³CO, and Δδ¹³C^β secondary shifts as a function of simulation time. As we discussed in Extent of Sampling section, a direct comparison between experiment and the whole length of the simulation is probably not meaningful due to the incomplete sampling of the unfolded state (see also Fig. 2). Nevertheless, this diagram is still useful since it demonstrates (a) the expected slow convergence of the χ ² values as simulation time increases (reaching at the end of the simulation values of 1.6, 1.4, and 0.8 for the Δδ¹³C^α, Δδ¹³CO, and Δδ¹³C^β secondary shifts respectively), and (b) the notable difference between the behavior of the Δδ¹³C^α and Δδ¹³CO shifts on one hand and Δδ¹³C^β on the other. As will be discussed below, the apparent “over‐fitting” of secondary shifts is not due to the increased accuracy of the estimated shifts per se, but rather, is due to their significantly higher simulation‐derived variances. It should be noted here that the observation that the shifts calculated from the whole trajectory do appear to converge toward the experimental values may indicate that the length of the simulation (15 μs) could be meaningfully approaching the timescales of the NMR experiment. Having said that, the significant variation of the χ ² values when comparing the first and second half of the trajectory, clearly indicates that convergence is very slow as expected.

The lower three panels in Figure 5 show a direct residue‐by‐residue comparison between the experimentally determined and simulation‐derived secondary shifts for all structures recorded from the major peptide conformer (see previous section and Fig. 4). All‐in‐all the agreement between experiment and simulation is reasonably good with overall reduced χ ² values of 0.8, 0.7, and 0.3 for the Δδ¹³C^α, Δδ¹³C^β, and Δδ¹³CO secondary shifts, respectively. The general motif of the “strong‐weak‐strong” shifts (corresponding to the helix‐turn‐helix structure) is accurately followed, with the only consistent difference being an underestimation—on the part of the simulation—of the Δδ¹³C^α and Δδ¹³CO shifts in the first (N‐terminal) residues of the first helix. This probably implies that the simulation overestimates the flexibility of the N‐terminal part of helix I, but it can also be argued that it is an artifact arising from the application of adaptive tempering: the clustering procedure described in The Major Peptide Conformation is a Native‐like Helix‐Turn‐Helix Structure section includes structures whose corresponding adaptive tempering temperatures are higher than the temperature at which the NMR experiments were performed, thus increasing the apparent mobility of the peptide's N‐ and C‐termini. This line of thought could also explain the rather low χ ² values observed: due to the higher temperatures (and, thus, peptide mobility) the simulation‐derived variances are overestimated which leads to a concomitant reduction of the χ ² values.

To address the issue of the effect of adapting tempering on the derived quantities we have compared the values of secondary shifts obtained from two very different temperature ranges (see Supporting Information Fig. S1). The first set included all structures whose corresponding temperature was <300 K, and thus, have a negligibly small temperature variation. The second set included all structures whose corresponding temperatures ranged from the lowest observed to 340 K. To make the calculation even more demanding and meaningful, for this calculation we have used the whole of the trajectory and not just the major peptide conformer (as shown in the diagrams of Fig. 5). The results presented in Supporting Information Figure S1 clearly indicate that the effects on the chemical shifts of including structures with a higher adaptive tempering temperature are negligibly small compared with the variance arising from the peptide's structural heterogeneity. The very small effect of including in the calculation structures with significantly different temperatures is not very surprising: adaptive tempering53 produces a distribution of temperatures of the form (1/β) which means that higher temperature structures are inversely represented in the sample when compared with the low temperature structures. It is for these reasons that no additional correction has been deemed necessary for the results shown both in Figures 5 and 6 (noting the temperature cutoff of 320 K for secondary structure calculation as discussed in the next section).

Figure 6.

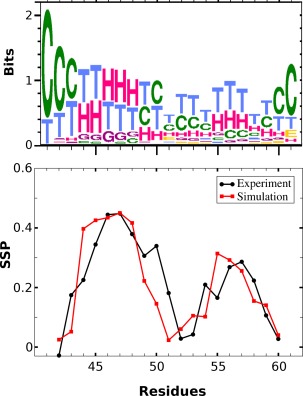
Secondary structure analysis. The top panel is a weblogo‐like representation of the per residue secondary structure preferences for all low temperature (T<320 K) structures recorded from the trajectory (H‐G: helical, C: coil, T: turn, E: extended β structure). The lower panel is a direct comparison between the per residue secondary structure propensity score (SSP) as determined from the experiment (black line) versus the simulation‐derived one (red line).

To quantify the agreement between the experimental and simulation‐derived secondary shifts shown in Figure 5 we have calculated the values of the linear correlation coefficient between them. These were found to be 0.83, 0.88, and 0.74 for the Δδ¹³C^α, Δδ¹³CO, and Δδ¹³C^β secondary shifts respectively, again verifying the reasonable agreement between experiment and simulation. As a side note, we should mention here that for the specific case of the Δδ¹³C^β secondary shifts, the simulation actually performs better at predicting their values than using directly the shifts obtained from HP36 (in the case of HP36 almost all residues have strongly negative Δδ¹³C^β secondary shifts, see Fig. 3 from the Raleigh paper49).

The experimental and simulation‐derived secondary structure propensities are in excellent agreement

The previous two sections established the good agreement between experiment and simulation especially with respect to the characterization of the major peptide conformer. Although—and as established in Extent of Sampling section—this is possibly a fair representation of what can be achieved due to the necessarily limited sampling for such a flexible system, we can nevertheless perform another test aiming to examine the general distribution of the peptide's secondary structure preferences. The calculation is based on a comparison between the SSP (secondary structure propensity) scores determined by the Raleigh group49 with the secondary structure assignments obtained from the simulation.

The results are shown in Figure 6. The upper panel is a graphical (weblogo66) representation of the simulation‐derived per residue secondary structure assignments for all structures with a corresponding adaptive tempering temperature of <320 K. The residues involved in the formation of the two helices (H assignments) are immediately obvious, as well as the lower stability of the second helix. The lower panel shows the per residue comparison between the experimentally derived data (black curve) and the simulation (red curve). Not only does the simulation reproduce the general characteristics of the distribution, it also accurately captures the persistence of the secondary structure elements with SSP values for the first helix reaching values of ∼0.45, compared with ∼0.30 for helix II. The exact limits of the helical regions are not as well defined, which is possibly a consequence of the limited sampling of other marginally stable peptide conformations.

Discussion

Highly flexible systems—with their associated dimensionality curse—are inherently difficult to study with molecular dynamics simulations. We believe that the calculations presented above indicate that even for such systems useful and experimentally verifiable information can be obtained from the simulation as long as the aim of the analysis is concerned with the transiently stable conformers (and not with the necessarily under‐sampled disordered state). The simulation clearly showed that HP21 is mostly disordered, correctly identified a native‐like structure as the most stable conformer, accurately predicted the associated secondary shifts, and faithfully reproduced the secondary structure preferences of the peptide. Having said that—and as the top diagram in Figure 5 demonstrated—obtaining useful averages from the whole length of the trajectory would be computationally prohibitive with such a slow rate of convergence, a finding which sets definitive limits for the interpretation of the trajectory as was extensively discussed in Extent of Sampling section. On a more technical note, we believe that the HP21 case study presented in this communication can—and should—be counted as yet another useful and physically relevant application of the AMBER99SB‐ILDN family of force fields for the study of peptide structure and dynamics.

Supporting information

Supporting Information