Detecting adaptive evolution based on association with ecological gradients: Orientation matters!

Abstract

Population genetic signatures of local adaptation are frequently investigated by identifying loci with allele frequencies that exhibit high correlation with ecological variables. One difficulty with this approach is that ecological associations might be confounded by geographic variation at selectively neutral loci. Here, we consider populations that underwent spatial expansion from their original range, and for which geographical variation of adaptive allele frequency coincides with habitat gradients. Using range expansion simulations, we asked whether our ability to detect genomic regions involved in adaptation could be impacted by the orientation of the ecological gradients. For three ecological association methods tested, we found, counter-intuitively, fewer false-positive associations when ecological gradients aligned along the main axis of expansion than when they aligned along any other direction. This result has important consequences for the analysis of genomic data under non-equilibrium population genetic models. Alignment of gradients with expansion axes is likely to be common in scenarios in which expanding species track their ecological niche during climate change while adapting to changing environments at their rear edge.

Detecting adaptive genetic responses using ecological gradients

The fossil record is replete with examples of species modifying their geographical distributions following environmental change (Comes and Kadereit, 1998; Blois and Hadly, 2009). On the basis of evidence from the past, range shifts are commonly viewed as an expected response of species to climate change (Parmesan and Yohe, 2003). In addition to range modifications, changing conditions and natural selection can also trigger genetic modifications allowing species to adapt to new local environments encountered during migration (Davis and Shaw, 2001; Davis et al., 2005; Jump and Penuelas, 2005). Under these conditions, researchers have suggested that gene frequencies may change gradually as natural selection acts on standing genetic variation or new mutations to favor adaptive phenotypes (Hermisson and Pennings, 2005; Hancock et al., 2010; Pritchard et al., 2010). In addition, natural selection may cause shifts in allele frequency at multiple genetic loci simultaneously, leaving subtle signatures of adaptive genetic change (Vitti et al., 2013).

Detecting gradual parallel genetic change is a difficult challenge (Pritchard et al., 2010), and range expansion scenarios may complicate the identification of adaptive alleles among selectively neutral polymorphisms. Range expansions can generate extreme genetic drift in the direction of colonization, driving allele frequencies close to fixation in a pattern that mimics the signature of selective sweeps (Edmonds et al., 2004). These results imply that traditional outlier methods based on allele frequency differentiation may be inappropriate to detect genetic signatures of local adaptation in species that underwent range expansion in the past. Allele frequency differentiation tests indeed lack the power to detect soft sweep signatures, and they are prone to high false-positive rates in this situation (Teshima et al., 2006; Hermisson, 2009).

A way to investigate signatures of local adaptation when selective alleles have weak phenotypic effects is by identifying loci with allele frequencies that exhibit high correlation with ecological variables (Joost et al., 2007; Hancock et al., 2008). Genome scan methods based on association of loci with ecological gradients assume that environmental factors vary throughout geographical space, and provide good proxies for unobserved selective pressures. Ecological association methods have performed well in simulation studies, often detecting adaptive loci when outlier allele frequency differentiation tests have failed, as in cases, for example, where selection varies geographically (De Mita et al., 2013), or when adaptive phenotypes evolve as polygenic traits (De Villemereuil et al., 2014).

An unanswered question is whether ecological association methods are impacted by the shape and orientation of gradients used as proxies for selection. Answering this question is essential to the interpretation of ecological association tests and to the use of ecological predictors that would produce the smallest proportion of false-positive associations. In this study, we considered a fictive species in which adaptive allele frequency gradients correlate with the geographical variation of some known environmental variables after the species expanded from its original range. For empirical examples, consider the evidence for genetic change associated with the ongoing range expansion of the bank vole (Myodes glareolus) in Ireland, or with the recent range expansion of the British butterfly (Aricia agestis) in response to climate change (Buckley et al., 2012; White et al., 2013). Under the situation described above, we argue that the performance of genome scan methods based on associations with ecological gradients will depend on the orientation of the gradient relative to the expansion axis as well as the test used. We provide evidence of spurious association at selectively neutral alleles for some gradients, and show that the most favourable case is when the gradients align along the direction of expansion. These results provide guidelines for researchers to analyse results when testing genetic data with ecological association methods.

Ecological association methods identifying genomic signatures of local adaptation

Genome scans based on correlations of allele frequencies with ecological gradients use multiple statistical tests to detect significant association at each locus. The list of loci showing associations with local environment are considered as candidate loci potentially targeted by selection. These associations are commonly tested using regression models (Joost et al., 2007). For example, regression models have been employed to identify ecologically relevant loci in humans (Hancock et al., 2008; Fumagalli et al., 2011; Frichot et al., 2013). Jones et al. (2012) used ecological correlation methods in their comparison of marine and freshwater sticklebacks to detect loci associated with habitat. Eckert et al. (2010) used regression methods to identify loci linked to climatic gradients in loblolly pines.

More specifically, statistical methods that evaluate the association of gene frequencies with ecological gradients can be classified into three main categories. Some of these methods include corrections for confounding effects due to population structure, whereas some others do not. The first category of methods tests for correlations using linear or logistic regression models or simple Mantel tests (Joost et al., 2007). These methods are appropriate for continuous populations or populations interconnected by high rates of gene flow. In other contexts, these simple regression models generate large numbers of false-positive associations (Schoville et al., 2012; De Mita et al., 2013; Frichot et al., 2013).

A second category of methods explicitly considers geographic structure in the data, and corrects for confounding effects created by shared demographic history and patterns of isolation by distance. Those models estimate the effect of the ecological variable on allele frequencies allowing for statistical dependence in residual terms. Interestingly, correction for confounding effects in ecological association methods relies on principles that are similar to phylogenetic comparative methods (Grafen, 1989; Harvey and Pagel, 1991). Phylogenetic comparative methods use information in phylogenetic trees to test for correlated evolutionary changes in two traits. In ecological association tests, confounding effects are corrected by introducing a known covariance matrix that models allele frequency dependencies. Evidence for local adaptation at a specific locus is then evaluated by testing a null model with this particular covariance structure. Our analogy with phylogenetic comparative methods postulates that background correlation in ecological association methods could be modeled on the basis of geographic or population genetic distance instead of phylogenetic distance (cf. Felsenstein, 2002).

For example, Poncet et al. (2010) used a generalized estimation equation model that assumes a covariance matrix in which nearby individuals are genetically more similar than individuals located farther apart. Another approach estimates the empirical covariance of allele frequencies among populations and uses it as the null model (Coop et al., 2010). This approach was implemented in the computer program BAYENV, and uses the full covariance matrix of allele frequencies. The BAYENV model can be extended to consider low rank approximations of the covariance matrix. It is then similar to using a regression model in which a fixed number of principal components of the data matrix are included as fixed effects in the model.

A third category of methods has been inspired by genome-wide association studies and mixed models (for example, Yu et al., 2006; Frichot et al., 2013; Yoder et al., 2014). Association between ecological gradients and allele frequencies are tested while estimating the effects of unobserved latent factors. In mixed models, the latent factors include background levels of population structure due to demographic history or background genetic variation, and the fixed effects model the correlation between allele frequencies and the observed selection gradients. The mixed model approach implemented in the software LFMM 2.1 (Frichot et al., 2013) proved to be among the most reliable approaches in a recent evaluation of several genome scan methods (De Villemereuil et al., 2014).

In this study, we used LFMM in conjunction with two other ecological association tests based on regression methods to investigate the confounding effect of range expansions on our ability to identify genomic signatures of selection. The two methods used a linear regression model without correction, and a linear regression model in which a fixed number of principal components of the data matrix are included as fixed effects. For linear regression methods, we used classical testing procedures based on z-scores and t-tests. Using LFMM, the number of latent factors, K, was chosen on the basis of the empirical distribution of locus-specific P-values after each program run. More specifically, we ran LFMM five times for each value of K with run-lengths of 10 000 cycles and burn-in periods of 5000 cycles, and we combined the P-values and the z-scores resulting from each run using the Fisher-Stouffer method (Brown, 1975). Following Devlin and Roeder (1999), we obtained a genomic inflation factor after computing the median of the squared (combined) z-scores for each K, divided by the median of the chi-square distribution with one degree of freedom. We selected the smallest value of K for which the genomic inflation factor value dropped below 1, using it to correct the test P-values.

Spatial simulation of neutral and adaptive allele frequencies

We considered a fictive species that underwent a range expansion 1000 generations ago. For this species, we simulated a demographic model in which a rectangular area was colonized from a unique source population located south of the area, and we considered population samples from the whole species range at the end of colonization.

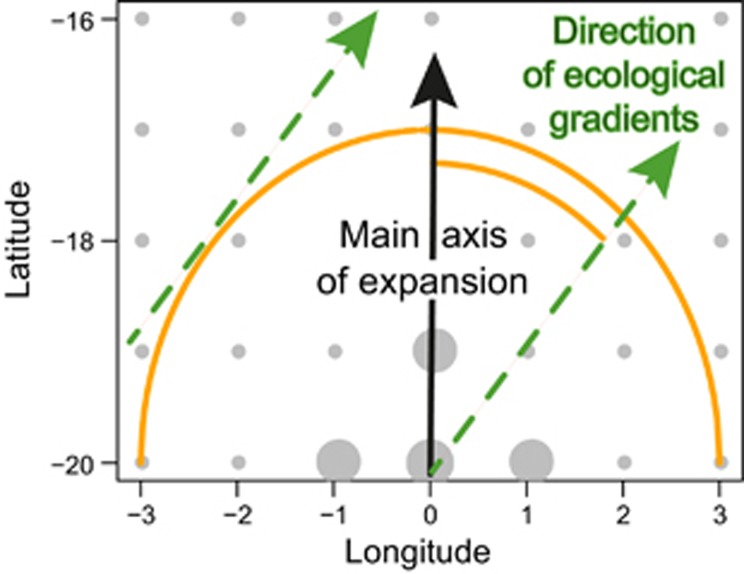
In our simulations, the main axis of expansion was oriented in the northward direction. We used the Haldane cline model to simulate geographic variation at adaptive loci based on ecological gradients (see below). A reference ecological gradient was defined to be parallel to the main axis of expansion. Then the axis of the reference gradient was rotated by angles of 11.25 degrees from the original position. We considered a total of 17 distinct angles ranging from −90 to +90 degrees. See Figure 1 for a representation of our simulation framework. An angle of 0 degree represented a selection gradient parallel to the main axis of expansion. We simulated independent genetic variation at 4900 neutral and at 100 adaptive single nucleotide polymorphisms. Our simulated data sets contained low percentages of true associations with ecological gradients (2%). We also simulated single nucleotide polymorphism data using 4500 neutral and 500 adaptive loci.

Figure 1.

Schematic representation of evolutionary scenarios. Populations (demes) are represented by a regular array of dots, the larger ones indicating the origin of expansion. The main direction of expansion is shown by black arrow (solid line), the circular wave front is shown by an orange circle. The main axis of the ecological gradient is shown by a green arrow (dashed line) which angle varies from −90 degrees to +90 degrees.

Data sets consisting of selectively neutral multi-locus genotypes were created using the computer program SPLATCHE (Currat et al., 2004). Range expansion scenarios were implemented using non-equilibrium stepping-stone models based on a regular array of 165 demes organized in a rectangle of size 11-by-15. A rectangular area was colonized from a unique source located south of the area (Figure 1). For each deme, the migration rate was equal to m =0.4, the expansion rate was equal to r =0.4, and the carrying capacity was equal to C=100. The ‘density overflow' option was used to spread the source population over eight demes.

Four genotypes were sampled from each of the 165 demes for a total number of 660 genotypes. To create associations between loci and ecological gradients, we linked allele frequencies to ecological gradients by using Haldane's transform (Haldane, 1948). The Haldane transform simulates a geographic trend, that is, continuous variation through geographic space, that reproduces clinal allele frequency patterns as expected under spatially varying selection intensities. In addition, we used a model of correlated residuals that generates the same background population genetic structure at adaptive loci as observed at neutral loci. To implement it, we introduced residual errors based on the empirical covariance matrix of the neutral loci (Coop et al., 2010). The shape parameter for Haldane's clines was set to mimic weak selection, not easily detectable using classical population differentiation methods. To check this, we computed the first axis of a principal component analysis for a typical set of neutral single nucleotide polymorphismss (Supplementary Figure S1A). This axis clearly separated populations defined at the right and left of the expansion axis. For all data sets, we computed the empirical distributions of F_ST for populations defined at the right and left of the expansion axis. Running tests with statistical power greater than 80%, we found that the false discovery rate (FDR) for adaptive loci was greater than 62% in all simulations. Supplementary Figure S1B displays the map of a selection gradient obtained by rotation of 45 degrees from the reference axis, and Supplementary Figure S1C displays the map of a selection gradient collinear to the direction of expansion.

In summary, adaptive loci were simulated so that the geographic distribution of the derived allele frequency correlated with the geographic distribution of the observed ecological gradient. Thus, we modelled a situation in which allele frequencies at adaptive loci are truly associated with the observed ecological gradient and exhibit background population structure similar to allele frequencies at neutral loci.

The orientation of ecological gradients impacts the identification of adaptive loci

To demonstrate the universal properties of methods rather than showing differences in their relative performances, we focused on three methods that can be considered representative of ecological association tests. Our first method was based on a simple linear regression model, our second method used a linear model including correction for population structure based on the first principal component of the genotypic matrix, and our third method was based on latent factor mixed models.

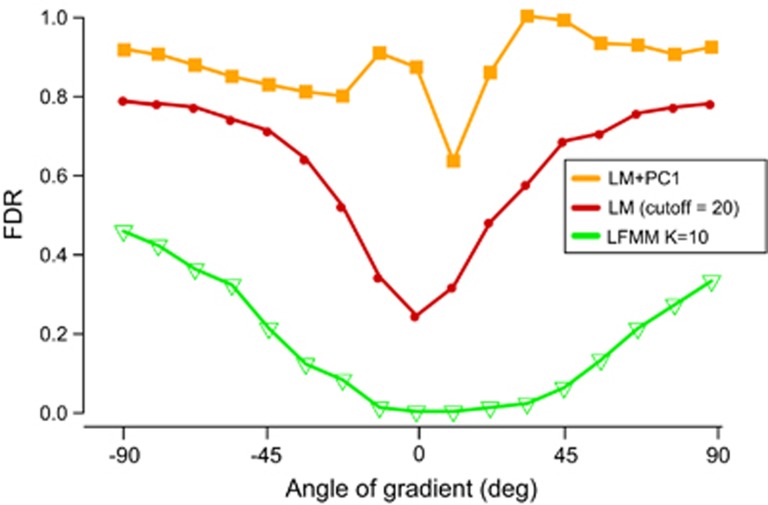
On the basis of simulated data, we computed a FDR for the three association tests and for 17 distinct orientations of ecological gradients. For each simulation, the FDR was computed as the number of times that a positive test detected a selectively neutral locus. We used Bonferroni correction for multiple testing at a nominal type I error of 1%. For all ecological association methods, we found that all test performances were influenced by the angle between the selection gradient and the main axis of range expansion (Figure 2).

Figure 2.

FDR for ecological association tests. Values of the FDR as a function of the orientation of ecological gradients relative to the main axis of range expansion. We used 17 angle values varying from −90 degrees to +90 degrees and three association tests: simple linear regression, principal component regression using the first PC of the genotypic matrix and a latent factor model using K=8 latent factors.

When we applied linear regression models and used Bonferroni correction, the FDR remained greater than 60% for all orientations of the ecological gradients (orange curve in Figure 2). For standard regression models, the excess of extreme P-values could be explained by the test not being correctly calibrated (see Supplementary Figure S2). Including a correction for population structure did not improve the performances of linear regression methods. In contrast, increasing the cut-off threshold for multiple testing correction to −log₁₀ P>20 or correcting for genomic inflation using the genomic inflation factor improved the performances of the regression models substantially (red curve in Figure 2). Using an increased cut-off threshold, the FDR curve exhibited a minimum at angular values close to zero, and the FDR was around 20% for those values (Figure 2, red curve). These results show that some gradient orientations are more favourable for detecting adaptive loci than other orientations. The most favorable case clearly occurs when selection gradients align with the main direction of range expansion. In more specific terms, this occurs when the orientation of the main axis of neutral genetic variation—as described by the first principal component of the neutral genotypic matrix—is perpendicular to the environmental predictor (François et al., 2010; Arenas et al., 2013; De Giorgio and Rosenberg, 2013). Ecological association methods perform well if they reduce the confounding effect created by population structure by capturing a significant proportion of genetic variation at neutral alleles in the residual error of the regression model.

Latent factor mixed models provide a general approach to correct for the undesired effect of population structure in ecological association methods (Frichot et al., 2013). In our simulations, the number of hidden factors was chosen to make the distribution of P-values closest to a uniform distribution. We found that this value was around K=8, consistent with the number of clusters detected by the ancestry estimation programs STRUCTURE, TESS and sNMF (Pritchard et al., 2000; Chen et al., 2007; Frichot et al., 2014). For K=8 factors, the performance of LFMM was expected to be superior to those of classic regression models whatever the orientation of the selection gradient. The FDR curve confirmed this expectation (Figure 2). Consistently with other regression models, the most favourable case happened when selection gradients aligned along the direction of range expansion. Our explanation is that nominal error rates are better calibrated when selection gradients are parallel to the axis of expansion than when they are oriented in other directions.

Extending our results to other methods, we observed that logistic regression models led to results very similar to those of linear regression models. Although we reported results for models including the first principal component of the genotypic matrix, we observed that including more components led to qualitatively equivalent results. We did not use BAYENV because of high run-to-run variability. This inherent variability makes conclusions about genome-wide patterns of adaptation more difficult than for other methods (Blair et al., 2014). As the BAYENV approach is similar to a logistic regression method including correction for population structure, the same behaviour is expected for BAYENV as for the other methods investigated here.

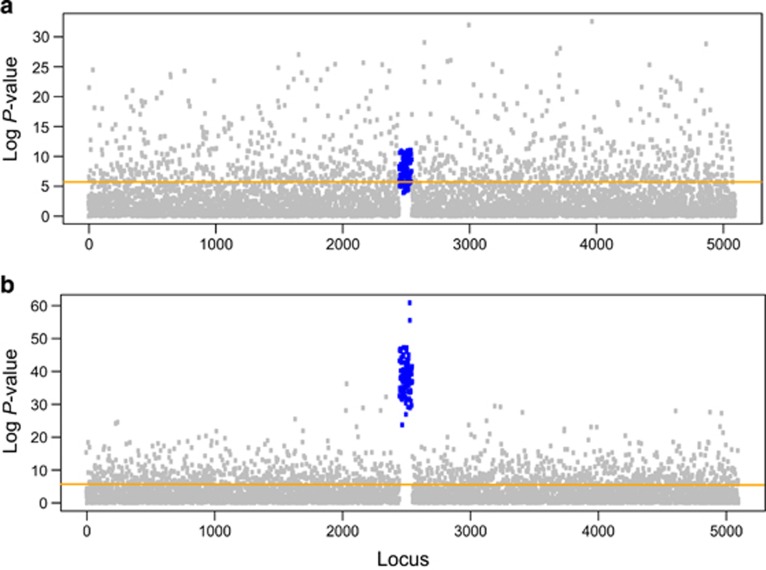
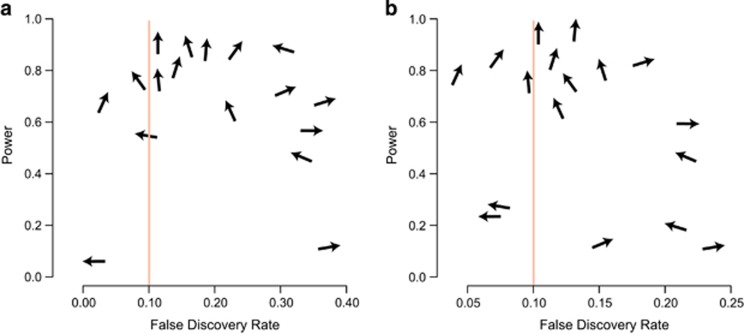
To investigate the power of ecological association tests under various orientations of ecological gradients, we applied the Benjamini-Hochberg algorithm to control the FDR at level q=10% for all methods. For each data set, we evaluated the sensitivity of tests as the proportion of loci with positive tests among adaptive loci. Sensitivity was generally high for linear regression methods, but the observed FDR reached values greater than 90% for those tests (for example, Figures 3a and b that shows excessively large numbers of neutral loci with P-values above the threshold). In contrast, the testing procedure based on latent factor models provided reasonable control of the FDR using the Benjamini-Hochberg algorithm. Note that the increased performance of LFMM resulted from the use of genomic inflation factor corrections combined with the meta-analysis of multiple runs, which is computationally more intensive than running simple regression models. For data sets containing 100 adaptive loci, the observed FDR ranged between 5 and 35% (10% expected, Figure 4a). For data sets containing 500 adaptive loci, the observed FDR ranged between 3 and 23% (Figure 4b). Using LFMM, the observed FDR was closer to its expected value when ecological gradients aligned along the direction of range expansion than along any other directions. The test power reached values greater than 75%, and it increased when ecological gradients aligned along the direction of range expansion. Power was less than 60% when ecological gradients were approximately perpendicular to the direction of range expansion (Figure 4).

Figure 3.

Manhattan plot for linear model association tests under two distinct angles of selection gradient (0 and 90 degrees). Graphical representation of minus log₁₀ P-values of linear regression tests at each locus. The horizontal line represents the value of the Bonferroni correction threshold. P-values for (a) ecological gradients perpendicular to the direction of expansion and (b) parallel to the direction of expansion.

Figure 4.

FDR—Power plot for LFMM tests and 17 distinct orientations of ecological gradients. Each data set is represented by an arrow displaying the direction of the ecological gradient in the simulated data. Vertical arrows indicate that the ecological gradient aligns along the direction of expansion. The expected FDR, q=10%, is shown by a vertical line. Each arrow position corresponds to the sensitivity (power) of tests and the percentage of false discoveries in the lists of loci obtained with the Benjamini-Hochberg algorithm. (a) 100 adaptive loci, (b) 500 adaptive loci. Five runs and K=8 factors were used in LFMM.

Discussion

Range expansions following climatic or other environmental changes are commonly associated with adaptive changes within migrant species genomes. This happens frequently in cases of species invasions (Kirk et al., 2013), postglacial recolonization (Hewitt, 1999) and even in crop or animal domestication (Doebley et al., 2006). Researchers can investigate these changes by applying genome scan methods based on association with ecological gradients (Joost et al., 2007; Hancock et al., 2008; Jay et al., 2012). Here, we provide new insights into the use of ecological association methods when species have expanded their spatial range. Our simulation study addressed the intuitive idea that the orientation of allele frequency gradients in geographic space could reveal signatures of natural selection (for example, Fix, 1996). If allele frequency gradients perpendicular to the axis of expansion can be linked to neutral population structure, allele frequency gradients that align along the direction of expansion could be linked to selection. We found that ecological association approaches are useful ways to formalise these conceptual ideas.

Using spatially explicit simulations, our first result was that association tests are sensitive to the orientation of ecological gradients relative to the main axis of expansion. We found that the angle made by the axis of expansion and the axis of selection had a strong influence on the FDR (and power) of ecological association tests. Even for the best method, we observed up to 35% FDR in unfavourable cases.

Although we kept the origin of expansion fixed and modified the direction of selection gradients, our approach also applies to the symmetric case where a fixed ecological gradient is considered and the geographic origin of expansion is modified. Our second result is that the list of candidate genes obtained from association methods contained fewer false associations when the test variables exhibited geographic gradients that paralleled the direction of expansion than in other directions. Though the performance of methods could differ significantly, all association tests exhibited better performance when the selection gradient was parallel to the axis of expansion. When this gradient was orthogonal to the axis of expansion, the FDR increased in all methods.

The reason for the lower rates of false positives in the case of a North-South ecological gradient was that population genetic structure was organized West-East. Under population genetic models of range expansion and a broad set of conditions, the gradient of principal component maps are oriented along a direction perpendicular to the axis of the expansion, rather than parallel to expansion (François et al., 2010; De Giorgio and Rosenberg, 2013). This pattern is an outcome of the ‘allele surfing' phenomenon, which creates patches of high allele-frequency differentiation that align perpendicular to the direction of the expansion, and complicates the detection of selection when ecological gradients do not align with the expansion axis. François et al. (2010) suggest that the results presented here will be valid for geometries more complex than a rectangular array, for example, range expansions in the European continent. They also suggest that admixture events have an impact on test performances. De Giorgio and Rosenberg (2013) provided evidence that population sampling can modify principal component analysis, which impacts the power and FDR of tests. Although the allele surfing phenomenon may strongly bias allele-frequency differentiation tests, we observed that the undesired effects can be corrected when we sample throughout the whole species range and test gradients that are perpendicular to the first principal axis of neutral variation.

The most likely explanation for the high FDRs observed in linear regression models is that those methods use an incorrect model to test the null hypothesis. In the linear model, residual errors are considered statistically independent of each other ignoring population genetic structure shaped by range expansion (Figure 3,Supplementary Figure S2). Using corrections based on principal components improved the FDR only slightly, and the results were qualitatively similar to those of linear regression methods. We also observed that increasing the number of principal components reduced the power to reject the null hypothesis (not reported).

The FDR of linear regression methods decreased substantially when an ultra-conservative cut-off threshold defined the test significance level. Again, we found that conservative tests exhibited better performances when ecological gradients paralleled the expansion axis. Because the calibration of P-values based on linear models is usually incorrect, researchers must be cautious about interpretations of the candidate locus list. In addition, they must be aware that their results come without any control of the FDR.

Latent factor mixed linear models were associated with much lower levels of FDR than simple linear regression models and models using correction based on principal components. Instead of principal components, LFMM uses unknown factors in addition to the fixed environmental effects. The LFMM algorithm estimates the unknown factors from the data at the same time as it estimates the effect of ecological variables. Choosing the number of factors according to the flatness of the P-values histogram, as measured by the genomic inflation factor, provides assurance that association tests were correctly calibrated, and models of background variation (or correlated residual errors) remained at acceptable levels. An important advantage of this choice procedure is to allow researchers to analyse ranked lists of loci while they control the FDR using classical procedures (Benjamini and Hochberg, 1995). Greater power will be found in ecological gradients that parallel the axis of expansion, and fewer false discoveries will be done in data sets where the number of adaptive loci is high compared with the number of neutral loci.

Recent simulation studies have evaluated the sensitivity and specificity of genome scans for selection, and compared ecological association methods with methods based on allele frequency differentiation (De Mita et al., 2013; De Villemereuil et al., 2014). These simulation studies have shown that ecological methods have higher power to detect adaptive genetic variation than outlier-based methods when adaptive traits are influenced by several genes and when population structure is hierarchical (De Villemereuil et al., 2014). Our study confirmed that ecological association methods could detect adaptive genetic variation when populations have undergone range expansion, and have high power to detect adaptive genetic variation when expansion and ecological gradients follow the same direction.

Following our observations, we encourage researchers to use ecological association methods when screening genomes for local adaptation in spatially expanding populations. For example, ecological gradients that align along the axis of expansion occur for species that colonized Europe following the most recent glacial period (Hewitt, 2000). More generally, our results are particularly relevant to global change scenarios where species track their ecological niche during range expansion while adapting to changing environments at their rear edge (Jump and Penuelas, 2005). In this case, researchers using ecological association approaches should be aware that detecting genomic signature of adaptation can be facilitated when gradients align along the main axis of expansion.

Data archiving

There were no data to deposit.

The authors declare no conflict of interest.