Abstract
Association mapping has become a widely applied genomic approach to dissect the genetic architecture of complex traits. A major issue for association mapping is the need to control for the confounding effects of population structure, which is commonly done by mixed models incorporating kinship information. In this case study, we employed experimental data from a large sugar beet population to evaluate multi-locus models for association mapping. As in linkage mapping, markers are selected as cofactors to control for population structure and genetic background variation. We compared different biometric models with regard to important quantitative trait locus (QTL) mapping parameters like the false-positive rate, the QTL detection power and the predictive power for the proportion of explained genotypic variance. Employing different approaches we show that the multi-locus model, that is, incorporating cofactors, outperforms the other models, including the mixed model used as a reference model. Thus, multi-locus models are an attractive alternative for association mapping to efficiently detect QTL for knowledge-based breeding.
Introduction
Association mapping has been developed by human geneticists but in recent years has been adopted by plant geneticists and become an increasingly popular genomic tool to dissect the genetic architecture of complex traits in plants (Nordborg and Weigel, 2008; Hamblin et al., 2011; Würschum, 2012). It has successfully been used to detect quantitative trait loci (QTL) for agronomically important traits in many crop species including maize (for example, Harjes et al., 2008), wheat (for example, Breseghello and Sorrells, 2006; Reif et al., 2011a, 2011b), barley (for example, Wang et al., 2012; Berger et al., 2013) and rice (for example, Huang et al., 2010). Traditional approaches for QTL detection in plants are based on linkage mapping in bi-parental populations. By contrast, association mapping is based on a diverse panel of plants with varying degrees of relatedness.
An assumption underlying the concept of association mapping studies is that the individuals are mutually independent, that is, unrelated or equally related to each other (Sillanpää, 2011). This assumption is, however, usually not met and diversity panels as employed for association mapping are characterized by population stratification and cryptic relatedness (Lander and Schork, 1994; Astle and Balding, 2009; Sillanpää, 2011). Population stratification refers to the origin of individuals from two or more source populations whereas cryptic relatedness describes the different covariances between individuals due to their relatedness. The presence of such population structure must be regarded as confounding factor in association mapping as it can result in the detection of false-positive QTL. To control the false-positive rate, it is thus important to correct for these confounding effects by an appropriate biometric approach (Price et al., 2010; Lippert et al., 2011; Sillanpää, 2011; Tucker et al., 2014; Yang et al., 2014). Association mapping in plants is nowadays commonly done by mixed model analysis that allows to account for cryptic relatedness by a random polygenic term modeled with a covariance structure that is defined by a kinship matrix (Yu et al., 2006). In addition, population stratification can be accounted for by structured association, that is, incorporating cluster membership information as covariate or by approaches that incorporate principal components as covariates (Price et al., 2006; Stich et al., 2008). It must be noted that a stringent correction for population structure will also reduce the QTL detection power (Würschum et al., 2011). Consequently, an appropriate biometric model should provide a balance between an adequate control of the false-positive rate and a high QTL detection power (that is, low false-negative rate).
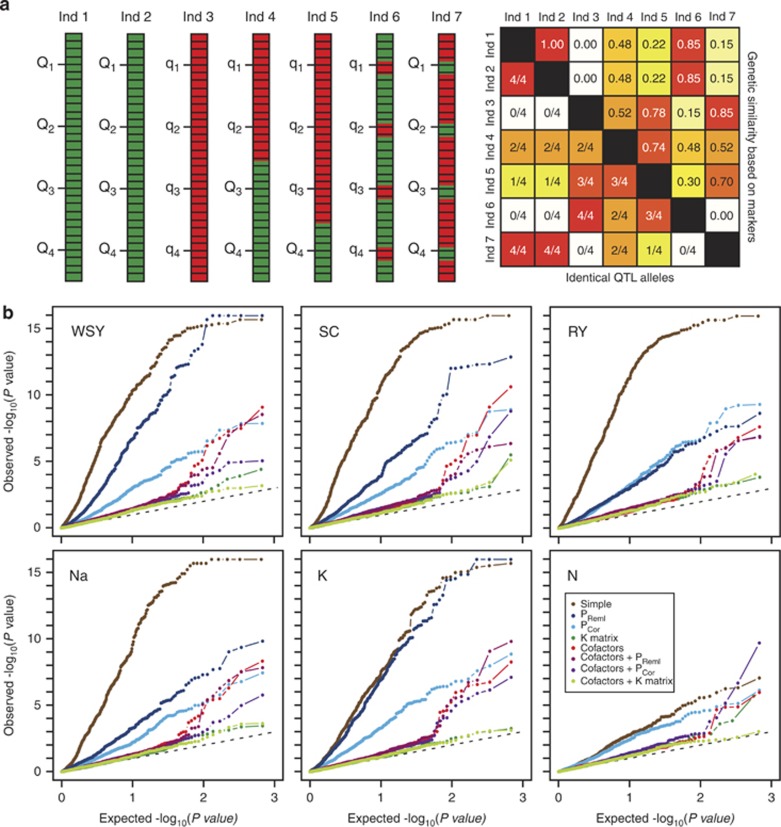
The control of the genetic background by a kinship matrix incorporates information from all chromosomal regions covered by markers, which with high-density genotyping means the entire genome. Crucial for an adequate control are, however, the QTL positions. As depicted schematically in Figure 1, the kinship estimates based on genome-wide marker data will generally provide good estimates for the similarity at the QTL positions. Nevertheless, Figure 1 also illustrates that, albeit exaggerated to emphasize this point, individuals may be highly similar based on genome-wide marker data but possess different alleles at QTL loci (Ind 1–Ind 6) or vice versa (Ind 1–Ind 7). In this example, the phenotypic covariance between individuals cannot be predicted based on their genetic relatedness estimated by genotypic information across the entire genome. In such cases, considering the QTL positions might provide a better control of the genetic background than a genome-wide kinship estimate.
Figure 1.
(a) Schematic illustration of the information captured by a kinship matrix. Seven individuals with a single chromosome are shown harboring four QTL with two alleles (Q, q). The horizontal lines indicate markers and red and green indicate different alleles at the marker loci. The heatplot indicates genetic similarity among the seven individuals estimated based on marker information (above diagonal) and their identity at the four QTL (below diagonal). (b) Distribution of observed −log10(P-values) against expected −log10(P-values) for the different biometric models shown for six traits.
A milestone in the development of linkage mapping methodology was the use of cofactors (Jansen and Stam, 1994; Zeng, 1994). These cofactors represent selected markers that are included in the analysis to increase the efficiency of QTL mapping as they control the genetic background variation of QTL outside the chromosomal region under consideration. In the context of association mapping, the incorporation of a single marker that is informative about ancestry (that is, the source populations) as cofactor in the model has also been shown to provide a certain control for population stratification (Wang et al., 2005). Setakis et al. (2006) suggested the use of a much larger number of null markers as regression covariates to eliminate most of the variation due to population structure. In addition, multilocus models have been shown to possess the potential to account for population stratification, potentially as the variable selection process selects also those markers that explain a part of the confounding variation (Iwata et al., 2007; Pikkuhookana and Sillanpää, 2009; Kärkkäinen and Sillanpää, 2012). Another benefit of simultaneously taking multiple QTL into account in the model is that the QTL detection power may also be enhanced (Iwata et al., 2007). Conceptually, the above-mentioned approaches aimed at incorporating one or several markers as covariates to control for the presence of population structure. Segura et al. (2012) have recently applied the concept of cofactors to association mapping. Their results suggested that multi-locus mixed models, that is, models incorporating a kinship matrix and selected cofactors, performed better with regard to the false-discovery rate and the QTL detection power than a model incorporating only a kinship matrix or only cofactors. A related approach has been proposed by Rakitsch et al. (2013), however, using Lasso instead of stepwise forward selection.
The aim of this study was to further evaluate the potential of multi-locus models to control the genetic background variation in association mapping, especially with regard to important QTL parameters. In particular our objectives were to employ a large sugar beet panel consisting of 924 lines to compare different models incorporating cofactors and standard approaches with regard to (1) the potential to control the false-positive rate, (2) the QTL detection power, (3) the predictive power for the proportion of explained genotypic variance and (4) the bias in the estimation of genotypic variance explained by detected QTL assessed by cross-validation.
Materials and methods
Plant materials, field experiments and molecular markers
The present study was based on a total of 924 diploid sugar beet (Beta vulgaris L.) inbred lines from the breeding program of Syngenta Seeds AB (Sweden) that have been described by Würschum et al. (2011). For all genotypes testcross progenies were produced through crosses to a single-cross hybrid as tester. The 924 testcross progenies were evaluated in multi-location field trials for the following traits: white sugar yield (t ha−1), sugar content (%), root yield (RY, t ha−1), potassium (K, mM), sodium (Na, mM) and α-amino nitrogen (N, mM).
All lines were genotyped with 677 single-nucleotide polymorphism markers, which provide a high coverage of the entire sugar beet genome (total map length of 698 cM).
Phenotypic data analyses
Adjusted entry means (BLUEs) were calculated for each location as described by Würschum et al. (2011). Principal coordinate analysis (Gower, 1966) based on the modified Rogers' distances of the individuals (Wright, 1978) was applied to analyze associations among the 924 genotypes, employing the software package Plabsoft (Maurer et al., 2008).
Association mapping
The mixed model for the association mapping approach was yijp=μ+ap+gi+lj+eijp, where yijp is the adjusted entry mean of the ith sugar beet line at the jth location carrying allele p, μ the intercept term, ap the allele substitution effect of allele p, gi the genetic effect of the ith sugar beet line, lj the effect of the jth location, and eijp the residual. The genotypic and the location effects, gi and lj, were treated as random effects while the allele substitution effect ap was a fixed effect. To control for potentially confounding effects of population structure, different approaches were tested: models that included only principal coordinates (PReml and PCor), a model with a kinship matrix, a model incorporating cofactors, and models that in addition to the cofactors included the principal coordinates or the kinship matrix.
The models PReml and PCor included different numbers of principal coordinates, as described in Würschum et al. (2011). For the PReml model, the Wald F statistic was used to identify the first principal coordinate that was not significant any more as fixed effect at P<0.01. By contrast, the PCor model included all principal coordinates that were found to be significantly associated (P<0.01) with the adjusted entry means of the six traits.
For models including the kinship matrix K, the variance of the random genetic effect was assumed to be Var(g)=KσG2, where σG2 refers to the additive genetic variance estimated by REML and K was a 924 × 924 matrix of kinship coefficients that define the degree of genetic covariance between all pairs of entries. This kinship matrix was not based on pedigree data as this would not have allowed to differentiate genotypes derived from the same cross. Rather, it is the realized relationship matrix estimated based on the genome-wide distributed molecular markers. Following the suggestion of Bernardo (1993), we calculated the kinship coefficient Kij between inbred lines i and j on the basis of marker data as Kij=1+(Sij−1)/(1−Tij), where Sij refers to the proportion of marker loci with shared variants between entries i and j, and Tij is the average probability that a variant from one parent of inbred i and a variant from one parent of inbred j are alike in state, even if they are not identical by descent. The coefficient Tij was separately estimated for each trait and model by REML, and resulting negative kinship values between inbred lines were set to zero (Stich et al., 2008). The kinship matrices obtained by this approach were invertible and consequently no further modifications to make them positive definite were required.
For the models incorporating cofactors, the mixed model described above was used for stepwise selection of the cofactors as described by Sillanpää and Corander (2002) which has been applied for example by Bauer et al. (2009). The first round of cofactor selection corresponds to the single-marker analysis. The marker which is most significantly associated with the trait, based on the P value from the Wald F statistic, is selected as first cofactor. In the next round, this marker is included in the model as a fixed effect before the marker to be tested, and all markers except the cofactor are tested again. This procedure is repeated until a full marker scan yields no further markers that are significantly associated with the trait. The final QTL scan includes all selected cofactors as fixed effects, and all markers (including those selected as cofactors) are sequentially tested for their association with the trait.
A genome-wide scan for marker–trait associations was done to detect main effect QTL, correcting for multiple testing by a false-discovery rate of 0.20 (Benjamini and Hochberg, 1995; Kraakman et al., 2004). The total proportion of genotypic variance (pG) explained by the detected QTL was obtained by a simultaneous fit of the QTL in a linear model to obtain Radj2. The ratio pG=Radj2/h2, where h2 refers to the heritability of the trait, then yielded pG (Utz et al., 2000). For the Venn diagrams, marker–trait associations were declared as identifying the same QTL if they fell within an arbitrarily defined ±5 cM interval. All mixed model calculations were performed using the software ASReml 3.0 (Gilmour et al., 2009).
Cross-validation
To obtain asymptotically unbiased estimates of the proportion of genotypic variance that could be explained by the detected QTL, a cross-validation approach was applied (Würschum and Kraft, 2014). We used fivefold cross-validation which means that 80% of the genotypes were used as estimation set (ES) for QTL detection employing the models described above. The remaining 20% of the genotypes constituted the test set (TS), which was used for validation of the estimated QTL effects. Notably, validation was not done based on the models used for QTL detection but based on a linear model: the detected QTL were simultaneously fitted in a linear model to estimate their effects in the ES that were subsequently used to predict the genotypic values of the lines in the TS. Thus, for validation, the QTL effect estimates obtained from the ES were used to predict the genotypic value of line j in TS QTS.ESj according to QTS.ESj=XTSj βES, where XTSj is the vector of marker data of line j at the identified QTL positions, and βES is the vector of genetic effects of these QTL estimated as partial regression coefficients from a simultaneous fit in the ES (Utz et al., 2000). Subsequently, the proportion of genotypic variance explained by the QTL in the TS (pG-TS) was calculated as follows: for the lines in the TS, the adjusted squared correlation coefficient (Radj2) between their observed phenotypic values and the predicted genotypic values QTS.ESj was obtained and divided by the heritability of the trait. The results presented here are averaged across 300 cross-validation runs. The difference in pG between the ES (pG-ES) and the TS (pG-TS) was used to estimate the bias in the proportion of explained genotypic variance and the relative bias was derived as 1−(pG-TS/pG-ES). The QTL frequency distributions were obtained from the cross-validation runs.
Simulation study
The simulation study was done based on the genotypic data of the experimental population. Ten markers were randomly sampled and defined as QTL. Each QTL was assigned a QTL effect, which in a population with equal allele frequencies would explain 10% of the variance. QTL mapping was then done with the kinship matrix model and the cofactors model in 100 simulation runs.
Results
A simple simulation study showed that the average probability of a detected QTL being a true positive QTL was comparable for the kinship matrix model and a model incorporating cofactors, thus corroborating previous results from Segura et al. (2012) on the competitiveness of multi-locus models. To further evaluate the performance of models with cofactors in experimental data sets, we employed a large panel of sugar beet lines that have been evaluated in multi-location field trials for three yield-related traits (white sugar yield, WSY; sugar content, SC; root yield, RY) and three quality-related traits (sodium content, Na; potassium content, K; α-amino nitrogen content, N) (Würschum et al., 2011). For this data set, the model incorporating a kinship matrix has been shown to perform well with regard to the false-positive rate and generally provided a higher QTL detection power as compared with models that in addition included principal coordinates to control for population structure. In this study, we compared eight biometric models: a simple model without any correction for population structure, two models incorporating different numbers of principal coordinates (PReml and PCor), the model with a kinship matrix (K matrix), a multi-locus model with selected cofactors, models that in addition to the cofactors incorporated the principal coordinates (PReml or PCor) and a model incorporating cofactors and the kinship matrix. For the latter models, the cofactors were selected in the presence of the principal coordinates or the kinship matrix, respectively. We first assessed the potential of these models to control the false-positive rate. The plots of observed versus expected −log10(P-values) indicated that with the exception of the simple model and the models incorporating only principal coordinates, the distributions closely followed the diagonal indicating a good control of the population structure (Figure 1b). The model with cofactors or cofactors in combination with principal coordinates or kinship matrix showed a similar distribution as the reference model incorporating the kinship matrix.
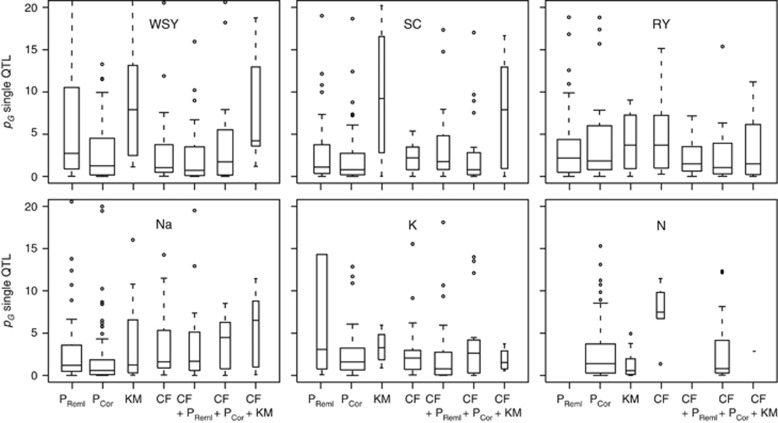
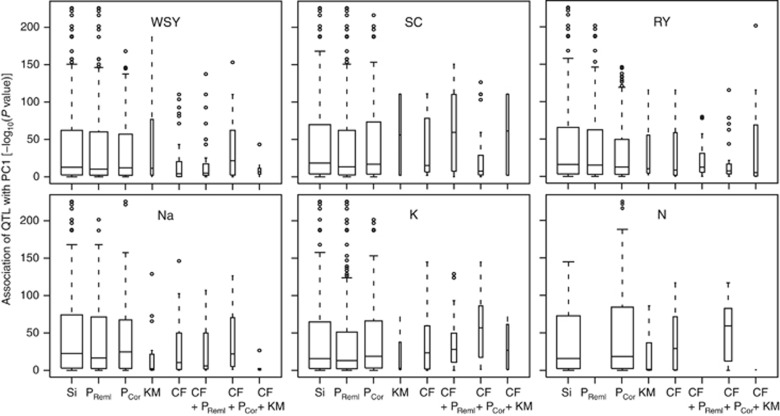
The models incorporating cofactors as well as cofactors and principal coordinates generally detected a substantially higher number of QTL as compared with the K matrix model while the model with cofactors in addition to the K matrix identified approximately the same number of QTL as the K matrix model (Table 1). The proportion of genotypic variance (pG) explained by the detected QTL followed this trend and was also higher for the model with cofactors and cofactors with principal coordinates as compared with the K matrix model. The distributions of the pG of the single QTL indicated that the models with cofactors appeared to capture also QTL with smaller effects as compared with the K matrix model (Figure 2). We next assessed the association of the detected QTL with population structure, which revealed no difference between the K matrix model and the models incorporating cofactors (Figure 3, Supplementary Figures S1 and S2). The QTL detected with the models incorporating cofactors were generally equally associated with population structure as the QTL from the K matrix model.
Table 1. Comparison of the number of detected main effect QTL and the genotypic variance explained by these QTL (p G in %) for the different models.
| Model | WSY | SC | RY | Na | K | N |
|---|---|---|---|---|---|---|
| Simple | ||||||
| QTL | 523 | 503 | 549 | 468 | 441 | 200 |
| pG | NA | NA | NA | NA | NA | NA |
| PReml | ||||||
| QTL | 372 | 312 | 275 | 244 | 419 | — |
| pG | NA | NA | NA | NA | NA | — |
| PCor | ||||||
| QTL | 208 | 218 | 236 | 163 | 283 | 174 |
| pG | NA | NA | NA | NA | NA | NA |
| K matrix | ||||||
| QTL | 8 | 4 | 10 | 15 | 4 | 9 |
| pG | 73.4 | 38.1 | 63.1 | 58.7 | 12.8 | 10.4 |
| Cofactors | ||||||
| QTL | 31 | 24 | 15 | 25 | 26 | 6 |
| pG | 100 | 74.9 | 85.7 | 88.7 | 77.2 | 42.6 |
| Cofactors+PReml | ||||||
| QTL | 37 | 21 | 27 | 18 | 28 | — |
| pG | 100 | 75.3 | 75.2 | 66.4 | 63.9 | — |
| Cofactors+PCor | ||||||
| QTL | 26 | 25 | 25 | 16 | 15 | 20 |
| pG | 85.2 | 58.3 | 73.6 | 58.4 | 58.7 | 49.4 |
| Cofactors+K matrix | ||||||
| QTL | 7 | 6 | 16 | 6 | 4 | 1 |
| pG | 70.8 | 45.5 | 60.2 | 33.2 | 6.7 | 2.6 |
Abbreviations: K, potassium content; N, α-amino nitrogen content; Na, sodium content; RY, root yield; SC, sugar content; WSY, white sugar yield.
Results are shown for six traits.
Figure 2.
Box-Whisker plots of the proportion of genotypic variance (pG) explained by the single QTL detected by the different biometric models shown for six traits. P, principal coordinates; KM, K matrix; CF, cofactors; the variable width indicates the number of QTL.
Figure 3.
Association of the QTL detected with the different biometric models with population structure (first principal coordinate). P, principal coordinates; KM, K matrix; CF, cofactors; the variable width indicates the number of QTL.
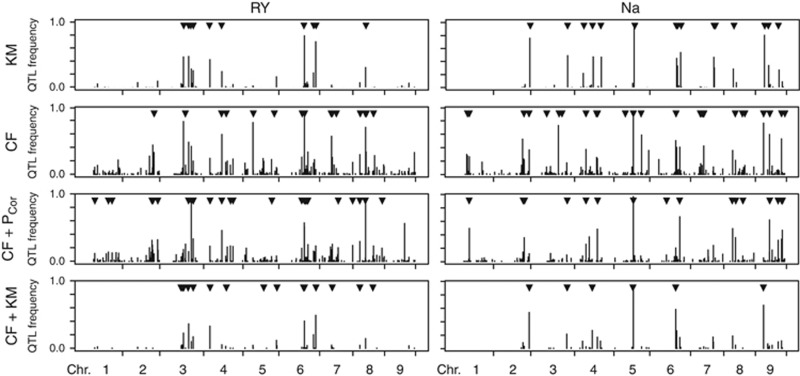
A comparison of the Manhattan plots as well as the Venn diagrams revealed model-specific QTL but also few QTL that were detected across all models, for example, the sodium content QTL on chromosome 5 (Figure 4). As visualized in the Manhattan plots, the associations between QTL and the trait were generally weaker for the models incorporating the kinship matrix as compared with the other models, while the average −log10(P-values) were comparable between them. For the model incorporating cofactors and the K matrix, only few cofactors were selected and the Manhattan plots more closely resembled those of the K matrix model as compared with the model with cofactors.
Figure 4.
Manhattan plot of the marker P-values for four biometric models shown for RY and Na. The filled arrowheads indicate the positions of the selected cofactors and the empty arrowheads the positions of the detected marker–trait associations. Venn diagrams for the QTL detected by these models. KM, K matrix; CF, cofactors; PCor, principal coordinates.
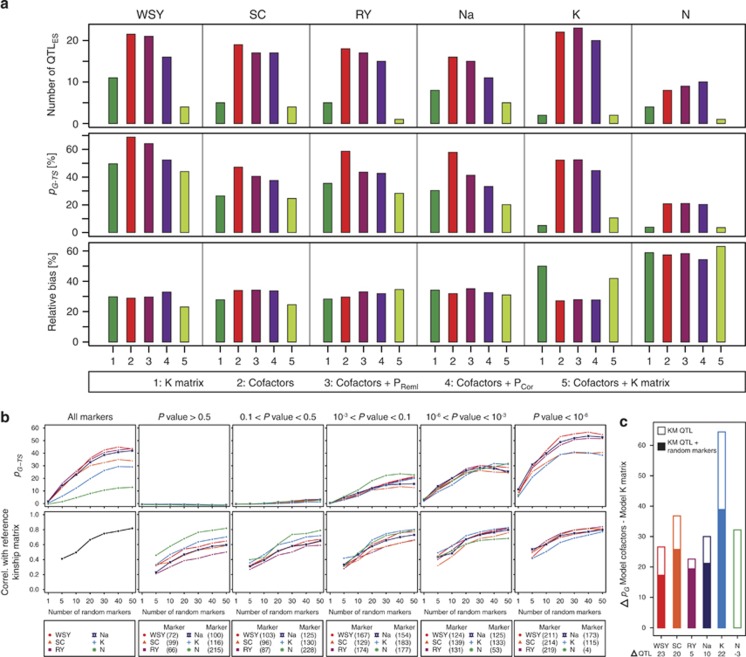
The QTL frequency distributions derived from fivefold cross-validation revealed that for all models some QTL were identified in a high number of runs, whereas other QTL were only identified with low frequency (Figure 5). The fivefold cross-validation confirmed the higher number of QTL detected by the models with cofactors and cofactors with principal coordinates as compared with the models with kinship matrix (Figure 6a). With regard to the cross-validated proportion of genotypic variance explained by detected QTL (pG-TS), the model incorporating cofactors outperformed the other models for all traits. A substantially lower pG-TS was observed for the K matrix model and the model with cofactors in combination with the K matrix. The relative bias in the estimation of pG, that is, the difference between pG-TS and pG-ES was, however, comparable for all models across all traits.
Figure 5.
QTL frequency distributions from fivefold cross-validation for four biometric models shown for RY and Na. The arrowheads indicate the positions of the QTL detected in the full data set. KM, K matrix; CF, cofactors; PCor, principal coordinates.
Figure 6.
(a) Results from fivefold cross-validation. Number of QTL detected in ESs, cross-validated proportion of genotypic variance (pG-TS) and the relative bias in the estimation of the proportion of explained genotypic variance. (b) Cross-validated proportion of explained genotypic variance (pG-TS) and correlation with the kinship matrix based on all markers for different numbers of randomly sampled markers. Results are shown for all markers or subsets of markers based on their association with the trait (P-values) in the simple model. (c) Difference in the proportion of genotypic variance (Δ pG) explained by the QTL detected with the cofactors model and the K matrix (KM) model as well as the K matrix model QTL supplemented with random QTL (Δ QTL) to total the same number of QTL as the cofactors model.
As the cofactors model identified a substantially higher number of QTL as compared with the K matrix model, we assessed the effect of the number of QTL on the proportion of explained genotypic variance. To this end, we randomly selected different numbers of markers and estimated the pG-TS that can be explained by them (Figure 6b). For all traits, we observed that the pG-TS increased with increasing numbers of markers until it reached a maximum at approximately 40 markers after which it slowly declined. This analysis showed that for the markers identified as QTL in the ESs of the cross-validation (QTLES) (Figure 6a), the pG-TS was substantially higher than expected based on the same number of randomly sampled markers. The difference in pG between the cofactors model and the K matrix model was substantial (Figure 6c) but the above analysis indicated that this cannot simply be attributed to the higher number of markers selected as QTL with the cofactors model. We used the QTL identified by the K matrix model and complemented them with randomly selected markers to yield the same total number of QTL as identified by the cofactors model. Nevertheless, the pG of the cofactors model was still considerably higher than that of the K matrix model QTL supplemented with random markers (Figure 6c).
The cross-validated proportion of explained genotypic variance by randomly sampled markers was surprisingly high which prompted us to perform the same analysis but instead of with random markers with subsets of markers that were chosen based on their association with the traits in the simple model (Figure 6b). This revealed that the pG-TS strongly depended on the association of the markers with the traits. Only the subsets of markers with a certain association with the traits (P<0.1) did show a pG-TS larger than zero and pG-TS increased with the strength of the association of the markers with the traits as well as with the number of markers in each subset. In addition, we assessed how well these subsets of markers are still representative for the entire genome by correlating the kinship matrix calculated with them to the kinship matrix based on all markers (Figure 6b). This revealed that the higher the number of sampled markers, the higher the correlation with the reference kinship matrix. Apart from that there were only slight differences between the subsets of markers and the subsets with a higher number of markers to sample from yielded higher correlations, probably due to the coverage of a higher proportion of the genome.
Discussion
The presence of population stratification and cryptic relatedness is a major issue for association mapping approaches and must be accounted for in the analysis, which is commonly achieved by the incorporation of a kinship matrix in the biometric model. However, as exemplified in Figure 1a this approach may have shortcomings under certain scenarios. A major step in the development of QTL linkage mapping methodology was the incorporation of cofactors to control the genetic background variation. Although association mapping and QTL linkage mapping are different approaches, they share the basic problem of controlling the genetic background, and thus may profit from each others methodological achievements. While the incorporation of a kinship matrix has been tested in QTL linkage mapping and shown to provide good results (Bernardo, 2013), the use of cofactors to control for population structure in association mapping has been proposed (Segura et al., 2012) but not yet intensively validated. In this study, we used a large sugar beet population to evaluate the performance of the kinship matrix model as a reference model for association mapping and models incorporating cofactors, in particular with regard to the estimation of important QTL parameters.
Control of the false-positive rate
The plots of observed versus expected −log10(P-values) can be employed to assess the overall control of the false-positive rate (Figure 1b). In the absence of QTL, the P-values are expected to follow a uniform distribution and thus the diagonal in the plot. Deviations from the diagonal in the region of large expected −log10(P-values) indicate the presence of QTL while stronger deviations from the diagonal are characteristic for an inflated false-positive rate. Taking the commonly used K matrix model as a reference, the models employing cofactors alone as well as in combination with principal coordinates or the K matrix provided an equally good control of the population structure and thus the false-positive rate for all six traits. It must be noted that these plots of observed versus expected −log10(P-values) do not rule out the presence of false-positive QTL and the higher number of QTL detected by the cofactors model as compared with the K matrix model might still be due to some false-positive QTL. There are, however, no approaches to prove that an identified QTL is a true-positive QTL. A marker associated with population structure can be identified as QTL, albeit a false-positive QTL, if it escapes the control for population structure by the biometric model. Such a QTL can explain a proportion of the genotypic variance and might even be confirmed by cross-validation if the population structure it is associated with is maintained in the cross-validation subsets. This, however, applies to all models and also QTL identified by the K matrix model may be false-positive QTL. In general, we should be aware that the results from a QTL mapping are statistical results and any identified QTL should be thoroughly validated before it is implemented in a marker-assisted selection program. Nevertheless, a number of approaches can be applied to substantiate the true nature of identified QTL.
While it is not possible to unambiguously determine whether a QTL is a true QTL, a strong association of the detected QTL with population structure can be interpreted as an increased risk of them being false positives and only identified due to their association with population structure not accounted for by the biometric model. These analyses revealed, however, no substantial difference between the reference K matrix model and the model incorporating cofactors (Figure 3, Supplementary Figures S1 and S2) indicating that the cofactors model QTL are no more likely to be false-positive QTL than the K matrix model QTL. Another measure for the quality of the detected QTL is the bias in the proportion of explained genotypic variance assessed by cross-validation. A high number of false-positive QTL may result in a large bias as their estimated effects can negatively affect the prediction in the independent validation set. The results from the cross-validation revealed no difference in the relative bias among the models for all traits (Figure 6a). Taken together, our results illustrate that the models incorporating cofactors are equally well suited to control for the presence of population structure and thus the false-positive rate as the standard model incorporating a kinship matrix. The different approaches employed here indicate that the QTL identified by the cofactors model are no more likely to be false positives as the QTL from the K matrix model serving as a reference and consequently are as likely to be true-positive QTL.
QTL detection power
While the control of the false-positive rate is essential in association mapping, appropriate biometric models should also maintain a high QTL detection power, that is, provide a low false-negative rate. With the exception of α-amino nitrogen for which fewer QTL were detected, the cofactors model identified on average four times more QTL than the K matrix model (Table 1). This trend was also confirmed by the substantially higher number of QTL detected in the ESs of the cross-validation approach (Figure 6a). Furthermore, the QTL frequency distributions can be employed to assess how consistently QTL are detected across ESs in cross-validation which revealed no difference between the K matrix model and the cofactors model (Figure 5). Interestingly, the K matrix model appeared to detect mainly large effect QTL as opposed to the cofactors model, which also detected QTL with smaller effects (Figure 2). The comparison of the identified QTL showed some QTL overlapping between both models (Figure 4), which were mainly major QTL explaining a high proportion of genotypic variance. These QTL were also identified in a high number of cross-validation runs for both models. The QTL specific for the cofactors model mainly had a low pG and were detected in fewer cross-validation runs. This however does not mean that they are not true-positive QTL as it must be noted here that the QTL detection power, especially for small effect QTL, strongly depends on population size and they would probably be detected more consistently in cross-validation given a larger mapping population. This corroborates previous findings from association mapping in multiple families, which also observed a lower QTL detection power of the K matrix model as compared with models incorporating cofactors (Würschum et al., 2012). In addition, the Manhattan plots showed that the associations of the identified QTL with the trait were weaker for the K matrix model than they were for the cofactors model while the average P-values of all markers were comparable for both models (Figure 4). This indicates that for a given significance threshold the K matrix model appears to be more stringent toward QTL detection as compared with the cofactors model. Thus, while both the K matrix model and the cofactors model provide a similar control of the false-positive rate, their mode of control appears to be different as reflected by the differences in the QTL detection power. This may indicate an overcorrection of the K matrix model resulting in the observed reduction of the QTL detection power.
Predictive power for the proportion of explained genotypic variance
An important parameter for QTL mapping approaches is the proportion of genotypic variance that can be explained by the detected QTL. The cofactors model had a substantially higher predictive power with regard to this parameter than the K matrix model which was confirmed by cross-validation (Table 1, Figure 6a). For all six traits, the model incorporating cofactors performed best with regard to the cross-validated proportion of explained genotypic variance. The two models which in addition included principal coordinates were slightly inferior to the cofactors model while the model with cofactors and K matrix performed comparable to the K matrix model. The superiority of the cofactors model over the K matrix model is likely due to the higher number of detected QTL which as described above are unlikely to all be false-positives. Consistently, we found that complementing the K matrix model QTL with random markers to total a similar number of QTL as identified by the cofactors model did not increase the proportion of explained genotypic variance to the same level as that obtained with the cofactors model QTL (Figure 6c).
We observed a rather high proportion of explained genotypic variance by randomly sampled markers (Figure 6b). This can be explained by the small size of the sugar beet genome and the quantitative nature of the studied traits. Consequently, most regions of the genome will harbor QTL which increase the probability that a marker in a QTL region is randomly selected. This was substantiated by randomly sampling the same numbers from subsets of markers that were made based on the association of the markers with the traits in the simple model. Markers which with the simple model showed no association with the trait are likely residing in chromosomal regions without QTL and consequently we observed no substantial pG-TS with these subsets even for 50 sampled markers. However, markers used in a statistical model to estimate marker effects for prediction can also capture additive genetic relationships between individuals and it has been shown through simulation studies that even if markers are used for prediction that are not in LD with QTL, the prediction accuracies are non-zero (Habier et al., 2007). We used the correlation with the reference kinship matrix calculated based on all markers to illustrate that all marker subsets appear to represent the genome equally well (Figure 6b). The observation that the markers from the non-associated subsets did not enable prediction suggests that the exploitation of additive genetic relationships has no or only a minor role for the observed prediction accuracies. The obtained cross-validated prediction accuracies rather appear to rely on the identification of QTL and precise estimation of their effects.
In summary, the cofactors model outperformed all other models, including the K matrix model, with regard to the predictive power for the proportion of explained genotypic variance, an essential parameter for marker-assisted selection.
Conclusions
Segura et al. (2012) have recently shown that a mixed model that in addition to a kinship matrix also included cofactors performed better with regard to the false-discovery rate and the QTL detection power than models incorporating either the kinship matrix or cofactors. By contrast, our results suggest that a model incorporating cofactors alone is equally well suited to control for population structure and consequently the false-positive rate as the K matrix model, but outperforms this reference model with regard to the QTL detection power and the predictive power for the proportion of explained genotypic variance. The model with cofactors in addition to the K matrix was similar to the K matrix model and thus the additional inclusion of cofactors offered no advantage. Our results suggest that the lower QTL detection power and predictive power of the models incorporating the K matrix may result from an overcorrection by this model. While the kinship matrix provides a genome-wide control of genetic kinship, cofactors control population structure but also the genetic background variation, that is, the genetic noise produced by other QTL, thus enabling a better evaluation of the marker under consideration. This may be particularly powerful for traits with a genetic architecture that in addition to small effect QTL also contains several medium or large effect QTL. It must be noted, however, that for traits for which the genetic architecture approaches a polygenic model of many loci with small effects, the cofactors model will suffer as no or only few cofactors can be selected and consequently no adequate correction is provided. For such highly polygenic traits, a model incorporating a kinship matrix might perform better. Thus, in addition to population structure, the genetic architecture of the trait is another important parameter affecting the performance of association mapping models. This is also a possible reason for the different performance of the models in our data set and that of Segura et al. (2012), which illustrates that the optimum model for association mapping strongly depends on the data set (for example, Kärkkäinen and Sillanpää, 2012).
In combination with missing marker imputation, the cofactors model as presented here could also be implemented as a linear model, taking advantage of the regression framework, as used for QTL linkage mapping, that is robust and computationally fast. In conclusion, our results demonstrate that multi-locus models, that is, selection and incorporation of cofactors, can be used in association mapping to control for the presence of population structure as well as genetic background variation. The multi-locus model provided a sufficient control of the false-positive rate while maintaining a high QTL detection power and consequently outperformed the kinship matrix model, used as ‘gold standard', with regard to the predictive power for the proportion of explained genotypic variance. Thus, depending on the population structure and the genetic architecture of the trait, the use of multi-locus models for association mapping represents an interesting and powerful alternative to the commonly used mixed model approach with kinship information.
Data archieving
This study is based on the data provided by Würschum and Kraft (2014).
The authors declare no conflict of interest.
Footnotes
Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)
Supplementary Material
References
- Astle W, Balding DJ. (2009) . Population structure and cryptic relatedness in genetic association studies. Stat Sci 24: 451–471. [Google Scholar]
- Bauer AM, Hoti F, Von Korff M, Pillen K, Léon J, Sillanpää MJ. (2009) . Advanced backcross-QTL analysis in spring barley (H. vulgare ssp. spontaneum) comparing a REML versus a Bayesian model in multi-environmental field trials. Theor Appl Genet 119: 105–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. (1995) . Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc 57: 289–300. [Google Scholar]
- Berger GL, Liu S, Hall MD, Brooks WS, Chao S, Muehlbauer GJ et al. (2013) . Marker-trait associations in Virginia Tech winter barley identified using genome-wide mapping. Theor Appl Genet 126: 693–710. [DOI] [PubMed] [Google Scholar]
- Bernardo R. (1993) . Estimation of coefficient of coancestry using molecular markers in maize. Theor Appl Genet 85: 1055–1062. [DOI] [PubMed] [Google Scholar]
- Bernardo R. (2013) . Genomewide markers as cofactors for precision mapping of quantitative trait loci. Theor Appl Genet 126: 999–1009. [DOI] [PubMed] [Google Scholar]
- Breseghello F, Sorrells ME. (2006) . Association mapping of kernel size and milling quality in wheat (Triticum aestivum L.) cultivars. Genetics 172: 1165–1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmour AR, Gogel BJ, Cullis BR, Thompson R. (2009). ASReml User Guide Release 3.0. VSN International Ltd: Hemel Hempstead, UK.
- Gower JC. (1966) . Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika 53: 325–338. [Google Scholar]
- Habier D, Fernando RL, Dekkers JCM. (2007) . The impact of genetic relationship information on genome-assisted breeding values. Genetics 177: 2389–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamblin MT, Buckler ES, Jannink J-L. (2011) . Population genetics of genomics-based crop improvement methods. Trends Genet 27: 98–106. [DOI] [PubMed] [Google Scholar]
- Harjes CE, Rocheford TR, Bai L, Brutnell TP, Kandianis CB, Sowinski SG et al. (2008) . Natural genetic variation in lycopene epsilon cyclase tapped for maize biofortification. Science 319: 330–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X, Wei X, Sang T, Zhao Q, Feng Q, Zhao Y et al. (2010) . Genome-wide association studies of 14 agronomic traits in rice landraces. Nat Genet 42: 961–967. [DOI] [PubMed] [Google Scholar]
- Iwata H, Uga Y, Yoshioka Y, Ebana K, Hayashi T. (2007) . Bayesian association mapping of multiple quantitative trait loci and its application to the analysis of genetic variation among Oryza sativa L. germplasms. Theor Appl Genet 114: 1437–1449. [DOI] [PubMed] [Google Scholar]
- Jansen RC, Stam P. (1994) . High resolution of quantitative traits into multiple loci via interval mapping. Genetics 136: 1447–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kärkkäinen HP, Sillanpää MJ. (2012) . Robustness of Bayesian multilocus association models to cryptic relatedness. Ann Hum Genet 76: 510–523. [DOI] [PubMed] [Google Scholar]
- Kraakman ATW, Niks RE, Van den Berg PMMM, Stam P, Van Eeuwijk FA. (2004) . Linkage disequilibrium mapping of yield and yield stability in modern spring barley cultivars. Genetics 168: 435–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Schork NJ. (1994) . Genetic dissection of complex traits. Science 265: 2037–2048. [DOI] [PubMed] [Google Scholar]
- Lippert C, Listgarten J, Liu Y, Kadie CM, Davidson RI, Heckerman D. (2011) . FaST linear mixed models for genome-wide association studies. Nat Methods 8: 833–835. [DOI] [PubMed] [Google Scholar]
- Maurer HP, Melchinger AE, Frisch M. (2008) . Population genetic simulation and data analysis with Plabsoft. Euphytica 161: 133–139. [Google Scholar]
- Nordborg M, Weigel D. (2008) . Next-generation genetics in plants. Nature 456: 720–723. [DOI] [PubMed] [Google Scholar]
- Pikkuhookana P, Sillanpää MJ. (2009) . Correcting for relatedness in Bayesian models for genomic data association analysis. Heredity 103: 223–237. [DOI] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. (2006) . Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet 38: 904–909. [DOI] [PubMed] [Google Scholar]
- Price AL, Zaitlen NA, Reich D, Patterson N. (2010) . New approaches to population stratification in genome-wide association studies. Nat Rev Genet 11: 459–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakitsch B, Lippert C, Stegle O, Borgwardt K. (2013) . A Lasso multi-marker mixed model for association mapping with population structure correction. Bioinformatics 29: 206–214. [DOI] [PubMed] [Google Scholar]
- Reif JC, Gowda M, Maurer HP, Longin CFH, Korzun V, Ebmeyer E et al. (2011. a) . Association mapping for quality traits in soft winter wheat. Theor Appl Genet 122: 961–970. [DOI] [PubMed] [Google Scholar]
- Reif JC, Maurer HP, Korzun V, Ebmeyer E, Miedaner T, Würschum T. (2011. b) . Mapping QTLs with main and epistatic effects underlying grain yield and heading time in soft winter wheat. Theor Appl Genet 123: 283–292. [DOI] [PubMed] [Google Scholar]
- Segura V, Vilhjálmsson BJ, Platt A, Korte A, Seren Ü, Long Q et al. (2012) . An efficient multi-locus mixed model approach for genome-wide association studies in structured populations. Nat Genet 44: 825–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setakis E, Stirnadel H, Balding DJ. (2006) . Logistic regression protects against population structure in genetic association studies. Genome Res 16: 290–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillanpää MJ, Corander J. (2002) . Model choice in gene mapping: what and why. Trends Genet 18: 301–307. [DOI] [PubMed] [Google Scholar]
- Sillanpää MJ. (2011) . Overview of techniques to account for confounding due to population stratification and cryptic relatedness in genomic data association analyses. Heredity 106: 511–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stich B, Möhring J, Piepho HP, Heckenberger M, Buckler ES, Melchinger AE. (2008) . Comparison of mixed-model approaches for association mapping. Genetics 178: 1745–1754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker G, Price AL, Berger B. (2014) . Improving the power of GWAS and avoiding confounding from population stratification with PC-Select. Genetics 197: 1045–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Utz HF, Melchinger AE, Schön CC. (2000) . Bias and sampling error of the estimated proportion of genotypic variance explained by quantitative trait loci determined from experimental data in maize using cross validation and validation with independent samples. Genetics 154: 1839–1849. [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Localio R, Rebbeck TR. (2005) . Bias correction with a single null marker for population stratification in candidate gene association studies. Hum Hered 59: 165–175. [DOI] [PubMed] [Google Scholar]
- Wang M, Jiang N, Jia T, Leach L, Cockram J, Waugh R et al. (2012) . Genome-wide association mapping of agronomic and morphologic traits in highly structured populations of barley cultivars. Theor Appl Genet 124: 233–246. [DOI] [PubMed] [Google Scholar]
- Wright S. (1978). Evolution and Genetics of Populations, Variability Within and Among Natural Populations Vol 4, The University of Chicago Press: Chicago. p 91. [Google Scholar]
- Würschum T, Maurer HP, Kraft T, Janssen G, Nilsson C, Reif JC. (2011). Genome-wide association mapping of agronomic traits in sugar beet. Theor Appl Genet 123: 1121–1131. [DOI] [PubMed] [Google Scholar]
- Würschum T. (2012) . Mapping QTL for agronomic traits in breeding populations. Theor Appl Genet 125: 201–210. [DOI] [PubMed] [Google Scholar]
- Würschum T, Liu W, Gowda M, Maurer HP, Fischer S, Schechert A et al. (2012) . Comparison of biometrical models for joint linkage association mapping. Heredity 108: 332–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Würschum T, Kraft T. (2014) . Cross-validation in association mapping and its relevance for the estimation of QTL parameters of complex traits. Heredity 112: 463–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Zaitlen NA, Goddard ME, Visscher PM, Price AL. (2014) . Advantages and pitfalls in the application of mixed-model association methods. Nat Genet 46: 100–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Pressoir G, Briggs WH, Vroh Bi I, Yamasaki M et al. (2006) . A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet 38: 203–208. [DOI] [PubMed] [Google Scholar]
- Zeng ZB. (1994) . Precision mapping of quantitative trait loci. Genetics 136: 1457–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.