Genomic prediction in biparental tropical maize populations in water-stressed and well-watered environments using low-density and GBS SNPs

Abstract

One of the most important applications of genomic selection in maize breeding is to predict and identify the best untested lines from biparental populations, when the training and validation sets are derived from the same cross. Nineteen tropical maize biparental populations evaluated in multienvironment trials were used in this study to assess prediction accuracy of different quantitative traits using low-density (~200 markers) and genotyping-by-sequencing (GBS) single-nucleotide polymorphisms (SNPs), respectively. An extension of the Genomic Best Linear Unbiased Predictor that incorporates genotype × environment (GE) interaction was used to predict genotypic values; cross-validation methods were applied to quantify prediction accuracy. Our results showed that: (1) low-density SNPs (~200 markers) were largely sufficient to get good prediction in biparental maize populations for simple traits with moderate-to-high heritability, but GBS outperformed low-density SNPs for complex traits and simple traits evaluated under stress conditions with low-to-moderate heritability; (2) heritability and genetic architecture of target traits affected prediction performance, prediction accuracy of complex traits (grain yield) were consistently lower than those of simple traits (anthesis date and plant height) and prediction accuracy under stress conditions was consistently lower and more variable than under well-watered conditions for all the target traits because of their poor heritability under stress conditions; and (3) the prediction accuracy of GE models was found to be superior to that of non-GE models for complex traits and marginal for simple traits.

Introduction

In genomic selection (GS), the effect of all markers is estimated simultaneously from a training population that has been both phenotyped and genotyped, and then the genomic estimated breeding values of the untested genotyped lines are computed as the sum of all marker effects (Meuwissen et al., 2001). In GS, lines in the prediction population are not phenotyped, only genotyped, thus reducing the breeding cycle time and increasing the genetic gain per unit time. In GS, all markers are fitted simultaneously to avoid biased marker effects and capture all the small effects (Heffner et al., 2009, 2010). In plants, Bernardo and Yu (2007) were the first to show, by simulation, the benefits of GS in terms of genetic gains as compared with marker-assisted selection. Also, de los Campos et al. (2009) and Crossa et al. (2010, 2011, 2013a), using extensive empirical maize and wheat data, demonstrated that using low-to-intermediate marker density and pedigree information increased the prediction accuracy of unobserved phenotypes. Massman et al. (2013a), in one biparental population, gave empirical evidence that GS produced higher genetic gains than marker-assisted selection for several traits.

Regarding the number of markers, it could be speculated that for certain types of breeding populations and a specific range of markers, more accurate genomic prediction could be achieved with high marker density; however, increasing marker density above a certain level does not produce an increase in prediction accuracy, as shown by de los Campos et al. (2012) for height in a human population.

Genotyping-by-sequencing (GBS) is a high-throughput, multiplex and short read sequencing approach that reduces genome complexity via restriction enzymes, generates high-density genome-wide markers (~1 million) at a low per-sample cost by tagging randomly shared DNA fragments from different samples with unique, short DNA sequences (barcodes) and pooling samples into a single sequencing channel (Elshire et al., 2011). The GBS cost per sample is comparable to (or lower than) the price of single-plex or array-based single-nucleotide polymorphisms (SNPs). A GBS platform was recently used to generate large numbers of SNPs in many species, exploring within-species diversity and studying trait association in a diverse seed bank collection (Poland et al., 2012a; Lu et al., 2013; Romay et al., 2013; Glaubitz et al., 2014); GBS is also a promising genotyping method for GS application. The first evidence of the prediction accuracy of GBS in plants came from Poland et al. (2012b), who showed good accuracy using GBS in prediction models for polyploid wheat breeding, and from Crossa et al. (2013a), who predicted doubled-haploid maize lines using pedigree as well as imputed and unimputed GBS data.

Prediction within biparental populations is the most favorable situation for GS in which the relationship between the training and prediction sets is close, as they are derived from the same cross, with the maximum linkage disequilibrium between quantitative trait loci and markers (Bernardo and Yu, 2007). Several studies showed that moderate-to-high prediction accuracy could be obtained in biparental populations for traits with high heritability, even using low marker density and a training population of relatively small size. A marker density of 10–20 cM, corresponding to ~150 markers, is sufficient to deliver good prediction accuracy within biparental maize populations (Lorenzana and Bernardo, 2009; Albrecht et al., 2011; Lian et al., 2014). In contrast, other studies mention that a high-density genotyping platform (for example, GBS) may improve prediction accuracy (Poland et al., 2012a; Crossa et al., 2013a; Massman et al., 2013b). Further studies are still necessary to investigate the impacts of GBS on prediction accuracy in biparental maize populations.

Despite the fact that, in maize (Zea mays L.) and other species, different breeding schemes for GS have been examined (Bernardo and Yu, 2007; Heffner et al., 2010; Riedelsheimer et al., 2012, 2013; Schulz-Streeckab et al., 2012; Wang et al., 2012; Windhausen et al., 2012), the most important issue for GS to be time and cost-saving is that the correlation between predicted and true genotypic values (r_MG =r_MP/h, where r_MP is the correlation between predicted and observed values and h is the square root of the heritability of the trait) must be high. Recently, Lian et al. (2014) reported the mean and variability of r_MG for different traits in 969 biparental maize populations. The authors found that for grain yield (GY) across the 969 biparental populations, the mean r_MG was 0.45, ranging from −0.59 to 1.03; the lines within each cross were genotyped with 31–119 SNPs, and the parents of the biparental population were genotyped with 2911 SNPs. Crossa et al. (2013b) showed prediction results from two biparental populations that were genotyped with 250 SNPs and evaluated under severely water-stressed (SS) and well-watered (WW) environments. Depending on the heritability of the trait, the number of markers, the number of lines within the biparental population and the prediction model used, the correlation between observed and predicted values reached 0.40 in one population when combining all SS and WW environments.

In plant breeding, multienvironment trials assessing genotype × environment interactions (GE) have an important role in selecting phenotypes with good performance and stability. Environmental conditions modulate gene expression and this induces GE such that the estimated genetic correlations of an individual line's performance across environments summarize the collective action of genes and environmental conditions, regardless of how different regions of the genome interact with different environmental factors. Despite the importance of GE in plant breeding trials, most previous GS studies only used single-environment prediction models; it was not until very recently that studies demonstrated that multienvironment linear mixed models can account for correlated environmental structures within the Genomic Best Linear Unbiased Predictor (GBLUP) framework and thus can predict performance of unobserved phenotypes using pedigree and molecular markers. Burgueño et al. (2012) used marker and pedigree GBLUP models for assessing GE under genomic prediction and Heslot et al. (2014) incorporated crop modeling data for studying genomic GE. In a recent study, Jarquín et al. (2014) proposed a random-effects model where the main and interaction effects of markers and environmental covariates are introduced using covariance structures.

Common studies for assessing genomic prediction have not taken advantage of the response in correlated environments and thus have not exploited the potential of these environmental structures for use in genomic prediction. For example, the prediction accuracy for GY in biparental populations does not seem to rise above a 0.4–0.5 accuracy level (Crossa et al., 2013a; Lian et al., 2014). A question that has yet to be answered is whether denser markers coupled with exploiting correlated environmental structures improve the prediction accuracy for different traits measured under SS and WW environments. Therefore, the main objectives of this study were to: (1) evaluate the prediction accuracy for different traits in 19 biparental maize populations (a total of 3273 lines) using low-density (~200 markers) and GBS SNPs; (2) study the effects of marker density on prediction accuracy by comparing the prediction accuracy obtained from low-density SNPs with that obtained from GBS SNPs; (3) examine the impact of a multienvironment model incorporating GE on prediction accuracy for several traits with different levels of genetic architecture complexity (GY, anthesis date (AD) and plant height (PH)) and evaluated under different environmental conditions (that is, SS and WW environments). We also calculated the prediction accuracy of lines within a biparental population that were not observed in any environment versus those that were observed in some environments but not in others under SS and WW conditions. Models incorporating GE and non-GE were evaluated with low-density or GBS SNPs and both simultaneously.

Materials and methods

Phenotypic data

This study comprised a total of 3273 lines derived from 19 crosses or backcrosses between 23 elite maize inbred lines. Basic information regarding these 19 biparental populations is provided in Table 1: 11 of the 19 are F₂ families and the remaining 8 populations are BC₁F₂ families. The number of lines in each population ranged from 126 to 184, with a mean of 172. All the lines in each biparental cross were testcrossed to a single-cross tester from the opposite heterotic group. Eleven populations were testcrossed with tester T1, and the remaining eight populations were testcrossed with T2, the other tester. Testcross progenies were evaluated for GY, AD and PH in four WW and three to four SS environments in Kenya and Zimbabwe in 2010 and 2011. GY in SS environments ranged from 0.2 to 4.2 t ha⁻¹, whereas GY in WW environments varied from 4.8 to 9.0 t ha⁻¹.

Table 1. Biparental testcross population parameters, number of lines and number of polymorphic low-density and GBS SNPs within 19 maize biparental populations, and heritability of target trait–environment combinations (GY, AD and PH in WW and SS environments).

Pop. no.	Pedigree	Tester	Pop. type	Na	Nb	Nc	Heritability
							GY_WW	GY_SS	AD_WW	AD_SS	PH_WW	PH_SS
1	P1 × P2	T1	F2	165	201	62 776	0.31	0.32	0.56	0.53	0.82	0.31
2	P2 × P3	T1	F2	162	188	56 891	0.22	0.18	0.54	0.40	0.69	0.69
3	P2 × P4	T1	F2	126	183	55 583	0.35	0.00	0.34	0.31	0.52	0.44
4	P2 × P5	T1	F2	163	209	65 223	0.27	0.00	0.56	0.44	0.39	0.22
5	P4 × P1	T1	F2	183	208	60 039	0.40	0.07	0.33	0.38	0.63	0.56
6	P6 × P7	T1	F2	173	195	48 662	0.37	0.00	0.71	0.73	0.76	0.21
7	P8 × P9	T1	F2	181	212	52 546	0.40	0.26	0.74	0.51	0.61	0.40
8	P8 × P7	T1	F2	184	212	55 039	0.55	0.10	0.77	0.59	0.80	0.34
9	P10 × P11	T1	F2	184	211	58 594	0.29	0.16	0.56	0.45	0.75	0.61
10	P12 × P13	T1	F2	174	194	55 301	0.31	0.11	0.53	0.52	0.74	0.06
11	P14 × P15	T2	BC1F2	184	170	54 208	0.11	0.01	0.60	0.50	0.81	0.37
12	P14 × P16	T2	BC1F2	184	165	53 761	0.28	0.05	0.64	0.39	0.71	0.26
13	P17 × P18	T2	BC1F2	184	185	70 728	0.45	0.35	0.64	0.34	0.75	0.52
14	P18 × P19	T2	BC1F2	160	162	52 468	0.44	0.27	0.68	0.56	0.62	0.39
15	P19 × P15	T2	BC1F2	178	176	49 126	0.00	0.38	0.61	0.41	0.66	0.02
16	P15 × P5	T1	BC1F2	184	183	67 178	0.31	0.00	0.65	0.57	0.78	0.52
17	P20 × P17	T2	F2	173	166	61 036	0.45	0.27	0.70	0.50	0.88	0.56
18	P21 × P22	T2	BC1F2	176	172	78 005	0.00	0.21	0.72	0.55	0.79	0.57
19	P22 × P23	T2	BC1F2	155	184	66 109	0.39	0.39	0.69	0.62	0.77	0.36
			Avg	172	188	58 731	0.31	0.16	0.61	0.49	0.71	0.39

Abbreviations: AD, anthesis day; GBS, genotyping-by-sequencing; GY, grain yield; PH, plant height; SNP, single-nucleotide polymorphism; SS, water-stressed; WW, well-watered.

^aNumber of lines in each biparental population.

^bNumber of polymorphic low-density SNPs in each biparental population.

^cNumber of polymorphic GBS high-density SNPs in each biparental population.

In total, six trait–environment combinations (that is, GY_WW, AD_WW, PH_WW, GY_SS, AD_SS and PH_SS) were considered in this study. The experimental design in each environment was an α-lattice incomplete block design with two replications, and data were balanced across the four WW and three to four SS environments. Phenotypic data were preadjusted using estimates of block and environmental effects derived from a linear model that accounted for the incomplete block design within the environment and for environmental effects. Combined trial analyses were performed within WW and SS environments.

Traits with heritability below 0.05 in individual locations were not included in the combined analysis. Broad-sense heritability of the combined analysis across environments was calculated as 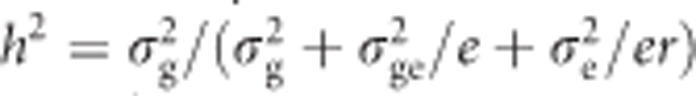, where 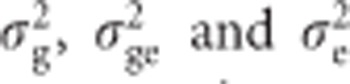are the genotypic, genotype-by-environment interaction and error variance components, respectively, and e and r are the number of environments and of replicates within each environment included in the corresponding analysis, respectively.

Genotypic data

All the lines in each biparental cross were genotyped with low-density SNPs polymorphic between parents. Low-density SNPs were distributed evenly on 10 maize chromosomes, and the number of polymorphic SNPs in each population ranged from 162 to 212, with a mean of 188 (Table 1). All the lines in each cross were genotyped by GBS SNPs as well. A GBS protocol commonly used by the maize research community was applied in this study (Elshire et al., 2011). The protocol was described in detail by Crossa et al. (2013a) and is briefly described here. GBS libraries were constructed in 96-plex, and genomic DNA was digested with the restriction enzyme ApeK1. Each library was sequenced on a single lane of Illumina flow cell (Cornell Life Science Core Laboratory Center, Ithaca, NY, USA). To increase the genome coverage and read depth for SNP discovery, raw read data from the sequencing samples were analyzed together with an additional 30 000 global maize collections. SNP identification was performed using TASSEL 4.0 GBS Discovery Pipeline with B73 as the reference genome. The source code and the TASSEL GBS discovery pipeline are available at http://www.maizegenetics.net and the SourceForge Tassel project (http://sourceforge.net/projects/tassel/). Initially, 955 690 SNPs evenly distributed on maize chromosomes were identified for all the lines in each population, and only high-quality SNPs with minor allele frequency >0.05 and <10% missing values were used for prediction within each population after filtering

Statistical models

Recently Jarquín et al. (2014) proposed a class of random-effect models where the main effects of markers, environments and their interactions are introduced using covariance structures that are functions of marker genotypes and environmental covariates. These models are extensions of the GBLUP models for incorporating interaction between markers and environments into genomic prediction.

In this study, the models developed by Jarquín et al. (2014) include low-density or/and GBS SNPs in the 19 biparental maize populations. We considered a sequence of models along the lines of those proposed by Jarquín et al. (2014). A brief description of these models is given below.

Baseline main-effects model

The phenotypes (y_ij) are described as

where μ is the overall mean, E_i(i=1,…,I) is the random effect of the ith environment, L_j is the random effect of the jth line (j=1,…,J) and e_ij is a random error term. The standard assumptions of random models are 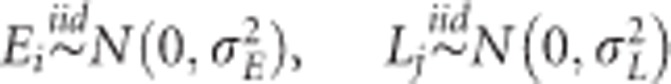and 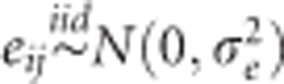, with N(.,.) denoting a normal density; iid stands for independent and identically distributed. In this baseline model, the random effects are independent.

Main-effects model (G1 or G2)

As previously described in model (1), the random effect of the line can be replaced by g_j, which is the regression on marker covariates 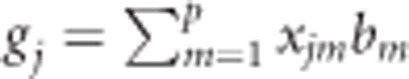, where x_jm is the genotype of the jth line at the mth marker, and b_m is the effect of the mth marker with the assumption that 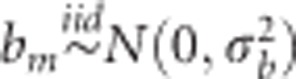(m=1,…,p) and 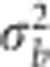is the variance of the marker effects. The vector g=(g₁,…,g_J)′ contains the genomic values of all the lines and is assumed to follow a multivariate normal density with zero mean and covariance matrix Cov (g)=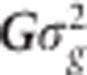, where G is the genomic relationship matrix and 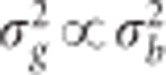is the genomic variance. Therefore, the equation

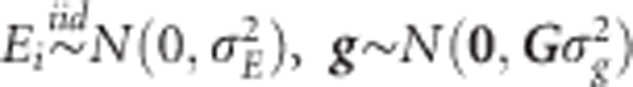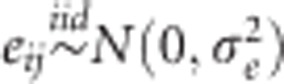assuming and . The random-effects g=(g₁,…,g_J)′ are correlated such that model (2) allows borrowing of information across lines. Therefore, model G1 is defined by setting G=G1, where G1 is a genomic relationship matrix derived from the low-density SNPs (see VanRaden, 2007, 2008). Similarly, model G2 is obtained by setting G=G2, where G2 is a genomic relationship matrix derived from GBS data. The random effect of the lines and the random genomic effects are both part of the total genetic value.

Main-effects and interaction models (G1E or G2E)

These random-effects models account for the effects of lines (L), of markers (genomic effects) (g), of environments (E), of the interaction between lines and environment (LE) and of the interaction between markers and environments (Eg). These models are obtained by extending models G1 or G2 (2) to include interaction effects (G1E or G2E). Predictions can be obtained with the model:

where EL_ij denotes the interaction of the ith line on the jth environment with 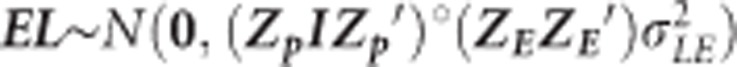, where Z_p and Z_E are the incidence matrices for phenotypes and environments, respectively, 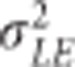is the variance component of EL and ‘°' stands for Hadamart product between two matrices. Also, Eg_ij is the interaction between the genetic value of the ith genotype in the jth environment and 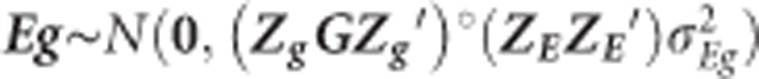, where Z_g is the incidence matrix for the effects of the genetic values of the genotypes. Then, models G1E and G2E are obtained by setting G=G1 and G=G2 for low-density and GBS SNPs, respectively.

Main-effects and interaction models (G1E and G2E)

This model includes the effect of the line (L), the environment (E) and the interaction between lines and environment. Interaction is built by simultaneously including the two sources of genomic information: G1E with SNPs and G2E with GBS. The model is:

where 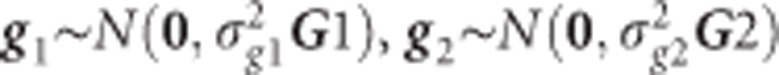and similar to Eg in Equation (3), but including both sources of genomic information 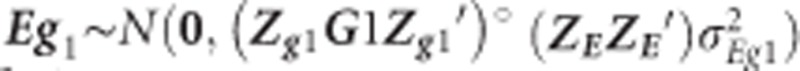and 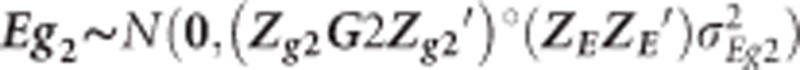for low-density and GBS SNPs, respectively.

Model implementation and cross-validation

To evaluate the impact of modeling the GE covariance structure for multienvironment trials, two distinct cross-validation schemes were designed to mimic two real situations that a breeder could potentially face (Burgueño et al., 2012). The first cross-validation scheme (CV1) consists of evaluating the predictive ability of models when new genotypes have not been evaluated in the field in any environment. Predictions derived using CV1 are based entirely on phenotypic records of other lines. The second cross-validation scheme (CV2) consists of evaluating the predictive ability of models when some lines have been evaluated in some environments but not in others. In CV2 prediction, information from related lines and the correlated environments is used, and prediction assessment can benefit from borrowing information between lines within an environment, between lines across environments and among correlated environments.

In both CV1 and CV2, a fivefold cross-validation scheme was used to generate the training and validation sets and assess the prediction ability and prediction accuracy within each population. For all trait–environment combinations within each population, the data were randomly divided into five subsets, with 80% of the lines assigned to the training set and 20% assigned to the testing set. Four subsets were combined to form the training set, and the remaining subset was used as the validation set. Permutation of five subsets led to five possible training and validation data sets. This procedure was repeated 20 times, and a total of 100 runs were performed in each population for each trait–environment combination. The average value of the correlations between the phenotype and the genomic estimated breeding values from 100 runs was calculated in each population for each trait–environment combination, and was defined as the prediction ability (r_MP). The prediction accuracy (r_MG) was estimated as the correlation between the true breeding value and the genomic estimated breeding value, where r_MG =r_MP/h, and h is the square root of the heritability of the target trait.

Software

All models were fitted in R (R-Core Team, 2014) using the BGLR package (de los Campos and Pérez-Rodríguez, 2013) to implement the models described in de los Campos et al. (2009).

Results

Heritability of predicted traits

Broad-sense heritabilities of the trait–environment combinations were low to moderate for GY in WW and SS environments, and they were consistently higher under WW conditions than under SS conditions in almost all populations (Table 1). Heritability of GY_WW had a mean value of 0.31 and ranged from 0.11 to 0.55 across all 19 populations except two, in which the GY_WW heritability was zero. Heritability of GY_SS had a mean of 0.16 and ranged from 0.01 to 0.39 across all populations except four, which had zero heritability.

Broad-sense heritabilities of AD and PH were relatively high under WW conditions, ranging from 0.33 to 0.77, with a mean of 0.61 for AD_WW, and from 0.39 to 0.88, with a mean of 0.71 for PH_WW in all 19 populations. Broad-sense heritabilities of AD and PH were moderate under SS conditions (Table 1); they ranged from 0.31 to 0.73, with a mean of 0.49 for AD_SS, and from 0.02 to 0.69, with a mean of 0.39 for PH_SS in all 19 populations. Heritabilities of AD and PH under WW conditions were consistently higher than those under SS conditions across all populations.

GBS data

The initial imputed GBS data before filtering had 955 690 markers evenly distributed on 10 maize chromosomes. The number of SNPs per chromosome ranged from 148 752 on chromosome 1 to 67 216 on chromosome 10. Across all populations, the missing proportion of SNPs ranged from 13.91 to 21.32%, with a mean value of 17.49%, and the heterozygosity proportion of SNPs ranged from 2.78 to 5.84%, with a mean value of 4.52%. In 11 F2 populations, average percentages of missing SNPs and heterozygous SNPs were 18.60% and 4.89%, respectively, which were higher than those in eight BC1F2 populations. The average missing proportion was 15.97% and the average heterozygosity proportion was 4.02% in all eight BC1F2 populations.

After filtering the GBS markers by applying two criteria (that is, <10% missing values and a minor allele frequency >0.05), the number of polymorphic SNPs in each population varied and ranged from 48 662 to 78 005, with a mean value of 58 731. Naïve imputation was performed in each population to impute all the missing SNPs.

Prediction accuracy in SS and WW environments within biparental populations using low-density SNPs

Shown in Table 2 is the prediction accuracy obtained with CV1 and CV2 for all target traits evaluated under WW conditions when low-density SNPs were considered for prediction. In both cases (CV1 and CV2), the r_MG value of each population differed among all predicted traits because of their heritability and genetic architecture. The r_MG values of GY_WW across all populations were consistently lower than those of AD_WW and PH_WW. In CV1, the r_MG values ranged from 0.10 to 0.54, with a mean of 0.27 for GY_WW, from 0.05 to 0.63, with a mean of 0.31 for AD_WW, and from 0.20 to 0.68, with a mean of 0.44 for PH_WW. In CV2, these values ranged from 0.19 to 0.44, with a mean of 0.34 for GY_WW, from 0.24 to 0.82, with a mean of 0.47 for AD_WW, and from 0.38 to 0.76, with a mean of 0.59 for PH_WW. As expected, the average r_MG values in CV1 were consistently lower than those in CV2 for all target traits, that is, predicting the performance of newly developed lines that have never been evaluated in the field (CV1) is more challenging than predicting the performance of lines that have been evaluated in different but correlated environments (CV2).

Table 2. Prediction accuracy (r _MG ) of all target traits evaluated under well-watered conditions, when low-density SNPs were included in the prediction model.

Population no.	Prediction accuracy in CV1						Prediction accuracy in CV2
	GY_WW		AD_WW		PH_WW		GY_WW		AD_WW		PH_WW
	G1	G1E	G1	G1E	G1	G1E	G1	G1E	G1	G1E	G1	G1E
1	0.17	0.26	0.05	0.01	0.49	0.51	0.35	0.45	0.24	0.21	0.67	0.69
2	0.10	0.17	0.27	0.25	—	—	0.28	0.33	0.43	0.45	—	—
3	0.16	0.27	0.63	0.64	0.40	0.39	0.33		0.82	0.85	0.55	0.55
4	0.20	0.23	0.24	0.23	0.41	0.41	0.42	0.47	0.50	0.51	0.76	0.77
5	0.39	0.41	0.11	0.26	0.47	0.46	0.38	0.45	0.24	0.28	0.56	0.55
6	0.12	0.13	0.30	0.30	0.36	0.39	0.19	0.19	0.47	0.47	0.56	0.58
7	0.21	0.23	0.38	0.37	0.25	0.24	0.35	0.38	0.50	0.50	0.38	0.37
8	0.36	0.36	0.24	0.23	0.48	0.48	0.37	0.40	0.38	0.34	0.59	0.60
9	0.18	0.39	0.39	0.42	0.46	0.48	0.24	0.38	0.50	0.52	0.62	0.64
10	0.19	0.21	0.30	0.26	0.35	0.37	0.29	0.32	0.48	0.47	0.59	0.61
11	0.54	1.46	0.41	0.43	0.52	0.54	0.35	1.42	0.51	0.52	0.61	0.62
12	0.43	0.58	0.45	0.44	0.45	0.45	0.35	0.56	0.53	0.54	0.52	0.53
13	0.38	0.43	0.44	0.45	0.52	0.57	0.40	0.49	0.55	0.56	0.58	0.64
14	0.16	0.24	0.21	0.25	0.20	0.23	0.32	0.37	0.36	0.37	0.42	0.43
15	—	—	0.37	0.39	0.34	0.33	—	—	0.42	0.45	0.47	0.47
16	0.28	0.43	0.35	0.40	0.53	0.55	0.25	0.37	0.45	0.50	0.65	0.66
17	0.31	0.40	0.43	0.45	0.59	0.60	0.44	0.56	0.54	0.53	0.75	0.76
18	—	—	0.51	0.54	0.68	0.69	—	—	0.60	0.63	0.73	0.74
19	0.38	0.45	0.26	0.27	0.48	0.46	0.44	0.56	0.51	0.52	0.59	0.59
Average	0.27	0.39	0.33	0.35	0.44	0.45	0.34	0.48	0.47	0.49	0.59	0.60

Abbreviations: CV, cross-validation scheme; SNP, single-nucleotide polymorphism.

Multienvironment models incorporating GE gave better prediction accuracy than single-environment prediction models that ignored GE; the increase in prediction accuracy because of incorporating GE was clearer in complex traits (GY) than in less complex traits (AD and PH). In CV1, the mean r_MG value increased from 0.27 to 0.39 for GY, from 0.33 to 0.35 for AD and from 0.44 to 0.45 for PH when GE was incorporated into the multienvironment models. Similar trends were found in CV2 but with higher accuracies than for CV1. In both CV1 and CV2, the r_MG value of GY_WW in population 11 exceeded 1.0 when model G1E was performed; this overestimation of the r_MG value was caused by sampling variation in both r_MP and h², because r_MG was estimated indirectly as r_MP/h, where r_MP is the correlation between observed and predicted phenotypic values.

Table 3 shows r_MG values obtained for all target traits evaluated under SS environmental conditions, when low-density SNPs were included in the prediction model. Results from Table 3 are similar to those found in Table 2, but r_MG values for all target traits under SS conditions are consistently lower than under WW conditions because of poor heritability estimation. The r_MG values under SS conditions were more often negative or above 1.0 than under WW conditions, which indicates the importance of improving field evaluations under stress conditions.

Table 3. Prediction accuracy (r _MG ) of all target traits evaluated under water-stressed conditions, when low-density SNPs were included in the prediction model.

Population no.	Prediction accuracy in CV1						Prediction accuracy in CV2
	GY_SS		AD_SS		PH_SS		GY_SS		AD_SS		PH_SS
	G1	G1E	G1	G1E	G1	G1E	G1	G1E	G1	G1E	G1	G1E
1	0.23	0.16	0.29	0.30	0.37	0.38	0.34	0.32	0.34	0.34	0.56	0.58
2	0.14	0.23	0.31	0.31	—	—	0.00	−0.04	0.38	0.39	—	—
3	—	—	0.27	0.23	0.11	0.03	—	—	0.49	0.49	0.16	0.11
4	—	—	0.27	0.33	0.11	0.20	—	—	0.38	0.40	0.07	0.15
5	0.29	0.46	0.23	0.22	0.00	0.00	0.05	0.15	0.32	0.34	—	—
6	—	—	0.27	0.27	0.13	0.28	—	—	0.53	0.53	0.21	0.32
7	0.02	0.19	0.25	0.25	−0.05	0.02	0.14	0.24	0.39	0.38	0.19	0.21
8	0.13	0.01	0.23	0.20	0.02	0.01	0.26	0.29	0.37	0.37	0.24	0.25
9	0.37	0.41	0.05	0.03	0.20	0.30	0.38	0.45	0.11	0.09	0.28	0.34
10	0.41	0.58	0.24	0.22	0.48	0.67	0.26	0.48	0.40	0.37	0.42	0.69
11	1.00	1.10	0.38	0.40	0.50	0.50	0.52	0.95	0.43	0.44	0.36	0.39
12	0.69	0.92	0.51	0.51	0.51	0.50	0.41	0.72	0.50	0.55	0.42	0.43
13	0.17	0.36	0.07	0.02	0.38	0.38	0.16	0.39	0.07	0.06	0.41	0.43
14	−0.27	−0.16	−0.05	−0.03	0.11	0.06	0.18	0.09	0.02	0.03	0.10	0.02
15	0.01	0.06	0.31	0.27	0.33	−0.06	0.23	0.24	0.41	0.46	0.01	−0.15
16	—	—	0.33	0.35	0.41	0.45	—	—	0.40	0.45	0.47	0.50
17	0.10	0.23	0.34	0.36	0.38	0.39	0.20	0.30	0.46	0.48	0.51	0.53
18	0.29	0.51	0.46	0.51	0.52	0.53	0.32	0.55	0.53	0.56	0.56	0.57
19	0.10	0.16	0.31	0.31	0.42	0.46	0.30	0.33	0.46	0.45	0.42	0.46
Average	0.25	0.35	0.26	0.27	0.27	0.28	0.25	0.36	0.37	0.38	0.32	0.34

Abbreviations: CV, cross-validation scheme; SNP, single-nucleotide polymorphism.

Prediction accuracy in SS and WW environments within biparental populations using GBS SNPs

Shown in Table 4 is the prediction accuracy obtained for all target traits evaluated in WW environments when GBS SNPs were included in the prediction model. This shows that GBS SNPs outperformed the prediction accuracy of low-density SNPs for complex trait prediction. The average r_MG values of GY_WW are higher than those in Table 2. When high-density GBS SNPs instead of low-density SNPs were used in the prediction model, average r_MG values of GY_WW increased from 0.27 to 0.33 in CV1 and from 0.34 to 0.37 in CV2 in non-GE models. In GE models, r_MG values increased from 0.39 to 0.43 in CV1 and from 0.48 to 0.49 in CV2. These results indicate that increasing marker density improved the prediction accuracy of complex traits (GY_WW and GY_SS).

Table 4. Prediction accuracy (r _MG ) of all target traits evaluated under well-watered conditions, when high-density GBS markers were included in the prediction model.

Population no.	Prediction accuracy in CV1						Prediction accuracy in CV2
	GY_WW		AD_WW		PH_WW		GY_WW		AD_WW		PH_WW
	G2	G2E	G2	G2E	G2	G2E	G2	G2E	G2	G2E	G2	G2E
1	0.38	0.47	0.15	0.16	0.62	0.64	0.42	0.58	0.26	0.27	0.70	0.72
2	0.41	0.48	0.37	0.39	—	—	0.38	0.45	0.46	0.49	—	—
3	0.22	0.28	0.65	0.63	0.55	0.55	0.34	0.35	0.83	0.83	0.60	0.59
4	0.48	0.48	0.39	0.39	0.48	0.47	0.50	0.53	0.52	0.52	0.78	0.76
5	0.43	0.46	0.20	0.24	0.56	0.56	0.42	0.47	0.25	0.26	0.60	0.59
6	0.29	0.33	0.43	0.45	0.50	0.53	0.29	0.39	0.51	0.53	0.59	0.62
7	0.22	0.25	0.51	0.50	0.34	0.33	0.35	0.41	0.55	0.55	0.40	0.38
8	0.42	0.45	0.34	0.32	0.45	0.46	0.43	0.46	0.41	0.37	0.59	0.61
9	0.27	0.42	0.52	0.53	0.58	0.59	0.27	0.43	0.56	0.59	0.66	0.67
10	0.32	0.43	0.39	0.37	0.55	0.58	0.32	0.41	0.51	0.50	0.62	0.62
11	0.60	1.38	0.41	0.42	0.56	0.57	0.39	1.34	0.51	0.52	0.62	0.63
12	0.03	0.13	−0.09	−0.05	−0.08	−0.12	0.21	0.25	0.45	0.45	0.47	0.44
13	0.38	0.42	0.47	0.48	0.59	0.64	0.41	0.46	0.57	0.59	0.61	0.65
14	0.28	0.38	0.20	0.22	0.22	0.23	0.32	0.38	0.36	0.35	0.42	0.42
15	—	—	0.09	0.10	0.01	0.02	—	—	0.39	0.39	0.45	0.43
16	0.24	0.27	0.36	0.38	0.54	0.56	0.29	0.31	0.46	0.49	0.66	0.67
17	0.42	0.50	0.49	0.51	0.72	0.75	0.49	0.59	0.56	0.58	0.77	0.80
18	—	—	0.47	0.48	0.61	0.61	—	—	0.59	0.61	0.72	0.73
19	0.17	0.25	0.04	0.02	0.19	0.17	0.38	0.43	0.50	0.49	0.56	0.55
Average	0.33	0.43	0.34	0.34	0.45	0.45	0.37	0.49	0.49	0.49	0.60	0.60

Abbreviations: CV, cross-validation scheme; SNP, single-nucleotide polymorphism.

When high-density GBS SNPs instead of low-density SNPs were used in the prediction model, only slight increases in prediction accuracy were found for less complex traits (AD_WW and PH_WW). The r_MG values of most populations in Table 4 are generally higher than the corresponding values in Table 2, but as marker density increases, there is either a slight increase or none at all in average r_MG values. Meanwhile, the r_MG values in Table 4 are underestimated in more populations whose prediction accuracies were close to zero or negative.

Prediction accuracies obtained with GBS SNPs for all target traits evaluated in SS environments are shown in Table 5. Compared with prediction accuracies in Table 4, the corresponding values in Table 5 are lower; this was caused by poor heritability estimation in SS environments. Increasing marker density improved the prediction ability of both complex and simple traits evaluated in SS environments. The average r_MG values in CV1 increased from 0.25 to 0.28 for GY_SS, from 0.26 to 0.29 for AD_SS and from 0.27 to 0.34 for PH_SS in non-GE models. In CV2, the average r_MG values increased from 0.25 to 0.31 for GY_SS, from 0.37 to 0.38 for AD_SS and from 0.32 to 0.36 for PH_SS in non-GE models. Similar results were found in GE models. High-density markers are required to achieve good prediction accuracy for both simple and complex traits, if their estimated heritability in stress environments is relatively low.

Table 5. Prediction accuracy (r _MG ) of all target traits evaluated under water-stressed conditions, when high-density GBS markers were included in the prediction model.

Population no.	Prediction accuracy in CV1						Prediction accuracy in CV2
	GY_SS		AD_SS		PH_SS		GY_SS		AD_SS		PH_SS
	G2	G2E	G2	G2E	G2	G2E	G2	G2E	G2	G2E	G2	G2E
1	0.25	0.23	0.32	0.35	0.69	0.70	0.37	0.37	0.37	0.39	0.68	0.72
2	0.31	0.38	0.28	0.29	—	—	0.15	0.18	0.39	0.38	—	—
3	—	—	0.27	0.28	0.02	−0.02	—	—	0.52	0.52	0.16	0.15
4	—	—	0.33	0.37	0.28	0.25	—	—	0.41	0.40	0.16	0.17
5	0.37	0.61	0.32	0.32	0.00	0.00	0.18	0.45	0.36	0.36	—	—
6	—	—	0.41	0.40	0.24	0.31	—	—	0.58	0.57	0.31	0.41
7	0.20	0.29	0.37	0.39	0.05	0.08	0.17	0.27	0.45	0.46	0.19	0.17
8	0.20	0.18	0.39	0.39	0.12	0.08	0.35	0.39	0.43	0.44	0.29	0.23
9	0.35	0.46	0.09	0.10	0.41	0.45	0.42	0.60	0.12	0.12	0.38	0.42
10	0.49	0.58	0.40	0.42	0.74	0.93	0.44	0.64	0.47	0.46	0.56	0.88
11	1.03	1.14	0.41	0.43	0.48	0.50	0.72	1.11	0.46	0.48	0.39	0.41
12	0.35	0.07	0.13	0.09	−0.04	−0.07	0.40	0.20	0.38	0.33	0.25	0.22
13	0.21	0.33	0.07	0.03	0.45	0.45	0.18	0.34	0.09	0.09	0.44	0.46
14	−0.21	−0.08	−0.02	−0.01	0.10	0.03	0.19	0.16	0.02	0.02	0.12	0.02
15	0.08	0.05	0.18	0.21	1.00	0.92	0.23	0.21	0.38	0.37	0.22	0.43
16	—	—	0.37	0.39	0.35	0.38	—	—	0.42	0.45	0.46	0.49
17	0.26	0.29	0.51	0.57	0.42	0.45	0.26	0.27	0.51	0.53	0.53	0.56
18	0.30	0.37	0.37	0.44	0.48	0.48	0.31	0.43	0.50	0.53	0.55	0.54
19	0.10	0.13	0.21	0.17	0.27	0.36	0.27	0.28	0.44	0.42	0.36	0.45
Average	0.28	0.33	0.29	0.30	0.34	0.35	0.31	0.39	0.38	0.38	0.36	0.40

Abbreviations: CV, cross-validation scheme; SNP, single-nucleotide polymorphism.

Prediction accuracy in SS and WW environments within populations using both low-density and GBS SNPs

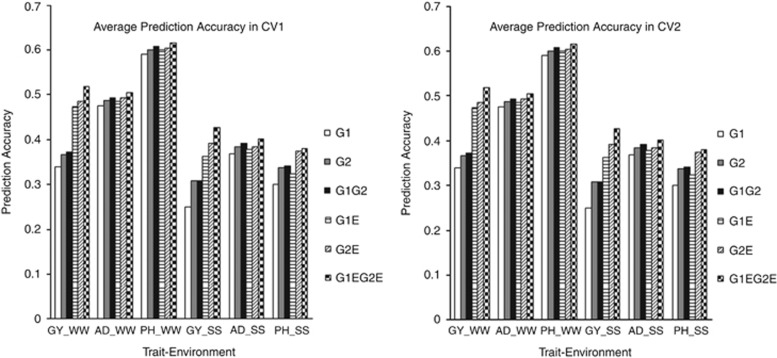
Average prediction accuracies obtained from the joint application of low-density and GBS SNPs (models G1G2 and G1EG2E) in all the models are shown in Figure 1 for all trait–environment combinations. In non-GE models, average prediction accuracies obtained from the joint application of low-density and GBS SNPs (model G1G2) were similar or a little higher than the corresponding r_MG values obtained using only GBS SNPs (model G2) for all trait–environment combinations. However, the differences between models G2 and G1G2 became obvious for all trait–environment combinations in GE models, especially for GY. These results clearly indicate the benefits of incorporating GE into the genomic models when using only low-density SNPs (G1E), only GBS SNPs (G2E) or both together (G1EG2E), especially for complex traits such as GY under SS and WW environments.

Figure 1.

Average prediction accuracy in CV1 and CV2 for all trait–environment combinations in all prediction models.

Discussion

In maize breeding, one of the most promising applications of genomic selection is to predict the performance of unphenotyped lines within biparental populations, where the training and validation sets are derived from the same cross. Owing to the close relationship between the training and validation sets and the strong linkage disequilibrium between quantitative trait loci and markers in biparental populations, moderate-to-high accuracies of genomic prediction for various traits could be obtained using low marker density and a small population size (Windhausen et al., 2012). In this study, 19 biparental tropical maize populations were used to assess the effects of marker density, trait heritability, trait genetic architecture, trait–environment combination, and non-GE and GE modeling on prediction accuracy. We found that, compared with low-density SNPs (~200 markers), GBS improved prediction ability; heritability and the genetic architecture of target traits can also affect the prediction ability in both GE and non-GE models. Prediction of all target traits under stress conditions was lower than under WW conditions, and multienvironment models incorporating GE gave better prediction accuracy in most cases, especially for complex traits such as GY.

Increasing marker density was previously found to be an important factor for improving prediction accuracy, but some studies have indicated that the r_MG value in biparental maize populations is at or near maximum when target trait heritability is relatively high and the genome is covered with sufficient markers, that is, when the mean distance between markers is <10–20 cM or around 150 markers evenly cover the whole genome (Lorenzana and Bernardo, 2009; Lian et al., 2014). In this study, we found that high-density GBS SNPs did not increase the r_MG values of simple traits (AD and PH) evaluated under WW conditions (AD_WW and PH_WW) as compared with low-density SNPs (~200 markers). This indicated that ~200 markers are usually sufficient to achieve good prediction in biparental maize populations for simple traits with moderate-to-high heritability. However, prediction accuracies obtained from GBS outperformed those obtained from low-density SNPs, when predicting complex traits in SS and WW environments (GY_WW and GY_SS) or simple traits (AD_SS and PH_SS) with low-to-moderate heritability evaluated under stress conditions. These results indicate that heritability and the genetic architecture of target traits affect prediction ability in biparental populations, and that high-density markers (GBS) are still required to obtain good prediction accuracy for both simple and complex traits, if their heritabilities are low under stress conditions. This is the first report to compare prediction accuracies obtained from GBS with those obtained from single-plex SNP assays having similar costs in plant breeding. In this study, GBS is shown to be a competitive alternative for economically increasing by many-fold the number of markers used and for improving prediction accuracy. However, GBS data always come with a large percentage of uncalled genotypes and a lower heterozygosity proportion than expected when highly heterozygous breeding materials or populations are genotyped with GBS. Preliminary results of this study indicated that the average r_MG values in 8 BC1F2 populations were consistently higher than those in 11 F2 populations when GBS markers were included in the prediction. This may be caused by the greater difference between the real heterozygosity proportion and the expected value in F2 populations. How imputation of missing and heterozygous genotypic data can affect prediction accuracies when GBS data are used in genomic prediction needs to be investigated in future research.

Genotype × environment interaction in maize is usually strong for complex quantitative traits, and maize hybrids are always tested in multiple environments. However, most of the current genomic prediction studies have only applied a single-environment model and have not considered predictive models having correlated environmental structures (Guo et al., 2013). Burgueño et al. (2012) were the first to include GE in the GBLUP model using markers and pedigree, whereas Jarquín et al. (2014) developed the models used in this study, which incorporate random structures of highly dimensional environmental and marker information. In this study, the impact of modeling GE variance structures for multienvironment trials was investigated, and our results indicate that the mean r_MG values derived from GE models were higher than the corresponding values from non-GE models across all cross-validations, marker densities and trait–environment combinations, especially for complex traits.

Across all populations, the differences between GE models and non-GE models were important and consistent for GY_WW and GY_SS. However, as expected, the superiority of the GE model was small for less complex traits (AD and PH), and the r_MG values were more frequently underestimated (below zero) or overestimated (above 1.0) with the GE models than with the non-GE models, especially when target traits were evaluated under SS conditions or high-density GBS markers were used for prediction. Besides sampling variation in both r_MP and h², underestimated and overestimated r_MG values may be caused by collinearity between high-density markers and linkage disequilibrium between quantitative trait loci and SNPs that were not stable across environments. Results of this study expand the conclusions reported by Burgueño et al. (2012) and Jarquín et al. (2014) that modeling GE gives better prediction accuracy than prediction models ignoring GE in wheat multienvironments trials. Our results indicate that multienvironment genomic prediction models, rather than simple-environment models, should be included in future research on complex traits. Results of this study also showed, as expected, that r_MG values in CV1 were consistently lower than the values in CV2 across all populations, marker densities and trait–environment combinations, which indicates that predicting the performance of newly developed lines that have never been evaluated in the field (CV1) is more challenging than predicting the performance of lines that have been evaluated in different but correlated environments (CV2).

Genomic prediction could also be improved by pooling multiple related biparental populations into the training set (Schulz-Streeckab et al., 2012). However, this study only focused on the prediction accuracy within each biparental maize population, and further research is needed to assess prediction accuracy across multiple biparental populations, both related and unrelated.

Conclusions

This study, comprising 19 biparental maize populations evaluated in several SS and WW environments and genotyped with low-density and GBS SNPs, had several objectives. The first objective was to compare the prediction accuracy under SS and WW environmental conditions of three traits with different complexity (GY, AD and PH) using low- and high-density SNPs with models that incorporate GE and non-GE. Another objective was to examine prediction accuracy when lines in one biparental population had not been observed in any environment (CV1) and when some of them had been observed in some environments but not in others (CV2).

In general, results within each biparental population are clear. First, as expected, predictions were higher in WW environments than in SS environments. Second, results indicated important increases in prediction accuracy when using GBS over low-density SNPs for a complex trait (GY) but not much of an increase for simpler traits such as AD and PH.

In models that incorporate low-density SNPs and GBS SNPs and their interaction with the environment (G1E or G2E), results for complex traits clearly showed the higher prediction accuracy of G1E or G2E as compared with models including only the main effects (G1 or G2) for both prediction cases (CV1 and CV2). This increase in prediction accuracy achieved using models with GE occurred for less complex traits such as AD and PH, but to a lesser degree than that observed for GY. Results of this study agree with those already reported by Burgueño et al. (2012), as well as with the results of the highly dimensional model proposed by Jarquín et al. (2014) in wheat, which suggested that the inclusion of the random-effects environment structure of GE allows exploiting information from correlated environments. This produces an increase in the prediction accuracy of the GBLUP model by borrowing information not only from related lines expressed in the genomic relationship matrix but also from related environmental conditions that in turn modulate gene effects differently.

Data archiving

Data available from the following repository: http://repository.cimmyt.org/xmlui/handle/10883/4071.

The authors declare no conflict of interest.