Evolutionary responses of tree phenology to the combined effects of assortative mating, gene flow and divergent selection

Abstract

The timing of bud burst (TBB) in temperate trees is a key adaptive trait, the expression of which is triggered by temperature gradients across the landscape. TBB is strongly correlated with flowering time and is therefore probably mediated by assortative mating. We derived theoretical predictions and realized numerical simulations of evolutionary changes in TBB in response to divergent selection and gene flow in a metapopulation. We showed that the combination of the environmental gradient of TBB and assortative mating creates contrasting genetic clines, depending on the direction of divergent selection. If divergent selection acts in the same direction as the environmental gradient (cogradient settings), genetic clines are established and inflated by assortative mating. Conversely, under divergent selection of the same strength but acting in the opposite direction (countergradient selection), genetic clines are slightly constrained. We explored the consequences of these dynamics for population maladaptation, by monitoring pollen swamping. Depending on the direction of divergent selection with respect to the environmental gradient, pollen filtering owing to assortative mating either facilitates or impedes adaptation in peripheral populations.

Introduction

Ongoing climate change and climatic predictions have sparked serious concerns about the persistence of tree species in many temperate and boreal areas. As forests have a crucial role in human societies through the maintenance of sustainable ecosystem services, considerable effort is currently being devoted to assessments of their possible evolutionary responses. A number of predictions based on climate change and greenhouse gas emission models have forecasted major shifts in the bioclimatic envelopes of temperate tree species (Thuiller, 2003; Cheaib et al., 2012); however, these predictions did not take genetic variation explicitly into account. Common garden experiments have highlighted high levels of genetic diversity within and among tree populations (Wright, 1976; Hamrick et al., 1992), reporting strong clinal genetic variations along environmental gradients (Mimura and Aitken, 2007; Savolainen et al., 2007), which suggests strong adaptive responses to past environmental changes. Genetic clines vary both in magnitude and orientation in comparison with phenotypic clines, corresponding to the so-called co- and countergradient variation (Conover and Schultz, 1995; Conover et al., 2009). Cogradient variation refers to cases when genetic population differences observed in common garden experiments covary positively with phenotypic differences observed in situ along the same environmental gradient. Countergradient corresponds to cases where genetic and phenotypic differences covary in opposite directions. Co- and countergradient patterns witness, therefore, contrasting responses of populations to natural selection (Soularue and Kremer, 2012; Kremer et al., 2014). Indeed, oaks (Vitasse et al., 2009a) and ashes (Vitasse et al., 2009b) exhibit cogradient variations in the timing of bud burst (TBB), whereas beech and most conifers exhibit countergradient variations. It is now necessary to determine which combinations of evolutionary factors were responsible for generating these differentiation patterns when trying to predict how a species might evolve in response to current and future rapid changes in climate.

TBB is a key adaptive trait of trees in the context of climate change, for three main reasons: (1) TBB varies predominantly with temperature (Vitasse et al., 2011), (2) TBB is related to the fitness of trees owing to its influence on growing season (Chuine and Beaubien, 2001) and (3) TBB is strongly correlated with flowering time (Franjic et al., 2011), suggesting that this trait may be subject to assortative mating. Clinal patterns of differentiation along environmental gradients have mostly been interpreted as resulting from divergent selection, but we have shown that the interaction between assortative mating and gene flow may cause TBB to vary with the environmental gradient (variation in the same direction, cogradient variation) without divergent selection (Soularue and Kremer, 2012), which confirms earlier results reported by Stam (1983). We showed that the synchronicity constraint imposed by assortative mating reversed the mixing effect of pollen flow, inducing genetic differentiation among populations. Indeed, across environmental gradients, gene flow over large distances, with filtering by assortative mating, leads to the import of alleles with genetic values very different from the mean genetic values of the recipient populations. Larger distances between the two mating parents are associated with larger differences in their genetic values, owing to the environmental gradient. Thus, the net result of intra- and interpopulation matings is a shift in the genetic values of the populations along the environmental gradient, creating a cogradient genetic cline (Soularue and Kremer, 2012). Additionally, we showed that the scale of the asymptotic differentiation was related to the slope of the environmental cline and the patterns of pollen dispersal. Here, we extended this approach to the context of divergent selection. The combined effects of assortative mating and natural selection in plant species have been investigated, theoretically and experimentally, several times, but usually in single populations. Analytical predictions and numerical simulations have mostly predicted a stronger response to selection in the presence of positive assortative mating than in conditions in which selection is applied to randomly mated populations, through an increase in genetic variation (Gianola, 1982; Jorjani et al., 1997; Fox, 2003). A few studies have also indicated that negative assortative mating may soften the impact of selection (De Lange, 1974; Jorjani et al., 1997). Most of the theoretical predictions and observations to date have considered single isolated populations and none has yet explored the balance between assortative mating and the various patterns of selection occurring in populations positioned along environmental gradients and interconnected by gene flow. As gene flow may either prevent adaptation (Kirkpatrick and Barton, 1997; Yeaman and Guillaume, 2009) or enhance evolutionary change (Bridle et al., 2009; Kremer et al., 2012), we also showed that the degree of TBB differentiation generated by assortative mating in the absence of selection depends strongly on the pollen dispersal model applied (Soularue and Kremer, 2012). We thereby also investigated here the interaction between gene flow and assortative mating in the presence of selection.

In summary, we investigated the interactions between three major evolutionary drivers of the TBB: divergent selection, assortative mating and gene flow. It is essential to consider the directional nature of these drivers when trying to understand their joint effects. Indeed, the environmental gradient triggers assortative mating for TBB by constraining preferential matings between neighboring populations in a given direction. Similarly, divergent selection may also act in the same direction as the environmental gradient or in the opposite direction, generating co- or countergradient variation. Finally, gene flow has also a directional component: in the case of latitudinal gradients, populations from northern latitudes can, for example, only receive pollen from more southerly latitudes. Here, we compared the evolutionary response of TBB for various evolutionary scenarios within numerical simulations. Our main objectives was to monitor the combined impact of the various forces on the evolutionary response and to determine which conditions and scenarios are associated with an enhancement or restriction of adaptation. We predict that assortative mating may either amplify or constrain the response to selection, depending on the combination of the directions and the extent of the environmental and selection gradients considered.

Materials and methods

Evolutionary change in populations under hypotheses of assortative mating, divergent selection and gene flow

We considered a set of populations connected by gene flow, with each population undergoing stabilizing selection. Within each population, the fitness of an individual k was given by a Gaussian function (Lande, 1976a):

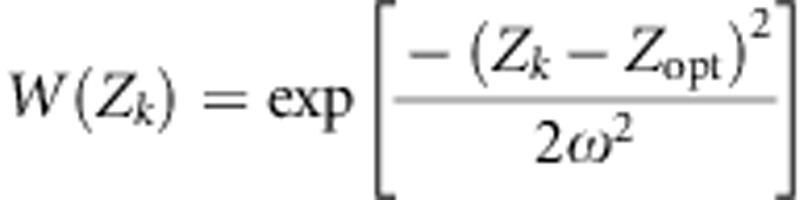where Z_k is the phenotypic value of individual k, Z_opt is the optimum value of the given population and ω² is the strength of stabilizing selection. We considered here that divergent selection in the landscape is driving populations toward different Z_opt values and assumed that the strength of within-population selection is identical in different populations. We were interested in the evolutionary change, over successive generations, within a given population, as a result of the various evolutionary forces. We further assumed that gene flow effects on genetic values are mostly due to pollen flow. On the basis of standard quantitative genetics principles, we subdivided the within-population phenotypic value of each tree in the population of interest into a genetic and a random environmental component: Z=G+ɛ, where G is the sum of the additive effects of the alleles carried by the tree and contributing to the trait. We assumed that there is no dominance or epistasis as suggested by high heritability values reported for TBB (Alberto et al., 2011). The mean genetic value of the population at generation t, before selection, is G_t, whereas that after selection is 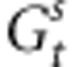. As ɛ has a mean value of 0 in each population, G_t=Z_t, where Z_t is the mean phenotypic value of the population. The mean genetic value of a population at the generation immediately following syngamy and preceding selection can thus be written as

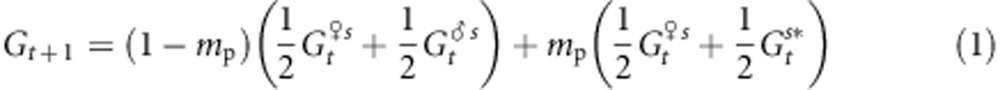where m_p is the rate of pollen immigration, 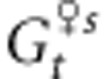and 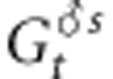are the mean genetic values for the female and male parents within the population after selection and 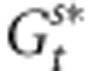is the mean genetic value of male parents outside the population after selection. We assume here that 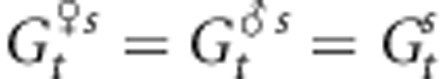. In addition, 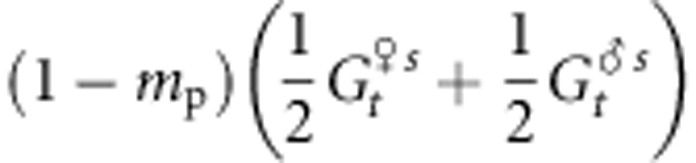represents the proportion of the genetic value owing to intrapopulation matings and 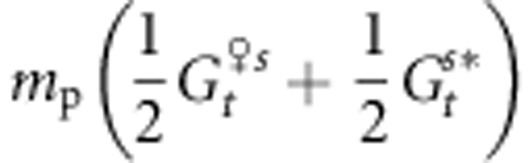represents the proportion of the genetic value owing to interpopulation matings.

We accounted for assortative matings involving parents from different populations, by also defining the overall phenotypic value of a tree as Y=G+E+ɛ, making it possible to compare phenotypic values across populations. E is a macroenvironmental component of identical magnitude for all trees in a given population and 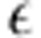a microenvironmental component assigned independently to each tree. Within a population, the mean phenotypic value of the male parents corresponding to the immigrant alleles can be expressed as

whereas the mean phenotypic value of the female parents is

where E and E* are the macroenvironmental components of the phenotypes of the female and male parents, while ε and ε* stand for the microenvironmental components of their phenotypes, respectively. Assuming full assortative mating, the phenotypic values of both parents should be equal, and the mean genetic value of the external male parents can then be written as

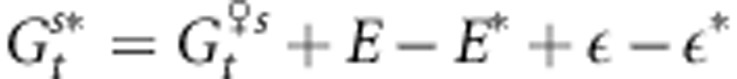Assuming ε−ε* is negligible compared with E−E*, we have

As selection is acting on the Z values, and assortative mating is shaped by the Y values, we can express the shift Δ_t of the genetic value of a population G_t+1−G_t after rewriting Equation (1):

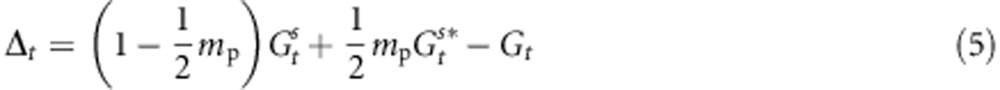The mean genetic value of the population after selection can be written as (Bulmer, 1980; Lopez et al., 2008):

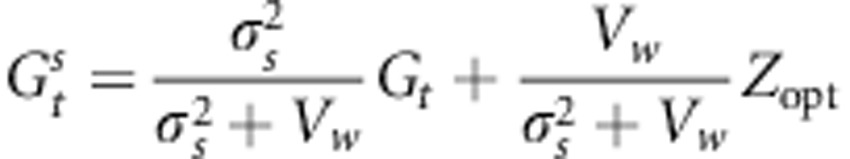where 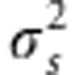is the sum of the variance of the random environmental deviation 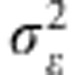and the selection intensity ω², V_w stands for the genetic variance observed within the population of interest and Z_opt is its phenotypic optimum. Replacing 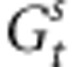and 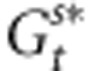in Equation (5), we obtain:

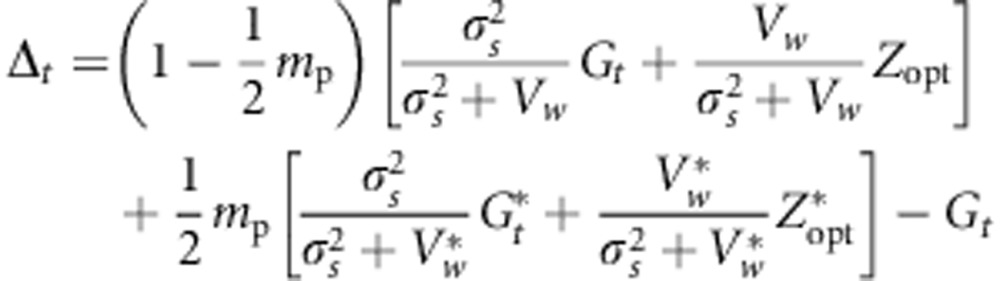If we assume that V_w is the same for all populations, then

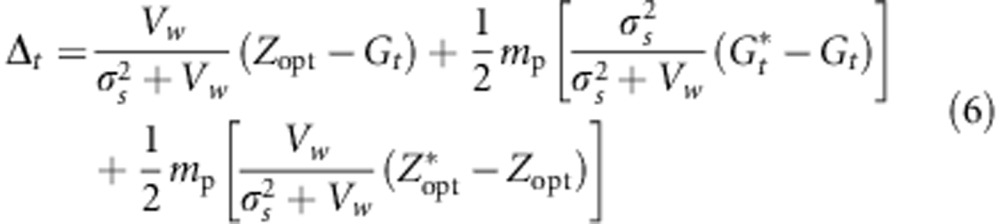Equation (6) partitions the evolutionary change within populations into three terms: Δ_t=A+B+C. The A term accounts for evolutionary change owing to stabilizing selection within the population of interest; it corresponds to the analytical prediction of evolutionary change for a single population under stabilizing selection, as suggested in previous studies (Lande, 1976b; Gomulkiewicz and Houle, 2009). It depends mainly on the strength of selection (σ²_s) and the degree of maladaptation Z_opt−G_t. The B and C terms account for evolutionary change owing to cross-pollination with trees from other populations. The B term expresses indirectly the influence of the environmental gradient as the difference between populations' mean genetic values depends on environmental gradients (Equation (4)). Finally, the C term expresses the influence of the selection gradient.

Clearly, the evolutionary shift of populations will depend on the selective pressures, the macroenvironmental component of the phenotypic values and the dispersal of pollen. Besides, from Equations (2, 3, 4), varying adaptive responses can be expected in the case of selection and environmental gradients. Assuming selective pressures sufficiently strong to drive the genetic values of individual toward a phenotypic optimum, we can assume that 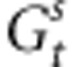and 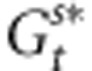will rapidly approach the Z_opt values of populations. Thereby, owing to the opposition between the selection and the environmental gradients, the phenotypic difference between distant individuals 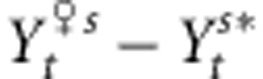will be less important in the case of countergradient settings, which will promote matings among distant individuals (see Soularue and Kremer (2012) for more details about matings between individuals from distinct populations across environmental gradients). Distant pollen flow will thus import alleles with additive contribution strongly diverging from the phenotypic optimum of the recipient populations, which will constrain the adaptive response of populations over the landscape. Conversely, in the case of cogradient settings, the mean phenotypic values of distant populations will be so important that distant mating will be impossible. As a result of limited distant pollen flow, assortative mating will in this case rapidly inflate the adaptive response of populations to selective pressures as indicated in the previous theory (Fox, 2003). Additionally, we expect the extent of the selection and environmental gradients to mediate the effects of assortative mating. However, very steep gradient might totally even out the evolutionary impact of assortative mating.

Finally, the evolutionary responses of populations may be amplified by the dispersal of pollen occurring in the direction of the environmental gradient under assortative mating. By contrast, pollen dispersal against the environmental gradient will tend to reduce the genetic cline. Finally, directional pollen flow would be expected to have a significant impact on the evolution of populations in conditions of uniform selection.

To sum up, Equation (6) indicates that assortative mating and gene flow are likely to shape evolutionary change. Our equations are, however, constructed assuming that: (1) seed dispersal is negligible with regard to pollen dispersal, (2) assortative mating is complete and (3) there is overlapping of phenotypic values among populations. We therefore extended our approach by using simulations that would match more closely real settings.

Simulations

We compared our expectations with the results of forward and individual-based simulations. To this end, we simulated the evolution of a subdivided population over successive generations with Metapop, a tractable numerical simulating framework focusing on evolutionary processes. Descriptions of this software have been provided elsewhere (Le Corre and Kremer, 2003). We recently described the way in which the environmental gradient and assortative mating were introduced into the simulations (Soularue and Kremer, 2012).

Environmental and genetic gradients

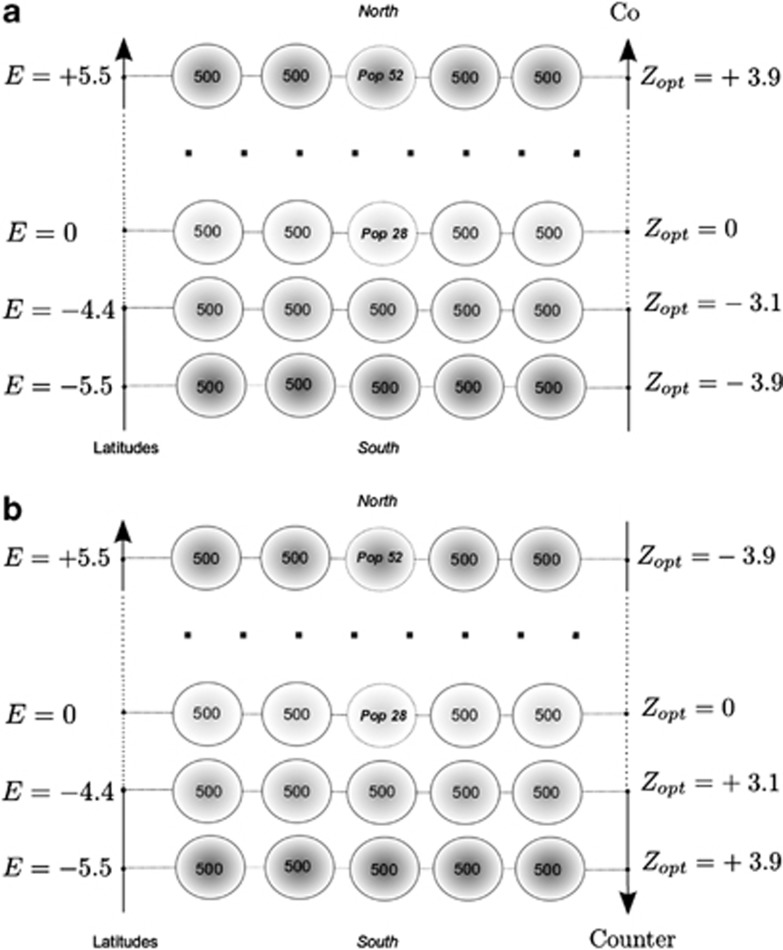
We considered a set of 55 populations spatially distributed over a two-dimensional grid, representing discrete schematic settings of populations distributed in a landscape (Figure 1). For the sake of simplicity, we use here ‘latitude' and ‘longitude' to label the two dimensions, these terms are used to facilitate the understanding of our analysis and do not refer to real geographic settings. We assumed that the macroenvironmental value E was distributed along one dimension, here latitudinal gradient, such that all populations at a given latitude had the same E value (see Soularue and Kremer (2012) for further details). These settings for E values mimic the patterns reported in situ for latitudinal gradients of flushing date in trees (Chuine and Cour, 1999; Vitasse et al., 2009a; Alberto et al., 2011). Each population was composed of 500 individuals, this number remaining constant among populations and over successive generations.

Figure 1.

Spatial settings of populations, environmental and selection gradients. Fifty-five populations of 500 individuals each were spread homogeneously on a 5 × 11 grid along 11 latitudinal positions. E represents the environmental effect at a given latitude (see Soularue and Kremer (2012) for more details). Co- and countergradient divergent selection were mimicked by assigning different Z_opt values at different latitudes. In the cogradient case, Z_opt values are positively correlated to latitudes, as the E values. In countergradient settings, Z_opt values are negatively correlated to latitudes, and hence are negatively correlated to the E values. Both examples correspond to k_E=2 and to 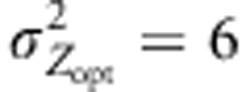. We considered mostly cases with ω²=50 and 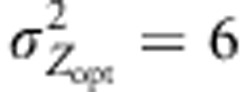, some cases were explored with ω²=5 or 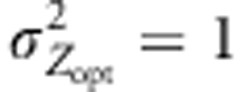. Finally, uniform selection was simulated with .

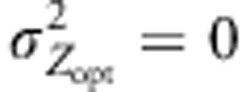Within Metapop, selection is implemented via the gaussian model of stabilizing selection (Lande, 1976a):

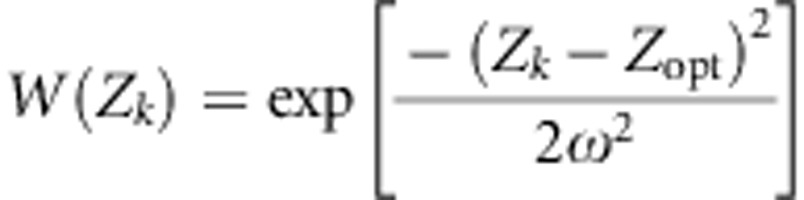where W(Z_k) is the fitness value assigned to the phenotype Z_k given, ω², the intensity of selection and Z_opt the optimal trait value in the population of interest. We simulated divergent selection among populations by assigning different Z_opt values to populations along a one-dimensional latitudinal gradient. All populations occupying the same latitude were given the same Z_opt. We also considered the gradients of E and Z_opt values to be running in the same direction (cogradient settings) or in opposite directions (countergradient settings) (Figure 1). In some cases, we simulated uniform selection, by applying a single Z_opt value (Z_opt=0) to the entire landscape. The environmental cline was scaled by its slope k_E (Soularue and Kremer, 2012), and the genetic cline by the variance of optimal values 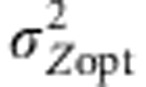. We mainly simulated steep environmental clines (k_E=2) that provided the most significant results in our earlier paper. In addition, we considered two steepness of selection gradient, 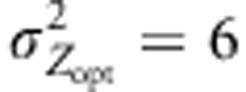and 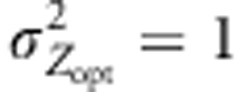, to further explore the interplay between the magnitudes of the environmental and selection gradients. The strength of stabilizing selection was mostly moderate (ω²=50). Assortative mating was scaled by the correlation of the phenotypic values ρ of mating parents (see Soularue and Kremer (2012) for further details). In the simulations, k_E, 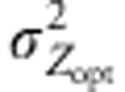and ρ were set at generation 0 and kept constant over successive generations. Finally, the starting metapopulation was at mutation–migration–drift equilibrium and all populations were considered to have a genetic value of 0 at generation 0.

Gene flow: directional and long-distance dispersal

Interest in the dispersal of tree pollen by wind has recently increased, with the confirmation that viable pollen can be dispersed over very long distances (for a review, see Schueler et al., 2005; Nathan et al., 2008; Kremer et al., 2012). In many regions, winds tend to blow in one particular direction, owing to the rotation of the Earth and pressure gradients (http://www.wcc.nrcs.usda.gov/), with major potential consequences for pollen dispersal, as observed in a previous experimental study (Bohrerova et al., 2009). We included, in the simulations, the preferential dispersal of pollen in one particular direction, such that most dispersal among populations occurred latitudinally, either northwards or southwards. Under the long-distance directional migration model, the exchange of pollen among populations was scaled by calculating the ratio of latitudinal to longitudinal dispersal. Ninety-five percent of the pollen shed from each population were disseminated latitudinally, and the remaining 5% were disseminated longitudinally. Latitudinal pollen dispersal occurred over long distances, with migration rates following a Weibull distribution mimicking fat-tailed dispersion (Austerlitz et al., 2004). We used the parameters (3, 1), which led to very rare exchange of pollen between extreme populations: only 0.5‰ of the pollen shed latitudinally by a northern population could reach a population from extreme south, in the case of preferential dispersal toward south. On the other hand, longitudinal dispersal of pollen was shed in similar proportions to the two closest neighboring populations. Below, long-distance dispersal models oriented toward the north are referred to as LDN, whereas those oriented toward the south are referred to as LDS. In addition to the unidirectional pollen migration model, we also considered pollen migration according to the island model (IMM). Seed migration was systematically considered to follow the island migration model.

We also assessed incoming pollen flow, with filtering due to the combined effects of assortative mating and pollen dispersal, a posteriori. To this end, we monitored exhaustively over a number of generations, the origin of the external pollen reaching the female parents of a population located at the northern edge of the landscape. We then determined numerically the distribution of the origin of the alleles received by the population of interest.

Simulation settings

To run the simulations, initial values for 16 parameters need to be set (Tables 1 and 2). Fixed values for 11 of the parameters (Table 1) were inferred from earlier investigations conducted in population and quantitative genetics of oaks. For example, levels of gene flow and selfing rate stem from earlier analysis of reproduction in oak stands (Bacilieri et al., 1996) and inferred from population structure (Kremer et al., 2010). Overall, pollen dispersal occurred at a much higher rate than seed dispersal, as indicated by experimental data in many broad-leaved and conifer tree species (Ennos, 1994). Genetic architecture, allelic effects originate from Derory et al. (2010), and heritability values stem from Alberto et al. (2011). Based on our earlier simulations (Soularue and Kremer, 2012), and in situ and common garden observations (Vitasse et al., 2009a, 2009b), k_E was set to 2, meaning that the variance of E values across the landscape is twofold larger than the phenotypic variance of TBB within a given population. We now illustrate how our chosen settings would fit in a real landscape. Starting from the field observations that the within-population standard deviation of TBB is about 4.6 days (Franjic et al., 2011), and assuming that TBB follows a gaussian distribution within populations, extreme southern populations would flush on average at day 15, with 95% of the trees flushing between days 5.8 and 24.2. With k_E=2, the mean day of flushing of northern populations is 33, and 95% of trees within northern populations would flush between days 23.8 and 42.2. Average mean flushing dates (in number of days) would be distributed along the 11 latitudes as follows from southern to northern populations: 15, 17, 19, 21, 23, 25, 27, 29, 31 and 33. Under such settings, assortative mating may still occur at low frequency between extreme southern and extreme northern populations, although mating between extremely distant populations is not necessary to occur within one generation to generate the evolutionary change. Long-distant migration over successive generations will as well result in the genetic shift of populations. The mean phenotypic shift of TBB in oaks is 7.5 days per °C of temperature change (Vitasse et al., 2009a). Given that on average the mean temperature change is 3 °C per 500 km shift in latitude, our grid distribution with k_E=2 would correspond to a geographic latitudinal range of 400 km. As a result, populations would be spread every 40 km on the grid. Although genetic connectivity through pollen flow would be extremely low between extreme populations within one generation, it would be rather frequent between adjacent populations on the grid (Buschbom et al., 2011; Kremer et al., 2012). Finally, we assigned a range of values for those parameters that we purposely investigated: pollen migration models, level of divergent selection, intensity of stabilizing selection, degree of assortative mating and directions of environmental and genetic gradients (Table 2). The range of values have been investigated through sensitivity analysis in earlier investigations using Metapop (Le Corre and Kremer, 2003; Kremer and Le Corre, 2011; Soularue and Kremer, 2012). In total, we considered 42 scenarios and ran 30 independent replicates over 1000 generations for each of them.

Table 1. Fixed parameters.

Parameter	Value
Heritability	0.83
Selfing rate	0.02
No. of populations	55
No. of individual per population	500
Seed migration model	IMM
Level of gene flow Nm	10.2
Pollen (mp) vs seed (ms) migration rates	mp=100ms
No. of QTL, n	10
Mutation rate μ	10−5
No. of latitude levels Y	11
Interval of latitudes Y	[−0.5, +0.5]
Steepness of environmental cline E scaled by kE	2

Abbreviation: QTL, Quantitative trait locus.

Table 2. Variable parameters.

Parameter	Value
Pollen migration models	IMM, LDN, LDS
Intensity of divergent selection	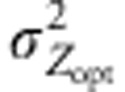0, 1, 6
Intensity of stabilizing selection ω2	5, 50
Level of assortative mating ρ	0, 0.8
Directions of environmental and genetic gradients	cogradient, countergradient

Abbreviations: IMM, island model; LDN, long-distance dispersal models oriented toward the north; LDS, long-distance dispersal models oriented toward the south.

Results

Genetic differentiation

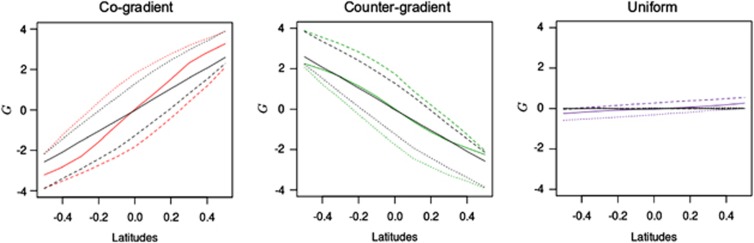
We first examined the shift in the mean genetic value of populations at the landscape scale when steep selection gradients 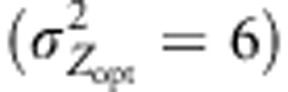were simulated (Figure 2). We focused here principally on the genetic values stabilized at the end of the simulation process, at generation 1000. Because of the joint influence of natural selection and assortative mating across the selection and the environmental gradients, the mean genetic values of populations were shifted rapidly and genetic clines were built up. The effects of assortative mating were particularly visible near the two edges of the landscape owing to the environmental gradient and long-distance pollen flow, which resulted in differentiation roughly clinal under IMM (Figure 2). Overall, assortative mating clearly increased the level of differentiation under cogradient divergent selection. Conversely, countergradient settings slightly decreased the differentiation observed at generation 1000. Under IMM, the slope of the genetic cline generated averaged 6.2 in cogradient conditions, greater than the slope of 4.7 obtained without assortative mating. Countergradient selection induced the shallowest cline with a slope of −4.2. Interestingly, assortative mating combined with uniform selection generated clinal differentiation as well (0.8 under IMM), even though populations shared similar optimal trait values. As expected, under random mating, without filter of pollen, the mean genetic value of populations remained close to the Z_opt values assigned.

Figure 2.

Variations in mean population genetic values at different latitudes. The value for each latitude is the average of the five mean genetic values for the populations concerned at generation 1000. Latitudinal means were computed and reported for cogradient (red), countergradient (green) and uniform selection (purple). Co- and countergradient selection involved steep selection gradients 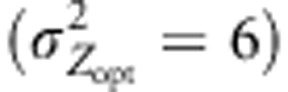, uniform selection was simulated with 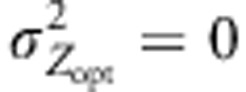. Intensity of stabilizing selection was moderate (ω²=50). Steep environmental gradients were simulated in all cases (k_E=2). The color lines indicate assortative mating (ρ=0.8), the black lines indicate random mating (ρ=0). All simulations were conducted under three migration models with moderate gene flow (N_m=10.2): IMM (plain lines), LDN (dashed lines) and LDS (dotted lines). Each line represents the mean of 30 independent replicates.

Directional migration models shifted uniformly the genetic values of the populations. Although they induced larger shift of the genetic values of central populations, they had few consequences on the magnitude of the differentiation among populations at generation 1000 in the presence of steep selection gradients. However, more pronounced effects were observed in earlier generations when selection gradients with lower slopes were simulated (Supplementary Figure 1). In conditions of uniform selection, directional pollen flow increased substantially the slope of the genetic clines induced by assortative mating (0.7 under LDN or LDS) (Figure 2).

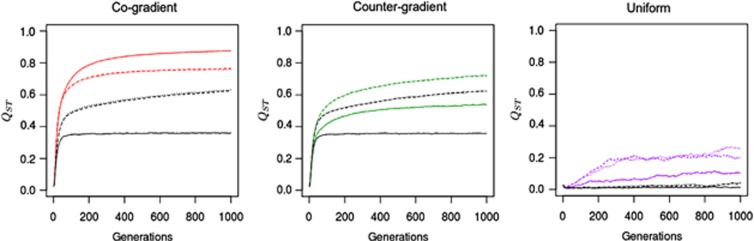
Beyond the monitoring of the genetic cline, we also assessed the overall genetic differentiation of TBB by calculating Q_st, which is a standardized measure of genetic differentiation for a quantitative trait:

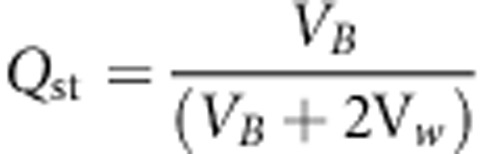where V_B and V_w stand for variance between or within populations, respectively. Q_st variation was driven by the establishment of clines: the highest Q_st value was obtained across cogradient landscapes (0.85), whereas assortative mating across countergradient landscapes resulted in Q_st values of 0.5 and random mating yielded the lowest Q_st value of 0.35. Additional simulations discarding seed flow or involving higher seed dispersal rates resulted in similar patterns (data not shown). When combined with uniform selection, assortative mating resulted in a significant differentiation of 0.09 under IMM and 0.2 under directional dispersal models (Figure 3).

Figure 3.

Variations in Q_st under different evolutionary scenarios. Variations monitored under assortative mating combined with cogradient (red), countergradient (green) and uniform (purple) selection. Co- and countergradient selection involved steep selection gradients 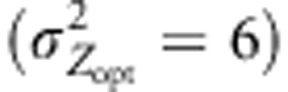; uniform selection was simulated with 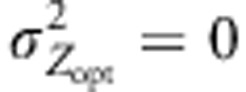. Intensity of stabilizing selection was moderate (ω²=50). Steep environmental gradients were simulated (k_E=2). In these scenarios, the black lines represent the values generated under random mating (ρ=0), and the colored lines represents the Q_st values obtained under assortative mating (ρ=0.8). All simulations were conducted under three migration models with moderate gene flow (N_m=10.2). Three dispersal models were used here: IMM (plain line), LDN (dashed-line), LDS (dotted-line). Each line represents the mean of 30 independent replicates for each evolutionary scenario.

Maladaptation

We then monitored changes in the mean level of adaptation of population 52, located at the northern edge of the landscape, and population 28, located in the center of the landscape. While the examination of genetic clines yields a spatial and static information, the monitoring of evolutionary change of single populations gives insights into the evolutionary and adaptive dynamics. The level of adaptation of populations can be assessed by calculating the difference between their phenotypic optima and their current mean genetic values (|Z_opt−G_t|), larger differences indicating a greater degree of maladaptation.

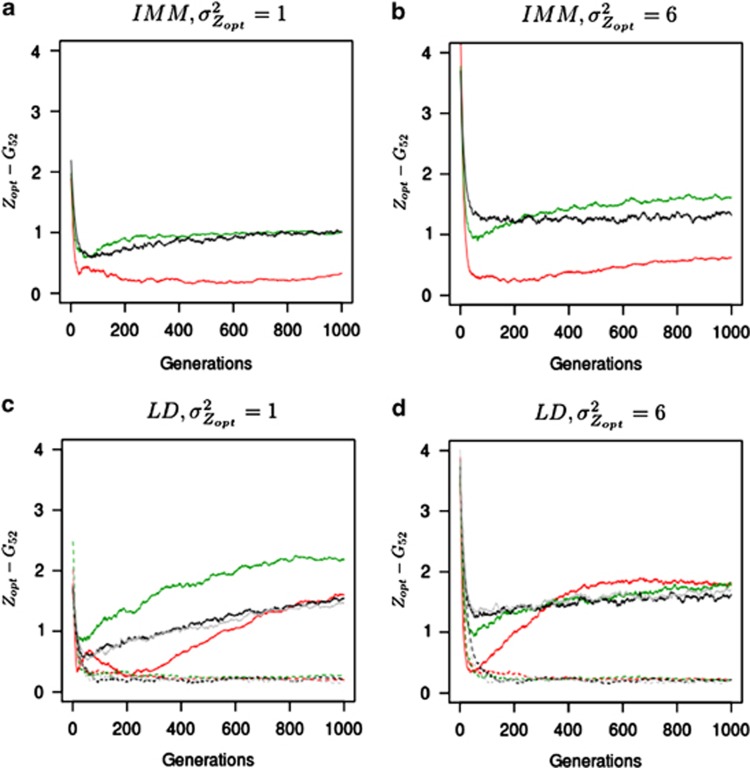
Genetic values were shifted very rapidly toward their optimal values in the first generations, and levels of maladaptation therefore rapidly decreased (Figure 4). At the northern edge, maladaptation decreased most strongly in cogradient conditions: a mean maladaptation rate of 0.3 was observed at generation 50, vs 1.0 in countergradient conditions and 1.3 under random mating. As the metapopulation was at the mutation–migration–drift equilibrium at the beginning of the simulation process, alleles were randomly spread over the landscape and populations had similar mean genetic values. Thus, during the early generations, the adaptative response of populations was inflated as long as alleles were not significantly sorted across the environmental gradient through long-distance pollen flow filtered by assortative mating (Soularue and Kremer, 2012). However, after generation 50, pollen flow from distant sources decreased rapidly the preliminary adaptation, especially in countergradient settings (Figure 4). Indeed, the import of alleles with additive effects strongly diverging from the local optimum of recipient populations gradually restored and amplified maladaptation that reached a level significantly more important than under random mating (1.5 vs 1.2 under IMM, respectively, at generation 1000). However, this swamping effect was considerably reduced under cogradient settings, which induced a much lower maladaptation level of 0.5 at generation 1000 for population 52, as a result of more stringent pollen filtering severely constraining long-distance pollen flow (Figure 5). Besides, under IMM, the differences among the adaptive responses were maximized when moderate selection across steep selection gradient was simulated (Figure 4b). On the other hand, weaker selection gradients 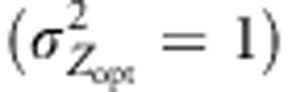and higher stabilizing selection intensity (ω²=5) reduced and canceled the differences observed among the scenarios, respectively (Figure 4a and Supplementary Figure 2).

Figure 4.

Variation in maladaptation level of a northern population. The difference between the phenotypic optima and the mean genetic values of population 52 was monitored within four scenarios involving moderate 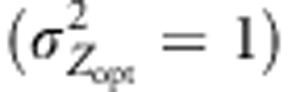and steep selection gradients 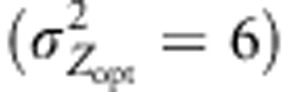. Overall, the intensity of selection was moderate (ω²=50). Assortative mating (ρ=0.8) was simulated and combined either with cogradient (red) or countergradient (green) selection. Alternatively, random mating was simulated: black lines represent the maladaptation level monitored when the selection gradient covaried positively with the latitudinal gradient. Gray lines, only represented in (c) and (d), stand for the maladaptation level observed under random mating when directional dispersal models were associated with a reversed selection gradient. Because the direction of the selection gradient had no importance under IMM and random mating, this latter case was only explored when directional dispersal models were simulated. Three dispersal models were simulated: IMM (plain lines in (a and b)), LDN (plain lines in (c and d)) and LDS (dashed lines in (c and d)). LD mentioned in the titles of the sub-figures (c) and (d) means ‘long-distance and directional dispersal', it refers both to LDN and LDS. Each line represents the mean of 30 independent replicates for each evolutionary scenario.

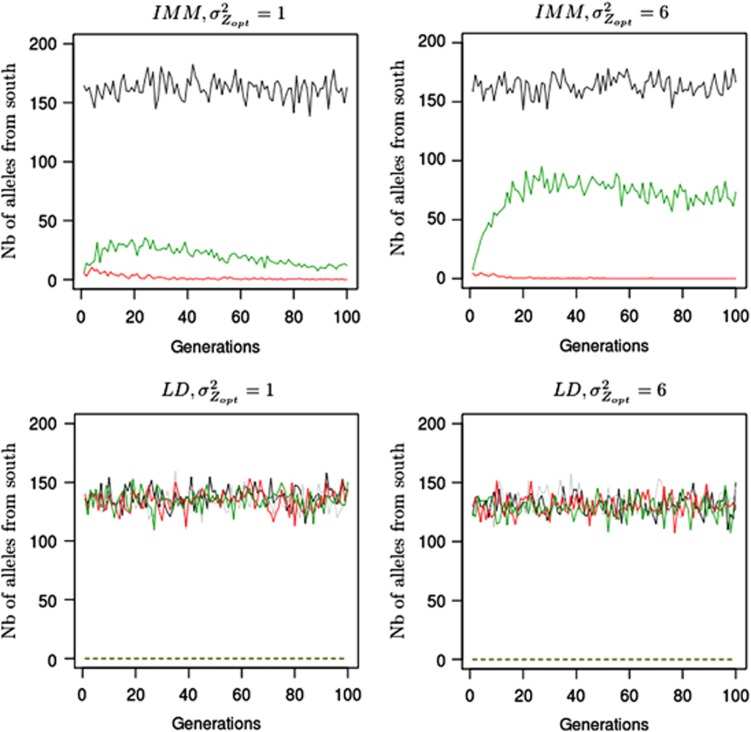
Figure 5.

Amount of southern immigrant alleles received by a northern population over generations. Absolute number of immigrant alleles into a population located at the extreme northern latitude (pop 52) and coming from southern latitudes (−0.5 to −0.1). Only gene flow between populations is represented here. Numbers on the y axis are counts of alleles at a given generation (x axis). Counts of alleles were monitored for two distinct selection gradients (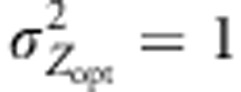, 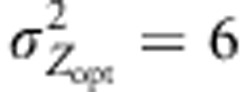), three models of pollen dispersal (IMM, LDS and LDN) and two mating systems (assortative or random mating). Title of the figures indicates the steepness of the selection gradient and the dispersal model simulated. LD means that the pollen dispersal in the scenario is of ‘long-distance and directional' type, it refers both to LDN (plain line) and LDS (dashed line). The color lines indicate assortative mating (ρ=0.8), red standing for cogradient and green for countergradient directional selection. The black and gray lines stand for random mating with the selection gradient covarying positively or negatively with latitudes, respectively. However, because under random mating the direction of the selection gradient has no impact when combined with IMM, the latter case was only considered when directional dispersal models were simulated (LD with 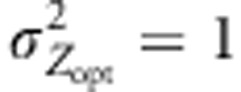and LD with 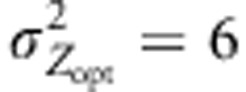). Each line represents the mean of 30 independent replicates for each evolutionary scenario.

Under LDS, because the northern population of interest received no pollen from distant sources, maladaptation remained close to 0 throughout the simulation process, in all landscape configurations. By contrast, LDN was the migration model for which the number of distant alleles was the largest in population 52 (Figure 5). Indeed, LDN swamped the pollen filtering occurring under assortative mating with distant pollen originating from southerly populations, hence promoting even more matings among distant individuals. As a result, overall LDN induced the highest maladaptation levels in population 52 (Figures 4c and d). Nonetheless, in this case, contrasts among cogradient, countergradient and random mating settings were particularly visible when selection gradients with low slope were simulated 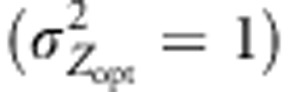(Figure 4c). In this scenario, LDN thus amplified the trend observed under IMM, the level of maladaptation reaching 1.3 at generation 200 and 2.1 at generation 1000 in conditions of countergradient variation. In the absence of assortative mating, the maladaptation level reached 0.8 at generation 200 and 1.3 at generation 1000 under LDN. Interestingly, the swamping effect of distant gene flow was considerably limited by cogradient selection: 0.3 at generation 200 and 1.4 at generation 1000. Steeper selection gradients 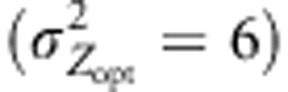resulted in initial adaptive responses strongly amplified by cogradient selection; however, after 300 generations, the maladaptation levels observed were similar among the configurations simulated (Figure 4d). Indeed, in this latter case, LDN combined with the reduced differences among southerly and northern individuals canceled the filtering effect of assortative mating and lead to the highest maladaptation levels observed.

Similar trends were observed in the middle of the landscape (population 28) when directional pollen migration models were simulated (Supplementary Figure 3). The level of maladaptation increased, particularly rapidly, under countergradient settings (1.0 at generation 200), whereas it was limited under cogradient settings during the first 300 generations (0.6 at generation 200). In comparison, the level of maladaptation of population 28 equaled 0.8 at generation 200 under random mating. However, the final level of maladaptation observed at generation 1000 was similar under co- and countergradient settings (1.8) and exceeded the value observed under random mating (1.2). When IMM was simulated, incoming pollen flow was balanced in relation to the environmental gradient in population 28, as a result, no significant effect on maladaptation was induced by assortative mating in this latter case.

At last, under conditions of uniform selection, the Z_opt value of all populations equaled 0. The level of maladaptation corresponded thus to the mean genetic values of the populations (Figure 2). In this configuration, assortative mating generated significant levels of maladaptation, which nevertheless remained below those obtained with divergent selection. For example, population 52 showed a level of maladaptation of 0.3 at generation 1000 under IMM and 0.6 under LDN.

Overall stochastic variation of the level of maladaptation, the clinal response and the differentiation of TBB were low and slightly larger for the level of maladaptation (Supplementary Figure 4).

Discussion

Assortative mating and spatial subdivision of genetic variation

In silico simulations were consistent with our expectations, suggesting that the combination of assortative mating with gene flow and pre-existing environmental clines can generate contrasting distributions of genetic variation for traits across the landscape. Under clinal divergent selection acting in the same direction as the environmental cline (cogradient conditions), genetic clines and differentiation are inflated by assortative mating. Conversely, under divergent selection of the same strength but acting in the opposite direction (countergradient selection), the slope of the genetic clines was slightly decreased. Finally, even under uniform selection, genetic clines are established that mimic cogradient variation (Figure 2). Whether under co- or countergradient conditions, the overall genetic differentiation (Q_st) of TBB is substantially larger under assortative mating in comparison with random mating. Thus, assortative mating inflates divergence in natural populations. The theoretical settings considered here are entirely appropriate for TBB, as TBB is triggered by temperature and is strongly correlated with flowering time in trees. Interestingly, trees display strong clinal genetic variation in provenance tests, also known as common garden experiments (Wright, 1976; Morgenstern, 1996; Savolainen et al., 2007). Our results suggest that cogradient genetic clines should be steeper than countergradient clines. Unfortunately, few reviews of experimental results in diverse species are available, making comparisons with theoretical predictions difficult. However, in a recent comparative study conducted along the same gradient of elevation in European oaks and beech, which display co- and countergradient variations, respectively, genetic clines were found to be steeper for the oaks than for beech (Vitasse et al., 2009a, 2009b, 2011).

Assortative mating and temporal dynamics of differentiation and maladaptation

In addition to the overall effects on clines, we were also able to monitor the temporal dynamics of adaptive trajectories of populations. The combined effects of assortative mating and pollen flow serve to filter external male parents for synchrony to female parents in the recipient populations. This filtering effect changes over generations, with the spatial dispersal of alleles across the landscape (Figure 5). The overall pattern of the evolution of maladaptation showed an initial adaptation state followed by an increase in the maladaptation rate whose extent strongly varied among scenarios when assortative mating was simulated. In cogradient conditions, assortative mating significantly inflated the initial responses of recipient populations to selection, by filtering distant pollen flow and favoring the import of alleles helping in the tracking of optimal values. This finding confirms and extends previous results (Jorjani et al., 1997; Fox, 2003), indicating that positive assortative mating induces the strongest response to selection in single populations. Additionally, in combination with cogradient divergent selection, assortative mating tends to reduce the time to adaptation (Figure 4). However, our models and simulations revealed that, when combined with countergradient selection, assortative mating decreases the ability of populations to track the shift of optimal values (Figure 4). Moreover, in such a configuration, less stringent pollen filtering results in assortative mating increasing the time to adaptation, such that it may become critical for the population concerned (Burger and Lynch, 1995). Overall, the contrast observed in the early generations between co- and countergradient settings was particularly visible when steep selection and environmental gradients were simulated (Figures 4b and c). These findings are of prime importance in the context of climate change. Global warming will probably shift the optimal values of populations (Lynch and Lande, 1993), which we considered to remain constant over successive generations in our simulations, thereby increasing the time to adaptation. Under such circumstances, in case of moderate selection intensity, assortative mating in cogradient settings will probably favor adaptation and recovery, whereas, in countergradient settings, it may greatly delay adaptation and rescue.

Interestingly, phenological assortative mating gave rise to a striking difference at later time points. Indeed, in our simulations, the initial adaptation phase was short (30–50 generations) and was followed by the maintenance of adaptation or by a gradual loss of the state of adaptation initially attained by populations (Figure 4). Despite a slight loss of adaptation level, especially present in case of countergradient conditions, the initial adaptation state attained by the populations was pretty well conserved under IMM, owing to the efficient filter of pollen realized by assortative mating (Figure 5). However, when we modified the content of the pollen cloud by simulating directional dispersal models allowing for long-distance pollen flow, large backward shifts of the genetic values of the populations occurred, steadily increasing their degree of maladaptation (Figures 4b and c and Supplementary Figure 3). This swamping effect was strongest at the edge of the landscape, where pollen from distant sources was more abundant. These findings are reminiscent of those of previous studies showing that peripheral populations are more likely to be swamped by maladapted gene flow originating principally from central populations (Kirckpatrick and Barton, 1997; Holliday et al., 2012). This swamping effect was most readily triggered in countergradient landscapes under conditions of extensive long-distance gene flow. By contrast, it was greatly delayed and constrained by assortative mating, especially across cogradient landscapes exhibiting selection gradients of low slope. Interestingly, maladaptation of population 52 remained lower under cogradient selection than under random mating during 800 generations. Nonetheless, the long-term filtering effect of assortative mating was reduced by steep selection gradients that increased even more the swamping effect of directional dispersal models (Figure 4d). Besides, the simulation of a very strong selection intensity evened out the effects of assortative mating (Supplementary Figure 2).

Maladaptation is difficult to assess in long-lived species, as it is difficult to record optimal population values and selection intensity. We are therefore unable to make comparisons with observed values for maladaptation, for the confirmation or rejection of our theoretical predictions. However, overall, this suggests that, below a very high threshold of long-distance pollen flow stemming from dispersal patterns, the filtering effect of assortative mating in the cogradient configuration may be strong enough to transform the swamping effect of distant pollen flow into a favorable effect, promoting durable adaptation within peripheral populations. In this interesting configuration, our results are consistent with those of Davis and Shaw (2001), indicating that preadapted alleles from central populations may promote adaptation within recipient peripheral populations (Davis and Shaw, 2001).

We considered constant environmental variation over generations within our simulations, but field observations have shown that the slope of the environmental gradient may differ among tree species (Vitasse et al., 2009a, 2009b). For example, Vitasse et al. (2009a, 2009b) showed that environmental gradients were more marked in oak and ash than in beech. We predicted that the impact of assortative mating would be dependent on the slope of the environmental gradient (Equation (6)) and we confirmed these predictions by numerical simulation (Soularue and Kremer, 2012). Empirical and theoretical temperature–phenology relationships have been well described in a number of temperate tree species (Vitasse et al., 2011), whereas comparisons with common garden observations are less frequent but can identify co- and countergradient settings (Wright, 1976; Morgenstern, 1996; Savolainen et al., 2007). This obtainable information should make it possible to predict the evolutionary responses of various temperate tree species in the context of future climate change.

Limitations and future applications

We used analytical calculations and simulations to predict the distribution of genetic variation of TBB in an heterogeneous landscape, by considering the joint effects of divergent selection, gene flow, assortative mating and environmental gradients. Earlier investigations were either limited to single population (Fox, 2003; Devaux and Lande, 2010) or did not consider selection on the phenological trait (Stam, 1983; Gavrilets and Vose, 2007). Our analytical calculations resulted in complex predictions (Equation (6)), and naturally lead to the use of numerical simulations. But even in simulations, combining the different evolutionary forces requires some form of simplification and abstraction to disentangle their individual and joint effects, and thus restricts generalizations to real situations. In our case, we reduce the landscape to a two-dimensional grid setting, with one-dimensional gradient of divergent selection and environmental variation. Gene flow, divergent selection and environmental gradients have indeed a directional component, and the grid system allowed to orientate their effect and track their impact. Particularly, our representation allowed to evaluate their effects when they act in the same or opposing direction (for example, co- and countergradient settings). Potential transposition to real settings can be made by considering external knowledge of potential direction of the evolutionary forces: direction of pollen flow, direction of gradient of selection as observed in provenance tests and climatic gradient across the landscape. A second level of simplification in our simulations was that the initial direction and intensity of the evolutionary forces was maintained constant over generations. This may be considered as a limitation, especially in the context of climate change that will trigger changes in strength of divergent selection and in environmental gradients. However, this step was necessary and is considered as a reference scenario to which responses under changing environments could be compared. A central issue that could be addressed in future investigations is whether assortative mating and gene flow will reshape the extant geographic distribution of genetic variation of TBB and facilitate adaptation in the central or peripheral populations of a species distribution.

Data Archiving

There were no data to deposit.

The authors declare no conflict of interest.