Abstract
Quantitative seed provisioning is an important life-history trait with strong effects on offspring phenotype and fitness. As for any other trait, heritability estimates are vital for understanding its evolutionary dynamics. However, being a trait in between two generations, estimating additive genetic variation of seed provisioning requires complex quantitative genetic approaches for distinguishing between true genetic and environmental maternal effects. Here, using Maritime pine as a long-lived plant model, we quantified additive genetic variation of cone and seed weight (SW) mean and SW within-individual variation. We used a powerful approach combining both half-sib analysis and parent–offspring regression using several common garden tests established in contrasting environments to separate G, E and G × E effects. Both cone weight and SW mean showed significant genetic variation but were also influenced by the maternal environment. Most of the large variation in SW mean was attributable to additive genetic effects (h2=0.55–0.74). SW showed no apparent G × E interaction, particularly when accounting for cone weight covariation, suggesting that the maternal genotypes actively control the SW mean irrespective of the amount of resources allocated to cones. Within-individual variation in SW was low (12%) relative to between-individual variation (88%), and showed no genetic variation but was largely affected by the maternal environment, with greater variation in the less favourable sites for pine growth. In summary, results were very consistent between the parental and the offspring common garden tests, and clearly indicated heritable genetic variation for SW mean but not for within-individual variation in SW.
Introduction
Seed weight (SW) is an important life-history trait with strong effects on offspring phenotype and ultimately on fitness. The influence of SW on germination (Norden et al., 2009), early growth (Hanley et al., 2007), survival (Metz et al., 2010), abiotic stress tolerance (Gomaa and Xavier Pico, 2011) and biotic resistance (Solla et al., 2011) of the offspring is well documented for many different plant species, including conifer trees (Sorensen and Campbell, 1993; Surles et al., 1993; Castro, 1999; Wennstrom et al., 2002; Parker et al., 2006; Blade and Vallejo, 2008). Given the relevance of SW for offspring fitness, it could be expected that SW would show little variation within populations as a result of stabilizing selection forces (Silvertown, 1989). The scientific literature is, however, replete of empirical studies reporting large intraspecific variation in SW (reviewed in Castro et al., 2006). Both maternal environmental effects (Roach and Wulff, 1987) and the size-number trade-off (Sadras, 2007) have been repeatedly identified as relevant factors maintaining intraspecific variation in SW. However, many other factors can all also contribute, including parental–offspring (de Jong et al., 2011) or paternal–maternal (Willi, 2013) conflicts in the optimum seed size, sibling competition within plants or fruits (Banuelos and Obeso, 2003), temporal and spatial instability of the optimum size (Charpentier et al., 2012), limited resources constraining the ability of plants to control individual seed size (Vaughton and Ramsey, 1998), and conflicting selective pressures acting on SW depending on the phase of recruitment (Gomez, 2004; Lazaro and Traveset, 2009). This unpredicted intraspecific variation has driven an interesting field of research in recent decades.
The theoretical prediction of reduced additive variance in SW within populations arises because natural selection is expected to eliminate genotypes with SW departing from the optimum for each environment. However, to evolve in such a way, phenotypic variation in SW must have a genetic basis, and this genetic variation must be heritable (Silvertown, 1989; Sadras, 2007). Separating the environmental and genetic effects in seed traits is, however, a complicated task (Zas et al., 2013). SW is a complex trait that bridges the transition between plant generations. Seeds include tissues of both maternal and embryonic origin, with triploid (or maternal-haploid in gymnosperms) and diploid genetic material. Because of their close connection with the mother plant, seeds are influenced not only by their own genotype (House et al., 2010), but also by the maternal genotype (Schwaegerle and Levin, 1990; Platenkamp and Shaw, 1993; Wolfe, 1995) and by the environmental conditions where the mother plant has grown (Roach and Wulff, 1987). The maternal environmental effect has often been confounded by the effect of the maternal genotype (Vaughton and Ramsey, 1998; Susko and Lovett-Doust, 2000; Voeller et al., 2012; Sober and Ramula, 2013), which, in turn involves both nuclear and extranuclear effects (Lipow and Wyatt, 1999) and can differentially affect the different seed tissues because of their different genetic contributions (Lacey et al., 1997). Accurate quantification of additive genetic variation—essential for understanding the evolution of SW—will thus require complex quantitative genetic approaches that allow the relative genetic and environmental maternal effects to be distinguished (Mazer, 1987). Such experimental approaches are difficult to implement, especially in long-lived plants such as conifer trees (Zas et al., 2013), and this may explain why there are no previous studies reporting narrow-sense heritability for seed traits in long-lived trees, in which these confounding factors are properly accounted for. Previous studies with conifer trees have reported total genetic variation for seed traits (without distinguishing additive and non-additive variance) but failed to differentiate the effect of the maternal genotype from that of the maternal environment (Matziris, 1998; Castro, 1999; Roy et al., 2004; Bilir et al., 2008; Carles et al., 2009). Taking advantage of a long-term experimental device of common garden tests established within a tree breeding programme, in the present paper, we were able to properly differentiate these factors and accurately estimate narrow-sense heritability of seed traits of Maritime pine.
The strong plasticity and the low heritability estimates of SW observed in wild populations of several species have motivated some authors to question the idea of stabilizing selection on SW (Silvertown, 1989). However, a more recent meta-analysis found considerable heritability estimates for SW in many herbaceous crops, despite the fact that domestication and breeding are supposed to have led to a reduction in the available genetic variation (Sadras, 2007). This apparent contradiction between wild populations and crops may arise from the difficulties in accurately estimating the heritability of wild populations in which many confounding factors (e.g., maternal effects, genotype × environment (G × E) interaction) can operate. Additionally, most of the studies have focused on the heritability of SW mean and neglected the within-individual variation in SW, which, in many cases, can be as high as or even higher than between-individual variation (Holland et al., 2009). Within-individual variation in SW has, in fact, been considered a fitness-correlated trait, as SW variability may provide fitness benefits in heterogeneous or unpredictable environments, providing a buffer against environmental variability and constituting a form of bet-hedging (Charpentier et al., 2012). When the temporal or spatial environmental heterogeneity impedes to settle an optimum seed size, producing variable seed sizes could be an advantageous strategy that maximizes the fitness of the mother plant. Again, heritable variation in this trait should exist to allow evolutionary responses to environmental selective pressures. However, very few previous studies have quantified the heritability of within-individual variation in SW (Halpern, 2005; Castellanos et al., 2008) and none in long-lived woody plants.
Recently, analysing two clonal seed orchards established in contrasting environmental conditions, we have found the SW of Maritime pine to be extremely variable and highly influenced by both the maternal environment and the maternal genotype (Zas et al., 2013). SW also influenced offspring performance mediating the transmission of both genetic and environmental maternal effects (Zas et al., 2013). In this study, we went a step further by aiming to determine (i) the extent to which the observed genetic variation in SW is heritable and (ii) whether there is a genetic correlation between SW and adult tree growth potential. Here, we analysed mean SW and individual SW variation of the open-pollinated progenies of the genotypes included in those clonal seed orchards analysed in the previous paper (Zas et al., 2013). This allowed us to estimate narrow-sense heritability using both half-sib analysis and parent–offspring regression, using in both cases several common garden tests established in contrasting environmental conditions to disentangle G, E and G × E effects. Results will help to understand the adaptive value and evolutionary dynamics of these interesting traits.
Materials and methods
Experimental approach
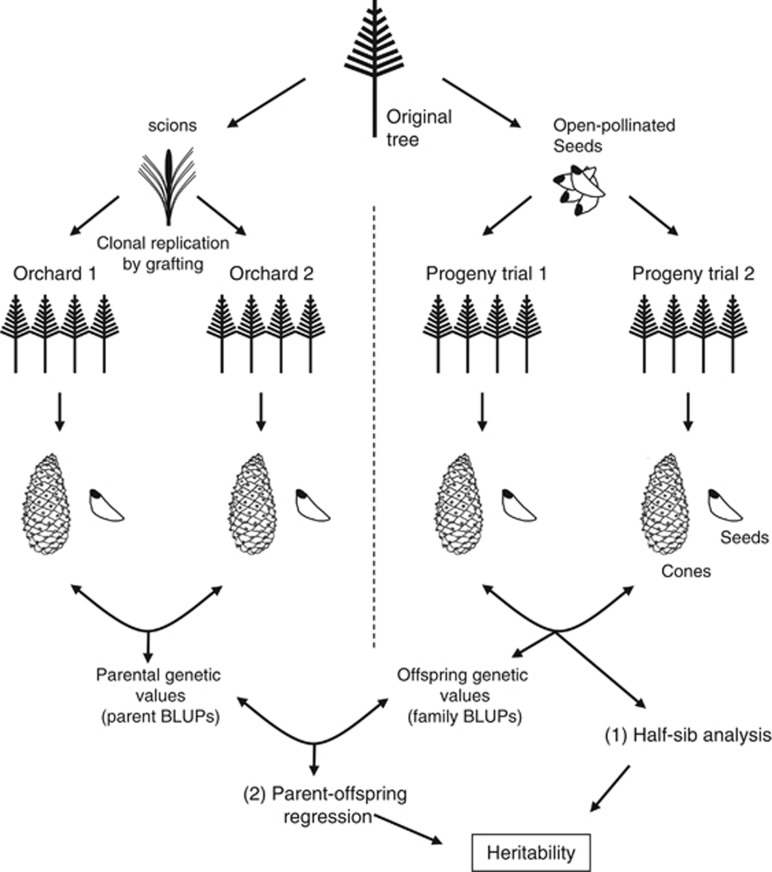
To address our objectives, we took advantage of different genetic trials established within the frame of the breeding programme of Maritime pine in Galicia (NW Spain, Consellería de Medio Rural, Xunta de Galicia). Within that programme, unrelated superior genotypes (‘plus trees' with outstanding phenotypes in terms of growth, stem form and branching habit for timber production) were selected in the early 80s from an extensive field survey in natural and man-made plantations within the Spanish North West Coastal provenance of Maritime pine. Open-pollinated seeds and scions collected from those plus trees were used for the establishment of a series of open-pollinated progeny trials and two twin clonal seed orchards, respectively (see Figure 1).
Figure 1.
Schematic representation of the experimental approach. Heritability of cone and seed weight was estimated both through (1) a half-sibling analysis of cone and seed traits assessed in two open-pollinated progeny trials, and (2) parent–offspring regression between the parent and offspring genetic values (BLUPs) estimated across the two clonal seed orchards and the two open-pollinated progeny trials, respectively.
Several open-pollinated progeny trials were established in 1994–95 across NW Spain following a randomized block design, with 10 blocks and five-tree row plots (Zas et al., 2004). In the present study, we analysed cones and seeds from two of those progeny trials: Lalin (42.64° N, 7.99° W) and Cortegada (42.21° N, 8.11° W), which were the worst and the best sites, respectively, in terms of growth (Zas et al., 2004).
In the clonal seed orchards, the scions were grafted on 2-year-old seedlings by substituting the terminal bud to obtain several clonal replicates of each genotype. Ten copies (ramets) of each plus-tree genotype were established in each of two clonal seed orchards (‘Sergude' and ‘Monfero') following a randomized block design with 10 blocks and one ramet of each genotype per block. Environmental conditions drastically differed between the two seed orchards, one of them (Sergude, 42.82° N, 8.45° W) with favourable conditions for pine growth and reproduction, and the other (Monfero, 43.52° N, 7.93° W) with stressful edaphoclimatic conditions (environmental stresses with low winter temperatures, exposed to continuous and intense winds, and shallow and impoverished soils) (Table 1).
Table 1. Climatic, edaphic and dasometric characteristics of the two maternal seed orchards (Sergude and Monfero) and the two open-pollinated family trials (Cortegada and Lalin).
|
Seed orchards |
Progeny trials |
|||
|---|---|---|---|---|
| Monfero | Sergude | Cortegada | Lalin | |
| Latitude (°N) | 43.52 | 42.82 | 42.21 | 42.64 |
| Longitude (°W) | 7.93 | 8.45 | 8.11 | 7.99 |
| Altitude (m) | 615 | 258 | 530 | 700 |
| Mean annual temperature (°C) | 10.6 | 13.2 | 12.6 | 11.3 |
| Annual precipitation (mm) | 1435 | 1445 | 1106 | 1202 |
| Soil pH in H2O (soil:water, 1:2.5) | 4.5 | 5.1 | 4.6 | 4.6 |
| Soil depth (cm) | 45.1 | >120 cm | 60.9 | 59.5 |
| Tree age at sampling | 20 | 27 | 14 | 14 |
| Spacing | 5 × 5 | 5 × 5 | 3 × 3 | 3 × 3 |
| Mean tree diameter at breast height (cm) | 6.1±0.3 | 20.9±0.6 | 10.0±0.1 | 7.7±0.1 |
| Mean tree height (cm) | — | — | 558.1±3.1 | 440.9±2.1 |
Sampling and assessments
In this study, we analysed cone and seed traits in 10 genotypes randomly selected among the 116 genotypes included in each seed orchard, and in 10 open-pollinated families established in the two progeny trials, 9 of which corresponded to the maternal genotypes studied in the seed orchards.
In each progeny trial, and for each selected open-pollinated family, up to three mature cones were collected from three out of the five trees per block, in five randomly selected blocks (i.e., 15 individual half-sib trees per family). Because of tree mortality and lack of available cones for sampling in some trees, we sampled 133 and 143 trees in Cortegada and Lalin, respectively, resulting in a total of 773 sampled cones. Sampling was performed in March 2009 when trees were 14 years old.
In the two seed orchards, three to four mature cones were collected from four to six ramets of each selected genotype in each of the two clonal seed orchards. A total of 373 cones were sampled from 103 different individual trees. The analysis of the sources of variation of SW in this collection of cones and its influence on offspring performance has been published elsewhere (Zas et al., 2013). Sampling was performed in January 2009, when trees were 20 years old in Monfero and 27 years old in Sergude.
Cones were randomly selected within the crown of each tree, collected using ladders and climbing tools and individually labelled. Damaged cones or cones in damaged branches were avoided. Cones were opened in the oven at 35 °C, weighed, and all seeds collected and stored at 4 °C in labelled PET vials. Empty seeds were separated from filled seeds by decantation in cold water. A subsample of filled seeds (n=24 in the seed orchards and n=16 in the progeny trials) was randomly sampled from each cone and seeds were individually weighed (±0.0001 g). A total of 8924 seeds from the seed orchards and 12 464 seeds from the progeny trials were considered in the analyses. Individual cone weight mean, SW mean and within-individual variation in SW were computed for each sampled tree. To estimate the variation of SW within individual trees, we used the coefficient of variation as it is the parameter least influenced by the variation in the mean (Crean and Marshall, 2009). Diameter at breast height was measured for all sampled trees.
Statistical analyses
In the present study, we estimated additive genetic variance and narrow sense heritability of cone and seed traits by analysing (i) the relation between family and within-family variances as estimated by mixed model analyses in the progeny trials and (ii) parent–offspring regression between the genetic values estimated in the clonal seed orchard and the progeny trials (Figure 1).
Tree diameter, mean cone weight, and the mean and within-individual tree variation in SW in the progeny trials were analysed by fitting mixed models with site as a fixed factor, and family and family × site interaction as random factors. Blocks within sites and the interaction of blocks and families (representing the variation among multi-tree plots) were also included in the models as random factors. Variance components were estimated using the REML method as implemented in the MIXED procedure of SAS (Littell et al., 2006). To explore and interpret the G × E interaction, we first fitted a full mixed model in which we assumed heterogeneity of residual variance and an unstructured family (co)variance structure. Then, by fitting different reduced models constraining different elements of the family and residual covariance structures, we tested for different hypotheses on the causes of the G × E interaction (see details in de la Mata and Zas, 2010). Specifically, we tested whether there was heterogeneity of residual and family variances across sites, and whether the genetic correlation between sites was significantly greater than zero (zero being complete independence) and significantly lower than one (one indicating perfect correlation or parallel reaction norms). Hypothesis testing regarding the constraints imposed on the residual and family covariance structures was carried out by comparing the restricted log-likelihoods of the reduced model and the full model, where the differences in two times the log-likelihood of these two nested models are distributed as one-tailed χ2 with degrees of freedom given by the difference in the number of covariance parameters between both models (Fry, 2004). The statistical significance of each specific variance component was also assessed using likelihood ratio tests by fitting reduced models in which we fixed the given (co)variance parameter to 0. Finally, we used the most parsimonious model (i.e., that with the lowest number of parameters that fitted as well as the full model) to estimate the best linear unbiased predictors (BLUPs) for each family (i.e., the offspring genetic values).
To compute parent–offspring regressions, we used the estimates of the parental values for seed and cone weight in the two clonal seed orchards obtained by Zas et al. (2013). Analyses of the cone weight mean and the mean and variation in SW were performed by fitting mixed models with the sites as a fixed factor and the blocks within sites, the genotypes and the site × genotype interaction as random factors (Zas et al., 2013). BLUPs as obtained from those mixed models were used to characterize the parental genetic values for each trait.
For the SW mean, we implemented two types of analyses for both the progeny trials and the seed orchards, including and excluding the cone weight as a covariate in the statistical models. The two approaches led to different covariance parameter estimates and BLUPs and thus to different heritability estimates.
Narrow-sense heritability was estimated both by means of parent–offspring regression and by analysing the similarities between half siblings in the progeny trials. In the first case, we regressed the BLUPs of the open-pollinated families on the BLUPs of their respective maternal parents as estimated from the mixed models described above. As the original maternal trees were located far away from each other, they are assumed to be unrelated and thus the heritability was estimated as two times the slope of the parent–offspring linear relationship (Roff, 1997). Similarly, the standard error of the heritability was twice the standard error of the regression slope. On the other hand, heritability was also calculated as the ratio of additive genetic variance to total phenotypic variance, with variance estimates derived from the analyses of the open-pollinated progeny trials. Pine families were assumed to be true half-sibs, and thus the additive genetic variance was estimated as four times the family variance (σ2A=4·σ2F, where σ2F is the family variance). Phenotypic variance was estimated as the sum of family, among-plot and within-plot (residual) variances. In this case, s.e. of heritability were estimated by the Delta method upon the asymptotic estimates of the variances and covariances of the variance components of the mixed model (Lynch and Walsh, 1997). Pines are wind-pollinated and predominantly outcrossers, and self pollination and correlated paternity have been shown to be extremely low in Maritime pine (de-Lucas et al., 2008). However, we cannot discard some level of full-sibling within our studied families.
To estimate genetic correlations between different traits, we carried out mixed bivariate repeated measures analyses (Holland, 2006) on the data obtained in the progeny trials. For each pair of traits, we assumed that the values of the two traits on a given tree are repeated measures on the same subject.
Results
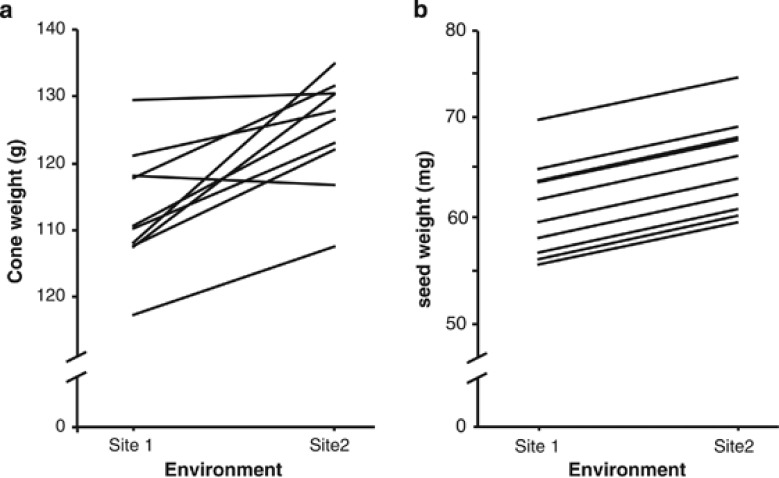
In the progeny trials, we found significant variation among families for cone weight mean and SW mean but not for tree diameter and within-individual variation in SW (Table 2). All these four traits were significantly influenced by the environment (Table 2). Trees were smaller in Lalin than in Cortegada, but cones and seeds were significantly greater in the former than in the latter site (Table 3). Individual variation of SW was, however, larger in Cortegada, that is, the site with lighter seeds (Table 3). The effect of the environment on the different traits was apparently similar for all the 10 studied families, as revealed by the lack of any significant family × site interaction (Table 2). However, the likelihood-based analyses of the G × E interaction revealed different interpretations of the interaction depending on the trait being considered. No trait showed a correlation estimate that significantly differed from one (i.e., perfect correlation, Table 4), but this was due to the high standard errors for the estimate of the genetic correlation between sites. In fact, the estimate of genetic correlation was significantly different from zero only in the case of the mean SW (Table 4), suggesting that only for this trait can we actually assume a high correlation between sites. Consequently, reaction norms for SW were parallel but those for cone weight showed large ranking changes across environments (Figure 2). Family variances were similar in the two sites for all the four traits but residual variances significantly differed between sites in the case of tree diameter and individual variation in SW (Table 4).
Table 2. Summary of the mixed model for the analysis of cone weight, seed weight mean and variation of seed weight within individual trees in the two progeny trials.
| Fixed factors |
Cone weight |
Seed weight mean |
Seed weight variation |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DF | F | P>F | DF | F | P>F | DF | F | P>F | ||
| Environment (E) | 1,16 | 5.6 | 0.031 | 1,16 | 8.3 | 0.011 | 1,16 | 13.7 | 0.002 | |
| Random factors | Var Comp | χ2 | P>χ2 | Var Comp | χ2 | P>χ2 | Var Comp | χ2 | P>χ2 | |
| Family (F) | 40.6±55.8 | 9.0 | 0.001 | 24±13.8 | 19.3 | 0.000 | 0.91±1.37 | 2.2 | 0.069 | |
| F × E | 57.1±59.1 | 1.9 | 0.084 | 0±0 | 0.0 | 0.500 | 0.4±1.5 | 0.1 | 0.376 | |
| (Cortegada) | 69.7±8.8 | |||||||||
| Residual | 709.9±73.5 | 85.3±9.0 | ||||||||
| (Lalin) | 22.2±2.7 | |||||||||
Abbreviations: DF, degrees of freedom; F × E, family × environment.
Environment was treated as a fixed factor, and family, blocks (not shown) and the interactions involving these terms were considered random factors. DF, F ratios and associated probability values are shown for fixed effects. REML estimates of variance components (±s.e.) and the likelihood ratio test (χ2) testing whether they are significantly greater than zero are shown for random factors. Significant probability values (P<0.05) are given in boldface. A heterogeneous residual mixed model was fitted for variation in seed weight.
Table 3. Least square means (±s.e.) for tree diameter, cone weight, seed weight mean and within-individual variation of seed weight in Pinus pinaster based on the analysis of two clonal seed orchards (Monfero and Sergude) and two open-pollinated progeny trials (Cortegada and Lalin) as estimated from the corresponding mixed models.
| Variable |
Clonal seed orchards |
Progeny trials |
||
|---|---|---|---|---|
| Monfero | Sergude | Cortegada | Lalin | |
| Tree diameter (cm) | 6.1±0.3 | 20.9±0.6 | 18.6±0.7 | 16.2±0.7 |
| Cone weight mean (g) | 101.5±10.1 | 150.6±9.6 | 113.2±4.1 | 125.3±4.1 |
| Seed weight mean (mg) | 53.2±0.2 | 79.1±0.3 | 60.9±1.8 | 65.1±1.9 |
| Seed weight coefficient of variation (%) | 14.4±0.6 | 10.8±0.5 | 19.4±0.8 | 15.9±0.6 |
Table 4. Results of different likelihood ratio tests for testing different hypothesis on the relevance and interpretation of the family × environment interaction across the two progeny trials.
| Hypothesis testing |
Tree diameter |
Cone weight |
Mean SW |
Variation SW |
||||
|---|---|---|---|---|---|---|---|---|
| X2 | P>χ | χ2 | P>χ | χ2 | P>χ | χ2 | P>χ | |
| Homogeneity of family variances | 0.0 | 0.500 | 0.1 | 0.376 | 0.1 | 0.376 | 0.2 | 0.327 |
| Homogeneity of residual variances | 16.9 | 0.000 | 0.3 | 0.292 | 2.4 | 0.061 | 38.2 | 0.000 |
| Genetic correlation not different from zero | 0.0 | 0.500 | 0.6 | 0.219 | 10.9 | 0.000 | 0.4 | 0.264 |
| Genetic correlation not different from one | 0.0 | 0.500 | 1.7 | 0.096 | 0.0 | 0.500 | 0.1 | 0.376 |
Abbreviation: SW, seed weight. Significant probability values (P<0.05) are given in boldface.
Figure 2.
Reaction norms for within-individual cone weight (a) and SW mean (b) of 10 half-sib families of Pinus pinaster across two progeny trials (Site 1=Cortegada; Site 2=Lalin). BLUPs as obtained from the corresponding mixed models are shown.
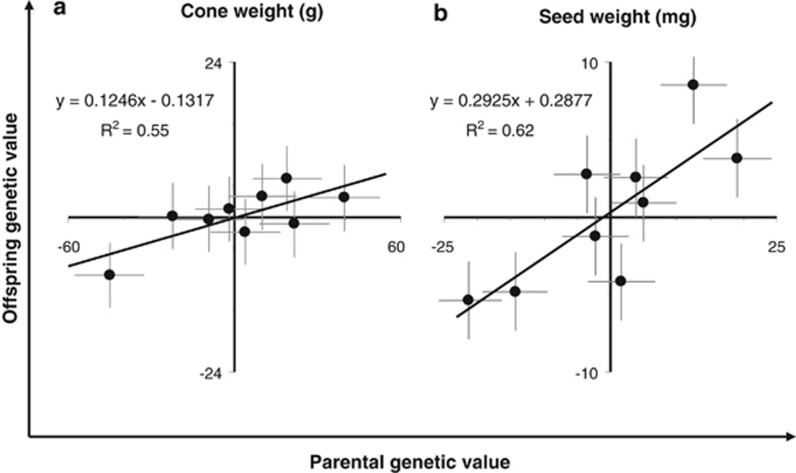
Heritability estimates were low for cone weight but moderate to high for SW mean (Table 5, Figure 3). The two estimation methods (parent–offspring regression, and half-sibling design) led to fairly similar heritability estimates, with no clear trend differentiating the methods (Table 5, Figure 3). Using the half-sibling design, heritability estimate of SW was higher when the analysis did not account for cone weight covariation, but the inclusion of the covariate did not affect the heritability when estimated using parent–offspring regression (Table 5).
Table 5. Narrow sense heritability estimates (h 2±s.e.) for cone weight and seed weight mean of Pinus pinaster derived from the analysis of similarities between half-sibs in progeny trials and from parental–offspring relationships.
|
Seed weight |
|||
|---|---|---|---|
| Cone weight | Not accounting for cone weight covariation | Accounting for cone weight covariation | |
| Half-sibs relationship | 0.17±0.08 | 0.74±0.27 | 0.56±0.12 |
| Parent–offspring regression | 0.25±0.09 | 0.58±0.17 | 0.55±0.19 |
Heritability of seed weight is shown with and without accounting for the covariation with cone weight in the corresponding mixed models.
Figure 3.
Parent–offspring regression for cone weight and SW mean of Pinus pinaster. Each point represents the BLUP of the parental value and the offspring value as obtained from the analysis of two clonal seed orchards (parents) and two half-sib progeny trials (offspring). N=9 parental genotypes and 9 half-sib families. Error bars denote the standard error of the corresponding BLUPs.
Cone weight and the SW mean were just moderately correlated at the phenotypic level (r=0.628, N=773, P<0.001), but showed a strong positive genetic correlation (Table 6). However, we found no significant genetic correlation among the other studied traits. Genetic correlations with tree diameter were inestimable because of the lack of additive genetic variation for this trait (Table 6).
Table 6. Restricted maximum likelihood estimates of genetic correlation (±s.e.) between tree diameter, CW, SW mean and SW variation within individual trees, estimated as CV-SW.
| CW | SW | CV-SW | |
|---|---|---|---|
| Diameter | 1.52±1.87ns | 1.47±1.87ns | 0.00±1.07ns |
| CW mean (CW) | — | 0.99±0.06*** | 0.54±0.69ns |
| SW mean (SW) | — | 0.19±0.53ns | |
| Variation in SW (CV-SW) | — |
Abbreviations: CW, cone weight; CV-SW, coefficient of variation-seed weight; SW, seed weight; ns, not significant.
***=P<0.001.
Significant correlation estimates (P<0.05) are given in boldface. N=10 open-pollinated families.
Discussion
Heritability of mean SW
Despite being a plastic trait subjected to environmental variation, SW mean appeared to be a genetically variable and highly heritable trait in this pine species, with most of the large observed genetic variation being attributable to additive genetic effects. Results also indicate that the genetic variation was consistent across sites, with parallel reaction norms despite the large differences in environmental conditions. Interestingly, results from the parental and offspring common gardens were consistently similar, with strong differences in SW between sites, large total or additive genetic variances and lack of G × E interaction in both cases (see also Zas et al., 2013). Because in this study parental trees proceed from a single artificial phenotypic selection event, the chances are that only a small range of the actual genetic variation of the original population is explored. It is therefore likely that the additive genetic variance in SW mean within the whole population could actually be even larger than that reported here. On the other hand, heritability was estimated assuming that families are true half sibs, but we cannot completely rule out that some of the seedlings from the same maternal tree are, in fact, full siblings. Although not very likely because of the mating system and gene flow in Maritime pine (de-Lucas et al., 2008), this could have caused a slight heritability overestimation.
The vast majority of the many studies exploring the sources of variation of SW (most of them performed in herbaceous or annual plants) have identified the variation among mother plants as the most important source of variation (Castro, 1999; Halpern, 2005; Lazaro and Traveset, 2009; Sober and Ramula, 2013). However, most of these studies failed to distinguish whether this effect has an additive genetic component or whether it is related to phenotypic plasticity (i.e., maternal environmental effects) or genetic maternal effects (e.g., Voeller et al., 2012). When these effects have been successfully isolated, SW mean has not always shown a strong genetic control; indeed, several studies on wild species have either failed to detect within-population genetic variation in SW mean (Schwaegerle and Levin, 1990; Wolfe, 1995; Castellanos et al., 2008) or have reported very low heritability estimates (Mazer, 1987; Biere, 1991; Platenkamp and Shaw, 1993). These reports of low heritability of SW have prompted some authors to challenge the idea of stabilizing selection for a particular seed size (Silvertown, 1989). However, there is now ample evidence that SW is a variable and heritable trait that can respond to the selection pressures imposed by the environmental conditions. Empirical evidence for the evolution of SW arises, for example, from studies showing strong genetic differentiation in SW among plant populations growing in contrasting environmental conditions, with the SW of each population matching the optimal predicted SW (Lazaro and Traveset, 2009). Accordingly, climatic or geographic gradients in SW have been described in many different plant species (Murray et al., 2004), including conifers (Liu et al., 2013), although in most cases, it is not clear whether the observed variation is due to genetic differentiation or phenotypic plasticity.
Importantly, the controversy around the heritability of seed traits may be related to the difficulties associated with the determination of the genetic architecture of a trait that is in between two generations. Many studies have considered all seed properties to be offspring traits (e.g., Byers et al., 1997), and accordingly have interpreted the seeds of each mother plant as half-sibs (e.g., Carles et al., 2009). In most of these cases, including almost all the studies reporting heritability for seed mass in conifer trees (Matziris, 1998; Bilir et al., 2008; Sivacioglu and Ayan, 2008; Carles et al., 2009), the reported heritability estimates were, in fact, clonal repeatability estimates. The statistical analyses used have not accounted, however, for the fact that seeds of a given mother plant are, indeed, non-independent repeated measures within the same subject (Carles et al., 2009). In other cases, seed traits have been assumed to be a property of the mother plant, and separation of the effects of the maternal environment and the maternal genotype is difficult unless the maternal plants are replicated in contrasting environments (Mazer and Gorchov, 1996). Separating genetic and environmental effects is, however, essential for estimating the narrow-sense heritability of SW accurately (Mazer and Gorchov, 1996). This has been typically approached by means of diallel or related breeding designs, in which the differences among paternal families are assumed to be due to additive genetic effects, whereas differences among half-sib maternal families include not only the additive genetic variance but also maternal environment and maternal genetic effects (Schwaegerle and Levin, 1990; Wolfe, 1995; Mazer and Gorchov, 1996; Lipow and Wyatt, 1999). Here, we used an alternative approach based on parental–offspring regression and maternal half-sibs resemblance. Both approaches have been recognized as problematic, as the resemblance of maternal half-sibs may be due to causes other than additive Mendelian genetic variation (Mazer and Gorchov, 1996). For example, the use of mother–offspring regression for estimating heritability of SW mean has been criticized because the maternal environmental effect—usually one of the most important sources of variation of SW (Zas et al., 2013)—can be transmitted through several generations, so that the offspring from mother plants with large seeds may be more vigorous, and, in turn, may also bear large seeds independent of the genotype (Mazer, 1987). Our experimental approach resists this criticism for three reasons. Firstly, although it is well known that big pine seeds lead to bigger seedlings (Castro, 1999), the effect of SW on the offspring is usually limited to early stages and tends to diminish or even disappear at older ages (Vivas et al., 2013). Secondly, and more relevant, both parent and offspring genetic values were estimated in two common garden tests sited in contrasting environmental conditions, thereby increasing the reliability of our results. On the one hand, most environmental maternal effects were successfully accounted for by clonally replicating the parental genotypes in the two contrasting environments (Zas et al., 2013). On the other hand, by replicating each maternal genotype within each macro-environment into several individual copies (ramets) established following a block design, we also accounted for microenvironmental variation within each site, diminishing at the same time the possible interference of the rootstock variation on seed traits (Zas et al., 2013). Thirdly, the seeds used for the establishment of the progeny trials were collected from the original selected trees in which scions were also sampled for vegetative propagation and establishment of the clonal seed orchards. Thus, the parental values of SW were estimated using individual trees different from those in which seeds were collected for the establishment of the progeny trials. Across-generation maternal effects are thus not likely to have influenced our results, although it is acknowledged that they cannot be completely ruled out.
Although we cannot completely discard the idea that observed differences between the maternal half-sibs could be partially due to non-genetic factors such as environmental or genetic maternal effects, the close resemblance between maternal and offspring SW suggests that SW is, in any case, transmitted through generations and thus, the resulting phenotypic variation could respond to selection pressures. There is now increasing evidence that the biological information transmitted from one generation to the next is not limited to the DNA sequence (Jablonka and Raz, 2009). Non-genetic information, including parental effects, can also be inherited across generations, contributing to the resemblance between individuals, and thus to the evolutionary dynamics of populations (Rapp and Wendel, 2005; Bossdorf et al., 2008; Danchin et al., 2011). This has been recently formalized into the term inclusive heritability, which represents the percentage of phenotypic variation that is transmitted across generations irrespective of the mechanisms of transmission, that is, including both genetic and non-genetic inheritance (Danchin et al., 2011). The heritability estimate of SW reported here could therefore to some extent be reflecting an estimation of the inclusive heritability of SW, including both direct additive genetic effects and the transgenerational transmission of other information related to the maternal genotype and the maternal environment. Although our experimental approach suggests that non-genetic effects are likely to be of less relevance than additive genetic effects (see discussion above), the relative contribution of both sources of inheritance should be formally tested as they affect evolutionary dynamics in different ways (Danchin et al., 2011). For example, evolutionary changes due to additive genetic effects are commonly irreversible whereas those due to non-genetic inheritance are not, and ancestral phenotypes could be recovered when the environmental conditions revert (Rapp and Wendel, 2005). The lack of consistence in the reported heritability estimates of SW for crops and wild populations (Silvertown, 1989; Sadras, 2007) may be also related to the degree to which genetic and non-genetic inheritance are experimentally differentiated.
Another interesting result regarding the quantitative genetics of the mean SW in this pine species is the lack of any G × E interaction in both the parental and the offspring series of common garden tests (see also Zas et al., 2013). Despite the large environmental effect, the genetic variation in mean SW remained almost the same in the different environments, with nearly parallel reaction norms across environments. This was especially the case when accounting for cone weight covariation, suggesting that the maternal genotypes actively control the mean SW irrespective of the amount of resources allocated to the cones (Zas et al., 2013). The lack of G × E interactions agrees with other studies in perennial plants that found a high correspondence across years in the relative variation in mean SW among maternal individuals (Castro, 1999; Koenig et al., 2009). These observations have been interpreted as further evidence of a high maternal genetic control of SW (Castro, 1999). It should be noted, however, that the lack of G × E interaction in the present study may be simply due to the selection process of the parental genotypes, that is likely to have reduced the available genetic variation within the studied population (Zas et al., 2013). Additionally, the low number of families analysed may have also favoured a reduced G × E interaction. We cannot discard that increasing the number of families and extending the range of the explored within-population variation, the G × E interaction could become larger.
Within-individual SW variability
Contrary to what was observed for mean SW, within-individual variation in SW showed no genetic variation associated with the maternal lineage. The results were, again, very consistent between the parental and the offspring common garden tests (see also Zas et al., 2013). Although both the maternal genotypes and the half-sibs did not statistically differ in the variation of SW within individual trees, the environmental conditions appeared to have an important effect, with greater variation in the sites least favourable for pine growth, that is, in those sites with the lowest SW mean. Producing seeds of different sizes might be an adaptive strategy to heterogeneous or unpredictable environments in which the optimum seed size is not clearly defined (Castellanos et al., 2008; Charpentier et al., 2012) or, alternatively, may simply be an indirect consequence of the physiological constraints that limit equal provision among all seeds when resources are scarce (Vaughton and Ramsey, 1998).
Variation in SW within individual plants is often among the most substantial sources of intraspecific variation in SW (Vaughton and Ramsey, 1998; Susko and Lovett-Doust, 2000). Our results do not show, however, a high variation in SW within individual trees. From the analyses of the parental common garden tests, within-individual variation in SW (including among and within cone variation) explained around 12% of the total observed phenotypic variation, whereas variation between individuals (including genetic maternal effects and macro and microenvironmental maternal effects) was 88% (Zas et al., 2013). These results suggest that individual trees of this pine species effectively control the mean size of the seeds they produce, and agree with the strong genetic control of mean SW discussed above. On the other hand, both the lower within-individual variation in SW and the lack of genetic differences among half-sibs or among parental genotypes in the variation of seed size within individual trees suggest that within-individual variation in SW has little potential to evolve as an adaptive trait per se.
Data archiving
Data available from the Dryad Digital Repository: doi:10.5061/dryad.60j76.
Acknowledgments
This study was financed by the Spanish National Research Grants RTA2007-100 and AGL2012-40151 (FENOPIN), both co-financed by EU-FEDER. The progeny trials and the clonal seed orchards are part of the experimental set up of the Maritime pine breeding programme developed by the Centro de Investigación Forestal de Lourizán, Xunta de Galicia. We thank César Cendán, Benito Santos, Raúl de la Mata, Enrique Diz, Aurea Pazos, Oscar Vilariño, Bretema Dorado and Montse Peso for their help in field assessment and cone sampling. Rocío Campanó and Luz Pato also helped in SW determinations. We also thank David Brown for language correction, and the comments and suggestions by two anonymous referees, which contributed to improve the manuscript.
The authors declare no conflict of interest.
References
- Banuelos MJ, Obeso JR. (2003). Maternal provisioning, sibling rivalry and seed mass variability in the dioecious shrub Rhamnus alpinus. Evol Ecol 17: 19–31. [Google Scholar]
- Biere A. (1991). Parental effects in Lychnis-Flos-Cuculi. 2. Selection on time of emergence and seedling performance in the field. J Evol Biol 4: 467–486. [Google Scholar]
- Bilir N, Prescher F, Lindgren D, Kroon J. (2008). Variation in cone and seed characters in clonal seed orchards of Pinus sylvestris. New For 36: 187–199. [Google Scholar]
- Blade C, Vallejo VR. (2008). Seed mass effects on performance of Pinus halepensis Mill. seedlings sown after fire. For Ecol Manage 255: 2362–2372. [Google Scholar]
- Bossdorf O, Richards CL, Pigliucci M. (2008). Epigenetics for ecologists. Ecol Lett 11: 106–115. [DOI] [PubMed] [Google Scholar]
- Byers DL, Platenkamp GAJ, Shaw RG. (1997). Variation in seed characters in Nemophila menziesii: Evidence of a genetic basis for maternal effect. Evolution 51: 1445–1456. [DOI] [PubMed] [Google Scholar]
- Carles S, Lamhamedi MS, Beaulieu J, Stowe DC, Colas F, Margolis HA. (2009). Genetic variation in seed size and germination patterns and their effect on white spruce seedling characteristics. Silvae Genet 58: 152–161. [Google Scholar]
- Castellanos MC, Medrano M, Herrera CM. (2008). Subindividual variation and genetic versus environmental effects on seed traits in a European Aquilegia. Botany 86: 1125–1132. [Google Scholar]
- Castro J. (1999). Seed mass versus seedling performance in Scots pine: a maternally dependent trait. New Phytol 144: 153–161. [Google Scholar]
- Castro J, Hódar JA, Gómez JM. (2006). Seed size. In: Basra AS (ed) Handbook of seed science and technology. Haworth Press: New York. pp 397–428. [Google Scholar]
- Crean AJ, Marshall DJ. (2009). Coping with environmental uncertainty: dynamic bet hedging as a maternal effect. Phil Trans Royal Soc B 364: 1087–1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charpentier A, Anand M, Bauch CT. (2012). Variable offspring size as an adaptation to environmental heterogeneity in a clonal plant species: integrating experimental and modelling approaches. J Ecol 100: 184–195. [Google Scholar]
- Danchin E, Charmantier A, Champagne FA, Mesoudi A, Pujol B, Blanchet S. (2011). Beyond DNA: integrating inclusive inheritance into an extended theory of evolution. Nature Rev Genet 12: 475–486. [DOI] [PubMed] [Google Scholar]
- de-Lucas AI, Robledo-Arnuncio JJ, Hidalgo E, González-Martínez SC. (2008). Mating system and pollen gene flow in Mediterranean maritime pine. Heredity 100: 390–399. [DOI] [PubMed] [Google Scholar]
- de Jong TJ, Hermans CM, van der Veen-van Wijk KAM. (2011). Paternal effects on seed mass in Arabidopsis thaliana. Plant Biol 13: 71–77. [DOI] [PubMed] [Google Scholar]
- de la Mata R, Zas R. (2010). Transferring Atlantic maritime pine improved material to a region with marked Mediterranean influence in inland NW Spain: a likelihood-based approach on spatially adjusted field data. Eu J For Res 129: 645–658. [Google Scholar]
- Fry JD. (2004). Estimation of genetic variances and covariances by restricted maximum likelihood using PROC MIXED. In: Saxton AM (ed) Genetic analysis of complex traits using SAS. SAS Institute: Cary, NC. pp 11–34. [Google Scholar]
- Gomaa NH, Xavier Pico F. (2011). Seed germination, seedling traits, and seed bank of the tree Moringa peregrina (Moringaceae) in a hyper-arid environment. Am J Bot 98: 1024–1030. [DOI] [PubMed] [Google Scholar]
- Gomez JM. (2004). Bigger is not always better: Conflicting selective pressures on seed size in Quercus ilex. Evolution 58: 71–80. [DOI] [PubMed] [Google Scholar]
- Halpern SL. (2005). Sources and consequences of seed size variation in Lupinus perennis (Fabaceae): Adaptive and non-adaptive hypotheses'. Am J Bot 92: 205–213. [DOI] [PubMed] [Google Scholar]
- Hanley ME, Cordier PK, May O, Kelly CK. (2007). Seed size and seedling growth: differential response of Australian and British Fabaceae to nutrient limitation. New Phytol 174: 381–388. [DOI] [PubMed] [Google Scholar]
- Holland JB. (2006). Estimating genotypic correlations and their standard errors using multivariate restricted maximum likelihood estimation with SAS Proc MIXED. Crop Sci 46: 642–654. [Google Scholar]
- Holland JN, Chamberlain SA, Waguespack AM, Kinyo AS. (2009). Effects of pollen load and donor diversity on seed and fruit mass in the columnar cactus, Pachycereus schottii (Cactaceae). Int J Plant Sci 170: 467–475. [Google Scholar]
- House C, Roth C, Hunt J, Kover PX. (2010). Paternal effects in Arabidopsis indicate that offspring can influence their own size. Proc Royal Soc B 277: 2885–2893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jablonka E, Raz G. (2009). Transgenerational epigenetic inheritance: prevalence, mechanisms, and implications for the study of heredity and evolution. Quat Rev Biol 84: 131–176. [DOI] [PubMed] [Google Scholar]
- Koenig WD, Knops JMH, Carmen WJ, Sage RD. (2009). No trade-off between seed size and number in the Valley oak Quercus lobata. Am Nat 173: 682–688. [DOI] [PubMed] [Google Scholar]
- Lacey EP, Smith S, Case AL. (1997). Parental effects on seed mass: seed coat but not embryo/endosperm effects. Am J Bot 84: 1617–1620. [PubMed] [Google Scholar]
- Lazaro A, Traveset A. (2009). Does the spatial variation in selective pressures explain among-site differences in seed mass? A test with Buxus balearica. Evol Ecol 23: 847–865. [Google Scholar]
- Lipow SR, Wyatt R. (1999). Diallel crosses reveal patterns of variation in fruit-set, seed mass, and seed number in Asclepias incarnata. Heredity 83: 310–318. [DOI] [PubMed] [Google Scholar]
- Littell RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenberger O. (2006) SAS System for mixed models 2nd edn. SAS Institute: Cary, NC. [Google Scholar]
- Liu J, Bai Y, Lamb EG, Simpson D, Liu G, Wei Y et al. (2013). Patterns of cross-continental variation in tree seed mass in the Canadian boreal forest. Plos One 8: e61060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Walsh B. (1997) Genetics and analysis of quantitative traits. Sinauer Associates, Inc.: Sunderland, Massachusetts, USA. [Google Scholar]
- Matziris D. (1998). Genetic variation in cone and seed characteristics in a clonal seed orchard of Aleppo pine grown in Greece. Silvae Genet 47: 37–41. [Google Scholar]
- Mazer SJ. (1987). The quantitative genetics of life-history and fitness components in Raphanus raphanistrum L (Brassicaceae): Ecological and evolutionary consequences of seed-weight variation. Am Nat 130: 891–914. [Google Scholar]
- Mazer SJ, Gorchov DL. (1996). Parental effects on progeny phenotype in plants: Distinguishing genetic and environmental causes. Evolution 50: 44–53. [DOI] [PubMed] [Google Scholar]
- Metz J, Liancourt P, Kigel J, Harel D, Sternberg M, Tielboerger K. (2010). Plant survival in relation to seed size along environmental gradients: a long-term study from semi-arid and Mediterranean annual plant communities. J Ecol 98: 697–704. [Google Scholar]
- Murray BR, Brown AHD, Dickman CR, Crowther MS. (2004). Geographical gradients in seed mass in relation to climate. J Biogeo 31: 379–388. [Google Scholar]
- Norden N, Daws MI, Antoine C, Gonzalez Mailyn A, Garwood NC, Chave J. (2009). The relationship between seed mass and mean time to germination for 1037 tree species across five tropical forests. Func Ecol 23: 203–210. [Google Scholar]
- Parker WC, Noland TL, Morneault AE. (2006). The effects of seed mass on germination, seedling emergence, and early seedling growth of eastern white pine (Pinus strobus L.). New For 32: 33–49. [Google Scholar]
- Platenkamp GAJ, Shaw RG. (1993). Environmental and genetic maternal effects on seed characters in Nemophila-menziesii. Evolution 47: 540–555. [DOI] [PubMed] [Google Scholar]
- Rapp RA, Wendel JF. (2005). Epigenetics and plant evolution. New Phytol 168: 81–91. [DOI] [PubMed] [Google Scholar]
- Roach DA, Wulff RD. (1987). Maternal effects in plants. Ann Rev Ecol Syst 18: 209–235. [Google Scholar]
- Roff DA. (1997) Evolutionary quantitative genetics. Chapman & Hall: NY. [Google Scholar]
- Roy SM, Thapliyal RC, Phartyal SS. (2004). Seed source variation in cone, seed and seedling characteristic across the natural distribution of Himalayan low level pine Pinus roxburghii sarg. Silvae Genet 53: 116–123. [Google Scholar]
- Sadras VO. (2007). Evolutionary aspects of the trade-off between seed size and number in crops. Field Crop Res 100: 125–138. [Google Scholar]
- Schwaegerle KE, Levin DA. (1990). Quantitative genetics of seed size variation in Phlox. Evol Ecol 4: 143–148. [Google Scholar]
- Silvertown J. (1989). The paradox of seed size and adaptation. Trends Ecol Evol 4: 24–26. [DOI] [PubMed] [Google Scholar]
- Sivacioglu A, Ayan S. (2008). Variation in cone and seed characteristics in a clonal seed orchard of Anatolian black pine [Pinus nigra Arnold subsp pallasiana (Lamb.) Holmboe]. J Environ Biol 31: 119–123. [PubMed] [Google Scholar]
- Sober V, Ramula S. (2013). Seed number and environmental conditions do not explain seed size variability for the invasive herb Lupinus polyphyllus. Plant Ecol 214: 883–892. [Google Scholar]
- Solla A, Aguín O, Cubera E, Sampedro L, Mansilla P, Zas R. (2011). Survival time analysis of Pinus pinaster inoculated with Armillaria ostoyae: genetic variation and relevance of seed and root traits. Eu J Plant Pathol 130: 477–488. [Google Scholar]
- Sorensen FC, Campbell RK. (1993). Seed weight - seedling size correlation in coastal Douglas-fir: genetic and environmental components. Can J For Res 23: 275–285. [Google Scholar]
- Surles SE, White TL, Hodge GR, Duryea ML. (1993). Relationships among seed weight components, seedling growth traits, and predicted field breeding values in slash pine. Can J For Res 23: 1550–1556. [Google Scholar]
- Susko DJ, Lovett-Doust L. (2000). Patterns of seed mass variation and their effects on seedling traits in Alliaria petiolata (Brassicaceae). Am J Bot 87: 56–66. [PubMed] [Google Scholar]
- Vaughton G, Ramsey M. (1998). Sources and consequences of seed mass variation in Banksia marginata (Proteaceae). J Ecol 86: 563–573. [Google Scholar]
- Vivas M, Zas R, Sampedro L, Solla A. (2013). Environmental maternal effects mediate the resistance of Maritime pine to biotic stress. PlosOne 8: e70148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voeller E, Auge H, Prati D, Fischer M, Hemp A, Bossdorf O. (2012). Geographical and land-use effects on seed-mass variation in common grassland plants. Basic App Ecol 13: 395–404. [Google Scholar]
- Wennstrom U, Bergsten U, Nilsson JE. (2002). Effects of seed weight and seed type on early seedling growth of Pinus sylvestris under harsh and optimal conditions. Scan J For Res 17: 118–130. [Google Scholar]
- Willi Y. (2013). The battle of the sexes over seed size: Support for both kinship genomic imprinting and interlocus contest evolution. Am Nat 181: 787–798. [DOI] [PubMed] [Google Scholar]
- Wolfe LM. (1995). The genetics and ecology of seed size variation in a biennial plant, Hydrophyllum appendiculatum (Hydrophyllaceae). Oecologia 101: 343–352. [DOI] [PubMed] [Google Scholar]
- Zas R, Cendán C, Sampedro L. (2013). Mediation of seed provisioning in the transmission of environmental maternal effects in Pinus pinaster. Heredity 111: 248–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zas R, Merlo E, Fernandez-Lopez J. (2004). Genotype x environment interaction in maritime pine families in Galicia, northwest Spain. Silvae Genet 53: 175–182. [Google Scholar]