Abstract
Variation in the environment can induce different patterns of genetic and phenotypic differentiation among populations. Both neutral processes and selection can influence phenotypic differentiation. Altitudinal phenotypic variation is of particular interest in disentangling the interplay between neutral processes and selection in the dynamics of local adaptation processes but remains little explored. We conducted a common garden experiment to study the phenotypic divergence in larval life-history traits among nine populations of the common toad (Bufo bufo) along an altitudinal gradient in France. We further used correlation among population pairwise estimates of quantitative trait (QST) and neutral genetic divergence (FST from neutral microsatellite markers), as well as altitudinal difference, to estimate the relative role of divergent selection and neutral genetic processes in phenotypic divergence. We provided evidence for a neutral genetic differentiation resulting from both isolation by distance and difference in altitude. We found evidence for phenotypic divergence along the altitudinal gradient (faster development, lower growth rate and smaller metamorphic size). The correlation between pairwise QSTs–FSTs and altitude differences suggested that this phenotypic differentiation was most likely driven by altitude-mediated selection rather than by neutral genetic processes. Moreover, we found different divergence patterns for larval traits, suggesting that different selective agents may act on these traits and/or selection on one trait may constrain the evolution on another through genetic correlation. Our study highlighted the need to design more integrative studies on the common toad to unravel the underlying processes of phenotypic divergence and its selective agents in the context of environmental clines.
Introduction
Spatial heterogeneity of environment induces adaptive divergence when each local population can evolve traits that provide a better fitness under local environmental conditions (Kawecki and Ebert, 2004). Local adaptation is expected when spatial variation in natural selection is strong enough to eliminate the deleterious alleles from populations over evolutionary time and to cause advantageous alleles in a given environment to increase (Kawecki and Ebert, 2004). Neutral processes, especially gene flow and genetic drift, can also influence phenotypic differentiation in space (for example, Lande, 1992). Genetic drift drives random loss and fixation of alleles and causes random phenotypic variation among populations that may be confounded with adaptive divergence (Whitlock et al., 2000). Gene flow among populations can influence genetic and phenotypic divergence in different ways (see recent reviews: Orsini et al., 2013; Sexton et al., 2013). Gene flow has often been considered a random and constraining force to local selection because strong gene flow has a homogenizing effect among populations that limits neutral genetic and quantitative differentiation, and thus hinders local adaptation by swamping locally beneficial genes (Lenormand, 2002; Räsänen and Hendry, 2008). However, gene flow can also alleviate the negative effects of genetic drift and provide genetic variation for selection to act upon (Garant et al., 2007). Gene flow is reduced when geographic distance increases between populations because of limitations on organism dispersal. This results in a classic pattern of isolation by distance (IBD) determined by a positive correlation between genetic differentiation among populations and geographic distances (Wright, 1943). Alternatively, when local selection occurs in natural habitats, the resulting adaptive divergence can promote barriers to gene flow between populations from ecologically divergent habitats and result in a positive correlation between adaptive phenotypic and neutral genetic population divergence (isolation by adaptation, IBA; Nosil et al., 2005). Subsequently, IBA may generate asymmetric gene flow among environments because of selection against immigrants or nonrandom gene flow, leading to a positive relationship between environmental differences and population differentiation (isolation by environment pattern, IBE; for example, Nosil et al., 2005; Crispo et al., 2006; Räsänen and Hendry, 2008; Lee and Mitchell-Olds, 2011). The gene flow-(genetic drift)-selection balance can therefore lead to different patterns of genetic and phenotypic differentiation across the mosaic of habitats within the range of species distribution (Gould and Johnston, 1972; Storz, 2002; Vasemagi, 2006). In this context, comparisons of population differentiation at quantitative traits (QST) to differentiation at neutral genetic markers (FST) are particularly useful to disentangle the relative roles of selection, genetic drift and gene flow (Merilä and Crnokrak, 2001; McKay and Latta, 2002; Leinonen et al., 2008; Whitlock, 2008).
Environmental gradients occurring from small to large geographical scales provide opportunities to study local adaption processes in a range of gene flow intensity. In the absence of gene flow (that is, populations are geographically isolated along a gradient), phenotypic divergence can result from adaptation to varying selection; however, a non-negligible proportion of this phenotypic variation may also be an outcome of neutral evolution because of IBD among populations along the gradient (Vasemagi, 2006). In the face of gene flow (small spatial scale), the phenotypic divergence observed along the gradient can result from both selection (when strong enough to counter the homogenizing effect of gene flow) and/or nonrandom gene flow because of IBA (Richter-Boix et al., 2010, 2013). Many studies show phenotypic divergence among populations along environmental gradients (for example, latitudinal gradient: Palo et al., 2003, Antoniazza et al., 2010; environmental stress gradient: Räsänen et al., 2003; Gomez-Mestre and Tejedo, 2004; Hangartner et al., 2011). When conducted as common garden or transplant experiments, these studies provide evidence for a genetic basis for quantitative trait differentiation among populations (Connover and Schultz, 1995). However, few studies have attempted to determine the relative contributions of different processes that contribute to genetic and phenotypic divergence along environmental gradients (but see Antoniazza et al., 2010; Hangartner et al., 2012; Muir et al., 2014).
Altitudinal gradients are especially interesting because environmental transitions occur at a small spatial scale, which limits the confounding effects such as distinct regional evolutionary histories (Keller et al., 2013). Moreover, altitudinal gradients provide an opportunity to investigate how adaptive divergence is possible in the face of gene flow (strong selection and/or nonrandom dispersal) when species dispersal distance is close to the environmental transition scale (Keller et al., 2013). Many studies on plants have shown differences in growth form or leaf morphology associated with the environmental variability along altitudinal gradients (reviewed in Körner, 2003). There have been fewer studies focused on environmental variability in animals, particularly on vertebrates, but the available data show that significant genetic and phenotypic differences among populations are common and taxonomically widespread, involving traits such as growth and development rates, mass, length or longevity (for a recent review, see Keller et al., 2013). Although some studies on plants have conducted QST–FST comparisons on populations along altitudinal gradients (for example, Scheepens et al., 2010; Alberto et al., 2011), they are surprisingly rare and it is difficult to see a clear pattern.
Many amphibians have wide altitudinal distribution range and some studies provide evidence of phenotypic differences along altitudinal gradients (review in Miaud and Merilä, 2001; Morrison and Hero, 2003). Delayed age at maturity at high altitude is common in most species (for example, Oromi et al., 2012) and often associated with a subsequent increase in longevity (for example, Miaud et al., 1999). The intraspecific variation of body size along altitudinal gradients seems to differ among species (Morrison and Hero, 2003; Cvetković et al., 2009). Growth and development rates seem to follow a countergradient pattern (that is, individuals from colder environments grow or develop more slowly in situ, but are able to grow or develop more rapidly than conspecifics from warmer parts of the range when compared in a common garden setting; Conover and Schultz, 1995, Ficetola and De Bernardi, 2005, 2006; Marquis and Miaud, 2008) but exceptions exist (for example, Sommer and Pearman, 2003) and explicit tests of local adaptation are lacking ((Berven, 1982a, 1982b) but see Muir et al., 2014).
The aims of our study were (i) to provide evidence for phenotypic variation and its genetic basis in the common toad Bufo bufo along an altitudinal gradient in France and (ii) to estimate the relative importance of divergent natural selection and neutral genetic processes in trait divergence. The common toad is one of the most widely distributed and abundant anuran species of Europe (Sillero et al., 2014), but there is only one study that has documented the age and growth patterns of adult individuals occurring along an altitudinal gradient (Hemelaar, 1988). We conducted a common garden experiment to compare the quantitative trait differentiation (larval period, metamorphic mass and growth rate) among altitudinal regions (low, medium and high altitudes) and among nine local populations. We performed correlations between population pairwise QSTs (larval life-history traits), FSTs (microsatellite markers), geographic distance and difference in altitude to estimate the relative importance of divergent selection and neutral genetic processes in phenotypic divergence. The difference in altitude between pairwise populations was considered a substitute for a score of environmental variables changing with altitude, most notably season length and temperature (for example, Monty and Mahy, 2009; Scheepens et al., 2010). First, we predicted strong phenotypic divergence among altitudinal regions and particularly faster developmental and growth rates corresponding with increasing altitude (countergradient pattern hypothesis). As fast development in amphibians is usually associated with reduced size at metamorphosis (for example, Wilbur and Collins, 1973; Newman, 1992; Laurila et al., 2002), we expected to find a negative relationship between mass at metamorphosis and altitude. Second, we expected that correlations between QST–FST and difference in altitude (after accounting for geographic distance) should be nonsignificant if phenotypic divergence differentiation is only because of neutral processes, or positive if altitude-mediated selection is driving phenotypic divergence.
Materials and methods
Study species and populations
The common toad B. bufo is a widespread species in Europe, which breeds in a great diversity of wetlands (Loman and Lardner, 2006) and is highly tolerant to various aquatic conditions. This species breeds over a few day period (that is, explosive breeder). The usual altitudinal range for breeding in France is 0–2000 m but some breeding of common toad has been occasionally observed at 2500 m (Sillero et al., 2014).
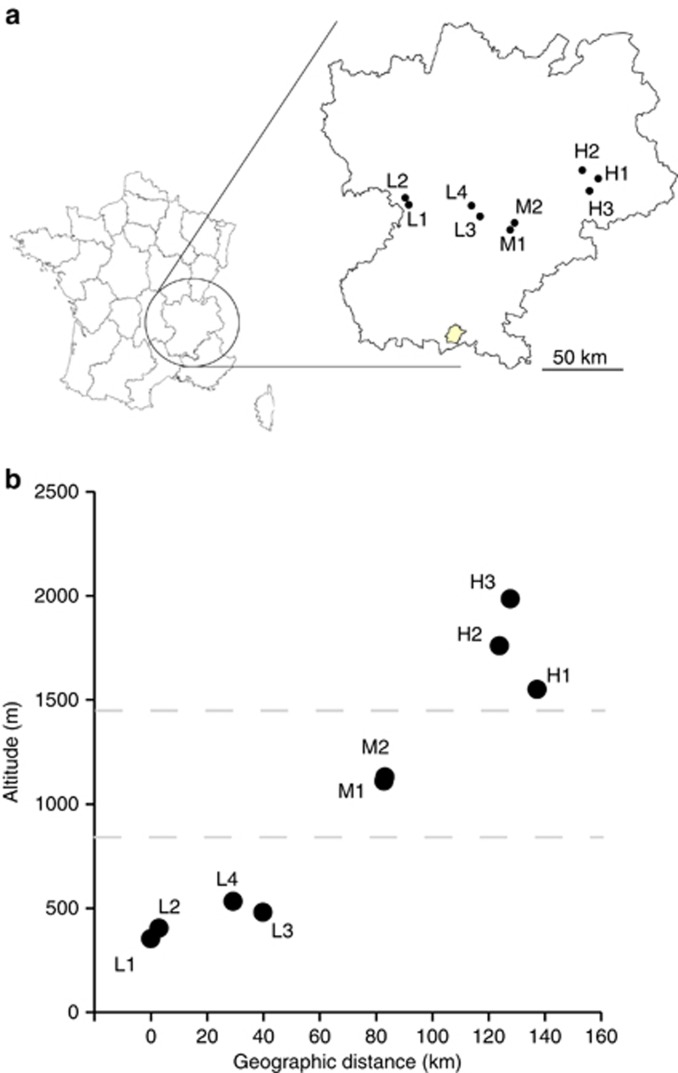
Nine populations were used in this study and were situated at different altitudes from low (<1000 m, four populations, L1–L4) to medium (1000–1500 m, two populations, M1 and M2) and high altitude (>1500 m, three populations, H1–H3) in South-Eastern France (Table 1; Figure 1). The resulting altitudinal gradient was located across several mountains. All our study populations breed in large permanent ponds (max depth<2 m) close to a forested area. The onset of the breeding season between the low- and high-altitude populations differs by ca. 60 days (Table 1).
Table 1. Altitudes and coordinates of ponds, breeding periods and genetic properties of the Bufo bufo study populations.
| Altitude | Population | Altitude (m) | Coordinates | Breeding period |
Microsatellite genotyping |
||
|---|---|---|---|---|---|---|---|
| Sample size (F/M) | HE (s.e.) | AR (s.e.) | |||||
| High | 0.774 (0.016) | 6.018 (0.340) | |||||
| H3 | 1984 | 45°33′08.21″N, 6°32′57.45″E | May | 20 (–/20) | 0.762 (0.040) | 5.343 (0.436) | |
| H2 | 1760 | 45°47′56.04″N, 6°26′09.75″E | May | 10 Clutches | 0.755 (0.077) | 6.429 (0.997) | |
| H1 | 1550 | 45°42′13.74″N, 6°38′47.09″E | May | 8 Clutches | 0.806 (0.055) | 6.281 (0.722) | |
| Medium | 0.797 (0.015) | 6.431 (0.386) | |||||
| M2 | 1130 | 45°11′13.75″N, 5°54′02.91″E | April | 28 (13/15) | 0.812 (0.043) | 6.045 (0.478) | |
| M1 | 1109 | 45°08′26.49″N, 5°52′00.94″E | April | 21 (12/9) | 0.782 (0.028) | 6.817 (0.534) | |
| Low | 0.798 (0.007) | 6.314 (0.172) | |||||
| L4 | 533 | 45°24′49.44″N, 5°16′59.86″E | March | 24 (11/13) | 0.796 (0.032) | 6.820 (0.673) | |
| L3 | 480 | 45°19′21.63″N, 5°22′53.51″E | March | 27 (13/14) | 0.806 (0.031) | 6.057 (0.581) | |
| L2 | 404 | 45°29′09.91″N, 4°53′17.19″E | March | 25 (11/14) | 0.779 (0.044) | 6.149 (0.803) | |
| L1 | 353 | 45°28′05.86″N, 4°54′59.73″E | March | 25 (12/13) | 0.811 (0.027) | 6.230 (0.783) | |
Abbreviations: AR, allelic richness; F/M, number of females and males in the sample; HE, gene diversity.
Figure 1.
(a) Location of the nine B. bufo populations in France. (b) Altitude of the study populations plotted against geographic distances from the L1 population (=0 km).
Microsatellite genotyping and population structure analyses
To investigate molecular genetic variation of the study populations, we collected 20–28 adults per population (for sample size and sex ratio, see Table 1), except in high-altitude H1 and H2 populations where we sampled clutches because no adults were found. For each collected adult, we performed buccal swabs (method according to Pidancier et al., 2003 and Broquet et al., 2007). For the high-altitude H1 and H2 populations, one larva per clutch from 8 to 10 clutches was randomly collected for further genetic analysis. The individuals were genotyped at nine polymorphic microsatellite loci (Bbufμ11, Bbufμ13, Bbufμ15, Bbufμ24, Bbufμ39, Bbufμ47, Bbufμ54, Bbufμ62 and Bbufμ65) according to Brede et al. (2001). Genotyping results were controlled by a secondary analysis on 32 randomly selected individuals. Potential genotyping errors such as presence of null alleles, shuttering and allelic dropouts were analyzed using MICRO-CHECKER 2.2.3 (Van Oosterhout et al., 2004). No evidence for such errors was detected but both Bbufμ11 and Bbufμ62 markers were subsequently removed from the data set because of deviation from Hardy–Weinberg equilibrium in all populations and linkage disequilibrium with other loci, respectively.
Expected and observed heterozygosity, allelic richness, tests for linkage disequilibrium between pairs of loci, and departures from Hardy–Weinberg at all loci were computed in FSTAT 2.9.3 (Goudet, 2001). To estimate neutral genetic differentiation, global and pairwise FSTs were estimated according to Weir and Cockerham's (1984). This method is appropriate for pairwise QST–FST comparisons, because variance among groups is calculated in the same way as for QST (Whitlock, 2008). In addition, we estimated the differentiation statistic DEST between populations (Jost, 2008) and Slatkin's RST (Slatkin, 1995) in response to recent concerns raised about the reliability of FST in highly polymorphic systems (Jost, 2008; Ryman and Leimar, 2009). In contrast to FST, DEST partitions total genetic variance into statistically independent within- and between-population components and thereby guards against deflated differentiation measures that can arise in measures such as to FST if within-population exceeds between-population genetic diversity (Jost, 2008). RST accounts for microsatellite mutation pattern and is better suited than FST when mutation is important relative to migration (Slatkin, 1995; Balloux and Goudet, 2002). We tested whether FST and DEST values deviated significantly from zero by bootstrapping with 1500 permutations and with Bonferroni corrections. To test for a geographic structure of IBD, we analyzed the relationship between the neutral genetic differentiation (FST, DEST or RST) and the logarithm of geographic distance between populations. Significance of the regression was tested by a nonparametric, permutation-based, Mantel test, running 10 000 bootstrap iterations. DEST and RST estimates were computed in DEMEtics R-package (Gerlach et al., 2010) and GENEPOP version 4.0.6 (Rousset, 2008), respectively. All other analyses were conducted in FSTAT 2.9.3 (Goudet, 2001).
Common garden experiment
We conducted a common garden experiment on tadpoles to measure the larval phenotypic divergence along the altitudinal gradient and to calculate QST estimates. To generate experimental tadpoles, we collected adults (adults previously used for genetic sampling) from each population at the onset of the breeding season, formed pairs, and left them to mate for up to 24 h in a climate chamber (17 °C) at Lyon1 University, France. Pairs were held in transparent tanks (17.5 × 33 × 18.5 cm) filled with dechlorinated, aged tap water and vegetation. In addition, we measured the snout-vent length and body mass of females in the four low-altitude populations to investigate maternal effects. We were able to generate 10 clutches per population, except in the high-altitude H1 and H2 populations where we sampled 1–2 days old clutches because no adults were found allowing to limit the environmental effects on embryonic development and the subsequent carry-over effects. Owing to the large difference in the onset of breeding period among populations (Table 1), these clutches were obtained on 23 March 2010, 20 April 2010 and 28 May 2010 for low-, medium- and high-altitude populations, respectively. All clutches were separately reared under standard laboratory conditions and consistent with conditions encountered in the wild (constant 17 °C with 12:12-h light–dark cycles) in 10 l plastic tanks until hatching.
When tadpoles reached Gosner stage 25 (complete gill absorption and initiation of independent feeding, Gosner, 1960; day 0 of the experiment), three were randomly selected from each clutch for each population and transferred to individual Nunc 75 cm2-Easy Flasks (250 ml, NUNC A/S, Roskilde, Denmark) containing tap water, to allow them to develop. The tadpoles were fed ad libitum (that is, uneaten food left after each feeding) every 2 days with mixed spinach. Water was completely changed every fourth day before feeding.
Starting from 20 days from the initiation of the experiment, the containers were checked at least twice a day for metamorph detection. At metamorphosis (defined as the emergence of the first forelimb: Gosner stage 42), the individuals were removed from the containers and weighed to the nearest 0.1 mg with an electronic balance (mass at metamorphosis). Length of larval period was defined as days elapsed from the start of the experiment (day 0) to metamorphosis. Average individual growth rate (mg day−1) was defined as the ratio of mass at metamorphosis/larval period.
Statistical and quantitative genetic analyses
The effect of altitude of populations on larval life-history traits (larval period, metamorphic mass and growth rate) was analyzed using linear mixed models with restricted maximum likelihood estimation and Kenward and Roger's approximation for degrees of freedom (Pinheiro and Bates, 2000). In these analyses, altitudinal region (low, medium and high altitude) was included as a fixed factor, population (nested within altitudinal region) and clutch (nested within population and altitudinal region) were considered as random effects. Differences among groups were analyzed using the contrast method.
The relative importance of neutral processes and natural selection on the evolution of life-history traits in populations located along the altitudinal gradient was evaluated by comparing population differentiation at quantitative traits (QST) and neutral genetic markers (FST). FST is a metric of population differentiation at neutral genetic markers (Weir and Cockerham, 1984) and QST is its analog of genetic differentiation at quantitative traits (Wright, 1951; Spitze, 1993; Whitlock, 2008). Comparing QST with other indices of neutral divergence (for example, DEST or RST) is not advised, because these indices are not theoretically equivalent to QST (Edelarr et al., 2011). Selection affects regions harboring the quantitative trait loci underlying the phenotypic trait and the nearby regions, while neutral processes have an equal effect all over the genome. If selection causes divergent evolution of phenotypes among populations, because selection is exerted on either quantitative traits measured or on genetically correlated traits, phenotypic differentiation is expected to exceed neutral differentiation (that is, QST>FST). A lack of significant differences (that is, QST=FST) means that the relative effects of neutral processes and selection on population differentiation cannot be separated, and lower divergence (that is, QST<FST) is evidence for stabilizing selection (for example, Raymond and Rousset, 1995; Merilä and Crnokrak, 2001). The population structure for phenotypic traits was estimated as (Spitze, 1993; O'Hara and Merilä, 2005):
QST trait=Vb/(2Vw+Vb), where Vb is the between population genetic variance and Vw the within-population genetic variance. The variance components were calculated for each trait by conducting mixed model analyses separately for each population pair. In these models, population and clutch (nested within population) were included as random factors; the random clutch factor was allowed to account for relatedness of individuals within clutches. Vb was obtained directly from the estimated variance component for the population effect (between populations) and the within-population variance (Vw) was estimated using the among family variance component (Vf) and multiplied by 2 (Vw=2 Vf) as we used a full-sibling design (Roff, 1997). When a population pairwise was not statistically significant (Vb=0), the QST estimate was considered as null. When the random effect of clutch was not significant (Vw=0), the QST estimate was considered as equal to 1. The environmental source of phenotypic variance that can bias QST estimates was excluded because our data were obtained from a common garden experiment (Pujol et al., 2008). A potential limitation in our study was that it used only full-sib data from F1 offspring and the QST estimates were broad sense estimates of genetic variance and may therefore be influenced by non additive genetic and maternal sources of variance (Lynch and Walsh, 1998; Whitlock, 1999; Merilä and Crnokrak, 2001; Goudet and Buchi, 2006). All mixed model analyses were done in JMP 7.0 (SAS Institute, Cary, NC, USA).
First, we tested the null hypothesis that there was no difference between the QST for each trait and the QST expected for a neutrally evolving trait using the approach of Whitlock and Guillaume (2009). This approach considers that the proper null hypothesis to test is to compare the estimated QST with the distribution of possible values of QST expected under neutrality. We estimated the predicted sample variance for QST of a neutral trait by simulating it with information on FST (using neutral markers) and the within-population additive variance for the trait analyzed. Using the R-script provided by Richter-Boix et al. (2013) and developed by Lind et al. (2011), we tested whether the (QST–FST) of each trait differed from the neutral expectations. To estimate significance, we calculated the expected among-population variance component for a neutral trait using the observed values of FST and the within-population variance (see Equation (4) in Lind et al., 2011). QST of a neutral trait was estimated using the measured within-population variation and the expected among-population variation. The difference between both statistics (QST–FST) was simulated 50 000 times to create a distribution of neutral trait to compare the observed QST–FST. Giving that FST using neutral markers should be similar to QST for a neutral trait, QST–FST can be used as a test statistic, where the observed QST–FST difference is compared with the 95% distribution of the simulated (QST–FST) values (Lind et al., 2011; Richter-Boix et al., 2013).
Second, we used the approach by Antoniazza et al. (2010) and Hangartner et al. (2012), where pairwise estimates of FST and QST are correlated with geographic distance and environmental differences (altitude) between-population pairs. This approach is based on Mantel tests and partial Mantel tests, which allow analyses of association patterns between distance matrices (Castellano and Balletto, 2002). The first step determines if neutral genetic differentiation explains divergence in quantitative traits by examining correlations between pairwise FSTs and QSTs. The second step estimates the effect of environmental differences (here difference in altitude) on phenotypic differentiation by analyzing the correlations between pairwise QSTs with the matrix of difference in altitude. The final step tests if phenotypic divergence is more likely driven by divergent selection or neutral processes in correlating the matrix of pairwise differences between QST and FST (QST–FST) with the matrix of environmental differences (Antoniazza et al., 2010; Hangartner et al., 2012). QST and FST are supposed to be identical under the null hypothesis of absence of divergent selection on phenotype. This method removes the neutral genetic component from the phenotypic differentiation and to test if correlation between phenotypic differentiation (accounting for neutral genetic divergence) and environmental distance remains. When the two matrices are uncorrelated, phenotypic differentiation is only due to neutral processes. In contrast, a positive correlation between them would strongly indicate that selection by an environmental factor is driving phenotypic divergence (Antoniazza et al., 2010; Hangartner et al., 2012). This approach provides a robust test of gradually varying selection because comparing pairwise FST and QST with environmental differences does not depend on the absolute values of phenotypic and genetic divergence but on the slopes of the respective regressions (Antoniazza et al., 2010). All Mantel tests were performed separately for the three phenotypic traits using 10 000 permutations in the FSTAT 2.9.3 program (Goudet, 2001).
In addition, we performed spatial autocorrelation analyses through non-directional Mantel correlograms to determine at which altitude difference the quantitative traits were significantly similar or dissimilar between-population pairs (Legendre and Legendre, 2012). This method computes an appropriate resemblance matrix among populations on the basis of the quantitative trait data (here phenotypic differentiation accounting for neutral genetic divergence, QST–FST), and for each class of difference in altitude. This matrix was compared using simple Mantel tests with 10 000 permutations to a model matrix where pairs of populations belonging to the same distance class received value 1 and other pairs received value 0 (Borcard and Legendre, 2012). The Mantel correlogram plotted Mantel's r values over classes of difference in altitude between-population pairs, with a 95% confidence interval (CI) determined by bootstrap resampling (1000 iterations). The Mantel correlograms were generated using the mgram() function in the ecodist package (Goslee and Urban, 2007) in R (R Development Core Team, 2010).
Results
Neutral genetic differentiation
A total of 188 individuals from nine populations were genotyped at seven microsatellite loci (two markers of the initial set of nine microsatellites were rejected). Levels of expected heterozygosity within populations ranged from 0.75 to 0.81 and allelic richness from 5.34 to 6.82 (Table 1). Gene diversity (P=0.26) and allelic richness (P=0.60) were all similar among altitudinal regions (Table 1).
The overall FST was 0.046 (95% CI=0.035–0.062; P<0.001) and revealed significant genetic differentiation among the nine populations. The FSTs for each altitudinal region were all similar (low: FST=0.024, medium: FST=0.011, high: FST=0.077; P=0.17). Pairwise FSTs between populations ranged from 0.003 to 0.115 (Supplementary Table S1), and were significantly different from 0 except for 7 out of 36 populations pairs (Supplementary Table S1). The overall DEST (0.215, 95% CI=0.185–0.248; P<0.001) and RST (0.104) were higher than the overall FST (0.046). Pairwise DESTs ranged from 0.047 to 0.461 (Supplementary Table S1) and were significantly correlated with FSTs (Supplementary Figure S1; Mantel's r=0.92, P<0.001). Pairwise RSTs ranged from −0.025 to 0.429 (Supplementary Table S1) and were significantly correlated with FSTs (Supplementary Figure S1; Mantel's r=0.33, P=0.048).
Pairwise FSTs were positively correlated with difference in altitude (Supplementary Figure S2; Mantel's r=0.51, P<0.001) and geographic distance (Supplementary Figure S2; Mantel's r=0.39, P<0.001). Similar patterns of differentiation for DEST and RST (marginally significant) were found with difference in altitude (Supplementary Figure S2; Mantel's r=0.53, P=0.008 and Mantel's r=0.33, P=0.05, respectively) and geographic distance (Supplementary Figure S2; Mantel's r=0.44, P=0.007 and Mantel's r=0.29, P=0.08, respectively). The IBD pattern likely arose because of the strong correlation between difference in altitude and geographic distance (Figure 1b; Mantel's r=0.90, P<0.001). Partial mantel tests revealed that the neutral divergence among these populations is more strongly a result of difference in altitude than geographic distance (FST: partial Mantel's raltitude=0.50, P<0.001 and rgeo. distance=−0.15, P=0.39; DEST: raltitude=0.52, P<0.001 and rgeo. distance=−0.08, P=0.61; RST: raltitude=0.33, P=0.05 and rgeo. distance=−0.005, P=0.97). Only FST was used in the following analyses, as it is statistically directly comparable to QST (Whitlock, 2008).
Divergence in larval life-history traits
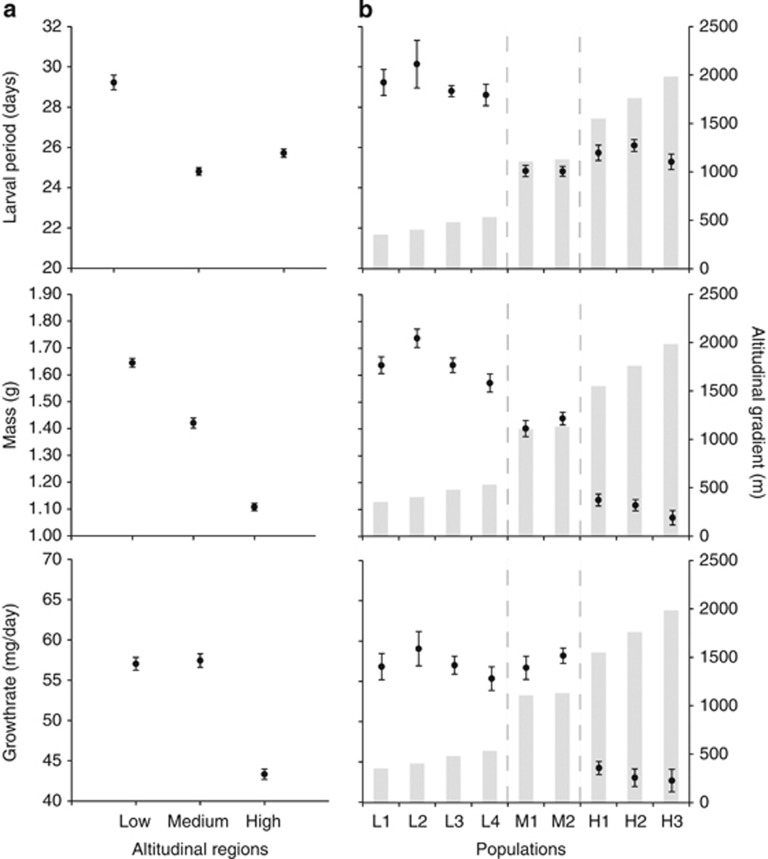
The length of larval period differed with the altitudinal regions (Table 2; Figure 2a). The larvae from medium and high altitudinal populations had similar lengths of larval period (contrast method, t5.26=−1.79, P=0.13) and had about 15% (ca. 4 days) shorter larval periods than those from the low-altitude populations (contrast method, medium altitude: t5.27=9.13, P<0.001; high altitude: t5.54=8.11, P<0.001). Within altitudinal regions, the local populations had similar lengths of larval period (Table 2; Figure 2b).
Table 2. Results of mixed model ANOVAs on the effects of altitudinal status, population (nested within altitudinal status) and clutch (nested within population and altitudinal status) on larval quantitative traits (larval period, mass at metamorphosis and growth rate).
| Fixed effect |
Larval period |
Mass at metamorphosis |
Growth rate |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| df | Dendf | F | P-value | df | Dendf | F | P-value | df | Dendf | F | P-value | |
| Altitudinal status | 2 | 5.37 | 54.05 | <0.001 | 2 | 5.84 | 85.35 | <0.001 | 2 | 5.38 | 121.93 | <0.001 |
| Random effects | Var | Var (s.e.) | Z | P- value | Var | Var (s.e.) | Z | P- value | Var | Var (s.e.) | Z | P- value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Population (altitude status) | 0.00047 | 0.202 | 0.002 | 0.50 | 1799.41 | 1715.06 | 1.05 | 0.15 | 0.94 | 1.01 | 0.93 | 0.18 |
| Clutch (Pop[altitudinal status]) | 0.503 | 0.607 | 0.83 | 0.20 | 4895.57 | 1937.46 | 2.53 | 0.006 | 9.14 | 4.40 | 2.08 | 0.02 |
Abbreviation: ANOVAs, analyses of variance.
Bold values indicate significant effects.
Figure 2.
Mean and 1±s.e. of larval life-history traits (larval period, metamorphic mass and growth rate) from each (a) altitudinal regions (low, medium and high altitude) and (b) populations along the altitudinal gradient. Altitude of populations is shown as gray bars.
The mass at metamorphosis significantly decreased according to altitude (Table 2; Figure 2a). The tadpoles from the low-altitude populations were 14% and 33% heavier than the tadpoles from medium- and high-altitude populations, respectively (contrast method, medium altitude: t5.79=4.85, P=0.003; high altitude: t5.89=13.06, P<0.001). The medium-altitude populations had 22% heavier tadpoles than those from high-altitude populations (contrast method, t5.81=6.37, P<0.001). Within altitudinal regions, there was no difference in mass at metamorphosis among local populations (Table 2; Figure 2b).
There was a significant variation in growth rate among the altitudinal regions (Table 2; Figure 2a). Although the populations from high altitude had a lower growth rate relative to medium-altitude populations (contrast method, t5.28=12.50, P<0.001), the latter had a similar growth rate to the low-altitude populations (contrast method, t5.23=−0.42, P=0.76). The growth rate did not vary among local populations within altitudinal regions (Table 2; Figure 2b).
Comparisons of neutral genetic and quantitative trait differentiation
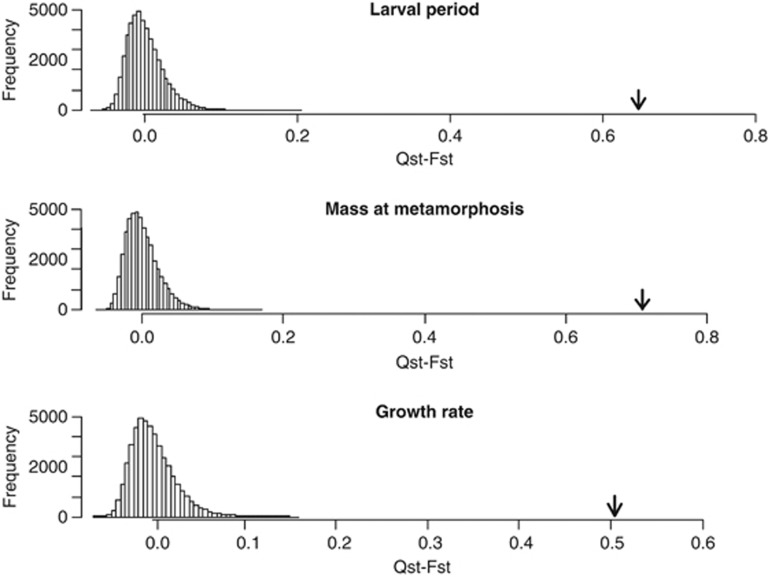
The overall differentiation among populations was higher for quantitative traits than for neutral markers. Divergence in the three larval life-history traits was about 15 times higher for larval period (QST=0.69, P(QST>FST)<0.001; Figure 3), about 16 times for metamorphic mass (QST=0.76, P(QST>FST)<0.001; Figure 3) and about 12 times for growth rate (QST=0.55, P(QST>FST)<0.001; Figure 3) than FST (0.046). Pairwise FSTs were not correlated with pairwise QST for larval period (Table 3) and were marginally correlated with pairwise QSTs for metamorphic mass and growth rate (Table 3).
Figure 3.
QST–FST comparison for the life-history traits measured: larval period, mass at metamorphosis and growth rate. The arrows indicate the point estimate for the difference between both statistics (QST–FST). Histograms represent the distribution of the 50 000 simulated (QST–FST) values for a neutral trait.
Table 3. Mantel tests for correlations between-population pairwise Q STs for the three quantitative traits (larval period, metamorphic mass and growth rate), difference in altitude and geographic distance.
|
Matrix 1 |
Matrix 2 |
|||
|---|---|---|---|---|
| Dependent matrix | Trait | Independent matrix | r | P-value |
| QST | Larval period | FST | 0.08 | 0.64 |
| Altitude difference | 0.71 | <0.001 | ||
| Geo. distance | 0.68 | <0.001 | ||
| Mass | FST | 0.28 | 0.09 | |
| Altitude difference | 0.80 | <0.001 | ||
| Geo. distance | 0.83 | <0.001 | ||
| Growth | FST | 0.29 | 0.09 | |
| Altitude difference | 0.60 | <0.001 | ||
| Geo. distance | 0.66 | <0.001 | ||
Matrix 1 is the dependent variable (QST), whereas matrix 2 is the independent variable (FST, difference in altitude or geographic distance).P-value <0.05 are indicated in bold font.
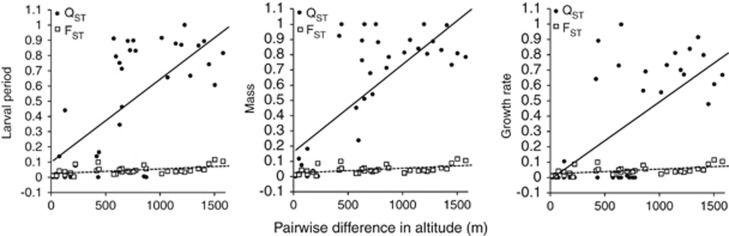
The linear regressions of pairwise QSTs for all traits against pairwise difference in altitude between populations revealed a strong differentiation in quantitative traits along the altitudinal gradient (Figure 4; Table 3).
Figure 4.
Pairwise quantitative trait (QST) divergence of larval period, metamorphic mass and growth rate and neutral genetic (FST) divergence between population pairs plotted against pairwise differences in altitude (m). FST are shown as open squares, QST as filled circles.
Phenotypic differentiation after accounting for neutral genetic divergence
For all larval traits, the QST–FST matrix was more strongly correlated with difference in altitude than with geographic distances, suggesting that the altitudinal effect on larval trait differentiation holds when eliminating the baseline level of differentiation resulting from historical and demographic factors (Table 4).
Table 4. Partial Mantel tests for correlation between Q ST and F ST matrices for each quantitative trait, difference in altitude and geographic distance.
|
Matrix 1 |
Matrix 2 |
Matrix 3 |
|||||
|---|---|---|---|---|---|---|---|
| Dependent matrix | Trait | Independent matrix | r | P-value | Independent matrix | r | P-value |
| QST–FST | Larval period | Altitude difference | 0.68 | <0.001 | Geo. distance | 0.10 | 0.54 |
| Mass | Altitude difference | 0.78 | <0.001 | Geo. distance | 0.26 | 0.12 | |
| Growth | Altitude difference | −0.58 | <0.001 | Geo. distance | 0.28 | 0.10 | |
Matrix 1 is the dependent variable (QST), whereas matrices 2 and 3 are the independent variables (difference in altitude and geographic distance).P-value <0.05 are indicated in bold font.
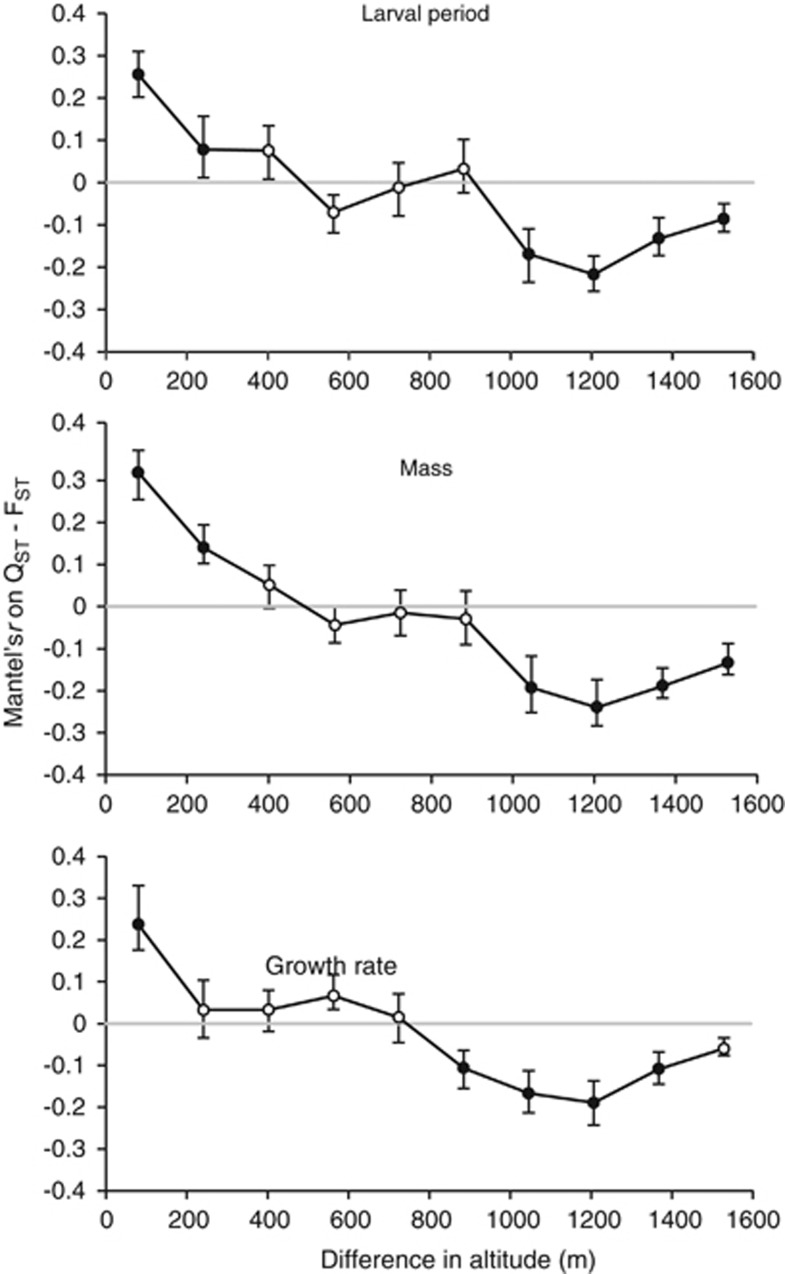
The Mantel correlograms showed the correlations of the QST–FST matrix with altitude difference classes and revealed significant phenotypic similarity (r>0) and dissimilarity (r<0) according to the difference in altitude between populations (Figure 5). For larval period and metamorphic mass, the correlograms showed significant phenotypic similarity when the difference in altitude among populations is <200 m, no significant correlations between ca 400 and 900 m, and significant phenotypic dissimilarity when the altitude differs by ca. 1000 m among populations (Figure 5). The growth rate was significantly similar among populations localized <100 m of difference in altitude apart and significantly dissimilar among populations that differ by ca. 900 m in altitude (Figure 5).
Figure 5.
Correlations of the QST–FST matrix with altitude difference classes (m, defined according to the Sturge's rule) using Mantel correlogramms. The Mantel correlogram plotted Mantel's r values over classes of difference in altitude between pairwise populations, with a 95% CI determined by bootstrap resampling (1000 iterations). Significant Mantel's r are as shown as filled symbols.
Discussion
Clinal phenotypic variation is of particular interest in disentangling the interplay between neutral processes and selection in the dynamics of local adaptation processes. We provided evidence for (i) both IBD and altitude structuring neutral genetic differentiation, (ii) strong phenotypic divergence among altitudinal regions of B. bufo populations in a common-garden setting, suggesting a genetic basis for phenotypic differentiation and (iii) altitude-mediated divergent selection driving this divergence in life-history traits.
Evidence for adaptive divergence
In our study, divergence in FSTs was weak, but showed both significant IBD patterns and differentiation according to altitude, indicating that neutral genetic processes can drive divergence among populations. We found further a positive relationship between FSTs and altitudinal difference after accounting for geographical distance. The same relationships were consistently found using the other indices of genetic differentiation (Jost's DEST and Slatkin's RST). This finding that neutral differentiation depends on environmental differences is in agreement with the IBE pattern (that is, heterogeneous gene flow among environments; Sacks et al., 2008; Méndez et al., 2010). However, it seems difficult to disentangle this pattern from IBD in our system. Although some populations not sampled along the altitudinal gradient could allow stepwise genetic exchange, most geographical distances among altitudinal regions were higher than individual dispersal capacity of common toad (maximum dispersal distance estimated is 3–4 km; Smith and Green, 2005) and could limit the gene flow along the altitudinal gradient. Both IBD and IBE patterns are likely involved in structuring the neutral genetic differentiation among populations along altitudinal gradient.
QST–FST comparisons provide a powerful means for inferring the relative role of divergent selection and neutral process in phenotypic diversification (Whitlock, 2008), particularly when environmental differences and geographic distance are positively correlated. A potential limitation of our study is that we cannot totally discard that broad sense QST estimates (full-sibling families) are not biased by maternal or nonadditive effects. Although the maternal effects seem relatively weak (no relationship between female body size and larval life-history traits; Supplementary Figure S3; Supplementary Table S2), other sources of maternal effects are possible and are not accounted for here (for example, Laugen et al., 2002). However, we can consider that our QST estimates for larval traits are likely conservative because the nonadditive effects do not seem to introduce strong bias to QST–FST comparisons (Whitlock, 2008).
QST–FST comparisons showed a higher degree of population differentiation for all quantitative traits as compared with neutral marker loci. Our study further showed that quantitative trait divergence along the altitudinal gradient is more strongly correlated with differences in altitude than with neutral genetic divergence, meaning that the altitudinal effect on larval trait differentiation holds when eliminating the baseline level of differentiation resulting from neutral processes. These several lines of evidence demonstrate that altitude-mediated selection has a major role in phenotypic differentiation in this system and corroborate amphibian quantitative genetic studies showing significant additive genetic variance components and heritabilities in length of larval period and size at metamorphosis (for example, Berven and Gill, 1983; Berven, 1987; Travis et al., 1987; Newman, 1988; Blouin, 1992; Semlitsh, 1993; Laurila et al., 2002). Incorporating measurements of environmental variation into QST–FST comparisons (genotype-by-environment interactions) could improve our inferential power about the agents of natural selection in this system (Hangartner et al., 2012).
This adaptive divergence may have generated selection on both divergent habitat preference and/or reproductive timing that can lead to IBE patterns observed in our study (Rundle and Nosil, 2005). Theoretical studies have indeed shown that IBE can result from strong selection in the whole or in large parts of the genome, especially when assortative mating mechanisms occur (mate choice, differences in reproductive timing or habitat choice; Thibert-Plante and Hendry, 2009, 2010, 2011). In addition to geographical distance, such a divergence in habitat preference and reproductive timing may in turn constrain the gene flow among populations along the gradient and contribute to the maintenance of local adaptation (IBA; Nosil et al., 2005). This should result in a positive correlation between adaptive phenotypic and neutral genetic population divergence. We found only marginal correlations between quantitative and neutral differentiation for mass and growth rate and a nonsignificant relationship for development rate. Although these results seem consistent with the IBA process, the relative importance of IBD and IBA cannot be evaluated in our biological system because the selection gradient is uni-dimensional and all these factors act in the same direction. Moreover, altitude difference between populations is a rough proxy of environmental difference along altitudinal gradient because it captures both ecological and space variation. In the case of common toads, the breeding habitat choice in altitude could be limited because lowland ponds probably are beyond the migration distance. A powerful approach to disentangle these processes is to investigate this correlation at a local scale where the selective agent is not correlated with geographic distances, preventing IBD within the area (Richter-Boix et al., 2013).
Local adaptation to altitude
Local adaptation is expected to arise because of fitness trade-offs among contrasting environments. In particular, growth and development of tadpoles are limited by time constraints imposed by habitat duration, seasonality or other climatic factors (Wilbur and Collins, 1973; Rowe and Ludwig, 1991; Laurila et al., 2002). We show a strong divergence in larval life-history traits along the altitudinal gradient and provide evidence that an altitude-mediated selection was driving this phenotypic variation. Tadpoles from medium- and high-altitude populations developed faster (shorter larval period) but grew slower (in high altitude) and metamorphosed at a smaller size in common garden. The higher development rate counteracts the effects of colder temperatures and shorter growth season in altitude (that is, genetic and environmental influences on phenotypes oppose one another). Selection for fast-developing genotypes in altitude increases the probability that metamorphosis is reached before the environmental conditions deteriorate. We noted that the length of larval period was similar in medium and high altitude (altitude difference of ca. 900 m). This result could mean that the strength of divergent selection may not be different enough between medium and high altitudes to drive differentiation in development rate or that there are constraints for the maximum development rate (Porcher et al., 2004; Hangartner et al., 2012; Muir et al., 2014). The autocorrelogram shows that a significant differentiation in larval period should indeed occur in our system when the difference in altitude is at least 1000 m. Such a countergradient variation pattern has been already demonstrated in various organisms, including amphibians, especially along latitudinal gradient (review in Conover et al., 2009). However, some amphibian studies have provided evidence also for a countergradient variation in growth rate (for example, Berven and Gill, 1983; Lindgren and Laurila, 2005, 2009; Laurila et al., 2008; Orizaola et al., 2010; Muir et al., 2014), which is not the case in our study. The growth rate was slower only in high altitude and metamorphic mass was gradually reduced with increasing altitude. These different patterns of phenotypic variation between larval growth and development along the altitudinal gradient can arise because both selection from different sources acts on these traits and/or a trade-off occurs between larval period length and metamorphic size. Indeed, we show that differentiation in development rate occurred between low and medium/high altitude, while the growth rate differentiation arose from high altitude. This suggests that selection contribution to these traits acts at different spatial scales, perhaps because of different selective agents. Our study does not determine the specific selective agents contributing to these divergences. However, we can suggest that divergence in larval period duration is most closely related to seasonal factors constraining the time of development, while a putative selective agent on growth rate may be predation (possibly in combination with other pond characteristics). Increased predation risk of fast-growing phenotypes is considered as a major cost of fast growth (Dmitriew, 2011) and has been demonstrated in anuran populations: high activity level of fast-growing individuals exposes them to predation (Laurila et al., 2006, 2008). Hangartner et al. (2012) found evidence in R. arvalis populations, located along both acidification and latitudinal gradients, that growth rate was positively related to predator densities, while larval period was negatively related to latitude. Future work is essential to track the detailed selective agents involved in the process of local adaptation to B. bufo in altitude (investigation of the genotype-by-environment interactions in QST–FST comparisons).
In addition, we show that fast-developing genotypes reached smaller size at metamorphosis. Although we cannot totally exclude the possibility that maternal effects drive size at metamorphosis in altitude, it seems unlikely because larger individuals are usually observed in altitudes (for B. bufo: Hemelaar, 1988; Miaud and Merilä, 2001; Morrisson and Hero, 2003) that should instead lead to larger offspring and no further maternal effects have been detected in low-altitude populations (Supplementary Figure S1; Supplementary Table S2). Smaller sizes of fast-developing genotypes instead suggests a negative genetic correlation between these traits, and then a fitness cost to develop faster because large size at metamorphosis generally confers higher fitness through improved juvenile survival (for example, Berven, 1990; Goater, 1994; Altwegg and Reyer, 2003) and higher adult reproductive success (for example, Scott, 1994; Altwegg and Reyer, 2003). Although this trade-off can arise from a selection against fast development in altitude, it may also contribute to the growth rate divergence along altitudinal gradient. The altitude-mediated divergent selection on development rate can indirectly drive differentiation in metamorphic mass through this trade-off. In this study, we cannot disentangle whether the growth rate divergence along altitudinal gradient results from selection against fast-growing individuals in altitude or an indirect effect via the trade-off between larval period and metamorphic size. It is likely that both these processes may simultaneously occur in our system and need to be unraveled in future studies.
Conclusion
Our study showed that IBD and IBE may likely act in concert to structure neutral genetic differentiation among populations along an altitudinal gradient. We found evidence for phenotypic divergence along the altitudinal gradient (faster development, lower growth rate and smaller metamorphic size). Correlations between pairwise QSTs and FSTs suggested that this phenotypic differentiation was most likely driven by divergent natural selection rather than by neutral genetic processes. The different divergence patterns of larval traits along altitudinal gradient indicates that different selective agents may act on these traits and/or selection on a trait may constraint the evolution on another through genetic correlation. These processes have yet to be unraveled in the context of altitudinal gradients. Finally, our study highlights how organisms locally adapt their timing of critical life-history stages to seasonal variation using an environmental gradient, which is becoming urgent in the context of climate change. However, the genetic basis underlying such adaptations is still relatively unknown. With the advent of molecular techniques, a future path of research will tracking down life-history trait evolution to the molecular level, while investigating the genetic basis of adaptation to seasonal variation and how natural selection shapes these adaptive genetic traits.
Data archiving
Data available from the Dryad Digital Repository: doi:10.5061/dryad.7fj38.
Acknowledgments
Funding for this study was provided by grants from the Conseil Général de l'Isère (JPL and SP). Thanks to A Appelgren, B Achard, M-L Carpentier, V Dumont, C Pigeard and J Devillechabrolle for their help during field and lab work and A Valentini for help on the molecular analyses. We also thank A Laurila, A Richter-Boix, G Orizaola, GF Ficetola and two anonymous reviewers for providing valuable comments on the manuscript and P Muralidhar, a native English speaker, for helping with text editing. This study was conducted with the approval of Préfecture de l'Isère, in accordance with the current laws in France and under the approval of the Direction of Veterinary Services (DSV permit no. 692661232).
The authors declare no conflict of interest.
Footnotes
Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)
Supplementary Material
References
- Alberto F, Bouffier L, Louvet JM, Lamy JB, Delzon S, Kremer A. (2011). Adaptive responses for seed and leaf phenology in natural populations of sessile oak along an altitudinal gradient. J Evol Biol 24: 1442–1454. [DOI] [PubMed] [Google Scholar]
- Altwegg R, Reyer HU. (2003). Patterns of natural selection on size at metamorphosis in water frogs. Evolution 57: 872–882. [DOI] [PubMed] [Google Scholar]
- Antoniazza S, Burri R, Fumagalli L, Goudet J, Roulin A. (2010). Local adaptation maintains clinal variation in melanin-based coloration of European barn owls (Tyto Alba). Evolution 64: 1944–1954. [DOI] [PubMed] [Google Scholar]
- Balloux F, Goudet J. (2002). Statistical properties of population differentiation estimators under stepwise mutation in a finite island model. Mol Ecol 11: 771–783. [DOI] [PubMed] [Google Scholar]
- Berven KA. (1982. a). The genetic basis of altitudinal variation in the wood frog Rana sylvatica. I. An experimental analysis of life history traits. Evolution 36: 962–983. [DOI] [PubMed] [Google Scholar]
- Berven KA. (1982. b). The genetic basis of altitudinal variation in the wood frog Rana sylvatica. II. An experimental analysis of larval development. Oecologia 52: 360–369. [DOI] [PubMed] [Google Scholar]
- Berven KA. (1987). The heritable basis of variation in larval developmental patterns within populations of the wood frog (Rana sylvatica). Evolution 41: 1088–1097. [DOI] [PubMed] [Google Scholar]
- Berven KA. (1990). Factors affecting population fluctuations in larval and adult stages of the wood frog (Rana sylvatica). Ecology 71: 1599–1608. [Google Scholar]
- Berven KA, Gill DE. (1983). Interpreting geographic variation in life history traits. Am Zool 23: 85–97. [Google Scholar]
- Blouin MS. (1992). Genetic correlations among morphometric traits and rates of growth and differentiation in the green frog, Hyla cinerea. Evolution 46: 735–744. [DOI] [PubMed] [Google Scholar]
- Borcard D, Legendre P. (2012). Is the Mantel correlogram powerful enough to be useful in ecological analysis? A simulation study. Ecology 93: 1473–1481. [DOI] [PubMed] [Google Scholar]
- Brede EG, Rowe G, Trojanowski J, Beebee TC. (2001). Polymerase chain reaction primers for microsatellite loci in the Common Toad Bufo bufo. Mol Ecol Notes 1: 308–310. [Google Scholar]
- Broquet T, Berset-Braendli L, Emaresi G, Fumagalli L. (2007). Buccal swabs allow efficient and reliable microsatellite genotyping in amphibians. Cons Genet 8: 509–511. [Google Scholar]
- Castellano S, Balletto E. (2002). Is the partial Mantel test inadequate? Evolution 56: 1871–1873. [DOI] [PubMed] [Google Scholar]
- Conover DO, Schultz ET. (1995). Phenotypic similarity and the evolutionary significance of countergradient variation. Trends Ecol Evol 10: 248–252. [DOI] [PubMed] [Google Scholar]
- Conover DO, Duffy TA, Hice LA. (2009). The covariance between genetic and environmental influences across ecological gradients—reassessing the evolutionary significance of countergradient and cogradient variation. Year Evol Biol 1168: 100–129. [DOI] [PubMed] [Google Scholar]
- Crispo E, Bentzen P, Reznick DN, Kinnison MT, Hendry AP. (2006). The relative influence of natural selection and geography on gene flow in guppies. Mol Ecol 15: 49–62. [DOI] [PubMed] [Google Scholar]
- Cvetković D, Tomašević N, Ficetola GF, Crnobrnja-Isailović J, Miaud C. (2009). Bergmann's rule in amphibians: combining demographic and ecological parameters to explain body size variation among populations in the common toad Bufo bufo. J Zoo Syst Evol Res 47: 171–180. [Google Scholar]
- Dmitriew CM. (2011). The evolution of growth trajectories: what limits growth rate? Biol Rev 86: 97–116. [DOI] [PubMed] [Google Scholar]
- Edelaar P, Burraco P, Gomez-Mestre I. (2011). Comparisons between QST and FST—how wrong have we been? Mol Ecol 20: 4830–4839. [DOI] [PubMed] [Google Scholar]
- Ficetola GF, De Bernardi F. (2005). Supplementation or in situ conservation? Evidence of local adaptation in the Italian agile frog Rana latastei and consequences for the management of populations. Anim Conserv 8: 33–40. [Google Scholar]
- Ficetola GF, De Bernardi F. (2006). Trade-off between larval development rate and post-metamorphic traits in the frog Rana latastei. Evol Ecol 20: 143–158. [Google Scholar]
- Garant D, Forde SE, Hendry AP. (2007). The multifarious effects of dispersal and gene flow on contemporary adaptation. Funct Ecol 21: 434–443. [Google Scholar]
- Gerlach G, Jueterbock A, Kraemer P, Deppermann J, Harmand P. (2010). Calculations of population differentiation based on G(ST) and D: forget G(ST) but not all of statistics!. Mol Ecol 19: 3845–3852. [DOI] [PubMed] [Google Scholar]
- Goater CP. (1994). Growth and survival of postmetamorphic toads: interactions among larval history, density, and parasitism. Ecology 75: 2264–2274. [Google Scholar]
- Gomez-Mestre I, Tejedo M. (2004). Contrasting patterns of quantitative and neutral genetic variation in locally adapted populations of the natterjack toad, Bufo calamita. Evolution 58: 2343–2352. [DOI] [PubMed] [Google Scholar]
- Goslee SC, Urban DL. (2007). The ecodist package for dissimilarity-based analysis of ecological data. J Stat Soft 22: 1–19. [Google Scholar]
- Gosner KL. (1960). A simplified table for staging anuran embryos and larvae with notes on identification. Herpetologica 16: 183–190. [Google Scholar]
- Goudet J. (2001) FSTAT, A Program to Estimate and Test Gene Diversities and Fixation Indices (Version 2.9.3). Université de Lausanne: Switzerland. [Google Scholar]
- Goudet J, Buchi L. (2006). The effects of dominance, regular inbreeding and sampling design on QST, an estimator of population differentiation for quantitative traits. Genetics 172: 1337–1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gould SJ, Johnston RF. (1972). Geographic variation. Ann Rev Ecol Syst 3: 485–486. [Google Scholar]
- Hangartner SB, Laurila A, Räsänen K. (2011). Adaptive divergence of the moor frog (Rana arvalis) along an acidification gradient. BMC Evol Biol 11: 366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hangartner S, Laurila A, Rasanen K. (2012). Adaptive divergence in moor frog (Rana arvalis) populations along an acidification gradient: inferences from Qst-Fst correlations. Evolution 66: 867–881. [DOI] [PubMed] [Google Scholar]
- Hemelaar A. (1988). Age, growth and other population characteristics of Bufo bufo from different latitudes and altitudes. J Herpetol 22: 369–388. [Google Scholar]
- Jost L. (2008). GST and its relatives do not measure differentiation. Mol Ecol 17: 4015–4026. [DOI] [PubMed] [Google Scholar]
- Kawecki TJ, Ebert D. (2004). Conceptual issues in local adaptation. Ecol Lett 7: 1225–1241. [Google Scholar]
- Keller I, Alexander JM, Holderegger R, Edwards PJ. (2013). Widespread phenotypic and genetic divergence along altitudinal gradients in animals. J Evol Biol 26: 2527–2543. [DOI] [PubMed] [Google Scholar]
- Körner C. (2003) Alpine Plant Life: Functional Plant Ecology of High Mountain Ecosystems. Springer: Berlin. [Google Scholar]
- Lande R. (1992). Neutral theory of quantitative genetic variance in an island model with local extinction and colonization. Evolution 46: 381–389. [DOI] [PubMed] [Google Scholar]
- Laugen AT, Laurila A, Merila J. (2002). Maternal and genetic contributions to geographical variation in Rana temporaria larval life-history traits. Biol. J. Linn. Soc. 76: 61–70. [Google Scholar]
- Laurila A, Karttunen S, Merila J. (2002). Adaptive phenotypic plasticity and genetics of larval life histories in two Rana temporaria populations. Evolution 56: 617–627. [DOI] [PubMed] [Google Scholar]
- Laurila A, Pakkasmaa S, Merilä J. (2006). Population divergence in growth rate and antipredator defences in Rana arvalis. Oecologia 147: 585595. [DOI] [PubMed] [Google Scholar]
- Laurila A, Lindgren B, Laugen AT. (2008). Antipredator defenses along a latitudinal gradient in Rana temporaria. Ecology 89: 13991413. [DOI] [PubMed] [Google Scholar]
- Lee CR, Mitchell-Olds T. (2011). Quantifying effects of environmental and geographical factors on patterns of genetic differentiation. Mol Ecol 20: 4631–4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legendre P, Legendre L. (2012) Numerical Ecology. Third English Edition. Elsevier Science BV: Amsterdam, The Netherlands. [Google Scholar]
- Leinonen T, O'Hara RB, Cano JM, Merilä J. (2008). Comparative studies of quantitative trait and neutral marker divergence: a meta-analysis. J Evol Biol 21: 1–17. [DOI] [PubMed] [Google Scholar]
- Lenormand T. (2002). Gene flow and the limits to natural selection. Trends Ecol Evol 17: 183–189. [Google Scholar]
- Lind MI, Ingvarsson PK, Johansson H, Hall D, Johansson F. (2011). Gene flow and selection on phenotypic plasticity in an island system of Rana temporaria. Evolution 65: 684–697. [DOI] [PubMed] [Google Scholar]
- Lindgren B, Laurila A. (2005). Proximate causes of adaptive growth rates: growth efficiency variation among latitudinal populations of Rana temporaria. J Evol Biol 18: 820–828. [DOI] [PubMed] [Google Scholar]
- Lindgren B, Laurila A. (2009). Physiological variation along latitudinal gradients: standard metabolic rate in Rana temporaria tadpoles. Biol J Linn Soc 98: 217–224. [Google Scholar]
- Loman J, Lardner B. (2006). Does pond quality limit frogs Rana arvalis and Rana temporaria in agricultural landscapes? A field experiment. J Appl Ecol 43: 690–700. [Google Scholar]
- Lynch M, Walsh B. (1998) Genetics and Analysis of Quantitative Traits. Sinauer: Sunderland. [Google Scholar]
- Marquis O, Miaud C. (2008). Variation in UV sensitivity among common frog Rana temporaria populations along an altitudinal gradient. Zoology 111: 309–317. [DOI] [PubMed] [Google Scholar]
- McKay JK, Latta RG. (2002). Adaptive population divergence: markers, QTL and traits. Trends Ecol Evol 17: 285–291. [Google Scholar]
- Méndez M, Rosenbaum H C, Subramaniam A, Yackulic C, Bordino P. (2010). Isolation by environmental distance in mobile marine species: molecular ecology of franciscana dolphins at their southern range. Mol Ecol 19: 2212–2228. [DOI] [PubMed] [Google Scholar]
- Merilä J, Crnokrak P. (2001). Comparison of genetic differentiation at marker loci and quantitative traits. J Evol Biol 14: 892–903. [Google Scholar]
- Miaud C, Guyetant R, Elmberg J. (1999). Variations in life-history traits in the common frog Rana temporaria (Amphibia: Anura): a literature review and new data from the French Alps. J Zool 249: 61–73. [Google Scholar]
- Miaud C, Merilä J. (2001). Local adaptation or environmental induction? Causes of population differentiation in alpine amphibians. Biota 21: 31–50. [Google Scholar]
- Monty A, Mahy G. (2009). Clinal differentiation during invasion: Senecio inaequidens (Asteraceae) along altitudinal gradients in Europe. Oecologia 159: 305–315. [DOI] [PubMed] [Google Scholar]
- Morrison C, Hero JM. (2003). Geographic variation in life history characteristics of amphibians: a review. J Anim Ecol 72: 270–279. [Google Scholar]
- Muir AP, Biek R, Thomas R, Mable BK. (2014). Local adaptation with high gene flow: temperature parameters drive adaptation to altitude in the common frog (Rana temporaria). Mol Ecol 23: 561–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman RA. (1988). Genetic variation for larval anuran (Scaphiopus couchii) development time in an uncertain environment. Evolution 42: 763–773. [DOI] [PubMed] [Google Scholar]
- Newman RA. (1992). Adaptive plasticity in amphibian metamorphosis. BioScience 42: 671–678. [Google Scholar]
- Nosil P, Vines TH, Funk DJ, Harrison R. (2005). Perspective: reproductive isolation caused by natural selection against immigrants from divergent habitats. Evolution 59: 705–719. [PubMed] [Google Scholar]
- O'Hara RB, Merilä J. (2005). Bias and precision in QST estimates: problems and some solutions. Genetics 171: 1331–1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oromi N, Sanuy D, Sinsch U. (2012). Altitudinal variation of demographic life-history traits does not mimic latitudinal variation in natterjack toads (Bufo calamita). Zoology 115: 30–37. [DOI] [PubMed] [Google Scholar]
- Orizaola G, Quintela M, Laurila A. (2010). Climatic adaptation in an isolated and genetically impoverished amphibian population. Ecography 33: 730–737. [Google Scholar]
- Orsini L, Vanoverbeke J, Swillen I, Mergeay J, De Meester L. (2013). Drivers of population genetic differentiation in the wild: isolation by dispersal limitation, isolation by adaptation and isolation by colonization. Mol Ecol 22: 5983–5999. [DOI] [PubMed] [Google Scholar]
- Palo JU, O'Hara RB, Laugen AT, Laurila A, Primmer CR, Merilä J. (2003). Latitudinal divergence of common frog (Rana temporaria) life history traits by natural selection: evidence from a comparison of molecular and quantitative genetic data. Mol Ecol 12: 1963–1978. [DOI] [PubMed] [Google Scholar]
- Pidancier N, Miquel C, Miaud C. (2003). Buccal swabs as a non-destructive tissue sampling method for DNA analysis in amphibians. Herpetol J 13: 175–178. [Google Scholar]
- Pinheiro JC, Bates DM. (2000) Mixed-effects Models in S and S-PLUS. Springer: New York. [Google Scholar]
- Porcher E, Giraud T, Goldringer I, Lavigne C. (2004). Experimental demonstration of a causal relationship between heterogeneity of selection and genetic differentiation in quantitative traits. Evolution 58: 1434–1445. [DOI] [PubMed] [Google Scholar]
- Pujol B, Wilson AJ, Ross RIC, Pannell JR. (2008). Are QST–FST comparisons for natural populations meaningful? Mol Ecol 17: 4782–4785. [DOI] [PubMed] [Google Scholar]
- Räsänen K, Laurila A, Merilä J. (2003). Geographic variation in acid stress tolerance of the moor frog, Rana arvalis. I. Local adaptation. Evolution 57: 352–362. [PubMed] [Google Scholar]
- Räsänen K, Hendry AP. (2008). Disentangling interactions between adaptive divergence and gene flow when ecology drives diversification. Ecol Lett 11: 624–636. [DOI] [PubMed] [Google Scholar]
- Raymond M, Rousset F. (1995). An exact test for population differentiation. Evolution 49: 1280–1283. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. (2010) R version 2.11.1. R Project for Statistical Computing, Vienna, Austria www.r-project.org.
- Richter-Boix A, Teplitsky C, Rogell B, Laurila A. (2010). Local selection modifies phenotypic divergence among Rana temporaria populations in the presence of gene flow. Mol Ecol 19: 716–731. [DOI] [PubMed] [Google Scholar]
- Richter-Boix A, Quintela M, Kierczak M, Laurila A. (2013). Fine-grained adaptive divergence in an amphibian: genetic basis of phenotypic divergence and the role of non-random gene flow in restricting effective migration among wetlands. Mol Ecol 22: 1322–1340. [DOI] [PubMed] [Google Scholar]
- Roff D. (1997). Evolutionay quantitative genetics:. Chapman & Hall, New York.
- Rousset F. (2008). Genepop'007: a complete re-implementation of the Genepop software for Window and Linux. Mol Ecol Notes 8: 103–106. [DOI] [PubMed] [Google Scholar]
- Rowe L, Ludwig D. (1991). Size and timing of metamorphosis in complex life cycles: time constraints and variation. Ecology 72: 413–427. [Google Scholar]
- Rundle HD, Nosil P. (2005). Ecological speciation. Ecology Letters 8: 336–352. [Google Scholar]
- Ryman N, Leimar O. (2009). GST is still a useful measure of genetic differentiation—a comment on Jost's D. Mol Ecol 18: 2084–2087. [DOI] [PubMed] [Google Scholar]
- Sacks BN, Bannasch DL, Chomel BB, Ernest HB. (2008). Coyotes demonstrate how habitat specialization by individuals of a generalist species can diversify populations in a heterogeneous ecoregion. Mol Biol Evol 25: 1384–1394. [DOI] [PubMed] [Google Scholar]
- Slatkin M. (1995). A measure of population subdivision based on microsatellite allele frequencies. Genetics 139: 457–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheepens JF, Frei ES, Stöcklin J. (2010). Genotypic and environmental variation in specific leaf area in a widespread Alpine plant after transplantation to different altitudes. Oecologia 164: 141–150. [DOI] [PubMed] [Google Scholar]
- Scott DE. (1994). The effect of larval density on adult demographic traits in Ambystoma opacum. Ecology 75: 1383–1396. [Google Scholar]
- Semlitsch RD. (1993). Adaptive genetic variation in growth and development of tadpoles of the hybridogenetic Rana esculenta complex. Evolution 47: 1805–1818. [DOI] [PubMed] [Google Scholar]
- Sexton JP, Hangartner SB, Hoffmann AA. (2013). Genetic isolation by environment or distance: which pattern of gene flow is most common? Evolution 68: 1–15. [DOI] [PubMed] [Google Scholar]
- Sillero N, Campos J, Bonardi A, Corti C, Creemers R, Crochet PA et al. (2014). Updated distribution and biogeography of amphibians and reptiles of Europe based on a compilation of countrywide mapping studies. Amphibia-Reptilia 35: 1–31. [Google Scholar]
- Smith MA, Green DM. (2005). Dispersal and the metapopulation paradigm in amphibian ecology and conservation: are all amphibian populations metapopulations? Ecography 28: 110–128. [Google Scholar]
- Sommer S, Pearman PB. (2003). Quantitative genetic analysis of larval life history traits in two alpine populations of Rana temporaria. Genetica 118: 1–10. [DOI] [PubMed] [Google Scholar]
- Spitze K. (1993). Population-structure in Daphnia obtusa—quantitative genetic and allozymic variation. Genetics 135: 367–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storz JF. (2002). Contrasting patterns of divergence in quantitative traits and neutral DNA markers: analysis of clinal variation. Mol Ecol 11: 2537–2551. [DOI] [PubMed] [Google Scholar]
- Thibert-Plante X, Hendry AP. (2009). Five questions on ecological speciation addressed with individual-based simulations. J Evol Biol 22: 109–123. [DOI] [PubMed] [Google Scholar]
- Thibert-Plante X, Hendry AP. (2010). When can ecological speciation be detected with neutral loci? Mol Ecol 19: 2301–2314. [DOI] [PubMed] [Google Scholar]
- Thibert-Plante X, Hendry AP. (2011). Factors influencing progress toward sympatric speciation. J Evol Biol 24: 2186–2196. [DOI] [PubMed] [Google Scholar]
- Travis J, Emerson SB, Blouin M. (1987). A quantitative genetic analysis of larval life-history traits in Hyla crucifer. Evolution 41: 145–156. [DOI] [PubMed] [Google Scholar]
- Vasemagi A. (2006). The adaptive hypothesis of clinal variation revisited: single-locus clines as a result of spatially restricted gene flow. Genetics 173: 2411–2414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Oosterhout CV, Hutchinson WF, Wills DPM, Shipley P. (2004). MICRO-CHECKER: software for identifying and correcting genotyping errors in microsatellite data. Mol Ecol Notes 4: 535–538. [Google Scholar]
- Weir BS, Cockerham CC. (1984). Estimating F-statistics for the analysis of population structure. Evolution 38: 1358–1370. [DOI] [PubMed] [Google Scholar]
- Whitlock M. (1999). Neutral additive variance in a metaopulation. Genet Res 74: 215–221. [DOI] [PubMed] [Google Scholar]
- Whitlock MC, Ingvarsson PK, Hatfield T. (2000). Local drift load and the heterosis of interconnected populations. Heredity 84: 452–457. [DOI] [PubMed] [Google Scholar]
- Whitlock MC. (2008). Evolutionary inference from QST. Mol Ecol 17: 1885–1896. [DOI] [PubMed] [Google Scholar]
- Whitlock MC, Guillaume F. (2009). Testing for spatially divergent selection: comparing QST to FST. Genetics 183: 1055–1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilbur HM, Collins JP. (1973). Ecological aspects on amphibian metamorphosis. Science 182: 1305–1314. [DOI] [PubMed] [Google Scholar]
- Wright S. (1943). Isolation by distance. Genetics 28: 114–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. (1951). The genetical structure of populations. Annals Eugen 15: 323–354. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.