Patterns of pollen dispersal in a small population of the Canarian endemic palm (Phoenix canariensis)

Abstract

The genetic diversity of small populations is greatly influenced by local dispersal patterns and genetic connectivity among populations, with pollen dispersal being the major component of gene flow in many plants species. Patterns of pollen dispersal, mating system parameters and spatial genetic structure were investigated in a small isolated population of the emblematic palm Phoenix canariensis in Gran Canaria island (Canary Islands). All adult palms present in the study population (n=182), as well as 616 seeds collected from 22 female palms, were mapped and genotyped at 8 microsatellite loci. Mating system analysis revealed an average of 5.8 effective pollen donors (N_ep) per female. There was strong variation in correlated paternity rates across maternal progenies (ranging from null to 0.9) that could not be explained by the location and density of local males around focal females. Paternity analysis revealed a mean effective pollen dispersal distance of ∼71 m, with ∼70% of effective pollen originating from a distance of <75 m, and 90% from <200 m. A spatially explicit mating model indicated a leptokurtic pollen dispersal kernel, significant pollen immigration (12%) from external palm groves and a directional pollen dispersal pattern that seems consistent with local altitudinal air movement. No evidence of inbreeding or genetic diversity erosion was found, but spatial genetic structure was detected in the small palm population. Overall, the results suggest substantial pollen dispersal over the studied population, genetic connectivity among different palm groves and some resilience to neutral genetic erosion and subsequently to fragmentation.

Introduction

The evolutionary dynamics of plants depends on gene flow within and among populations, the patterns of which largely influence spatial genetic structuring (Loveless and Hamrick, 1984; Smouse and Sork, 2004). At the microevolutionary level, gene flow by pollen dispersal is a major determinant of mating patterns, within-population genetic diversity and among-population connectivity in spatially structured plant species, counteracting the effect of isolation by distance (Wright, 1943). Of particular concern is the loss of genetic diversity potentially resulting from mate limitation and gene flow disruptions associated with population size reduction (Jump and Peñuelas, 2006). However, some mechanisms such as effective pollen and seed dispersal and traits such as the longevity of trees could increase their resilience to the negative effects of small population size (Hamrick, 2004; Jump and Peñuelas, 2006). Thus, assessing spatial patterns of pollen movement, as well as their interaction with mating systems, pollination syndromes and ecological and demographic factors has become an important topic in experimental ecological and evolutionary studies, especially with the availability of highly polymorphic microsatellite markers (Smouse et al., 2001; Burczyk et al., 2002; Robledo-Arnuncio et al., 2006). Mating distance distributions typically exhibit an excess of nearby events (Levin and Kerster, 1974), a short-distance component of effective pollen dispersal that greatly determines correlated paternity rates (that is, the fraction of sibling pairs that share the same father) and the probability of identity of two uniting gametes within a population (that is, the inverse of the ‘neighbourhood size', sensu Wright, 1943; see Crawford, 1984; Robledo-Arnuncio and Austerlitz, 2006; Pluess et al., 2009). Short-distance pollen dispersal can be efficiently assessed via paternity analysis of parent–offspring genotypic samples (Jones et al., 2010) that also allows investigating the effect of phenotypic traits and ecological variables on individual male reproductive success (Nielsen et al., 2001; Oddou-Muratorio et al., 2003). Rare long-distance pollen dispersal events, on the other hand, although much harder to detect and quantify, are the vector of genetic connectivity among populations, especially across fragmented landscapes (Trakhtenbrot et al., 2005; Klein et al., 2006), that bears potentially important consequences for local adaptation in changing environments (Kremer et al., 2012).

Although accurately estimating the frequency and origin of long-distance effective pollen dispersal events remains an enormous experimental challenge (Kremer et al., 2012), local paternity analysis can provide some hints on its frequency through the estimation of pollen immigration rates into isolated populations and the examination of the shape of the tail of (locally) estimated dispersal functions (Burczyk et al., 2002; Austerlitz et al., 2004; Oddou-Muratorio et al., 2005; Klein et al., 2006). One of the most frequent approaches to estimate local mating patterns is maximum-likelihood categorical paternity assignment (see, for example, Marshall et al., 1998) that enables individually explicit characterization of effective pollen dispersal at the cost of frequently large numbers of unassigned offspring and substantial type II errors (Oddou-Muratorio et al., 2003). Fractional paternity analysis (see, for example, Nielsen et al., 2001) alleviates sample size reductions inherent in the categorical analysis and, although it does not identify fathers categorically, it provides an alternative way to estimate the distribution of mating distances. Finally, spatially explicit mating models (Burczyk et al., 2002; Oddou-Muratorio et al., 2005) provide an inclusive tool to jointly estimate the pollen dispersal kernel, pollen immigration rates into the study area and phenotypic and ecological correlates of male reproductive success.

Phoenix canariensis Chabaud (Arecaceae) is an endemic and very representative palm species in the Canary Islands. Like all other species belonging to the Canarian thermophilous woodland, Canarian palm populations suffered severe fragmentation after the Spanish conquest and colonization in the fifteenth century because the fertile areas that it inhabited were rapidly deforested for agriculture. Thermophilous woodlands of the Canary islands grow preferentially between 300 and 500 m above sea level on windward wetter slopes, and between 500 and 900 m on leeward drier slopes, as determined by the east–west distribution of the main mountain chains and the predominant northeastern trade winds (Fernández-Palacios and Whittaker, 2008). The current natural distribution of P. canariensis consists of palm groves that remain of a bygone wider natural distribution, being mainly restricted to the bottom of ravines and slopes with high moisture. It is most abundant in La Gomera and Gran Canaria islands, but it can be found across the entire archipelago. Besides fragmentation, P. canariensis is affected by several factors of disturbance such as several pests (like the weevils Rhynchophorus ferrugineus and Diocalandra frumenti), infections (especially that caused by the fungus Fusarium oxysporum) and hybridization with the allochthonous congener Phoenix dactylifera, massively introduced into the Canarian archipelago and with which it forms fertile hybrids (González-Pérez et al., 2004). Nowadays, the Canarian palm groves are catalogued as priority habitats of European Union Natura 2000 network of protection areas, and the Canarian Government has designated the species as vegetal symbol of the archipelago. However, despite the importance of the species and the potential reduction in population viability posed by fragmentation and other human-induced disturbances, there are few scientific studies about the genetic structure and reproductive biology of P. canariensis, and none about the extent of pollen dispersal within or between its natural populations that would be instrumental to understand and manage the genetic consequences of fragmentation.

This study investigates effective pollen dispersal patterns of P. canariensis using fractional paternity analysis and spatially explicit mating models, based on microsatellite markers. The general goal is to provide information on Canarian palm grove mating patterns and genetic connectivity, and on potential phenotypic and ecological correlates of individual dispersal parameters. Such information could serve as reference for future investigations in other palms in the genus Phoenix, for which similar studies are absent in the literature, despite their economic and ecological relevance in their natural habitats (Dransfield et al., 2008). There are indeed few effective pollen dispersal studies for palms in general (Gaiotto et al., 2003; Sezen et al., 2007; Ottewell et al., 2012), and to our knowledge no pollen dispersal kernel has ever been estimated for an oceanic island plant. Our specific aims were to: (1) estimate mating system and effective pollen dispersal parameters within and into an isolated Canarian palm population; (2) investigate phenotypic and ecological correlates of individual mating system parameters; and (3) assess patterns of fine-scale spatial genetic structure of a small natural isolated Canarian palm population.

Materials and methods

Study species and study site

P. canariensis is a diploid (n=18), long-lived, slow-growing, arborescent monocot with a solitary trunk that grows up to ∼20 m, but most frequently between 5 and 10 m. Numerous small yellowish male and female flowers cluster in spadices that develop on separate plants, being a dioecious species with dimorphic flower and crown morphology traits. Flower anthesis happens at night or dawn and the flowering period lasts from few hours to 3 days in males and from 2 to 5 days in females, whereas fruit ripening takes 1 year after fertilization. There is substantial flowering asynchrony between individuals within populations, being frequent to find at least some flowering individuals through all the summer and autumn, that should facilitate outcrossing with palms from other groves. Although traditionally described as anemophilous, this pollination syndrome has been questioned because of male inflorescence traits and the presence of insects as flower visitors, both characters suggesting entomophily pollination (Meekijjaroenroj and Anstett, 2003). Our recent observations failed to detect any insect entering in female flowers, and therefore we favour the hypothesis that pollination is mainly by wind and that insects are just flower visitors (I Saro, unpublished data).

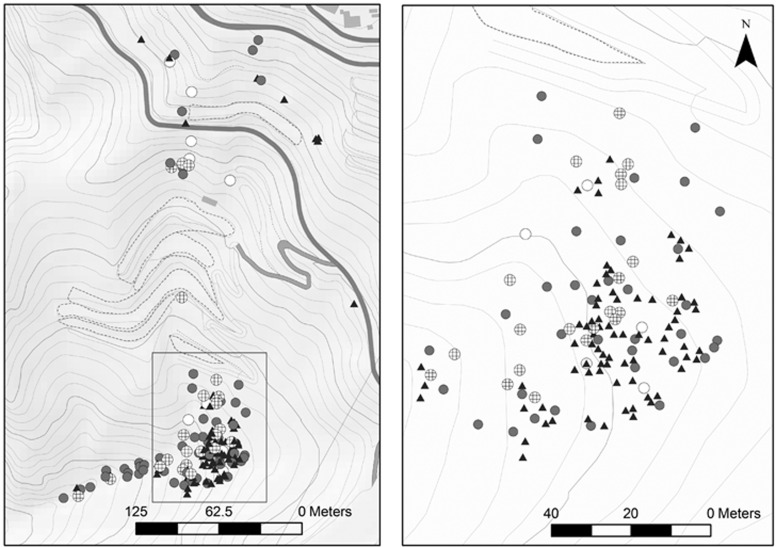
The study area was the Acusa Verde population, located on a leeward slope in northwestern Gran Canaria island (27° 59.85′ N, 15° 41.33′ O; at elevations from 505 to 686 m above sea level). This stand is one of the only four populations registered as pure basic material for the collection of P. canariensis forest reproductive material (BOE, 2006). It was chosen for its small size (∼10 ha), which allowed exhaustive individual sampling, and its isolation from other populations by deep ravines (the closest population is 600 m away, with an abrupt landscape between the two). The surrounding vegetation consists mainly of transition scrubland and pastures, with some vegetable crops grown between the northern limit of the stand and the denser core of the population in the south (Figure 1).

Figure 1.

Spatial distribution of palms present in Acusa Verde population: sampled mother female palms (crossed circles), unsampled female palms (white dots), male palms (grey dots) and immature palms (black triangles). (a) The whole study area (dark grey lines are roads and dashed lines represent crop boundaries), is shown. (b) A zoom of the denser core on the southeast side of study area (inner rectangle within left panel).

Sample collection and genetic analysis

Sampling

We mapped with a GPS (GPSmap 76CS, Garmin, Kansas City, USA) and collected leaf material from all 182 palms found in the study population. In order to assess reproductive status, we checked the crowns of every palm for evidence of old or emerging inflorescences (withered inflorescences typically remain in the palm for several years). We thus found 56 males, 47 females and 79 nonreproductive palms. The latter bore no trace of inflorescences, and hence we assumed that they did not participate in the reproductive cycle under study. A total of 22 seeds were randomly collected from well-ripened fruits born in the reproductive branches of each of 28 female palms; these palms are referred to as ‘mothers' hereafter. Seeds from each maternal family were stored in separate bags along with leaf tissue from the corresponding mother, used to determine the maternal gametic contribution to the embryos. Seeds were first treated by removing the outer fleshy covering and were then sowed in an outdoor nursery at the Forest Nursery of Gran Canaria island Council until seedlings had 1 month of growth. All 616 collected seeds germinated successfully and were used for molecular analysis.

DNA isolation and microsatellite analysis

Total genomic DNA was extracted from ∼1 g of silica-dried leaf tissue from each sampled adult and germinated seedling, following Dellaporta et al. (1983), after grinding plant material with a Mixer Mill MM300 (RETSCH, Haan, Germany). The obtained DNA solution was purified using GenElute PCR Clean-Up Kit (SIGMA-ALDRICH, St Louis, MO, USA). DNA concentration was evaluated on a spectrophotometer to verify a minimum of 20 ng μl⁻¹. We tested 14 dinucleotide (GA) microsatellite loci previously developed for P. dactylifera (Billotte et al., 2004), finding that only 8 of them (mPdCIR010, mPdCIR025, mPdCIR048, mPdCIR050, mPdCIR057, mPdCIR063, mPdCIR070 and mPdCIR085) amplified and were polymorphic in P. canariensis (results not shown). DNA fragments were amplified in two PCR multiplex reactions with four loci each, using the Qiagen Multiplex PCR kit (QIAGEN, Valencia, CA, USA) and following the manufacturer's instructions, but accommodating reagent proportions to a final volume of 15 ml. Amplification products were run on an ABI3730 capillary sequencer using an internal size standard (GS500 (−250) LIZ) and fragment sizes were manually scored using GENEMAPPER software (Applied Biosystems, Foster City, CA, USA). Samples with dubious scorings at particular loci, including mother–offspring mismatches identified by CERVUS v 3.0 (Kalinowski et al., 2007), were regenotyped to minimize genotyping errors (yielding a final zero mother–offspring mismatch rate) (Data available from the Dryad Digital Repositor; doi:10.5061/dryad.1pb6t).

Data analysis

Mating system

We estimated correlated paternity rates (r_p) at the population and individual-mother level with MLTR v3.2 (Ritland, 2002), using the following settings: outcrossing rate fixed at t_m=1 (as P. canariensis is dioecious and because no evidence of biparental inbreeding was detected in preliminary analyses; results not shown), known maternal genotype (obtained from maternal leaf tissue), ovule and pollen gene frequencies estimated separately, Newton–Raphson optimization algorithm and 1000 bootstrap resamples of maternal families to obtain standards errors for the population estimate. The effective number of fathers per mother (N_ep) was then calculated as N_ep=1/r_p. We also quantified the genetic differentiation among the male gametes pollinating each of the 28 mothers by calculating the Φ_FT intraclass correlation parameter of the TwoGener method, as implemented in GENALEX v6.5 (Smouse and Sork, 2004; Peakall and Smouse, 2006).

Paternity assignment

In order to infer the mating distance distribution, we assessed paternity for sampled seeds from the 28 mothers through fractional assignment methods in PATRI (Nielsen et al., 2001; Signorovitch and Nielsen, 2002). We chose to use fractional (rather than categorical) paternity assignment because it does not need independent information about the breeding male population size, and because our primary goal was not to delineate parental relationships, but to infer the mating distance distribution, for which it is desirable to use the full seed sample, without incurring the high unassignment rates typical of categorical parentage analysis (Oddou-Muratorio et al., 2003). We jointly estimated (1) the male population size (N), assuming a uniform prior distribution in the (56, 1000) interval, (2) posterior probabilities of paternity for every candidate male and (3) the posterior expectation of the proportion of sampled seeds sired by sampled fathers. We initially included nonreproductive individuals (as indicated by the absence of flowers) as candidate males, but null or virtually null posterior probabilities of paternity confirmed their nonreproductive status, and hence they were excluded from the final paternity analysis. The effective pollination distance within the population was then calculated for each of the 606 seeds without missing data (not allowed by PATRI) as the weighted average of the distances between the corresponding mother and every candidate male, using the posterior probabilities of paternity as weights.

We used nonparametric Kolmogorov–Smirnov tests implemented in ‘R' (R Development Core Team, 2008) to assess whether the observed mating distance distribution departed significantly from the null hypothesis of random mating, and we did this by comparing the frequency distribution of effective pollination distances and the frequency distribution of all pairwise distances among all sampled males and the 28 mother palms.

Spatially explicit mating model

We fit within-population pollen dispersal kernels using a spatially explicit mating model, or NEIGHBOURHOOD model (Burczyk et al., 2002; Oddou-Muratorio et al., 2005), implemented in the software NM+ v 1.1 (Chybicki and Burczyk, 2010). Besides the pollen dispersal kernel parameters, this method jointly estimates the pollen immigration rate into the study population and correlations between male reproductive success and phenotypic and ecological variables (Burczyk et al., 2006; Chybicki and Burczyk, 2010). Basically, the model assumes that each offspring sampled from a mother palm was sired by a paternal gamete either via self-pollination (with probability s), pollen immigration from outside the study area (with probability m_p) or pollen from a sampled male within the study area (with probability 1−m_p−s); the dispersal kernel parameters are estimated jointly with m_p and s following a maximum-likelihood method based on Mendelian transition probabilities, without discarding ambiguous-paternity cases and considering the effect of cryptic gene flow (Burczyk et al., 2006). As program settings, we fixed the neighbourhood parameter to ‘infinite' in order to include all sampled adults as candidate fathers (Chybicki and Burczyk, 2010), and the selfing rate s at zero, and we jointly estimated genotyping error rates. We assumed five different pollen dispersal kernels: exponential, exponential-power, Weibull, geometric and 2Dt. We included male height and local palm density around male individuals (measured in radii of 5, 15 and 30 m) as variables potentially affecting male reproductive success. In this way we tested whether high total local densities around males could reduce their mating success by hampering free pollen movement to a larger number of distant females. Given that the software assumes a monoecious species, we additionally assumed a fictitious phenotypic trait that forced the male reproductive success of females to zero while not affecting the relative success of different males. Finally, we tested for directional effective pollen dispersal using the von Misses distribution with prevalent direction parameter θ_p (measured from true north) and rate (intensity) parameter K_p (Chybicki and Burczyk, 2010). To avoid local optima, we manually tested different initial values for all parameters. Moreover, following NM+ user's manual instructions, we obtained initial estimates for each parameter by adding parameters one at a time, although we jointly estimated all parameters in the final fit. Akaike information criterion (AIC) was used to evaluate relative goodness of fit, calculated as AIC=−2(logL)+2K, with logL being the logarithm of the maximized likelihood and K the number of estimated parameters.

Demographic correlates of local mating parameters

We assessed the influence of demographic variables on local variation in the effective pollen cloud by estimating Spearman's rank correlation coefficients using SPSS Statistic v.19 (IBM Corporation, Armonk, NY, USA) between mating and density parameters for individual maternal plants. For each mother palm, we considered the correlated paternity rate (r_p) and the mean effective dispersal distance (d_eff) as mating parameters (as estimated by MLTR v3.2 software and paternity assignment, respectively) and the following local density variables: mean distance to all male palms (d_mean), distance to the nearest male palm (d_min) and number of males at distance x or less from the mother (N_mx). We considered different values for the radius x, 5, 15, 20, 30, 40 and 50 m, that encompassed the different clump sizes found in the study population.

Genetic diversity and spatial genetic structure

We tested for Hardy–Weinberg equilibrium and calculated the following standard genetic diversity parameters for the adult population and the seed sample separately as implemented in GENALEX v6.5 (Peakall and Smouse, 2006): mean effective number of alleles per locus (N_e), observed (H_o) and expected (H_e) heterozygosity and inbreeding (F_/S). The allelic richness (N_a) was estimated using the rarefaction method implemented in HP-RARE 1.0 (Kalinowski, 2005) in order to account for the unequal sample sizes of adult and seed samples. We assessed fine-scale spatial genetic structure among adult trees using the spatial autocorrelation analysis implemented in SPAGeDi 1.3 (Hardy and Vekemans, 2002), with the kinship coefficients (F_ij) of Loiselle et al. (1995). We set 10 distance classes containing equal numbers of pairwise comparisons each, and conducting 1000 random permutations of individual locations among plants to obtain 95% confidence intervals around the null hypothesis of random genetic structure. Standard errors of observed kinship values were estimated using Jackknife procedure over loci 1000 times. The extent of spatial genetic structure was quantified using the Sp statistics proposed in Vekemans and Hardy (2004), estimated by the ratio −b_F (1−F₁), where b_F is the mean slope of the regression of kinship coefficient on Ln (distance) and F₁ is the average kinship coefficient over the first distance interval.

Results

Mating system and paternity assignment

The MLTR correlated mating model estimated a moderate degree of correlated paternity within maternal progeny arrays (population average r_p=0.173), indicating that ∼17% of seed pairs were full-sibs. This paternal identity rate within progeny arrays translated into an average estimate of N_ep=5.8 effective pollen donors per female (Table 1). Family-level estimates of correlated paternity showed high variation, ranging from negative values (suggesting null parametric values) to 0.902 (N_ep range: 1.1–45.4) (Table 2). The TwoGener approach showed moderate to low but significant global differentiation among the pollen pools fertilizing different mother palms (Φ_FT=0.057, P=0.001; Table 1) that translates into an estimate of 1/2Φ_FT=8.8 effective pollen donors per female, assuming null correlated paternity among mother pairs (see Equation 27 in Austerlitz and Smouse, 2001). The latter assumption is probably not true among the nearby females of the study population, which would explain the positive bias of TwoGener N_ep estimate relative to that of MLTR.

Table 1. Population-level estimates of mating system and pollen dispersal statistics for Phoenix canariensis.

Mating system
Parental F-estimate	−0.179±s.e. 0.032
Correlated paternity (rp)	0.173±s.e. 0.032
Effective number of pollen donors (Nep)	5.78±s.e. 1.07
Genetics differentiation of seed families (ΦFT)	0.057, P=0.001
Paternity analysis
Mean/median/minimum/maximum potential pollen dispersal distance	96.2/58.5/2.2/391.6 m
Mean/median/minimum/maximum pollen dispersal distance on PATRI	71.5/47.9/4.6/377.2 m

Methods section contains details on each analysis.

Table 2. Family-level mating system for Phoenix canariensis.

Maternal tree ID	nprogeny	rp	Nep	Mean PDD (m)	Mean EDD (m)
02	22	0.155±0.074	6.5±3.1	121.68	85.03
09	22	0.110±0.053	9.1±4.4	98.70	77.14
20	22	0.186±0.088	5.4±2.5	76.65	59.83
24	22	−0.084±0.042	NA	74.04	58.90
28	22	0.095±0.045	10.5±5.0	74.59	39.58
38	22	0.056±0.027	17.9±8.6	73.79	51.95
39	22	0.064±0.031	15.6±7.6	72.32	65.14
40	22	0.342±0.143	2.9±1.2	70.13	44.02
49	22	0.110±0.052	9.1±4.3	70.07	42.57
51	22	0.330±0.156	3.0±1.4	69.34	40.61
73	22	0.022±0.011	45.4±22.7	69.68	91.06
81	22	0.195±0.093	5.1±2.4	70.24	41.99
82	22	0.037±0.018	27.0±13.1	70.35	55.01
83	22	0.067±0.033	14.9±7.4	69.86	67.63
95	22	0.073±0.035	13.7±6.6	70.58	26.67
104	22	0.147±0.070	6.8±3.2	74.58	48.31
125	22	0.371±0.018	2.7±0.1	72.13	61.28
130	22	0.126±0.061	7.9±3.8	70.74	54.54
140	22	0.126±0.061	7.9±3.8	126.24	116.43
141	22	0.065±0.031	15.4±7.3	86.92	85.19
144	22	0.085±0.041	11.8±5.7	79.36	92.94
146	22	0.120±0.058	8.3±4.0	80.50	61.75
149	22	0.113±0.054	8.8±4.2	78.97	66.04
150	22	0.061±0.030	16.4±8.1	77.85	62.45
157	22	0.902±0.428	1.1±0.5	195.71	47.97
160	22	0.353±0.168	2.8±1.3	196.15	123.74
162	22	0.130±0.063	7.7±3.7	197.38	175.23
167	22	0.087±0.042	11.5±5.5	204.25	192.04
Average	22	—	—	96.17	72.68

Abbreviation: NA, cannot be computed.

Number of seeds sampled for each mother (n_progeny), correlated paternity (r_p) as calculated by MLTR (Ritland, 2002), effective number of pollen donors (N_ep), mean separation distance between the focal maternal palm and all male palms (potential dispersal distance; PDD) and mean distance between pollen donors and the focal maternal palm (effective dispersal distance; EDD), as calculated from paternity analysis results using PATRI (Nielsen et al., 2001), are shown.

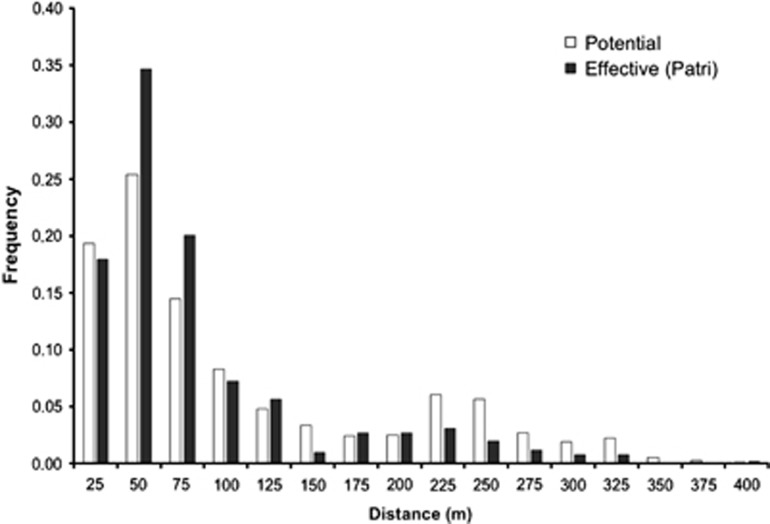
Assuming no genotyping errors, PATRI fractional paternity analysis estimated 25% of sampled offspring not sired by sampled candidate fathers, and a breeding male population size of 74.3 (95% confidence interval: 70.8–79.6). In particular, estimated mean mating distances were 71 m for PATRI, and the minimum, median and maximum values ranging from 3 to 377 m (Table 1). At the level of individual maternal progenies, there was substantial variation in the mean mating distance that ranged from 26.6 to 192 m according to PATRI results (Table 2). The mating distance distribution exhibited an excess of short-distance pollination (Figure 2); ∼70% of effective pollen has its origin in a distance of <75 m, and 90% from <200 m. The range of effective pollen dispersal was lower than expected under random mating: the mean and median pairwise distance between mothers and all candidate males were 96.2 and 58.5, respectively, that are larger than the estimated mean and median mating distances (Table 1). Kolmogorov–Smirnov tests confirmed that the observed and potential frequency distributions of mating distances were significantly different to effective distances calculated from PATRI results (D=0.145, P<0.001).

Figure 2.

Frequency distribution of potential distances among females and males (white bars) and intermate distances observed by fractional assignments (black bars).

Spatially explicit mating model

NM+ software yielded pollen immigration estimates that were slightly sensitive to the assumed dispersal kernel, ranging from 12 to 14% (Table 3). This rate (12% of seeds sired by immigrant pollen) is smaller than the 25% estimate from PATRI, which should be regarded as a maximum estimate because it assumes no genotyping errors. The within-population random dispersal assumption yielded the worst fit, indicating that a panmictic mating model is unlikely, whereas the best model fits were achieved assuming biparametric leptokurtic pollen dispersal kernels with either thin (Weibull with b>1) or fat (exponential-power with b<1) tails (Table 3; see Austerlitz et al., 2004). However, all biparametric kernels considered yielded unrealistically large mean pollen dispersal distances. This is a possible behaviour of the model for biparametric kernels when dispersal is leptokurtic and the spatial scale of analysis (beyond which we are implicitly extrapolating) is limited, being advisable in this case to fix the shape parameter in order to estimate other parameters (I Chybicki, personal communication). We thus assumed an exponential kernel for subsequent estimation of anisotropy and reproductive success parameters. Under the exponential kernel assumption, adding both palm height (as correlate of male reproductive success) and anisotropic dispersal kernel parameters substantially reduced AIC, whereas local density parameters around males did not significantly improve or even worsened the fit (Table 3). The model with smaller AIC yielded a mean pollen dispersal distance of 198±24 m and a 12% pollen immigration rate, with a prevalent dispersal direction to the northwest (296.32°±9.21° from the true north), and with the height of male palms positively influencing their mating success (β=0.24±0.07).

Table 3. Dispersal parameters estimated with NM+(Chybicki and Burczyk, 2010).

Model	mp	dp	a	b	Kp	ap	h	Np5	Np15	Np30	LogL	AIC
Random dispersal	0.139 (0.019)	Infa	5 × 10299 a	1a	—	—	—	—	—	—	−6830.3	13 662.6
Exponential	0.126 (0.018)	184.9 (22.0)	92.5	1a	—	—	—	—	—	—	−6777.9	13 561.8
Exponential-power	0.121 (0.018)	6.44 × 1016	—	0.03 (0.01)	—	—	—	—	—	—	−6745.7	13 499.4
Weibull	0.121 (0.018)	32 × 104 (34 × 106)	34 × 104	1.24 (0.05)	—	—	—	—	—	—	−6745.5	13 499.1
Geometric	0.126 (0.018)	8.46 × 103 (4.06 × 103)	122.7	3.03 (0.014)	—	—	—	—	—	—	−6766.2	13 540.4
2Dt	0.129 (0.019)	4.11 × 103 (1.81 × 103)	100.8	1.51 (0.006)	—	—	—	—	—	—	−6786.7	13 581.4
Exponential	0.123 (0.018)	197.3 (22.8)	98.6	1a	0.59 (0.10)	297.92 (8.58)	—	—	—	—	−6760.7	13 531.4
	0.124 (0.018)	205.6 (25.2)	102.8	1a	0.55 (0.10)	296.32 (9.21)	0.26 (0.07)	—	—	—	−6753.8	13 519.6
	0.125 (0.018)	198.5 (23.9)	99.2	1a	0.48 (0.11)	294.04 (10.6)	0.24 (0.07)	−0.16 (0.11)	—	—	−6752.6	13 519.2
	0.125 (0.018)	199.9 (24.6)	99.9	1a	0.49 (0.12)	294.64 (10.5)	0.24 (0.07)	−0.19 (0.13)	0.04 (0.12)	—	−6752.5	13 521
	0.125 (0.018)	195.2 (24.1)	99.1	1a	0.47 (0.13)	293.84 (11.4)	0.24 (0.07)	−0.18 (0.14)	0.11 (0.16)	−0.09 (0.15)	−6752.3	13 522.6

Abbreviation: AIC, Akaike information criterion.

Pollen immigration rate (m_p), mean distance of pollen dispersal (d_p), scale (a) and shape (b) parameters of the dispersal kernel, directionality effect (K_p) and direction at angle (a_p) of pollen dispersal are shown. Male reproductive success gradient was assessed for the height of male palms (h) and local density around male palms in ratios of 5 m (Np5), 15 m (Np15) and 30 m (Np30). The s.d. values are in parenthesis.

The symbol ‘—‘ indicates that the parameter was not estimated.

^aFixed value.

Demographic correlates of local mating parameters

Neither the mean distance to all males nor the distance to the nearest male were significantly associated with correlated paternity rates of focal maternal palms (respectively: r_s=0.125, P=0.53 and r_s=0.160, P=0.415). Neither did the number of nearby males explained variation in correlated paternity among maternal families for any of the radii considered (all tests with r_s⩽ −0.02 and P>0.26). Variation in mean mating distance among maternal families, on the other hand, was not associated with correlated paternity values (r_s=−0.146, P=0.458). There was however a significant negative correlation between mean effective pollination distance and local male density. The relationship was stronger for radii >15 m (r_s⩽−0.498, P⩽0.007). Overall, lower the local male density around females, the longer their mean mating distance, without an effect on correlated paternity rates.

Genetic diversity and spatial genetic structure

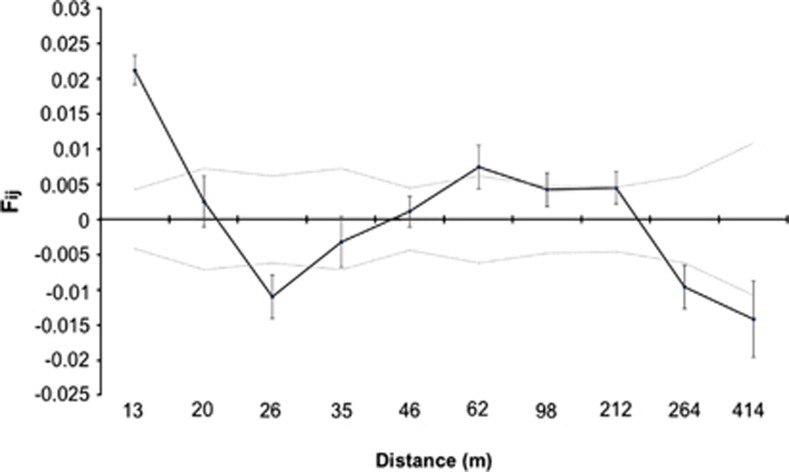
We found similar moderately high levels of genetic diversity (H_e, N_a and N_e) among the adults and the seeds (Table 4). There was no evidence of inbreeding in natural palms or in the seed pool, with both actually exhibiting heterozygote excess, although H_o was somewhat lower (and F_IS somewhat larger) for the seed sample, suggesting some degree of (biparental) consanguineous mating that diminishes at the adult stage (Table 4). The spatial autocorrelations analysis revealed weak but significant spatial genetic structure in the first distance class only, with palms located up to 21 m from each other being genetically more related than the average (Figure 3).

Table 4. Mean values of genetic diversity statistics for adult individuals of Phoenix canariensis at Acusa Verde population and seeds collected from mother palms.

Analysis level	N	Na	Ne	Ho	He	FIS
Mean population	182	3.18	3.23	0.664	0.598	−0.108*
Mean seeds	616	3.08	2.94	0.597	0.578	−0.031*

Abbreviations: Number of samples (N), rarefied allelic richness (N_a), number of effective alleles (N_e), observed heterozygosity (H_o), expected heterozygosity (H_e) and inbreeding coefficient (F_IS) are shown.

*P<0.05.

Figure 3.

Analysis of within-population spatial genetic structure of P. canariensis. Mean kinship coefficient (F_ij) and 95% confidence intervals (vertical lines) between adult individual pairs for 10 distance classes. The two dashed lines delimit 95% confidence intervals around the null hypothesis of spatial randomness, as determined by permutations.

Discussion

Our study provides new insights about the mating system and dispersal patterns of P. canariensis. Here, we provide detailed information about a major component of the dispersal process, focussing on pollen gene flow within and into an isolated population of the species.

The analysis of the effective pollen pool revealed restricted dispersal and uneven paternal contributions, resulting in moderate to low differentiation among pollen gametes siring different maternal progenies. The estimated effective number of fathers per maternal plant (N_ep=5.8) lies, respectively, in the medium and lower range of studied animal- and wind-pollinated trees (Smouse and Sork, 2004), although being very similar to the value obtained for the only other palm species studied so far (N_ep=5.4 for the widespread Oenocarpus bataua; Ottewell et al., 2012). Correlated paternity rates varied substantially among maternal progenies (ranging from null to 0.902), a variation that could not be explained by the spatial distribution of males relative to focal females. Other factors such as individual male fecundity variation and asynchronous flowering phenology could have determined the observed variation in individual mating system parameters.

The estimated within-population mating distance distributions revealed nonrandom mating, with a rapid decrease of effective pollen dispersal frequency over short distances but at same time a nonnegligible (10%) frequency of mating events over 200 m and a maximum mating distance that matched the maximum distance between individuals in the population. This leptokurtic pattern resembles the ones reported for different wind-pollinated tree species (Dow and Ashley, 1998; Streiff et al., 1999; Robledo-Arnuncio and Gil, 2005; Pakkad et al., 2008; Pluess et al., 2009). Considering the small size and geometry (with a densest main core) of the studied population, the observed mean dispersal distance (71 m) indicates that effective pollen moves across the whole population area, consistently with the contribution of most sampled males to the seed crop. The mean mating distance for P. canariensis is somewhat lower than values reported for some small population of wind-pollinated trees, such as Araucaria angustifolia (83 m; Bittencourt and Sebbenn, 2007) or Pinus sylvestris (83 m; Robledo-Arnuncio and Gil, 2005), but greater than estimates obtained within forest fragments of the anemophilous Fagus sylvatica (42–59 m; Piotti et al., 2012). Besides potential interspecific variation in dispersal capacity, variation in tree dispersal distance estimates in the literature is not surprising, given that the mating distance distribution can be expected to depend strongly on the spatial geometry of the population (size, density, continuity, shape and so on), as confirmed by several empirical studies (Hanson et al., 2008; Piotti et al., 2012). Further studies of pollen dispersal within more continuous areas of P. canariensis would be necessary to contrast the pattern observed in the small grove studied here. Moreover, many population of P. canariensis are limited to isolated crop boundaries, and it would be interesting to assess the consequences for pollen dispersal of this and other habitat changes (Hanson et al., 2008), as well as different kind of managements (Piotti et al., 2012).

Overall, the analysis of the correlation between local population demography and mating patterns showed no association between correlated paternity and effective pollination distance at the maternal progeny level, unlike previous observations for other tree species (Fuchs et al., 2003; Robledo-Arnuncio and Gil, 2005). As suggested by Ottewell et al. (2012), this independence puts into question simplistic general predictions of the effective number of fathers as simple functions of effective dispersal distance. Other factors independent of dispersal distance are indeed expected to affect effective paternal numbers under passive dispersal, such as local density and phenological asynchronies (Robledo-Arnuncio and Austerlitz, 2006; Hanson et al., 2008). We failed to detect any effect of local density around females on the effective number of males they mate with, and this would suggest that asynchronous phenology may be the key determinant of the latter and would be worthy of further investigation. Although flowering phenology was not measured during the study period, we have observed a temporally diffuse pattern of flowering in some other populations of P. canariensis during 2011 and 2012, with a 6- to 7-month long flowering period at the population level that contrasts with the short anthesis of inflorescences. In addition, the number of inflorescences per individual observed at any given time varies substantially, from approximately 1 to 6 in females and from 1 to 10 in males (I Saro, unpublished data). All this variability influences the daily rate of flowering overlap among the sexes and could explain the differentiation between effective pollen clouds received by different mother palms (Streiff et al., 1999; Kitamoto et al., 2006). Flowering asynchronies among sexes within populations, on the other hand, might increase the proportion of gene immigration from other groves, if local females become receptive when no local pollen is available. Further investigation on flowering phenology overlap among populations, sufficiently replicated to capture the expected variation across years (Pakkad et al., 2008), could help better understand the potential for long-distance effective pollen flow and its temporal variation in P. canariensis.

The spatially explicit mating model also rejected the random mating null model, yielding the best fits for biparametric leptokurtic pollen dispersal kernels. Several of these leptokurtic functions (such as the exponential-power and Weibull) could be suitable for modelling short-distance pollen dispersal for the species, at least over the scale of our study area, although extrapolation of these models over long distances would be risky, as indicated by their unrealistic means. It is well known that models with fairly different tails can fit about equally well the observed data (Austerlitz et al., 2004; Pluess et al., 2009), exemplifying the problematic characterization of both short- and long-distance pollination with a simple phenomenological function fitted over short distances only (Goto et al., 2006). Even if there was high uncertainty around our kernel's tail estimates (as is expected when using paternity data, see Niggemann et al., 2012), however, the mating model clearly supported a moderate amount of long-distance dispersal, with an estimated 12% of pollen immigration from outside the population. This estimate demonstrates potential for genetic connectivity among P. canariensis remnant populations, and it suggests that effective pollen dispersal can be better described by a combination of two processes in the species: local dispersion and long-distance transport, as found in other wind-pollinated species (Streiff et al., 1999; Oddou-Muratorio et al., 2005; Pluess et al., 2009). Compared with other wind-pollinated species, the estimated pollen immigration rate lies below values found in continuous or weakly fragmented populations (Dow and Ashley, 1998; Streiff et al., 1999), and above estimates reported for more strongly isolated populations (Robledo-Arnuncio and Gil, 2005). This significant quantity of immigrant pollen, to the extent that it were translated into effective gene flow among established seedlings, could greatly contribute to population genetic diversity, avoiding the drift-induced erosion of genetic variability expected for such a small local population size (Hamrick, 2004; Bittencourt and Sebbenn, 2007; Pakkad et al., 2008). Gene flow among palm groves would tend at the same time to homogenize neutral genetic variation over greater scales, at least among fragments within islands. An interesting topic for future studies would be to assess whether distant groves are also demographically connected via seed dispersal.

The mating model also revealed a significant pattern of anisotropic pollen flow, with a predominant northwest direction. Several factors may be invoked to explain anisotropic pollen flow, such as prevailing wind directions at the regional and local scales, and air turbulences within the canopy. The Acusa Verde population grows within a ravine to leeward of the prevailing northeastern winds in the island that are thus unlikely to have a large impact on local air movement. Previous studies for wind-pollinated species have found a similarly weak influence of prevailing regional winds on pollen dispersal direction (Austerlitz et al., 2007; Pluess et al., 2009), suggesting that local winds, probably variable across years, may be major determinants of pollen movement. Altitude and orientation have a large influence on local climatic conditions in the Canary Islands; the pollination season (summer) is climatically the most stable, with an inversion layer at an altitude of 800–1000 m separating lower moist and cool from upper dry and warm air. Our study population is located at an elevation of 500–600 m, and hence we would expect local air movement being mainly determined by diurnal ascendant anabatic wind and nocturnal descendant katabatic wind, along the north to northwest oriented ravine (Figure 1), with the upper inversion layer acting as a barrier and the high buoyancy of P. canariensis pollen (maximum diameter of 30 μm, usually from 12 to 25 μm; Reille, 1998) favouring its altitudinal airborne transport. It would indeed be worth testing the possibility that among-population pollen exchange were restricted to palm groves within the same ravine, or at neighbouring ravines, as long as they are not on opposite extremes of the inversion layer. The fact that most effective pollen flows to northwestern areas might be indicating that pollination takes place largely at night or dawn (consistently with anthesis timing), to the extent that such altitudinal wind patterns are truly determining mating patterns. At the densest cores of the population, on the other hand, pollen will probably be subject to vertical and lateral stochastic turbulences within the canopy (Levin and Kerster, 1974; Di-Giovanni and Kevan, 1991; Streiff et al., 1999), with an unpredictable directional outcome.

Although we lack information on prefragmentation diversity levels, the moderate to high level of genetic variety observed might indicate some resilience of the genetic diversity of the species (neutral) to demographic disturbance. Moreover, the genetic diversity level found in the adult individuals remained similarly high in the seed crop (H_e values of 0.59 and 0.57, respectively), with a similar allelic richness in the progeny (N_a=3.18 versus 3.08, respectively), consistently with the maintenance of genetic diversity across generations (possibly enhanced by gene flow). On the other hand, we found heterozygote excess in both seeds and adults (F_IS=−0.027, P<0.05, and F_IS=−0.098, P<0.05, respectively). Selective factors are not likely to have affected the heterozygosity levels of the employed, putatively neutral, microsatellite markers. The observed pollen immigration rate, if originating in genetically divergent populations, could however have enhanced the heterozygosis of the seed crop. Moreover, heterozygote excess is expected in small populations of strictly outcrossing species that could explain the observed levels for both adults and seeds (Balloux, 2004).

Considering the relatively large range of pollen dispersal, one could have expected an effective mixing of genes by pollen flow within the study of P. canariensis population, hampering spatial genetic structuring. However, spatial genetic structure is also determined by restricted seed dispersal, all the more with large correlated paternity among seed progenies (Vekemans and Hardy, 2004). The seed dispersal system of P. canariensis is not well known. The common raven (Corvus corax) has been cited as an effective seed disperser of the species (Nogales et al., 1999), although there are possibly other dispersers. However, it seems that the vast majority of fruits fall and remain within few metres of the maternal palm (I Saro, personal observation), and it is likely that seed dispersal is more restricted than pollen movement in this palm species. The relatively high value of S_p is comparable with reported values for species with rather restricted pollen and seed dispersal, particularly similar to those of barochorous species (Vekemans and Hardy, 2004). A joint analysis of seed and pollen dispersal would be necessary to measure their relative contribution to effective gene flow among established seedlings.

Implications for conservation

The dispersal and genetic parameters estimated in this study may prove useful for eventual genetic conservation plans of P. canariensis. On one hand, the genetic structure of the effective pollen cloud and the large variability in correlated paternity rates among maternal families calls for abundant replication at the family level in any germplasm collection for ex situ conservation. Moreover, the observed spatial genetic structure among adult palms and the estimated average pollination distance suggest a minimum separation distance of 70 m among mothers for seed collection in order to reduce relatedness among maternal families. On the other hand, given the evidence of significant intraspecific pollen dispersal into an isolated P. canariensis population found in the present study, the possibility of interspecific genetic introgression via pollen flow from allochthonous Phoenix species cannot be disregarded, at least considering spatial factors alone. For instance, the presence of individuals of P. dactylifera in both urban gardens and cultivated populations, even if distant, could be more threatening than previously thought and renders necessary the assessment of pollen exchange between natural and allochthonous stands.

Data archiving

Genotypes for the data set of 798 samples are available from the Dryad Digital Repository: doi:10.5061/dryad.1pb6t.

The authors declare no conflict of interest.