Evaluating Public Health Interventions: 2. Stepping Up to Routine Public Health Evaluation With the Stepped Wedge Design

Abstract

In a stepped wedge design (SWD), an intervention is rolled out in a staggered manner over time, in groups of experimental units, so that by the end, all units experience the intervention. For example, in the MaxART study, the date at which to offer universal antiretroviral therapy to otherwise ineligible clients is being randomly assigned in nine “steps” of four months duration so that after three years, all 14 facilities in northern and central Swaziland will be offering early treatment.

In the common alternative, the cluster randomized trial (CRT), experimental units are randomly allocated on a single common start date to the interventions to be compared. Often, the SWD is more feasible than the CRT, both for practical and ethical reasons, but takes longer to complete. The SWD permits both within- and between- unit comparisons, while the CRT only allows between-unit comparisons. Thus, confounding bias with respect to time-invariant factors tends to be lower in an SWD than a CRT, but the SWD cannot as readily control for confounding by time-varying factors. SWDs have generally more statistical power than CRTs, especially as the intraunit correlation and the number of participants within unit increases.

Software for both designs are available, although for a more limited set of SWD scenarios.

This is my second commentary for the section, “AJPH Evaluating Public Health Interventions,” which addresses critical methodological issues that arise in the course of evaluating public health interventions. In the first commentary,¹ I defined implementation science, impact evaluation, program evaluation, and cost-effectiveness research, and argued that from a methodological perspective, these various disciplines largely overlap. In this commentary, I will launch a discussion of best practices for the design of studies for this overlapping set of disciplines, including some new and not-so-new developments. I start with the stepped wedge design (SWD), because of the promise of this largely underutilized approach to greatly expand causal evaluations of public health interventions in the routine course of rolling them out.^2,3 In fact, a well-written summary of this topic has appeared previously in AJPH, with the major difference being the nomenclature.⁴ In this earlier article, the SWD was called the multiple baseline design (MBD). So readers, please note: SWD = MBD, and if you already understand the advantages and disadvantages of the MBD, as well as how to adequately power studies utilizing this design, you need to read no further.

For the rest, let’s start with the fundamental question: What is an SWD? It is a design in which an intervention is rolled out in a staggered manner over time, in groups of experimental units, so that as time goes on, more and more units experience the intervention. By the end, all units experience the intervention. In a randomized SWD, the time at which each unit begins to receive the intervention is randomly assigned. In the observational version, the intervention start time for each facility is not randomized.

EXAMPLES

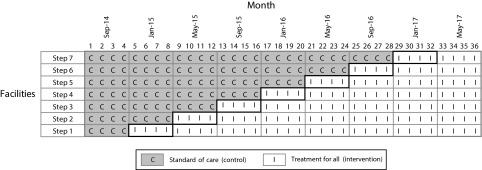
Since I learn best from the specific to the general and I imagine many of you do as well, that is, loosely speaking, inductively, I’ll give two examples from my current work. First, with the Swaziland Ministry of Health in partnership with the MaxART Consortium, we are using an SWD to evaluate the impact of offering antiretroviral therapy (ART) regardless of CD4 count or disease stage to all HIV-positive clients among the 14 health facilities serving northern and central Swaziland (MaxART). After an initial four-month period of observation, the date at which universal ART access would be offered to new and returning pre-ART patients was randomly assigned to the 14 facilities in nine “steps” of four months duration. By the end of the three-year study period, all 14 facilities will be offering early ART access. (Figure 1). Within the context of a growing body of evidence worldwide that early access to ART promotes healthier and longer living for people with HIV, while at the same time reducing HIV transmission rates,^5,6 questions remain about the feasibility of early access in resource limited settings, its impact on sicker patients already initiated to ART, and its acceptability to early stage patients yet to experience the adverse effects of their disease. Thus, in the context of Swaziland’s position as a country with one of the world’s highest HIV prevalence rates (31%),⁷ the SWD emerged as an attractive evaluative tool to study the “real-world” implementation questions that the Swaziland Ministry of Health was facing, with sound ethical implications.

FIGURE 1—

MaxART Stepped Wedge Design, Swaziland

Another project I am currently working on, together with colleagues, involves the assessment of postpartum intrauterine device (IUD) insertion as a safe, acceptable, and effective means to prevent unintended pregnancy closely following a current birth. Recently launched in Sri Lanka, Nepal, and Tanzania in collaboration with the International Federation of Gynecology and Obstetrics, after a three-month baseline period of observation, three randomly assigned facilities will start the postpartum IUD program, which will run for nine months. Six months after the first three facilities start, the second three facilities will start, with the program running for three months at these facilities, so that nine months after the study has begun, the program will be in place everywhere. As in MaxART above, although there is substantial evidence that postpartum IUD insertion will reduce unintended pregnancy, questions remain about the safety, acceptability, and sustainability of this intervention in low- and middle-income countries where uptake is currently quite low. In 2013, 14% of married or in-union women aged 15 to 49 years were using IUDs, but only 1% in the least developed countries and 0.7% in sub-Saharan Africa.⁸ Although the Ministry of Health in each country was eager to begin offering the program, they did agree to the staggered roll-out, both for practical reasons and to make it possible to obtain a rigorous evaluation of the program’s effectiveness.

STEPPED WEDGE DESIGN

In an SWD design, there is an initial baseline period of observation in which no experimental unit experiences the intervention. Usually, the time at which the intervention begins at each unit is randomized, imparting causal rigor by design, although observational versions of this design can be considered as well, for which causal inference can be facilitated at the analysis stage. The SWD is a special case of a cluster randomized design because the experimental units are typically facilities, practices, villages or neighborhoods, which contain a common or varying number of participants. Outcomes can be continuous, binary or of survival form, and can also be of a repeated continuous or binary nature.

The first publication using this design was a trial in Gambia looking at the effectiveness of a childhood vaccination program against hepatitis B to prevent the incidence of chronic liver disease and hepatocellular carcinoma, phasing in the program in three-month steps over a four-year period for a total of 16 steps across the 17 regions of the country covering 1.2 million children in total.⁹ Another of the largest and most well known examples of the use of this design was in the evaluation of former Harvard School of Public Health’s Dean Julio Frenk’s PROGRESA (Programa de Educación, Salud, y Alimentación) program, later renamed Oportunidades, launched when Frenk served as Minister of Health for Mexico. PROGRESA/Oportunidades was a conditional cash transfer program targeting the country’s poorest families, providing them with financial incentives for uptake of recommended public health and nutrition practices and for keeping children in school. Incentives were contingent on regular attendance at health clinics that supplied these essential health and nutrition services. PROGRESA was evaluated through a staggered roll-out of these policies among 495 communities, 314 of whom were randomized to program initiation in the first two years and the remaining 181 communities were initiated in the program’s third year.¹⁰ This is an example of the simplest version of an SWD, with only three steps: baseline, the first two-year intervention period, and then, the second intervention period. The postpartum IUD project I described above also has this three-step design.

These are but a few examples of SWDs in practice. A citation search on the seminal 2007 Hussey and Hughes paper on SWD design and analysis¹¹ or the term “stepped wedge” brought up around 300 relevant publications between 2003 to the present, of which a small fraction were methodological in nature, the remainder exemplifying applications of the design in a wide range of public health settings, including occupational health, HIV/AIDS care and treatment, chronic disease screening, gerontology, substance abuse treatment, obesity prevention and mitigation, and many more.

STEPPED WEDGE DESIGN VS CLUSTER RANDOMIZED TRIAL

In my experience, an SWD is considered as a possible alternative to a parallel group” cluster randomized trial (CRT), where clusters are randomized to intervention or control on a single common start date. Table 1 provides a schematic illustration contrasting these two options. In both situations, the treatment is, or can be, balanced so that the same number of clusters and participants receive intervention and its comparator. The choice between these two options is driven by considerations of feasibility, validity, and power. I will next consider the advantages and disadvantages of these two designs with respect to each of these features.

TABLE 1—

Enrollment and Randomization Plans for a Hypothetical Cluster Randomized Trial (CRT) and Stepped Wedge Design With the Same Number of Clusters and Same Proportion Randomized to the Intervention

	CRT	Stepped Wedge Design
Cluster	Time	Time	Time	Time	Time	Time
1	1	1	2	3	4	5
2	x	o	x	x	x	x
3	x	o	x	x	x	x
4	x	o	o	x	x	x
5	x	o	o	x	x	x
6	o	o	o	o	x	x
7	o	o	o	o	x	x
8	o	o	o	o	o	x
9	o	o	o	o	o	x

Feasibility

SWDs are often the only option for including a randomized component in a public health evaluation, implementation science projects, pragmatic trials, program evaluations, and impact evaluations, for political, ethical or practical reasons, or some combination thereof. Politically, it is often the case that the entity hosting the evaluation, henceforth called the “host,” cannot or will not permit any other version of randomization. (By host, I mean those responsible for implementing the intervention and its evaluation, to be distinguished from the funder, although in some cases, and hopefully as time goes on more so, they are the same. For example, the hosts of MaxART are the Swazi Ministry of Health and clinical staff at the 14 facilities at which the evaluation is taking place, while the funder is the Dutch Postal Code Lottery and other funding consortium members.) Politically, randomization and experimentation on human participants is unacceptable in many programmatic settings, and politicians and policymakers do not wish to expend political capital advocating for such, in what may well be a losing battle in the end. In Oportunidades, hosts needed to be persuaded even to allow the SWD roll-out. Somewhat related to the political reasons, once an intervention has advanced beyond the evaluation of its efficacy to an evaluation of its effectiveness, ethicists may argue that the evidence is beyond that which can reasonably be considered to be in equipoise, and standard randomization methods may no longer be acceptable. On the other hand, it can reasonably be argued that although efficacy has been “proven,” effectiveness is still in equipoise, thus justifying randomization by either the SWD or CRT approach. There are many examples where efficacious interventions have been found to be ineffective, providing strong support for this ethical argument.^12,13 In any event, if ethics are at all in question, the SWD clearly dominates, since the intervention will be put in place at all facilities by the end of the study.

There are practical reasons why an SWD is desirable: simply put, program implementers are not able to roll out an intervention of interest at the same time in multiple locations. Thus, the CRT, even if preferred for other reasons, is often infeasible. Adding an element of randomization to the timing of roll-out, that is, implementing a SWD, may often add little complexity to the overall program roll-out, yet greatly strengthen the validity of the causal inference to be obtained subsequently in the evaluation. On the other hand, an important advantage of the CRT is underscored by Table 1: the CRT enrollment period is completed in 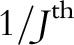the time it takes to complete the SWD evaluation, where 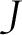is the number of step times (the columns in Table 1). Note that this schematic illustrates the enrollment plan, not the follow-up plan. The duration of participant follow-up for ascertaining outcomes needs to be added to the duration of the enrollment period to obtain the total study time. The feasibility of SWDs is discussed in further detail in a recent article that, interestingly, took a qualitative research approach to its investigation, interviewing practitioners from low-, middle-, and high-income countries engaged in SWD-based research.¹⁴

Validity

Although both CRTs and SWDs use randomization to control for confounding, thereby allowing valid causal inferences to be made, they each have some limitations from a causal inference perspective. To consider the relative validity advantages and disadvantages of these two options, we need to assess their potential for bias attributable to confounding. In a cluster-randomized design, randomization guarantees on average—that is, over infinite replications of the same study, no bias. Under the null, when there is no intervention effect, the P value of the test of no intervention effect on the outcome expresses the probability, exactly or approximately depending on the statistical test used, that the observed imbalance in the outcome distribution between the two arms or anything more extreme could have occurred by chance when there is no intervention effect. Randomization is truly useful with regard to hypothesis testing. However, as shown in the box on this page, randomization does not guarantee unbiasedness of the effect estimate or its confidence intervals in any given study.

Confounding Can Commonly Occur in Cluster Randomized Trials Despite Randomization

To illustrate why randomization does not guarantee unbiasedness of the effect estimate or its confidence intervals in any given study, let’s take a look at the Mwanza Trial of Sexually Transmitted Disease Treatment of HIV Prevention,^15–17 discussed in Hayes and Moulton’s book on cluster randomized trials.¹⁸ This study cluster-randomized 12 rural Tanzanian communities to a sexually transmitted disease prevention intervention or standard of care, matching the communities by expected HIV prevalence rates ranging from 1.6% to 8.6%. There are 12 choose 6, equal to 924 unique ways to assign 6 of 12 communities to the intervention and 6 to control, and these can be enumerated through combinatorial analysis. I thus calculated that, assuming the range of baseline HIV rates observed in these study communities, “bad luck” randomizations leading to a relative risk of 1.1 or greater, or 0.9 or less, would occur, on average, 73.4% of the time, and “bad luck” randomizations leading to a relative risk of 1.2 or greater or 0.8 or less would occur 50.5% of the time. For example, with a probability 1 in 924 (∼0.1%), the communities with the 6 highest HIV prevalence rates would be randomly assigned to the control and the communities with the 6 lowest to the intervention. In this case, given the observed rates (Table 5.1 in Hayes and Moulton¹⁸), the effect estimate would be 0.5 on the relative risk scale, suggesting a strongly beneficial intervention when there may not be one at all.

SWDs are also susceptible to these residual imbalances, as they, too, will typically include a similarly small number of clusters. However, this design has a major important advantage—the staggered roll-out allows for within-cluster comparisons of intervention effects across time, as well as time-specific between-cluster comparisons. When outcomes rates do not vary by calendar time over the duration of the study, the within-cluster comparisons will provide causal estimates of the intervention effect. In studies of relatively short duration, that assumption is likely to be met for all practical purposes, but in studies of longer duration, the assumption will be less tenable and the between-cluster comparisons become very important to examine as well, since those are controlled for confounding by time as well as randomized to provide balance, on average, over infinite replications of the same trial. By contrast, although as shown in the box on this page, the CRT can be plagued with residual confounding for effect estimation despite randomization, it controls completely, by design, for confounding attributable to time. SWDs are ideally suited for short-term outcomes and point exposures, in which case, control for confounding by time is likely unnecessary. These points have implications for analysis, to which we will return to in a later column.

Efficiency

If one design is invalid or infeasible for reasons discussed above, it is inadvisable to consider it any further. Otherwise, once feasibility and validity of both designs is established, we can next consider relative efficiency. Although there is a very large body of work on efficient design of CRTs, covered in great detail in three books,^18–20 and a number of publications on methodology for efficient SWDs,^3,11,21 there are only a few published comparisons of the relative efficiency of SWDs and CRTs. The most recent work concludes that, for studies in which the outcome is a single continuous variable, although this could easily be adapted to include a change score, that is, a within-subject before-after difference, the relative efficiency of the two designs varies most strongly as a function of the intracluster correlation coefficient (ICC) and the number of participants within each cluster. The ICC measures the extent to which the outcome varies between clusters, presumably because of unmeasured risk factors. When the ICC is small—that is, when, in the absence of the intervention, the outcome is similar across clusters—the CRT tends to be more efficient; when the ICC is large, the SWD tends to be more efficient. The power of the CRT decreases dramatically as a function of the ICC, and after a certain value, the CRT becomes infeasible because of the drastic sample size requirements. The power advantages of the SWD increase as the number of steps increase, and, in general, CRT power improves faster with increasing number of clusters, while the SWD power increases faster with increasing number of participants within clusters. The extent to which the results for SWDs with continuous endpoints apply to studies with binary outcomes, as is typically the case in much public health research, or survival endpoints, is unknown. In addition, the extent to which these results are altered by a varying number of participants within clusters, known to dramatically reduce power in CRTs^22,23 and a common feature of many evaluative settings, has not yet been explored. These results all assume the existence of a time effect; the relative advantages of the two approaches have not yet been studied when a time effect can be reasonably be ignored.

SOFTWARE

Some of these topics are active areas of work in my own group at Harvard. Software for CRTs is readily available^24,25 and, in my experience, easy-to-use. Hughes’ free, easy to use Excel spreadsheet and R package can be downloaded for SWD with continuous and binary endpoints.²⁶ Please note that in Hughes’ spreadsheets, 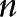is the number of observations per time step per cluster, that is, the spreadsheet cell count, not the total number of observations per time step as it is labeled in the spreadsheet, that is, not the spreadsheet column total. In addition, the Hughes’ materials parameterize between-cluster variation by the between-cluster coefficient of variation, following,¹⁸ rather than by the ICC, as in,¹⁹ a formulation I find more intuitive. It is easy to prove that, for binary endpoints,

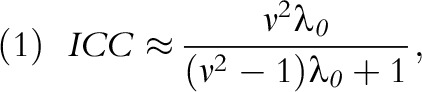where 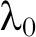is the average baseline rate in the control group and 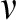is the between-cluster coefficient of variation (i.e., the square root of the between-cluster variance divided by the average baseline rate).

CONCLUSIONS

In conclusion, the SWD has improved validity over an observational evaluation of a public health intervention, although even the latter is substantially better than no evaluation at all. When a small number of clusters are available, as is often the case, the SWD may be the only feasible option for randomized evaluation. Its major disadvantage compared with a CRT is its considerably longer duration. Ethical advantages are perceived by implementers and the design often matches the natural schedule of program roll-outs. I encourage public health practitioners to incorporate an SWD in the roll-out of new programs and interventions, to enhance the causal rigor of subsequent evaluations.