Estimation of Musculotendon Kinematics under Controlled Tendon Indentation

Abstract

The effects of tendon indentation on musculotendon unit mechanics have been left largely unexplored. Tendon indentation is however routinely used in the tendon reflex exam to diagnose the state of reflex pathways. Because muscle mechanoreceptors are sensitive to mechanical changes of the musculotendon unit, this gap in knowledge could potentially impact our understanding of these neurological exams.

Accordingly, we have used ultrasound (US) imaging to compare the effects of tendon indentation with the effects angular rotation of the elbow in six neurologically intact individuals. We used sagittal ultrasound movies of the biceps brachii to compare length changes induced by each of these perturbations. Length changes were quantified using a pixel-tracking protocol.

Our results show that a 20 mm indentation of the distal tendon is broadly equivalent to a 15° elbow rotation. We also show that within the imaging window the strain differences between the two stretching protocols are statistically insignificant. Finally, we show that there exists a significant linear relationship between the two stretching techniques and that this relationship spans a large rotational angle to indentation depth.

We have used a novel tendon probe to administer controlled tendon indentations as a way to characterize musculotendon kinematics. Using this probe, we confirm that tendon indentation can be physiologically equated with joint rotation, and can thus be used as an input for muscle stretching protocols. Furthermore, this is potentially a simpler and more practical alternative to externally imposed angular joint motion.

I. Introduction

In the course of the standard neurological exam, a clinician records myotatic reflexes by stretching muscles in two ways: by rotating a joint, or by tapping a tendon with a reflex hammer. Both techniques stretch the muscle, and both stimulate the muscle receptors that trigger the reflex responses. To the best of our knowledge, however, the kinematic relationship between each stretching paradigm has not been explored. Furthermore, the muscle kinematics recorded in response to tendon indentation alone are also largely unexplored, potentially hindering our basic understanding of stretch reflex mechanisms.

We now know that the tendon reflex response is dependent on several controllable factors, such as the amplitude of the tendon tap and the frequency with which the tap is delivered (Voerman (2005)). More recently, we have shown that controlling the depth of tendon indentation prior to the tap also elicits reflex patterns resembling ones found for progressive whole limb rotation (Chardon (2014)). Accordingly, there is potentially a strong correlation between the parameters impacting the tendon reflex and the kinematics of the muscle prior, during and after the tendon tap. However, we do not currently know how much stretch is delivered by tendon indentation, and how this stretch compares with that generated by a standard angular joint rotation.

Presently, global musculotendon unit movements are routinely studied using ultrasound (US) medical imaging, because of its unparalleled ability to record tissue motion in vivo. However, the majority of the studies stretch a muscle using controlled joint rotation (Blemker (2007)). In contrast, tissue indentation protocols are often used to assess local muscle mechanics. When applied in cadaveric specimens (Palevskial (2006); Van Loocke (2006&2008)) or on muscle belly (Iivarinen (2011); Leonard (2001); Uchiyama (2000)), the indenter is used to record compression force and the associated tissue displacement, recorded either from the indenter motion, or from imaging techniques (Moerman (2011); Zheng (1996)). While extremely important, these indentation paradigms can only provide insights about local rather than global musculotendon unit mechanics. There is also no way currently to integrate findings drawn from joint rotation with those derived from tissue indentation.

In this study, we explore and compare whole muscle kinematics of the biceps brachii (BIC) muscle under tendon indentation and during a standard joint rotation at the elbow. We plan to use US imaging as a tool to record internal muscle deformation. We further seek to demonstrate whether muscle length changes during tendon indentation can be equated with joint rotation, and whether such tendon indentation produces physiologically meaningful changes in muscle length. We chose the BIC as our model system because it has an easily accessible distal tendon. For our muscle kinematics measures, we used B-mode US imaging.

II. Method

A. Participants

Six neurologically intact individuals, of age 31±5.2 years, were recruited and their dominant side was tested once. All participants gave informed consent via protocols approved by the Institutional Review Board under the Office for the Protection of Human Subjects at Northwestern University.

B. Experimental Setup

Each subject was seated in a Biodex chair and the forearm was braced to a custom arm rotation device (Fig. 1-A). The subject’s position was adjusted such that shoulder-abduction was 10°, shoulder-flexion 10°, elbow-flexion was 120° and forearm-supination was 0°. The arm brace was also adjusted such that the axis of rotation of the elbow was collinear to the axis of rotation of the rotation device.

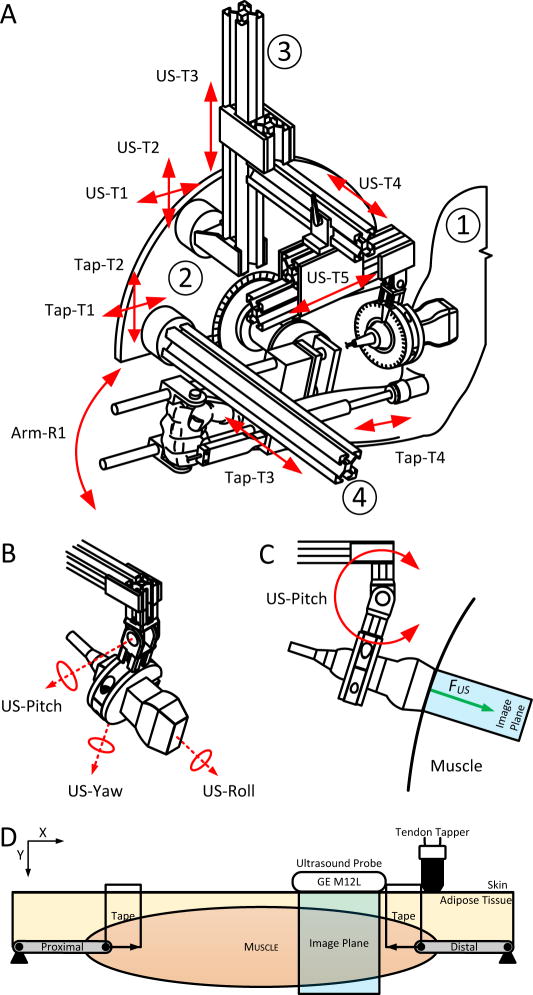
Fig. 1.

Experimental Setup. (A) Schematic of the whole experimental setup. There are four parts to the schematic. ➀ is the cutout of the subject’s arm. ➁ is the rotational motor to which is attached the brace for the lower arm. ➂ is the ultrasound probe holder with the probe. ➃ is the tendon tapper holder with the tendon tapper. (B) Close up of the schematic of the end effector of the ultrasound probe holder. The design allows the probe to be adjusted in the roll, pitch and yaw to optimize for the quality of the ultrasound image. (C) Shows the interaction force – FUS – with the skin and muscle. (D) Schematic of the placement of the different probes relative to the biceps brachii. From left to right, the tendon tapper is set above the tendon-muscle junction. A piece of clear tape from the tendon tapper, acts as the reference for the ultrasound probe.

The US probe and tendon tapper were placed near to the distal muscle-tendon junction of the BIC, identified using US and marked by tape (Fig. 1). Specifically, using the 8 adjustments of a custom US probe holder, we placed the probe orthogonal to the shorter axis of the BIC (sagittal-plane), closest to the distal tendon at 1cm distance. We then used the rotational adjustments to increase the reflectivity of the tissue below and further ensured that the muscle could be tracked throughout the range of angles. We then placed the tendon tapper such that its tip indented the distal end of the BIC muscle at an angle of attack 90° to the humerus.

Each protocol had 5 trials. In a single rotation trial, the forearm was extended at a PID controlled velocity (0.08rad/s) from 120° elbow flexion to 150° and then rotated back after a 5 second pause. For a single indentation trial, the tendon tapper was lowered onto the tendon at a PID controlled velocity (5mm/s) from skin (0mm) to a distance of 20mm and was then returned after a 5 second pause. Subjects were instructed to keep their muscles quiescent during the trials.

The US movies were collected using a GE-Logiq9-R6.0.5 and a GE-M12L probe set at a frequency of 14MHz, gain of 63dB at a recording depth of 30mm and width of 50mm. For each rotation and tendon indentation cycle, we stored for later analysis (533×436) grayscale DICOM movies. We used Matlab-xPC-2011a to collect, to control the trajectories of motors and to synchronize the motors with the US machine.

C. Data Analysis

1. Motion Tracking – X, Y & Total Distance

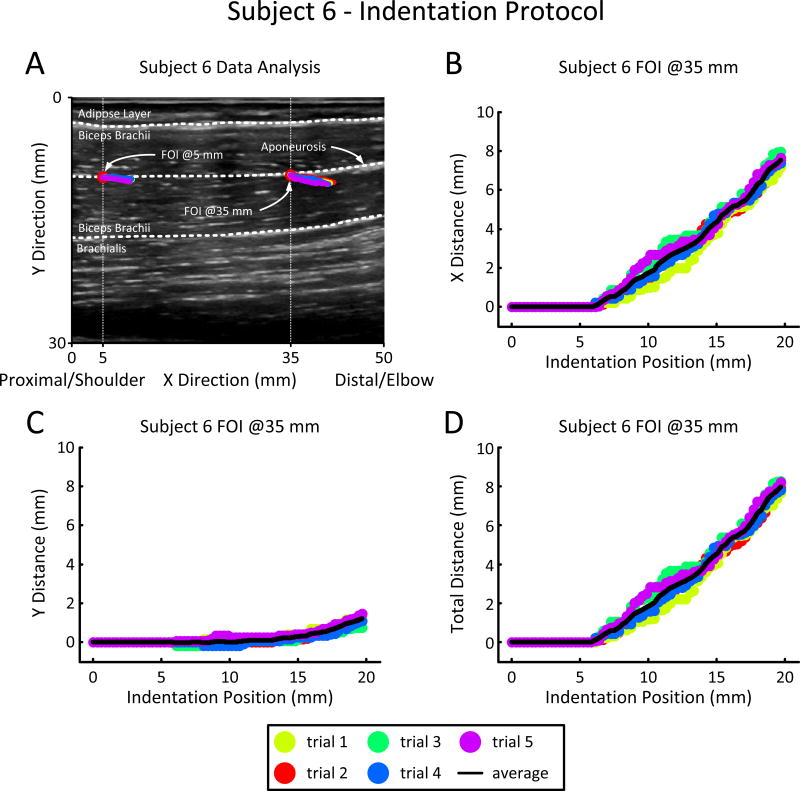
The motion or kinematics of the BIC for each stretching protocol was estimated by tracking features within the US images by eye. Prior to tracking, two feature of interest (FOIs) were identified along the main axis of the muscle along the aponeurosis (dashed middle white line in Fig. 2-A) at an ultrasound image width location of 5mm and 35mm respectively. In order to qualify, the FOI had to be present in both protocols and had to remain trackable for all movie frames (f = 1,2, …, m).

Fig. 2.

Example of tracking features of interest (FOI) using ultrasound movies for the indentation protocol. (A) Initial ultrasound image prior to being indented. The image is 50 mm wide and 30 mm deep with the depth starting at the top (i.e. skin-US probe layer). The biceps brachii is sectioned by the upper and lower dotted white lines. The adipose layer is above the upper dotted white line and the brachialis is below the dotted white line. The center dotted white line follows the aponeurosis of the biceps brachii. Along the aponeurosis are the FOI @5mm and the FOI @35mm shown by red dots and referenced to the image width by vertical dotted lines. Superimposed on the FOIs, in color, are the five different tracking trajectories during the 20 mm indentation of the distal tendon from skin. (B & C) Displacement/Indentation Position plots of the Y and X pixel as the distal tendon is being indented. (D) Distance/Indentation Position plots of the FOI as the distal tendon is being indented.

Given the FOIs, the US movies were analyzed by hand by two different raters using a custom script. Each rater was given the location of the FOI only for the initial frame. The first rater reanalyzed the US movies at a later date to test within-rater repeatability.

Subsequent to tracking, the raw pixel vectors [X_f,Y_f] of the FOI (Fig. 2-A) were offset from their initial positions and converted into metric units. Given the protocol, the [X_f,Y_f] pairs were synchronized with the rotation angle or the indentation position giving two (f x 2) vectors [P_f,X_f] & [P_f,Y_f] where P is either rotation angle or the indentation position (ex: vectors plotted against each other (Fig. 2-B&C)). Finally, the Total Distance (TD) vector [P_f,TD_f] travelled by the FOI was calculated with the following cumulative sum equation:

$${TD}_f=\sum _{i=2}^f\sqrt{{(x_i-x_{i-1})}^2+{(y_i-y_{i-1})}^2}\text{with}\{\begin{array}{c}{TD}_1=0\\ (f=2,\dots ,m)\end{array}$$

where x_i and y_i are the sequential pixels in the X and Y direction (Fig. 2-D).

2. Rotation-Indentation Map

The Rotation-Indentation Map relates joint angle to tendon indentation position. The map was calculated by finding the matching distances travelled by the FOI for each protocol and subsequently matching their respective rotation angle and indentation position (Fig. 3-C).

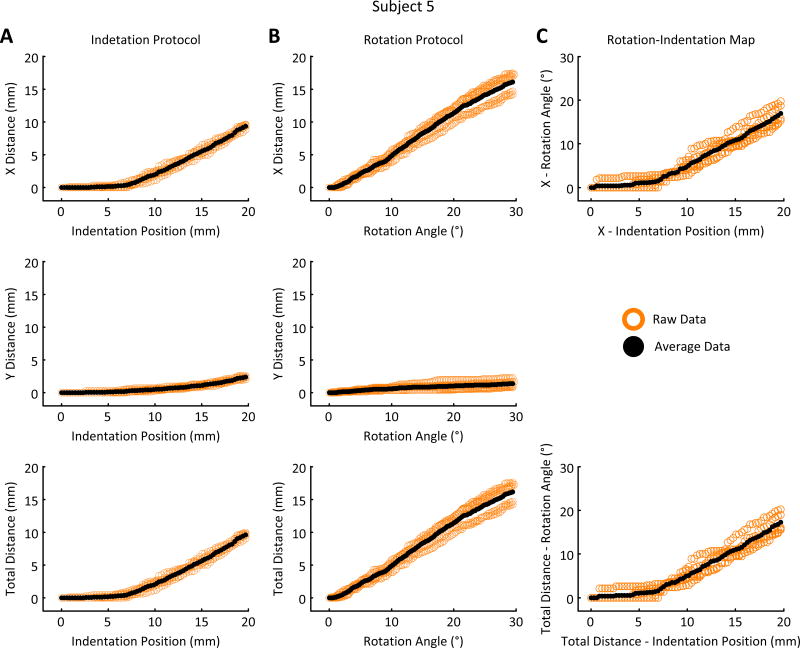
Fig. 3.

Example of the average results obtained from tracking the feature of interest (FOI) for the indentation of the distal tendon of the biceps (A), the rotation of the elbow (B) and the Rotation-Indentation Map (C) for a single subject. These results are the average of the five measured cycles – in/out for indentation or extend/flex for rotation. (A & B – top) Shows the FOI’s distance travelled in the x direction relative to the indentation position and the rotation angle. (A & B – middle) Shows the FOI’s distance travelled in the y direction relative to the indentation position and the rotation angle. (A & B – bottom) Shows the FOI’s total distance travelled in the x and y direction relative to the indentation position and the rotation angle. (C – top & bottom) Shows the Rotation-Indentation Map in the x direction and for the total distance. This map was created by combining the data displayed in A & B – top & bottom (see Section II.C.2).

3. Regional Strain

Regional strain provides an estimate of the strain registered along the main axis of the imaged BIC for each stretch protocol. It is estimated using the following equation:

$${\epsilon }_{\mathit{regional}}=\frac{{TD}_{@35}^{\mathit{max}}-{TD}_{@5}^{\mathit{max}}}{L_{@35}^0-L_{@5}^0}.$$ Eq. 1

${TD}_{@35}^{\mathit{max}}$ is the maximum TD travelled by the FOI@40mm, ${TD}_{@5}^{\mathit{max}}$ is the maximum TD travelled by the FOI@5mm, $L_{@35}^0$ is the initial X position of the FOI@35mm and $L_{@5}^0$ is the initial X position of the FOI@5mm.

D. Statistical Analysis

1. Models

For each data set (5-trials), we fit three models: a linear curve (f(x) = p₁x + p₂), an exponential (f(x) = p₁e^p₂x), and a piecewise continuous function as described by Quapp 1998:

$$f(x)=\{\begin{array}{ll}\hfill a_1{e}^{b_{1}x}+c_1,& x\le x_1\hfill \\ \hfill a_{2}x+c_2,& x>x_1\hfill \end{array}\text{such}\text{that}\{\begin{array}{c}{a}_1{e}^{b_1{x}_1}+c_1=a_2{x}_1+c_2\\ a_1{b}_1{e}^{b_1{x}_1}=a_2\\ b_1>0\\ f(0)=a_1+c_1\end{array}$$ Eq. 2

where a₁, b₁, c₁, a₂ and c₂ are parameters to be optimized and x₁ is the connection point between the two curves.

For each data set, we retained the model with the lowest Akaike information criteria (AIC) (Kullback (1951)). The confidence interval of each of the piecewise parameters was estimated by a 1E4 iteration bootstrap of the fit using the residuals of the fit with largest R² in a 500 random initial conditions search (Table-1).

Table 1.

Pooled results along the X, Y and Total Distance directions for the Rotation and Indentation protocol, as well as the Rotation to Indentation Map.^a

Measure	Direction	Rotation (n = 6)	Indentation (n = 6)	Map (n = 6)
Max Distance (mm)	X Direction	10.17 (±3.30)RDX	6.56 (±1.83)IDX	14.49 (±2.15)MAX
	Y Direction	0.68 (±0.67)RDY	1.34 (±0.76)IDY
	Total Distance	10.60 (±3.38)RDT	7.16 (±1.98)IDT	14.94 (±2.10)MAT
Slope (mm/mm)	X Direction	0.39 (±0.11)RSX	0.54 (±0.13)ISX	1.26 (±0.19)MSX
	Y Direction	0.03 (±0.04)RSY
	Total Distance	0.40 (±0.11)RST	0.57 (±0.14)IST	1.34 (±0.23)MST
Transition Point (mm)	X Direction		10.78 (±1.51)ITPX	10.08 (±2.69)MTPX
	Y Direction
	Total Distance		10.95 (±1.42)ITPT	11.41 (±0.93)MTPT
Lowest AIC	X Direction	line	piecewise	piecewise
	Y Direction	line
	Total Distance	line	piecewise	piecewise
Direction Ratios	X/TD	96% (±0.02)	92% (±0.03)
	Y/TD	4% (±0.02)	8% (±0.03)

a: Data are mean (± SD).

RDX, RDT, IDX, IDY, IDT,MAX, MAT: Max Distance/Angle Data are statistically different than 0 (p-value < 0.05).

RDY: Max Distance Data are not statistically different than 0 (p-value < 0.05).

RDX, IDX: Max Distance Data are statistically different (p-value < 0.05).

RDT, IDT: Max Distance Data are statistically different (p-value < 0.05).

RDY, IDY: Max Distance Data are statistically different (p-value < 0.05).

ITPX, ITPT: Subject Individual Transition Point Data are not statistically different (p < 0.05)

2. Statistical Tests

To test the significance between parameters we either used a paired t-test within 5% or determined if their distribution spanned 0 within 95%, Bonferroni corrected for multiple comparison (Motulsky (2004)).

3. Rater Consistency and Reliability

Rater performance was assessed using the intraclass correlation coefficient (ICC) (McGraw (1996)). The in-between-rater ICC as well as the within-rater ICC were very high, with an average of 0.94(±0.03) and 0.97(±0.01) respectively. Detailed rater analysis results can be found in Table-2.

Table 2. Intraclass Correlation Coefficient (ICC).

The ICC chosen is based on the analysis of variance using a two-way mixed effect model with row and column interaction.

Subject	Rater vs. Original	Protocol	ICC Method	ICC	Rating
subj 1	Rater 1 Redo	Indentation	A-k	0.94	Excellent
		Rotation	A-k	0.98	Excellent
	Rater 2	Indentation	A-k	0.92	Excellent
		Rotation	A-k	0.97	Excellent
subj 2	Rater 1 Redo	Indentation	A-k	0.96	Excellent
		Rotation	A-k	0.99	Excellent
	Rater 2	Indentation	A-k	0.94	Excellent
		Rotation	A-k	0.91	Excellent
subj 3	Rater 1 Redo	Indentation	A-k	0.95	Excellent
		Rotation	A-k	0.97	Excellent
	Rater 2	Indentation	A-k	0.95	Excellent
		Rotation	A-k	0.96	Excellent
subj 4	Rater 1 Redo	Indentation	A-k	0.95	Excellent
		Rotation	A-k	0.96	Excellent
	Rater 2	Indentation	A-k	0.93	Excellent
		Rotation	A-k	0.89	Excellent
subj 5	Rater 1 Redo	Indentation	A-k	0.98	Excellent
		Rotation	A-k	0.96	Excellent
	Rater 2	Indentation	A-k	0.99	Excellent
		Rotation	A-k	0.91	Excellent
subj 6	Rater 1 Redo	Indentation	A-k	0.96	Excellent
		Rotation	A-k	0.98	Excellent
	Rater 2	Indentation	A-k	0.95	Excellent
		Rotation	A-k	0.95	Excellent

ICC Value	Rating
0.0 ≤ ICC < 0.4	Poor
0.4 ≤ ICC< 0.6	Fair
0.6 ≤ ICC < 0.75	Good
0.75 ≤ ICC < 1	Excellent
ICC Method: A-k is defined as: “The degree of absolute agreement for measurements that are based on k independent measurements made under the fixed levels of the column factor” (McGraw & Wong, 1996).

III. Results

We analyzed successive frames of US movies, to quantify motion of the FOI in a muscle, as the muscle is being stretched by elbow rotation, or as it is being stretched by tendon indentation at the elbow.

To evaluate and compare each stretch condition we extracted the following parameters from the US-images:

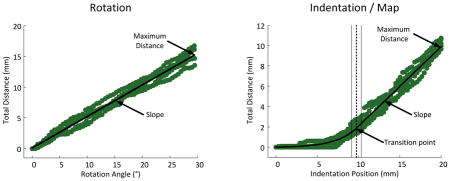
• the “Maximum Distance” is the maximum distance travelled by the FOI,

• the “Slope” is the rate of rise of the linear portion of the displacement of the FOI,

• the “Transition Point” is the indentation location at which the displacements transitions to a linear behavior,

• the “Lowest AIC” describes which model best fits the displacement of the FOI and,

• the “Direction Ratio” is the percentage of the displacement that is in the X direction.

The definitions, statistics and estimates of these values are described in Table-1 & Fig. 4.

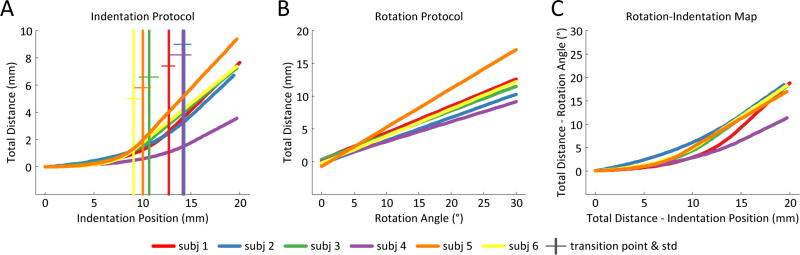
Fig. 4.

Results for all subjects. (A) Shows the piecewise continuous fits for the Total Distance travelled for each subject under the Indentation protocol. (B) Shows the linear fits for the Total Distance travelled for each subject under the Rotation protocol. (C) Shows the Rotation-Indentation piecewise continuous maps for the Total Distance travelled for each subject.

A. Rotation Protocol

For the rotation protocol, the FOI of all the subjects moved measurably in the X (longitudinal) direction. Conversely, in 4/6 subjects, the FOI did not move more than 0.3mm in the Y direction and 0.7mm for the remaining 2. These results are reflected in the direction ratios, in which the X direction is responsible for 96% of the TD. From here, we will only report on the TD for the model fits as X data mirrors the TD. The model that best fit the rotation data, with the lowest AIC score, is a line for all the subjects tested. The individual slopes are significantly different from each other, but lie within the same order of magnitude averaging 0.40(±0.11)°/mm.

B. Indentation Protocol

For the indentation protocol, the FOI of all the subjects moved significantly in the X direction. In contrast to the rotation protocol, the FOI of 5/6 subjects moved more than 1.5mm in the Y direction, and reached 2mm for one subject. The direction ratios reflect these results in that 92% of the TD is due to the displacement in the X direction. The indentation protocol is best fit, with the lowest AIC score, by a piecewise continuous model for all the subjects tested.

Focusing on the linear portion of the model, we found that the transition points between the non-linear and linear portion of the fit were not statistically different from each other for 4/6 subjects and lay, on average, at 10.95(±1.42)mm. The individual slopes statistics suggests two different groups; however they are all within the same order of magnitude 0.57(±0.14)mm/mm.

C. Rotation-Indentation Map

We established a Rotation-Indentation Map for all the subjects tested. The model that best fit the Map, with the lowest AIC score, was piecewise continuous. The transition points between the non-linear and linear portion of the fit were not statistically different from each other for 4/6 subjects and were on average 11.41(±0.93)mm. The slopes of the linear portion of the fit were found to group similarly to indentation and are of the same order of magnitude.

Our main result is that there exists a linear relationship between joint rotation and tendon indention with a 1.34(± 0.23)°/mm ratio. Furthermore, this linear relationship applies over 50% of the indentation range, and is equivalent to a 14.94(±2.16)° elbow rotation for a 20mm indentation.

D. Regional Strain

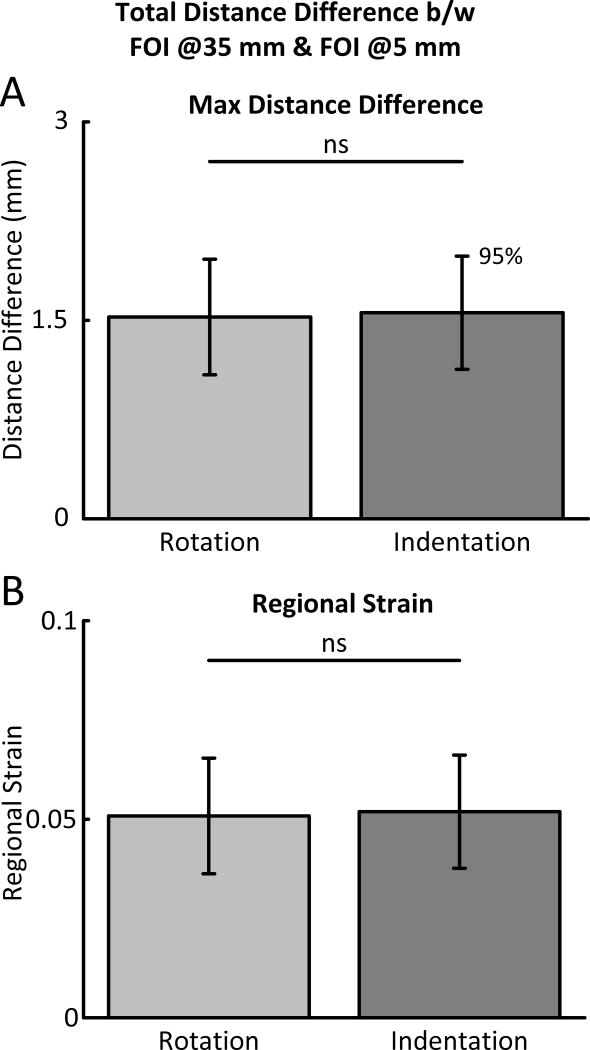
The regional strain (see equation 1) provides an estimate of the strain registered along the main axis of the BIC for each stretch protocol. As illustrated in the bar plots in Fig. 5-B, we find that along its main axis the average BIC strains 0.05(±0.014) under rotation and 0.051(±0.014) under indentation. These strains show statistically insignificant differences.

Fig. 5.

Bar plots of the maximum distance difference and regional strain as calculated from the FOI @ 35 mm and the FOI @5 mm. The solid black line above the bars represent the statistical link between the bars and ns stands for: not significant. (A) Shows the Maximum Distance difference between the FOI @35 mm and the FOI @5 mm for both the Rotation and Indentation protocol. (B) Shows the same information as (A) however the information has been normalized by the initial length between the two FOIs of 30 mm.

IV. Discussion

The goal of this study was to determine whether muscle length changes induced by tendon indentation were broadly comparable to those induced by elbow joint rotation. Our rationale was threefold:

1. tendon indentation is commonly used clinically as part of the neurological exam,

2. better description could improve the study of the musculotendon unit, and

3. indentation could substitute for joint rotation in motion sensitive imaging.

Using B-mode US movies, we estimated local muscle kinematics for each stretch condition by tracking a FOI in that muscle. We produced FOI distance results and used them to compare each protocol.

A. Physiological meaning for the X and Y distance

The distance values in the X and Y direction do not have physiological meaning in themselves, as they are points extracted from an image that has no fixed relation to the underlying anatomy of the BIC. To assign meaning to these values we looked first at the distances travelled in the X and Y direction for the physiologically normal muscle stretch (or the rotation protocol). Our results show that the morphology of the distance travelled by the FOI in both the X and the Y direction is best fit by a two parameter linear regression. In the X direction the slope relating angular rotation of the BIC joint to the distance travelled is 0.37(±0.09)mm/degree. In the Y direction however, the slope is on average, 0.02(±0.04)mm/degree and is not significantly different from zero (p<0.05). This suggests that in this experimental setup, the data most representative of normal physiological stretching are reflected by pixel motion in the X direction.

B. Evaluation of the rotation protocol

We compared the results obtained for the rotation protocol with data in the literature that most closely resembled our experimental setup. These data came from Murray (1995) who reported the displacement of the BIC, at the tip of the distal tendon, in human cadavers relative to elbow rotation. We also used OpenSim-3.0, implementing the Stanford VA upper limb model (Holzbaur (2005)).

For an equivalent elbow extension (120°–150°), the BIC is stretched 16.02(±0.3)mm for Murray (1995) and 15.72mm for OpenSim compared to our average 10.17(±1.10)mm in the X direction and 10.60(±1.09)mm for the TD. This ~30% difference is multifaceted in origin. First, though previous data was collected using fresh cadaveric BIC, the muscle was detached from its surrounding tissue thus allowing for greater motion. Second, since the US probe is fixed relative to the muscle, its field of view behaves just like a flow field. Therefore being 1/3 distance of the total muscle away from the tip of the distal tendon, the probe’s field captured roughly 2/3 of the stretching effects assuming an ideal linear muscle. The proportion of each effect on the results is not known however both could explain the ~30% difference.

The morphology of the Murray (1995) and OpenSim data matches ours. The model that best fit both data sets, with the lowest AIC score, is a linear curve (R²≥99%) and both data sets have a 0.97 correlation coefficient with the X and TD data.

C. Evaluation of the Indentation Protocol

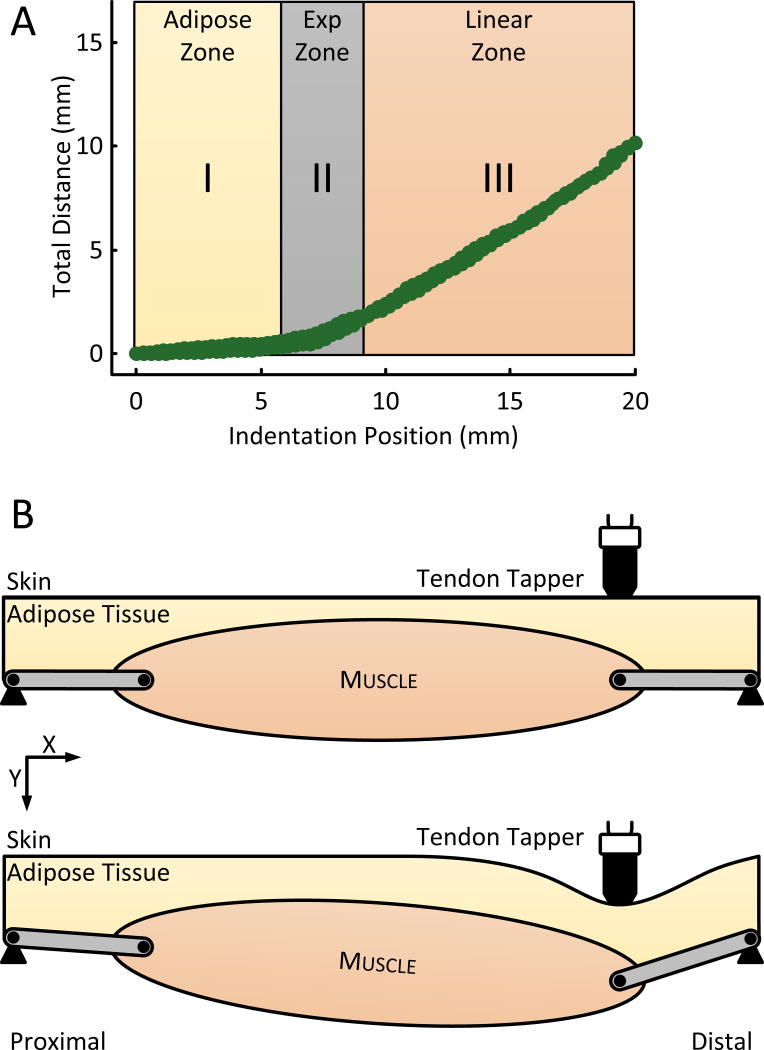
In comparison to the Rotation protocol, the displacement-indentation relationship of the indentation protocol is nonlinear and has three distinctive parts. The first is a proposed “adipose-zone” in which the displacement is minimal. The second is an “exponential-zone” in which the displacement quickly increases. And the third is a “linear-zone” in which the displacement grows linearly (Fig. 6). We believe that these indentation zones are related to the soft tissue configuration underneath the indenter, as identified from our US-images as two layers: the skin-adipose layer and the tendon-muscle layer.

Fig. 6.

Physiology of the indentation protocol. (A) Shows the Total Distance travelled by the FOI under the indentation protocol overlaid atop the three possible physiological zones. (B) Schematic of the indentation protocol. The initial condition (top) shows the indenter at the skin above the tendon-muscular junction. The full indentation condition (bottom) shows the deformation of the layers under the indenter.

The “adipose-zone” can be explained by the mechanics of the combined skin-adipose layer. From a biomechanics point of view, the indenter compresses the skin and adipose layer in the Y direction as if under a uniaxial unconfined compression test at low strain rates (ε̇ ~ 0.25 s⁻¹). Under such conditions, the nominal stress-strain relationship of adipose tissue has been shown, for strains ε ≤ 10%, to behave linearly, to have a bulk modulus 1.15E3Pa and to have 1E3-2E3Pa stress at 10% strain (Comley (2009); Miller-Young (2002)). Given these properties and the surface area of our indenter, 25πmm², the first 10% of the indentation will generate a ~0.15N force which is too small to displace the tendon-muscle layer given its combined 8.8E6Pa bulk modulus (Blemker (2005); Weiss (2002)).

The “exponential-zone” can be explained by two phenomena. First, as the indenter continues beyond the 10% strain, the stresses on the adipose layer increases exponentially until they become large enough to displace the tendon-muscle layer (Comley (2009)). Second, as the force increases, the combined strain of the tendon-muscle layer will increase exponentially as the collagen fibers of the tendon, together with fibers and muscle connective tissue begin to straighten (Quapp (1998);Zajac (1988)).

In the “linear-zone”, the tendon and muscle fibers have reached a length where their combined strains behave linearly relative to stress. Work on whole muscle mechanics, performed primarily in in-vivo animal preparations, has shown a similar trends (Joyce (1969); Matthews (1959)). Even though direct evidence of the effect of indentation of the skin-adipose-tendon-muscle complex is not available, we believe that the morphology of the displacement-indentation relationship of the indentation protocol is consistent with known passive material properties.

D. Is the indentation stretch physiologically relevant?

Our results suggest three major finding with respect to the physiology of the tendon stretch. First, large scale tendon indentation of the BIC substantially stretches the muscle, because the TD travelled by the FOI is on average only 32% smaller than the TD travelled by the FOI during a rotational stretch. This result is partially confounded by the “adipose zone” in which there is an indentation region where the displacement of the FOI is minimal. However, using the linear portion of the piecewise curve that best fit the indentation data (Table-1), we calculated the theoretical maximum TD if the “adipose-zone” did not exist and found that the 32% difference in TD travelled disappears between the two protocols. This means basically that the indentation actions can be ignored until the tendon-muscle complex is loaded, and begins to move with increasing indentation.

The second major finding is that 92% of the TD travelled during the indentation protocol is in the longitudinal or X direction. The X direction is most representative of normal physiological displacement, because we recorded no significant displacements in the Y direction during the rotation protocol. Furthermore, because the FOI motion had large displacements values in the X direction in both protocols, we can conclude that the physiology of a tendon stretch is broadly analogous to normal physiological stretch.

Third, on average our estimate of the regional strain along the main axis of the muscle for both stretching protocols show insignificant statistical differences, suggesting that the tendon indentation and joint rotation will strain the muscle similarly along the main axis of the muscle. Considering that muscle receptors respond to local strain this finding indicates that an equivalent amount of proprioceptive feedback will presumably reach the spinal cord, regardless of stretching protocol.

We do expect however, that the strain rate will be different for each protocol, due to the nonlinear kinematics of tendon indentation. While the static information of the proprioceptive information will presumably be equivalent, we expect the dynamic information to differ in its delivery rate. Therefore, to truly match the two protocols, rotational and indentation speed must be taken into account. On a regional analysis however, the non-linear behavior of the indentation kinematics disappears, further supporting the premise that each protocol stretches the muscle equivalently.

The results presented strongly indicate that a 20mm indentation of the region above the distal tendon of the BIC is broadly equivalent to a 15° elbow rotation. By removing the “adipose-zone”, the relationship becomes linear with a 1/2 indentation-rotation ratio. Furthermore, each stretching protocol strains the main axis of the muscle equivalently.

E. Benefits & Limitations of this stretching technique

Even though further validation is needed, tendon indentation has multiple benefits for the study muscle-tendon mechanics. It allows for the exploration of a muscle’s properties without needing large-scale joint rotation which is particularly useful in pathological states. It allows for the study of muscles associated with joints having range of motion too large for certain imaging techniques. Finally tendon indentation allows the exploration of the mechanics of muscles spanning a joint independently of joint motion, or in concert.

A limitation of this technique is that it is best-suited to muscles with an accessible tendon allowing for indentation (i.e. away from bone). Joints can be adjusted to maximize the indentation distance; however this technique would thus far exclude deep muscles.

Finally, although our approach enables direct comparison between two stretching techniques, (rotation and indentation) it does not encompass musculotendon kinematics during a tendon tap. The high velocity nature of a tap should introduce highly nonlinear features into the system in part due to muscle stiction, tendon and extracellular matrix properties. To capture such events warrants high speed medical imaging. This topic warrants further study.

F. Methodological Considerations

1. Choice of Feature of Interest

In order to be consistent across subjects, we chose the FOIs to be in similar regions of the muscle, as well as being visible in both stretch protocols. The FOIs were chosen to be along the axis of the aponeurosis (Fig. 2-A) and we chose the @5mm location to be as proximal as possible and the @35mm location in order to emulate the Murray (1995) experiments which measured BIC displacement from the tip of its distal tendon.

2. Effect of US probe placement on measurements

A reported source of measurement error in B-mode US imaging is US probe placement & handling (Bénard (2009); Kristjansson (2004); Kwah (2013)). To minimize error, we reduced the contact of the probe on the muscle to its sensing surface and leveraged gravity to control the “probe-muscle” interaction force by letting the probe freely rotate around US-Pitch (Fig. 1-C). We further aligned the image plane of the probe such that it would return maximum reflectivity. Finally, we constrained the subject in space and co-aligned the rotation axis of the elbow and the motor to minimize motion from the subject.

V. Conclusion

Tendon indentation is the basis of many neurological tests, such as the deep tendon reflex, however its effect on muscle kinematics and subsequently on spindle receptor mechanical transduction has been largely unexplored. Understanding the effects of indentation on muscle kinematics would further our understanding of the neural control of movement. These data will also help design novel tendon tapping apparatus to refine neurological tests, gather of global musculotendon unit mechanics and perhaps serve as a surrogate to joint rotation.