Assessment of regional ventilation and deformation using 4D-CT imaging for healthy human lungs during tidal breathing

Abstract

This study aims to assess regional ventilation, nonlinearity, and hysteresis of human lungs during dynamic breathing via image registration of four-dimensional computed tomography (4D-CT) scans. Six healthy adult humans were studied by spiral multidetector-row CT during controlled tidal breathing as well as during total lung capacity and functional residual capacity breath holds. Static images were utilized to contrast static vs. dynamic (deep vs. tidal) breathing. A rolling-seal piston system was employed to maintain consistent tidal breathing during 4D-CT spiral image acquisition, providing required between-breath consistency for physiologically meaningful reconstructed respiratory motion. Registration-derived variables including local air volume and anisotropic deformation index (ADI, an indicator of preferential deformation in response to local force) were employed to assess regional ventilation and lung deformation. Lobar distributions of air volume change during tidal breathing were correlated with those of deep breathing (R² ≈ 0.84). Small discrepancies between tidal and deep breathing were shown to be likely due to different distributions of air volume change in the left and the right lungs. We also demonstrated an asymmetric characteristic of flow rate between inhalation and exhalation. With ADI, we were able to quantify nonlinearity and hysteresis of lung deformation that can only be captured in dynamic images. Nonlinearity quantified by ADI is greater during inhalation, and it is stronger in the lower lobes (P < 0.05). Lung hysteresis estimated by the difference of ADI between inhalation and exhalation is more significant in the right lungs than that in the left lungs.

precise analysis of lung motion during respiration is essential to study sensitive structure and function relationships at the local level. Several studies have used imaging tools such as magnetic resonance imaging (MRI) (3, 14) and single-photon-emission computed tomography (SPECT) (22, 34). The studies have shown regional lung information such as regional ventilation and perfusion to perform physiological evaluation of those imaging modalities. Although MRI is radiation free and SPECT has the ability to analyze ventilation-perfusion, the low resolution and long acquisition time of these imaging techniques limit precise evaluation of lung function and reduce the number of examinations. Multidetector-row CT (MDCT) imaging equipped with a two-dimensional array of detectors (multiple detector rows) greatly shortens image acquisition time, allowing acquisition of a large number (128 in this case) of slices simultaneously for assessment of detailed structure and function of the lung (7, 10). In applications such as four-dimensional CT (4D-CT) imaging in which the travel of the table bed is slowed during spiral acquisitions and the air flow at the mouth is recorded along with the projection images, one can reconstruct the lung volume using only projections from a select portion of the respiratory cycle. By repeating this for many points in the respiratory cycle (gathered in a single spiral acquisition), the result is a 4D digital representation of the lung. With its advantage of fast acquisition and more coverage of lung volume, MDCT can be utilized to improve the 4D-CT imaging process.

4D-CT dynamic imaging can provide more detailed physiological information of lung motion during tidal breathing. However, in addition to lowered spatial resolution (attributable to motion and a need to limit radiation dose) compared with static imaging, there are limitations with previous studies because of inconsistencies of tidal breathing during scan acquisition (21). For example, if tidal breaths vary, the actual lung volume varies along the z-axis (apical to basal). This can clearly lead to erroneous physiological representations. Thus critical to this process, when one seeks to define the mechanical characteristics of the lung, is maintenance of a consistent tidal volume and respiratory rate during scanning. This is critical both for the reconstruction of a meaningful lung volume at each point of the respiratory cycle in a single acquisition and also when one seeks to compare subjects and to evaluate regional lung mechanics longitudinally. To resolve this issue, Fuld et al. (11) have devised a dual rolling-seal piston system that maintains the same lung tidal volumes over multiple breathing cycles for wash-in xenon CT studies.

Recent advances in image-registration techniques provide accurate matching of local lung volumes, mapping pairs of lung images to a common coordinate system (33). The image-registration techniques have been utilized to compute regional lung deformation and ventilation (1, 7, 23). For example, Yin et al. (31) have used a (tissue) mass-preserving nonrigid registration method (33) to match two static MDCT images to compute lung deformation and regional ventilation. Later, Yin et al. (32) proposed a method to derive nonlinear characteristics of lung deformation in three static MDCT images. Jahani et al. (16) then compared regional lung mechanics between two and three static images to analyze lung motion at different inflation levels. Unlike the two-image-based method, the three-image-based method was able to capture nonlinear characteristics of lung deformation. However, static image-based analysis could not capture asymmetric physiological characteristics and irreversible nonlinearity of the lung motion, so-called hysteresis, between inhalation and exhalation. To assess those characteristics, image-registration methods also have been applied to the 4D-CT volumetric images to estimate continuous displacement fields of a lung and to derive more sensitive local functional variables during dynamic breathing. For example, Christensen et al. (8) have applied image registration to a few selected lung slices (i.e., not the whole lung) acquired at limited breathing cycles. They have demonstrated a strong correlation between the lung motion evaluated by image registration and the change of air volume measured by spirometry. Boldea et al. (4) have introduced new parameters based on trajectories of material points in the 4D-CT images over exhalation and inhalation to quantify nonlinearity and hysteresis. When comparing motion of tumor volume to healthy tissue, they found that hysteresis motion in the tumor volume is larger. White et al. (27) have applied a lung tissue trajectory model that depends on tidal volume and air flow to registration-processed 4D-CT images to study lung tissue hysteresis. They observed significant differences in hysteresis values between lower and upper lung regions.

The main objective of this study was to derive the displacement fields of image voxels by image registration to assess regional ventilation, lung anisotropic deformation and nonlinearity, and hysteresis of anisotropic deformation for healthy human lungs during volume-controlled free breathing (VCFB). The novelty of the study is twofold. First, tidal volumes during dynamic imaging are controlled with a unique dual rolling-seal piston for accurate image reconstruction that is important for assessment of regional lung functions. Second, displacement fields obtained from registration are used to derive sensitive local variables, such as air volume and flow rate for assessing regional ventilation and anisotropic deformation index (ADI) for quantifying nonlinearity and hysteresis of lung motion. A driving motivation for our work is to use regional lung dynamic flow for improved boundary conditions required for the application of computational fluid dynamics (CFD) to study lung function (32). This may potentially lead to a better understanding of particle deposition patterns, shear forces at the airway surfaces, or regional distribution of and clearance of inhaled gases (19, 28, 29). These 4D-CT-derived regional air volumes and flow rates are also compared with those estimated by linear or nonlinear assumption in the static scans (16). The comparison allows quantification of the differences between static vs. dynamic breathing. Furthermore, much of the motivation, to date, for assessing lung motion and hysteresis via 4D-CT is based on the desire to adjust for regional lung motion during radiation-treatment planning, e.g., by tracking tumor structures (9, 24, 30).

METHODS

Static and dynamic image acquisition.

Six healthy human volunteers (50% men/women) were recruited for this study. Before CT scanning, pulmonary function tests (PFTs), including body plethysmography (nSpire Health, Longmont, CO), were performed to obtain preliminary lung volume information, such as total lung capacity (TLC), functional residual capacity (FRC), residual volume (RV), vital capacity (VC), forced VC, and forced expiratory volume in 1 s in upright body posture. During a CT scanning session, both static and dynamic MDCT image scans were performed in the supine position for each subject. For static CT (SCT) imaging, accurate breath-hold volumes were achieved by use of a pneumotachometer-controlled device (11). This system uses a balloon occlusion valve that closes when the individual is at the desired percentage of their VC. In this study, we targeted 95% VC and 15% VC, approximating TLC and FRC, respectively. This method has been validated to provide strong correlations with the corresponding PFT-based TLC and FRC, significantly improved over simple coaching methods used at other imaging centers (5). The repeatability of the method has previously been demonstrated from multiple visits relative to breath-hold verbal coaching (15).

For dynamic scans and 4D-CT volumetric reconstruction, a dual rolling-seal piston system (11) was employed to guide the subject's inspiratory and expiratory depths of breathing, and subjects were coached to breath at least 12 breaths per minute (bpm) because of scanning limitations. This 12-bpm lower limit is dictated by the scanner rotation speed, the table translation rate, and radiation dose limits. Scanning time took ∼1 min to acquire the projection images covering the full apex-to-base extent of the lungs. Tidal depth was set based on assessment of a comfortable minute ventilation obtained for each subject during PFT as a first approximation. This was then adjusted in the CT facility to accommodate what the subject perceived as a comfortable depth for the desired >12-bpm ventilation rate. Subjects rehearsed breathing through the rolling-seal piston device and coached to breath at a consistent, comfortable respiratory rate above 12 bpm. With five subjects, we were able to achieve consistent multislice MDCT lung volumes between end inhalation (EI) and the end exhalation (EE) for multiple breathing cycles. One subject dropped below this 12-breath limit during scanning. In this case, we were unable to collect an adequate number of projects for use in reconstruction of each phase of the respiratory cycle. Thus this subject was eliminated from further analysis. This was the first subject studied and motivated additional coaching before scanning in the subsequent six subjects, leading to scanning success in all of the remaining five subjects.

The imaging protocols for acquiring MDCT human lung volumetric images were approved by the University of Iowa Institutional Review Board and the radiation safety committee. Written, informed consent was obtained for each subject after we explained the goals and the risks of the present study. For the static and dynamic scanning, a Siemens Somatom Definition Flash dual-source 128-slice MDCT scanner (Forchheim, Germany) was employed. The scanner parameters of scan type, peak voltage, effective current, and slice thickness were set to spiral, 120 kV, 75 mA, and 0.75 mm, respectively. Each volumetric data set was acquired at a section spacing of 0.5 mm and a reconstruction matrix of 512 × 512 using the B35f kernel. Semiautomatic segmentation software, Apollo (VIDA Diagnostics, Coralville, IA), was utilized to segment the airways, lungs, and lobes of both static and dynamic images.

Figure 1 illustrates the process of lung volume reconstruction at a selected phase. For each subject, 4D-CT volumetric image datasets were reconstructed by the scanner at 8-10 automatically defined phases based on the signal provided by the turbine-based flow meter recorded together with the projection images. To achieve a greater number of reconstructed phases of the respiratory cycle, there was an option for the user to manually identify additional points within the respiratory cycle. The air volumes obtained from the initial, automatically defined 8–10 phases were used for validation of air volumes assessed by image matching. The additional reconstructed time points were required for spline interpolation analysis in which eight exhalation and eight inhalation phases were utilized. Because the phases at EE (minimum volume) and EI (maximum volume) were common for exhalation and inhalation, there were a total of 14 phases for each breathing cycle.

Fig. 1.

A flow chart of lung volume reconstruction process at a certain phase.

Average of respiratory cycles.

Because the inhalation period, the exhalation period, and the tidal volume vary from subject to subject, times (t) in respective inhalation and exhalation phases and continuous air volumes measured with a flow meter (V_air,m) were normalized as follows:

$$\begin{array}{l}{t}_{\mathrm{i}\mathrm{n}}^{*n}=\frac{t-t_{\text{EE}}^{n-1}}{t_{\text{EI}}^n-t_{\text{EE}}^{n-1}};t_{\text{ex}}^{*n}=\frac{t-t_{\text{EI}}^n}{t_{\text{EE}}^n-t_{\text{EI}}^n},\hspace{0.17em}\text{where}\hspace{0.17em}{t}_{\text{EE}}^{n-1}\le t\le t_{\text{EE}}^n\hspace{0.17em}\text{and}\hspace{0.17em}{t}_{\text{EE}}^0=0\\ {\text{V}}_{\text{air},\text{m}}^{*n}\left(t^{*n}\right)=\frac{{\text{V}}_{\text{air},\text{m}}\left(t\right)-{\text{V}}_{\text{air},\text{m},\text{EE}}^n}{{\text{V}}_{\text{air},\text{m},\text{EI}}^n-{\text{V}}_{\text{air},\text{m},\text{EE}}^n},\hspace{0.17em}\text{where}\hspace{0.17em}{t}^{*n}=\{\begin{array}{l}{t}_{\mathrm{i}\mathrm{n}}^{*n},\hspace{0.17em}\mathrm{i}\mathrm{f}\hspace{0.17em}{t}_{\text{EE}}^{n-1}\le t\le t_{\text{EI}}^n\\ t_{\mathrm{e}\text{x}}^{*n},\hspace{0.17em}\mathrm{i}\mathrm{f}\hspace{0.17em}{t}_{\text{EI}}^n\le t\le t_{\text{EE}}^n\end{array}\end{array}$$ (1)

t_in^*n, t_ex^*n, and V_air,m^*n are normalized inhalation time, normalized exhalation time, and normalized flow-meter-measured air volume, respectively, at the n^th cycle. Thus $t_{\mathrm{in}}^{*}$ = 0 (or $t_{\mathrm{ex}}^{*}$ = 0) corresponds to the beginning of inhalation (or exhalation), and t_in^*n, t_ex^*n, and V_air,m^*n all range from 0 and 1. Then, the mean was computed as ${\text{V}}_{\text{air},\text{m}}^{*}(t^{*}=t^{*n})=\sum _{n=1}^N{V}_{air,m}^{*n}\left(t^{*n}\right)/N,$ where N is the total number of cycles, along with its SE. With the normalized mean air volume (V_air,m^*), we obtained the normalized total flow rate at any time point t_p^* [Q^*(t_p^*)] using a central finite difference scheme as follows:

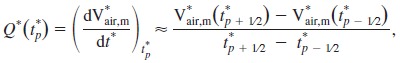(2)

where the time interval (t^*_{p + 1/2} − t^*_{p − 1/2}) is taken as 0.01 in this study.

Image registration.

Given the image density in Hounsfield units (HU) at position x, the air and tissue fractions were estimated by

$${\beta }_{\text{air}}\left(\mathbf{\text{x}}\right)=\frac{{\text{HU}}_{\text{tissue}}-I\left(\mathbf{\text{x}}\right)}{{\text{HU}}_{\text{tissue}}-{\text{HU}}_{\text{air}}}\hspace{0.17em}\text{and}\hspace{0.17em}{\beta }_{\text{tissue}}\left(\mathbf{\text{x}}\right)=\frac{I\left(\mathbf{\text{x}}\right)-{\text{HU}}_{\text{air}}}{{\text{HU}}_{\text{tissue}}-{\text{HU}}_{\text{air}}}$$ (3)

where β_air(x), β_tissue(x), I(x), HU_tissue, and HU_air denote air fraction, tissue fraction, CT density, HU of tissue, and HU of air, respectively. HU_air and HU_tissue were set to −1,000 and 55, respectively (13). We employed a mass-preserving image-registration method to match two CT lung images, one as a reference image and the other as a moving image. A spatial transformation, T(x), was determined to minimize a cost function E, based on the sum of squared tissue volume difference between two images (33).

$$E={\displaystyle \sum _{\mathit{x}\in \Omega }{\left[{\text{v}}_1\left(\mathbf{\text{x}}\right){\beta }_{\text{tissue},1}\left(\mathbf{\text{x}}\right)-{\text{v}}_2\left(\mathbf{\text{T}}\left(\mathbf{\text{x}}\right)\right){\beta }_{\text{tissue},2}\left(\mathbf{\text{T}}\left(\mathbf{\text{x}}\right)\right)\right]}^2}$$ (4)

where v₁ and v₂ are local volumes of the corresponding regions of reference and moving images, respectively.

Registration-derived variables.

For each registration between a pair of CT images, local air volume for the moving image at position x of the reference image was calculated as

$${\text{v}}_{\text{air}}\left(\mathbf{\text{x}}\right)=\text{v}\left(\mathbf{\text{T}}\left(\mathbf{\text{x}}\right)\right){\beta }_{\text{air}}\left(\mathbf{\text{T}}\left(\mathbf{\text{x}}\right)\right)$$ (5)

where v_air (or v) is the local air volume (or local volume). We employed TLC of static scan and EE of dynamic scan as reference images. The summation of v_air within the whole lung is equal to total air volume of a CT image (V_air,CT), and the local air volume fraction v_f,air is defined as the ratio of v_air to V_air,CT. In addition, local air volume (v_air) at dynamic scan was normalized as

(6)

Because the measured air volume should be equal to the corresponding CT image-derived air volume, we compared them using linear regression to validate the equality of V_air^* = V_air,m^* = V_air,CT^*.

In addition, we employed SCT-based TLC and FRC for V_air,CT and corresponding %VC of the TLC and FRC to derive RV and VC in the supine position of a subject as follows:

$$\%\mathrm{V}\mathrm{C}=\left({\mathrm{V}}_{\mathrm{a}\mathrm{i}\mathrm{r},\mathrm{C}\mathrm{T}}-\mathrm{R}\mathrm{V}\right)/\mathrm{V}\mathrm{C}\times 100$$ (7)

We then computed %VC of each phase with corresponding total air volume of a dynamic scan for V_air,CT and the obtained VC and RV using Eq. 7.

Furthermore, to calculate lung deformation at a local position x, we computed the principle strains of lung tissue deformation, λ_i (1), where λ₁ > λ₂ > λ₃. We used the principle strains to estimate ADI as follows:

$$\mathrm{A}\mathrm{D}\mathrm{I}=\sqrt{{\left(\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_2}\right)}^2+{\left(\frac{{\lambda }_2-{\lambda }_3}{{\lambda }_3}\right)}^2}$$ (8)

ADI indicates the preferential deformation of local lung volume in one or two directions. In this study, ADI was computed from the lung volume at EE and normalized by its maximum value at EI state (ADI^*) for intersubject comparisons. To quantify nonlinearity of lung motion in dynamic breathing, we defined a new quantity δ_ADI* that is based on the ADI^* difference at a certain phase from the corresponding point on the straight line between EE and EI. That is, the straight line is expected of linear behaviors, whereas any deviation from the line reflects nonlinear behaviors. Similarly, the hysteresis of the lung motion is defined as a function of ADI^* at each point [Hys_ADI*(x)] as the absolute difference between the ADI^* values of inhalation and exhalation at the same phases.

$$\mathrm{H}\mathrm{y}{\mathrm{s}}_{\mathrm{A}\mathrm{D}{\mathrm{I}}^{\ast }}\left(\mathbf{x}\right)=|\mathrm{A}\mathrm{D}{\mathrm{I}}^{*}{\left(\mathbf{x}\right)}_{inh\mathrm{a}lation}-AD{\mathrm{I}}^{\ast }{\left(\mathbf{x}\right)}_{exhalation}|$$ (9)

Interpolation method.

In this study, we used a cubic spline interpolation method to construct a continuous function of a local variable s, such as v_air and ADI at various V_air^* based on those derived from CT images at the discrete phases. The interpolation function is piecewise cubic polynomials for a set of q + 1 phases $\left\{(V_{air,0}^{*},s_0),\hspace{0.17em}\mathrm{.}\hspace{0.17em}\mathrm{.}\hspace{0.17em}\mathrm{.}\hspace{0.17em},(V_{air,q}^{*},s_q)\right\}$.

The function in each interval (V_air,i^*, V_{air,i + 1}^*) is defined as

$$s_i\left({\mathrm{V}}_{air}^{\ast }\right)=a_i{\left({\mathrm{V}}_{air}^{\ast }-{\mathrm{V}}_{air,i}^{*}\right)}^3+{\mathrm{b}}_i{\left({\mathrm{V}}_{air}^{*}-{\mathrm{V}}_{air,i}^{*}\right)}^2+c_i\left({\mathrm{V}}_{air}^{*}-{\mathrm{V}}_{air,i}^{*}\right)+d_i$$ (10)

where the constructed functions pass through q + 1 control points. This method is twice continuously differentiable and used for inhalation and exhalation separately. Combining the breathing waveform (dV_air^*/dt^*) with interpolated variables (s) allowed us to find the time rate of s as follows,

$$\frac{\mathrm{d}{s}_i\left({\mathrm{V}}_{air}^{*}\right)}{\mathrm{d}{t}^{*}}=\frac{\mathrm{d}{s}_i}{\mathrm{d}{\mathrm{V}}_{air}^{*}}\left(\frac{\mathrm{d}{\mathrm{V}}_{air}^{*}}{\mathrm{d}{t}^{*}}\right)=\left[3a_i{\left({\mathrm{V}}_{air}^{*}-{\mathrm{V}}_{air,i}^{*}\right)}^2+2b_i\left({\mathrm{V}}_{air}^{*}-{\mathrm{V}}_{air,i}^{*}\right)+c_i\right]\left(\frac{\mathrm{d}{\mathrm{V}}_{air}^{*}}{\mathrm{d}{t}^{*}}\right)$$ (11)

For example, to assess regional ventilation, the local normalized flow rate, q^*, can be calculated as

$$q^{*}=\frac{\mathrm{d}{\mathrm{v}}_{air}^{*}}{\mathrm{d}{t}^{*}}=\frac{\mathrm{d}{\mathrm{v}}_{air}^{*}}{\mathrm{d}{\mathrm{V}}_{air}^{*}}\frac{\mathrm{d}{\mathrm{V}}_{air}^{*}}{\mathrm{d}{t}^{*}}$$ (12)

In addition to the measured waveform, we also performed a symmetric sinusoidal waveform [V_air^* = 1/2(1 − cos(πt^*)) for inhalation and V_air^* = 1/2(1 − cosπ(1 − t^*)) for exhalation] to evaluate the effect of waveform on regional flow rate and on intersubject variability. Furthermore, the flow rate fraction (q_f) in each region is defined as the flow rate in that region over total flow rate. In dynamic analysis, q_f is computed as follows:

$$q_{\mathrm{f}}=\frac{q^{*}}{Q^{*}}=\frac{\mathrm{d}{\mathrm{v}}_{air}^{*}}{\mathrm{d}{\mathrm{V}}_{air}^{*}}$$ (13)

It is noted that q_f is independent from the waveform. In two static images, q_f is equivalent to the ratio of local air volume change to total air volume change (Δv_air/ΔV_air,CT), so it could be used for CFD boundary condition if only two CT images are available (31). The flow rate fraction q_f is mainly used to compare the distributions of air volume changes derived from dynamic vs. static scans.

Furthermore, all the variables plotted in results were derived from their corresponding continuous functions, but we only plotted a certain number of SE for clarity.

RESULTS

Reliability of dynamic lung volume controller system.

Demographic information and PFT data of the six healthy subjects are shown in Table 1. The percentage of predicted values of the six subjects indicates that the measurements were within normal ranges (12, 25). Meanwhile, 4D-CT analysis was performed for the five subjects for whom we were able to reconstruct volumetric image data sets. As discussed in methods, the respiratory rate of subject 1 fell below 12 bpm, limiting our ability to reconstruct volumetric image data. Figure 2, A and B, shows V_air,m^* (± SE) for exhalation and inhalation for subject 6. For all subjects, the SEs of the means were <4% between all the cycles. The results indicate that the dual-piston-based volume controller adequately maintained consistent tidal volumes over multiple breathing cycles. It was this consistency that provided for the consistent trends shown in the data across all five subjects.

Table 1.

Demographic information and PFT values for the 6 subjects

Subject	1	2	3	4	5	6
Sex	F	F	M	F	M	M
Age, yr	24	44	23	39	53	58
BMI, kg/m2	25	26	26	24	30	32
FEV1, liters	3.3 (99%)	2.6 (95%)	3.7 (91%)	3.0 (97%)	3.5 (87%)	3.4 (83%)
FVC, liters	4.1 (105%)	3.4 (101%)	4.6 (95%)	3.6 (97%)	4.6 (86%)	4.4 (82%)
FEV1/FVC	0.806	0.762	0.813	0.818	0.774	0.768
TLC, liters	4.8 (93%)	4.5 (99%)	5.4 (87%)	5.2 (104%)	6.6 (88%)	7.2 (93%)
FRC, liters	2.1 (76%)	2.2 (85%)	1.9 (71%)	2.8 (102%)	2.9 (79%)	2.9 (78%)
RV, liters	1.0 (73%)	1.1 (73%)	0.9 (69%)	1.5 (97%)	2.1 (90%)	2.3 (93%)
RV/TLC	0.209	0.249	0.157	0.296	0.315	0.318

All subjects are white non-Hispanic except subject 4 that is white Hispanic. Values in parentheses are % predicted normal values. BMI, body mass index; FEV1, forced expiratory volume in 1 s; FVC, forced vital capacity; TLC, total lung capacity; FRC, functional residual capacity; RV, residual volume.

Fig. 2.

Normalized air volume (± SE) for exhalation (A) and inhalation (B) for subject 6.

Total lung volume and flow rate.

On the basis of data acquired at the time of imaging, Table 2 shows the actual %VC achieved for the inspiratory and expiratory breath holds (TLC and FRC) in the supine body posture and the corresponding air volumes for these two breath holds along with the air volumes achieved for EI and EE of the 4D-CT scans of the five subjects. Table 2 also indicates the supine RV, VC, and %VC of EI and EE estimated by Eq. 7. TLC, FRC, and RV in Table 2 show strong correlations with those volumes obtained from PFT shown in Table 1 (R² > 0.89). Although the %VCs of EI and EE show large standard deviations of 14–15% among different subjects, the difference of %VC between EI and EE (%VC of tidal volume) has a standard deviation of 6% (Table 2).

Table 2.

Lung volume information at the TLC, FRC, EI, and EE states for the 5 subjects

Subject	2	3	4	5	6	Average	SD
%VC from measurement
TLC	92.7%	91.6%	88.2%	95.3%	89.9%	92%	3%
FRC	15.8%	13.3%	16.2%	11.5%	13.4%	14%	2%
CT lung volume, liters
TLC	4.73	5.19	5.31	6.82	7.77	5.96	1.28
FRC	2.41	2.21	2.87	3.34	3.69	2.90	0.62
EI	3.84	2.96	3.46	5.42	5.99	4.33	1.31
EE	3.69	2.08	2.67	4.56	4.88	3.58	1.20
Volume from Eq. 7, liters
RV	1.93	1.70	2.32	2.86	2.97	2.35	0.56
VC	3.02	3.81	3.38	4.15	5.33	3.93	0.88
%VC from Eq. 7
EI	63.2%	33.1%	33.7%	61.7%	56.5%	50%	15%
EE	28.5%	9.9%	10.3%	40.9%	35.8%	25%	14%
EI-EE	34.7%	23.2%	23.4%	20.8%	20.7%	25%	6%

VC, vital capacity; EI, end inhalation; EE, end exhalation.

Figure 3 shows the means (± SE) of normalized total flow rate Q^* for the five subjects during exhalation (positive values) and inhalation (negative values). The Q^* for each subject was used to calculate the normalized regional flow rate q^* by Eq. 12. To validate registration results, approximated values for normalized air volumes from the measurement (V_air,m^*) were compared with the corresponding air volumes in the whole lungs derived from image registration (V_air,CT^*). Because we compared the data at 8–10 phases automatically selected by the scanner, there were 42 data points. The comparisons for the five subjects are plotted in Fig. 4, demonstrating that V_air,CT^* is significantly correlated with V_air,m^* for the five subjects (R² ≈ 0.98). Thus it validates the assumption of V_air^* = V_air,CT^* = V_air,m^*.

Fig. 3.

Means (± SE) of normalized flow rates obtained from measurement for exhalation (+) and inhalation (-) in the whole lung for the 5 subjects.

Fig. 4.

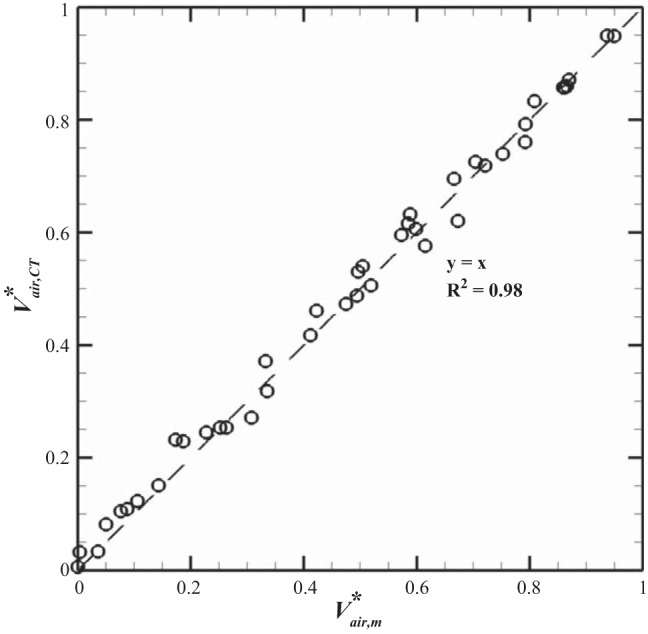
Linear regression between normalized measured air volume and normalized registration-derived air volume for the 5 subjects.

Local air volume and flow rate.

Figure 5 illustrates the mean (+SE) of lobar air volume fraction, v_f,air, during inhalation and exhalation for the five subjects. As the lung volume increases, v_f,air in the lower lobes increases while those in the upper and the middle lobes decrease. In addition, v_f,air values at EE (V_air^* = 0) and at EI states (V_air^* = 1) for both the lower and upper lobes are significantly different in the VCFB range (P < 0.005).

Fig. 5.

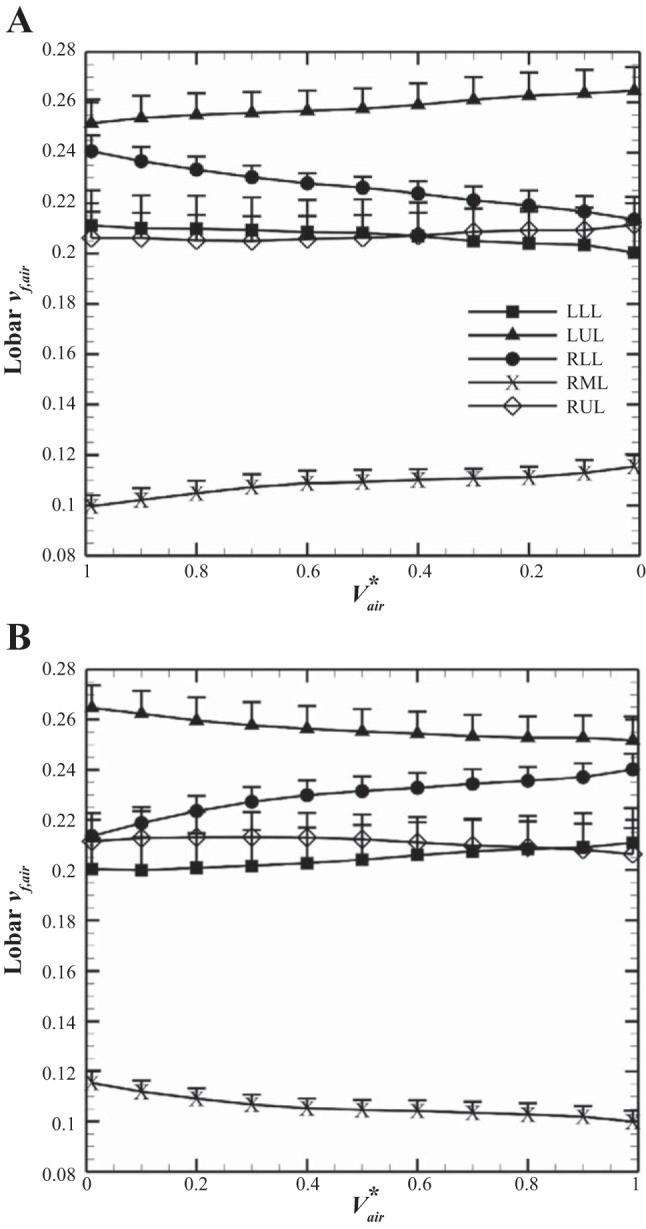
Mean (+SE) of lobar air volume fraction during exhalation (A) and inhalation (B) for the 5 subjects. LLL, left lower lobe; LUL, left upper lobe; RLL, right lower lobe; RML, right middle lobe; RUL, right upper lobe.

In regard to regional ventilation, Fig. 6, A and B, exhibits the mean (+SE) of medians q^* in each lobe as a function of V_air^* calculated using Eq. 12 for exhalation and inhalation, respectively. The results show that the q^* values of the lower lobes always remain greater than those of the upper and middle lobes during breathing. Next, to evaluate the effect of the waveform on asymmetric patterns of regional flow rates and on intersubject variability, instead of the measured waveforms, we imposed an ideal symmetric sinusoidal waveform to compute q^* for all subjects. Figure 6, C and D, demonstrates the mean (+SE) of the medians of lobar q^* at which the overall trends of q* remain similar with those using the measured waveform, and furthermore, intersubject variability does not vary significantly (mean of SE decreases from 24% to 23%). Although the sinusoidal waveform provides the same notion that q* of the lower lobes is greater than that of the upper and the middle lobes, the values and peak location of the sinusoidal waveform are different from those in the measured waveform, and the asymmetric pattern between inhalation and exhalation is reduced (Fig. 6).

Fig. 6.

Mean (+SE) of median of lobar flow rate during breathing for the 5 subjects. Plots correspond to results using the measured waveform for the left lobes (A) and the right lobes (B) and using sinusoidal waveform for the left lobes (C) and the right lobes (D).

Comparison of tidal and deep breathing (dynamic and static scans).

We compared air volume changes obtained from 4D-CT at VCFB with those obtained from SCT at deep breathing to see how deep breathing analysis is able to estimate regional ventilation in the VCFB range in the case that 4D-CT image data are not available. Linear interpolation (like Eq. 10 in which a_i and b_i equal 0) of lobar v_air from FRC to TLC for SCT gives a constant flow rate fraction, q_f, equivalent to lobar air volume difference over total air volume difference (q_f,SCT = LobarΔV_air,CT/TotalΔV_air,CT). We compared q_f,SCT with the average of flow rate fractions of 4D-CT obtained from Eq. 13 (q̄_f,4D-CT). Figure 7A shows the linear regression between q_f,SCT and q̄_f,4D-CT in all lobes for the five subjects, indicating good correlation (R² ≈ 0.84).

Fig. 7.

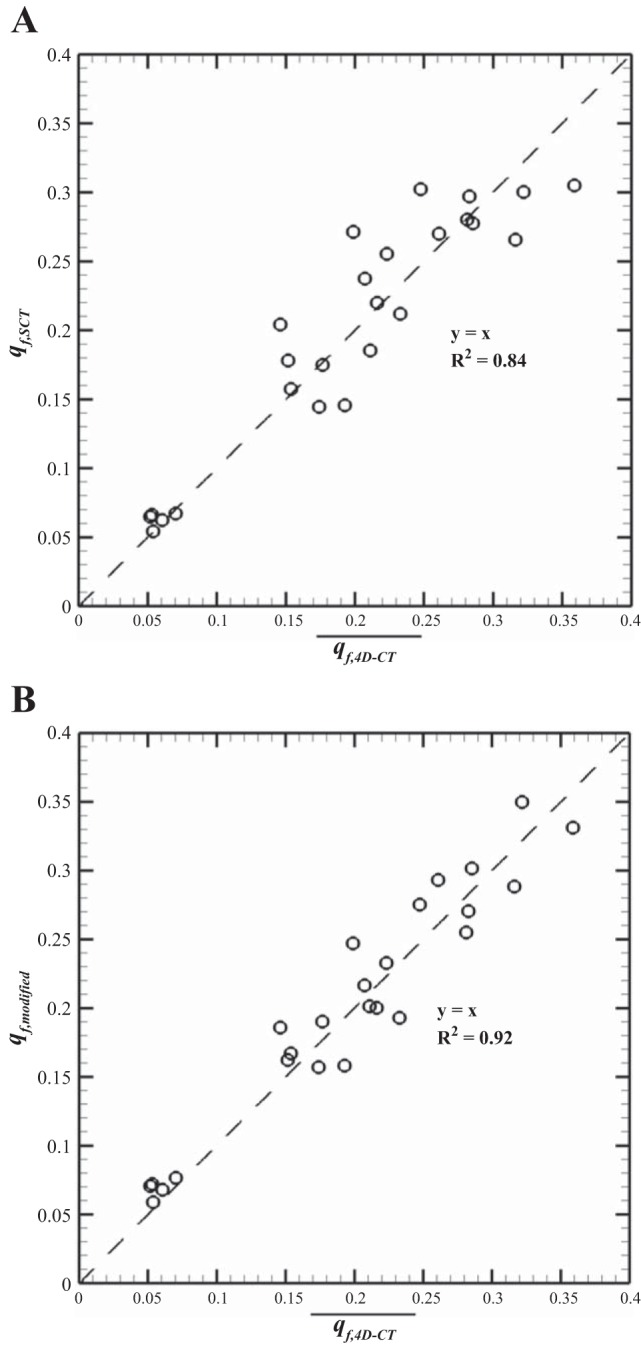
Linear regression between lobar q_f of static images (functional residual capacity-total lung capacity, FRC-TLC) and average q_f of dynamic (end exhalation-end inhalation, EE-EI) (A) and between lobar average q_f of dynamic (EE-EI) and q_f modified from static images (FRC-TLC) (B) for the 5 lobes of the 5 subjects. The values of 2 data points in the right middle lobe are too close to each other; thus it appears that there are 24 data points instead of 25.

However, the comparison of q_f in the left lungs (LL) with q_f in the right lungs (RL) for the five subjects indicates that in deep breathing, the contributions of the left and the right lungs in air volume change are almost the same (q̄_f,LL = 0.492, q̄_f,RL = 0.508), whereas in VCFB, the average contribution of the right lung in air volume change is significantly (P < 0.05) greater than that of the left lung (q̄_f,LL = 0.449, q̄_f,RL = 0.551). In addition, means of air volume fractions in the lower lung volumes (FRC, EE, and EI) are 0.56 < v_f,air < 0.58 for the right lung and 0.42 < v_f,air < 0.44 for the left lung, whereas the air volume fraction at full inspiration (TLC) was 0.53 ± 0.02 for the right lung and 0.47 ± 0.02 for the left lung. Because intersubject variability of q_f is small (SE < %2), we can compute flow rate fraction of the left and the right lungs at tidal breathing from deep breathing analysis with two correction-weighting factors of W_left = 0.449/0.492 = 0.913 and W_right = 0.551/0.508 = 1.085, respectively, for the all subjects. Therefore, to predict q_f during the VCFB range more accurately, we assume that W_left and W_right can be multiplied by q_f in any region of the left and right regions computed by the deep breathing analysis, respectively. Figure 7B shows the linear regression between q̄_f,4D-CT and q_f,SCT modified by W_left and W_right (denoted by q_f,modified). In this case, the correlation factor, R², was improved from 0.84 to 0.92 so that we can roughly use the equations (q_f,modified)_left = (q_f,SCT)_left × W_left and (q_f,modified)_right = (q_f,SCT)_right × W_right to predict air volume change during VCFB. A comparison between original and modified values of the left and right lungs showed that they are significantly different (P < 0.05).

Furthermore, the comparison of the left and right lungs for ADI of FRC-TLC normalized by total ADI at TLC (ADI_LL^* = 1.02, ADI_RL^* = 0.97) and ADI of EE-EI normalized by total ADI at EI (ADI_LL^* = 0.87, ADI_RL^* = 1.19) illustrates consistency with the left-right lung differences observed by air volume changes in each left and right lungs.

Nonlinearity and hysteresis of ADI.

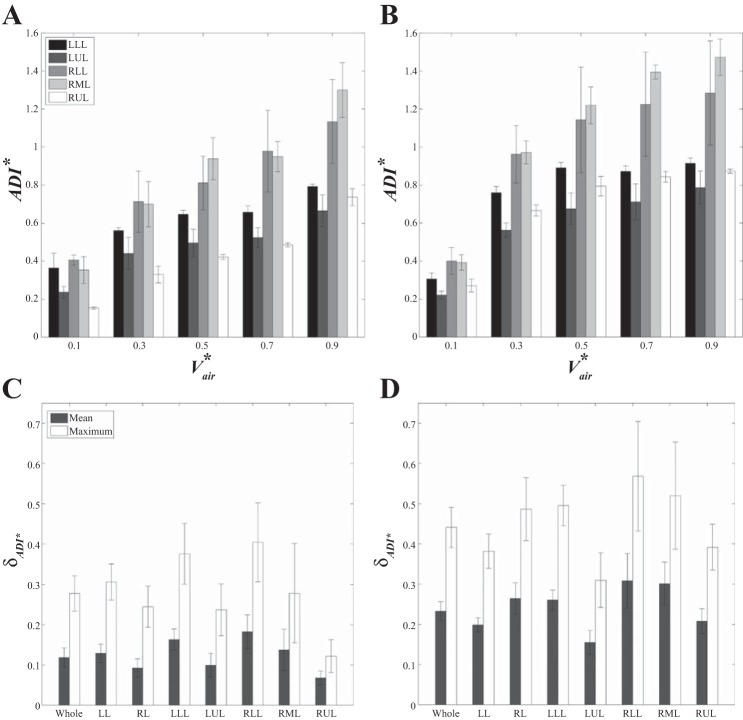
To observe nonlinearity and hysteresis of the lung motion during dynamic breathing, we examined ADI^* values during VCFB. Figure 8A shows the means (± SE) of ADI^* values in the whole lung at different V_air^* over a breathing cycle for the five subjects. The results showed that ADI^* values are not along a straight line and that the values of inhalation are greater than those of exhalation (P < 0.05), capturing nonlinear and asymmetric lung deformations between two certain points (EE and EI). In Fig. 8B, we also observed greater ADI^* values for the right lung rather than the left lung. Figure 9, A and B, shows the lobar distributions of ADI^* over exhalation and inhalation, respectively. We observed that ADI^* values in the middle and the lower lobes are greater than those in the upper lobes for both exhalation and inhalation. We further quantified the nonlinearity δ_ADI*. Figure 9, C and D, shows that δ_ADI* in inhalation is greater than that of exhalation, and lower and middle regions represent greater δ_ADI*. Furthermore, Fig. 10 shows mean and maximum of Hys_ADI* in the whole lung, the left and the right lungs, and each lobe for different phases. The results demonstrate that the right lung has greater Hys_ADI* than the left lung (P < 0.05).

Fig. 8.

A: mean (± SE) of anisotropic deformation index (ADI^*) in the whole lung. B: mean of ADI^* in the whole, left, and right lungs during volume-controlled free breathing for the 5 subjects.

Fig. 9.

Bar graph showing the mean (± SE) of lobar ADI^* values of exhalation (A) and inhalation (B) and the mean (± SE) and maximum (± SE) of lungs and lobar nonlinearity of exhalation (C) and inhalation (D).

Fig. 10.

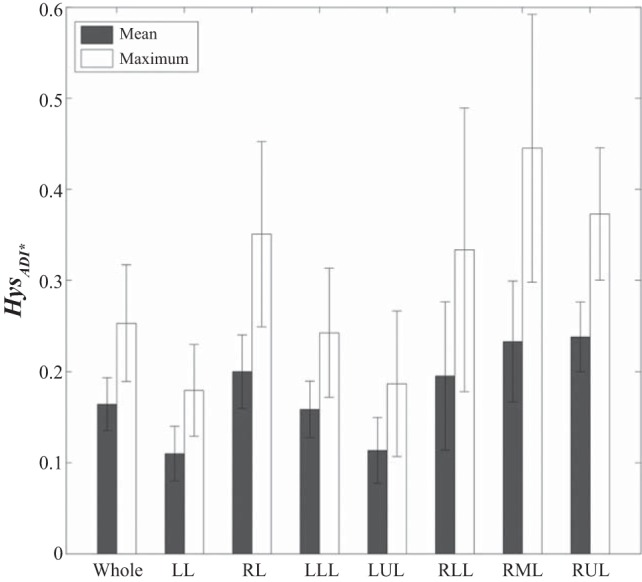
Bar graph showing mean (± SE) and maximum (± SE) of lungs and lobar hysteresis (Hys) for the 5 subjects.

DISCUSSION

Controlled tidal volume.

The limitations of inconsistent tidal volumes and irregular breathing patterns during 4D-CT have been recognized by others (4, 8, 21). The amplitude difference produces artificial motions in the reconstructed 4D volumetric CT data set, leading to erroneous assessment of regional mechanical behavior. With the introduction of a dual rolling-seal piston system (11) for control of tidal breathing during 4D-CT data collection, we presented a means of regionally assessing lung mechanics that provides physiologically meaningful metrics. The results demonstrated that the dual-piston system successfully controlled the subject's respiratory cycle to obtain consistent air volume change and breathing waveforms (SE < 4%), thus allowing for the collapse of multiple cycle data into a single cycle (Fig. 2, A and B). To further harmonize subject data, air volumes derived from registration were normalized, utilizing measurements via the same scheme as discussed in Eqs. 1 and 6. The strong correlation between the measured air volume and the air volume computed by image registration, not only validates the accuracy of 4D-CT data, but also enables use of a single normalized air volume for analysis of measurement and 4D-CT data. Because of intersubject variability in respiratory waveforms, other studies had to examine each subject separately (8, 27). In contrast, with use of a dual-piston system, we were able to derive consistent normalized flow rates and lobar air volume fractions during inhalation and exhalation in a group of healthy subjects (Figs. 3 and 5). This is particularly important for future studies that seek to define phenotypes based on altered regional mechanical properties in a patient population.

Regional air volume and flow rate.

Several studies used linear assumption between each two successive phases to estimate 4D-CT lung motion (4, 8). Piecewise linear interpolation yields discontinuity in calculation of air flow rate at each phase, whereas, in the present study, we used a cubic spline interpolation function to construct a continuous function for any local variable, which is independent of breathing waveform. Regional air volume and flow rates obtained from 4D-CT analysis showed that lower lobes always have more contribution to air volume change compared with upper and middle lobes during dynamic breathing (Figs. 5 and 6). This supports the analysis of Yin et al. (32) and Jahani et al. (16) based on interpolation of three static MDCT images. It is speculated that the predominance of diaphragm motion in driving lung expansion leads to the greater volume change in the lower lobes than the upper lobes.

Furthermore, because the interpolated function is independent of lung volume waveforms, it can be incorporated with any other lung volume curve for various waveforms. Thus, if measured temporal lung volume curves are not available, an ideal lung volume waveform can be assumed to compute local air flow rates (Eq. 12) for various respiratory conditions. For example, to examine the effect of waveform, we replaced the actual waveform with a sinusoidal one. Although the results showed similar trends when using a symmetric waveform, asymmetric patterns of local flow rates (Eq. 13) of exhalation and inhalation were reduced (Fig. 6).

Flow rate based on regional tidal vs. deep breathing (dynamic vs. static scans).

Several studies have utilized static scans acquired at static points to evaluate regional lung ventilation and deformation (13, 16, 31). Although 4D-CT images can provide more physiological information, they typically yield lower spatial resolution compared with static imaging and expose subjects to higher radiation doses. Newer-generation CT scanners are serving to dramatically drop radiation doses (20). Because of the need for high resolution acquired with lower radiation doses, lung mechanics studies have typically been carried out with static breath-hold imaging. Our study provides, possibly for the first time, a means of comparing the mechanical data derived from breath hold vs. dynamic imaging and provides a methodology, which, when coupled with newer methods for low-dose imaging, can provide important dynamic regional lung mechanics, and in the future, can be used as novel phenotypes, differentiating populations at early stages of lung disease. In some studies, FRC and TLC data (instead of end tidal lung volumes) have been used to derive mean flow rate fraction, equivalent to the fractions of lobar air volume change (6, 31). Our comparisons between tidal breathing (4D-CT) vs. static imaging at FRC and TLC demonstrated that fractions of lobar air volume change across lung volumes are in good correlation with the flow rate fractions in 4D-CTs (Fig. 7A). This suggests that, in normal subjects, static breath-hold-derived metrics may be adequate for certain lung mechanics studies. However, we found that, during VCFB, the air volume change fractions in the right lung are greater than that of the left lung, whereas the air volume change fractions of both lungs derived from static FRC and TLC images are almost the same, consistent with findings of Voorhees et al. (26). Because the left lung was less well expanded at lower lung volumes and during VCFB, it is able to expand more than the right lung when inspiring to full lung capacity, equalizing lung volume changes between the two lungs at TLC, whereas, at tidal breathing, one observes differences in distribution of lung volume changes. Flow rate fractions for the left and right lungs, between VCFB and deep breathing, are significantly different in which respective values for the five subjects were similar with small standard errors (SE < 2%). Therefore, we proposed two correction-weighting factors W_left = 0.913 and W_right = 1.085, which were multiplied by mean flow rate fractions, i.e., air volume change fractions, obtained from the SCT analysis in left and right lungs, respectively. The improved correlation implies that the proposed correction factors could be utilized to estimate regional ventilation predictions (Fig. 7B). Yin et al. (31) have proposed an image-based technique using two SCT lung data sets to estimate a subject-specific boundary condition for CFD simulation. Thus those two correction factors can be employed in their method to estimate more realistic boundary conditions for CFD simulation in tidal breathing range.

Yin et al. (32) and Jahani et al. (16) have used three static images to study nonlinear behaviors of lung mechanics with a sinusoidal waveform. They showed that, as lung volume increases for deep breathing, the peaks of flow rate occur earlier in the upper lobes than the peaks in the lower lobes, whereas our dynamic breathing analysis with the assumption of a sinusoidal waveform did not show any ascending or descending trend in lobar flow rate fractions (Fig. 6). One reason is that most regions in the upper lobes are fully inflated before the lung volume reaches its maximum volume, while the upper lobes in VCFB still have capacity to accommodate more air at the maximum volume of EI because of lower lung volume. In addition, acquiring 4D-CT data can allow assessment of the regional flow volume loop that is asymmetric between inhalation and exhalation (Fig. 6). In contrast to 4D-CT analysis, two static scans can provide only constant flow rate, and three static scans can provide a nonlinear but symmetric volume-dependent flow rate between inhalation and exhalation (32).

Nonlinearity and hysteresis.

In this study, ADI was used to quantify nonlinearity and hysteresis in lung deformation during VCFB. Our results indicated that ADI and nonlinearity are greater in inhalation, consistent with the parameters of anisotropic deformation and nonlinearity quantified by Jahani et al. (16) and Boldea et al. (4), respectively. Our observations may reflect the fact that the diaphragm and chest wall muscles are typically active only during inhalation, producing greater directional forces than occur during passive exhalation. It is noted that Boldea et al. (4) have used trajectories of material points to quantify nonlinearity. They assumed that local points have uniform motion relative to total volume change over inhalation and exhalation, whereas our study showed that local points might move nonuniformly relative to the motion of normalized total lung volume (Figs. 5 and 6). Similar to point trajectory, ADI is a Lagrangian quantity obtained via the registration-derived one-to-one mapping field.

Physiologically, the hysteresis of lung motion is attributed to the fact that some part of the transmitted energy in inhalation is dissipated because of local forces such as surface tension and tissue stress and is not recovered in exhalation (9a). Locally, those forces are correlated with strains. For example, Jahani et al. (16) have used shear strain expressed as (λ₁ − λ₃)/2 to quantify nonlinearity in the lung and have demonstrated a strong correlation between shear strain and ADI (R² > 0.89), consistent with our results. The significant difference between ADI values on inhalation and those on exhalation suggests that anisotropic deformation can be used to assess the hysteresis of lung motion. The computed hysteresis showed the maximum value at the middle of breathing and greater hysteresis in the right lung (Figs. 8 and 10).

Limitations and future work.

In this study, we investigated 4D-CT analysis for only five healthy subjects although more subjects are needed to fully define the characteristics of a normal population. Nonetheless, we performed t-tests between different regions (e.g., lower vs. upper lobes, left vs. right lung, and inhalation vs. exhalation) to assure that the reported characteristics are statistically significant. With P < 0.05, the heterogeneous pattern of lung characteristics is confirmed. Furthermore, to evaluate intersubject variability, means and standard errors between the five subjects were reported for all variables. To achieve more subjects, we need to resolve the remaining issues such as imaging protocol and limitation in breathing rates, and it will be desirable to identify lower dose protocols, taking advantage of newer scanner technologies (20). In addition, application of the current analysis to disease states, such as asthma, chronic obstructive lung disease, and interstitial fibrosis, is desirable because heterogeneity in diseased lungs may pose new challenges on normalization of intersubject data (6, 7). Several studies have applied CFD to simulate respiratory air flow in a breathing lung based on static image-derived flow boundary conditions (18, 32). The regional air flow distributions and flow rates extracted from the current 4D-CT analysis can be further used in CFD to better predict the distributions of flow-induced shear stress and pressure as well as temperature, water loss rate (28, 29). and particle depositions (19) for various applications. In addition, using the methods in this study for tracking the motion of lung cancers could provide more accurate information regarding lung motion required for the targeting of radiotherapy and for the assessment of regional, longitudinal changes in lung mechanics throughout therapy (2, 4, 9, 30).

GRANTS

This work was supported in part by NIH grants R01-HL094315, U01-HL114494, R01-HL112986, and S10-RR022421.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s). There is no conflict of interest although E. A. Hoffman is a shareholder in VIDA diagnostics, which is commercializing lung image analysis software derived from the University of Iowa lung imaging group. He is also a member of the Siemens CT advisory board.

AUTHOR CONTRIBUTIONS

Author contributions: N.J., E.A.H., and C.-L.L. conception and design of research; N.J., S.C., J.C., and K.I. performed experiments; N.J. analyzed data; N.J., S.C., J.C., and K.I. interpreted results of experiments; N.J. prepared figures; N.J. drafted manuscript; N.J., S.C., J.C., E.A.H., and C.-L.L. edited and revised manuscript; S.C. and C.-L.L. approved final version of manuscript.