A Primer on the Bayesian Approach to High-Density Single-Molecule Trajectories Analysis

Abstract

Tracking single molecules in living cells provides invaluable information on their environment and on the interactions that underlie their motion. New experimental techniques now permit the recording of large amounts of individual trajectories, enabling the implementation of advanced statistical tools for data analysis. In this primer, we present a Bayesian approach toward treating these data, and we discuss how it can be fruitfully employed to infer physical and biochemical parameters from single-molecule trajectories.

Main Text

In the past years, single-molecule measurements have become a tool of choice for the study of biological systems. In particular, single-molecule tracking techniques play an important role for probing the processes regulating the mobility of biomolecules in living cells. They have been successfully used to investigate the motion of, among others, membrane proteins, molecular motors, mRNAs, and transcription factors (1, 2). In practice, single-molecule tracking experiments involve capturing a sequence of images of biomolecules tagged with a fluorescent probe (usually fluorescent proteins, organic dyes, or nanoparticles). Fluorescent probes are then imaged on a sensitive camera and spatially localized (e.g., with a fitting algorithm). The positions are then connected between frames to construct individual molecule trajectories (3). From these trajectories, it is then possible to obtain information on the physical and biological parameters controlling the movement.

The throughput of single-molecule tracking experiments have long been limited to a few tens or hundreds of trajectories. However, the advent of high-density tracking methods, such as sptPALM (4) or uPAINT (5), has changed the scale at which individual motions can be recorded and made it possible to capture hundreds of thousands or even millions of individual trajectories. Importantly, it enables more advanced statistical methods to infer the motion parameters. Moreover, it means that sufficient data are available to determine these parameters in a spatially resolved manner.

In this primer, we discuss the use of Bayesian inference methods to analyze single-molecule trajectories. First, we recall the basic principles of Bayesian inference. Next, we detail its implementation for the analysis and mapping of the stochastic motion of proteins in living cells. Finally, we illustrate the Bayesian approach with experimental results on the dynamics of transmembrane proteins.

Bayesian framework

A general goal in data analysis is the determination of the parameters of a model (e.g., the diffusion coefficient in the case of Brownian particles) given a set of experimental observations (e.g., individual trajectories from single-molecule tracking experiments). Bayesian approaches provide a consistent and reliable framework for extracting information from experimental measurements (6, 7, 8, 9, 10, 11). As illustrated in this primer, a great benefit of Bayesian methods is that they easily incorporate hypotheses on the physical and biological properties of the system, as well as on experimental conditions. Classically, Bayesian inference features two steps: the derivation of the posterior probability distribution of the model parameters and sampling from the posterior distribution to estimate the parameters.

The starting point is Bayes’ law that reads as follows:

$$P\left(\left\{U\right\}|\left\{T\right\},M\right)=\frac{P\left(\left\{T\right\}|\left\{U\right\},M\right)P\left(\left\{U\right\}|M\right)}{P\left(\left\{T\right\}|M\right)},$$ (1)

where $\left\{T\right\}$ is the set of experimental observations, $\left\{U\right\}$ is the set of model parameters (to be evaluated), and M is the model chosen to describe the data. In standard terminology, $P\left(\left\{U\right\}|\left\{T\right\},M\right)$ is the posterior distribution, $P\left(\left\{T\right\}|\left\{U\right\},M\right)$ is the likelihood, $P\left(\left\{U\right\}|M\right)$ is the prior distribution, and $P\left(\left\{T\right\}|M\right)$ is the evidence of the model.

The likelihood embodies the physical model and hypotheses regarding the acquisition of data. In the context of tracking experiments, it encodes the model used to describe the motion of the molecules (including the presence of drift, or the Markovian/non-Markovian nature of the process), the positioning noise induced by the experimental conditions, and various hypotheses regarding characteristic scales of the environment.

Prior probability distributions are critical to Bayesian analysis (6, 7, 9, 10, 12). They represent knowledge on the parameters before any measurements, including various physical constraints that may not be present in the likelihood. Furthermore, they can impose that the posterior distribution is invariant under reparametrization (i.e., Jeffreys prior), and they can ensure that the posterior distribution is a well-behaved function. Finally, priors can be used to regularize the inferred parameters as discussed below.

The evidence allows access to the probability of a model. It is mostly used in the context of Bayesian model comparison (6, 7, 9, 10, 12) as follows:

$${\gamma }_{ij}=\frac{P\left(\left\{T\right\},M_i\right)}{P\left(\left\{T\right\},M_j\right)}=\frac{P\left(\left\{T\right\}|M_i\right)P\left(M_i\right)}{P\left(\left\{T\right\}|M_j\right)P\left(M_j\right)},$$ (2)

where $P\left(M_i\right)$ is the prior probability of the model $M_i$ and where the model with the highest evidence is chosen. In the context of single-molecule analysis, proper model selection is made semi-empirically with the use of numerical simulations and various statistical estimators (13, 14).

The final task of the Bayesian approach is sampling the posterior distribution. The most common estimator of the inferred parameters is the maximum a posteriori (MAP), i.e., the highest-probability parameter value from the posterior. It is usually accessed through direct optimization of the posterior distribution. In low dimensions, posterior sampling can be done by direct integration (9, 10). Otherwise, it is commonly performed using Monte Carlo sampling (7, 9, 10, 12, 15). Fine tuning of the Monte Carlo parameters is often required to obtain efficient sampling in large dimensions. Numerous discussions on Monte Carlo sampling can be found in (7, 9, 10, 12). It is worth noting that in the following and under most relevant assumptions (discussed in the next section), the posterior distributions, in our case, are well-behaved functions with well-defined maxima (usually not unique but with a main one). Hence, a common approximate method for posterior sampling (allowing faster computation than Monte Carlo sampling) is the Laplace approximation (12) of the posterior distribution at the MAP value of the parameters. It provides a Gaussian approximation of the posterior distribution (11, 16, 17). In most relevant hypotheses, it leads to overestimation of the error in parameter estimation, which stems from asymmetry of the diffusion posterior distribution that is imperfectly approximated by a Gaussian.

Mapping the parameters of single-molecule motion

As indicated above, a unique benefit of Bayesian approaches is that the likelihood and prior distributions can be used to account for noise and variability in experiments. Hence, before explicitly constructing the different terms required for Bayesian inference, it is important to note a few specific features of single-molecule tracking measurements in living cells. Different sources of noise and variability may be identified in single-molecule experiments. First, the dynamics of individual molecules in cells is primarily driven by thermal noise, leading to Brownian motion. Next, the cellular environment is highly heterogeneous. For example, this is the case of the plasma membrane where lipid microdomains, scaffold proteins, and molecular crowding (among other factors) contribute to variability in diffusive properties. Finally, single-molecule experiments are inherently single-cell experiments, meaning that they are subject to phenotypic variabilities between cells.

Given the vast spatial heterogeneity in the dynamics of molecules, it is natural to map the parameters controlling their motion rather than provide a single value averaged over the entire cell. There are a few implicit assumptions in the mapping procedure. First, it is necessary to mesh the cellular environment, meaning that there are scales at which the physical parameters can be considered approximately constant. In turn, the number of trajectories must be large enough so that sufficient information is gathered to infer the parameters in each zone of the mesh. A second assumption is that the cellular system does not significantly evolve over the durations of the measurements (note that slow evolutions may still be analyzed as in (18)). Experimental constraints associated with these assumptions have largely been alleviated with the advent of high-density single-particle tracking techniques that permit rapid recording of a large number of data points (up to several thousands per μm² in a few minutes).

Likelihood

We start our Bayesian analysis by constructing the likelihood. The dynamics of molecules, the characteristic scales of motion, the relaxation time of the velocity (10⁻¹⁸ − 10⁻¹⁰ s), and the heterogeneity of the environment suggest that the overdamped Langevin equation (19, 20, 21) can be used to model various kinds of motion. It reads as follows:

$$\frac{d\mathbf{r}}{dt}=\frac{\mathbf{F}\left(\mathbf{r}\right)}{\gamma \left(\mathbf{r}\right)}+\sqrt{2D\left(\mathbf{r}\right)}\xi \left(\mathbf{t}\right),$$ (3)

where $D\left(\mathbf{r}\right)$ is the diffusion, $\gamma \left(\mathbf{r}\right)$ is the friction, $\mathbf{F}\left(\mathbf{r}\right)$ is the force, and $\xi \left(t\right)$ is a zero-averaged Gaussian noise. Equation 3 describes the time evolution of the molecule in a heterogeneous environment where the diffusion, friction, and forces vary with space. If the force field is conservative, i.e., the energy is conserved, it can be written as the derivative of a potential $\mathbf{F}\left(\mathbf{r}\right)=-\nabla V\left(\mathbf{r}\right)$. The analysis is not limited to conservative force fields. Before analysis there is no information on the various scales at which these fields vary or even if they are present. Furthermore, the heterogeneous spatial diffusion potentially leads to the well-known (Itô-Stratonovich-Hänggi) dilemma (19, 20, 21, 22, 23, 24, 25, 26). The dilemma stems from the dependence of the results of stochastic integrals on the hypothesis made to evaluate them. In the case of the Langevin equation, it leads to the “spurious force” induced by diffusion gradients (as shown in Eq. 4).

The Fokker-Planck equation governing the time evolution of the transition probability of a molecule displacement associated to Eq. 3 reads (20) as follows:

$$\frac{\partial P\left(\mathbf{r},t|{\mathbf{r}}_0,t_0\right)}{\partial t}=-\nabla \left[\left(\frac{\mathbf{F}\left(\mathbf{r}\right)}{\gamma \left(\mathbf{r}\right)}+\lambda \nabla D\left(\mathbf{r}\right)\right)P\left(\mathbf{r},t|{\mathbf{r}}_0,t_0\right)\right]+\nabla \left[D\left(\mathbf{r}\right)\nabla P\left(\mathbf{r},t|{\mathbf{r}}_0,t_0\right)\right],$$ (4)

where ${\mathbf{r}}_0$ is the position of the molecule at time $t_0$; r is the position of the molecule at time t; and λ is a constant equal to $\lambda =0$ if Eq. 3 is interpreted by the Itô definition, $\lambda =1/2$ if it is interpreted by the Stratonovich definition, and $\lambda =1$ if it is interpreted by the Hänggi (isothermal) definition.

We can now compute the full likelihood. The motion being Markovian (or at least approximated as such), the probability of a trajectory of length N reads $P\left({\left\{{\mathbf{r}}_i,t_i\right\}}_{i=\mathrm{1..}N}\right)={\prod }_{i=1}^{N-1}P\left({\mathbf{r}}_{i+1},t_{i+1}|{\mathbf{r}}_i,t_i\right)$. It follows from Eq. 4 that the probability P can be expressed as a path integral (27, 28) over all paths $\mathbf{r}\left(s\right)$ connecting ${\mathbf{r}}_0$ to r as follows:

$$P\left(\mathbf{r},t|{\mathbf{r}}_0,t_0\right)\propto \int \mathcal{D}\mathbf{r}\left(s\right)e^{-\int dsQ\left(\mathbf{r}\left(s\right)\right)},$$ (5)

where

$$Q\left(\mathbf{r}\left(s\right)\right)\equiv \frac{1}{4D\left(\mathbf{r}\left(s\right)\right)}{\left(\frac{d\mathbf{r}\left(s\right)}{ds}-\frac{\mathbf{F}\left(\mathbf{r}\left(s\right)\right)}{\gamma \left(\mathbf{r}\left(s\right)\right)}+\lambda \nabla \mathbf{D}\left(\mathbf{r}\left(\mathbf{s}\right)\right)\right)}^2+\lambda \nabla \frac{\mathbf{F}\left(\mathbf{r}\left(\mathbf{s}\right)\right)}{\gamma \left(\mathbf{r}\left(\mathbf{s}\right)\right)}$$

is the classic Gaussian weight governing the probability of displacements over an infinitesimal time interval.

We now use the mapping hypothesis suggesting that trajectories close in space share the same properties. Hence, our analysis is performed in a spatially partitioned space: a mesh. We have recently described three methods of meshing in the context of single-molecule trajectories: square (11, 14), quad-tree (hierarchical), and Voronoi tessellation (via unsupervised clustering) (29). The goal of the mesh is to balance multiple constraints: local densities of translocations, characteristic sizes of motion heterogeneities, and local domain size scaling. A common property is that the size of the mesh is (at best) on the order of $\sqrt{D\Delta t}$ where D is the local diffusion coefficient and $\Delta t$ is the time between frames.

Thus, the solution of Eq. 5 can be approximated in mesh subdomains by the Laplace approximation with locally $D\left(\mathbf{r}\right)\approx D\left({\mathbf{r}}_c\right)$, $\gamma \left(\mathbf{r}\right)\approx \gamma \left({\mathbf{r}}_c\right)$, $\mathbf{F}\left(\mathbf{r}\right)\approx \mathbf{F}\left({\mathbf{r}}_c\right)$ and if the force field is conservative $\nabla V\left(\mathbf{r}\right)\approx \nabla V\left({\mathbf{r}}_c\right)$ with ${\mathbf{r}}_c$ the centroid of the mesh domain. Finally, events happening at smaller scales than the one imposed by the local diffusivity, $\sqrt{D\left(\mathbf{r}\right)\Delta t}$, cannot be directly analyzed without earlier knowledge (30). Note that these approximations collapse the three definitions of stochastic integrals previously mentioned onto the same value.

Depending on the physical modeling, on the characteristic scales of the fields and on the statistical properties of the data, many different likelihoods may be formulated (11, 13, 14, 16, 17, 18, 29, 31, 32). In this primer, we discuss the likelihood to infer heterogeneous diffusion in a potential field, thus with $\mathbf{F}\left(\mathbf{r}\right)=-\nabla V\left(\mathbf{r}\right)$. The full likelihood reads as follows:

$$P\left({\left\{T_k\right\}}_{\left(k\in \mathcal{T}\right)}|{\left\{\nabla V_l\right\}}_{\left(l\in \mathcal{M}\right)},{\left\{D_l\right\}}_{\left(l\in \mathcal{M}\right)}\right)\propto \prod _{\left(l\in \mathcal{M}\right)}\left(\prod _{k\in \mathcal{T}}\prod _{\mu :{\mathbf{r}}_{\mu }^k\in S_l}\frac{\text{exp}\left(-\frac{{\left({\mathbf{r}}_{\mu +1}^k-{\mathbf{r}}_{\mu }^k-D_l\nabla V_l\Delta t/k_{B}T\right)}^2}{4\left(D_l+\frac{{\sigma }^2}{\Delta t}\right)\Delta t}\right)}{{\left(4\pi \left(D_l+\frac{{\sigma }^2}{\Delta t}\right)\Delta t\right)}^{\frac{d}{2}}}\right),$$ (6)

where $\mathcal{M}$ is the mesh, $S_l$ is a subdomain in the mesh, $\mathcal{T}$ is the set or subset of trajectories, k is the superscript index of a trajectory in $\mathcal{T}$, μ is the subscript time index of a point in the trajectory, σ is the positioning noise modeled as a Gaussian process, and d the spatial dimensionality $\left(d\in \left\{\mathrm{1,2,3}\right\}\right)$. The local fluctuation-dissipation relation, $D_l=k_{B}T/{\gamma }_l$ is enforced directly in this likelihood. Note that, for a large number of points, the potential inferred converges onto the Boltzman equilibrium distribution (11, 13, 14, 16, 17, 18, 20, 21, 29, 31, 32).

Priors

To perform the analysis, we use as a prior the product of two priors: the Jeffreys prior and the field prior. In our case, the Jeffreys prior reads as follows:

$$P\left(D_l,V\right)\propto \frac{D_l^2}{{\left(D_l\Delta t+{\sigma }^2\right)}^2}.$$ (7)

In a practical manner, the Jeffreys prior prevents from inferring negative diffusion in local confinement domains because of positioning noise (31). The field prior is used to penalize strong gradients of the diffusive and potential fields. This prior reads as follows:

$$P\left(D\left(\mathbf{r}\right),V\left(\mathbf{r}\right)\right)\propto \text{exp}\left(-\mu \int d\mathbf{r}{\Vert \nabla D\left(\mathbf{r}\right)\Vert }^2-\lambda \int d\mathbf{r}{\Vert \nabla V\left(\mathbf{r}\right)\Vert }^2\right),$$ (8)

where μ and λ are weighting coefficients optimized using simulations matching experimental conditions. Note that the parameters $\left(\mu ,\lambda \right)$ can also be accessed directly from the experimental trajectories using the parametric empirical Bayesian approach (12, 33). This approach is an approximate Bayesian procedure in which the parameters of the prior are estimate directly from the data using Bayes law. The field prior encodes physical constraints on the medium properties and effectively reinforces the robustness of the parameter estimation. Among other things, it can impede the consequences of misconnected single-molecule trajectories. It damps the propagation during optimization of local region of high diffusion or potential that are induced by improper linking between two separate biomolecules.

Finally, the robustness of the results regarding misevaluation of the positioning noise should be tested. To this end, an empirical noise prior is introduced as follows:

$$P\left(\sigma \right)=\frac{1}{{\sigma }_0}\text{exp}\left(-\frac{\sigma }{{\sigma }_0}\right),$$ (9)

where ${\sigma }_0$ is the experimentally measured positioning noise. It is worth noting here that ${\sigma }_0$ includes all sources of noise, i.e., camera shot noise, single-molecule motion blur (34), localization algorithm, etc. The posterior distribution is then computed by numerically integrating the likelihood over all the possible values of σ as follows:

$$P\left(\left\{U\right\}|\left\{T\right\},M\right)\propto \int P\left(\left\{T\right\}|\left\{U\right\},\sigma ,M\right)P\left(\left\{U\right\}|M\right)P\left(\sigma \right)d\sigma .$$ (10)

Note that in both the likelihood and the prior, the physical model of the environment and the experimental conditions (acquisition time, number of translocations, localization error) are mixed allowing a full probabilistic view of the experiments.

Posterior distribution sampling

Estimators of parameters are linked to the Bayesian procedure (6, 7, 9, 10, 12). When numerous localizations are available, the posterior distribution is bound to be narrow. Thus, we use the MAP values as estimators. The MAP is evaluated by optimizing the posterior distribution using simplex or quasi-Newton methods in multiple dimensions (35) (other optimization procedures work also efficiently). When the analysis is performed with independent mesh domains, local posterior distributions of diffusivity and forces are evaluated by direct integration. When the analysis is performed on large-scale domains (or full cell surface) with coupling between mesh domains (either in the likelihood or the prior), approximate methods are often employed. As interaction and diffusivity fields are limited in their spatial extension, the posterior distribution sampling was performed by setting all the parameter values outside the area of interest to their MAP values. This procedure was used to perform direct integration of diffusion and force posterior distribution on local areas and also to evaluate confinement energy. Furthermore, a common approximation used when evaluating the posterior distribution of parameters in local domains is the Laplace approximation. This approximation leads to a Gaussian shape of the posterior distribution. The main effect in the case of single-molecule analysis is an overestimation of the error in diffusion analysis, which stems from the asymmetry of the diffusion distribution imperfectly approximated by a Gaussian.

Quantitative elements

The efficiency of the scheme regarding convergence, reliability of the maps, quality of the posterior distribution, and effect of the prior are discussed in great detail in (11, 13, 14, 16, 17, 18, 29, 31, 32). A few common rules can be shortly described. Numerous properties are problem dependent, however, generating a mesh with ≈20 points per zone ensures a well-behaved posterior distribution and reliably inferred maps. When handling various levels of single-molecule confinement, the Jeffreys prior ensures that no area will have a negative diffusivity induced by the combined effect of the positioning error and confinement. Finally, field priors have a useful property beyond smoothing. Numerous experiments and single-molecule tracking algorithms lead to trajectory misconnections during tracking that can have significant consequences on analyzed properties. Coupling mesh domains together with the field prior ensures that these events have limited statistical weight.

Globally, when handling any new problem, the inference procedure is optimized on numerical simulations. Trajectories are numerically generated in media mimicking both the biological system and the recording properties. Parameters are then optimized to infer the fields used to generate the trajectories. It is worth noting that single-molecule experiments enjoy a useful property: most possible configurations can be simply and efficiently simulated.

A biological example: dynamics of membrane proteins

We illustrate the application of our Bayesian approach in the case the dynamics of glycine receptors (GlyR) in living cells. The analysis was performed by means of InferenceMAP (29), an open source C++ software that implements the method discussed above. GlyR diffuses on the postsynaptic membrane of neurons and interacts with the scaffold protein gephyrin via an intracellular β-loop. The GlyR-gephyrin interaction is thought to be a key molecular mechanism of synaptic formation and plasticity in the inhibitory neuronal synapse (31, 36, 37). Gephryin scaffolds are stable on the timescale of a few minutes and, as previously shown (31), they can be described as potential wells in which receptors are transiently trapped.

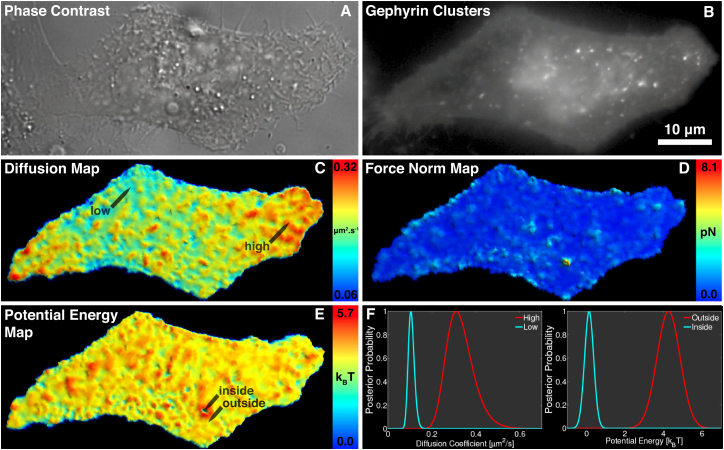
To reconstitute the interaction in a nonneuronal system, we used HeLa cells cotransfected with gephyrin and a transmembrane domain possessing the intracellular β-loop (38) and fused to an extracellular photoactivatable fluorescent probe (dendra2). Using sptPALM in total internal reflection fluorescence illumination, we recorded more than 160,000 individual trajectories in a 300 s acquisition. With the described mapping approach, we generated diffusion, force, and potential energy maps spanning the whole cell (Fig. 1). The map is based on an adaptive mesh, generated with an unsupervised clustering technique described in (29). There are more than 4,000 zones in the mesh, with the minimal spatial resolution being ∼120 nm. The full analysis required ≈30 min. Analysis of individual clusters only requires a few tens of seconds. The main time-consuming step is the optimization of the potential field, which strongly depends on the number of variables. Approximate methods to optimize large-scale fields, such as randomized optimization of mesh subsets (implemented in InferenceMAP (29)), reduce computation time and efficiently converges to the MAP values of the parameters.

Figure 1.

Bayesian approach to mapping single-molecule dynamics of a transmembrane protein that interacts with gephyrin clusters via an intracellular β-loop inside a HeLa cell: (A) phase contrast image of a HeLa cell; (B) fluorescent image of gephyrin clusters, visible as bright spots; (C) whole-cell diffusivity; (D) force norm; and (E) potential energy. (F) Example of posterior distributions of the diffusion and potential is shown. Positions are indicated by labeled arrows in (C) and (E). To see this figure in color, go online.

The maps display important features. For the diffusion, values range from 0.06 to 0.32 μm² × s⁻¹. The spatial variation of diffusivities is likely the result (among other things) of variations in lipid content of the membrane, local changes in membrane composition, crowding, and nonspecific interaction with the environment. Importantly, we verify that the posterior distribution of the low- and high-diffusivity regions are disjoint (Fig. 1 F), indicating that the measured differences are statistically significant. The map of the force norms reveals small regions of strong directional bias, which corresponds to potential wells of different depths in the potential energy map (Fig. 1 E). Importantly, the sites of these interaction regions are correlated to the location of gephyrin clusters inside the cell, seen in the gephyrin fluorescence image (Fig. 1 B). Outside the gephyrin clusters, the force and potential landscape is mostly flat meaning that the motion is predominantly diffusive. We can quantify the depths of the potential wells by sampling the posterior distribution of the potential energy inside and outside of the interaction region (Fig. 1 F). The potential energy difference of roughly ∼4 kT is evidence of a transient interaction, in which receptors are temporarily confined at the site of a gephyrin cluster.

Conclusion

To conclude, Bayesian inference constitutes a natural framework for single biomolecule trajectory analysis. It combines physical modeling of single-molecule motion with hypotheses on data recording into a full probabilistic framework. In future developments, it will be interesting to adapt the Bayesian approach described above to include the internal dynamics of the biomolecule (switching between different diffusive states), the multiscale nature of the environments, non-Markovian processes and, from a computational standpoint, adaptation of the methods to large data sets.

Author Contributions

M.E.B., S.T., and M.R. performed the experiments; A.T., M.D., A.A., and J.B.M. designed the experiments; M.E.B., S.T., and J.B.M. programmed the various scheme and inference software; J.B.M. designed the inference procedures; and M.E.B., A.A., M.D., and J.B.M. wrote the article.

Editor: Stanislav Shvartsman