Single-Molecule Chemo-Mechanical Spectroscopy Provides Structural Identity of Folding Intermediates

Abstract

Single-molecule force spectroscopy has emerged as a powerful tool for studying the folding of biological macromolecules. Mechanical manipulation has revealed a wealth of mechanistic information on transient and intermediate states. To date, the majority of state assignment of intermediates has relied on empirical demarcation. However, performing such experiments in the presence of different osmolytes provides an alternative approach that reports on the structural properties of intermediates. Here, we analyze the folding and unfolding of T4 lysozyme with optical tweezers under a chemo-mechanical perturbation by adding osmolytes. We find that two unrelated protective osmolytes, sorbitol and trimethylamine-n-oxide, function by marginally decelerating unfolding rates and specifically modulating early events in the folding process, stabilizing formation of an on-pathway intermediate. The chemo-mechanical perturbation provides access to two independent metrics of the relevant states during folding trajectories, the contour length, and the solvent-accessible surface area. We demonstrate that the dependence of the population of the intermediate in different osmolytes, in conjunction with its measured contour length, provides the ability to discriminate between potential structural models of intermediate states. Our study represents a general strategy that may be employed in the structural modeling of equilibrium intermediate states observed in single-molecule experiments.

Introduction

Single-molecule force spectroscopy has emerged as a powerful tool for studying protein folding (1, 2, 3). Devoid of ensemble averaging, mechanical manipulation of single protein molecules with optical tweezers has revealed a wealth of mechanistic information on transient states and intermediates that would otherwise have been obscured in ensemble measurements (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11). To date, state assignment of these intermediates and structural transitions has relied on changes in contour length and empirical domain boundary demarcation (7, 9, 10, 11). Only recently, studies have begun to identify structural intermediates through mutational analysis (6), although such experiments are time-consuming, difficult, and not applicable to all systems. Performing force spectroscopy experiments in the presence of osmolytes, however, represents an alternative approach, providing a chemo-mechanical perturbation that reports on the relative accessible surface area (ASA) of states in addition to contour length (2, 12, 13, 14, 15).

Protective osmolytes are ubiquitous small organic molecules that have evolved in nature to counteract the deleterious effects of harsh environmental conditions experienced by many organisms (16). In elasmobranchs, for example, up to 0.4 M urea can accumulate in the cytosol, introducing significant denaturing stresses to the proteins in the cytosolic milieu (16). Protective osmolytes function by stabilizing folded conformations of proteins, and despite the fact that osmolytes fall into different chemical classes (e.g., polyols and methylamines), and that different osmolytes interact to different extents with the protein backbone and side chains, the overall effect of stabilizing folded conformations relative to unfolded conformations appears similar (12, 15).

Despite the fact that the impact of osmolytes on protein stability can be accurately predicted from surface area changes (12, 13, 14, 15, 16), a mechanistic understanding of how osmolytes modulate the energy landscape of proteins (known as the osmophobic effect) remains elusive. In particular, it is clear from ensemble measurements that osmolytes affect both folding and unfolding kinetics (17, 18, 19, 20), yet mechanistic information on how they change the folding pathway is lacking. Although single-molecule studies with atomic force microscopy (AFM) have revealed that in high concentrations of osmolyte, the unfolding kinetics are slowed and compaction of unfolded species occurs faster when force is quenched (21, 22, 23, 24), those studies were performed in a force regime that did not permit direct observation of folding.

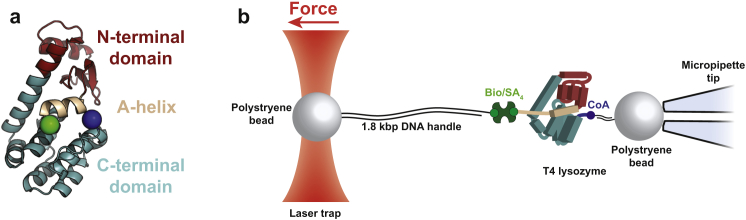
To address these limitations and to determine whether the known transfer free energy correlations (12, 13, 14) could be leveraged into single-molecule experiments, we performed single-molecule force spectroscopy on the cysteine-free variant of T4 lysozyme [T4^∗] (25) in different osmolytes using optical tweezers. T4^∗ consists of two coupled subdomains; a sequentially contiguous N-terminal domain and a sequentially discontiguous C-terminal domain (Fig. 1 a). T4^∗ has been extensively studied both at the ensemble (26, 27) and at the single-molecule level (5, 7), and is known to fold through an intermediate state. As such, it is an ideal system to perturb with osmolyte to characterize both the unfolded to intermediate, as well as the intermediate to native state transitions.

Figure 1.

T4 Lysozyme as a model system and single-molecule folding experimental setup. (a) Cartoon representation of T4 Lysozyme (PDB: 2LZM). Highlighted is the N-terminal A-helix (beige, residues 1–11), the N-terminal subdomain (red, residues 12–66), and the C-terminal subdomain (cyan, resides 67–164). Also shown are the attachment points for single-molecule force spectroscopy experiments (green and blue spheres). (b) In the experimental setup, a polystyrene bead is held in the trap that exerts force on the single molecule. The bead is covalently linked to 1.8 kbp of dsDNA, which is attached to biotin (green circle) at the other end. There is a noncovalent biotin/streptavidin interaction that then is linked to T4. CoA (blue circle) is covalently linked to T4 and another 50 bp of dsDNA that is attached to the polystyrene bead, which is held by suction. To see this figure in color, go online.

We conducted single-molecule experiments in the absence and the presence of two different osmolytes, sorbitol and TMAO (trimethylamine n-oxide), representing two different classes of osmolyte molecules (Fig. 1 b and Materials and Methods for details). Their impact on the mechanical unfolding and refolding rates was determined. Because our single-molecule force spectroscopy experiments provide the extension change as well as the different osmolyte sensitivities of the intermediate state population, we are able to reliably determine the structural properties of the intermediate state. In addition, we show that we are able to discriminate between multiple detailed structural models of the intermediate. The resultant approach may represent a general strategy for characterizing structures populated during protein folding, thereby adding to the library of information that can be gleaned from single-molecule experiments.

Materials and Methods

Pulling buffers and materials

All pulling experiments were conducted in buffer HKM (25 mM HEPES^∗KOH, 150 mM KCl, 5 mM MgCl₂, pH 7.4). TMAO (trimethylamine n-oxide dehydrate) was purchased from Sigma-Aldrich (St. Louis, MO) and dissolved with the components of pulling buffer. To remove impurities from TMAO synthesis, all buffers were stirred with activated carbon (12-20 mesh; Sigma-Aldrich) for 1 h while protected from light. Sorbitol was purchased from Sigma-Aldrich. The buffers were filtered (0.22 μm filter; Millipore, Billerica, MA), divided into aliquots, and stored at −80°C until use. All beads were purchased from Spherotech (Lake Forest, IL).

Protein purification

The plasmid harboring the single-molecule cysteine-free variant of T4 Lysozyme (T4^∗) was provided from Kaiser et al. (7). The construct contains an N-terminal Avi Tag for biotinylation (28), a flexible linker, the open reading frame of T4^∗, and then a YbbR tag on the C-terminus for addition of Coenzyme A (CoA) cross-linked to oligonucleotide (29). The insert was subcloned into a pET vector with a 9X-His-Tag and a TEV protease site adjacent to the Avi-tag used for biotinylation. The plasmid was transformed into Rosetta 2(DE3)pLysS (EMD Millipore) and plated on LB plates with 100 μg/mL ampicillin. The next day colonies were picked and grown to preparative volumes at 37°C 250 rpm until the OD_600nm reached 0.6–0.8. Expression was induced with 1 mM IPTG under the same conditions for 3 h. Cells were harvested by centrifugation and stored at −80°C. Pellets were resuspended in Lysis Buffer (50 mM NaH₂PO₄, 300 mM NaCl, 20 mM Imidazole, pH 8.0) and lysed by five passes through an EmulsiFlex C3 (Avestin, Ottawa, Ontario, Canada) at 15,000 psi. Lysates were clarified by centrifugation and immediately loaded onto HisPur Ni-NTA Superflow Agarose (Thermo Scientific, Waltham, MA) and eluted with a linear gradient with the same buffer containing 500 mM imidazole. Samples containing T4^∗ were pooled and dialyzed to TEV digestion buffer (50 mM Tris-HCl, 0.5 mM EDTA, 1 mM DTT, pH 8.0) along with TEV protease (1 μM final concentration). Cleaved T4^∗ was recovered by running through the same nickel affinity resin, dialyzed to 1× PBS, concentrated to 100 μM, and flash-frozen with liquid nitrogen. It should be noted that the single-molecule data collected indicate that T4^∗ is in its native state and unperturbed from the modification tags. This is indicated by the molecule folding cooperatively and reproducibly to a state that is not only consistent in dimensions to the native state, but also demonstrates reproducible kinetics of unfolding as previously demonstrated in Kaiser et al. (7).

Synthesis of oligonucleotide cross-linked to CoA

OligoCoA (oligonucleotide cross-linked to CoA) was synthesized as previously described in Kaiser et al. (7) and Maillard et al. (8) except OligoCoA was purified by reverse-phase high-performance liquid chromatography. After cross linking, samples were isopropanol-precipitated and resuspended in Milli-Q water (Millipore). The samples were then desalted by an illustra MicroSpin G-25 Column (GE Healthcare, Port Washington, NY) according to the manufacturer’s instructions. Samples were concentrated by vacuum centrifugation and then purified by semipreparative reverse-phase high-performance liquid chromatography on an 1100 Series instrument (Agilent Technologies, Santa Clara, CA). Modified oligonucleotide was separated using a 250 × 10 mm Jupiter C18 column (Phenomenex, Torrance, CA) packed with 5 μm particles. Mobile phase A was 100 mM TEAA (triethylammonium acetate) pH 7.0, and mobile phase B was the same except with the addition of 15% acetonitrile. The column was equilibrated to 60°C and samples were eluted by a linear gradient of 0–100% B over 30 min and then holding 100% B for another 30 min while detecting absorption at 260 nm. Pure fractions were confirmed by urea-polyacrylamide gel electrophoresis. Samples were finally isopropanol-precipitated and confirmed by matrix-assisted laser desorption/ionization time-of-flight mass spectrometry.

Labeling of protein for optical tweezer experiments

The labeling occurred in two major steps: a biotinylation reaction specific to the N-terminus followed by attachment of CoA (that was cross linked to double-stranded oligonucleotide) to the C-terminus. Before the optical tweezer experiments, modified protein molecules were ligated directly to polystyrene beads. During experiments, tethers were generated via a noncovalent biotin/streptavidin/biotin interaction in situ (i.e., in the microfluidics chamber) between the N-terminal biotin and the streptavidin/biotin complex on the surface of the DNA bead held in the trap (see below). Many of these methods are previously described in Kaiser et al. (7) and Maillard et al. (8), and modifications to these protocols are described for completeness.

The T4^∗ construct harbored an N-terminal Avi tag sequence (GLNDIFEAQKIEWHE) that is specifically modified by Escherichia coli biotin ligase (BirA) at lysine 10 in the sequence (28). BirA was purified as previously described in Kaiser et al. (7). Purified protein was mixed with 1× biotinylation buffer (20× = 500 μM D-biotin, 100 mM ATP, 100 mM Mg(OAc)), 2 μM BirA, and allowed to react for 2 h at room temperature. Samples were then dialyzed against 1× PBS to remove excess biotin. Biotinylated protein was purified by using Pierce Monomeric Avidin Resin (Thermo Scientific) according to manufacturer’s instructions. Samples containing biotinylated protein were dialyzed to 1× PBS.

The T4^∗ construct also harbored a C-terminal YbbR tag (DSLEFIASKLA), which is specifically modified at serine 2 by the phosphopantethein moiety of CoA in an enzymatic reaction catalyzed by the phosphopantethein transferase Sfp from Bacillus subtilis (30). Sfp was prepared as previously described in Yin et al. (29). OligoCoA was annealed to a complimentary strand that had a 4-bp overhang allowing for downstream annealing and ligation of protein to beads. Biotinylated T4^∗ (25 μM) was labeled by mixing freshly annealed dsOligo-CoA (50 μM), Sfp (10 μM), and 1× HM buffer (5× = 50 mM HEPES^∗KOH, 10 mm MgCl₂, pH 7.5) and incubating for 2 h at 37°C. Modification was confirmed by mobility shift in sodium dodecyl sulfate-polyacrylamide gel electrophoresis and unused dsOligo-CoA and Sfp were removed via Pierce Monomeric Avidin Resin (Thermo Scientific). Samples were then dialyzed to 1× PBS overnight, diluted to 5 μM, and flash-frozen with liquid nitrogen.

Synthesis of DNA handles

DNA handles were generated by cross linking a 5′-primer to polystyrene beads (31) and directly amplifying the handle on the bead in a PCR-like fashion. The DNA handle was ∼1.8 kbp with ∼50% GC content and was amplified from the λ-phage genome. Carboxylic acid coated polystyrene beads (2.8 μm diameter) were spun down and washed in 100 mM MES pH 6.0 multiple times to remove any residual material from manufacturing. The carboxyl groups on the beads were then activated with 40 μg/μL fresh EDC (1-Ethyl-3-[3-dimethylaminopropyl]carbodiimide hydrochloride) three times for a 15-min incubation period. Beads were then quickly washed in 50 mM HEPES pH 7.5 and excess 5′-primer was added (5′-NH₂-ACTGATGCAACTGACTCAGC-3′). The reaction was gently shaken at room temperature for 2 h before quenching via addition of 1 M Tris, pH 7.5 to a final concentration of 10 mM. The beads were then washed extensively with Milli-Q water (Millipore) to remove any unreacted product. The beads were finally spun down and resuspended in an equal volume of 5 mg/mL casein (Affymetrix, Santa Clara, CA) and 1% TWEEN-20 to prevent bead aggregation. The beads were treated as a 5′-primer in a PCR reaction with a 3′-primer harboring a biotin moiety on its 5′-end (5′-bio-GAAAGAATGGGCATGAGC-3′) as previously described in Kaiser et al. (7). After PCR, the beads were spun down and washed extensively using TE Buffer with 20% glycerol and then finally flash-frozen with liquid nitrogen and stored at −80°C. For optical tweezer measurements, beads were thawed and incubated with streptavidin before dilution and injection into the microfluidics chamber. This protocol yielded stable tethers for multiple rounds of pulling and relaxing up to the overstretching transition at 65 pN (32).

Synthesis of beads for protein ligation

Beads were synthesized as previously described in Kaiser et al. (7) except different primers were used. The two primers used were 5′-NH₂-CATGCGTCCTGATGTTAGCTCTCCG-3′ and 5′-CGCACGGAGAGCTAACATCAGGACGCATG-3′, which leaves a 4-bp overhang complementary to the OligoCoA/protein.

Optical tweezers measurements and analysis

The optical MiniTweezers system was built and calibrated according to directions available online (http://tweezerslab.unipr.it/). The instrument has a counterpropagating, dual-laser beam single-trap that measures force directly by the change in light momentum (33). Experiments were conducted in a microfluidics chamber with a micropipette tip that was purchased from Steve B. Smith Engineering (Los Lunas, NM). Beads ligated with protein were trapped, moved to a micropipette tip, and held by suction. Subsequently, a bead with DNA handles and streptavidin was trapped and brought within close physical proximity of the protein bead in the micropipette tip. Tethers were confirmed by exerting force and observing behavior described previously in Kaiser et al. (7). Single-molecules were confirmed by overstretching of DNA handles (34). Force and trap position were recorded at a sampling frequency of 400 Hz for all constant velocity (force ramp) and constant force (force clamp) experiments. The total number of single-molecule tethers generated under each condition was: N_Buffer = 32 molecules, N_Sorbitol = 20, and N_TMAO = 24 molecules. Constant force rates were determined from a significant number of transitions (total transitions: N_Buffer = 1173, N_Sorbitol = 605, and N_TMAO = 1237).

Steered molecular dynamics simulations

All simulations were performed with VMD and NAMD molecular dynamics software package (35) with the CHARMM36 force field (36). Initial structure of T4^∗ was obtained from the Protein Data Bank (PDB: 1L63). Due to the large extension of the fully elongated conformation (∼600 Å), explicit solvent was intractable given limited computational resources. All simulations were performed using an implicit solvent model: generalized Born with a cutoff radius of 12 Å and an ion concentration of 0.15 M similar to the optical tweezer experiments. Temperature was controlled using Langevin dynamics (damping coefficient 2/ps) at 300 K. Van der Waals interactions were treated as a Lennard-Jones 6-12 potential calculated using the switch method starting at 13 Å and smoothly cut off at 14 Å. The SHAKE method was used on all hydrogen atoms allowing integration steps of 2 fs expediting simulation time.

After hydrogens were built in, the structure was minimized by conjugate gradient for 1000 steps. The system was then equilibrated for 4 ns. Three random points were selected within a 2 ns window of the end of equilibration and used as different starting points in the subsequent simulations. Steered molecular dynamics (SMD) simulations were performed by fixing the C-terminal Cα and pulling on the N-terminal Cα with a spring constant of 1000 pN/Å and a velocity of 4 m/s. The system was pulled until the approximate contour length of T4^∗ was achieved (∼58.1 nm). Three trials of each of these simulations were performed. Trajectories were analyzed by using the VMD software and subsequent analysis scripts described below for surface area and energy calculations.

Structure-based calculations for the intermediate state

The ΔΔG values for intermediates were calculated based on the group transfer free-energy model, which uses experimentally measured free energies of transfer for every amino-acid side chain and the peptide backbone (12, 13). Potential unfolded states used in determining statistics of average ASA were generated by mechanically unfolding T4^∗ in silico (described above). Intermediate states were treated as having the crystal structure conformation for the folded portion and the unfolded conformation for the remainder. The ASA to a 1.4 Å rolling sphere was calculated for all states using a subroutine from the COREX algorithm (37). The change in ASA from unfolded to intermediate was calculated for every possible species (i.e., every possible combination of the N-terminus and C-terminus unfolded). Using these values, it was possible to calculate ΔΔG as follows:

$$\Delta \Delta G=\Delta Gtr,I-\Delta Gtr,U=-\left({\sum }_{\mathit{i}=\text{AA}\text{type}}\left[n_i\Delta g_{tr,i,sc}^o\Delta {\alpha }_i^{\text{SC}}\right]+\Delta g_{tr,\text{BB}}^o{\sum }_{i=\text{ΑΑ}\text{type}}\left[n_i\Delta {\alpha }_i^{\text{BB}}\right]\right),$$

where n_i is the total number of groups of amino acid (AA) type I, $\Delta g_{tr}^o$ is the free energy of transfer for the side chain (SC) or backbone (BB) from 0 to 1 M sorbitol or TMAO, and Δα_i is the fractional change in solvent ASA from the unfolded to the intermediate state (12, 13). The Δα_i values used in the calculation above were the mean values of those consistent with the unfolded state: i.e., all states that fell in the range μ_U ± σ_U = 25.3 ± 2.0 nm. Detailed derivation and treatment of intermediate states are described in Text S2 in the Supporting Material.

Results and Discussion

Osmolytes marginally decelerate unfolding rates

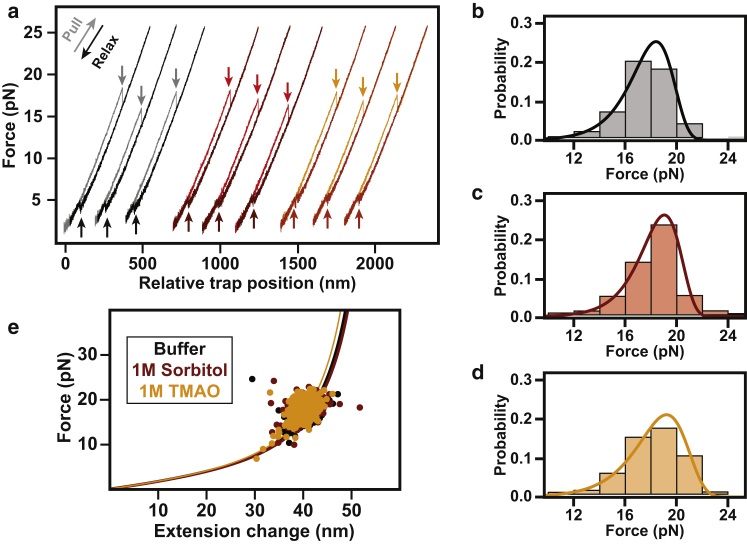
To fully characterize the effect of osmolyte on the energy landscape, we first performed mechanical unfolding experiments. Single molecules of T4^∗, subjected to continuously increasing force by moving the trap at a constant velocity (i.e., force-ramp experiments), exhibited cooperative unfolding (Fig. 2 a). The mean unfolding forces (〈F_unf〉) obtained in the presence and absence of osmolytes overlap significantly: F_unf,buffer = 17.6 ± 1.9 pN (N = 224), F_{unf,1M Sorbitol} = 18.2 ± 2.1 pN (N = 288), and F_{unf,1M TMAO} = 18.2 ± 2.2pN (N = 340), where the error values are the standard deviation (SD) of the force distributions. To quantitatively evaluate the unfolding from such experiments, several force-ramp data sets were collected and analyzed using a model that converts the force rupture distribution to an intrinsic lifetime and distance to transition state (38) (Fig. 2, b–d). The model reveals that the distance to the transition state (Δx^‡ = ∼2.7 nm) does not change appreciably in the presence of either osmolyte and that unfolding rates are marginally decelerated (Text S1 in Supporting Materials and Methods). Given that osmolytes stabilize the native states of proteins, our results are not unexpected, as osmolytes have been shown to decrease unfolding rates both in ensemble experiments (17, 18, 19) and at the single-molecule level (21, 22, 23, 24). It should be noted that osmolytes primarily act on the denatured state and we would expect a more pronounced effect on the folding pathway from the denatured state (discussed below). Additionally, osmolytes do not appear to impact the wormlike chain model that is used to describe the unfolded state of proteins in force spectroscopy experiments (1, 3, 7) (Fig. 2 e). As a result, we can rule out that osmolytes affect the persistence or contour length in our experiments, at least in the force range covered by the T4^∗ unfolding transitions (∼10–20 pN).

Figure 2.

The mechanical unfolding pathway is unaffected by osmolyte (a). Shown are representative force-extension curves for single molecules of T4 lysozyme generated under constant velocity (100 nm/s). Force-extension curves in buffer (black), sorbitol (red), and TMAO (orange) behave similarly. Unfolding transitions (lighter arrows pointing down) were observed in the 12–24 pN regime for all conditions. Refolding occurred in the 3–6 pN regime (darker arrows pointing up). (b–d) Force rupture probability distributions in the presence of buffer (black), sorbitol (red), and TMAO (orange), respectively. Overlaid on the distributions are the fits using a theoretical model that yields distances to the transition state and lifetimes of the folded state (38). The distributions are well determined and the errors of the fits are smaller than the thickness of the lines. (e) Shown are the unfolding transition extension changes (in nanometers) versus the forces of unfolding (in picoNewtons) for every transition observed. Data are color-coded similar to (a) and are fit to the wormlike-chain model (55). All contour length changes (ΔL_C) that are consistent with unfolding of the whole molecule are within error of each other. To see this figure in color, go online.

To more accurately probe the unfolding landscape, we directly measured unfolding rates in constant-force experiments at different forces. An example trace is shown in Fig. 3 a. The molecule initially (t = 0) populates the native state and is held at 15 pN until a cooperative unfolding transition occurs. Using data from multiple independent transitions, performed at different forces, we determined the distributions of lifetimes (τ_app) at each force, from which we calculated the force-dependent unfolding rate constants (k_app,unf) (Fig. 3 b). Over the experimentally accessible force range, we consistently observed a small yet significant deceleration of T4^∗ unfolding rates in the presence of TMAO and sorbitol consistent with the force-ramp experiments (Fig. 3 b).

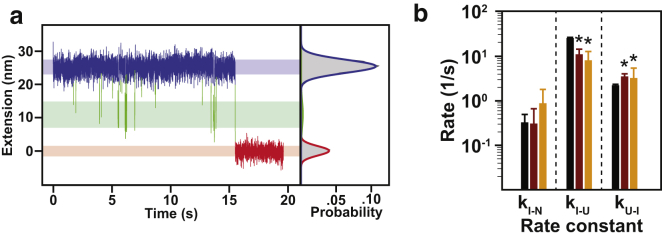
Figure 3.

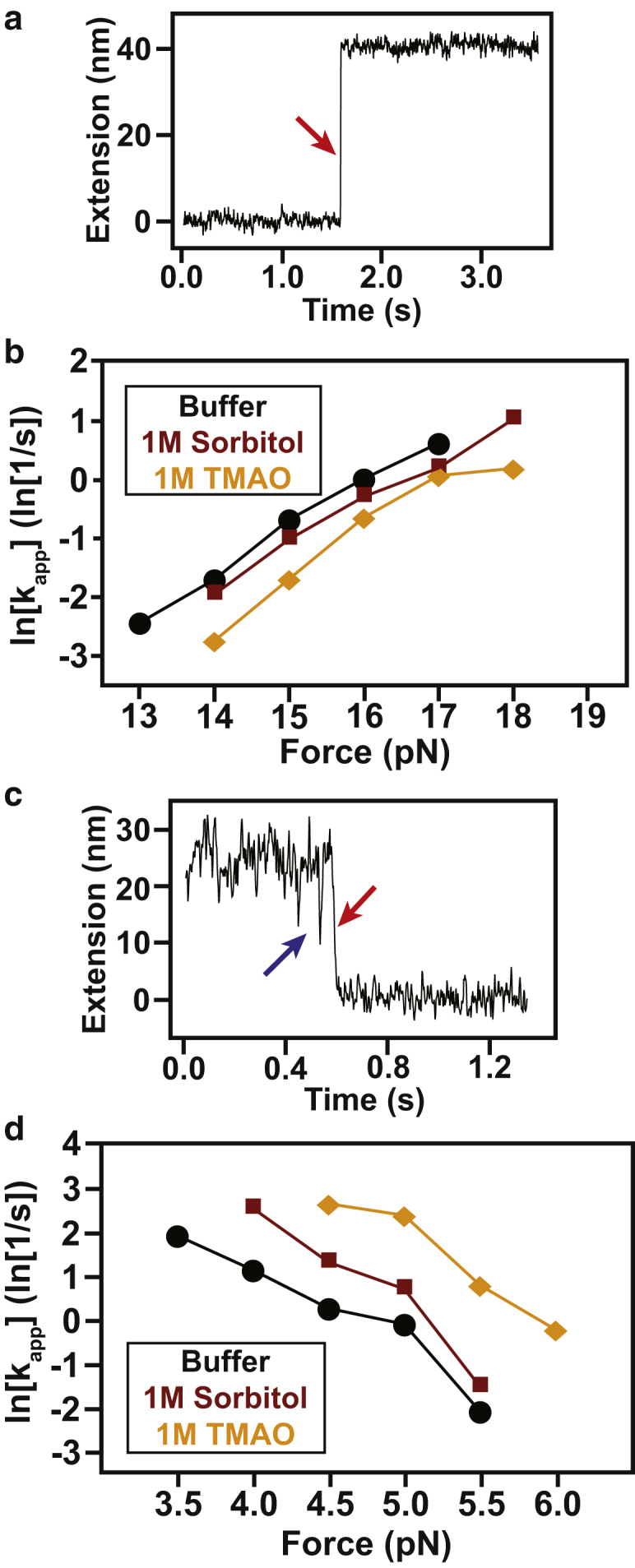
Osmolytes affect protein folding kinetics (a) Representative force-clamp unfolding transition. Shown is the extension as a function of time with the unfolding transition denoted by the red arrow. Unfolding results in an increase in the relative position of the trap. (b) Apparent unfolding kinetics as a function of force. Shown are the apparent kinetic rates under all three conditions tested. Error bars are smaller than the plot points and are thus not visible. (c) Representative force-clamp folding transition. Shown is the extension as a function of time with the folding transition denoted by the red arrow. There is a statistically significant on-pathway intermediate observed that is denoted by the blue arrow. (d) Apparent folding kinetics as a function of force. Shown are the apparent kinetic rates in all three conditions tested. Due to the significant change in the rates, it was not possible to obtain complete overlap of the force regime. Error bars are smaller than the points on the plot, and are thus not visible. To see this figure in color, go online.

Using Bell’s model (39), we determined the force dependence of the rate constant and the distance to the transition state. The fits with and without osmolyte are not statistically different, yielding zero force unfolding rates (i.e., intercept) within error of each other and Δx^‡ values (i.e., slope) that are comparable to the values obtained from force rupture distributions (Text S1 in Supporting Materials and Methods). This is in apparent contradiction to the force-ramp unfolding rates obtained using a different model. Both models require extrapolation from the unfolding force regime (∼15–20 pN) to zero force. As such, both models are subject to error propagation. However, Bell’s model does not explicitly take into account experimental parameters such as trap stiffness and elasticity of DNA handles. As a result, we believe that it is subject to more error and is unable to differentiate the small difference in zero force unfolding rates. This notion is supported by the fact that each unfolding rate is significantly decreased in the presence of osmolyte (Fig. 3 b), but to a small degree as discussed below.

The apparent unfolding rate at each force in the presence of sorbitol and TMAO decreases 1.39 ± 0.10 and 2.31 ± 0.56 fold, respectively (Table S1), relative to buffer only. Because the apparent rate is related to the activation energy of the process, it is possible to determine the change in activation energy across the overlapped force regimes:

$$k_{\text{app,unf}}\propto \text{exp}\left(\frac{-\Delta G^{‡}}{k_{\text{B}}\times T}\right).$$

The average difference in activation energy between these conditions is on the order of thermal noise, which may explain the inability of Bell’s model to differentiate zero force-unfolding rates: ΔΔG^‡_Sorb = −0.33 ± 0.07 k_BT and ΔΔG^‡_TMAO = −0.82 ± 0.25 k_BT. These changes in activation free energies and folding rates are smaller than what has been reported for other force spectroscopy studies using AFM (22, 23, 24). Importantly, our results indicate that at lower concentration of osmolyte and at a lower force regime, osmolytes do not affect unfolding kinetics as much as previously reported. In short, it is evident that osmolytes marginally decelerate unfolding rates and that all the data are consistent with the mechanical unfolding pathway remaining unperturbed.

Osmolytes accelerate early events in folding

Previous force-spectroscopy experiments in the presence of osmolytes have been unable to directly observe folding because of the high force-regime required for AFM. We empirically noted that the refolding forces observed in the force-ramp experiments (darker arrows in Fig. 2 a) are slightly higher in the presence of osmolyte, suggesting faster folding rates. Unfortunately, reliable estimates of the refolding force could not be obtained in force-ramp experiments due to the noise in the measurement and hopping behavior at this low force regime. Thus, we carried out force-clamp experiments to directly observe folding and to accurately determine the folding rates of T4^∗ (Fig. 3 c). In these measurements, the molecule is populating the unfolded state at time zero and refolds after some time (denoted by the red arrow) while being held at a low, constant force. Similarly, we determined the force dependence of the apparent refolding rate constant k_app,fold (Fig. 3 d; Table S2).

Two major conclusions can be drawn. First, the apparent folding rate at a given force is accelerated in the presence of osmolyte. The average folding rate is increased in the presence of sorbitol and TMAO by 2.75 ± 1.02 and 13.7 ± 3.8, respectively. These values correspond to ΔΔG^‡_Sorb = 0.96 ± 0.36 k_BT and ΔΔG^‡_TMAO = 2.59 ± 0.26 k_BT, demonstrating a more pronounced effect than on the unfolding rate deceleration. Second, the folding pathway is not well described by a two-state transition, apparent from the nonlinear dependence of k_app,fold on force. This observation suggests the presence of a folding intermediate. Indeed, despite the increased noise at the lower forces required for folding, the presence of an intermediate state between the unfolded and the native states is clearly apparent (blue arrow, Fig. 3 c). The weaker force dependence at low forces (owing to the change in the average transition state) indicates that the transition into the intermediate state is more dominant at low forces. Conversely, a higher force dependence is observed when the transition into the native state is more dominant at high forces (4).

From the data it can be inferred that the intermediate observed in the single-molecule folding traces appears to be on-pathway and essentially irreversible once folded to the native state (7). It should be noted that all the constant-force data are consistent with one intermediate state as previously reported in Kaiser et al. (7). Furthermore, upon addition of osmolyte, the kinetics data are still consistent with one intermediate in addition to the binned distribution of distances revealing a single species. It is highly unlikely that multiple intermediates have the same kinetics, extension, and osmolyte sensitivity. This allows the reaction to be schematically represented as:

$$U\begin{array}{c}{k}_{U-I}\\ \to \\ \leftarrow \\ k_{I-U}\end{array}I\begin{array}{c}{k}_{I-N}\\ \to \end{array}N,$$

where the unfolded (U) can exchange with the intermediate (I) until it irreversibly folds to the native state (N). To deconvolve the kinetic rate constants, k_U-I, k_I-U, and k_I-N (where k_A-B represents the rate of going from A to B), we implemented a Bayesian extension of a hidden Markov model (HMM) (40). Advantages of the Bayesian HMM are that it explicitly accounts for experimental noise in addition to distance fluctuations within each state, provides for state assignments as well as a deconvolution of the individual rate constants, and provides more precise values than HMMs by sampling the posterior (Fig. 4 a).

Figure 4.

Osmolytes specifically affect the first step in folding. (a) Representative refolding trace (force-clamp at 5 pN) fit to the Bayesian HMM. The graph shows the extension data with states assigned according to the Bayesian HMM: the unfolded state is shown in blue, the intermediate in green, and the native in red. The width of the shaded bars under the data represents the mean ± 1 SD, which in this case is: μ_U ± σ_U = 25.3 ± 2.0 nm, μ_I ± σ_I = 10.9 ± 3.8 nm, and μ_N ± σ_N = 0.0 ± 1.4 nm. On the right is the probability distribution of the states in this refolding transition. (b) Fits of each rate in the folding transition as determined by the BHMM for buffer (black), sorbitol (red), and TMAO (orange). The rates showing significant change are the k_I-U and k_U-I rates denoted by ^∗p < 0.05. To see this figure in color, go online.

At higher forces, k_I-U increases, resulting in lifetimes of the intermediate that are on average too short for our experimental approach to detect. Lower forces, as well as the addition of osmolyte, increase k_I-N, similarly reducing the lifetime of the intermediate to the point that it cannot be reliably detected. Nonetheless, we were able to obtain reliable values for all three rate constants at 5.0 pN (Fig. 4 b). Due to the nature of the osmophobic effect (i.e., stabilizing folded compact states over more extended states), it may be expected that the rate of formation of either the I state from the U state or the formation of the N state from the I state would be increased significantly as both the U to I and the I to N transitions presumably decrease exposure of the backbone to the solvent. Interestingly, such a conclusion is not borne out of this analysis. The increased apparent folding rate is instead due to a significant increase in k_U-I (i.e., k_U-I,Buffer = 2.17 s⁻¹ [1.88 s⁻¹, 2.29 s⁻¹] to k_{U-I,1M Sorbitol} = 3.45 s⁻¹ [3.00 s⁻¹, 3.93 s⁻¹] and k_{U-I,1M TMAO} = 3.17 s⁻¹ [2.57 s⁻¹, 5.30 s⁻¹]) and a decrease in k_I-U (i.e., k_I-U,Buffer = 24.98 s⁻¹ [22.03 s⁻¹, 26.00 s⁻¹] to k_{I-U,1M Sorbitol} = 10.80 s⁻¹ [9.51 s⁻¹, 14.08 s⁻¹] and k_{I-U,1M TMAO} = 7.91 s⁻¹ [6.25 s⁻¹, 12.50 s⁻¹]) (Fig. 4 b).

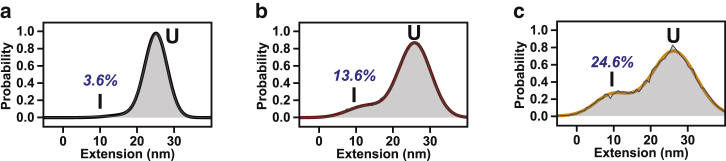
Interestingly, the rate constant confidence intervals for the final irreversible step have significant overlap, revealing very little, if any, change in the intermediate to native state transition: k_{I-N, Buffer} = 0.32 s⁻¹ [0.21 s⁻¹, 0.48 s⁻¹], k_{I-N,1M Sorbitol} = 0.30 s⁻¹ [0.08 s⁻¹, 0.65 s⁻¹], and k_{I-N,1M TMAO} = 0.86 s⁻¹ [0.32 s⁻¹, 1.76 s⁻¹]. Note that the values in brackets represent 95% confidence intervals as previously described in Kaiser et al. (7) and Chodera et al. (40). Although the increase in k_U-I and decrease in k_I-U does not explain the total change in the apparent kinetics (Fig. 3 d), these two rates are clearly dominating the changes that are observed in the force-clamp experiments. The modulation of a specific rate constant in the single-molecule folding pathway of T4^∗ has been reported previously. Specifically, the rate of N formation from I (k_I-N) is decreased when a nascent T4^∗ version folds on the ribosome (7). In direct contrast to the mechanism by which the ribosome affects T4^∗ folding, osmolytes are promoting intermediate formation, an effect that increases the apparent folding rate significantly. Indeed, the population of the intermediate relative to the unfolded state increases significantly from 3.6 to 13.6% and 24.6% from buffer to sorbitol and TMAO, respectively (Fig. 5). Importantly, both classes of osmolytes affect folding by the same mechanism, albeit to different degrees (on a per molar basis).

Figure 5.

Osmolytes stabilize formation of the intermediate (a–c) are binned extension distributions for all transitions used for fitting from buffer (black), sorbitol (red), and TMAO (orange), respectively, for unfolded (U) and intermediate (I) states. The mean values of extension have not changed appreciably; however, the relative populations of both have changed significantly from 3.6% to 13.6% and 24.6% from buffer to sorbitol and TMAO, respectively. To see this figure in color, go online.

Structural resolution of the intermediate state using single-molecule COREX: sCOREX

Because single-molecule force spectroscopy experiments conducted in the presence of osmolytes represent a chemo-mechanical perturbation of the protein, they provide a unique opportunity for characterizing the structural properties of the intermediate state. As noted above, analysis of the constant-force extension traces provides direct access to the contour length change between the I and U states of T4^∗, corresponding to 96–108 amino acids folded in the intermediate as previously reported in Kaiser et al. (7). Additionally, we do not observe compaction of the intermediate or a deviation from the wormlike chain model as a function of force for the intermediate, supporting the assertion that the intermediate is the same state in the presence of osmolyte. However, we note that the probability of the intermediate changes significantly upon addition of osmolyte, increasing by almost four- and sevenfold in the presence of sorbitol and TMAO, respectively (Fig. 5).

As described previously in Auton and Bolen (12, 13) and Auton et al. (14), the equilibrium effect of osmolytes on an intermediate state is based on the amount of ASA relative to the unfolded state. Importantly, because different osmolytes interact with backbone and side-chain surface area to different extents, the relative effect of two or more osmolytes will be unique to each intermediate. If this is the case, it should be possible to use the osmolyte dependence of the intermediate (in one or more osmolytes), in conjunction with the change in contour length from single-molecule experiments, to resolve the structural identity of the intermediate state.

To explore this possibility, we generated potential intermediate state models using a strategy similar to that employed in the COREX algorithm (37), wherein folded regions are treated as adopting the conformation in the native PDB structure and unfolded regions are treated as being extended. Specifically, states were generated by systematically unfolding residues from the N- and C-termini, one residue at a time in all combinations, leaving one contiguously folded region flanked by different amounts of unfolded residues on the N- and C-termini, as described in the Materials and Methods. Because the force-clamp data (Fig. 4) provides the equilibrium between the U and the I states, the energy difference between these states can be determined from the probabilities of each state with and without osmolytes (Fig. 5), thereby providing direct access to the degree to which the I state is stabilized (relative to U) in 1 M TMAO (ΔΔG = −RT ln (24.6/3.6) = −1.14 kcal/mol) and in 1 M sorbitol (ΔΔG = −RT ln (13.6/3.6) = −0.79 kcal/mol).

For comparison, the free energy of all of the potential intermediates can be determined from transfer free-energy values and the difference in solvent ASA between the U and the I state, as described by Auton and Bolen (12, 13). According to this relationship, the Gibbs Energy of transfer for any state can be expressed as:

$$\Delta \Delta {\text{G}}_{tr,I-U}=\Delta \text{Gtr},\text{I}-\Delta \text{Gtr},\text{U}=-\left({\sum }_{i=\mathit{{\rm A}{\rm A}}\mathit{type}}\left[n_i\Delta g_{tr,i,SC}^o\Delta {\alpha }_i^{SC}\right]+\Delta g_{tr,BB}^o{\sum }_{i=AAtype}\left[n_i\Delta {\alpha }_i^{BB}\right]\right),$$ (1)

where ΔΔG is the transfer energy of the intermediate relative to the unfolded state, n_i is the total number of groups of amino acid (AA) type i; $\Delta g_{tr}^o$ is the free energy of transfer for the side-chain (SC), or backbone (BB) to 1 M TMAO or sorbitol; and Δα_i is the fractional change in solvent ASA from the unfolded to the intermediate state, which is computed from the expression:

$$\Delta {\alpha }_i^{bb\text{or}sc}=\frac{{\sum }_{j=1}^{n_i}\left(AS{A}_{i,j,U}-AS{A}_{i,j,I}\right)}{n_{i}AS{A}_{i,Gly\cdot X\cdot Gly}},$$ (2)

where the numerator is summed over all amino acids j of type i, ASA_i,j,U is the ASA of the unfolded state, ASA_i,j,I is the ASA of the intermediate state, n_i is as defined in Eq. 1, and ASA_i,Gly.X.Gly is the standard side-chain or backbone solvent accessibility of Gly-X-Gly tripeptides presenting the maximally exposed surface area (X is the amino acid of type i) (41). See Text S2 in Supporting Materials and Methods for a full derivation.

The ASA of mechanically unfolded T4^∗ is presumably different from the chemically denatured state, complicating structural modeling. Although the fully extended conformation can be readily calculated from physical chemistry principles, T4^∗ is not fully elongated in the refolding experiments. At 5 pN, for example, the unfolded state is ∼25 nm more extended than the native state (Fig. 5 a) as opposed to the fully elongated state of ∼60 nm. A simple linear interpolation between the native state and fully elongated state may provide a first-order estimate of the ∼25 nm extended state ASA, but this simplification assumes linearity. To address this concern, we performed SMD to determine ASA and therefore the Δα_i^{bb or sc} dependence on extension between the native and fully elongated state. Briefly, the system was equilibrated and was subsequently pulled at a constant velocity until fully elongated, similar to Cheng et al. (42), Zheng (43), and Zhang and Lou (44). By performing multiple SMD simulations we were able to determine how Δα_i^{bb or sc} relates to extension, and to develop statistics on the ASA of the unfolded state (Figs. S1 and S2). From these values, we determined the free energy of transfer for the unfolded state (ΔG_tr,U in Eq. 1) and that of the intermediate (ΔG_tr,I in Eq. 1) as described above. Remarkably, the first-order estimates of ASA from linear interpolation are close to the values calculated from SMD, validating this assumption for future studies.

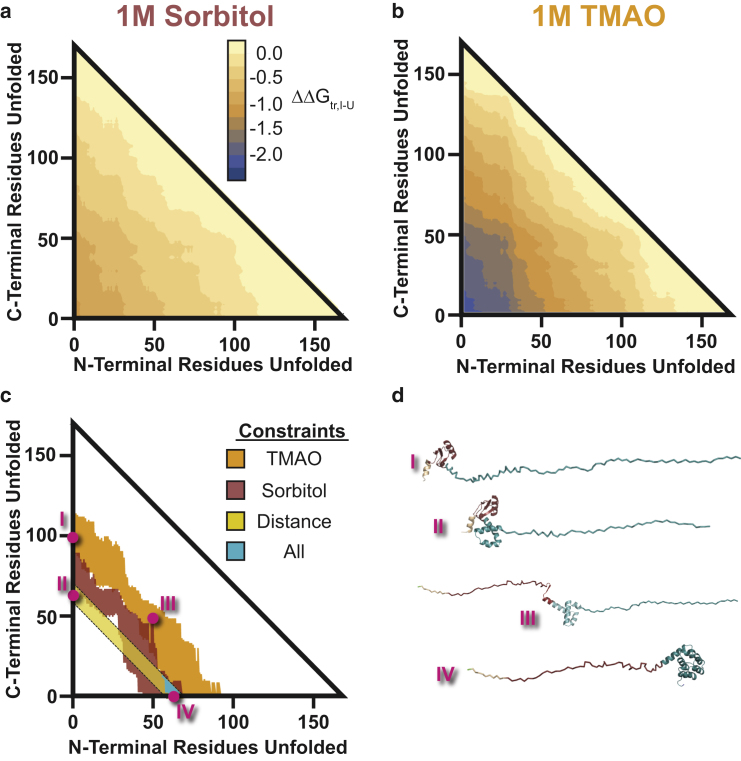
Using this method, we exhaustively enumerated all possible contiguously folded intermediate states for T4^∗ and determined the free energy of transfer to 1 M sorbitol and TMAO. A plot representing all possible partially folded species with varying unfolded termini are shown in Fig. 6, a and b, for sorbitol and TMAO, respectively. Several important features emerge. First, there are clear differences in ΔΔG_tr,I-U for unfolding the N-terminus versus the C-terminus in 1 M TMAO and sorbitol relative to the unfolded state (as evidenced by the asymmetry in Fig. 6, a and b). This asymmetry originates from differences in amino-acid composition between the N- and C-terminal segments of a given length. Second, the magnitude of the free energy difference in 1 M sorbitol is less than in 1 M TMAO, which is expected result given that TMAO is a more potent osmolyte (12, 13).

Figure 6.

Experimental discrimination of structural models of the T4^∗ folding intermediate. (a) Plot of the transfer free-energy difference between the I and U state (ΔΔG_tr,I-U) for every possible contiguously folded intermediate of T4^∗ to 1 M sorbitol. The axes represent the portion of the N-terminal or C-terminal residues unfolded in the intermediate. The values are shaded according to value as denoted by the key. (b) Shown is the same plot as (a), except for 1 M TMAO. Of note is that the values have higher magnitude, as expected from transfer free-energy models. (c) Shown are the experimental constraints on potential intermediates that are considered. Shaded in orange and red are intermediates that are consistent with the population changes in going from buffer to 1 M TMAO and 1 M sorbitol, respectively. The yellow diagonal bar is the dimensional contour-length-based constraint from the BHMM. Shaded in cyan are the intermediates consistent with all three constraints. These are all intermediates where the N-terminal domain is mostly unfolded and the C-terminal domain is primarily folded. (d) Potential structural models of intermediates. Color-coding is identical to Fig. 1a. (I) Depicted is the N-terminal subdomain that is consistent with the population constraint of TMAO (folded amino acids 60–72). (II) Depicted is the N-terminal subdomain portion along with C-terminal subdomain portion folded to be consistent with distance restraint (folded amino acids 96–108). (III) Depicted is an intermediate that has 50 amino acids of the N- and C-terminus unfolded. This intermediate is consistent with both population restraints. (IV) Depicted is the C-terminal subdomain structural model that is consistent with both constraints (C-terminus). This is the only intermediate that is consistent with all three pieces of experimental data. To see this figure in color, go online.

Importantly, when the range of free energies is used to determine intermediates that are consistent with the population changes upon going from buffer to 1 M sorbitol (Fig. 6 a) or 1 M TMAO (Fig. 6 b), only narrow portions of the potential unfolding combinations for the N- and C-termini agree with experiment (red- and orange-shaded regions, Fig. 6 c). Shown also in Fig. 6 d are four potential intermediate states that are tested using this methodology (I–IV), which represent unfolding; (I) 100 and (II) 65 residues from the C-terminus; (III) 50 residues each from the N- and C-termini; and (IV) 65 residues from the N-terminus.

Inspection of the red and orange regions in Fig. 6 c reveals that of all possible states, only a small subset is consistent with both the sorbitol and the TMAO free energy data (see dark red in Fig. 6 c). Importantly, this minimal overlap is due to the relative differences in how the different osmolytes affect backbone versus side-chain surface area (12, 13). In effect, performing the single-molecule experiments in more than one osmolyte significantly constrains the possible states that can produce the observed behavior. When the additional constraint associated with the experimental contour length change (i.e., extension of 96–108 amino acids) is also applied (Fig. 6 c, yellow diagonal bar), only one region is found where there is an overlap between all three of the experimental constraints (cyan-shaded region, Fig. 6 c).

The results indicate that the structural character of the intermediate state is most consistent with the C-terminal domain of T4^∗ being folded and the N-terminal domain being unfolded (Fig. 6 d, IV). Remarkably, the predicted intermediate is consistent with two previous experimental observations. First, the division of the structure falls precisely at the known structural domain boundary of T4^∗ previously identified by x-ray crystallography (45). Second, the N-terminus being unfolded is consistent with the known relative stability of this domain obtained from both ensemble experimental (46) and theoretical (47) studies. In short, these results suggest that the constraints imposed by performing optical tweezers experiments in multiple osmolytes provides sufficient information, when combined with the experimental contour length change, to distinguish the structural character of nativelike folding intermediates.

We note that recent studies have questioned whether general transfer free energy models based on surface area can mechanistically capture the relative energetic contribution of osmolytes to the transfer free energy of side chains versus backbone (48, 49). We make no claims about the underlying mechanism, and in fact, whether or not the molecular origins of the osmolyte effect are understood, the parameterization of the transfer free energies in terms of surface area is no less predictive, as clearly demonstrated by Auton and Bolen (12, 13). As such, this analysis provides quantitative insight into the structural character of the intermediate.

Finally, it is interesting to speculate on the potential implications of such an approach to systems in which structure is not known or in the case of intrinsically disordered proteins (IDPs). It is clear that marginally stable proteins and certain IDPs fold cooperatively upon the addition of ligands and osmolytes to their functional state(s) (50, 51, 52). Performing the experiments described here, under different osmolyte concentrations and forces, can yield multidimensional information about the states that are accessed during folding/unfolding. Because the transfer free energies have been shown here to be valid in single-molecule force spectroscopy experiments, it should be possible to study IDPs under osmolyte and force conditions where the folding is more probable, and to extrapolate the probabilities to functional conditions (i.e., 0 pN force and 0 M osmolytes), thereby providing a lens into the functional conformational transitions of IDPs. The applicability of this strategy to the analysis of IDPs awaits further study.

Conclusions

To our knowledge, we believe this study represents the first use of the osmophobic effect at the single-molecule level to discriminate between structural models of the intermediate state populated during folding. We observe an increase in folding rate consistent with what has previously been reported for the effect of osmolyte. However, our ability to directly observe folding together with a robust method to determine individual rate constants from the single-molecule traces (Fig. 4 b) reveals surprising details of how osmolytes modulate T4^∗ folding. Strikingly, formation of a folding intermediate is specifically modulated in the first step of the folding pathway: i.e., the population of the intermediate changes because k_U-I and k_I-U change, while k_I-N is relatively unperturbed. This finding is unexpected because approximately one-third of the molecule remains unfolded in the intermediate state, leaving a significant portion of the peptide backbone exposed to solvent. How is it possible, then, that k_I-N is not affected by osmolytes? Because the rate depends on how osmolyte is affecting the energy of the intermediate state relative to the transition state, the lack of a difference in k_I-N, with and without osmolyte suggests that the surface area exposed in the transition state, relative to the intermediate state, is approximately the same.

Regardless of the origin of the effect, the functional implications are clear. Low concentrations of osmolytes decrease the rate of the transition from I to U, in effect minimizing the probability of an excursion to higher energy states. This suggests an osmolyte-driven dampening of dynamics of the protein, an assertion that is consistent with results obtained from hydrogen exchange studies (53). We note that our results report the effect of osmolyte on one protein (T4^∗). The fact that we obtain similar results using two different osmolytes applied to one protein of course does not mean that the results will be the same for all proteins. Nonetheless, the results presented here reveal that single-molecule force spectroscopy provides a powerful tool to understand the impact of osmolytes on protein stability.

We note that at least in the case of T4^∗, osmolytes primarily affect the rate of the U to I transition, while the ribosome was recently shown to affect the I to N transition (7), indicating that osmolytes and ribosomes exert their impact on different parts of the T4^∗ folding reaction. Whether this effect is a general phenomenon remains to be seen. However, it is interesting to speculate on the benefits of biological systems being able to evolve orthogonal mechanisms that presumably can be effective both together and separately. Did osmolytes evolve so as to minimize the potential of adversely affecting cotranslational folding in organisms where osmolytes are colocalized with functioning ribosomes?

Perhaps most importantly, our results demonstrate that using osmolytes as a chemo-mechanical perturbation is a powerful approach for gleaning structural information about intermediates in the form of a second metric (i.e., solvent-accessible surface area). Although applied here to data obtained from optical tweezers, the strategy, in principle, is not limited to force spectroscopy. Other techniques, such as single-molecule fluorescence spectroscopy, providing access to changes in populations of states in different osmolyte concentrations, can also provide information about surface area. Whether this is indeed the case awaits further studies, although the relationship between Förster resonance energy transfer efficiency and absolute distance changes may be less certain than with optical tweezers.

Author Contributions

H.N.M., D.T., C.M.K., and V.J.H. designed the research; H.N.M. performed the research; and H.N.M., D.T., C.M.K., and V.J.H analyzed the data and wrote the article.

Editor: James Cole.

Supporting Citations

Reference (54) appears in the Supporting Material.