Abstract
Actin and myosin assemble into a thin layer of a highly dynamic network underneath the membrane of eukaryotic cells. This network generates the forces that drive cell- and tissue-scale morphogenetic processes. The effective material properties of this active network determine large-scale deformations and other morphogenetic events. For example, the characteristic time of stress relaxation (the Maxwell time ) in the actomyosin sets the timescale of large-scale deformation of the cortex. Similarly, the characteristic length of stress propagation (the hydrodynamic length λ) sets the length scale of slow deformations, and a large hydrodynamic length is a prerequisite for long-ranged cortical flows. Here we introduce a method to determine physical parameters of the actomyosin cortical layer in vivo directly from laser ablation experiments. For this we investigate the cortical response to laser ablation in the one-cell-stage Caenorhabditis elegans embryo and in the gastrulating zebrafish embryo. These responses can be interpreted using a coarse-grained physical description of the cortex in terms of a two-dimensional thin film of an active viscoelastic gel. To determine the Maxwell time , the hydrodynamic length λ, the ratio of active stress , and per-area friction γ, we evaluated the response to laser ablation in two different ways: by quantifying flow and density fields as a function of space and time, and by determining the time evolution of the shape of the ablated region. Importantly, both methods provide best-fit physical parameters that are in close agreement with each other and that are similar to previous estimates in the two systems. Our method provides an accurate and robust means for measuring physical parameters of the actomyosin cortical layer. It can be useful for investigations of actomyosin mechanics at the cellular-scale, but also for providing insights into the active mechanics processes that govern tissue-scale morphogenesis.
Introduction
Cells need to adopt their shape to drive tissue-scale morphogenetic processes (1, 2, 3, 4). A classical example is convergent extension, where cells reshape and intercalate to allow an epithelium to shrink in one direction, while expanding in the other (5). The actomyosin cortex also endows cells with the ability to reshape themselves (6). This thin layer beneath the membrane largely consists of cross-linked actin filaments and nonmuscle myosin motor proteins. Importantly, this thin structure can generate active stresses and contract (7, 8, 9). Active stresses emerge from the force-generation of myosin motors interacting with actin filaments, fueled by ATP hydrolysis (10). Such active molecular processes lead to the buildup of mechanical stress () on larger scales (11). To gain a physical insight into the stresses and the force balances that govern large-scale deformation and flows of the cell cortex, coarse-grained continuum mechanical descriptions have played an important role (8, 9, 12). Furthermore, cortical laser ablation (COLA) has emerged as a useful tool for investigating forces and stresses in the cortical layer (3, 8, 9). The aim of this article is to extend the analysis of the response of the actomyosin cortex to COLA by use of thin film active viscoelastic gel theory (13, 14, 15), to determine physical parameters that characterize the actomyosin cortical layer.
One biological example where a continuum mechanics description in the framework of active gels has been useful is epiboly in zebrafish gastrulation (8). Here, a ring of actomyosin cortex forms on the surface of the yolk cell (16). This ring contracts not only to generate circumferential stresses, but also to drive flow of actomyosin into the ring. The mechanical stresses that are generated in this process play an important role to pull the connected enveloping layer of cells (EVL) of the blastomere from the animal pole of the embryo toward the vegetal one. The stress distribution and the emerging large-scale actomyosin flow velocity field can be understood using thin film active gel theory. Cortical tension can also be investigated in experimental terms by COLA. Anisotropies of recoil velocities can be related to tension anisotropies resulting from flow, and viscous tension and the emerging flow fields depend on the large-scale physical parameters of the actomyosin cortical layer. Therefore, to understand the mechanics that underlie flow and deformation of the actomyosin cortical layer it is key to determine its large-scale physical properties, which has been difficult to achieve.
A second example that highlights the role of actomyosin in morphogenesis is polarizing the one-cell stage Caenorhabditis elegans embryo (17, 18). Here, gradients of active tension generate cortical flows that lead to the establishment of anterior-posterior cell polarity, which in turn is key for the subsequent asymmetric cell division (19, 20). Notably, cortical flow in this system can be well described by a thin film active gel theory (9). Also here, COLA has permitted the characterization of tension profiles by analyzing the initial recoil velocity of actomyosin after COLA (9). However, in earlier studies (8, 9), an estimation of physical parameters that characterize the actomyosin cortex, such as the effective two-dimensional (2D) viscosity η and the friction coefficient γ with respect to the membrane and the cytosol, have remained elusive.
Furthermore, the cortex behaves as an elastic solid on short times, while it is essentially viscous on long times (21). Thus, a dynamic description needs to take into account that the actomyosin cortical layer is viscoelastic. A simple model for viscoelastic behaviors that is limited to the slowest relaxation processes is the Maxwell model, which can be incorporated into the theory of active gels (13, 14, 15). Viscoelastic behavior of the cortex stems from the continuous remodeling of the cortical network by the turnover of actin filaments and other cortical constituents (22, 23, 24). This turnover occurs under the influence of regulatory and signaling molecules (10). Because of the turnover, the strain energy stored in the cortex elastic stress relaxes and the corresponding strain energy is dissipated (25, 26). The corresponding timescale of stress relaxation (the Maxwell time ) is an important physical quantity that determines cortex behavior. Mechanical perturbations that persist on times large compared to will lead to viscous deformations and flows (9). If, however, a mechanical perturbation persists only for times that are shorter than , strain energy will be stored and the cortical layer will respond elastically. To conclude, the timescale of cortical remodeling determines the characteristic timescale of stress relaxation , which in turn governs the cortical response to mechanical perturbations.
Another important parameter characterizing the coarse-grained spatiotemporal dynamics of the actomyosin cortex is its hydrodynamic length, . This length determines the range of stress propagation and sets the correlation length of the cortical flow field. Hence, a large hydrodynamic length λ leads to long-ranged cortical flows, which, for the case of C. elegans, is important for polarization (20).
In previous studies, analysis of COLA typically relied on the recoil velocity of the cortex in response to the ablation and the corresponding decay time (9). Even though the decay timescale is related to , a precise characterization of from COLA experiments remains to be performed. In addition, λ was determined by analyzing the distribution of myosin and the cortical flow field, in the long-time and viscous limit (9). Considering the broad applications of laser ablation experiment in cell- to tissue-scale mechanical studies, a full analysis of the cortical response to COLA on short- and intermediate timescales and in the viscoelastic regime is useful, to extract physical parameters of the cortical layer.
In this article we sought to determine key coarse-grained physical parameters of the cell cortex, by use of COLA experiments and by use of a theoretical description of the cortical layer in terms of a 2D active viscoelastic gel. We provide a complete description of flows in response to COLA, both on short and intermediate times. Besides determining the hydrodynamic length, our method can be used to determine the timescale of elastic stress relaxation within the layer as well as a parameter that characterizes myosin-dependent active stress. We apply our method to two model systems: the actomyosin ring that drives zebrafish epiboly, and the actomyosin cortical layer in the single cell embryo of C. elegans that drives cell polarization. We measure distinct physical properties of the cortex in the two systems, thus demonstrating a broad applicability of our method.
Materials and Methods
C. elegans strain and sample preparation
To image nonmuscle myosin II (NMY-2) in single cell embryos, we used transgenic line LP133 (nmy-2(cp8[NMY-2::GFP + unc-119(+)])I; unc-119 (ed3) III). The C. elegans maintenance and handling was as previously described in Brenner (27). We cultured the line at 20°C and shifted temperature up to 24°C 24 h before microscope imaging and COLA. Embryos were dissected in M9 buffer (0.1 M NaCl and 4% sucrose) and mounted onto the agar pads (2% agarose in water) to squish the embryos gently. All experiments were performed at 23–24°C.
Zebrafish transgenic lines and sample preparation
To visualize NMY-2 in the yolk syncytial layer (YSL) of zebrafish embryos throughout epiboly, we used transgenic line Tg(actb2:myl12.1-EGFP) (28). Maintenance of the fish line as well as embryo collection was conducted as previously described in Westerfield (29). Zebrafish embryos were incubated at 25–31°C in E3 medium and staged according to morphological criteria (30). For imaging and the performance of COLA, embryos were mounted in 1% low melting point agarose (Invitrogen, Carlsbad, CA) inside E3 medium on a glass bottom petri dish (MatTek, Ashland, MA).
Imaging and COLA
Zebrafish embryos and C. elegans embryos were imaged and ablated using modified versions of previously described spinning disk laser ablation systems (8, 9). In brief, the spinning disk system (Revolution Imaging System; Andor Technology, South Windsor, CT; and model No. CSU-X1; Yokogawa, Rutherford, NJ) was assembled onto the Axio Observer Z1 inverted microscope (Carl Zeiss, Jena, Germany) equipped with a 63× water immersion objective. Fluorescent images were acquired by an electron-multiplying charge-coupled device camera (iXon; Andor Technology) at the specified time intervals (for C. elegans, 1 s; for zebrafish, 0.5 s). The pulsed 355 nm-UV laser (Powerchip; Teem Photonics, Meylan, France) with a repetition rate of 1 kHz was coupled into the Axio Observer (Carl Zeiss) and steered for pointwise ablation by galvanometric mirrors (Lightning DS; Cambridge Technology, Bedford, MA). A custom-built LabVIEW program (National Instruments, Austin, TX) integrated all devices for simultaneous COLA and imaging. To see the cortical response in C. elegans embryos, we applied 20 pulses for each point spaced every 0.5 μm along a 10 μm line. The cut lines were chosen to be parallel with the long axis of the embryos, the future anterior/posterior (AP) axis. For zebrafish embryos we applied 25 pulses per point spaced at 0.5 μm along a 20 μm line. The cut line was placed within the YSL actomyosin ring at a distance of 20 μm from the EVL margin and parallel to that margin. The intensity of the UV laser was adjusted to achieve successful COLA in zebrafish embryos. Successful COLA was characterized by the visible opening of the cortex in response to the cut, subsequent recovery of the actomyosin cortex within the cut opening, and no wound-healing response, as previously described in Behrndt et al. (8) and Mayer et al. (9).
Comparison to theory
To determine the best-fit nondimensionalized model parameters α1, α2, α3, and the characteristic time (see Appendix A for the details), we performed the least-square fitting for the COLA responses in experimental observation by the theoretical one. We evaluated the spatial velocity profile at a time just after the COLA, temporal evolution of the width of the cut opening boundary, and the recovery timecourse (see Fig. 2 and main text for detail). Fitting was performed iteratively by using the Nelder-Mead method (31). First we obtained the best-fit value of with the arbitrary values of α1, α2, and α3 by fitting the recovery timecourse. We then nondimensionalized the experimental time course with determined value and obtained the best-fit values of α1, α2, and α3 through fitting the spatial velocity profile and the time evolution of the cut opening boundary. In next iteration step, we determined the best-fit value of with values of α1, α2, and α3 obtained in the previous iteration step. We stopped the iteration after the convergence of the fitting parameters.
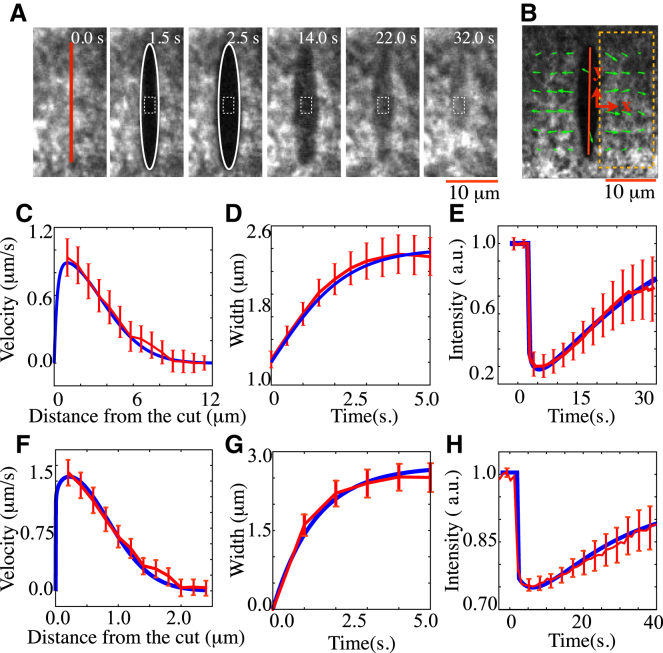
Figure 2.
COLA response in zebrafish and C. elegans. (A and B) Illustration of the analysis of the cortical response to COLA. (A) The time evolution of the cut boundary opening was characterized by fitting an ellipse to the cut boundary and measuring the minor radius of the fitted ellipse (white solid line). To analyze the regrowth of the cortical NMY-2 after the cut, we measured the average fluorescence intensity within the box (white broken line). The size of the box is 1.8 × 1.4 μm for zebrafish and 1.4 × 1.2 μm for C. elegans. (B) To obtain the velocity profile along the direction perpendicular to the cut line (red line), the x components of the velocity vectors inside the rectangular area surrounded by the orange broken line were averaged in the y direction (box size, zebrafish: 27 × 13 μm, C. elegans: 12 × 10 μm). (C and F) Velocity profile along the direction perpendicular to the cut line at the time just after the cut for zebrafish (C) and C. elegans (F). (D and G) Time evolution of the minor radius of the fitted ellipse to the cut boundary for zebrafish (D) and C. elegans (G). (E and H) Average concentration of cortical NMY-2 as a function of time after the cut opening for zebrafish (E) and C. elegans (H). (Red) Experimental results in zebrafish (C–E) and C. elegans (F–H). Error bars represents standard error, with n = 15 for all cases. (Blue lines) Theory curves utilizing the obtained least square fit parameters, see main text.
In parallel to this, we tested to find the best-fit parameter values by comparing the temporal development of the cut boundary between the experimental data and theoretical prediction. We determined the cut opening boundary by automatically detecting the cut opening region. The edge points were detected by using active contour method, a built-in function in MATLAB (The MathWorks, Natick, MA). Then we obtained the best-fit parameter values iteratively by using the Nelder-Mead method (31). In each iteration, we first determined the best-fit value of by fitting the recovery curve with arbitrary values of α1, α2, and α3, to set the timescale for the nondimensionalization. Then we computed the cut response numerically with the given parameter values. We next compared the edge points of the cut opening region between the experimental observation, , and theoretical prediction, , at the given time point, n. We computed the pairwise distances between and , , and then calculated the minimum distances, with respect to each j, . Then we took sum with respect to i, and average for the frames in analysis, to get the distance measure,
| (1) |
where N represents the number of frames in analysis. We minimized D to obtain the best-fit parameter values of α1, α2, and α3 with the given value of . The iteration is stopped after the convergence of the parameter values.
Results
Cortical response to COLA
We first sought to quantify precisely the spatiotemporal dynamics of cortical NMY-2 that arises in response to ablating the cortex along a line. For this, we used spinning disk microscopy to image NMY-2 fluorescence, in combination with a UV laser ablation setup to sever the cortical layer along a line (8, 9, 32). We recorded the spatiotemporal evolution of the surrounding NMY-2 in the cortex to follow the resealing process.
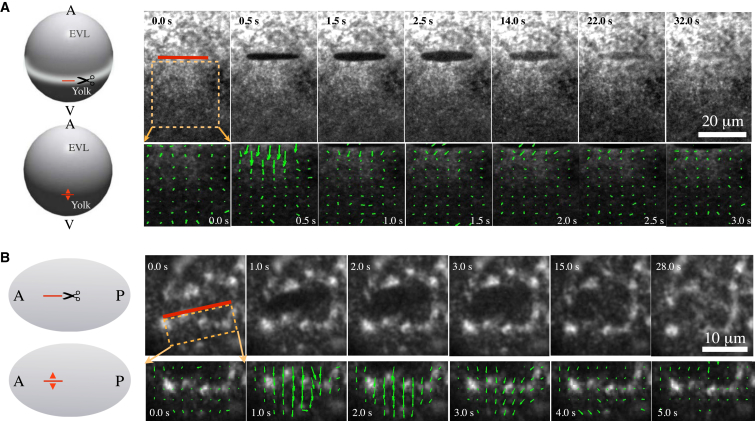
In the case of the zebrafish embryo, at the stage of 60–70% epiboly, COLA was performed within the YSL actomyosin ring and along a line parallel to EVL. In the case of the C. elegans one-cell embryo, the cortex was ablated just before the onset of cortical flow in the anterior half of the embryo and in a direction along the AP axis. In both systems the area surrounding the cut was imaged until the hole was no longer visible due to turnover and regrowth (Fig. 1, A and B, right upper).
Figure 1.
Probing cortical tension in the actomyosin ring of gastrulating zebrafish (A) and in the C. elegans (B) actomyosin cortex of single-cell embryos by COLA. (A) (Left) Schematic of COLA (scissors) in the actomyosin ring of zebrafish. COLA is performed along a 20 μm line (red line) at the stage of 65% epiboly. (Red arrowheads) Direction of cortical recoil after ablation. (Right) Upper images show a time series of cortical NMY-2-GFP after ablation; lower images show the corresponding velocity fields as determined by PIV. (B) (Left) Schematic of COLA on the actomyosin cortex of the C. elegans zygote. COLA is performed along a 10 μm line in parallel to the AP axis of the embryo. (Red arrowheads) Direction of cortical recoil after ablation. (Right) Upper images, time series of cortical NMY-2-GFP after ablation; lower images, corresponding velocity fields as determined by PIV.
COLA severs all connections within the cortex along the cut line and sets tension in the direction orthogonal to the cut line to zero. This results in tension gradients that drive an outward movement of the adjacent cortex away from the cut line (Fig. 1, A and B, right). Notably, despite significant differences in cortical structure and dynamics, both zebrafish and C. elegans share large similarities in the overall response to COLA and the spatiotemporal dynamics of cut opening and resealing. In both systems the outward movement of the cut boundary lasts for several seconds and turns the cut line into an approximately elliptically shaped opening. Furthermore, the adjacent cortex moves outward with a velocity that decays over time, followed by cortical regrowth within the cleared region until no visible mark of the COLA procedure remains.
To extract the characteristics of the response of the cortex to COLA and the characteristics of the resealing process, we analyzed the spatiotemporal dynamics of cortical NMY-2 after COLA in several ways. First, we determined the outward velocity of cortical NMY-2 adjacent to the cut line by particle image velocimetry (PIV) at a time just after the cut, as indicated by the arrows in Fig. 1, A and B (right, lower panels). Remarkably, the velocity profile along the direction perpendicular to the cut line was not uniform, but rather decayed over a characteristic distance away from the cutline as shown in Fig. 2, C and F. This spatial decay entails information about the characteristic distance λ over which mechanical stresses communicate in the 2D cortical layer. Second, we quantified the temporal evolution of the cut opening. For this, we determined the extent of the opening generated by COLA, by fitting an ellipse to this opening and determining the time evolution of the minor radius of this fitted ellipse as a measure of the width of the cut opening (Fig. 2 A). Notably, the width of the cut opening increased with time and reached maximum after ∼3–5 s (Fig. 2, D and G). The minor radius of the opening grows with a characteristic time governed by processes of stress relaxation in the actomyosin cortical layer. Third, we analyzed NMY-2 regrowth within the opening, by quantifying the average fluorescence intensity in a box that is placed at the center of the COLA opening (white broken line in Fig. 2 A). After an initial drop in intensity due to ablation and outward movement, NMY-2 intensity gradually recovered over ∼30 s (Fig. 2, E and H). Similar timescales have been observed in FRAP measurements that characterize NMY-2 turnover (9).
These observations lend credence to the assumption that the cortex behaves as an active viscoelastic material. The shape evolution of the cut opening is determined largely by elastic properties of the cortex as well as active tension provided by NMY-2. The velocity decay away from the cut line is largely determined by the decay length of tension in the layer, and thus by γ and λ. Finally, reassociation of myosin at the cut site is determined by actomyosin turnover. In what follows, we will compare the dynamics of opening and regrowth, as determined in our experiments by characterizing the spatial decay of the velocity field and the time evolution of the cut opening width and the myosin levels at the center of the hole, with theory.
Physical description of the actomyosin cortex
We next sought to calculate the cut response in a coarse-grained physical description of the cortical layer. Considering that the thickness of the cortex is small compared to the size of the cell, we describe the actomyosin cortex as an active 2D viscoelastic compressible fluid. We introduce a scalar field h(x,y,t) that denotes the local height of the cortical layer in the z direction, with x and y denoting spatial Cartesian coordinates within the plane of the cortical layer, and t denoting time. Considering a viscoelastic isotropic active fluid in the plane and integrating over the height of the cortex, we write the following constitutive equation:
| (2) |
where indices . The dynamic variables are the 2D stress tensor σ, the 2D active stress tensor σa, and the 2D velocity field v. The material properties are characterized by the 2D shear viscosity η, 2D bulk viscosity , and a characteristic Maxwell time of stress relaxation . Here, denotes the material time derivative. Turnover of the film is captured by the dynamics of the height given by
| (3) |
where the first term on the right-hand side accounts for advection of the gel by cortical flow, and the second term describes turnover that relaxes to the steady-state height . Note that both the turnover time and the relaxed height depend on actin and myosin turnover. The force balance equation reads (7, 8, 9, 33, 34)
| (4) |
where inertial forces have been neglected, and γ is a friction coefficient that describes frictional interactions between the cortex and its surrounding cytosol and membrane.
We consider an active gel that is incompressible in three dimensions (3D), with constant density through the height of the cortical layer. In this case, both the active stress and the 2D viscosities η and ηb of the cortex are proportional to cortex height h, and are written as
| (5) |
| (6) |
| (7) |
Here, denotes the isotropic active stress generated through ATP consumption of myosin, positive for contraction and dependent on the change in chemical potential associated with ATP hydrolysis . Furthermore, and denote the shear and bulk viscosities of the layer when . Three-dimensional incompressibility condition couples divergences in the 2D flow velocity field v to change the cortex height h according to Eq. 3, and we set (35). This is because the gel is considered to be incompressible in 3D, thus and , where is the viscosity in 3D. Equations 2–4 complete the model. For nondimensionalization, we choose the characteristic time of regrowth and the COLA cut length as the respective time- and length scales. Model equations with dimensionless variables can be rewritten with dimensionless parameters, , , and (see Appendix A).
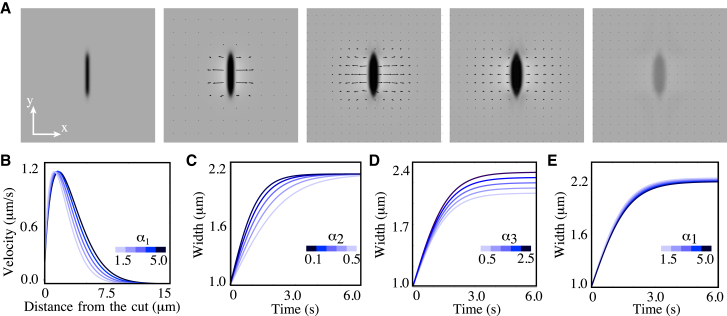
We next asked whether this description can reproduce the relaxation dynamics in response to COLA that we observed in our experiments. To this end, we numerically solved nondimensional versions of Eqs. 2–4 (see Appendix A) in a rectangular box of width L () in x and y, with periodic boundary conditions. As an initial condition, we choose uniform height and stress fields that correspond to the unperturbed stationary solution with v = 0. To account for COLA, this homogenous initial condition is perturbed at t = 0 by setting height h to zero within a thin rectangular strip of length and width . We then computed the resulting spatiotemporal dynamics. Fig. 3 A displays the time evolution of the resultant height and velocity fields. We observe that (1) the velocity field is not uniform through the cortex but decayed over a distance from the cut line; (2) the width of the boundary initially grows and reaches a maximum; and (3) in the cut region recovers to steady-state values on long times. These observations are consistent with those that we have made in our experiments, which lend credence to our approach.
Figure 3.
Numerical calculation of the spatiotemporal response of a 2D active viscoelastic fluid in response to COLA. (A) Representative calculated nondimensional height (gray) and velocity field (arrows) of the cortex at times 0, 0.02, 0.04, 0.06, 0.08, and 0.68 after COLA by setting the height to zero in the dark region around the red line in the leftmost image (see main text). (B) Effect of variation of α1 on the spatial velocity profile at 0.5 s after cut. The x component of velocity vectors was averaged along the y direction and within the box indicated by the broken orange line in the second panel of (A). (C–E) Effect of variation of α2 and α3 on the time evolution of the half-width of the cut opening, determined by fitting an ellipse to the opening boundary. Note that changing α1 has a small effect on time evolution of the width of the opening (E). Unless otherwise specified, parameter values are α1 = 2.0, α2 = 0.25, and α3 = 4.5. For (B)–(E), we have dimensionalized time by and length by .
Next we analyzed our results from theory in terms of the spatial profile of the velocity in the direction perpendicular to the cut line, the growth of the cut boundary, and the recovery of the cut region in a manner that is similar to how we analyzed the experimental data. Fig. 3, B–E, demonstrates that the essential features observed in the corresponding graphs from our experiments (Fig. 2, C–H) are reproduced in our theory. We next asked how changes of physical parameters of the cortical layer impact on the spatial profile of the velocity in the direction perpendicular to the cut line, the growth of the cut boundary, and the recovery of cortex height. To this end, we performed numerical simulations of COLA with different values of α1, α2, and α3. We find that increasing λ leads to a corresponding increase of the spatial decay length of the velocity profile in a direction perpendicular to the cut line (Fig. 3 B), but has little impact on the growth timecourse of cut boundary (Fig. 3 E). Furthermore, increasing results in a corresponding increase in the relaxation time to reach the maximal width of the opening (Fig. 3 C), with little effect on the final size of the hole. Taken together, key aspects of the relaxation process after COLA are separately determined by the characteristic length and time, λ and , of the cortical layer.
Comparison of theory and experiment for determination of physical parameters
To compare the response observed in experiment to the theoretical predictions, we sought to investigate the relationship between the florescence intensity of myosin, , and cortex height, . First, we consider a proportionality between cortex height and the cortical actin density per unit area, . As is given by integrating the cortical actin density per unit volume, , over z, , 3D incompressibility gives , in which is constant through the cortex. We next investigated the relationship between the per-area densities of actin and myosin. To this end we studied the regrowth of both myosin and actin densities after the ablation. Note that because the thickness of the cortical layer is smaller than the focal depth of the confocal microscope (∼1 μm), the fluorescence intensities from the actin and myosin are proportional to their densities integrated over the cortex height, which correspond to the respective densities per unit area. We ablated the cortex in C. elegans embryo that is expressing both NMY-2 GFP and lifeact RFP, as the probe for actin filaments, to see if upon regrowth in the region of cut opening the ratio between the actin and myosin fluorescence intensities remains constant over time. In Fig. S1 (in the Supporting Material), the fluorescence recoveries of actin and myosin intensities are proportional to each other, revealing a linear relationship between the two quantities. Given our assumption that the per-area density of actin is proportional to cortex height, this suggests that the per-area density of myosin is proportional to cortex height as well. Therefore, for our COLA response analysis we considered a proportional relationship between NMY-2 fluorescence intensity and the scalar height field , and relate and according to
| (8) |
Here, denotes the background signal obtained from the average intensity within the box located at the center of the cut opening in the first post-cut frame, and is the maximum intensity in each recorded image.
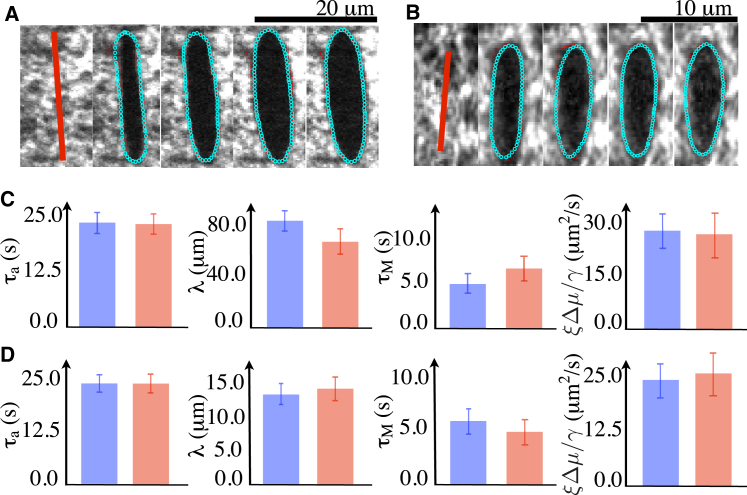
Next, we determined the best-fit nondimensionalized model parameters within a nonlinear least-square fitting scheme (31) by iteratively calculating the theoretical responses that best fit the experimental profiles (see blue curves in Fig. 2, C–H, in comparison to the experimental profile given by red curves). In Fig. 4, C and D, we report the physical parameters of the cell cortex () from the best-fit model parameters. We obtained , and for zebrafish, and , and for C. elegans. Note that these values were obtained by fitting each individual experiment (n = 15 for both systems), and we report the respective averages ± 95% confidence interval. Note also that the hydrodynamic lengths of ∼68 μm for the zebrafish actomyosin ring and ∼14 μm for the C. elegans cortex as well as the turnover times of ∼25 s show a close agreement with previous investigations (8, 9). This supports our method of extracting values of physical parameters by use of fitting the measured COLA response to that expected from theory. Note that we ablated the cortex along the lines of 20 μm for zebrafish and 10 μm for C. elegans in length, larger than the characteristic length associated with inhomogeneities of the cortical myosin distributions (myosin foci), and as such we do not expect them to contribute to the overall laser ablation response. Note also that our numerical analysis assumes a homogeneous distribution of myosin around the cut region, and thus does not take large-scale myosin gradients and flows into account. This is an accurate representation for C. elegans, but not for zebrafish. However, for the flow magnitudes reported, we expect that the associated errors in determining cortex material parameters are small (8).
Figure 4.
Determination of physical parameters by comparing the COLA responses observed in experiment to the computed response from the theory. (A and B) Representative examples of fitting the cut opening boundary in response to COLA of the actomyosin ring in zebrafish during epiboly (A) and the cortex in a single-cell embryo of C. elegans (B). (Red points) Automatically detected boundaries of the cut opening. Distances between the computed and the detected boundaries were minimized to find the best-fit parameter values. (Cyan) The theoretical boundaries that best fit the experimental ones. Images are 1 s apart. (C and D) Comparison of physical parameter values between the two methods utilized. (Red) The best-fit parameter values were determined by comparing the experimentally determined regrowth of the cut region, spatial decay of the outward velocity profile, and the time evolution of the cut opening boundary to theoretical prediction (see Fig. 2). (Blue) The best-fit parameter values obtained by comparing the cut opening boundaries between experiment and theory (see A and B). Note that both fitting procedures converge to similar values. Error bars are the 95% confidence interval of the mean with n = 15 for zebrafish and n = 10 for C. elegans.
The good agreement between theory and experiment indicates that the shape evolution of the cut opening might entail a sufficient amount of information for accurately determining both λ and . Because the spatial profile of the velocity field is governed by hydrodynamic length, λ, the temporal change of the shape of the cut opening boundary is likely to be affected by λ. On the other hand, the temporal decay of the outward velocity is characterized by the timescale of the stress relaxation, . Thus it is possible that the shape evolution of the cut boundary is, to a large extent, governed by these two physical parameters. In agreement with this statement, the shapes of the cut opening boundary are distinct between the zebrafish actomyosin ring and C. elegans embryo, which might reflect the respective differences in physical parameters.
Therefore, we asked if it is possible to determine the hydrodynamic length λ and the timescale of stress relaxation from the shape evolution of the cut opening boundary. To this end, we determined the values of α1, α2, and α3 by comparing the spatiotemporal development of the cut opening boundary shapes in experiment and theory. We detected the shape of the cut opening boundary observed in experiment to evaluate the difference with the shape from the theoretical prediction at the given parameter values. We computed the minimum distance from ith edge point detected in the experiment to the edge points obtained from the theory at the nth time frame, (see Materials and Methods for details). We then evaluated a merit function, , where N is the number frames analyzed (a useful choice for N was between 8 and 12 for a zebrafish, and between 4 and 6 for C. elegans). D was minimized iteratively to find the best-fit values of α1, α2, and α3 and . Fig. 4, A and B, shows the shape of the cut opening boundary from the theory with the best-fit parameter values with respect to the minimization of D, successfully reproducing the shape evolution of the cut opening boundary observed in experiment. Consequently, we obtained nondimensionalized model parameters α1, α2, α3, as well as the physical parameters , and for zebrafish and , and for C. elegans. Again, these values were obtained by fitting each individual experiment (n = 15 for zebrafish and n = 10 for C. elegans; in the latter, not all of our experimental datasets converged in the fitting procedure), and we report the respective averages ±95% confidence interval. The values of the parameters of the actomyosin network are in close agreement between this method of determination, and the method used before (see Fig. 4, C and D). We conclude that the shape evolution of the cut opening boundary entails a sufficient amount of information to determine the entire set of nondimensional physical parameters, and provides a second means of determining physical parameters of the actomyosin cortical layer.
Discussion
While COLA is a powerful tool to characterize the tension in the actomyosin cortex, obtaining the physical parameters to describe the cortical mechanics relies on an appropriate analytical method. Here we present a strategy to determine the physical parameters of actomyosin cortex from the cortical response to COLA. The method relies on the fitting of the COLA response to the theoretical prediction from the 2D active viscoelastic fluid model. We show that for the best-fit values of the hydrodynamic length, λ are in close agreement with previous estimates for the zebrafish actomyosin ring and the C. elegans single-cell embryo (8, 9). Notably, we can determine a whole set of parameters in a single experiment, in contrast to the previous estimates that require the ensemble averaging for the flow profile and myosin distribution. As shown in Fig. 4, the standard errors of the best-fit parameters are small in both methods, signifying the overall robustness of the approach. In addition, our method does not require any assumptions for boundary conditions in the flow and myosin profiles. Taken together, our method allows the precise determination of the physical parameters.
Importantly, our method also allows us to determine the characteristic time of stress relaxation, , which governs the timescale between elastic and viscous regime. The value sets the timescale for the large-scale movement of the actomyosin cortex, and morphogenetic deformations of the cortex that are driven by active stresses in the layer generally occur on timescales larger than . Recently active microrheology has been performed to measure the storage and loss moduli by manipulating a bead injected inside the cell (36). This method allows the precise determination of the characteristic time of stress relaxation of the cytoplasm. A particularly useful method applies a magnetic force to twist a magnetic bead attached to a cell surface (37). However, all these methods are only feasible in situations where the actomyosin cortex is accessible with a probe, which is not always the case in vivo. In contrast, our method allows us to directly determine physical parameters of the cortex in vivo and without any direct physical contact, and thus is complementary to active microrheology.
In summary, we have developed a robust and accurate method with broad applicability to determine the physical parameters of cortical mechanics from COLA experiment in conjunction with the coarse-grained mechanical theory. It provides us with the large-scale and biologically relevant parameters in terms of morphogenetic mechanics. Given the simple description of the cortex used in the article, we suggest that our method can be applied for complex multicellular systems such as epithelial tissues to determine the physical parameters that describe the tissue mechanics.
Author Contributions
A.S., F.J., and S.W.G. designed the research; M.B. and M.N. performed experiments under supervision of C.-P.H. and S.W.G.; A.S. and M.N. developed the theory and performed numerical simulations as well as the comparison to data under supervision of F.J. and S.W.G.; and M.N. and S.W.G. wrote the article with the help of A.S. and with support from F.J.
Acknowledgments
We are grateful to Daniel Dickinson for providing the LP133 C. elegans strain. We thank G. Salbreux, V. K. Krishnamurthy, and J. S. Bois for fruitful discussions.
S.W.G. acknowledges support by grant no. 281903 from the European Research Council and by grant No. GR-7271/2-1 from the Deutsche Forschungsgemeinschaft. S.W.G. and C.-P.H. acknowledge support through a grant from the Fonds zur Förderung der Wissenschaftlichen Forschung and the Deutsche Forschungsgemeinschaft (No. I930-B20).
Editor: Gijsje Koenderink.
Footnotes
Arnab Saha and Masatoshi Nishikawa contributed equally to this work.
Arnab Saha’s present address is Institut für Theoretische Physik II, Heinrich-Heine-Universität Düsseldorf, Germany, Düsseldorf, Germany.
One figure is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)00158-2.
Appendix A: Nondimensional Equations
We rescaled the time and the spatial coordinate by setting the cut length () as the length scale and as the timescale of the system. Equations 2–4 can be rewritten as
| (9) |
| (10) |
| (11) |
where represents the hydrodynamic length. The values , , and are three independent, dimensionless parameters of the model.
Supporting Material
References
- 1.Lecuit T., Lenne P.F. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat. Rev. Mol. Cell Biol. 2007;8:633–644. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
- 2.Eaton S., Jülicher F. Cell flow and tissue polarity patterns. Curr. Opin. Genet. Dev. 2011;21:747–752. doi: 10.1016/j.gde.2011.08.010. [DOI] [PubMed] [Google Scholar]
- 3.Hutson M.S., Tokutake Y., Edwards G.S. Forces for morphogenesis investigated with laser microsurgery and quantitative modeling. Science. 2003;300:145–149. doi: 10.1126/science.1079552. [DOI] [PubMed] [Google Scholar]
- 4.Solon J., Kaya-Copur A., Brunner D. Pulsed forces timed by a ratchet-like mechanism drive directed tissue movement during dorsal closure. Cell. 2009;137:1331–1342. doi: 10.1016/j.cell.2009.03.050. [DOI] [PubMed] [Google Scholar]
- 5.Tada M., Heisenberg C.P. Convergent extension: using collective cell migration and cell intercalation to shape embryos. Development. 2012;139:3897–3904. doi: 10.1242/dev.073007. [DOI] [PubMed] [Google Scholar]
- 6.Salbreux G., Charras G., Paluch E. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 2012;22:536–545. doi: 10.1016/j.tcb.2012.07.001. [DOI] [PubMed] [Google Scholar]
- 7.Salbreux G., Prost J., Joanny J.-F. Hydrodynamics of cellular cortical flows and the formation of contractile rings. Phys. Rev. Lett. 2009;103:058102. doi: 10.1103/PhysRevLett.103.058102. [DOI] [PubMed] [Google Scholar]
- 8.Behrndt M., Salbreux G., Heisenberg C.P. Forces driving epithelial spreading in zebrafish gastrulation. Science. 2012;338:257–260. doi: 10.1126/science.1224143. [DOI] [PubMed] [Google Scholar]
- 9.Mayer M., Depken M., Grill S.W. Anisotropies in cortical tension reveal the physical basis of polarizing cortical flows. Nature. 2010;467:617–621. doi: 10.1038/nature09376. [DOI] [PubMed] [Google Scholar]
- 10.Levayer R., Lecuit T. Biomechanical regulation of contractility: spatial control and dynamics. Trends Cell Biol. 2012;22:61–81. doi: 10.1016/j.tcb.2011.10.001. [DOI] [PubMed] [Google Scholar]
- 11.Koenderink G.H., Dogic Z., Weitz D.A. An active biopolymer network controlled by molecular motors. Proc. Natl. Acad. Sci. USA. 2009;106:15192–15197. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bergert M., Erzberger A., Paluch E.K. Force transmission during adhesion-independent migration. Nat. Cell Biol. 2015;17:524–529. doi: 10.1038/ncb3134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kruse K., Joanny J.-F., Sekimoto K. Asters, vortices, and rotating spirals in active gels of polar filaments. Phys. Rev. Lett. 2004;92:078101. doi: 10.1103/PhysRevLett.92.078101. [DOI] [PubMed] [Google Scholar]
- 14.Kruse K., Joanny J.-F., Sekimoto K. Generic theory of active polar gels: a paradigm for cytoskeletal dynamics. Eur. Phys. J. E. Soft Matter Biol. Phys. 2005;16:5–16. doi: 10.1140/epje/e2005-00002-5. [DOI] [PubMed] [Google Scholar]
- 15.Callan-Jones A., Jülicher F. Hydrodynamics of active permeating gels. New J. Phys. 2011;13:093027. [Google Scholar]
- 16.Köppen M., Fernández B.G., Heisenberg C.-P. Coordinated cell-shape changes control epithelial movement in zebrafish and Drosophila. Development. 2006;133:2671–2681. doi: 10.1242/dev.02439. [DOI] [PubMed] [Google Scholar]
- 17.Cuenca A.A., Schetter A., Seydoux G. Polarization of the C. elegans zygote proceeds via distinct establishment and maintenance phases. Development. 2003;130:1255–1265. doi: 10.1242/dev.00284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cheeks R.J., Canman J.C., Goldstein B. C. elegans PAR proteins function by mobilizing and stabilizing asymmetrically localized protein complexes. Curr. Biol. 2004;14:851–862. doi: 10.1016/j.cub.2004.05.022. [DOI] [PubMed] [Google Scholar]
- 19.Munro E., Nance J., Priess J.R. Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo. Dev. Cell. 2004;7:413–424. doi: 10.1016/j.devcel.2004.08.001. [DOI] [PubMed] [Google Scholar]
- 20.Goehring N.W., Trong P.K., Grill S.W. Polarization of PAR proteins by advective triggering of a pattern-forming system. Science. 2011;334:1137–1141. doi: 10.1126/science.1208619. [DOI] [PubMed] [Google Scholar]
- 21.Humphrey D., Duggan C., Käs J. Active fluidization of polymer networks through molecular motors. Nature. 2002;416:413–416. doi: 10.1038/416413a. [DOI] [PubMed] [Google Scholar]
- 22.Bausch A.R., Ziemann F., Sackmann E. Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys. J. 1998;75:2038–2049. doi: 10.1016/S0006-3495(98)77646-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wen Q., Janmey P.A. Polymer physics of the cytoskeleton. Curr. Opin. Solid State Mater. Sci. 2011;15:177–182. doi: 10.1016/j.cossms.2011.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Broedersz C.P., Depken M., MacKintosh F.C. Cross-link-governed dynamics of biopolymer networks. Phys. Rev. Lett. 2010;105:238101. doi: 10.1103/PhysRevLett.105.238101. [DOI] [PubMed] [Google Scholar]
- 25.Tawada K., Sekimoto K. Protein friction exerted by motor enzymes through a weak-binding interaction. J. Theor. Biol. 1991;150:193–200. doi: 10.1016/s0022-5193(05)80331-5. [DOI] [PubMed] [Google Scholar]
- 26.Bormuth V., Varga V., Schäffer E. Protein friction limits diffusive and directed movements of kinesin motors on microtubules. Science. 2009;325:870–873. doi: 10.1126/science.1174923. [DOI] [PubMed] [Google Scholar]
- 27.Brenner S. The genetics of Caenorhabditis elegans. Genetics. 1974;77:71–94. doi: 10.1093/genetics/77.1.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Maître J.-L., Berthoumieux H., Heisenberg C.-P. Adhesion functions in cell sorting by mechanically coupling the cortices of adhering cells. Science. 2012;338:253–256. doi: 10.1126/science.1225399. [DOI] [PubMed] [Google Scholar]
- 29.Westerfield M. University of Oregon Press; Eugene, OR: 2007. The Zebrafish Book: A Guide for the Laboratory Use of Zebrafish (Danio rerio) [Google Scholar]
- 30.Kimmel C.B., Ballard W.W., Schilling T.F. Stages of embryonic development of the zebrafish. Dev. Dyn. 1995;203:253–310. doi: 10.1002/aja.1002030302. [DOI] [PubMed] [Google Scholar]
- 31.Nelder J.A., Mead R. A simplex method for function minimization. Comput. J. 1965;7:308–313. [Google Scholar]
- 32.Colombelli J., Grill S.W., Stelzer E.H.K. Ultraviolet diffraction limited nanosurgery of live biological tissues. Rev. Sci. Instrum. 2004;75:472–478. [Google Scholar]
- 33.Bois J.S., Jülicher F., Grill S.W. Pattern formation in active fluids. Phys. Rev. Lett. 2011;106:028103. doi: 10.1103/PhysRevLett.106.028103. [DOI] [PubMed] [Google Scholar]
- 34.Vijay Kumar K., Bois J.S., Grill S.W. Pulsatory patterns in active fluids. Phys. Rev. Lett. 2014;112:208101. [Google Scholar]
- 35.Batchelor G.K. Cambridge University Press; Cambridge, UK: 2000. An Introduction to Fluid Dynamics. [Google Scholar]
- 36.Guo M., Ehrlicher A.J., Weitz D.A. Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell. 2014;158:822–832. doi: 10.1016/j.cell.2014.06.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Massiera G., van Citters K.M., Crocker J.C. Mechanics of single cells: rheology, time dependence, and fluctuations. Biophys. J. 2007;93:3703–3713. doi: 10.1529/biophysj.107.111641. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.