Abstract
Multiscale reactive molecular dynamics simulations are used to study proton transport through the central region of ClC-ec1, a widely studied ClC transporter that enables the stoichiometric exchange of 2 Cl– ions for 1 proton (H+). It has long been known that both Cl– and proton transport occur through partially congruent pathways, and that their exchange is strictly coupled. However, the nature of this coupling and the mechanism of antiporting remain topics of debate. Here multiscale simulations have been used to characterize proton transport between E203 (Gluin) and E148 (Gluex), the internal and external intermediate proton binding sites, respectively. Free energy profiles are presented, explicitly accounting for the binding of Cl– along the central pathway, the dynamically coupled hydration changes of the central region, and conformational changes of Gluin and Gluex. We find that proton transport between Gluin and Gluex is possible in both the presence and absence of Cl– in the central binding site, although it is facilitated by the anion presence. These results support the notion that the requisite coupling between Cl– and proton transport occurs elsewhere (e.g., during proton uptake or release). In addition, proton transport is explored in the E203K mutant, which maintains proton permeation despite the substitution of a basic residue for Gluin. This collection of calculations provides for the first time, to our knowledge, a detailed picture of the proton transport mechanism in the central region of ClC-ec1 at a molecular level.
Introduction
The ClC proteins are a family of chloride channels and transporters that are widely distributed in species ranging from bacteria to human beings (1). They have a broad range of physiological functions, including maintenance of the membrane potential, regulation of transepithelial Cl– transport, and control of pH in the cytoplasm and intracellular organelles (2, 3). In addition to their physiological importance, two aspects of ClC proteins have attracted interest in recent years. First, despite having very similar structures the ClC proteins can be either passive ion channels, facilitating selective anion transport down an electrochemical gradient, or secondary active transporters, coupling the uphill movement of protons (H+) to the downhill transport of Cl– ions (and vice versa) (4, 5, 6). Second, the mechanism of ClC transporters seems to be unique. Most exchangers transfer ions across the membrane in opposite directions in separate half reactions via large conformational changes in what is called a ping-pong or alternating access mechanism. However, ClC transporters can bind both ions simultaneously and transport them across the membrane through partially congruent pathways, resulting in an intriguing mechanism that has yet to be fully explained (7). Although recent experimental studies (8, 9, 10, 11) have suggested that there are some pH- or Cl–-dependent conformational changes in regions outside of the ion pathways, their magnitude and connection to ion transport remain unknown.
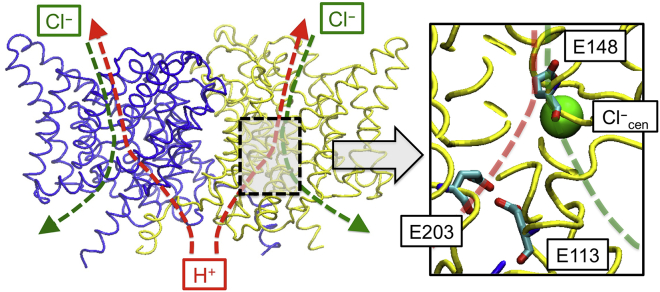
ClC-ec1, a bacterial ClC transporter homolog from Escherichia coli, controls the stoichiometric exchange of 2 Cl– for 1 H+ (12, 13). Following the determination of a high-resolution crystal structures for ClC-ec1 (14, 15), a series of electrophysiological experiments (12, 16, 17) and computational studies (18, 19, 20, 21) revealed the transport channels for the Cl– ions. Like all ClC transporters, ClC-ec1 forms a dimer in vivo and in vitro, and can function as a monomer in vitro (22). Each monomer has three intermediate binding sites for Cl– (Sext, Scen, and Sint) along the Cl– pathway (see Fig. 1) (15). The protonation of glutamic acid residue E148 (Gluex) at the center of the conducting pore allows Cl– ions to enter Scen from the extracellular side (23). The H+ pathway is thought to separate from the Cl– pathway on the intracellular side of Gluex, but the two pathways overlap on the extracellular side (16, 24, 25, 26). Sext and Scen are located along the H+ pathway, and Sint is separated from Scen by only 6.5 Å.
Figure 1.
Overview of the structure of the ClC-ec1 antiporter and transport pathways for Cl– (green dashed) and H+ (red dashed). ClC-ec1 consists of two monomers, where monomer A is colored in yellow, and monomer B is in blue. The central region is highlighted in the black box. Two pathways for Cl– and H+ meet at E148. In the figure, one Cl– is bound to Scen site, which is very close to the H+ pathway. The other Cl– binding sites (Sext and Sint) are not shown here. To see this figure in color, go online.
Site-directed mutagenesis studies (16, 27) revealed that two glutamate residues, E148 (Gluex) and E203 (Gluin), which are located near the external and internal sides of the membrane, respectively, are essential to proton transport (PT). Thus, it is assumed that Gluin accepts a proton from the intracellular side and transfers it to Gluex, but how it does so in concert with Cl– transport is unknown. Because the two residues are separated by ∼15 Å, water molecules or protonatable residues must occupy this space to facilitate PT. However, the residues surrounding this region (I109, L186, F199, F357, I402, and T407) are mostly hydrophobic before any possible large conformational changes (8, 9, 10, 11), and none of the crystal structures from E. coli (15) or other homologs (28) exhibit any crystallographic water molecules in this region. Moreover, it is unclear what influences the presence or absence of Cl– at the binding sites, or the protonation states of the surrounding residues, have on the PT from Gluin to Gluex. Thus, the molecular mechanism by which protons traverse the ClC-ec1 core, and the impact PT has on H+:Cl– antiporting, remains unclear.
In this study, PT through the central region is investigated by calculating the free energy profiles (potentials of mean force, PMFs) for explicit proton migration from Gluin to Gluex. Multiple PMFs are calculated to determine the effect of various factors on the migration of the excess proton: (1) the binding of Cl– at the central site (Cl–cen), (2) the dynamic hydration of the central region, and (3) the rotation of Gluin and Gluex. A combination of quantum mechanics/molecular mechanics (QM/MM) and multiscale reactive molecular dynamics (MS-RMD) (29, 30) is used to enable realistic description of the excess proton migration. The MS-RMD model, which is force-matched to ab initio data, also provides the required computational efficiency to enable extensive statistical sampling of the slow hydration dynamics in the central region along with the excess proton migration through the water and involved residues via Grotthuss shuttling. By virtue of MS-RMD’s accuracy and efficiency, this coupled behavior is quantitatively expressed for the first time, to our knowledge, in terms of two-dimensional (2D) PMFs calculated as a function of the excess proton coordinate and the water occupancy in the central region. The presented quantitative simulations build significantly upon our earlier and more preliminary work on this problem (24, 25), while at the same time being quite different from MD simulations that have studied the water occupancy alone in the absence of explicit proton transport (the latter then being inferred from the water hydration patterns rather than explicitly simulated) (26, 31).
Our results provide insight the elementary mechanism of PT in the ClC-ec1 central region. First, the excess proton, which likely resides on E113 or is shared between E113 and E203 in the crystal structure as previously predicted (32), is shown to transfer readily from E113 to E203 (Gluin) before PT to E148 (Gluex). Second, PT from Gluin to Gluex is shown to be dynamically coupled to the hydration of the central region (and vice versa). Third, the presence of Cl–cen is found to facilitate PT between Gluin and Gluex, despite blocking the downward rotation of Gluex. Surprisingly, however, we find that proton transport is also kinetically feasible in the absence of Cl–cen, when side-chain rotation facilitates PT, mimicking a classical heavy-light-heavy reaction (33). The calculated PT rate constants suggest that PT through the central region is not rate-determining, as suggested by experiments (34). Although experimentalists have proposed two mechanisms for wild-type (WT) ClC-ec1 (13, 35), differing in the presence or absence of Cl–cen during PT through the central region, our simulations reveal that PT can happen in either case, although the presence of the anion does lower the PT free energy barrier. This result further supports the notion that the requisite coupling between proton and Cl− transport occurs elsewhere in the overall PT process (e.g., during proton uptake to, or release from, residues E203 or E148), as previously suggested based on calculated pKa shifts of E148 depending on ion occupancy (36).
Finally, PT through the central region of the interesting E203K mutant is also explored. Despite the replacement of Gluin with a basic residue, experiments show that H+ permeation is not blocked and that the Cl–/H+ coupling remains intact (though slightly weaker) in this mutant (27). Our simulations suggest that PT from K203 to Gluex is indeed kinetically and thermodynamically possible, but only in the presence of Cl–cen. Similar to WT, the calculated rate for PT through the central region is not rate-limiting.
Materials and Methods
System setup
The initial configuration of the ClC-ec1 dimer (Protein Data Bank (PDB): 1OTS), embedded in 163 POPE lipids, 17 Cl– ions, and ∼11,000 water molecules in a 92 × 92 × 79 Å simulation box, was taken from our previous study (24). In this structure, Cl– ions were present at Scen and Sint of each monomer, as also given in the PDB structure. Consistent with pKa calculations (32), standard protonation states were chosen for all residues other than E113 in monomer B and D417 in monomer A, which were both protonated. Previous experiments have shown that ClC functions as a monomer (22); thus, all enhanced sampling used to calculate the PMFs was applied only to monomer A. Similarly, all variations in the core region (e.g., the presence or absence of Cl–, different protonation states, and the E203K substitution) were only made in monomer A. Removing all restraints used in previous studies, the system was equilibrated for 10 ns. The classical MD equilibration and simulation details are described in the Supporting Material.
QM/MM free energy profiles for PT from E113 to E203
The initial configurations for umbrella sampling (37) were prepared after 10 ns of equilibration MD runs with either Cl–cen present or absent. E113, which was protonated during equilibration, was deprotonated and a water molecule close to the center of each umbrella sampling window was replaced with a protonated water molecule (hydronium cation). The effective spatial position of the excess proton is defined as the center of excess charge (CEC), (38):
| (1) |
where the value is the position of the jth heavy atom in the QM region (one of the water oxygen atoms or glutamic acid carboxyl oxygen atoms), and the value is the position of the ith hydrogen atom bound to those heavy atoms. The weighting factor, , was set to be 2 for the water oxygen and 0 for the glutamic acid OE1 and OE2 atoms, which reflects the hydrogen coordination number in the deprotonated state of the heavy atom. The term here denotes the distance between and atoms, and the switching function is given as follows:
| (2) |
where is 0.04 Å and is 1.25 Å (39). The transfer of the CEC is mapped onto a one-dimensional collective variable (CV), denoted as , as a function of the distances between and the center of mass of the carboxyl group atoms of two Glu residues. For example, for the PMF of PT from E113 to E203 , is defined as
| (3) |
such that varies from 0 to 1 as the CEC moves from E113 to E203. The centers of the harmonic potential were separated by 0.1–0.2 Å between adjacent windows. The force constants for were chosen to be in the range of 1500–3000 kcal⋅mol−1, depending on the windows. Considering that the denominator of , , varies from 7 to 8 Å, the effective force constants acting on were 30–40 kcal⋅mol−1⋅Å−2. The initial configurations were taken from the classical MD simulations, which were described in the Supporting Material, and both E113 and E203 were set to be deprotonated. A water molecule located between E113 and E203 was converted to a hydronium, by adding a hydrogen atom to water oxygen. Then, the system was further equilibrated for 1 ns using the multistate empirical valence bond (MS-EVB) model (40, 41), ver. 3.1 (29). The simulation was performed with the RAPTOR software (42), interfaced with the LAMMPS MD package (http://lammps.sandia.gov) (43), and the harmonic potential was controlled by the PLUMED package (44).
The initial configurations for each window in the QM/MM umbrella sampling were taken from the final configurations of the 1 ns MS-EVB equilibration. The QM atoms were treated with the density functional theory (DFT) BLYP-D3/TZV2P level of theory (45, 46, 47) including the Grimme dispersion correction (48). The QM region included Cl–cen if present, the water molecules in the central region, and the side chains of residues E113, E148, E203, Y445, and S107 for the WT system. Y445 and S107 were included in the QM region because their side-chain OH groups are coordinated to Cl–cen. The waters within two solvation shells of E113 and E203 were also included in the QM region. The QM box size was set to be 20–30 Å in each dimension to ensure it was 6–8 Å larger than the size of the QM atoms. A quadratic confining wall potential was used to restrain the QM atoms within the QM box, with the wall skin thickness being 1 × 1 × 2 Å. The QM box size was chosen such that the quadratic wall potential did not affect the QM atoms for the vast majority of the simulation. The Gaussian expansion of the electrostatic potential scheme was used to treat the QM/MM electrostatic coupling with periodic boundary conditions (49, 50), and the spurious QM/QM periodic image interactions were decoupled following the method developed by Blochl (51). The chemical bonds that crossed the QM/MM boundary were capped with hydrogen atoms, the forces on which were calculated following the IMOMM scheme with a scaling factor of 1.50 (52). Otherwise, the QM setup was consistent with previous QM/MM umbrella sampling of PT in the influenza A M2 channel (53). The temperature was set to 300 K and controlled by a Nosé-Hoover thermostat (54). The QM/MM umbrella sampling was performed with the CP2K software package (55). All windows were equilibrated for 5 ps, followed by 20-ps production runs. The value of was collected every time step (0.5 fs). The PMF was constructed with the WHAM method (56).
The MS-RMD model configuration
The MS-RMD models were constructed for Gluin and Gluex in WT ClC, and for K203 and Gluex in the E203K mutant. Detailed procedures of the MS-RMD force-matching of QM/MM data have been described in previous studies, where the models were developed for describing the deprotonation reaction of Glu and Asp in aqueous solution (29) as well as in protein environments (30). The model parameters from that work were refit in this study to the QM/MM data calculated in protein environment. There were two different system setups in total for the WT, as well as depending on the presence of Cl–cen, four setups for E203K mutant, depending on the presence of Cl–cen and the protonation state of E202. The E202 residue was set to be deprotonated in the WT. For each system setup, two sets of umbrella sampling were performed from either E148 or E203 (K203 in E203K) to sample configurations for generating QM/MM force data. The harmonic potential with a force constant of 20 kcal⋅mol−1⋅Å−2 was applied to the CV, . The X in the previous expression is either E148 or E203 (or K203) for each set. The vector in E203K was defined as the center of mass of the nitrogen atom in the terminal ζ-position (NZ in the PDB) and the ε-carbon atom (CE in the PDB) in Lys. For each set the centers of the windows ranged from 2.0 to 4.0 Å, and were separated by 0.25 Å between adjacent windows. Approximately one-thousand configurations were evenly sampled for the CV in all ranges. Each configuration was selected with a 2 ps interval. For each configuration, a single point energy calculation was performed with the CP2K software to calculate the QM/MM forces on the atoms in the QM region. To avoid the boundary issues, more waters were included in the QM region, which were selected within the third solvation shell from E148 and E203 (or K203). The side chains of S107, E113, E148, E202, E203 (or K203), and Y445 were included in the QM region. Other simulation details were kept as the same with the QM/MM umbrella sampling. The MS-RMD force field was fit to the QM/MM reference forces by using the previously described force-fitting algorithm (29). Parameters for E148 and E203 in WT, and E148 and K203 in the E203K mutant, are given in Table S2.
The MS-RMD umbrella sampling
Four sets of the 2D PMFs were calculated in the WT, two for each of the Cl–cen present and absent cases, and two for each of two different sets of CVs. The two sets of CVs were defined as follows. In the first set, CV1 is the difference in the two distances from the CEC to the center of mass of the carboxyl group of either of E148 or E203, ; and CV2 is the distance between the center of mass of the carboxyl groups of two residues, . The vector in the MS-RMD umbrella sampling was defined by Eq. 1, using all water hydrogens for , and water oxygens and glutamic acid carboxyl oxygens for . The collective variable CV1 represents the migration of the excess proton from E203 to E148. The collective variable CV2 represents the rotation of E148 and E203, where it decreases as the side chains of the two residues rotate and face toward each other. In the second set of 2D PMFs, CV1 is the distance of the CEC along the pathway sampled from metadynamics, (described below), which represents PT, and CV2 is the water density, , for hydration of the central region.
The CV for water density (the effective number of water molecules in the central region) is defined as (57)
| (4) |
where is total number of the water molecules and is the occupancy of the ith water molecule in a defined rectangular box, given by
| (5) |
and is defined as
| (6) |
where is the position of the center of the box, which is chosen to be the midpoint between the center of mass of each of the carboxyl groups of E148 and E203, and values are the position of the oxygen atom of ith water molecule. The central axis of the box is aligned with the vector connecting the center of mass of the carboxyl group of E148 to that of E203. The distance d was chosen to be 5 Å. The parameters bx, by, and bz were set to be 3, 3, and 6 Å in the system for Cl–cen present, and 2, 2, and 5 Å in the system with Cl–cen absent, respectively. The size of the box is bigger in the case of Cl–cen present, because the side chain of E148 rotates up due to the hindrance by Cl–cen located between E148 and Y445 OH group, and the distance between E148 and E203 becomes longer. The boundary of the box was determined to avoid counting the waters outside the central region.
Metadynamics (MetaD) (58) simulations were used to determine the curvilinear CEC pathway (59), where CV1 in the second set of PMF calculations is defined as the distance along the pathway. The initial configurations for the MetaD simulations were taken from the classical MD simulations, where a continuous hydrogen-bond network formed in each system setup. The protonation states of the residues in the central region in the initial configurations are E148(0)E203(H) in the WT, and E148(0)K203(H) in E203K mutant. Note that 0 in the parentheses denotes the side chain is in the deprotonated state, and H for the protonated state. A Gaussian MetaD potential was added for the z coordinate of the CEC every 1 ps. The Gaussian height was set to be 0.2 kcal/mol. The wall potentials (half-sided harmonic potential) were added to the boundary of the central region, acting on the CEC when its z coordinate is located 2 Å above from the center of mass of the side chain of E148, or 2 Å below from E203, to prevent sampling the CEC outside of the central region. The MetaD was performed for each system setup, until the CEC moves between E148 and E203 (or K203) two to three times. The coordinate of the CEC was recorded every time step. The x and the y coordinates of the CEC were averaged with each 0.25 Å interval in the z coordinate. The CEC pathway (CV1 in the second set) is defined as a three-dimensional curvilinear path connecting the averaged points. In the umbrella sampling, the harmonic potential was applied to the tangent vector defined at the window center on the CEC pathway.
The 2D PMFs from the MS-RMD simulations were calculated by umbrella sampling. The force constants of the harmonic potentials in the umbrella sampling were set to be 30 and 5 kcal⋅mol−1⋅Å−2 for CV1 and CV2 of the first set, and 15 kcal⋅mol−1⋅Å−2 and 15 kcal⋅mol−1 for CV1 and CV2 of the second set, respectively. All windows had an equilibrium time of 100 ps after the harmonic potential is applied, and production sampling of ∼1 ns. For the E203K mutant, the one-dimensional PMF was calculated for the proton pathway sampled from the MetaD for each system setup. The PMF was constructed by the WHAM method. Statistical errors in the PMFs were estimated using the block average method by dividing each trajectory into four consecutive blocks. The average error in the PMF calculated in this way is ∼0.8 kcal⋅mol−1.
Committor analysis (60) was performed to check the appropriateness of the chosen CVs as reaction coordinates. A total of 10 configurations were captured from the windows at the top of the free energy barrier in the PMFs. Each configuration was spaced by 20 ps. The velocities of all atoms were randomized again for 300 K, following the Maxwell-Boltzmann distribution, and the bias potential from the umbrella sampling was released. The unconstrained committor simulations were performed from each configuration, until the system reached either the E148(0)E203(H) or E148(H)E203(0) state.
Proton transport rate constants
The minimum free energy path in the 2D PMF was calculated by using the string method (61). The rate for PT from E203 to E148 was then estimated by using transition state theory between the two states as follows (62):
| (7) |
where kB is Boltzmann’s constant; T is the temperature (300 K); and is the free energy barrier height along the minimum free energy path. The fundamental frequency is that of the reactant state oscillations around its minimum, which is defined as
| (8) |
where r is the local minimum in the PMFs for the protonated E203 (or K203). The effective mass of the excess proton CEC, , was determined using the equipartition theorem, , where the value of was calculated from the MS-RMD trajectory sampled at r. When calculating in the 2D PMFs, v is defined as , where is the displacement of the trajectory (CV1, CV2), projected onto the tangent vector of the lowest free energy path at r; and is the time step in the trajectory.
Results and Discussion
Proton transport from E113 to Gluin (E203)
The side chains of E113 and E203 are close together in the crystal structure, with their respective side-chain O atoms only 2.5 Å apart. Faraldo-Gómez and Roux (32) calculated the pKa of these residues using the Poisson-Boltzmann equation. Their results suggested that in the crystal structure (PDB: 1OTS) E113 is protonated, but shares a hydrogen bond with E203 such that the two residues share the excess proton. Additionally, experiments on the E113Q mutant provide indirect evidence of a coupling between the protonation states of E113 and E203, as the H+ permeation rate of this mutant is seven times lower than that of the WT (27). This presumably occurs because the electrically neutral Q113 suppresses the proton affinity of E203 (34). Importantly, the possibility that the excess proton is shared between E113 and E203 has not been explored in previous studies using nonreactive classical MD (24, 26, 63, 64) because the residues were simulated in fixed protonation states.
To assess the preferred location of the excess proton before PT from Gluin to Gluex, we calculated the PMF for the migration of the excess proton from E113 to E203 with DFT-based QM/MM umbrella sampling. The CV used in this PMF is defined in Eq. 3. As shown in Fig. 2, a shared excess proton between E113 and E203 is not the dominant state; it is ∼5 kcal/mol less stable than either protonated E113 () or protonated E203 (), regardless of the presence or absence of Cl–cen.. The PMF also shows that PT from E113 to E203 is slightly favored (by ∼1–2 kcal/mol). Given their similar proton affinities and the low barrier for PT between the two residues, it is possible that E113 plays a direct role in proton uptake (e.g., delivering the proton to E203 in the WT protein or in place of it in E203 mutants). Fig. S1 shows representative structures for when the excess proton resides on E113 or E203, and compares them with the crystal structure. When E203 is deprotonated, it forms a salt bridge with the positively charged R28 of the other monomer. This interaction is present in the crystal structure, indicating that E203 is likely deprotonated, which is consistent with previous calculations (32). As E203 is protonated, R28 breaks its salt bridge with E203 and moves closer to E113. The movement of R28 due to the protonation of E203 also has been reported in other computational work (63). These combined results suggest that ClC-ec1 evolves from E113(H)E203(0), as captured in the crystal structure, to E113(0)E203(H) before PT from E203 to E148. Thus, the proton was localized on E203, as opposed to being shared between E113 and E203, in the starting structure for our analysis of PT between E203 and E148.
Figure 2.
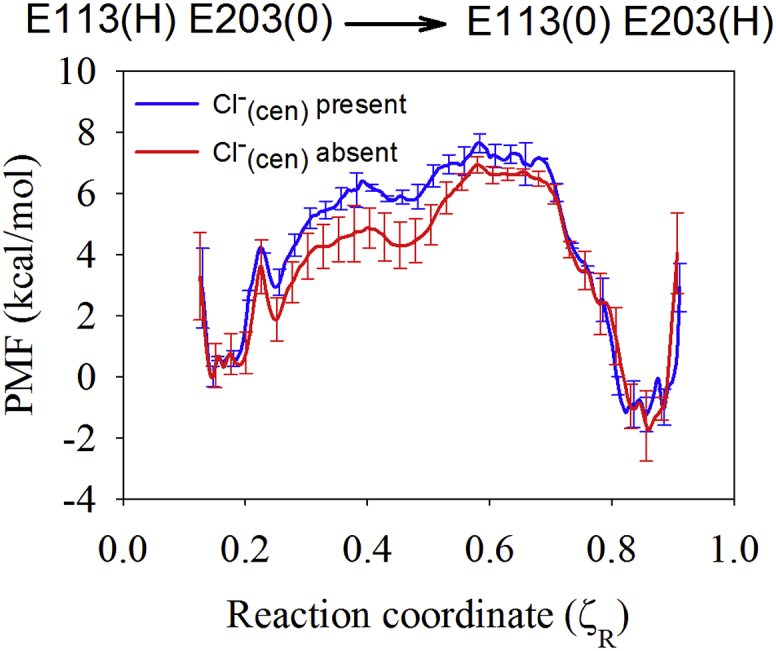
The PMF for PT from E113 to E203, calculated with the QM/MM umbrella sampling, when Cl–cen is present (blue) and absent (red). To see this figure in color, go online.
Hydration of the central region
The hydration state of the central region has been previously examined in a series of computational studies. Kuang et al. (31) predicted positions of three water molecules using the DOWSER program (65), which places waters in empty cavities of static structures given a favorable interaction energy between the water and the surrounding protein. E203 and E148 were not directly connected by the hydrogen-bonded network of these waters, but through the hydroxyl group of Y445 and Cl–cen. However, experiments demonstrated that proton permeation was conserved in Y445F mutant, suggesting that proton permeation does not necessitate the hydroxyl group (66). In a later study (67), four water positions connecting E203 and E148 were predicted by DOWSER, although their stability was never validated with MD simulations.
Several studies have used MD to evaluate the hydration of the central region, though none have focused on the protonation state most relevant to PT that is studied herein—namely E113(0)E203(H)E148(0). In our previous work, an MD simulation of E203(0)E148(0) demonstrated that some number of waters remained stable for 1.4–3.7 ns (24). Ko and Jo (63) simulated E203(H)E148(H) and found that water spontaneously entered the central region from the intracellular bulk when Cl–cen was absent and remained stable for ∼8 ns. Han et al. (26) observed the formation of transient water wire in the central region in their MD simulations, but for the E203(0)E148(0) state with Cl–cen present.
Herein, classical MD was performed for the protonation states most relevant to PT: E113(0)E203(H)E148(0) in WT and E113(0)K203(H)E148(0) in the E203K mutant. We found that a continuous hydrogen-bonded network can form in both the presence and absence of Cl–cen, but that it forms infrequently and its stability is transient (Fig. S2). As discussed below, hydration of the central region is thermodynamically uphill when E203 (or K203) is protonated and E148 is deprotonated, which is consistent with the rare hydration observed in previous MD simulations (26, 63). However, as discussed in Coupling to Hydration Changes, below, water molecules in the central region are stabilized by the entry of the excess proton to the first solvation shell above E148. Thus, the hydration stability changes significantly as the excess proton enters this region because the two processes are coupled.
Proton transport from Gluin (E203) to Gluex (E148)
Mechanistic predictions from experiment
The mechanism of the PT from Gluin to Gluex has been hypothesized based on experimental findings. Feng et al. (28) observed that the crystal structures from E. coli (ClC-ec1) and its eukaryotic homolog (cmClC) are different around the central region. They hypothesized that the two conformations capture different intermediate states, and proposed a mechanism in which Gluex moves from Sext to Scen in association with the movement of Cl– ions from Scen and Sint to the intracellular side. Thereafter, Gluex (still at Scen) receives a proton from Gluin. Hence, PT from Gluin to Gluex occurs with Cl–cen absent. A later study (35) showed that, although the E148A mutant is itself not H+-conducting, its proton conductivity recovers upon addition of a carboxylate-containing substrate as an analog for E148, even in the absence of Cl– ions. In an E148A crystal structure containing this substrate, the substrate’s carboxyl group is bound to Scen, displacing Cl–cen. These findings further suggest that PT in the central region from Gluin to Gluex can occur in the absence of Cl–cen.
Miller and Nguitragool (13) proposed a different mechanism wherein PT from Gluin to Gluex occurs with Cl–cen present and Gluex in position between Sext and Scen. They showed that the Cl–/H+ coupling of the WT and various Y445 mutants are correlated with the presence of an anion at Scen in the crystal structures (66). When Br–, which is a substitute for Cl– in the preparation of the crystal structure, is replaced by SeCN–, the protein could transport SeCN–, but H+ permeation was blocked. The corresponding crystal structures displayed no SeCN– density at Scen, suggesting the importance of an anion in this position for H+ permeation (68). It is important to recognize, however, that the observed coupling between H+ transport and an anion at Scen could occur somewhere other than the PT between Gluin and Gluex (e.g., during proton uptake or release). Indeed, Lim et al. (34) have also suggested that it is proton uptake that is rate-limiting for proton permeation. Nevertheless, these two proposed mechanisms (13, 35) differ in whether Cl–cen is present during PT from Gluin to Gluex. Interestingly, our MS-RMD simulations reported below show that PT can happen in either the presence or absence of Cl–cen, although the former has a kinetically faster rate.
MS-RMD simulation results
To examine the Cl–/H+ coupling using a computational approach, Zhang and Voth (25) calculated the PMF for PT from Gluin to Gluex using an older MS-EVB model, and showed that the free energy barrier for PT is decreased by Cl–cen. In this work, the free energy profile for PT from Gluin to Gluex is recalculated with more realistic initial configurations and more accurate and extensive MS-RMD simulations, such that the coupling between PT and the conformational changes of Gluin and Gluex as well as the hydration of the central region, can be explicitly characterized. The new initial configurations include the full dimer of the protein in the membrane, explicit waters, ions, and an equilibrium distribution of hydrogen-bonded water networks in the central region. The MS-RMD model (42, 69) was developed based on the MS-EVB framework, which has been employed to model proton dynamics in aqueous systems with high efficiency and accuracy (40, 41) and fit to high-level QM/MM data (see Materials and Methods). With this MS-RMD approach, mechanistically revealing 2D PMFs using two different sets of CVs (described in Materials and Methods) could be calculated both in the presence and the absence of Cl–cen. In turn, the minimum free energy path along the 2D PMFs could be obtained with the string method, which finds the most likely collective path (and the lowest free energy barrier) between the protonated Gluin and Gluex minima in the 2D PMF.
In addition, the committor probability (60) could be calculated to verify that the chosen CVs are representative of the correct reaction coordinate for PT from Gluin to Gluex. As described earlier in Materials and Methods, by starting from the configurations captured at the top of the free energy barrier in each PMF, unconstrained simulations were initiated with randomized velocities. Demonstrating that half of these trajectories proceed to reactant (Gluin protonated) and half to product (Gluex protonated) (Table S1) verifies that the free energy barriers in the presented PMFs represent a good transition state of the reaction. This analysis is often overlooked and is critical because relative distance coordinates (e.g., Eq. 3 for PT from Gluin to Gluex) can force the system to sample a more limited configuration space that is not reflective of the unconstrained reaction.
Coupling to conformational changes
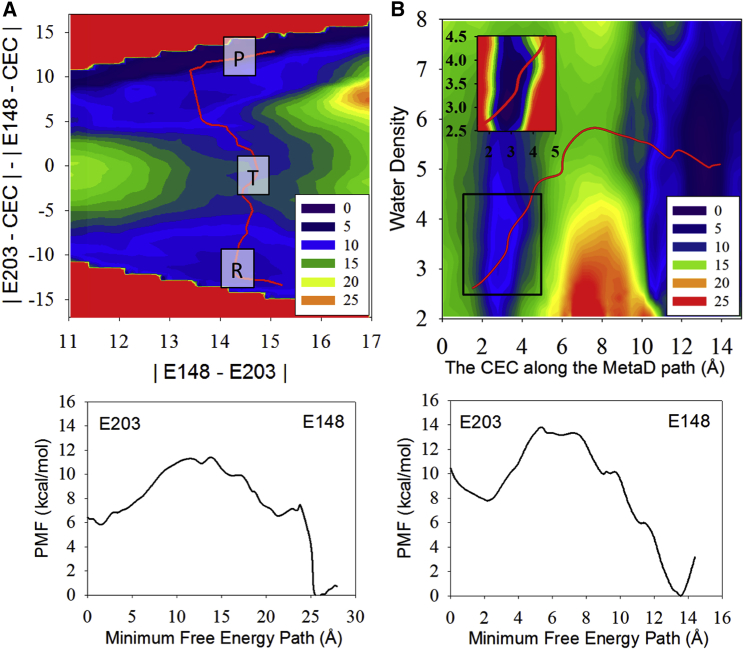
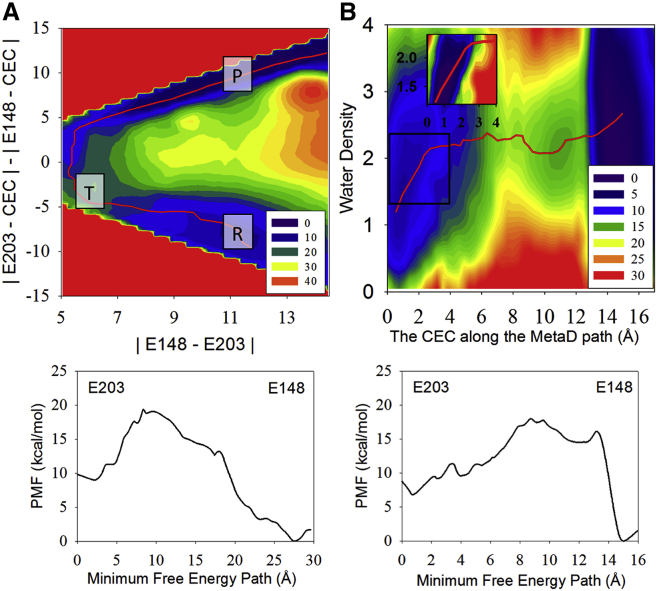
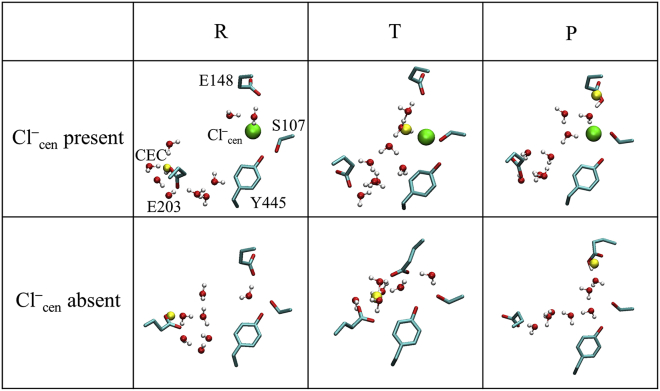
Figs. 3 A and 4 A show the coupling between PT from Gluin to Gluex and the interresidue distance. When Cl–cen is present this interresidue distance (CV1) does not change significantly, primarily because Cl–cen blocks the downward rotation of E148. However, when Cl–cen is absent the distance between the donor (E203) and acceptor (E148) changes significantly as the proton is transferred; similar to a heavy-light-heavy reaction, the interresidue distance (CV1, the horizontal axis coordinate in Fig. 4 A) decreases in the transition region when the excess proton is in between the residues, but lengthens in the reactant and product minima when either residue is protonated. The one-dimensional PMF along the minimum free energy path in each 2D PMF at the bottom of Figs. 3 and 4 show that PT from Gluin to Gluex is downhill process, in both the presence and the absence of Cl–cen. This may seem to contradict previous calculations of the pKa value of E148 in the crystal structure (32). However, the solvation environment that enables protonation of E148 changes significantly during the PT process (further described below) from that found in the crystal structure. Fig. 5 shows representative structures for the excess proton on E203 (R for reactant), in between E203 and E148 (T for transition), and on E148 (P for product). They show how the downward rotation of E148 is hindered by Cl–cen (Fig. 5 T, top), but possible when Cl–cen is absent, such that E148 rotates down and the E203 and E148 side chains face each other (Fig. 5 T, bottom). This downward orientation is also stable for state P, when E148 is protonated. We do not observe a stable, direct interaction between the excess proton and Cl– (forming HCl), as suggested in a previous experimental study (68). Instead the proton passes through water molecules. Because the protonation of Cl– was not included in our MS-RMD model, this conclusion was verified by the same finding in our DFT-level QM/MM PMF of the same system (30), where QM atoms in the central region, including Cl–cen, are all reactive. Nevertheless, the barrier for PT is decreased by ∼4 kcal/mol in the presence of Cl–cen, indicating that Cl–cen does, as expected, facilitate the deprotonation of E203 by stabilizing the excess proton in the central region.
Figure 3.
The 2D PMFs of WT, with Cl–cen present, calculated with MS-RMD. For (A), CV1 (the horizontal axis) is defined as the distance between E148 and E203, and CV2 (the vertical axis) is the difference in the two distances from the excess proton CEC to either E148 or E203. For (B), CV1 is the distance of the CEC along the proton pathway sampled by the MetaD, and CV2 is the water density in the central region. The red line on each 2D PMF represents the minimum free energy path for the transition from E203(H) to E148(H). The plot below each 2D PMF is the PMF calculated along that minimum free energy path. The boxes R, T, and P in (A) represent the positions of the reactant, transition state, and product state, respectively. The inset in (B) highlights the free energy in the reactant minimum more clearly with a finer color scale of purple through red corresponding to the PMF range of 7.5–10.5 kcal/mol. To see this figure in color, go online.
Figure 4.
(A and B) The 2D PMFs of WT, with Cl–cen absent and with all other quantities as otherwise described in the caption for Fig. 3. Note the higher water occupancy and degree of dynamical coupling to the proton CEC translocation evident from Fig. 3B, in this case of the Cl–cen present. To see this figure in color, go online.
Figure 5.
Representative configurations of the central region for each of the boxes R, T, and P in the 2D PMFs in Figs. 3A and 4A. (Top) All configurations from 1 ns of MD simulation are first aligned based on α-carbons >15 Å from the central region. Then intact residues and water molecules are overlaid on the average positions of the highlighted protein and water molecules. The positions of the intact residues are averaged over the trajectories, and the water molecules are taken from the last MD frame of each trajectory. (Bottom) The excess proton CEC is represented by a yellow sphere. To see this figure in color, go online.
Coupling to hydration changes
The 2D PMFs in Figs. 3 B and 4 B show that the hydration of the central region is coupled with the migration of the excess proton from Gluin to Gluex. In the reactant state (with the proton on Gluin) water molecules can transiently penetrate the central region, but there is an energetic cost to this process (Figs. 3 B and 4 B), making it infrequent (see Fig. S1). However, once the excess proton enters the first solvation shell of Gluin, more water molecules are pulled in from the intracellular bulk. Thus, the hydration of the central region is stabilized as the proton migrates to E148. Importantly, the presence of a (meta-)stable full water chain between Gluin and Gluex before the proton transfer event of Gluin is not a prerequisite for proton transport. Thus, we find an interesting phenomenon—the dynamic hydration of a hydrophobic space induced by an incoming excess proton, which was recently predicted in an idealized carbon nanotube system (57), but is here, to our knowledge for the first time, observed in a biomolecular system. The coupling between the excess proton motion and the hydration of this region is shown more clearly when Cl–cen is present (Fig. 3 B), due to the increased size of the central region accommodating more water.
Calculated rate constants
The rate constants of PT from E203 to E148 in the presence and absence of Cl–cen were calculated with transition state theory using the minimum free energy paths in Figs. 3 and 4 and reported in Table 1. The PT rate constant is roughly three orders-of-magnitude greater with Cl–cen present. However, in both cases the calculated rate constants are on the order of 0.7–380 μs−1, which is 3–4 orders-of-magnitude greater rate than the experimentally measured values for the H+ permeation (∼0.2–1 ms−1 depending on the Cl concentration gradient and for pH values between 4 and 7) (9, 34). It is critical to note, however, that these experimental values correspond to the complete permeation process, which not only includes the migration of an excess proton from one side of membrane to the other side, but also the associated Cl– migration. Thus, our results suggest that PT through the central region is facilitated by Cl–cen, but that it is also kinetically possible in the presence or absence of Cl–cen (i.e., it is not rate-limiting for H+ permeation in either case). This has indeed been proposed in previous experimental work (34). These results clearly suggest that the requisite Cl–/H+ coupling occurs during proton uptake to, or release from, E203 or E148. This is consistent with an early prediction from Yin et al. (36), who used continuum pKa calculations to show that the pKa of E148 is quite low in the absence of nearby anions.
Table 1.
The Rate Constants for PT in the WT ClC-ec1 and E203K Mutant
| Cl−cen | PMF | k (μs−1) | ΔF‡ (kcal/mol) | |
|---|---|---|---|---|
| WT | Present | Fig. 3A | (3.8 ± 1.8) × 102 | 5.1 |
| Fig. 3B | (6.4 ± 1.5) × 102 | 5.9 | ||
| Absent | Fig. 4A | 0.71 ± 0.25 | 10.2 | |
| Fig. 4B | 0.24 ± 0.09 | 10.9 | ||
| E203K | Present | Fig. 6A | (2.3 ± 0.3) × 102 | 11.4 |
| Fig. 6B | 1.2 ± 0.2 | 9.4 | ||
| Absent | Fig. 6C | (7.0 ± 0.7) × 10−9 | 20.4 | |
| Fig. 6D | (1.9 ± 0.9) × 10−2 | 12.0 |
The rate constants were calculated with transition state theory. Error in the rate constant was estimated using the block average method by calculating the rate constant in four consecutive blocks in the trajectories for each window. The experimental value for proton permeation rate in the WT protein is (1.0 ± 0.1) × 10−3μs−1 (34), while that for E203K is ∼3 times slower (27).
Proton transport in the E203K mutant
Gluin and Gluex are deemed essential to PT because replacement of either residue with a nonprotonatable side chain eliminates H+ transport, but retains Cl– transport (16). However, the chemical identity of Gluin (E203) is more flexible than one might guess. Most protonatable side chains (D, H, K, and R) retain Cl–/H+ exchange while others (C and Y) block H+ transport and significantly inhibit Cl– flow (27).
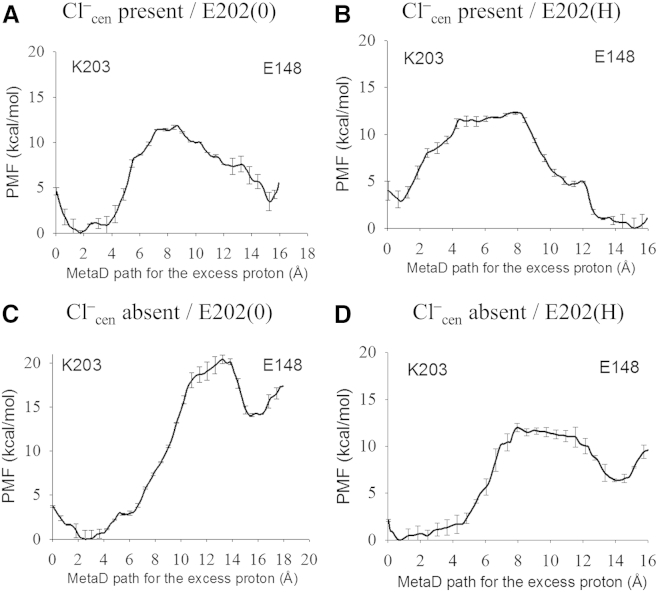
To explore how the replacement of E203 with a basic residue retains Cl–/H+ exchange capacity, we calculated the PMF for PT both in the presence and the absence of Cl–cen in the E203K mutant. The curvilinear pathway for PT from K203 to Gluex was determined with MetaD and the PMFs were calculated with umbrella sampling and force integration of the excess proton CEC along the determined pathways. The resulting PMFs are shown in Fig. 6. The free energy barrier for PT in the WT is decreased in the presence of Cl–cen. However, for the mutant this decrease is more significant both in magnitude and consequence. In the absence of Cl–cen the calculated rate constant (Table 1) is six orders-of-magnitude lower than that of the WT, yet experimentally the rate for H+ permeation is only seven times slower (27). Thus, Fig. 6 C indicates that H+ permeation is not allowed in E203K in the absence of Cl–cen, which is consistent with the decreased coupling observed for the E203K mutant (27). (Note that decreased coupling means fewer H+ ions are exchanged per Cl– ion.) Because the E203K mutant has the additional constraint to proton permeation that Cl–cen must be present, it follows that fewer H+ ions would be transferred from one side of the membrane to the other. This is not the case in the presence of the Cl–cen (Fig. 6 A) because PT is only 10 times lower than for the WT, which is still two orders-of-magnitude greater than the mutant’s lowest rate constant for H+ permeation. Although PT from K203 to E148 is slightly uphill, the thermodynamic cost could be compensated by coupled downhill steps (e.g., proton release going with a proton gradient or Cl– transport). Thus, excluding the participation of other residues (as discussed below), PT from K203 to Gluex is kinetically and thermodynamically possible, but only in the presence of Cl–cen. This may also speak to the overall mechanism of coupled ClC transport, suggesting that in WT the PT typically occurs with Cl–cen present, albeit with the PT not being the rate-limiting step(s) in the transport cycle, as stated earlier.
Figure 6.
The PMFs for PT in E203K mutant with Cl–cen present (A and B) or absent (C and D), and with deprotonated E202 (A and C) or protonated E202 (B and D). The reaction CV is defined as the distance of the excess proton CEC along the proton pathway sampled by the MetaD.
One interesting possibility is that other residues may also play a role in the PT process in the E203K mutant. Following a long equilibration (see Materials and Methods), we found that the side chain of E202, which is deprotonated in the WT, reorients toward K203, decreasing the average distance between the E202 carboxyl group and the K203 ζ-nitrogen (NZ in the PDB) to 4.5 Å (see Fig. S3). However, E202 is more likely to be protonated in E203K than in the WT, because a basic residue (K203) is located nearby. When E202 is protonated, the average distance between the two residues is increased to 10.2 Å. In the WT protein, E202 points away from the PT pathway regardless of its protonation state, such that the average distance between the carboxyl groups of E202 and E203 is 7.0 Å with E202 deprotonated and 6.5 Å with E202 protonated, respectively. Thus, the proton affinity of K203 is likely more influenced by the protonation state of E202 than E203 is in the WT protein.
To further explore the role of E202 in the E203K mutant, PMFs for the protonated E202 system were also calculated. The PMFs in Fig. 6, B and D, show that the free energy barriers for PT are significantly reduced in both the presence and the absence of Cl–cen. The free energy of the final states (protonated Gluex, deprotonated K203) are also decreased, making the PT process thermodynamically favorable in the presence of Cl–cen. The computed rate constants for PT with protonated E202 are both ∼10 μs−1 (Table 1), indicating that, as in the WT, PT through the central region would not be rate-determining for the overall PT process. Thus, it is tempting to conclude that E202 plays either a direct or an indirect role in the central PT process in this mutant. However, these results do not seem to explain the threefold decreased rate of H+ permeation for E203K (27), nor do our calculations account for the cost of protonating two residues (E202 and K203) in the ClC core.
Conclusions
We have performed extensive MS-RMD and QM/MM simulation studies of the PT process through the central region of the WT ClC-ec1 antiporter and its E203K mutant. MS-RMD was shown to offer an accurate and efficient way of sampling the reactive dynamics of an excess proton in this large biomolecular system while accounting for other slow dynamics, such as water movement in the central region, and by capturing longer timescales than are accessible to ab initio MD or QM/MM MD methods.
We first focused on the most likely starting protonation state for PT through the central region, which is an essential step in proton permeation through the protein. A free energy profile of PT between E113 and E203 shows that the proton more likely resides on E203 than being shared between E113 and E203 before transfer to E148. We then turned to the proper starting solvation state for the central region. Although our standard MD simulations suggested that water molecules can transiently enter the region between E203 and E148, their stability is limited. Thus, we turned to a combination of MS-RMD and QM/MM simulations to calculate 2D PMFs that describe not only the stability of hydration in the central region, but also its coupling to PT between E203 (Gluin) and E148 (Gluex). These 2D free energy profiles show that the hydration of the central region is indeed coupled with the proton translocation, such that waters enter this space as the excess proton migrates through it.
Using the Gluin to Gluex interresidue distance as an additional CV, we then calculated 2D free energy profiles to show that, during PT from Gluin to Gluex, the presence of a Cl– ion in the central site (Cl–cen) both blocks the downward rotation of Gluex and reduces the free energy barrier for PT. However, the calculated rate constants for both the Cl–cen present and absent cases are significantly greater than the experimental rate of proton permeation, suggesting that PT through the central region is kinetically possible, and not rate-limiting, in the presence or absence of Cl–cen. This suggests that the experimentally observed coupling between Cl– and H+ transport occurs outside of the central region. For additional comparisons to experiment, future simulations must account for PT in other regions (i.e., from the intracellular side to Gluin and from Gluex to the extracellular side), and the kinetic coupling to Cl– transport must be more explicitly determined. Attention should also be given to the potential role of the recently observed protein conformational changes (9, 10, 11). This work is in progress in our group. Nevertheless, the results presented herein provide an interesting new, to our knowledge, perspective on the story of coupling in the ClC antiporters; that PT from Gluin to Gluex can occur in either the presence or absence of Cl–cen (albeit the former is faster), thus supporting the notion that the requisite coupling between Cl– and H+ transport occurs outside of the central region. Our results neither support nor negate the experimentally suggested mechanisms for this particular PT step in the central region, which differ in the presence of Cl–cen (13, 35).
Lastly, we explored the PT process in the E203K mutant, for which H+ permeation remains intact experimentally despite the substitution of E203 with a basic residue. Our results suggest that PT from K203 to E148 is both kinetically and thermodynamically possible, but only when Cl–cen is present. Additionally, we find that E202 deviates from its position in the WT system, rotating such that it interacts more closely with K203. Although the PMFs and rate calculations show that PT is most favorable when E202 is protonated, this calculation does not account for the cost of protonating two residues in the ClC-ec1 core. Once again, PT through the central region is facilitated by Cl–cen but not expected to be rate-determining in the E203K mutant. These findings add to our understanding of how the ClC-ec1 protein exchanges ions through partially overlapping pathways. Our future efforts will aim to add further insight into our mechanistic understanding of this important antiporter.
Author Contributions
J.M.J.S. and G.A.V. designed the research; S.L. performed the research and analyzed the data with J.M.J.S. and G.A.V.; and S.L., J.M.J.S., and G.A.V. wrote the article.
Acknowledgments
We thank Professor Christopher Miller of Brandeis University for his invaluable input and many helpful comments on this work.
The personnel in this research were supported by the National Institutes of Health (NIH grant No. R01-GM053148). The computational resources in this research were provided in part by the Extreme Science and Engineering Discovery Environment, which is supported by National Science Foundation grant No. ACI-1053575; in part by a grant of computer time from the U.S. Department of Defense High Performance Computing Modernization Program at the Engineer Research and Development Center and Navy Department of Defense Supercomputing Resource Centers; in part by the University of Chicago Research Computing Center; and in part by the National Institutes of Health through resources provided by the Computation Institute and the Biological Sciences Division of the University of Chicago and Argonne National Laboratory, under grant No. 1S10OD018495-01.
Editor: Jose Faraldo-Gomez.
Footnotes
Supporting Materials and Methods, three figures, and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)00159-4.
Supporting Citations
References (70, 71, 72, 73, 74, 75) appear in the Supporting Material.
Supporting Material
References
- 1.Chen T.Y. Structure and function of CLC channels. Annu. Rev. Physiol. 2005;67:809–839. doi: 10.1146/annurev.physiol.67.032003.153012. [DOI] [PubMed] [Google Scholar]
- 2.Estévez R., Jentsch T.J. CLC chloride channels: correlating structure with function. Curr. Opin. Struct. Biol. 2002;12:531–539. doi: 10.1016/s0959-440x(02)00358-5. [DOI] [PubMed] [Google Scholar]
- 3.Jentsch T.J. CLC chloride channels and transporters: from genes to protein structure, pathology and physiology. Crit. Rev. Biochem. Mol. Biol. 2008;43:3–36. doi: 10.1080/10409230701829110. [DOI] [PubMed] [Google Scholar]
- 4.Maduke M., Miller C., Mindell J.A. A decade of CLC chloride channels: structure, mechanism, and many unsettled questions. Annu. Rev. Biophys. Biomol. Struct. 2000;29:411–438. doi: 10.1146/annurev.biophys.29.1.411. [DOI] [PubMed] [Google Scholar]
- 5.Chen T.Y., Hwang T.C. CLC-0 and CFTR: chloride channels evolved from transporters. Physiol. Rev. 2008;88:351–387. doi: 10.1152/physrev.00058.2006. [DOI] [PubMed] [Google Scholar]
- 6.Miller C. ClC chloride channels viewed through a transporter lens. Nature. 2006;440:484–489. doi: 10.1038/nature04713. [DOI] [PubMed] [Google Scholar]
- 7.Picollo A., Xu Y., Accardi A. Synergistic substrate binding determines the stoichiometry of transport of a prokaryotic H+/Cl− exchanger. Nat. Struct. Mol. Biol. 2012;19:525–531. doi: 10.1038/nsmb.2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Khantwal C.M., Abraham S.J., Maduke M. Revealing an outward-facing open conformational state in a CLC Cl/H exchange transporter. eLife. 2016;5:e11189. doi: 10.7554/eLife.11189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Basilio D., Noack K., Accardi A. Conformational changes required for H+/Cl− exchange mediated by a CLC transporter. Nat. Struct. Mol. Biol. 2014;21:456–463. doi: 10.1038/nsmb.2814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bell S.P., Curran P.K., Mindell J.A. Site-directed fluorescence studies of a prokaryotic ClC antiporter. Biochemistry. 2006;45:6773–6782. doi: 10.1021/bi0523815. [DOI] [PubMed] [Google Scholar]
- 11.Elvington S.M., Liu C.W., Maduke M.C. Substrate-driven conformational changes in ClC-ec1 observed by fluorine NMR. EMBO J. 2009;28:3090–3102. doi: 10.1038/emboj.2009.259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Accardi A., Miller C. Secondary active transport mediated by a prokaryotic homologue of ClC Cl− channels. Nature. 2004;427:803–807. doi: 10.1038/nature02314. [DOI] [PubMed] [Google Scholar]
- 13.Miller C., Nguitragool W. A provisional transport mechanism for a chloride channel-type Cl−/H+ exchanger. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2009;364:175–180. doi: 10.1098/rstb.2008.0138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dutzler R., Campbell E.B., MacKinnon R. X-ray structure of a ClC chloride channel at 3.0 Å reveals the molecular basis of anion selectivity. Nature. 2002;415:287–294. doi: 10.1038/415287a. [DOI] [PubMed] [Google Scholar]
- 15.Dutzler R., Campbell E.B., MacKinnon R. Gating the selectivity filter in ClC chloride channels. Science. 2003;300:108–112. doi: 10.1126/science.1082708. [DOI] [PubMed] [Google Scholar]
- 16.Accardi A., Walden M., Miller C. Separate ion pathways in a Cl−/H+ exchanger. J. Gen. Physiol. 2005;126:563–570. doi: 10.1085/jgp.200509417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Jayaram H., Accardi A., Miller C. Ion permeation through a Cl−-selective channel designed from a CLC Cl−/H+ exchanger. Proc. Natl. Acad. Sci. USA. 2008;105:11194–11199. doi: 10.1073/pnas.0804503105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bostick D.L., Berkowitz M.L. Exterior site occupancy infers chloride-induced proton gating in a prokaryotic homolog of the ClC chloride channel. Biophys. J. 2004;87:1686–1696. doi: 10.1529/biophysj.104.042465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gervasio F.L., Parrinello M., Klein M.L. Exploring the gating mechanism in the ClC chloride channel via metadynamics. J. Mol. Biol. 2006;361:390–398. doi: 10.1016/j.jmb.2006.06.034. [DOI] [PubMed] [Google Scholar]
- 20.Cheng M.H., Coalson R.D. Molecular dynamics investigation of Cl− and water transport through a eukaryotic CLC transporter. Biophys. J. 2012;102:1363–1371. doi: 10.1016/j.bpj.2012.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ko Y.J., Jo W.H. Chloride ion conduction without water coordination in the pore of ClC protein. J. Comput. Chem. 2010;31:603–611. doi: 10.1002/jcc.21432. [DOI] [PubMed] [Google Scholar]
- 22.Robertson J.L., Kolmakova-Partensky L., Miller C. Design, function and structure of a monomeric ClC transporter. Nature. 2010;468:844–847. doi: 10.1038/nature09556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Accardi A. Structure and gating of CLC channels and exchangers. J. Physiol. 2015;593:4129–4138. doi: 10.1113/JP270575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang D., Voth G.A. Proton transport pathway in the ClC Cl−/H+ antiporter. Biophys. J. 2009;97:121–131. doi: 10.1016/j.bpj.2009.04.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang Y., Voth G.A. The coupled proton transport in the ClC-ec1 Cl−/H+ antiporter. Biophys. J. 2011;101:L47–L49. doi: 10.1016/j.bpj.2011.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Han W., Cheng R.C., Tajkhorshid E. Water access points and hydration pathways in CLC H+/Cl− transporters. Proc. Natl. Acad. Sci. USA. 2014;111:1819–1824. doi: 10.1073/pnas.1317890111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lim H.H., Miller C. Intracellular proton-transfer mutants in a CLC Cl−/H+ exchanger. J. Gen. Physiol. 2009;133:131–138. doi: 10.1085/jgp.200810112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Feng L., Campbell E.B., MacKinnon R. Structure of a eukaryotic CLC transporter defines an intermediate state in the transport cycle. Science. 2010;330:635–641. doi: 10.1126/science.1195230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nelson J.G., Peng Y., Swanson J.M.J. Multiscale reactive molecular dynamics for absolute pKa predictions and amino acid deprotonation. J. Chem. Theory Comput. 2014;10:2729–2737. doi: 10.1021/ct500250f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee S., Liang R., Swanson J.M.J. Computationally efficient multiscale reactive molecular dynamics to describe amino acid deprotonation in proteins. J. Chem. Theory Comput. 2016;12:879–891. doi: 10.1021/acs.jctc.5b01109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kuang Z., Mahankali U., Beck T.L. Proton pathways and H+/Cl− stoichiometry in bacterial chloride transporters. Proteins. 2007;68:26–33. doi: 10.1002/prot.21441. [DOI] [PubMed] [Google Scholar]
- 32.Faraldo-Gómez J.D., Roux B. Electrostatics of ion stabilization in a ClC chloride channel homologue from Escherichia coli. J. Mol. Biol. 2004;339:981–1000. doi: 10.1016/j.jmb.2004.04.023. [DOI] [PubMed] [Google Scholar]
- 33.Skodje R.T. The adiabatic theory of heavy-light-heavy chemical reactions. Annu. Rev. Phys. Chem. 1993;44:145–172. [Google Scholar]
- 34.Lim H.H., Shane T., Miller C. Intracellular proton access in a Cl−/H+ antiporter. PLoS Biol. 2012;10:e1001441. doi: 10.1371/journal.pbio.1001441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Feng L., Campbell E.B., MacKinnon R. Molecular mechanism of proton transport in CLC Cl−/H+ exchange transporters. Proc. Natl. Acad. Sci. USA. 2012;109:11699–11704. doi: 10.1073/pnas.1205764109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yin J., Kuang Z., Beck T.L. Ion transit pathways and gating in ClC chloride channels. Proteins. 2004;57:414–421. doi: 10.1002/prot.20208. [DOI] [PubMed] [Google Scholar]
- 37.Torrie G.M., Valleau J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. J. Comput. Phys. 1977;23:187–199. [Google Scholar]
- 38.König P.H., Ghosh N., Cui Q. Toward theoretical analysis of long-range proton transfer kinetics in biomolecular pumps. J. Phys. Chem. A. 2006;110:548–563. doi: 10.1021/jp052328q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Riccardi D., König P., Cui Q. “Proton holes” in long-range proton transfer reactions in solution and enzymes: a theoretical analysis. J. Am. Chem. Soc. 2006;128:16302–16311. doi: 10.1021/ja065451j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Swanson J.M.J., Maupin C.M., Voth G.A. Proton solvation and transport in aqueous and biomolecular systems: insights from computer simulations. J. Phys. Chem. B. 2007;111:4300–4314. doi: 10.1021/jp070104x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wu Y., Chen H., Voth G.A. An improved multistate empirical valence bond model for aqueous proton solvation and transport. J. Phys. Chem. B. 2008;112:467–482. doi: 10.1021/jp076658h. [DOI] [PubMed] [Google Scholar]
- 42.Yamashita T., Peng Y., Voth G.A. Computationally efficient multiconfigurational reactive molecular dynamics. J. Chem. Theory Comput. 2012;8:4863–4875. doi: 10.1021/ct3006437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995;117:1–19. [Google Scholar]
- 44.Tribello G.A., Bonomi M., Bussi G. PLUMED 2: new feathers for an old bird. Comput. Phys. Commun. 2014;185:604–613. [Google Scholar]
- 45.Becke A.D. Density functional exchange energy approximation with correct asymptotic behavior. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 46.Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 47.Schäfer A., Huber C., Ahlrichs R. Fully optimized contracted Gaussian basis sets of triple ζ valence quality for atoms Li to Kr. J. Chem. Phys. 1994;100:5829–5835. [Google Scholar]
- 48.Grimme S., Antony J., Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 49.Laino T., Mohamed F., Parrinello M. An efficient linear-scaling electrostatic coupling for treating periodic boundary conditions in QM/MM simulations. J. Chem. Theory Comput. 2006;2:1370–1378. doi: 10.1021/ct6001169. [DOI] [PubMed] [Google Scholar]
- 50.Laino T., Mohamed F., Parrinello M. An efficient real space multigrid OM/MM electrostatic coupling. J. Chem. Theory Comput. 2005;1:1176–1184. doi: 10.1021/ct050123f. [DOI] [PubMed] [Google Scholar]
- 51.Blochl P.E. Electrostatic decoupling of periodic images of plane-wave-expanded densities and derived atomic point charges. J. Chem. Phys. 1995;103:7422–7428. [Google Scholar]
- 52.Maseras F., Morokuma K. IMOMM—a new integrated ab-initio plus molecular mechanics geometry optimization scheme of equilibrium structures and transition-states. J. Comput. Chem. 1995;16:1170–1179. [Google Scholar]
- 53.Liang R., Li H., Voth G.A. Multiscale simulation reveals a multifaceted mechanism of proton permeation through the influenza A M2 proton channel. Proc. Natl. Acad. Sci. USA. 2014;111:9396–9401. doi: 10.1073/pnas.1401997111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Nosé S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984;81:511–519. [Google Scholar]
- 55.VandeVondele J., Krack M., Hutter J. Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005;167:103–128. [Google Scholar]
- 56.Kumar S., Rosenberg J.M., Kollman P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 57.Peng Y., Swanson J.M.J., Voth G.A. Hydrated excess protons can create their own water wires. J. Phys. Chem. B. 2015;119:9212–9218. doi: 10.1021/jp5095118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Laio A., Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA. 2002;99:12562–12566. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhang Y., Voth G.A. A combined metadynamics and umbrella sampling method for the calculation of ion permeation free energy profiles. J. Chem. Theory Comput. 2011;7:2277–2283. doi: 10.1021/ct200100e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Dellago C., Bolhuis P. Transition path sampling simulations of biological systems. In: Reiher M., editor. Atomistic Approaches in Modern Biology. Springer; Berlin, Germany: 2007. pp. 291–317. [Google Scholar]
- 61.E W., Ren W., Vanden-Eijnden E. Simplified and improved string method for computing the minimum energy paths in barrier-crossing events. J. Chem. Phys. 2007;126:164103. doi: 10.1063/1.2720838. [DOI] [PubMed] [Google Scholar]
- 62.Chandler D. Oxford University Press; New York: 1987. Introduction to Modern Statistical Mechanics; pp. 234–270. [Google Scholar]
- 63.Ko Y.J., Jo W.H. Secondary water pore formation for proton transport in a ClC exchanger revealed by an atomistic molecular-dynamics simulation. Biophys. J. 2010;98:2163–2169. doi: 10.1016/j.bpj.2010.01.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Miloshevsky G.V., Hassanein A., Jordan P.C. Antiport mechanism for Cl−/H+ in ClC-ec1 from normal-mode analysis. Biophys. J. 2010;98:999–1008. doi: 10.1016/j.bpj.2009.11.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zhang L., Hermans J. Hydrophilicity of cavities in proteins. Proteins. 1996;24:433–438. doi: 10.1002/(SICI)1097-0134(199604)24:4<433::AID-PROT3>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 66.Accardi A., Lobet S., Dutzler R. Synergism between halide binding and proton transport in a CLC-type exchanger. J. Mol. Biol. 2006;362:691–699. doi: 10.1016/j.jmb.2006.07.081. [DOI] [PubMed] [Google Scholar]
- 67.Kieseritzky G., Knapp E.W. Charge transport in the ClC-type chloride-proton anti-porter from Escherichia coli. J. Biol. Chem. 2011;286:2976–2986. doi: 10.1074/jbc.M110.163246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Nguitragool W., Miller C. Uncoupling of a CLC Cl−/H+ exchange transporter by polyatomic anions. J. Mol. Biol. 2006;362:682–690. doi: 10.1016/j.jmb.2006.07.006. [DOI] [PubMed] [Google Scholar]
- 69.Knight C., Lindberg G.E., Voth G.A. Multiscale reactive molecular dynamics. J. Chem. Phys. 2012;137:22A525. doi: 10.1063/1.4743958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 71.MacKerell A.D., Bashford D., Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 72.Feller S.E., MacKerell A.D. An improved empirical potential energy function for molecular simulations of phospholipids. J. Phys. Chem. B. 2000;104:7510–7515. [Google Scholar]
- 73.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 74.Darden T., York D., Pedersen L. Particle mesh Ewald: an N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 75.Barducci A., Bussi G., Parrinello M. Well-tempered metadynamics: a smoothly converging and tunable free-energy method. Phys. Rev. Lett. 2008;100:020603. doi: 10.1103/PhysRevLett.100.020603. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.