Cross-Disciplinary Network Comparison: Matchmaking Between Hairballs

Abstract

Biological systems are complex. In particular, the interactions between molecular components often form dense networks that, more often than not, are criticized for being inscrutable ‘hairballs’. We argue that one way of untangling these hairballs is through cross-disciplinary network comparison—leveraging advances in other disciplines to obtain new biological insights. In some cases, such comparisons enable the direct transfer of mathematical formalism between disciplines, precisely describing the abstract associations between entities and allowing us to apply a variety of sophisticated formalisms to biology. In cases where the detailed structure of the network does not permit the transfer of complete formalisms between disciplines, comparison of mechanistic interactions in systems for which we have significant day-to-day experience can provide analogies for interpreting relatively more abstruse biological networks. Here, we illustrate how these comparisons benefit the field with a few specific examples related to network growth, organizational hierarchies, and the evolution of adaptive systems.

Introduction

A signature of biology in the “omic” era is the shift of attention away from the isolated interrogation of a few individual molecular components toward more holistic profiling of entire cellular systems (Baker, 2013). Molecular biologists used to studied protein complexes consisting of a few dozen proteins; however, proteomic methods are now able to probe the interactions between thousands of proteins. Similarly, geneticists who would previously manipulate a single gene for functional characterization can now employ high-throughput techniques to study the relationships between all genes in an organism. In many cases, genome-scale information describing how components interact is captured best by a network representation (Barabási and Oltvai, 2004). However, the cellular molecular networks probed by genomics and systems biology are of such great size and complexity that gaining intuition or novel insights about biology is not always easy (Lander, 2010).

What approaches might help in deciphering these network ‘hairballs’? Throughout the history of science, many advances in biology were catalyzed by discoveries in other disciplines. For instance, the maturation of X-ray diffraction facilitated the discovery of the double helix and, subsequently, the characterization of structures containing thousands of proteins. Thus, one may wonder whether ideas in other areas of science could help us with the “hairball challenge.” While the influx of ideas related to reductionism mostly originated from subfields of physics and chemistry, in order to understand biology from a systems perspective we may benefit from new catalysts originating in disciplines as diverse as engineering, behavioral science, and sociology. These new ideas are centered on the concept of the network. In fact, comparisons and analogies are not new to biology. For instance, to illustrate the principles of selection, Dawkins coined the meme, a unit carrying cultural information analogous to the gene in biology that undergoes a similar form of selection (Dawkins, 2006). This comparison has been further elaborated in the proto field of phylomemetics, which concerns itself with phylogenetic analysis of non-genetic data (Howe and Windram, 2011). Nevertheless, comparing a bio-molecular network with a complex network from a disparate field, e.g., sociology, may appear to be comparing apples to oranges. What kinds of comparison can truly deepen our understanding? The key is to find an optimal level of abstraction and simplification.

A spectrum of cellular descriptions

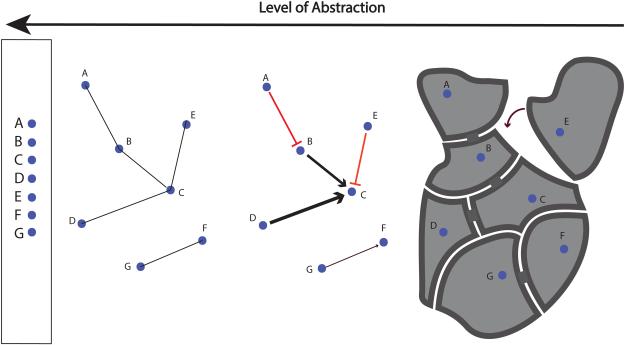
Given the complexity of the cell, a certain level of simplification is necessary for useful discussion. The description of cellular systems can be seen as a spectrum (Figure 1). On one extreme, there is a complete three- or four-dimensional picture of how cellular components and molecules interact in space and time. On the other extreme, there is a simple list of parts that enumerates each component without specifying any relationships. However, neither extreme affords the best understanding for the data we have to hand. The complete 4D picture of all the molecules in a cell is far too ambitious for the current state-of-the-art technology in data acquisition. Conversely, it is widely appreciated that the characteristics of a cellular system cannot be explained by the properties of individual components—the whole is greater than the sum of its parts—and the data we have to hand is considerably richer than the parts list representation. The network representation conveniently spans these extremes, capturing some of the relationships between individual components in a flexible fashion, especially where connectivity rather than exact spatial location determines function.

Figure 1.

A spectrum of cellular descriptions (from left to right). Networks help reveal and convey the relationships between components of a biological system. Different levels of information can be represented using a network. At an abstract level, a network can denote associations between various nodes. More details, such as excitatory and inhibitory regulatory relationships, can then be layered on top of this basic network. As additional information about the nodes and the relationships between them is added, the network begins to resemble the real-world entity it models. For example, the addition of 3D structural information and temporal dynamics onto a network of molecular machine components leads it to more closely resemble the molecular machine itself.

There are two approaches for thinking about networks. In the purest form, a network is an abstract representation of the connections (edges) between constituents (nodes). As physical associations between components in all sorts of complex systems can be viewed as networks, such an abstract approach to networks offers a common mathematical framework for different systems. In a biological context, in addition to physical associations, connections can be defined more loosely by statistical association. This is exemplified by disease networks (Goh et al., 2007; Menche et al., 2015) in which a gene (genotype) and a disease (phenotype) are connected via the statistical association between the existence of genomic variants and the occurrence of the disease. Networks derived from co-expression relationships provide another example (Stuart, 2003). Beyond the biological context, networks have long been used to study other systems. For example, the flow network was used to model and analyze traffic in road systems. In general, a network is a very useful data structure with a wide variety of applications in both biology and other data-intensive disciplines, such as computational social science, in the era of “Big Data.”

The second way of thinking about networks aims to decipher the organization principles behind a complex system. The underlying network is assumed to be a backbone that captures the essence of the system. This is particularly true for networks that capture the mechanistic interactions within systems—for instance, the cellular networks resulting from protein–protein interactions and transcriptional regulation. Thinking about networks in a mechanistic way is a process of concretization, as opposed to the approach in abstract, associative networks. Concrete mechanistic networks aim to get closer to the complete 4D picture. They are intended to describe and integrate many of the physical processes happening inside a living system—for instance, the processing of information, the chemistry of metabolites, and the assembly of molecular machines—and therefore focus on incorporating various details of interactions. Adding further mechanistic detail onto a simple nodes-and-edges skeleton can be visualized as decorating edges with direction, color, thickness, etc. However, incorporating too much detail makes the description intractable. In particular, the network formalism breaks down if we try to load spatial or temporal information as well as higher-order interactions onto the diagram. At a certain point, the actual 4D picture is required.

The two network approaches essentially complement each other. On one hand, thinking in an abstract fashion allows one to transfer mathematical formalism readily between disciplines. This can be beneficial for the biological sciences as it allows the application of formalism developed elsewhere to find fruitful application in biology. On the other hand, thinking mechanistically focuses more on the conceptual resemblances between networks. Comparison of appropriately matched networks may provide additional insight into the interactions between molecular components of cells by examining analogous interactions in complex systems for which we have more day-to-day experience.

Abstract approach: comparison leverages mathematical formalism

Let us first focus on the abstract association approach to biological networks, whose power lies in the simplicity of its formalism. A key point of comparison between various complex systems focuses on topology. The earliest and probably most important observation is that many networks organize themselves into scale-free architectures in which the majority of the nodes contain very few connections, while a few (also called “hubs”) are highly connected (Box 1) (Barabasi and Albert, 1999). A surprising variety of networks exhibit scale-free architecture; for example, the Internet, air transport routes, and many social networks (Barabasi, 2003).

Box 1. Network terminology.

Degree

the number of neighbors of a node.

Scale-free networks

The degree distribution of the network is a statistical property that can be used to understand some of the organizing principles of the network. The degree distribution of a random network is a Poisson distribution. Most real-world networks, including biological networks, are organized in the form of scale-free networks that contain a small number of hubs that are highly connected in the network. The degree distribution in a scale-free network is better modeled as a power-law distribution. Hubs in a scale-free network also lead to the formation of small-world networks.

Betweenness

The number of paths passing a node. Similar in spirit to heavily used bridges, highways, or intersections in transportation networks, a few centrally connected nodes funnel most of the paths between different parts of the network. High-betweenness nodes are referred to as “bottlenecks,” and the removal of these nodes could reduce the efficiency of communication between nodes (Newman, 2001).

Small-world network

A small-world network is a kind of network in which the distance between nodes in the network is much smaller than the size of the network even though most nodes are not connected to one another. Typically, the average distance between any two nodes in a small-world network scales as the logarithm of the number of nodes in the network.

Cliques

Cliques are defined as sub-networks in the graph that are completely connected, i.e., every pair of nodes in a clique contains an edge connecting them. Cliques form a single cohesive group in social networks and such groups tend to act together. Similarly, a clique can be formed from a large biomolecular complex, such as a ribosome, that functions as a single unit. This property of cliques has been used to find missing edges to predict the function of biomolecules.

Modules (community structure of networks)

Most real-world networks can be divided into smaller modules that have a large density of internal edges but relatively fewer edges that connect nodes from different modules. For instance, social networks tend to have communities within them due to the relatively larger number of interactions between people in the same neighborhood, school, or workplace. Similarly, in a biological context, a large number of biological components can form a single functional macromolecular complex, such as the ribosome. A wide variety of methods have been developed to uncover the modular structure of networks. Most of these methods are based on optimizing the modularity of the network that compares the number of intra- and inter-module links within the network.

PageRank algorithm

PageRank is a prominent example of measuring the importance of a node by taking into account the importance of its neighbors. Originally developed in social network analysis (Katz, 1953), PageRank utilizes an algorithm developed to rank relevant documents based on the rank of the websites that link to this document in a self-consistent manner; i.e., being linked to by higher-ranking nodes has a larger impact on the document’s ranking. This algorithm has been applied to food webs to prioritize species that are in danger of extinction (Allesina and Pascual, 2009) and has also been used to rank marker genes and predict clinical outcome for cancers (Winter et al., 2012).

Another important notion is that of a small-world network, in which any two nodes are, on average, separated by only a few steps (Box 1). Scale-free networks are also small-world networks because hubs ensure that the distance between any two nodes is small (Amaral et al., 2000; Watts and Strogatz, 1998). For example, the presence of hubs in the airport network is designed to make it possible to travel between any two cities in the world within a short interval of time. However, not every small-world network is scale-free, an example of which is the mammalian brain—and more specifically, the cerebral cortex. The cortical neuronal network is subdivided into more than 100 distinct, highly modular areas (Essen et al., 2012) that are dominated by connections internal to each area, with only ~20% of all connections being between neurons in different areas (Markov et al., 2013). Each area is considered to have a primary feature, for example, in processing sensory or cognitive signals. The cortical architecture has a high degree of clustering and a small average path length yet exhibits an exponential degree distribution (Modha and Singh, 2010).

The behavior of scale-free networks is dominated by a relatively small number of hubs. While this ensures that such networks are resistant to random, accidental failures, they are still vulnerable to coordinated attacks against the hubs (Albert et al., 2000). One can see analogous examples of this robustness in many contexts: just as the Internet functions without any major disruptions even though hundreds of routers malfunction at any given moment, individuals belonging to the same species in general can tolerate considerable numbers of random mutations. However, a cell is not likely to survive if a hub protein is knocked out. For example, highly connected proteins in the yeast protein–protein interaction network are three times more likely to be essential than proteins with only a small number of links (Jeong et al., 2001).

The number of connections of a node reflects its centrality in the network. There are more elaborate approaches to determining centrality than just counting neighbors, the most famous example of which is the original PageRank algorithm underlying the Google search approach (Box 1). One can also try to define centrality via network paths using such quantities as “betweenness” (Box 1). It has been reported that bottlenecks (nodes with high betweenness) in biological networks are more sensitive to mutations than the rest of the network—even more so than hubs for regulatory networks (Missiuro et al., 2009; Yu et al., 2007). Centrality is a property of an individual node; apart from such individual properties, it is important to define medium-scale structures called “network modules” (Box 1). A quantity dubbed “modularity” attempts to measure this by comparing the number of intra- and inter-module links in a network (Girvan and Newman, 2002).

A broad class of algorithms maps properties or features to the nodes in a network. This is particular true in the biological context (Figure 2) (Saito et al., 2012; V. Liluashvili). Apart from visualization, this mapping provides ways to organize the features. For instance, it has been reported that mapping somatic mutations to gene networks allows for stratification of cancer into subtypes (Hofree et al., 2013). Another important example is the inference of missing data using “guilt by association,” which is the idea that nodes with similar associations in the network tend to have similar properties. In a social context, if your friends in an online social network recommend a particular product, you are more likely to use this product and the advertisements you view online are personalized based on these recommendation systems (Breese et al., 1998). In a biological context, it has been observed that cellular components within the same network module are more closely associated with the same set of phenotypes than components belonging to different modules (Barabasi et al., 2011). As a result, one can infer, or at least hypothesize, the function of a gene or a non-coding element based on its neighbors. The diseases comorbidity network (Anna et al., 2014; Hidalgo et al., 2009; Liu et al., 2014) makes use of a similar idea. In such networks, a node represents a disease and two diseases are connected if they are carried by the same patient as shown in medical claims data. Diseases (phenotypes) that are next to each other in the network may operate similarly on a molecular level.

Figure 2.

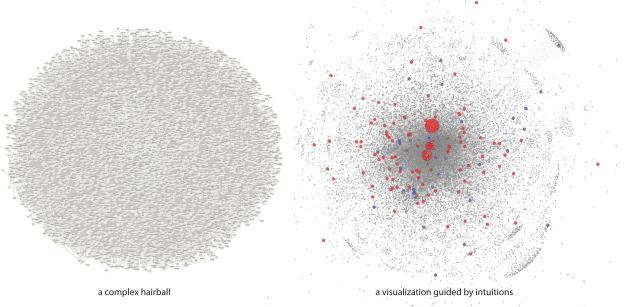
Intuitions guide visualizations of a complex network hairball. A mechanistic network with multiple kinds of edges (protein–protein interactions, metabolic reactions, transcription regulations, etc.) forms an ultimate hairball (left). The hairball is then visualized by scaling the size of nodes by the degree of genes (right). The red nodes are essential and the blue nodes are loss-of-function tolerant. Vaja Liluashvili and Zeynep H Gümüş generated the network layout using iCAVE (V. Liluashvili).

A particular way to utilize genes with special features is based on the concept of “seed” genes, a form of biological prior knowledge, to drive network creation. Instead of identifying central genes based on connectivity; i.e., hub genes, they can be defined in the literature as being causally implicated in a particular disease or phenotype. In one such example, genes implicated through copy number variation in autism were used to cluster an expression network in healthy brain development in order to identify larger sets of putative autism-related genes as candidates for future investigation and diagnosis (Willsey et al., 2013). Such approaches are attractive as they maintain the power and flexibility of a network-based organizational scheme, but are grounded from the start in a particular biological context.

We can further exploit the structure of a network with data on underlying dynamical processes. As mentioned earlier in terms of recommendation systems, online retailers are interested in using purchase records to study how customers influence each other (Domingos and Richardson, 2001). The same question is extremely common in biology, but is discussed using the term “reverse engineering.” For example, how can we infer the developmental gene regulatory network from temporal gene expression dynamics? Ideally, one could fit the relative temporal data using dynamical equations so as to infer the topology. However, cellular processes happen too fast and thus most functional genomics experiments do not contain enough time points. To overcome this drawback, data mining techniques such as matrix factorization are employed. For instance, given the genome-wide expression profile at different time points, one could project the high-dimensional gene expression data to low-dimensional space and write differential equations to model the dynamics of the projections (Wang et al., 2012).

In addition to the actual dynamic processes occurring in a network, one can explore evolutionary change by comparing networks. In a biological context, pairs of orthologous genes (nodes) can be used to define conserved edges, which are called “interologs” and “regulogs” for the protein– protein interaction and regulatory networks, respectively. These can then be used to align networks from different species (Singh et al., 2008) and to detect conserved or specific functional modules (Yan et al., 2014) across species. Based on a large collection of aligned networks between species, a mathematical formalism has been developed to measure the rewiring rate between networks using methods analogous to those used for quantifying sequence evolution. In this context, metabolic networks rewire at a slower rate compared to regulatory ones (Shou et al., 2011).

Criticisms concerning the abstract approach to networks

Despite an increasing number of studies applying networks in an abstract mathematical context, scientific concerns have been raised. A major concern regarding network analysis comes from the criticism that statistical patterns (e.g., the scale-free degree distribution mentioned above) offer limited insights. Other examples of these patterns include the enrichment of network motifs (small recurrent subgraphs in a network). Statistical patterns suggest that network structures are potentially interesting; nevertheless, understanding their actual functioning requires studying the detailed dynamics of each constitutive part (Ingram et al., 2006). While this is a reasonable criticism, such patterns, whether interpretable or not, can often be used as features in machine-learning frameworks for biological and clinical predictions.

More fundamentally, depending on their background, different researchers may have different interpretations of the meaning of “understanding” (Lander, 2010). In the ideal scenario, everyone wants to have a complete mechanistic picture. For perfectionists, in particular, networks have often proved frustrating because their abstract patterns do not always yield easily to precise molecular description. As an illustration, many stress that systems biology is the study of the behavior of complex biological organization and processes in terms of their underlying molecular constituents (Kirschner, 2005). Therefore, it is instructive to employ a mechanistic approach in order to provide a desired mechanistic interpretation.

Mechanistic approach: comparison provides intuition into biological complexity

The previous section discussed insights gained by applying formalisms from various social and technological networks to biological networks. Such wide-ranging insights were possible only because the detailed characterization of the nodes in the network was neglected in the abstract approach. On the other hand, if details are added to the picture, insights about a system become more specific, and in a sense, more meaningful. However, it is typically harder to apply the same formalism equivalently to two different networks characterized in this more detailed fashion. This situation is manifest, for example, when trying to explain the scale-free degree distribution of various networks described above.

Different mechanistic intuition for scale-free structure

It is well known that the scale-free network topology can be derived using two mathematically similar but conceptually different models. The first is the preferential attachment model (Barabasi and Albert, 1999). The scenario can be illustrated by the hub-and-spoke system of the airline network. Every time a new airport is created, the airlines have to balance available resources and customer satisfaction, i.e., the cost of adding a new flight and customer comfort due to connectivity between the new airport and a larger number of other airports. (We acknowledge that this is arguably an idealistic view. Some may argue that airline companies do not care about customer satisfaction at all and instead only care about their revenues. As a result, they consider customer satisfaction only within limits imposed by revenue maximization. Nevertheless, the motivation behind the airlines does not affect the conclusion of the model.) The most efficient use of these limited resources occurs if the new airport connects to pre-existing hubs in the network as this reduces the average travel time to any airport in the entire system due to the small-world nature of scale-free networks. The model is called “preferential attachment” because the newly created nodes prefer to connect to pre-existing hubs in the network.

The second model is duplication–divergence and it explains the evolution and growth of the World Wide Web. Here, a random pre-existing node and its associated edges are duplicated—for example, to make a webpage for a new product listed on Amazon.com, one could use a template shared by an existing product (Evlampiev and Isambert, 2008). After duplication, the content of two nodes and their connections diverge but a proportion of their edges are likely to be shared (Pastor-Satorras et al., 2003). In fact, as its name suggests, the same duplication–divergence mechanism can describe the patterns and occurrence of memes in online media (Simmons et al., 2011). Such a duplication–divergence model is, in a sense, equivalent to the preferential attachment model since it is more likely for a hub to increase its connectivity, simply because it is more likely to be attached to a neighbor that is being duplicated. However, the model provides more intuition for biological networks via comparison. As gene duplication is one of the major mechanisms driving the evolution of protein families, scale-free behavior in the protein–protein interaction network was proposed to arise via duplication–divergence (Vázquez et al., 2003). Of course, no model is perfect. Upon analyzing the structural interfaces involved in protein–protein interactions, one observes that there are differences in hubs that interact with many proteins by reusing the same interface versus those that simultaneously use many different interaction interfaces. The duplication–divergence model only applies to the former situation (with the duplicated protein reusing the same interface as its parent) (Kim et al., 2006).

Thus, many networks that exhibit similar topologies are the result of different underlying growth mechanisms. Specifically, in the case of scale-free networks, there exists a common topological property but a somewhat different mechanistic explanation in different domains (e.g., airline networks vs. gene networks). Some of the domains share the same mechanistic explanation— i.e., the scale-free structure in both protein–protein interaction and web-link networks can be explained by duplication and divergence. Moreover, this latter commonality provides additional intuition about the biological network through comparison to the more commonplace web network, which is conceptually much easier to understand.

More intuition from social networks

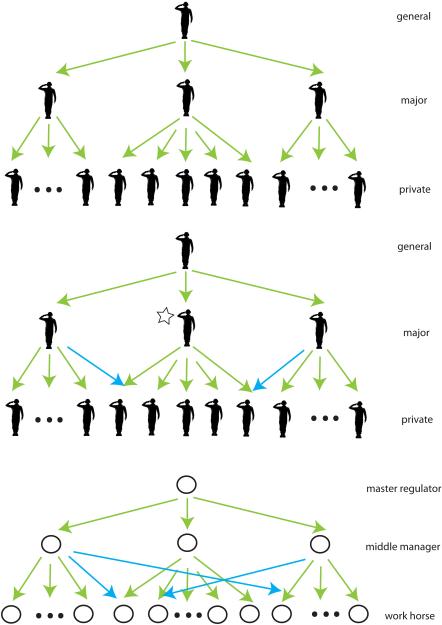
The ability to gain intuition about the often arcane world of molecular biology via comparison to commonplace systems is even more clear-cut when considering social networks, where people have very strong intuition for how a "system" can work. A good example of this is transferring understanding of organizational hierarchy to biology (Figure 3). Many biological networks, such as those involved in transcriptional regulation, have an intrinsic direction of information flow, forming a natural but loose hierarchy (Cosentino Lagomarsino et al., 2007; Ispolatov and Maslov, 2008; Yu and Gerstein, 2006). Likewise, society has many hierarchical structures, examples of which include a military command chain or a corporate "org chart" (Gerstein et al., 2012). In the purest form of a military hierarchy, multiple individuals of lower rank each report to a single individual of a higher rank and there are fewer and fewer individuals on the upper levels, eventually culminating in a single individual commanding an entire army. This structure naturally leads to information flow bottlenecks as all the orders and information related to many low-rank privates must flow through a limited number of mid-level majors. In a biological hierarchy of transcription factors (TFs), one sees a similar pattern, with bottlenecks in the middle. In many cases, such bottlenecks create vulnerabilities (Gerstein et al., 2012). Indeed, knockout experiments have shown that many of the bottleneck nodes in biological networks are essential (Yu et al., 2007). Structurally, hierarchies can insulate themselves from mid-level bottleneck vulnerability by allowing middle managers to co-regulate those under them. This eases information flow bottlenecks in an obvious way: if one major gets knocked out, the privates under them can receive orders through a second major. Moreover, many commentators have pointed out that in order to function smoothly, it is imperative for middle managers to work together in corporate hierarchies (Floyd and Wooldridge, 1992). It is striking that biological regulatory networks employ a similar strategy by having two mid-level TFs co-regulate targets below them, and this degree of co-regulation increases with overall organism complexity (Bhardwaj et al., 2010b). Thus, one can develop an intuition for the reason behind a particular biological structure through analogies to a commonplace social situation.

Figure 3.

Comparison between the hierarchical organizations in social networks versus biological networks illustrates design principles of biological networks. The hierarchical organization in biological networks resembles the chain of command in human society, e.g., in the context of the military. The top panel shows a conventional autocratic military hierarchy. The structure is intrinsically vulnerable in the sense that if a bottleneck agent (star) is disrupted, information propagation breaks down. The introduction of cross-links (blue) avoids the potential problem (middle panel) because the private at the bottom can then take commands from two different superiors above. The bottom panel shows the hierarchical organization of a biological network, with the existence of cross-links between pathways. These observations reflect a democratic hierarchy as opposed to an autocratic organization.

Moreover, further comparison provides easy intuition into the biological characteristics of regulators at different levels in the hierarchy. Conventionally, one expects the CEOs of companies to gather information from all their sources and make the widest-ranging and most influential decisions in the company. One also stereotypically expects people at the top of conventional social hierarchies to be the most “conservative” and resistant to change. Likewise, TFs at the top of the hierarchy tend to be more evolutionarily conserved. They are more connected in the protein–protein interaction network as they modulate gene expression based upon internal and external stimuli through these interactions (Cheng et al., 2011; Yu and Gerstein, 2006), and also more influential in driving gene expression (Erwin and Davidson, 2009). Rewiring the TF network at its upper levels also tends to have a larger effect on cell proliferation and survival (Bhardwaj et al., 2010a).

More intuition from technological systems: connectivity and constraints

The mapping between architecture and function lies at the heart of deciphering biological networks. As it is often hard to define “function” in complex biological settings, comparison with simple technological or engineered components with basic and well-defined functions is particularly insightful (Lim et al., 2013). Sarpeshkar and colleagues have explored the similarities between the biochemical reactions within cells and electron flow in analog circuits. These similarities have enabled the application of intuitive electronic circuit diagrams to describe the processes underlying TF networks. In this analogy, chemical concentrations are represented as electronic currents. For example, mRNA molecules can be thought of as accumulating on a capacitor while a resistor represents mRNA degradation. The analogy extends beyond simply intuitive representations since the mathematical formalisms describing electron flow in subthreshold transistors can be adapted to capture the dynamics of chemical reactions. Thus, this comparison allows us to potentially connect intuitions and mathematical models developed for electronics to transcription (Sarpeshkar, 2014). Similar ideas have been employed to map a transcriptional regulatory pathway to a combination of logic gates (Wang et al., 2015).

While biological networks and technological networks are similar in many respects (Alon, 2003), it is worth noting some of the differences. For example, in biological networks, more connected components (as measured by their degree or betweenness) tend to be under stronger constraint than less connected ones. This is evident in numerous studies that have analyzed the evolutionary rate of genes in many networks (e.g., protein interaction and transcription regulatory networks) in many organisms (e.g., humans, worms, yeast, E. coli) using many different metrics of selection (e.g., variation within a population or dN/dS for fixed differences) (Butland et al., 2005; Fraser et al., 2002; Fraser et al., 2003; Hahn and Kern, 2005). One’s intuition here is obvious: biological systems seek to decentralize functionality, minimizing average connectivity on nodes and making the system robust to a random mutation. However, this architecture requires a few hubs to connect everything and these more connected components are particularly vulnerable. Is this finding true in general? And if not, why? Software systems provide insight into this question: software engineers tend to reuse certain bits of code, leading to the sharing of components between modules and thus arriving at highly connected components (Fortuna et al., 2011). Analysis of the evolution of a canonical software system, the Linux kernel, revealed that the rate of evolution of its functions (routines) is distributed in a bimodal fashion; the more central components, e.g., the hubs, in the underlying network (call graph) are updated often (Yan et al., 2010). In other words, unlike biological networks whose hubs tend to evolve slowly, hubs in the software system evolve rapidly.

The concept of connectivity associated with constraint has many useful applications. In particular, there are many highly conserved genes that are very well connected in physical protein–protein and regulatory networks. Mutations in these genes are more likely to be deleterious, resulting in a loss of function, and it is therefore useful to prioritize these as potential disease drivers (Khurana et al., 2013b). The results are also extremely useful for therapeutics in which a drug targeting a highly connected target can have a very efficient effect on an entire cell, albeit often with the sacrifice of low specificity. However, the measurement of connectivity/constraint depends on the cellular context. In regulatory networks and similar systems involving information transfer, the measurement is often better conceptualized in terms of bottlenecks, while in protein–protein interactions it is often better conceptualized in terms of hubs. An example of a chemically exploitable hub in the regulatory network is the bacterial ribosome, which is the target of most antibiotics that broadly inhibit protein translation leading to the rapid death of the organism (Wilson, 2014). A subtler, but no less useful, route to the inhibition of protein translation is through bottleneck proteins such as mTOR and other key gates in cellular signaling cascades that are actively exploited in therapies for ailments as diverse as breast cancer (Vinayak and Carlson, 2013) and depression (Abelaira et al., 2014). Nevertheless, there is an exception for the observation regarding connectivity versus constraint: in metabolic networks, highly connected hub genes have more duplicated copies. Decentralization is achieved by a pair of duplicates compensating each other and they are generally more tolerant to loss-of-function mutations (Khurana et al., 2013a).

Conclusion

Biology is a subject with a strong tradition of utilizing comparative methods. One hundred years ago, biologists compared the phenotypes of different species. Since the discovery of DNA, biologists have been comparing the sequences of different genes and various “omes” across species. Perhaps we should extend the tradition further by comparing networks in biology to those in other disciplines. In fact, efforts have already been made in this direction (Figure 4). We have described how abstract approaches that focus on simple connections between entities allow the application of mathematical formalisms across disciplines. We then showed how mechanistic details can be placed onto these simple networks, thereby enabling them to better explain a real process, such as transcriptional regulation or software code development. In this case, the networks are often too detailed to allow for direct transfer of formalisms. Nevertheless, one can gain meaningful intuition about a biological system by comparing it to a more commonplace network, such as a social system, using a similar mechanistic description.

Figure 4.

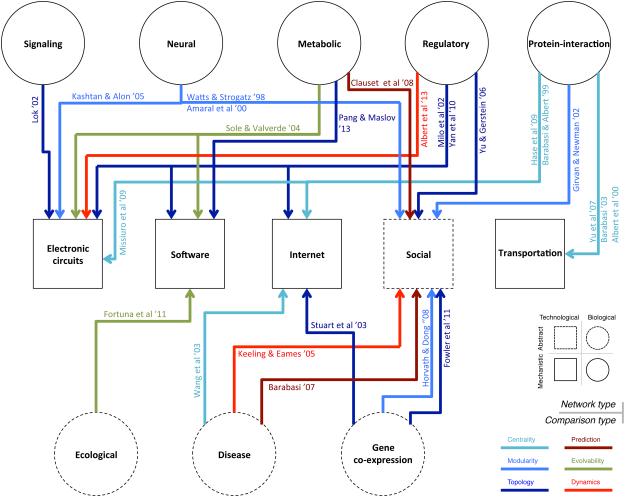
Interdisciplinary network comparison. Many papers have addressed the similarity and difference between biological networks (circle) and networks in social/technological systems (squares) (Albert et al., 2013; Barabasi, 2007; Clauset et al., 2008; Hase et al., 2009; Horvath and Dong, 2008; Kashtan and Alon, 2005; Keeling and Eames, 2005; Lok, 2002; Pang and Maslov, 2013; Solé and Valverde, 2004; Wang et al., 2003). Here we represent all of these comparisons in the form of a network where an edge associated with references represents a network comparison in a specific context (color). Moreover, these comparisons can take place in terms of abstract approaches where formalism is used equivalently in two domains (dotted lines) or mechanistic approaches where one only seeks analogies between disciplines (solid lines).

Seeking comparison between biological networks, social networks, and technological networks may echo the long-time aspiration of finding universality in all complex systems. In particular, the concept of universality has a long tradition in statistical physics literature, and the efforts of characterizing the underlying mechanisms of complex systems by a few scaling or critical exponents has long been an active area of research (Stanley, 1999; Wilson, 1975). The discovery of the scale-free degree distribution in many different networks, including biological networks, initially suggested such a possibility of universality for networks. However, very soon it was counterargued that a universal model does not exist: there are biological networks whose degree distributions do not follow a simple power law (Clauset et al., 2009; Tanaka et al., 2005); there are simply too many ways to generate a network with a broad degree distribution (Keller, 2005; Lima-Mendez and van Helden, 2009; Newman, 2005). Though scale-free distribution is not universal, there are still many open questions that hint at more general properties for biological networks. For example, in terms of building blocks, different network motifs exhibit different occurrence frequencies (Milo et al., 2002). It is quite remarkable that the transcriptional regulatory networks constructed in different cell lines as well as different species exhibit similar patterns (Boyle et al., 2014; Neph et al., 2012). In general, despite a lack of fundamental laws of networks, we believe that one should not be disappointed or simply turn away from network biology.

So then what is next? We envision that these cross-disciplinary network comparisons will become increasingly common as a result of data growth. One area that is especially ripe for comparison is multiplex networks, which concatenate different networks to form a multiplex structure (Holme and Saramaki, 2012; Mucha et al., 2010). This framework is commonly used in social science in which an individual may participate in multiple social circles (e.g., family, friends, and colleagues) or in an online setting, such as Facebook, LinkedIn, and Twitter; however, it has not been explored very well in biology. Nevertheless, the fundamental structure of biological data now extends beyond a single network to multiplex ones: the multiple layers could be formed by different categories of relationships (co-expression, genetic interactions, etc.). Furthermore, biological regulation occurs at multiple levels: transcriptional, post-transcriptional, and post-translational regulation occurs in a manner analogous to a city with electrical networks, water pipes, and phone lines. For example, next-generation sequencing technologies are generating a wide variety of gene regulatory data at various cellular scales, including transcription factor binding (ChIP-seq), RNA-binding proteins (CLIP-seq), histone modifications (ChIP-seq), and DNA methylations. One can thus systematically study gene regulatory mechanisms across cellular scales by integrating these datasets using multi-layer gene regulatory networks. Therefore, we are looking forward to multi-layer network formalisms developed in other contexts being applied to biology.

Apart from leveraging the ideas and methods developed in multiple disciplines through comparison, we can even imagine that comparisons will ultimately lead to real connections (i.e., not analogies) between biological networks and those in other disciplines. For instance, biologists and sociologists have started to investigate if there is any connection between genomics information and sociological information; for example, whether phenotypes or genotypes are correlated in friendship networks (Fowler et al., 2011). In addition, biological, technological, and social systems are not static. They all have dynamics, and thus how to identify the dynamic patterns that distinguish these systems could be an interesting topic in the future. For example, how have the biological mechanisms evolved in biological systems compared with the changes of engineering designs in technological systems?

We focused here on comparing networks across different disciplines in this paper. An individual discipline, however, has its own unique strength. In the future, it would be a promising direction to transfer each discipline’s strength to help understand other disciplines via comparative analysis. For example, one can easily gain intuition in a social network setting. Conversely, one can readily observe the design changes of a technological system and understand the particular mechanistic reasons why these changes are made in terms of engineers’ decisions. Finally, the strength of the biological context is that we can validate testable hypotheses by controlled lab experiments. Thus, abstractly one can imagine a scenario where one generates interesting testable hypotheses based on either studying social or technological networks and then transfers these hypotheses (via network comparison) to a biological setting where they can be validated in a controlled fashion.