Uncovering local trends in genetic effects of multiple phenotypes via functional linear models

Abstract

Recent technological advances equipped researchers with capabilities that go beyond traditional genotyping of loci known to be polymorphic in a general population. Genetic sequences of study participants can now be assessed directly. This capability removed technology-driven bias toward scoring predominantly common polymorphisms and let researchers reveal a wealth of rare and sample-specific variants. While the relative contributions of rare and common polymorphisms to trait variation are being debated, researchers are faced with the need for new statistical tools for simultaneous evaluation of all variants within a region. Several research groups demonstrated flexibility and good statistical power of the functional linear model approach. In this work we extend previous developments to allow inclusion of multiple traits and adjustment for additional covariates. Our functional approach is unique in that it provides a nuanced depiction of effects and interactions for the variables in the model by representing them as curves varying over a genetic region. We demonstrate flexibility and competitive power of our approach by contrasting its performance with commonly used statistical tools and illustrate its potential for discovery and characterization of genetic architecture of complex traits using sequencing data from the Dallas Heart Study.

1 Introduction

Genome-wide association studies (GWAS) have identified numerous risk loci for common complex diseases, and next-generation sequencing based association strategies are now emerging to characterize the contribution of rare genetic variants to human genetic disorders. Analysis of the ‘rare variant - common complex disease’ hypothesis requires tailored statistical methods, as single marker tests fail to uncover these rare variants [Carvajal-Carmona, 2010]. An entirely new powerful class of statistical methods based on non-parametric functions was recently developed for genetic association testing that can accommodate both rare and common variants, or the combination of the two [Fan et al., 2014, 2013; Lee et al., 2014; Luo et al., 2011, 2012a,b; Svishcheva et al., 2015; Vsevolozhskaya et al., 2014; Wang et al., 2015; Zhu and Xiong, 2012]. A comprehensive comparison of non-parametric functional-based methods (FBMs) via simulation studies and real data applications have repeatedly shown that FBMs have a valid type-I error rate and a substantially higher power to detect an association compared with alternative approaches. Additionally, FMBs were proven to be a powerful approach for genetic association studies with longitudinal data [Reimherr et al., 2014], or for the analysis of gene expression data [Storey et al., 2005].

Recently, our research group has demonstrated that within FBMs, functional analysis of variance (FANOVA) attains higher power to detect an association between a genetic region and a dichotomous trait compared to methods based on functional linear models (FLM) [Vsevolozhskaya et al., 2014]. Specifically, we have shown that FANOVA outperforms FLM for small to moderate effect sizes of the variants within a genetic region. Nonetheless, from a practical point of view, FANOVA had a notable limitation in that it was not able to accommodate quantitative traits or adjust for continuous covariates.

In light of these shortcomings, our aim was to extend the existing FANOVA method to association analyses of multiple quantitative and qualitative traits and to accommodate situations in which (1) a gene influences more than one trait (i.e., pleiotropy), (2) where there are confounding/mediation effects (due to population substructure or other sources), and (3) where the effect of disease risk can be modified by a trait or an exposure – a phenomena that we refer hereafter as “Treatment by Trait” (T×T) interaction.

To conceptualize T×T interaction, consider a study of genetic risk factors of substance abuse disorder. It is well known that personality traits like impulsivity and sensation-seeking are highly prevalent in drug-dependent individuals (e.g., [De Wit, 2009]). It is also known that personality traits are substantially influenced by genes (e.g., [Bouchard Jr and Loehlin, 2001]). Suppose there are genetic risk factors that contribute to the increased risk of developing drug addiction among individuals with high trait-impulsivity. Suppose, further, that a different genetic disposition might be involved in the increased risk of developing drug addiction among individuals with low trait-impulsively. Hence, risk alleles for drug-dependence (i.e., ‘treatment’) might vary by the level of personality traits, which will be modeled as T×T interaction in our generalized FANOVA approach – more on this later.

A distinctive contribution of the approach presented here to the emerging field of FBMs for genetic association studies is the introduction of an efficient way to estimate the effects of phenotypes, confounding factors and T×T interactions using continuous curves smoothly varying over genetic loci. Previously proposed functional methods for genetic association studies (e.g., [Fan et al., 2013; Luo et al., 2011, 2012a]) and other methods that combine information across multiple variants within a gene (e.g., [Liu and Leal, 2010; Wu et al., 2011]) aggregate across both the association signals of genetic variants as well as over covariate effects. We exploit the flexibility of the functional approach to unveil a more nuanced blueprint of how covariate and interaction effects vary within a genetic region by estimating partial regression coefficient curves that change over variant positions.

Unlike traditional statistical models that treat a disease phenotype as an outcome (i.e., on the left-hand side of the equation), our model puts non-genetic variables on the right-hand side, including traits, environmental exposures, and confounders. The response function in our model is an allelic dosage curve, fitted through genetic variants within a region. If we start our modeling by including a binary trait such as drug dependence as a single predictor, the continuous regression coefficient will be the difference between average allelic dosages over multiple variants of the two groups. That is, a continuous intercept curve will estimate smoothed average allelic dosage among non drug dependent controls, and a continuous regression coefficient will estimate a deviation from this baseline allelic dosage over multiple variants among drug-dependent cases. Further, if we include personality trait as a covariate, the regression coefficient curve for drug-addiction will be adjusted for personality trait. Finally, if we include a T×T interaction between drug-dependence status and a personality trait, the deviation from the baseline allelic dosage among drug-dependent cases will vary by the level of a personality trait.

Functional models where genetic predictor (X) and the outcome (Y) are swapped in the regression equation are reminiscent of the reverse regression approach [Maddala, 1992]. In general, coefficients of the direct and the reverse regressions are not the same, however the test statistic for the X (adjusted for any covariates) as well as the corresponding partial correlation coefficient remain the same after the swapping. For example, adjustment for confounding or mediation is unaffected and remains valid in the reverse regression approach.

To estimate continuous coefficient curves, our new generalized FANOVA approach utilizes a connection between penalized spline regression and best linear unbiased predictors (BLUPs), enabling a straightforward practical implementation using standard linear mixed models statistical software. A connection between BLUPs and penalized functional regression has been explored in statistical and machine learning literature [Brumback et al., 1999; Crainiceanu et al., 2005; Crainiceanu and Goldsmith, 2010; Eilers and Marx, 1996; Goldsmith et al., 2011; Ivanescu et al., 2014; Lian, 2007; Nosedal-Sanchez et al., 2012; Pearce and Wand, 2006; Ruppert et al., 2003; Wand and Ormerod, 2008; Wang, 1998]. However, this connection has largely been ignored in functional method approaches for genetic association studies.

We provide an illustration of our method using data from the Dallas Heart Study [Romeo et al., 2007], by characterizing associations of sequence variants with plasma triglyceride levels, modified by race and adjusted for sex. In addition to identifying the originally reported association between triglyceride levels and the ANGPTL4 gene, our new FANOVA approach identified specific sub-regions of the ANGPTL4 gene associated with plasma triglyceride levels among European Americans, African Americans, and Hispanics.

2 Methods

2.1 Genotypic functions: a brief overview

In brief, our method is an extension of the previously proposed FANOVA methodology, which seeks to quantify the relationship between scalar phenotypes X₁, X₂, . . . , X_k and smooth genotypic functions G(t)'s, with t indexing a genetic variant's position over a genetic region, t ∈ [0, τ] [Vsevolozhskaya et al., 2014]. By using the term ‘genotypic functions,’ we refer to nonparametric functions fitted with a basis expansion method [Ramsay and Silverman, 2005; Ruppert et al., 2003; Wood, 2006]. Thus, for each subject, the genetic data is not of a discrete (i.e., counted) nature, such as would be the case for genotype frequencies, but rather a single nonparametric genotypic function, G(t), of a continuous nature.

A genotypic function is obtained by either (i) a cubic B-spline basis expansion over a dense set of knots, κ₁, . . . , κ_K, over the range of the variant's genomic positions t_i's (in the one-base coordinate system) or (ii) penalized spline smoothing that avoids the knot selection problem completely (e.g., [Luo et al., 2012a; Vsevolozhskaya et al., 2014]). Earlier investigations of functional linear models designed for genetic association testing include comprehensive coverage of the estimation procedure for the genotypic functions G(t)'s [Fan et al., 2014, 2013; Lee et al., 2014; Luo et al., 2011, 2012a,b; Svishcheva et al., 2015; Vsevolozhskaya et al., 2014; Wang et al., 2015; Zhu and Xiong, 2012].

If we let G₁(t), . . . , G_N(t), t ∈ [0, τ] denote the functional genotypic data for N individuals, and we let X_1i, . . . , X_Pi, i = 1, . . . , N denote a set of P variables that consists of covariates and traits (either quantitative or qualitative) that may contribute to a disease, our model for each individual's genotypic function is:

$$G_i\left(t\right)={\beta }_0\left(t\right)+{\beta }_1\left(t\right)X_{1i}+\cdots +{\beta }_P\left(t\right)X_{Pi}+{ϵ}_i\left(t\right),$$ (1)

where β_i(t)'s are continuous regression coefficients that describe an association between a scalar trait and a set of variants in a genetic region t ∈ [0, τ], and where ε(t) is a residual function. Unlike traditional models where the outcome is regressed on a set of predictors, this model treats genetic information as an outcome. Outside of the functional approach, utility of such “reverse regressions” has been explored previously for analysis of genetic associations [Feng, 2014; Kwan et al., 2011]. While coefficient estimates change, in general, due to swapping of variables between two sides of a regression equation, the partial correlations as well as the test statistics and P-values for the coefficients remain invariant: this follows simply from expressing these quantities in terms of the entries of the inverse of the correlation matrix between all variables including the outcome. Thus, testing for effects or for validity of regression adjustments are preserved under the reversal. There is also convenience in having the same type of outcome (i.e., genetic information) and thus the same type of a link function regardless of the type and the number of other variables in the model. Additionally, within the functional approach, exploration of $\widehat{\beta }\left(t\right)$'s may allow researchers to determine sub-regions of [0, τ] that harbor causal genetic variants (i.e., sub-regions over which $\widehat{\beta }\left(t\right)\ne 0$).

To estimate $\widehat{\beta }\left(t\right)$'s, we place a function-on-scalar regression in Eq. 1 into the context of a mixed-effects model or, more generally, embed the penalized splines problem into the class of reproducing kernel methods. To introduce the method, we first present a case of a single curve estimation, and conclude with the general case that allows us to estimate continuous coefficients of multiple traits, construct their confidence intervals and test for an association. We finally note that in the context of this paper, the word “kernel” should not be confused with a weight function as in the local regression (or local smoothing), which is also called a kernel [Hastie et al., 2009].

2.2 Estimating a single curve

To draw connections between smoothing splines and reproducing kernels, first consider a simpler problem of estimating a single curve from the observed y_i's and t_i's, i = 1, . . . , n. One possible approach to estimating a nonparametric function f(t) from discrete data is to invoke penalized spline smoothing (e.g., [Wahba, 1990]). This smooth interpolation of the data is achieved by minimizing least squares fits with an additional roughness penalty (i.e., penalized sums of squares) as follows:

$$\min \{n^{-1}\sum _{i=1}^n{(y_i-f\left(t_i\right))}^2+\lambda {\int }_0^1{\left[Ly\left(t\right)\right]}^{2}dt\}.$$ (2)

Here, the roughness of a function is quantified by the square of a linear differential operator Ly(t) (a typical choice is Ly(t) = f″(t) that corresponds to penalizing curvature of the function). The constant term, λ, referred to as a smoothing or a tuning parameter, should be either specified by a user or determined through the generalized cross-validation (GCV) [Wood, 2006].

The above minimization problem is analogous to a corresponding regularization problem within the machine learning domain:

$$\underset{f\in \mathcal{H}}{\min }\{\sum _{i=1}^{n}L(y_i,f\left(t_i\right))+\lambda {\Vert Pf\Vert }_{\mathcal{H}}^2\},$$ (3)

where L(y_i, f(t_i)) is a loss function, ∥P f∥² penalizes f in terms of the variability of its function values, and $\mathcal{H}$ is the reproducing kernel Hilbert space (RKHS) of real functions f. The theory of RKHS was developed by Aronszajn [1950] and Saitoh [1988], with good overviews provided by Smola and Schölkopf [1998]; Wahba [1990] and Rasmussen and Williams [2006]. Briefly, a RKHS on ${\mathbb{R}}^d$ is a Hilbert space of real-valued functions generated by a bivariate symmetric, positive definite kernel k(·, ·) with the following properties: (i) for every t in ${\mathbb{R}}^d$, k(t, t′) is a function of t′ in $\mathcal{H}$ and (ii) k has the reproducing property ${\langle k(\cdot ,t_i),f\rangle }_{\mathcal{H}}=f\left(t_i\right)$, where 〈·, ·〉 denotes the inner product. To conceptualize penalized splines in Eq. (2) as BLUPs in a mixed model framework, we explore the solution to the regularization problem in Eq. (3) from the machine learning theory. Based on the results of the representer theorem [Kimeldorf and Wahba, 1971], it can be shown that each minimizer $f\in \mathcal{H}$ of Eq. (3) can be written as a linear combination of kernel functions, as follows:

$$f\left(t\right)=\sum _{i=1}^n{\alpha }_{i}k(t,t_i).$$ (4)

The solution for α = [α₁, . . . , α_n]′ can be obtained as $\widehat{\alpha }={(\mathbf{K}+\lambda {\mathbf{I}}_n)}^{-1}\mathbf{y}$, in which K is then n × n matrix with ijth entry of k(t_i, t_j), I is the n × n identity matrix, nad y is the n × 1 vector of observed y_i's [Hastie et al., 2009; Rasmussen and Williams, 2006]. Further, the vector of n fitted values is given by $\widehat{\mathbf{f}}=\mathit{K}\widehat{\alpha }$. This solution looks very similar to that from a linear regression model (i.e., $\widehat{\mathbf{y}}=\mathbf{T}\widehat{\beta }$ since we used t_i instead x_i in Eqs. (2-3)). Regrettably, this reproducing kernel transformation of t_i's does not simply move our non-linear problem into the ‘friendly’ linear model domain, because the solution for α depends on λ.

A slight variation to the representer theorem can be achieved by decomposing $\mathcal{H}$ into ${\mathcal{H}}_0\oplus {\mathcal{H}}_1$, where ${\mathcal{H}}_0$ is a finite-dimensional null space containing terms which will not be penalized, and ${\mathcal{H}}_1$ is it's orthogonal complement (i.e., penalized terms). For example, for ∥P f∥² defined by differential operators of the form Ly(t) = f^(m)(t), the null space ${\mathcal{H}}_0$ is spanned by polynomials of degree up to m – 1. More specifically, if m = 2, then constant and linear functions are in the null space, because they are not penalized for ‘curvature.’ With the decomposition of $\mathcal{H}$, the minimizer f of the regularization function in Eq. (3) now has the form:

$$f\left(t\right)=\sum _{j=1}^m{d}_j{\varphi }_j\left(t\right)+\sum _{i=1}^n{c}_i{k}_1(t,t_i),$$ (5)

where ϕ₁(t), . . . , ϕ_m(t) form the basis of ${\mathcal{H}}_0$ and k₁(·, ·) is a reproducing kernel that generates ${\mathcal{H}}_1$. If m = 2 as in the example above, then ϕ₁(t) = 1 and ϕ₂(t) = t span the null space of unpenalized functions.

There are relatively few published recommendations in the statistical literature on how to construct k₁(·, ·). For example, Lian [2007] writes “[...] the construction of k₁ in general is difficult and a search of the literature does not seem to provide us with any clues about how to construct a positive definite kernel in general.” Nonetheless, if we shift our attention to the machine learning literature, we see that k₁(t, t_i) = G(t, t_i), where G(t, t_i) is a Green's function of the linear differential operator Ly(t) [Fasshauer, 2012; Fasshauer and Ye, 2013; Poggio and Girosi, 1990; Rasmussen and Williams, 2006]. Note that the Green's function also depends on the boundary conditions. A ‘natural’ choice is the “Natural Boundary Condition” f^(j)(a) = f^(j)(b) = 0, j = 1, . . . , m; where a and b are the boundaries of the functional domain [Green and Silverman, 1993].

How can we estimate the fitted values of the coefficients d̂ and ĉ in Eq. (5) for a specific problem? If we re-write Eq. (5) using linear algebra notations as:

$$\widehat{\mathbf{f}}=\Phi \widehat{\mathbf{d}}+{\mathbf{K}}_1\widehat{\mathbf{c}},$$ (6)

it becomes evident that Eq. (6) represents a solution to the linear mixed-effects model with design matrices Φ and K₁, and d̂ and ĉ estimated as best linear unbiased predictors (BLUPs) from this model [Speed, 1991]. In addition, the BLUP solution for the coefficients is independent of the smoothing parameters λ, which is equal to the ratio of the variances of the residuals and random effects. For numerical stability reasons, the design matrices are specified for a sequence of knots k₁, . . . , k_κ places at sample quantilies over the range of t_i's [Ruppert, 2002] as:

$$\Phi =\left[\begin{array}{cc}\hfill 1\hfill & \hfill t_1\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill t_n\hfill \end{array}\right]\text{and}{\mathbf{K}}_1=\left[\begin{array}{ccc}\hfill {(t_1-k_1)}_{+}\hfill & \hfill \cdots \hfill & \hfill {(t_1-k_{\kappa })}_{+}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {(t_n-k_1)}_{+}\hfill & \hfill \cdots \hfill & \hfill {(t_n-t_{\kappa })}_{+}\hfill \end{array}\right],$$ (7)

where G(t_i, t_j) = (t_i – t_j)₊ is the Green's function of the linear differential operator f⁽²⁾(t), and x₊ = max{0, x}. This specification of the design matrices corresponds to a truncated lines series basis expansion $\widehat{f}\left(t\right)={\widehat{d}}_0+{\widehat{d}}_{1}t+{\sum }_{i=1}^{\kappa }{\widehat{c}}_i{(t-k_i)}_{+}$. Other choices of basis functions can also be used with corresponding changes to penalized terms. Possible choices include, but are not limited to, (a) truncated power basis ${(t-k_i)}_{+}^p$, (b) O'sullivan splines [Wand and Ormerod, 2008], (c) thin plate splines [Ivanescu et al., 2014], or (d) the Gaussian kernel [Lian, 2007].

Some readers might wonder whether the mixed model formulation for penalized splines bear the same parameter interpretation as in a typical application to nested hierarchical data. We should clarify that the functional representation in Eq. (6) is just a convenient way of shifting a non-linear problem into a linear domain, while simultaneously estimating a smoothing parameter. Similarly, the random effects in c, are just a convenience device to model the curvature in f and should not be interpreted as random effects, per se.

2.3 Estimating β(t)'s

With respect to the conceptual model in Eq. (1), continuous regression coefficients can be estimated as follows. For each subject, the genotypic function is evaluated on the grid of genomic positions t₁, . . . , t_n, i.e, Ĝ_i(t) = Ĝ_i(t₁), . . . , Ĝ_i(t_n). For the sequence of knots k₁, . . . , k_κ, each functional regression coefficient is expanded in terms of the linear combination of ϕ's and k₁'s. This expansion yields the following mixed-model representation of Eq. (1):

$$\begin{array}{cc}\hfill {\widehat{G}}_i\left(t\right)& ={\widehat{\beta }}_0\left(t\right)+{\widehat{\beta }}_1\left(t\right)X_{1i}+\cdots +{\widehat{\beta }}_P\left(t\right)X_{Pi}\hfill \\ \hfill & =\underset{{\widehat{\beta }}_0\left(t\right)}{\underbrace{({\widehat{d}}_1+{\widehat{d}}_{2}t+\sum _{i=1}^{\kappa }{k}_1(t,k_i){\widehat{c}}_i)}}\hfill \\ \hfill & +\underset{{\widehat{\beta }}_1\left(t\right)}{({\widehat{d}}_1^{\ast }+{\widehat{d}}_2^{\ast }t+\sum _{i=1}^{\kappa }{k}_1(t,k_i){\widehat{c}}_i^{\ast })}{X}_{1i}+\cdots \hfill \\ \hfill & +\underset{{\widehat{\beta }}_P\left(t\right)}{({{\widehat{d}}^{\prime }}_1+{{\widehat{d}}^{\prime }}_{2}t+\sum _{i=1}^{\kappa }k(t,k_i){{\widehat{c}}^{\prime }}_i)}{X}_{Pi}.\hfill \end{array}$$ (8)

Conceptually, the generalized FANOVA-based regression coefficients, β(t)'s, are similar to the genetic effect coefficients in the recently published paper by Wang et al. [2015]. Specifically, Wang et al. [2015] also proposed to estimate regression coefficients, β_l(t)'s, smoothly varying over the genetic position t. However, unlike the methodology proposed in the present study, their approach can not simultaneously handle quantitative and qualitative traits, adjust coefficients for confounders/mediators over a continuum [0, τ] or modify effects by the level of another trait. With our approach, this adjustments can be easily incorporated into the model.

Suppose we want to adjust the effect of a risk factor X₁ by trait X₂ over all t. The model will be written as:

$${\widehat{G}}_i\left(t\right)={\widehat{\beta }}_0\left(t\right)+{\widehat{\beta }}_1\left(t\right)X_{1i}+{\widehat{\beta }}_2\left(t\right)X_{2i}.$$

Suppose, further, we want to modify the effect of a risk factor X₁ by the level of trait X₂, i.e., model a T×T interaction (for simplicity, assume that X₂ has only two levels). The model can be expressed as:

$${\widehat{G}}_i\left(t\right)={\widehat{\beta }}_0\left(t\right)+{\widehat{\beta }}_1\left(t\right)X_{1i}+{\widehat{\beta }}_2\left(t\right)X_{2i}+{\widehat{\beta }}_{12}\left(t\right)X_{1i}{X}_{2i}.$$

Then, for the first level of X₂, dummy coded as 0, the association between a gene and X₁ will be estimated by ${\widehat{\beta }}_1\left(t\right)$:

$${\widehat{G}}_i\left(t\right)={\widehat{\beta }}_0\left(t\right)+{\widehat{\beta }}_1\left(t\right)X_{1i},$$

and for the second level of X₂, dummy coded as 1, the association between a gene and X₁ will be modified as:

$${\widehat{G}}_i\left(t\right)=({\widehat{\beta }}_0\left(t\right)+{\widehat{\beta }}_2\left(t\right))+({\widehat{\beta }}_1\left(t\right)+{\widehat{\beta }}_{12}\left(t\right))X_{1i}.$$

To facilitate the data analysis using mixed-effects software, an input response should be a vectorized matrix of genotype functions for N subjects evaluated on the grid of genomic positions, $\mathrm{vec}\left(\widehat{\mathbf{G}}\right)=[{\widehat{G}}_1\left(t_1\right),\dots ,{\widehat{G}}_1\left(t_n\right),\dots ,{\widehat{G}}_N\left(t_1\right),\dots ,{\widehat{G}}_N\left(t_n\right)]$. Input predictors should be N ·n×1 vectors X₁, . . . , X_P which are generated by repeating each phenotype observation n times and stacking them on top of one another. The fixed and the random effects design matrices, Φ and K₁, are then constructed as follows:

$$\begin{array}{cc}\hfill \Phi & =\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill t_1\hfill & \hfill X_{11}\hfill & \hfill t_1{X}_{11}\hfill & \hfill \cdots \hfill & \hfill X_{P1}\hfill & \hfill t_1{X}_{P1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill t_n\hfill & \hfill X_{11}\hfill & \hfill t_n{X}_{11}\hfill & \hfill \cdots \hfill & \hfill X_{P1}\hfill & \hfill t_n{X}_{P1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill t_1\hfill & \hfill X_{1N}\hfill & \hfill t_1{X}_{1N}\hfill & \hfill \cdots \hfill & \hfill X_{PN}\hfill & \hfill t_1{X}_{PN}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill t_n\hfill & \hfill X_{1N}\hfill & \hfill t_n{X}_{1N}\hfill & \hfill \cdots \hfill & \hfill X_{PN}\hfill & \hfill t_n{X}_{PN}\hfill \end{array}\right]\hfill \\ \hfill & =\left[1_N\otimes \left[\begin{array}{cc}\hfill 1\hfill & \hfill t_1\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill t_n\hfill \end{array}\right],{\mathbf{X}}_1\otimes \left[\begin{array}{cc}\hfill 1\hfill & \hfill t_1\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill t_n\hfill \end{array}\right],\dots ,{\mathbf{X}}_P\otimes \left[\begin{array}{cc}\hfill 1\hfill & \hfill t_1\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill t_n\hfill \end{array}\right]\right],\hfill \end{array}$$

and ${\mathbf{K}}_1=[1_N\otimes \mathbf{K},{\mathbf{X}}_1\otimes \mathbf{K},\dots ,{\mathbf{X}}_P\otimes \mathbf{K}]$, where 1_N is N × 1 vector of 1's, $\otimes$ is the Kronecker product, and K is the n × κ matrix with the ijth entry of k₁(t_i, k_j) calculated over the sequence of knots k₁, . . . , k_κ.

2.4 Confidence interval for $\widehat{\beta }\left(t\right)$

Since the conceptual model in Eq. (1) can be expressed as a mixed-effects model in Eq. (8), the typical inferential machinery for mixed-effects models can be used to obtain the variance-covariance estimates of the model parameters [Ruppert et al., 2003]. An explicit formulation for the estimated standard deviation of $\widehat{\beta }\left(t\right)$ is:

$$\widehat{\mathrm{st}.\mathrm{dev}}\left(\widehat{\beta }\left(t\right)\right)={\widehat{\sigma }}_{ϵ}\sqrt{\mathbf{C}{({\mathbf{C}}^{\mathsf{T}}\mathbf{C}+\widehat{\lambda }\mathbf{D})}^{-1}{\mathbf{C}}^{\mathsf{T}}\mathbf{C}{({\mathbf{C}}^{\mathsf{T}}\mathbf{C}+\widehat{\lambda }\mathbf{D})}^{-1}{\mathbf{C}}^{\mathsf{T}}},$$ (9)

where ${\widehat{\sigma }}_{ϵ}$ is a REML estimate of σ_ε, C = [Φ K₁] is formed by two design matrices described in Eq. (7), $\widehat{\lambda }={\widehat{\sigma }}_{ϵ}^2∕{\widehat{\sigma }}_c^2$ is the estimated smoothing parameter, and D is formed as follows:

$$\mathbf{D}=\left[\begin{array}{cc}\hfill 0_{m\times m}\hfill & \hfill 0_{m\times \kappa }\hfill \\ \hfill 0_{\kappa \times m}\hfill & \hfill {\mathbf{I}}_{\kappa \times \kappa }\hfill \end{array}\right],$$

where m is the number of ‘fixed effects’ and κ is the number of ‘random effects.’ An approximate point-wise 100%(1 – α) confidence interval is $\widehat{\beta }\left(t\right)\pm z_{(1-\alpha ∕2)}\widehat{\mathrm{st}.\mathrm{dev}}\left(\widehat{\beta }\left(t\right)\right)$ Alternatively, Bayesian credible intervals can be obtained by realizing a connection between Gaussian processes and spline construction [Crainiceanu et al., 2005; Rasmussen and Williams, 2006], or “subject re-sampling” bootstrap error bars can be obtained to construct the confidence intervals [Wu and Yu, 2002].

In the application of point-wise bands to functional genotype data, the issue of bias-variance trade-o associated with the selection of the degree of smoothing might deserve more careful attention. Specifically, in the context of the mixed-effects model in Eq. (8), the response variable is a fitted genotypic function Ĝ(t). If the fitted function is somewhat wiggly, this ‘noise’ will account for the increased width of the point-wise standard error bands for $\widehat{\beta }\left(t\right)$. We previously proposed the ‘flipping algorithm’ for genotype re-labeling that decreases the number of noisy oscillations for smoothed genotype data and showed that this approach results in a substantial increase of statistical power to detect a genetic association [Vsevolozhskaya et al., 2014]. Nonetheless, too smooth genotype functions might result in narrow standard error bands for $\widehat{\beta }\left(t\right)$ and thus estimate a biased version of a true function with great reliability. Further research is needed on the issue of optimal choice of a smoothing parameter in the context of genotype function fitting.

2.5 Testing for an association

In this section we turn our attention to a test statistic used for evaluating an association between a genetic region and one or more phenotypes. Whereas different types of point-wise confidence intervals for the coefficient curves can be constructed, the hypothesis testing problem of distinguishing an optimal sub-model of β(t)'s is still of interest. To address this issue, we will use the function $\mathcal{F}$ statistic [Shen and Faraway, 2004] as previously used in our FANOVA methodology [Vsevolozhskaya et al., 2014]. Specifically, suppose we want to test the nullity of a single predictor:

$$H_0:{\beta }_i\left(t\right)=0,i=1,\dots ,P.$$

By using Theorem 2 in Shen and Faraway [2004], a test statistic to determine if β(t) is equivalent to the zero function can be constructed as follows:

$$\mathcal{F}=\frac{(N-P)\int {\widehat{\beta }}_i^2\left(t\right)dt}{rs{s}_1{\left({\mathbf{X}}^{\mathsf{T}}\mathbf{X}\right)}_{ii}^{-1}},$$ (10)

where X = (1 XM₁ . . . X_P) is a design matrix for the full model containing all phenotypic variables, and $rs{s}_1={\sum }_{i=1}^N\int {({\widehat{G}}_i\left(t\right)-\mathbf{X}\widehat{\beta })}^{2}dt$ is the residual sum of squares for the full model. Under the null hypothesis, it can be easily shown (e.g. [Reimherr et al., 2014; Shen and Faraway, 2004; Zhang, 2013]) that the distribution of $\mathcal{F}$ can be approximated by an F-distribution as:

$$\mathcal{F}\sim F_{\widehat{d},(N-P)\widehat{d}},$$

where $\widehat{d}=\frac{{\left({\sum }_{i=1}^n{r}_i\right)}^2}{{\sum }_{i=1}^n{r}_i^2}$, with n being the number of genetic variants, and r_i is the ith order eigenvalue of the empirical variance-covariance matrix under the full model, ${\widehat{\Sigma }}^1$.

Alternatively, if we want to test the nullity of K predictors simultaneously, that is, to compare the full model:

$${\widehat{G}}_i\left(t\right)=\sum _{j=1}^P{\widehat{\beta }}_j\left(t\right)X_{ij},$$

to the reduced model:

$${\widehat{G}}_i\left(t\right)=\sum _{j=1}^{(P-K)}{\widehat{\beta }}_j\left(t\right)X_{ij},$$

the test statistic $\mathcal{F}$ can be defined in terms of the reduction in the sums of squared errors, as follows:

$$\mathcal{F}=\frac{(rs{s}_0-rs{s}_1)∕K}{rs{s}_1∕(N-P)}\approx \frac{\mathrm{trace}({\widehat{\Sigma }}^0-{\widehat{\Sigma }}^1)∕K}{\mathrm{trace}\left({\widehat{\Sigma }}^1\right)∕(N-P)},$$ (11)

where rss₀ is the residual sum of squares for the reduced model, and ${\widehat{\Sigma }}^0$ is the empirical variance-covariance matrix under the reduced model. Under the null hypothesis, the distribution of $\mathcal{F}$ is approximated by $F_{K\widehat{d},(N-P)\widehat{d}}$.

We note that the test statistic in Eq. (11) is computationally more complex than the one in Eq. (10). That is, if the goal is to test the nullity of only one predictor at a time, the test statistic in Eq. (10) can be calculated directly by fitting only the full model, and thus omitting fitting the reduced model. Further details and comparisons of the two formulas can be found in Shen and Faraway [2004].

3 Simulation Study

3.1 Design

The flexibility of our method allows us to accommodate various analysis settings and types of variables, including multiple, possibly correlated or pleiotropic phenotypes, and T×T interactions. One way to analyzing multiple traits is to test for an association one trait at a time. For a proper control of the experiment-wise false-discovery error rate, this ‘one at a time’ testing approach requires accounting for the number of tests performed and correcting for each individual trait's P-value. This individual correction typically leads to an inflation in the observed P-values. However, our method provides an efficient way of testing multiple traits simultaneously, with no P-value correction required, and thus naturally provides superior performance in terms of statistical power to detect an association. Moreover, to handle T×T interactions, or to assess modification of genetic susceptibility to disease by trait, our model requires a test of nullity for an interaction term. Previously, we investigated the power of FANOVA to detect an association with a single predictor [Vsevolozhskaya et al., 2014]. Simulation studies presented here reflect the extension of our previous basic model with the addition of mediation/confounding scenarios

Figure 1 aids in conceptualization of our data simulation process. We focused on a three variable system and hypothesized that there is a genetic predisposition (G) to continuous phenotypes (Z) and (X). We also assumed a relationship between (Z) and (X) and were interested in testing for an association between (G) and (X), while adjusting for the third variable (Z). Clearly, data generated under this scenario fits the mediation analysis framework, but MacKinnon et al. [2000] point out that the label of (Z) (i.e., either as a mediator or a confounder) depends on the framework used to conceptualize the phenomenon. From a statistical modeling point of view, directionality and the causality are indistinguishable, making these seemingly different concepts of mediation and confounding statistically equivalent. Therefore, data generated under our design can be used to check for both a mediator and a confounding control.

Figure 1.

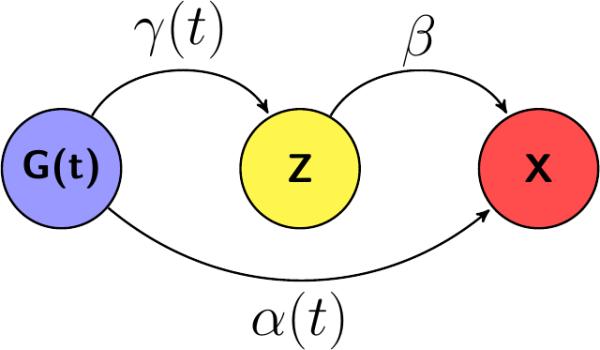
The genetic information (G(t)) is directly associated with the outcome of interest (X) and indirectly through the third variable (Z).

3.2 Data generation

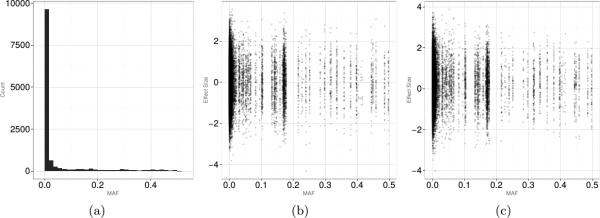
We generated genetic data (G) using the 1,000 genome project [Durbin et al., 2010] to mimic the real sequencing data structure (e.g., linkage disequilibrium patterns, allele frequencies, and randomly missing genotype data). Specifically, at each simulation iteration, a random 30 kb section of genetic region was drawn. Within this 30 kb region, each simulated data contained an average of 300 variants with minor allele frequencies (MAF) ranging from less than 0.001 to almost 0.5. The complete distribution of MAF for all variants across simulations is provided in the left panel of Figure 2.

Figure 2.

Panel (a): The range and the distribution of MAF for all variants. Panels (b)-(c): MAF distribution of causal variants by the effect size.

Next, a continuous trait (Z) was simulated as:

$$Z_i=\sum _{j=1}^n{G}_i^{\chi }\left(t_j\right)\times \gamma \left(t_j\right)+{ϵ}_i,i=1,\dots ,N,j=1,\dots ,n,$$ (12)

where N is the number of subjects, n is the number of variants, t_j indexes the position of variants, γ(t_j) is the effect of the variant in t_j's, ε_i ~ N(0, 1), and ”χ” indicates a subset of genetic variants harboring causal alleles. For example, if χ = 10%, then a random sample of 10% of all variants for subject i were causal, and the effect of each causal variant j, γ(t_j), was drawn from an $N({\mu }_{\gamma },{\sigma }_{\gamma }^2)$ distribution (the rest of γ(t)'s, corresponding to non-causal variants, were zero). If μ_γ = 0, the effect of a given causal variant was either protective or deleterious . If μ_γ > 0, then the majority of causal variants had the same direction of the effects (i.e., deleterious), and the magnitude of the effect size varied by manipulating ${\sigma }_{\gamma }^2$. The middle panel of Figure 2 illustrates simulated effects by MAF for the choice μ_γ = 0 and ${\sigma }_{\gamma }^2=1$; the right panel for μ_γ = 0.25 and ${\sigma }_{\gamma }^2=1$. The reader should note that under our simulation scenario, the causal variants can be both rare and common. Alternative situations with only rare or common causal variants were previously investigated by our group and showed favorable performance by FANOVA [Vsevolozhskaya et al., 2014].

Another continuous trait (X) was simulated as:

$$X_i=\sum _{j=1}^n{G}_i^{\chi }\left(t_j\right)\times \alpha \left(t_j\right)+\beta \times Z_i+{ϵ}_i.$$ (13)

Similar to $\gamma \left(t_j\right),\alpha \left(t_j\right)\sim N({\mu }_{\alpha },{\sigma }_{\alpha }^2)$ represents the effect of a causal variant j on the trait (X), and β ~ N(3,1) represents the effect of the third variable (Z) on the trait (X).

3.3 Type I error results

For empirical type I error simulations, we set the genetic effect on the continuous trait (X) to zero, i.e., α(t_j) = 0 for all j, and tested for an association between (G) and (X), while adjusting for (Z). The percentage of risk variants for the association between (G) and (Z) in Eq.(12) was set to χ = 30% and γ_j's were simulated from an N(μ_γ = 0, σ_γ = 3) distribution. For the different sample sizes, we compared the generalized FANOVA approach to the SKAT methodology [Wu et al., 2011]. The results are summarized in Table 1. For both methods, all empirical type I error rates are around the nominal α levels with the exception of SKAT for a small sample size. To further contrast the differences between FANOVA and SKAT, we proceeded to a comparison of power simulations.

Table 1.

Empirical type I error rates for the association tests between (G) and (X), while adjusting for (Z).

Sample size	Nominal level α	FANOVA	SKAT
50	0.05	0.04319	0.04164
	0.01	0.01037	0.00845
	0.001	0.00191	0.00018
	0.0001	0.00036	0.00000
500	0.05	0.04346	0.04854
	0.01	0.00941	0.01002
	0.001	0.00108	0.00123
	0.0001	0.00023	0.00000

3.4 Statistical power results

For the statistical power comparison, both traits (Z) and (X) shared the same percentage, but a random set of risk variants. The percent of risk variants were set to 5%, 10%, 30%, 50%, 70%, 90%, and 100%. The sample size values were N = 50, 500, 2500, and 5000. The execution time of a single iteration of the simulations (the statistical power is presented based on at least 1,000 iterations) on a single core (2.5Ghz Intel Xeon E5-2670v2) of high-performance computing center (HPCC: https://wiki.hpcc.msu.edu/) ranged from 20 seconds for N = 50 up to an hour for N = 5000. The allocated memory for N = 5000 subjects was 64GB.

Figure 3 summarizes empirical power results for the scenario with risk variants having either positive or negative effects (i.e., μ_γ = μ_α = 0) for the different number of subjects. In Figure 4 the majority of risk variants had deleterious effects for both traits (i.e., μ_γ > 0 and μ_α > 0). In each figure, the generalized FANOVA statistical power to detect an association between (G) and (X), while adjusting for (Z), is represented by a solid line, and the power of SKAT is represented by a dashed line.

Figure 3.

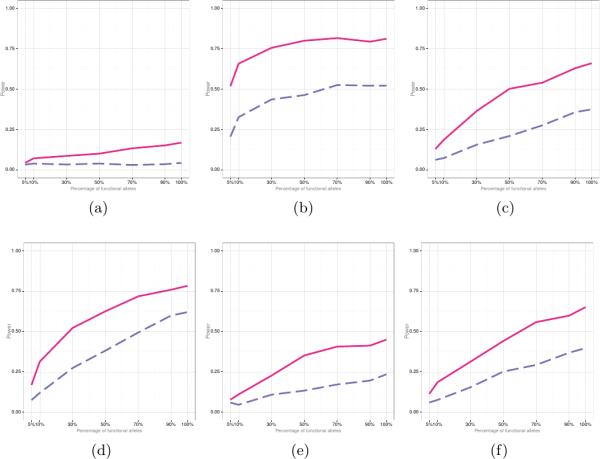
Empirical power of FANOVA (solid line) and SKAT (dashed line) when the variants can have either protective or deleterious effects (i.e., μ_γ = μ_α = 0). Panel (a): N = 50 σ_γ = σ_α = 0.05; (b): N = 50 σ_γ = σ_α = 1; (c): N = 500 σ_γ = σ_α = 0.05; (d): N = 1000 σ_γ = σ_α = 0.05; (e) N = 2500 σ_γ = σ_α = 0.015; (f) N = 5000 σ_γ = σ_α = 0.015.

Figure 4.

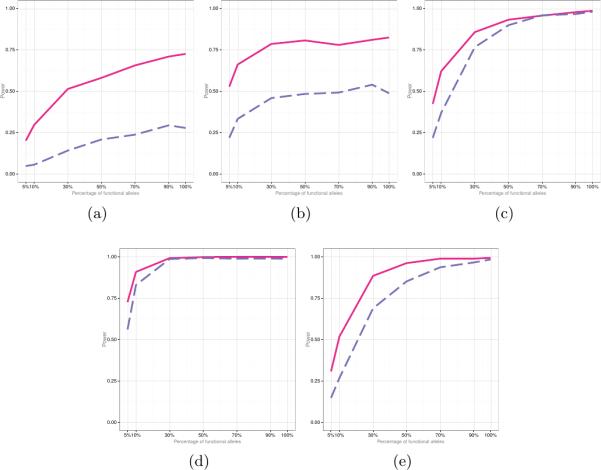
Empirical power of FANOVA (solid line) and SKAT (dashed line) when the majority of variants have deleterious effect (i.e, μ_γ > 0 μ_α > 0) . Panel (a): N = 50 μ_γ = μ_α = 0.05 σ_γ = σ_α = 0.25; (b): N = 50 μ_γ = μ_α = 0.05 σ_γ = σ_α = 1; (c): N = 500 μ_γ = μ_α = 0.05 σ_γ = σ_α = 0.15; (d): N = 500 μ_γ = μ_α = 0.25 σ_γ = σ_α = 0.15; (e): N = 1000 μ_γ = μ_α = 0.05 σ_γ = σ_α = 0.05

In general, the proposed FANOVA approach attained higher power than SKAT, especially for small sample sizes, small effect sizes, and when the percentage of risk variants is small. The empirical power of the two approaches become comparable if the effect sizes and the proportion of risk variants were large.

4 Application to real data: ANGPRL4 association with triglyceride

To further illustrate the utility of our generalized FANOVA approach, we turn to the issue of association testing between sequence variations in ANGPTL4 gene and lipid metabolism. In mice, the involvement of ANGPTL4 in lipid metabolism was shown by intravenous injection of recombinant ANGPTL4, resulting in an increase in plasma triglycerides (TG) levels [Yoshida et al., 2002]. In humans, the involvement of ANGPTL4 in lipid metabolism is probable and may be associated with a higher risk of cardiovascular disorder [Kathiresan et al., 2009; Muendlein et al., 2014; Romeo et al., 2007]. However, each individual ANGPTL4 variant confers a modest effect [Kathiresan et al., 2009], suggesting an improved statistical power for methods like generalized FANOVA that perform a joint gene-based association analysis.

We conducted an analysis of 93 sequence variations in ANGPTL4 that were identified among 3,551 participants in the Dallas Heart Study [Romeo et al., 2007]. To examine an increase in plasma TG levels, we binned individuals into the ‘low-triglyceride’ group (660 individuals with plasma triglyceride level ≤25th percentile) and into the ‘high-triglyceride’ group (679 individuals with plasma triglyceride level ≥75th percentile). The resulting sample included 443 individuals of mixed European descent, 651 African Americans, and 245 Hispanics.

As discussed elsewhere (e.g., [Svishcheva et al., 2015; Vsevolozhskaya et al., 2014]), statistical power of functional methods may depend on the quality of genotype data smoothing. To obtain smooth genotypic functions, we first coded allelic dosage based on the minor allele counts (i.e., either 0, 1 or 2) and applied the “flipping algorithm” [Vsevolozhskaya et al., 2014] to minimize the number of 0-2 (or 2-0) patterns in every two subsequent variant positions. However, because the majority of 93 sequenced variants were rare [Romeo et al., 2007], the coding based on minor allele counts was concluded to be optimal and no re-coding of allelic dosage was necessary.

To examine an effect of increase in TG levels, modified by race and adjusted for sex, we built the following model:

$$\begin{array}{cc}\hfill {\widehat{G}}_i\left(t_j\right)=& {\beta }_0\left(t_j\right)+{\beta }_1\left(t_j\right)X_{\mathbf{TG}i}+\hfill \\ \hfill & {\beta }_2\left(t_j\right)X_{\mathbf{AA}i}+{\beta }_3\left(t_j\right)X_{\mathbf{H}i}+{\beta }_{12}\left(t_j\right)X_{\mathbf{TG}i}{X}_{\mathbf{AA}i}+{\beta }_{13}\left(t_j\right)X_{\mathbf{TG}i}\left(t_j\right)X_{\mathbf{H}i}+\hfill \\ \hfill & {\beta }_4\left(t_j\right)X_{\mathbf{Sex}i}+{ϵ}_i\left(t_j\right),\hfill \end{array}$$

where β₀(t_j) is the smoothed baseline allelic dosage j = 1, . . . , 93; β₁(t_j) is the effect of TG-increase on allelic dosage. The next four terms are added to examine T×T interaction or whether the effect of TG increase varies among European Americans (β₁(t_j)), African Americans (β₁(t_j) + β₁₂(t_j)), and Hispanics (β₁(t_j) + β₁₃(t_j)). Finally, β₄(t_j) is the adjustment for sex.

To determine the most parsimonious model, we first performed a test for T×T interaction, i.e., H₀ : β₁₂(t_j) = β₁₃(t_j) = 0 for all t_j, and found statistically significant differences in TG-increasing effect among individuals of different racial descent (P-value=0.0028). We note that the magnitude of this P-value remained the same for different choices of kernels and as such, we proceeded to explore specific sub-regions of the ANGPTL4 gene that may harbor causal variants for the different racial groups.

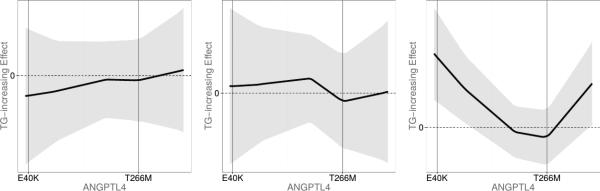
Each panel of Figure 5 illustrates the estimated TG-increasing effect among different racial groups and across 93 variants of the ANGPTL4 gene. Further, the positions of the recently identified variants E40K and T266M [Romeo et al., 2007; Talmud et al., 2008] are added as vertical lines to each panel. The left panel of Figure (5) shows ${\widehat{\beta }}_1\left(t\right)$ or the estimated effect of TG increase among European Americans. From this panel we can infer that the region around the E40K variant has the top contribution among European Americans, since it is the region over which ${\widehat{\beta }}_1\left(t\right)$ deviates the most from the zero line. Additionally, the direction of ${\widehat{\beta }}_1\left(t\right)$ around E40K is negative, indicating that TG increase is associated with a lower dosage of E40K variant, which implies that European American E40K carriers can be expected to have lower TG levels. However, the confidence bands for ${\widehat{\beta }}_1\left(t\right)$ include zero and indicate lack of statistical significance.

Figure 5.

TG-increasing effect among European Americans (left panel), African Americans (middle panel), and Hispanics (right panel) with the 95% confidence bands (shaded regions).

The right panel of Figure 5 shows ${\widehat{\beta }}_1\left(t\right)+{\widehat{\beta }}_{13}\left(t\right)$ or the estimated effect of TG increase among Hispanics. Once again, the effect has the top magnitude around E40K region, but it's direction is reversed, indicating that Hispanic E40K carriers tend to have higher TG levels. Additionally, among Hispanics, E40K region association with TG-increase reached statistical significance.

The middle panel of Figure 5 shows ${\widehat{\beta }}_1\left(t\right)+{\widehat{\beta }}_{12}\left(t\right)$ or the estimated effect of TG increase among African Americans. Unlike European Americans and Hispanics, the contribution of E40K variant does not appear to be appreciably associated with TG increase. Also, no contribution of T266M variant to either TG increase (or decrease) was found among any racial groups.

Finally, to compare our T×T interaction results to SKAT, we performed a subgroup analysis on data from European Americans, African Americans, and Hispanics. The P-values, adjusted for sex, for the test of an association between TG-levels and variants in the ANGPTL4 gene were as follows: among European Americans P_SKAT = 0.0006, P_FANOVA = 0.0262; among Hispanics P_SKAT = 0.1738, P_FANOVA = 0.0001; among African Americans P_SKAT = 0.2321, P_FANOVA = 0.9447. Accordingly, both methods concluded an association between ANGPTL4 variants and plasma triglycerides levels among European Americans, no association among African Americans, and discordant results among Hispanics. The reader should not be surprised by seemingly disagreeing FANOVA conclusions for European Americans summarized via the confidence bends in Figure 5 and via the P-value for an association test. It has been noted multiple times, including by our research group [Vsevolozhskaya et al., 2015], that a combination of multiple “marginally significant” outcomes across different variants may result in the overall significance for a genetic region.

5 Discussion

By generalizing previously proposed FANOVA methodology, we offer a novel approach not previously explored in FLM-based association studies for estimating multiple phenotype-specific effects smoothly varying over genetic variants. Furthermore, by treating genetic information as the response variable and all traits as predictors (qualitative or quantitative), the generalized FANOVA provides a straightforward way to account for hidden population stratification, confounders, mediators and T×T interactions. The established connection between penalized least squares and best linear unbiased predictors allows for a straightforward implementation of the proposed methodology using standard mixed linear model software.

The introduced notion of T×T interaction deserves additional clarification. We are not necessarily putting emphasis on the interaction itself or the value of its coefficient. Rather, the inclusion of this term gives a simple way of detecting possible effects of various combinations of treatment and trait values that may go beyond what is captured by the sum of their individual effects.

How well do our generalized FANOVA regression coefficient estimates replicate what others have found in prior studies of ANGPTL4 ? Studies of Romeo et al. [2007] and Talmud et al. [2008] revealed that among European Americans E40K carriers have significantly lower TG levels. Talmud et al. [2008] also showed TG-lowering effect of T266M variant, but only among E40K carriers (i.e., whenever E40K men were excluded from the reanalysis, there was no longer a significant association between T266M and TG levels). T266M is more prevalent than E40K and in our sample out of 620 T266M carriers only 16 were also carriers of E40K, which may be a reason behind lack of association. Furthermore, no studies presented conclusive findings over TG-lowering effect and mutations in ANGPTL4, so a replication of the reported association is required.

Our generalized FANOVA model is a functional model analogue of “reverse regression” (e.g., [Maddala, 1992]), where genetic information, X, becomes the response while phenotypes, Y , are treated as predictors. Regression coefficients are not invariant to swapping of predictor and response variables. However, partial correlations, as well as test statistics and the corresponding P-values remain the same after swapping. Thus, effects of adjustments for covariates in a direct model are properly preserved when testing for association in a reverse model. With multiple correlated predictors at an arbitrary variant's position t_j, the test statistic for the regression coefficient β_i can be re-expressed based on the partial correlation between Y and X_i, which is not affected by swapping of variables, and the test statistic (and therefore the P-value) is also invariant under the reversal in a functional model. One limitation of this approach is that for the direct and reverse tests to be equivalent, X_i cannot enter any interaction terms with other variables.

The generalized FANOVA is an extension of the previously proposed FANOVA approach and thus inherits some of its features. For example, generalized FANOVA fully utilizes variants’ position information and linkage-disequilibrium structure when computing the test statistic $\mathcal{F}$. However, unlike the previously proposed FANOVA, our current approach allows inclusion of multiple traits and adjustment for additional covariates. Moreover, our new functional approach provides a unique way of graphically depicting phenotypic effects and interactions by representing them as continuous curves varying over a genetic region. We also hypothesize that the functional approach may hold increased robustness to genotyping errors. This may be due to the fact that the estimated genotype functions, Ĝ(t), are used for the analysis in place of allele frequencies of the marked locus. It is noted that genotyping errors can have severe consequences for the analysis of low frequency alleles (e.g., [Abecasis et al., 2001]). Although genotype functions are estimated via allele counts, they incorporate a certain degree of smoothing, therefore the fitted functions are expected to be less prone to genotyping errors.

In terms of the application of the generalized FANOVA methodology, practitioners can use standard mixed-effects software to estimate continuous regression coefficients as illustrated in the Methods section of this article. Previous research in penalized regression models [Scheipl and Greven, 2012] suggests that a penalty with a small null space should be preferred (a typical choice for the number of “fixed effects” is 2) and a ‘rule of thumb’ for the number of “random effects” is κ = 35. However, the specific number of kernel functions is unimportant as long as the fitted genotype functions are not too smooth.