When Optimal Strategy Matters to Prey Fish

Abstract

Predator–prey interactions are commonly studied with an interest in determining the optimal strategy for prey. However, the implications of deviating from optimal strategy are often unclear. The present study considered these consequences by studying how the direction of an escape response affects the strategy of prey fish. We simulated these interactions with numerical and analytical mathematics and compared our predictions with measurements in zebrafish larvae (Danio rerio), which are preyed upon by adults of the same species. Consistent with existing theory, we treated the minimum distance between predator and prey as the strategic payoff that prey aim to maximize. We found that these interactions may be characterized by three strategic domains that are defined by the speed of predator relative to the prey. The “fast predator” domain occurs when the predator is more than an order of magnitude faster than the prey. The escape direction of the prey had only a small effect on the minimum distance under these conditions. For the “slow predator” domain, when the prey is faster than the predator, we found that differences in direction had no effect on the minimum distance for a broad range of escape angles. This was the regime in which zebrafish were found to operate. In contrast, the optimal escape angle offers a large benefit to the minimum distance in the intermediate strategic domain. Therefore, optimal strategy is most meaningful to prey fish when predators are faster than prey by less than a factor of 10. This demonstrates that the strategy of a prey animal does not matter under certain conditions that are created by the behavior of the predator.

Introduction

Biologists have long-appreciated the importance of predation in the ecology and evolution of prey species. This subject is extensive enough to fill the pages of books about the fascinating diversity of strategies that prey use to avoid encounters with predators (e.g., Ruxton et al. 2004) or to defend themselves when discovered (e.g., Emlen 2014; Evans and Schmidt 1990). In contrast, our understanding for how prey evade capture by locomotion is relatively rudimentary. Although biomechanical studies commonly speculate on the importance of locomotor performance to survival, relatively few have tested what aspects of locomotion are most meaningful in these interactions. Studies that have explored this subject (reviewed by Domenici and Blagburn 2011) underscore the common-sense notion that the direction of an escape matters to a prey’s survival. This idea has been formalized by pursuit-evasion models that aim to determine the optimal direction for an escape. The present study examined such a model, based on Weihs and Webb (1984), to consider the strategic consequences of deviating from optimal strategy in piscivorous interactions. We compared the model’s predictions to experimental results in zebrafish (Danio rerio) (Stewart et al. 2014) and arrived at new interpretations of this theory on prey strategy.

A pursuit-evasion model originates from an area of game theory that offers a basis for examining locomotor behavior in strategic terms. There is recent interest in revisiting such models (e.g., Howland 1974; Weihs and Webb 1984; Djemai et al. 2010; Gal and Casas 2014) with experimental studies that consider the behavior both of predators and of prey. This includes work on running (e.g., Wilson et al. 2013) and flying (e.g., Kullberg et al. 1998; Ghose et al. 2006) in vertebrates, running (Domenici et al. 2008) and flying (e.g., Combes et al. 2012) in insects, and swimming in zooplankton (e.g., Arnott et al. 1999; Heuch et al. 2007) and fishes (e.g., Domenici et al. 2000). These efforts offer the potential to reveal how sensory and motor systems govern the outcome of predator–prey interactions.

Piscivorous interactions offer some advantages for examining the sensory-motor basis for evading predators. In many cases, this interaction can be studied in a laboratory, where predatory fishes will attempt to feed on prey and prey initiate a “fast-start” escape response (Fig. 1) (Weihs 1973). Both animals operate with motion that is largely two-dimensional and therefore relatively simple to measure and describe. Adult zebrafish prey on larvae of the same species (Stewart et al. 2013). This is a species that offers a growing wealth of understanding in physiology and neuroscience (e.g., McLean and Fetcho 2011; Briggs 2002) that may be leveraged for mechanistic insight into predator–prey interactions. In addition, fish offer one of the few biological pursuit-evasion systems that have been mathematically modeled (Weihs and Webb 1984). This modeling offers specific predictions of swimming trajectories that may be tested with kinematic measurements.

Fig. 1.

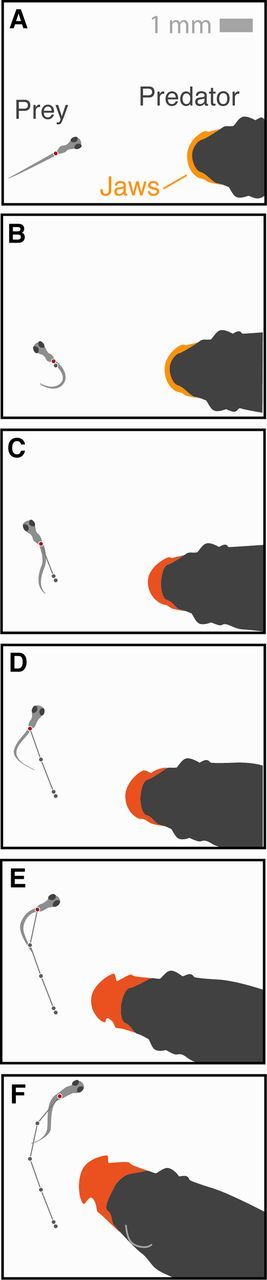
A predator–prey interaction in zebrafish. Silhouettes of zebrafish from a dorsal perspective have been traced from videographic stills (5 ms interval) as an adult attempts to capture a larva with a suction-feeding strike. (A and B) On the predator’s approach, the prey initiates a “fast-start” response to accelerate away from the predator. The strike has yet to begin, as shown by the lack of protrusion by the jaws of the predator. (C and D) The predator initiates a strike, which is visible from the jaw’s protrusion. (E and F) With its jaws fully extended, the predator fails to capture the prey, which proceeds to move away from the predator by employing rapid undulatory swimming. Recording from Stewart et al. (2014). (This figure is available in black and white in print and in color at Integrative and Comparative Biology online.)

Deviation from optimal strategy has been interpreted as a strategic adaptation in fish and other systems. The protean hypothesis suggests that unpredictable prey have an advantage over predictable prey in evading predators (Humphries and Driver 1970). This idea may apply to the erratic motion of an individual or a population of prey that collectively exhibit a variety of motion, which challenges an individual predator’s ability to learn or opposes the adaptation of a lineage of a predatory species to an optimal strategy. Therefore, variability in the direction of the fast-start may be an adaptation for unpredictability in a prey species. This raises the potential for a trade-off between the escape direction that generates optimal displacement from a predator and one that is unpredictable.

Interpretations of the motion of prey generally have not considered the implications of deviating from optimal strategy. For example, it is not clear whether an escape that is 5° or 50° from the optimum predicted by Weihs and Webb (1984) has a major or negligible effect on the success of evasion. If the performance of an escape is insensitive to differences in the direction taken, then no trade-off should exist between evasiveness and predictability. In short, it is unclear when optimal strategy matters. The present study therefore revisited the mathematics of the Weihs and Webb (1984) model to examine how deviation from optimal strategy affects the performance of evasion. We expanded this model and performed numerical simulations for comparison with experimental results. In this effort, we identified three strategic domains that are defined by the relative speed of the predator and prey. In two of these domains, the direction of escape was found to have little or no effect on the evasiveness of prey.

Optimal strategy for the prey

The Homicidal Chauffeur is the colorful title for a pursuit-evasion game that has been applied to a variety of systems, including predator–prey interactions (Isaacs 1965). These games consider the trajectories of its players to address the strategic effects of directional decision–making. Weihs and Webb (1984) adopted the Homicidal Chauffeur to model the responses of a prey fish that encounters a predatory fish. Here we offer a brief review of this model to explain the basis for our expansion of this theory. See the original study for a more complete derivation (Weihs and Webb 1984).

The payoff is a quantity used in game models to define the beneficial or detrimental consequences of using a particular strategy (Webb 2007). For pursuit-evasion models, the payoff often is defined as the minimum distance between predator and prey with respect to time. This quantity reflects the condition when the predator has the best opportunity to capture the prey. The optimal strategy for an evasive prey is therefore defined as the escape angle that yields the greatest minimum distance (Weihs and Webb 1984).

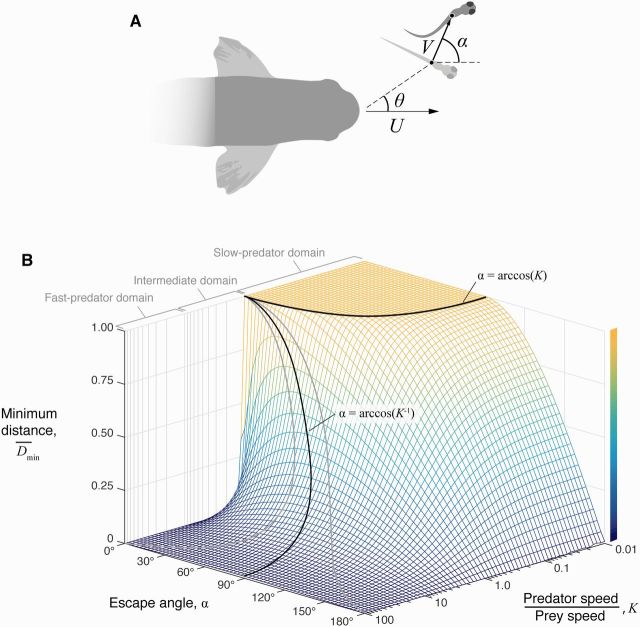
Predicting the distance between predator and prey requires relatively few parameters under some simplifying assumptions. In the rapid events of a predatory strike, it is reasonable to approximate the predator’s motion as a constant speed, U. If one neglects the acceleration period of the fast-start (∼20 ms), then the prey’s motion may also be approximated with a constant speed, V, at an escape angle α, defined with respect to the heading of the predator (Fig. 2A). Under these conditions, the distance between predator and prey, D, may be calculated over time:

$$D^2={((X_0-Ut)+Vt\text{cos}\alpha )}^2+{(Vt\text{sin}\alpha )}^2,$$ (1)

where X₀ is the starting position of the prey.

Fig. 2.

A pursuit-evasion model for predator–prey interactions in fish. (A) Pursuit-evasion models consider the motion of a predator (viewed from dorsal perspective) with speed U and a prey with speed V and escape angle α. Some versions of this model consider prey positioned lateral to the predator’s approach (${\theta }_0>0$). (B) Numerical simulations were run at varying escape angle and at different speeds of approach by the predator (with ${\theta }_0=0$) to examine variation in the minimum distance. The effect of escape angle on minimum distance was found to differ among the slow-predator domain (K < 1), the fast-predator domain (K > 10), and the intermediate domain (1 < K < 10). For the intermediate and fast-predator domains, the optimal angle (black curve) was predicted analytically (Equation (5), based on Weihs and Webb 1984). The effect of deviation from the optimum is indicated by the boundaries of a decrease of ${0.1}_{}{\overline{D}}_{\text{min}}$ (gray curves). In the slow-predator domain, the boundary of the performance plateau where ${\overline{D}}_{\text{min}}=1$ is predicted by Equation (7). (This figure is available in black and white in print and in color at Integrative and Comparative Biology online.)

The minimum distance, the payoff in this game, may be calculated from the distance equation. This is first achieved by calculating the time, $t_{\text{min}}$, at which the minimum distance occurs. This may be found from the root of the first derivative of Equation (1) with respect to time, which yields the following expression:

$$t_{\text{min}}=\frac{X_0}{V}\frac{K-\text{cos}\alpha }{1-2K\text{cos}\alpha +K^2},$$ (2)

where K indicates the speed of the predator relative to the prey ($K=U/V$). This equation yields negative values of time when K < 1 and therefore only applies when the predator is faster than the prey. The minimum distance was consequently determined for K > 1 by solving for distance (Equation (1)) at $t_{\text{min}}$:

$${\overline{D}}_{\text{min}}^2=\frac{D_{\text{min}}^2}{X_0^2}=\frac{{\text{sin}}^2\alpha }{K^2-2K\text{cos}\alpha +1},$$ (3)

where ${\overline{D}}_{\text{min}}$ is the minimum distance normalized by the starting position of the prey.

Finally, the optimal strategy is determined by finding the escape angle that yields the greatest minimum distance. This occurs when the derivative of Equation (3) with respect to α is equal to zero, which is explicitly described by the following equation:

$$0=\frac{{\partial \overline{D}}_{\text{min}}^2}{\partial \alpha }=\frac{2\text{sin}\alpha \text{cos}\alpha (K^2-2K\text{cos}\alpha +1)-2K{\text{sin}}^3\alpha }{{(K^2-2K\text{cos}\alpha +1)}^2}.$$ (4)

Among the solutions that satisfy this equation, Weihs and Webb proposed that the following indicates the optimal strategy when the predator is faster than the prey (K > 1):

$${\alpha }_{\text{opt}}=\pm \text{arccos}{K}^{-1}.$$ (5)

We added the ± symbol to this expression to indicate that prey are equally effective if escaping at an optimal angle toward the left ($\alpha >0$) or right ($\alpha <0$) of the predator’s heading. For relatively fast prey (K < 1), Weihs and Webb suggested that the optimal solution consists of swimming directly away from the predator (α = 0) (Weihs and Webb 1984). Therefore, for any speed of the predator, this model offers predictions for how a prey can direct its escape to maximize its chances for survival by creating the greatest distance from the predator.

Three strategic domains

The significance of an optimum is different if it corresponds to a sharp global maximum, a local peak much smaller than the global maximum, or a shallow peak in performance. We considered the conditions that surround optimal strategies by calculating how the payoff in this pursuit-evasion model, the minimum distance (Weihs and Webb 1984), varies with escape angle and the relative speed of the predator. As an alternative to analytical mathematics, we first formulated this performance landscape with a numerical approach that we implemented in Matlab (v2014b, MathWorks, Natick, MA). This was simply done by defining a series of time values at a regular interval to calculate the positions of the predator ($X_{\text{pred}}=Ut,Y_{\text{pred}}=0$) and prey ($X_{\text{prey}}=X_0+Vt\text{cos}\alpha ,Y_{\text{prey}}=Vt\text{sin}\alpha$). The minimum value of the distance between them was determined in this way for variable escape angle and the predator’s speed, over a range of K and α values (Fig. 2B). This yielded results that were coincident with the analytical equation for ${\overline{D}}_{\text{min}}$ formulated by Weihs and Webb (1984) for relatively fast predators (K > 1, Equation (3)). However, the advantage of this numerical calculation was that it allowed us to examine variation in the minimum distance for slower predators (i.e., K < 1) as well. The resulting performance landscape (Fig. 2B) illustrates how the minimum distance varies over a broad range of values of the relative speed of the predator.

Our results suggest that the fast-start is unlikely to be effective at any escape angle when a prey is approached by a very fast predator. We will refer to this condition as the “fast-predator” domain, which corresponds to interactions where the predator is an order of magnitude faster than the prey (K $\ge$ 10). For example, if a predator is 10-fold faster than the prey (K = 10), then the prey can do no better than displace its body by 10% of its initial distance (Fig. 2B). An escape that is 24.5° larger or smaller than the optimum yields a minimum distance that is less than the value at the optimum by 0.1 (i.e., 1% of the starting position of the prey). These metrics become increasingly unfavorable for the prey when approached by an even faster predator (Fig. 2B). Therefore, deviation from optimal strategy in the fast-predator domain has little effect on the performance of prey. In this regime, inaccuracy in the strike by the predator is likely a more decisive factor to the prey’s survival than anything the prey may do in response.

A different picture emerges when one considers prey that move more quickly than their predators. This occurs when predators brake or glide slowly on their approach toward a prey (Higham et al. 2005; Higham 2007) while the prey initiates a rapid escape. We term this condition the “slow-predator” domain (K < 1) where we have found that the fast-start causes the predator to reach no closer than the starting distance (i.e., ${\overline{D}}_{\text{min}}=1$, Fig. 2B) for a variety of escape angles. To define the bounds of these effective escape angles, it is useful to consider the first derivative of the distance function with respect to time (see Supplementary Materials for details):

$$\frac{\partial D^2}{\partial t}=2(t(U^2+V^2)-U{X}_0+V(X_0-2tU)\text{cos}\alpha ).$$ (6)

A prey achieves an optimal escape (${\overline{D}}_{\text{min}}=1$) when the distance function never decreases as a function of time (i.e., $\frac{\partial D^2}{\partial t}\ge 0$). This holds true for α = 0, which Weihs and Webb proposed as the optimal direction (Weihs and Webb 1984). However, it also holds true that the distance increases for another solution to Equation (4) ($\alpha =\pm \arccos K$) and all values in between (see Supplementary Materials for details). Therefore, the following defines a domain of a performance plateau in minimum distance for the escape direction when the prey is faster than the predator (K < 1):

$${\overline{D}}_{\text{min}}=1{{\displaystyle }}^{}\text{if}{{\displaystyle }}^{}|\alpha |\le \text{arccos}(K).$$ (7)

This suggests that if the escape response of a prey is capable of exceeding the approach speed of the predator, then a wide range of angles yield equally successful escapes for the prey.

Optimal strategy matters the most in the intermediate domain, between when the prey and the predator are equivalent in speed and when the predator is an order of magnitude faster ($1<K<10$). In this domain, prey are capable of attaining appreciable minimum distance values and there is a penalty for deviating from the optimal angle (Fig. 2B). Therefore, a prey fish has a strong incentive to conform to the predicted optimum when encountering a predator that can move slightly faster than itself.

Comparing models with measurements

We were interested in examining how optimal strategy is related to experimental measurements. This was addressed by recent studies on larval zebrafish that were preyed upon by adults of the same species (Stewart et al. 2013). This included experiments that used a robot to simulate the approach of a predator toward prey in the dark. The position at which the prey responded with a fast-start and the direction of that response to the robot were recorded (Stewart et al. 2014). This evasive action was stimulated by the lateral line system of the prey, which detected the flow of water generated by the approaching predator robot, in a manner analogous to flow sensing in insects (Casas and Steinmann 2014).

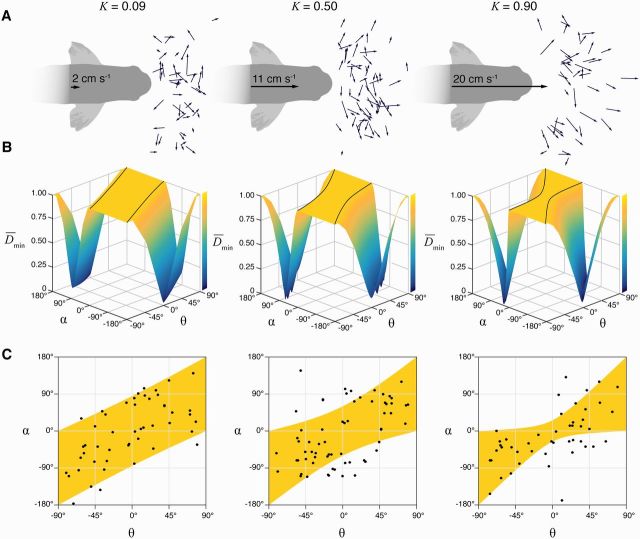
As detailed above, the predictions of the present model depend on the speed of the predator relative to the prey. The approach speed of the robot, and consequently K, was varied to span the range of values observed for live predators (Stewart et al. 2013). Our calculations of K used a prey speed ($V={22}_{}{\text{cm}}_{}{\text{s}}^{-1}$) from the literature that approximated the maximum value attained during a fast-start for larvae of this species (Budick and O’Malley 2000; Müller and van Leeuwen 2004). As a consequence of the relatively slow approach made by these suction-feeding predators, the prey had the potential to move faster at all approach speeds, which yielded K-values of less than unity (Fig. 3A). Therefore, zebrafish adults and larvae operate in the slow-predator domain (Fig. 2B).

Fig. 3.

Predictions of the model and measurements of the fast-start in the slow-predator domain. The pursuit-evasion model was compared with experiments that recorded the responses of larval zebrafish that were approached by a robotic predator at three speeds (2, 11, and 20 cm s−¹) (Stewart et al. 2014). The results of experiments and modeling are arranged in columns that correspond to each of these speeds. (A) The fast-starts are illustrated by the center-of-body displacement over the two stages of the behavior (small arrows). (B) Numerical results of the simulated interactions show how the minimum distance (${\overline{D}}_{\text{min}}$) varies with the escape angle (α) and the initial position (θ₀). The plateau region (defined by Equation (11)) shows an area where ${\overline{D}}_{\text{min}}=1$. (C) This area is plotted with measurements of the initial position and the escape angle of the measured responses shown in (A). (This figure is available in black and white in print and in color at Integrative and Comparative Biology online.)

One discrepancy between the model and our experiments was that the majority of prey fish were not aligned with the heading of the robotic predator before the fast-start. This condition has biological relevance because it corresponds to a situation in which a predator fails to approach a prey with perfect accuracy. We therefore modified Weihs’ and Webb’s model by adding a lateral component to the initial position of the prey in our distance function. Following the same procedure (Equations (2)–(3)), we arrived at a minimum distance function (see Supplementary Materials for details). This function was simplified using polar coordinates, as in the following equation:

$${\overline{D}}_{\text{min}}^2=\frac{D_{\text{min}}^2}{R_0^2}=\frac{{\left(\text{sin}(\alpha -{\theta }_0)+K\text{sin}{\theta }_0\right)}^2}{K^2-2K\text{cos}\alpha +1}$$ (8)

where R₀ and θ₀ are the initial radial and angular positions of the prey relative to the mouth of the predator (Fig. 2A). Numerical solutions to this equation showed a broad range of angular positions and escape angles that defined a performance plateau where ${\overline{D}}_{\text{min}}=1$ (Fig. 3B). We found the margins of this plateau using a similar procedure as outlined above (Equation (4)). Specifically, we solved for the conditions when the derivative of the minimum distance with respect to α was equal to zero:

$$0=\frac{\partial {\overline{D}}_{\text{min}}^2}{\partial \alpha }=\frac{\left\{\begin{array}{c}2(K\text{cos}\alpha -1)(K\text{cos}{\theta }_0-\text{cos}(\alpha -{\theta }_0))\\ \times (K\text{sin}{\theta }_0+\text{sin}(\alpha -{\theta }_0))\end{array}\right\}}{{(K^2-2K\text{cos}\alpha +1)}^2}.$$ (9)

We found solutions that satisfy this equation by setting the terms in the numerator equal to zero. The solution for K > 1 was similar to Equation (5), although the initial angular position determines the sign of the optimal angle:

$${\alpha }_{\text{opt}}=\frac{{\theta }_0}{|{\theta }_0|}\text{arccos}(K^{-1}).$$ (10)

This solution indicates that the same optimal direction exists when the predator is faster than the prey, irrespective of the prey’s initial position. As detailed above, we found that the escape angle is equally effective (i.e., ${\overline{D}}_{\text{min}}=1$) when the prey is aligned with the predator for a broad range of values (Equation (7)). This result holds true when prey are positioned lateral to the predator, but this performance plateau depends on the initial angular position of the prey. We found that the following equation defines the bounds of this plateau among the solutions that satisfy Equation (8) for K < 1:

$${\overline{D}}_{\text{min}}=1{{\displaystyle }}^{}\text{if}{{\displaystyle }}^{}|\alpha -{\theta }_0|\le \text{arccos}(K\text{cos}{\theta }_0).$$ (11)

This demonstrates that the performance plateau reduces in area with increasing speed of the predator (Fig. 3B). Therefore, fewer combinations of starting positions and escape angles yield equivalent effectiveness of escape from faster predators.

Using this formulation of the pursuit-evasion model, we evaluated how the measured responses of prey compared to the model’s predictions (Fig. 3C). This revealed that the vast majority of larvae operated within the performance plateau and therefore were predicted to yield maximal performance (${\overline{D}}_{\text{min}}=1$). This was true even at the fastest approach by a predator (K = 0.90), where the plateau encompassed a smaller area of the performance landscape. Therefore, the large variation in the observed direction of escape incurs no penalty in the evasive performance of most larvae. Zebrafish larvae may therefore be variable, and therefore less predictable, and also achieve maximal escape performance.

The predator’s strategy

Although the present pursuit-evasion model was formulated with a focus on the prey, it also provides an opportunity to consider strategy from the standpoint of a predator. The minimum distance, the payoff considered by this model, is normalized by the response distance, which is the distance between predator and prey when the prey initiates its escape (Figs. 2 and 3). Because the absolute distance traversed is therefore predicted to be proportional to the response distance, the predator may first do well to minimize this distance. This may be achieved by approaching more slowly and thereby reducing the intensity of stimulation of the visual (Dill 1974) and lateral line (Stewart et al. 2014) systems of the prey. This is one benefit to the braking behavior that suction-feeding predators exhibit before a strike (Higham et al. 2005; Higham 2007). Another advantage to a slow approach is the potential for greater accuracy in the timing and direction of a suction-feeding strike, which is restricted to a brief duration over a relatively small region around a predator’s mouth (Wainwright et al. 2001). Therefore, although the slow-predator domain offers the opportunity for prey to successfully escape in a variety of directions (Figs. 2 and 3), predators may approach slowly and thereby minimize the response distance and enhance the accuracy of their strike.

Our results also indicate some of the strategic advantages for fast predators. Moving faster than the escaping prey greatly diminishes the escape angles that are beneficial for evasion (Fig. 2B). As we discussed above (in “Optimal prey strategy”), the fast-start can become ineffective at offering any benefit to the prey’s evasion when the predator is substantially faster and headed directly at the prey. However, such a high-speed approach may present a challenge for a predator to coordinate the timing of the strike (Higham et al. 2005; Higham 2007). Therefore, the fast-predator domain will be most successful for ram-feeding predators that are capable of a well-timed and accurately-directed strike.

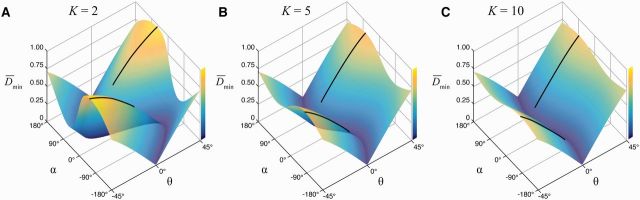
We conducted a series of simulations in the intermediate strategic domain to examine the effect of a predator’s accuracy in striking. As in our comparison with experimental results (Fig. 3), we calculated the minimum distance for a range of values in escape angle and initial position, but this time considered predators that were faster than prey (K > 1). We interpreted deviation from a zero angular position as a measure of inaccuracy in the strike of the predator, under the assumption that fish lack the interception strategy of targeting used by bats (Ghose et al. 2006) and birds (Kane and Zamani 2014). This measure of inaccuracy neglects the increasing challenge of correct timing in the opening of the jaws (Kane and Higham 2011, 2014), but does address the effect of error in the direction of the approach.

The results of these simulations illustrate the relative contribution of escape angle and the accuracy of a strike on evasion for different speeds of approach. For a predator that is twice as fast as the prey (K = 2), the minimum distance varied substantially both with escape direction and the accuracy of strike (Fig. 4A). For example, the optimal escape angle (${\alpha }_{\text{opt}}=60.0$°) generated a minimum distance (${\overline{D}}_{\text{min}}=0.71$) that was more than two-orders of magnitude greater than what was achieved with the least effective direction of escape (${\overline{D}}_{\text{min}}=0.002$), when the prey was positioned at 15° from the predator’s heading. This advantage in minimum distance was not greatly reduced (${\overline{D}}_{\text{min}}=0.50$ at ${\alpha }_{\text{opt}}=60$°) if the predator successfully aligned its strike (${\theta }_0=0$°). However, the escape angle played a reduced role in aiding evasion at faster speeds of approach by the predator. For example, when the predator was 10-times faster (Fig. 4C) and inaccurate (${\theta }_0=15$°), then the optimal escape angle (${\alpha }_{\text{opt}}=84.3$°) was only slightly more than twice the value (${\overline{D}}_{\text{min}}=0.35$) for the least effective angle (${\overline{D}}_{\text{min}}=0.16$). Furthermore, the optimal minimum distance (${\overline{D}}_{\text{min}}=0.10$) was relatively ineffective for an accurate strike (${\theta }_0=0$°). Therefore, the accuracy of a predator’s strike becomes an increasingly dominant factor in determining the prey’s survival with predators that are many times faster than the prey.

Fig. 4.

Evasive performance in the intermediate strategic domain. Numerical simulations calculated the minimum distance for variable initial position (θ₀) and escape angle (α) of the prey for predators that are faster than the prey by a factor of 2 (A), 5 (B), and 10 (C). (This figure is available in black and white in print and in color at Integrative and Comparative Biology online.)

Conclusions

The present theoretical study suggests that predator–prey interactions in fish may be characterized by three strategic domains. In the slow-predator domain, prey have the opportunity to escape in a variety of directions (Figs. 2B, 3B–C). In the fast-predator domain, the accuracy of the predator’s heading becomes a major determinant in the outcome. It is in the intermediate domain for which optimal prey strategy is meaningful because the minimum distance varies greatly with the direction of an escape (Fig. 2B).

It may appear counterintuitive that any predator would choose to move slowly. Predatory fishes are commonly between 2-fold and 20-fold greater in length than their prey (Fuiman 1994) and generally are capable of swimming many times their body length per second by rapid undulation (Bainbridge 1958). However, fishes also exhibit a large scope of swimming speeds and may move slowly by the coordinated braking action of their many fins (Videler 1981; McHenry and Lauder 2005). Many suction-feeding predators take advantage of this hydrodynamic plasticity to swim slowly on the approach of a feeding strike. This braking results in swimming that is in the lower range of potential speeds, at rates below a single body length per second (Higham et al. 2005; Higham 2007). In contrast, a startled prey may act to maximize its distance from a predator with its fastest swimming possible. Even a larval fish may attain speeds in excess of 50 lengths s^–1 during a fast-start (Müller and van Leeuwen 2004). Therefore, prey may compensate for their smaller size if the predator brakes for suction feeding to operate in the slow-predator domain (K < 1, Fig. 3).

As we have demonstrated, a key characteristic of the slow-predator domain is the ability of prey to escape in a variety of directions with equal effectiveness (Equation (11), Fig. 3). This strategic benefit for the prey is compatible with our thinking about the motor control of the escape response. Zebrafish larvae respond to a robotic predator with directionality that is no more specific than moving away from the side of the body stimulated by a faster flow stimulus (Stewart et al. 2014). Such crude decision-making may be achieved through relatively few synapses that serve to create motion with brief latency (Liu and Fetcho 1999). The present results suggest that there is little strategic disadvantage to this motor control. A short latency allows the prey to respond at greater distance and the direction of most responses is equally effective (Fig. 3C).

A failure of prey to conform to a single escape direction could be interpreted as deviation from optimal strategy. As explained above, the benefit to a population of prey responding in this way is that they become unpredictable to predators (Humphries and Driver 1970). However, this interpretation should not apply to interactions in the slow-predator domain. In this regime, a performance plateau, and not an optimum, permits maximal evasiveness for a large range of directions during escape (Fig. 3B–C). In this region of parameter space, no trade-off exists between predictability and evasiveness.

Different strategic dynamics come into play when the predator is slightly faster than the prey. In this intermediate domain ($1<K<10$), deviation from optimal strategy has the potential for large adverse consequences (Figs. 2B, 4A–B) and optimal strategy consequently is meaningful for the prey. Therefore, the intermediate domain should be most revealing of a prey’s capacity to attain optimal behavior. The present model is similar to most pursuit-evasion models in its assumption that the prey operates with perfect information about the predator. Therefore, the prey must detect the heading and speed of the predator in order to move in the optimal direction. Based on our understanding of the sensory biology of fish, this is likely to be achieved by the visual or lateral line systems (Dill 1974; Higgs and Fuiman 1996; Paglianti and Domenici 2006; Stewart et al. 2013). This use of the lateral line system is analogous to the sensing of flow by wood crickets when evading predatory wolf spiders (Casas and Steinmann 2014). It is additionally necessary that the motor system be capable of rapidly propelling a prey in the optimal direction. As noted by Domenici and Blagburn (2011), constraints on the sensory and motor systems can prohibit a prey from conforming to an optimum.

Sensory-motor constraints may play a role in the escape performance of guppies (Poecilia reticulata) that are preyed upon by pike cichlids (Crenicichla alta) (Walker et al. 2005). These predators are approximately twice as fast as the prey and therefore operate in the intermediate domain. Despite the potential benefit for prey to escape at the optimal direction, these guppies were observed to direct their escape with high variability. The survivorship of prey that escaped directly toward the predators ($\alpha \sim 180$°) was greater than in those that responded in the direction that our model would predict as optimal (${\alpha }_{\text{opt}}=60.0$°). It is additionally possible that the pike may accelerate to a degree that substantially violates the constant-velocity assumption of our model.

Our model predicts that the accuracy of a predator’s strike becomes a dominant factor in the outcome of an interaction in the fast-predator domain (K > 10). We found that differences in escape angle had a minor effect on the minimum distance across a broad range of escape angles (Fig. 2B). It remains possible that these differences in distance are more meaningful to the hydrodynamics of prey evasion when the predator is attempting a rapid strike. Resolving this issue would be aided by an explicit consideration of the hydrodynamics of feeding and of the escape response (as in Holzman et al. 2011).

We have identified conditions under which the outcome of a predatory strike differs little between optimal and suboptimal strategies. In particular, the optimal strategy for prey is not particularly meaningful in the slow-predator and fast-predator domains. In contrast, the direction of an escape is predicted to be a critical factor in the intermediate domain. That these domains are defined by the relative speed of the predator and prey underscores the coupled nature of strategy in pursuit-evasion games. The present interpretations have the potential to inform our reading of previous studies and to structure future experimental investigations not only of piscivorous interactions, but of other predator–prey interactions that may be characterized by pursuit-evasion models. We see this as a highly promising area for future experimental and theoretical study that is concerned with understanding the key factors that determine the outcome of predator–prey interactions.

Funding

This work was supported by grants from NSF (IOS-0952344 and IOS-1354842).

Supplementary data

Supplementary Data available at ICB online.