Microbial catabolic activities are naturally selected by metabolic energy harvest rate

Abstract

The fundamental trade-off between yield and rate of energy harvest per unit of substrate has been largely discussed as a main characteristic for microbial established cooperation or competition. In this study, this point is addressed by developing a generalized model that simulates competition between existing and not experimentally reported microbial catabolic activities defined only based on well-known biochemical pathways. No specific microbial physiological adaptations are considered, growth yield is calculated coupled to catabolism energetics and a common maximum biomass-specific catabolism rate (expressed as electron transfer rate) is assumed for all microbial groups. Under this approach, successful microbial metabolisms are predicted in line with experimental observations under the hypothesis of maximum energy harvest rate. Two microbial ecosystems, typically found in wastewater treatment plants, are simulated, namely: (i) the anaerobic fermentation of glucose and (ii) the oxidation and reduction of nitrogen under aerobic autotrophic (nitrification) and anoxic heterotrophic and autotrophic (denitrification) conditions. The experimentally observed cross feeding in glucose fermentation, through multiple intermediate fermentation pathways, towards ultimately methane and carbon dioxide is predicted. Analogously, two-stage nitrification (by ammonium and nitrite oxidizers) is predicted as prevailing over nitrification in one stage. Conversely, denitrification is predicted in one stage (by denitrifiers) as well as anammox (anaerobic ammonium oxidation). The model results suggest that these observations are a direct consequence of the different energy yields per electron transferred at the different steps of the pathways. Overall, our results theoretically support the hypothesis that successful microbial catabolic activities are selected by an overall maximum energy harvest rate.

Introduction

According to the second law of thermodynamics, systems with a high degree of organization are maintained by the input of external energy. Microorganisms, similar to other living systems, can be described as open systems exchanging material and energy with their surroundings (von Stockar et al., 2006). They obtain the required chemical energy input by the transformation from high- into low-energy content chemical components (Morowitz, 1968; Westerhoff et al., 2009).

Evidence suggests that the successful microbial metabolic strategies which still survive today in natural ecosystems could constitute the most efficient forms of energy harvest developed over millions of years of evolution (Vallino, 2003; Lane and Martin, 2010; Pascal and Boiteau, 2011; Lane et al., 2013). Successful microbial groups, when competing in energy-limited environments, consume the available energy and might prevent less efficient groups to thrive. This competition can be considered as a natural selection towards the most efficient microbial strategies and drives adaptation in energy-limited environments as well as improvements in the biochemical energy harvest mechanisms (Pfeiffer and Bonhoeffer, 2004; Pfeiffer et al., 2001), pursuing the minimization of energy losses (Jackson and McInerney, 2002; Hoehler and Jørgensen, 2013).

In natural ecosystems, a microorganism capable of harvesting more energy per unit of substrate consumed (that is, higher adenosine triphosphate (ATP) yield) appears, in principle, as in competitive advantage. But in systems where substrate availability is the limiting factor, a microorganism capable of harvesting more energy per unit of time (that is, higher ATP rate) could overcome the previous one (Pfeiffer et al., 2001; Schuster et al., 2008). Longer catabolic pathways favour higher yields by harvesting more energy per mol of substrate while shorter pathway metabolisms can achieve faster specific uptake turnover rates. This makes not always clear whether a system would evolve towards a maximization of the growth yield or growth rate.

This trade-off between yield and rate of energy harvest is believed to be a key factor for ecological interactions. Cooperation, selfishness, altruism and competition have been widely observed in microbial ecosystems (Pfeiffer et al., 2001; Pfeiffer and Bonhoeffer, 2004; Kreft and Bonhoeffer, 2005; MacLean, 2008). In particular, syntrophic relations between species have been strongly hypothesized as predecessor stages for a later evolved endosymbiosis, which ended up in the formation of new species (Margulis and Chapman, 1998; López-García and Moreira, 1999; Stams and Plugge, 2009; Lane and Martin, 2010).

In this study, we propose that the success of certain experimentally observed microbial metabolisms and syntrophic relationships over others (theoretically possible but never experimentally found to be conducted by one single cell) might be determined by bioenergetic considerations. For this purpose, an energy-based model has been developed, which includes thermodynamic information (potential energy harvested from a specific catabolism) and kinetic information (related to catabolic pathway length and substrate availability), to study the competition between different proposed microbial metabolisms. The catabolic activities are limited to known enzymatic reactions and carried out by cells with no specific adaptations to the environment. The model aims at describing not only the growth of the different microbial groups considered but also the impact of their activities in the environment (that is, changes in the media chemical concentrations) such that syntrophic relationships between microorganisms in the ecosystem might emerge or be limited.

Materials and methods

Model description

In order to test the hypothesis of bioenergetics as the main selector for the success of specific microbial metabolisms, an energy-based model (following concepts proposed in Rodríguez et al., 2008) has been developed to be applied to specific microbial ecosystems hypothesized in this study. A detailed description of the model equations is included in Supplementary Information S1. The model simulates the activity of simple microbial groups (non-adapted in terms of specific advantages to any environment) carrying out different specific catabolic processes defined as combinations of well-known biochemical reactions present in microorganisms.

Generalized metabolism stoichiometry (growth yield) from bioenergetics

Microorganisms must survive with the energy they harvest (typically as ATP) from the total available in the overall catabolism reactions (ΔG_cat, see table of symbols in Supplementary Information S4). Part of this energy must be invested in the maintenance and the rest is available to drive growth through anabolic reactions. Catabolism is here defined as a chemical reaction that converts substrates (S, eD (electron donor)) into lower-energy products (P) and anabolism as the process that converts a carbon source (C_S) and a nitrogen source (N_S) into cells' biomass (C_X) with energy consumption (Equation 1).

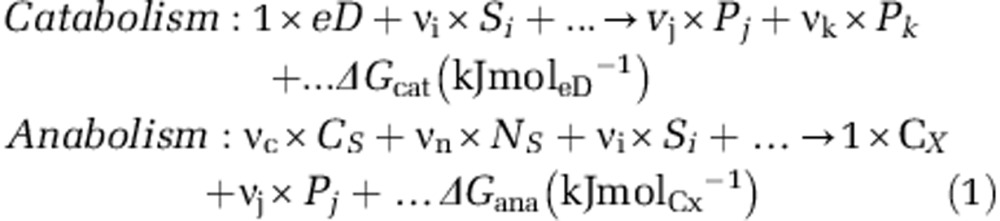Catabolism and anabolism are described as two mass-balanced independent processes only linked by the energy exchange through the production and consumption of ATP. Both processes are quantitatively coupled by the number of times that catabolism needs to run to yield the necessary energy to form one C-mol of biomass λ_cat (mol_eD mol_Cx⁻¹) (Heijnen and Kleerebezem, 2010). Under this approach, if catabolism and anabolism reactions are known, the overall metabolism becomes a function of λ_cat (Met=Ana+λ_cat × Cat).

Not all the energy harvested through catabolism can be available for growth as part must be dissipated mainly during anabolism (ΔG_dis, kJ mol_Cx⁻¹). The energy dissipated has been previously estimated based on the carbon source molecule size and degree of reduction (Heijnen and van Dijken, 1992; Heijnen et al., 1992). This approach allows for the overall metabolism to be estimated by means of an energy balance to the system (von Stockar et al., 2006; Kleerebezem and van Loosdrecht, 2010) Equation 2, in which the energy dissipated in catabolism is negligible with respect to anabolism, is based on the much lower number of reactions and minimized energy losses in catabolic reactions (microorganisms are able to survive in systems even with strong energy limitations (Jackson and McInerney, 2002; González-Cabaleiro et al., 2013). The inverse of λ_cat is analogous to the maximum growth yield if the electron donor for anabolism and catabolism are different (Y_XS^max, mol_Cx mol_eD⁻¹) (Heijnen and Kleerebezem, 2010.

This generalized approach allows for the overall metabolism stoichiometry and yield to be described as a sole function of bioenergetics (ΔG_cat, ΔG_ana, ΔG_dis) for any postulated microbial metabolism (see example on Supplementary Information S1.2).

Generalized kinetics from maximum electron transfer in the catabolism

The reported attempts to estimate the rate of microbial growth from bioenergetics (for example, using an approximation of the energy dissipation in the catabolic pathway) have not been fully successful (Waddell et al., 1999; Manchester, 2000). Growth rate has, however, been considered as limited by the length of the pathway by relating the need for higher enzyme concentrations with higher energy consumptions (Pfeiffer and Bonhoeffer, 2004) or directly by relating the growth rate with the number of reaction steps required in the catabolism (Costa et al., 2006).

Experimental evidences of a maximum specific rate of electron transport in the catabolism (referred to enzymatically catalysed oxidations or reductions) have been reported and used in similar models (Andersen and von Meyenburg, 1980; van de Leemput et al., 2011). In this work, the number of electrons transferred has been used as the general representative measure of catabolic activity and a constant maximum value (3 mol_e− (mol_Cx·h)⁻¹) adopted across the board for all microbial activities considered. This has been implemented in the form of a specific maximum substrate uptake rate (q_S^max, mol_eD (mol_Cx·h)⁻¹) using Equation 4 (Heijnen and Kleerebezem, 2010), in which N_e (mol_e− mol_eD⁻¹) is the number of electrons transfers attributed throughout a catabolism per mol of the electron donor substrate.

Full details of how N_e values are calculated for each catabolic pathway can be found in Supplementary Information S1.3.

In addition to the above q_S^max, the metabolic rate depends also on the availability of the limiting substrate. Monod-like saturation terms (Equation 5), as commonly used in microbial kinetic models, are adopted. The minimum among all substrate saturation terms (that is, the limiting substrate, S_lim) is defining the metabolic rate (Equation 5).

Monod half saturation values (K_S) are typically obtained experimentally (Heijnen and Kleerebezem, 2010) and no general agreement on their mechanistic interpretation has been achieved (Liu, 2007; Wang et al., 1998; Snoep et al., 2009). For the purpose of this model, a general theoretical approach was proposed based only on the relative differences between the diffusivities of the different substrates (which implies no differences in the K_S values for the species competing for the same substrate) to estimate Ks values of both the existing and postulated microbial metabolic activities (more details on the K_S modelling are presented in Supplementary Information S1.4). The main goal of the K_S implementation is to maintain a working realistic dynamics of the microbial ecosystem while avoiding much interference with the bioenergetics hypothesis subject of the study. It is important to highlight that all microorganisms are modelled as non-specialized to any particular environment and as physiologically non-differentiated, being also equally efficient in harvesting the energy from their catabolic activities. Experimentally observed physiological differences among microbial species leading to differences in the parameters describing their kinetics can be attributed to later evolutionary adaptations and specializations of species conducting a catabolic activity. Considering that this modelling approach addresses the competition between microbial activities, these specific adaptation differences cannot be and are not considered. In the model presented, microbial groups compete based on energetic considerations.

For this reason, the same values for q_S^max and for Ks are applied to all the microbial activities considered in the model. The uncertainty and impact of the numerical values used, owing to the limited experimental information available, was assessed with a sensitivity analysis for both K_S and q^max values. The results (presented in the Supplementary Information S3 and Supplementary Figures S4–S11) support the relative independence of the study conclusions from the values assumed for these two parameters, which display only numerical and minor impacts.

Kinetics of microbial growth and decay

Although the specific microbial growth rate of each postulated microbial group (μ, h⁻¹) is determined by the total energy harvest rate from its specific catabolism (E_cat, kJ (mol_Cx·h)⁻¹) (Equation 7), not all the energy harvested can be used for growth. The maintenance energy required to sustain the population (m_G, kJ (mol_Cx·h)⁻¹), reducing the actual growth yield, is assumed constant and equal for all the microorganisms considered (Supplementary Information S1.5)

The actual Gibbs energy change of each catabolic reaction (ΔG_cat), function of the concentrations of the chemical components in the system, is precisely computed at each simulation time step and the specific catabolic energy harvest rate is calculated according to Equation 6.

With this approach, three possible modes of the microbial growth exist (detailed equations are presented in Supplementary Information S1.6).

Positive net growth: occurs when the rate of energy harvest exceeds that required for the maintenance of the existing cell population (Equation 7). Here substrate uptake goes to both growth and catabolism purposes as,

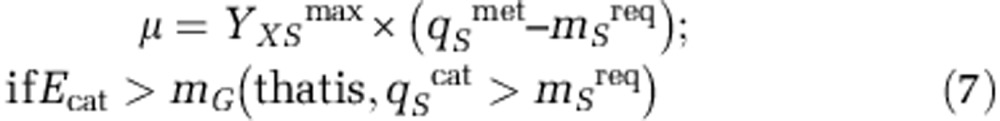where q_S^met kinetics (Equation 5) includes anabolism-related possible limiting substrates (for example, nitrogen source).

Zero net growth: occurs when the energy available exactly meets the requirements for maintenance of the existing cell population. In this mode, no net growth or decay takes place, only substrate consumption in order to provide the necessary energy for maintenance of the microbial population.

Negative net growth (decay): occurs when the energy available is not sufficient to meet the maintenance requirements of the existing cell population. A net decay rate is modelled as proportional to the energy shortage with respect to that required for maintenance. This process is defined as converting active biomass into death biomass (X_d), Equation 8. In this and in the previous zero net growth mode, substrate uptake goes only to catabolism (q_S^cat),

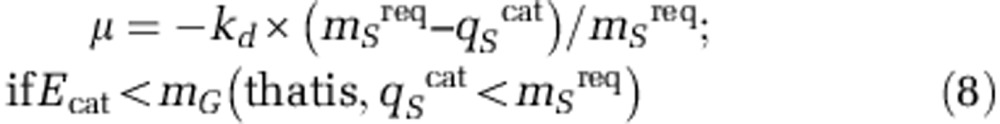where k_d (h⁻¹) is a decay kinetic parameter, whose value is assumed to be 8.33 × 10⁻⁴ h⁻¹ for all postulated microorganisms (Batstone et al., 2002) and q_S^cat kinetics (Equation 5) includes only catabolism-related possible limiting substrates as no cell growth occurs in this scenario.

Dead biomass is assumed as biodegradable and hydrolysed into glucose or acetate equivalents in a first-order kinetics (Equation 9) as commonly found in literature (Batstone et al., 2002),

where X_d is the concentration of dead biomass (mo l⁻¹) and K_Hyd is the first-order constant for death biomass hydrolysis (h⁻¹). The value of 0.01 h⁻¹ is used for all the microorganisms considered (Batstone et al., 2002).

Results and discussion

The model, as described above, was applied to the simulation of two microbial ecosystems under different environmental conditions. First, the anaerobic fermentation of glucose at pH 7 and 5 with controlled hydrogen partial pressure is studied. Second, the aerobic autotrophic oxidation of inorganic nitrogen compounds and the reduction of nitrogen oxides with and without organic carbon source are studied. Tables 1 and 2 present the list of potential catabolic activities considered in each microbial ecosystem, including both reported and postulated. The considered hypothetical catabolic activities never observed in nature consist only of possible combinations of other observed ones; therefore activities involving unknown biochemistry have not been included.

Table 1. Catabolic reactions considered in the glucose anaerobic fermentation microbial ecosystem.

Anaerobic fermentation of glucose
Xi	Catabolism reaction	Ne, mole− moleD−1	ΔG01a, kJ moleD−1	ΔG01/e−, kJ mole−−1
1	C6H12O6 + 2H2O → 2C2H3O2− + 2CO2 + 4H2 + 2H+	8	−215.90	−26.99
2	C6H12O6 → C4H7O2− + 2CO2 + 2H2 + H+	12	−264.10	−22.01
3	C6H12O6 + 2H2 → 2C3H5O2 + 2H+ + 2H2O	12	−359.25	−29.94
4	C6H12O6 → 2C2H6O + 2CO2	16	−235.00	−14.69
5	C2H3O2− + H+ → CH4 + CO2	2	−35.78	−17.89
6	C2H3O2− + H+ + 2H2O → 2CO2 + 4H2	8	95.02	11.88
7	½CO2 + H2 → ¼C2H3O2− + ¼H+ + ½H2O	2	−23.76	−11.88
8	H2 + ¼CO2 → ¼CH4 + ½H2O	2	−32.70	−16.35
9	C4H7O2− + 2H2O → 2C2H3O2− + H+ + 2H2	4	48.20	12.05
10	C3H5O2− + 2H2O → C2H3O2− + 3H2 + CO2	6	71.68	11.95
11	C2H6O + H2O → C2H3O2− + H+ + 2H2	4	9.55	2.39
12	C6H12O6 + 6H2O → 6CO2 + 12H2	24	−25.85	−1.08
13	C6H12O6 + 2H2O → 2CH4 + 4CO2 + 4H2	12	−287.46	−17.97
14	C6H12O6 → 3C2H3O2− + 3H+	16	−310.92	−19.43
15	C6H12O6 →3CH4 + 3CO2	20	−418.26	−20.91
16	C4H7O2− + H+ + 6H2O → 4CO2 + 10H2	20	238.25	11.91
17	C4H7O2− + H+ + 2H2O → 2CH4 + 2CO2 + 2H2	8	−23.36	−1.95
18	C3H5O2− + H+ + 4H2O → 3CO2 + 7H2	14	166.70	11.91
19	C3H5O2− + H+ + 2H2O → CH4 + 2CO2+3H2	8	35.90	3.59
20	C2H6O + 3H2O → 2CO2 + 6H2	12	104.57	8.71
21	C2H6O + H2O → CH4 + CO2 + 2H2	6	−26.23	−3.28

^aConsidering pH 7 and 298.15 K. Liquid concentrations 1 m and 1 bar for gas components (CH₄, CO₂ and H₂).

Table 2. Catabolic reactions considered in the inorganic nitrogen oxidation–reduction microbial ecosystem.

Nitrogen oxidation and reduction
Xi	Catabolism reaction	Ne,mole− moleD−1	ΔG01a, kJ  moleD−1	ΔG01/e−, kJ mole−−1
1	NH4+ + 1.5O2 → NO2− + 2H+ + H2O	6	−269.90	−44.98
2	NO2− + ½ O2 → NO3−	2	−76.50	−38.25
3	NH4+ + 2O2 → NO3− + 2H+ + H2O	8	−346.40	−43.30
4	C2H3O2− + 8/5NO3− + 13/5H+ → 4/5N2 + 2CO2 + 14/5H2O	8	−805.60	−100.70
5	C2H3O2− + 8/3 NO2− + 11/3 H+ → 4/3N2 + 2CO2 + 10/3H2O	8	−977.50	−122.19
6	C2H3O2− + 2NO3− + 3H+ → N2O + 2CO2 + 3H2O	8	−689.40	−86.18
7	C2H3O2− + 4NO2− + 5H+ → 2N2O + 2CO2 + 4H2O	8	−831.00	−103.88
8	C2H3O2− + 4N2O + H+ → 4N2 + 2CO2 + 2H2O	8	−1270.50	−158.81
9	C2H3O2− + 4NO3− + H+ → 4NO2− + 2CO2 + 2H2O	8	−547.70	−68.46
10	C2H3O2− + NO3− + 3H+ → NH4+ + 2CO2 + H2O	8	−507.30	−63.41
11	C2H3O2− + 4/3NO2− + 11/3H+ → 4/3NH4+ + 2CO2 + 2/3H2O	8	−493.80	−61.73
12	NH4+ + NO2− → N2 + 2H2O	4	−362.80	−90.70

^aConsidering pH 7 and 298.15 K. Liquid concentrations 1 m and 1 bar for gas components (N₂, N₂O and CO₂).

For the anabolic reaction, the same electron donor as in catabolism is taken as carbon or nitrogen source when it contains carbon or nitrogen, respectively. Alternatively, CO₂ is considered as carbon source and NH₄⁺ as the nitrogen source.

All the simulation case studies are started with equal concentrations of all microbial groups. A continuous stirred tank reactor (CSTR) model with high solids retention time (average cell age) was selected to describe the hydrodynamics of the process. A CSTR system was selected as analogous systems are frequently found in nature and in most wastewater treatment plants. Full details of the operational conditions simulated are presented in Supplementary Table S1 and Supplementary Information S2.

Anaerobic fermentation of glucose

Anaerobic digestion is a well-established process widely used in waste and wastewater treatment owing to its potential as biogas producer (Appels et al., 2008). In anaerobic digesters, the importance of an efficient syntrophic cooperation between different bacteria and archaea, fermenting glucose to methane and carbon dioxide, is well known (Schink, 1997; Schink and Stams, 2006). This microbial ecosystem was selected to investigate, among other questions, whether, under this approach, a hypothetic microorganism capable of producing methane directly from glucose would be competitive over the experimentally reported volatile fatty acid (VFAs) synthesizers in synergy with methane-producing archaea. Methanogens have been reported to possess the biochemical mechanisms to metabolize carbohydrates (König et al., 1985; Murray and Zinder, 1987); however, there is no experimental evidence of any microorganism producing methane directly from a carbohydrate as substrate (Schink, 1997).

The anaerobic glucose-fermenting microbial ecosystem studied is defined by also initially considering the presence of microorganisms that hypothetically would be able to completely convert glucose or different VFAs and ethanol to CH₄ and CO₂ or H₂ and CO₂ in addition to those well known that convert glucose or VFAs and ethanol first to acetate and then to CH₄, CO₂ and H₂ (Table 1).

Two operational conditions were simulated: (i) anaerobic fermentation of glucose towards methane production and (ii) non-methanogenic fermentation of glucose at controlled hydrogen partial pressure (see Supplementary Table S1 for full details). The latter is an operation mode of current interest in process development towards the production of higher energy density liquid products from VFAs (González-Cabaleiro et al., 2013).

Glucose fermentation to methane

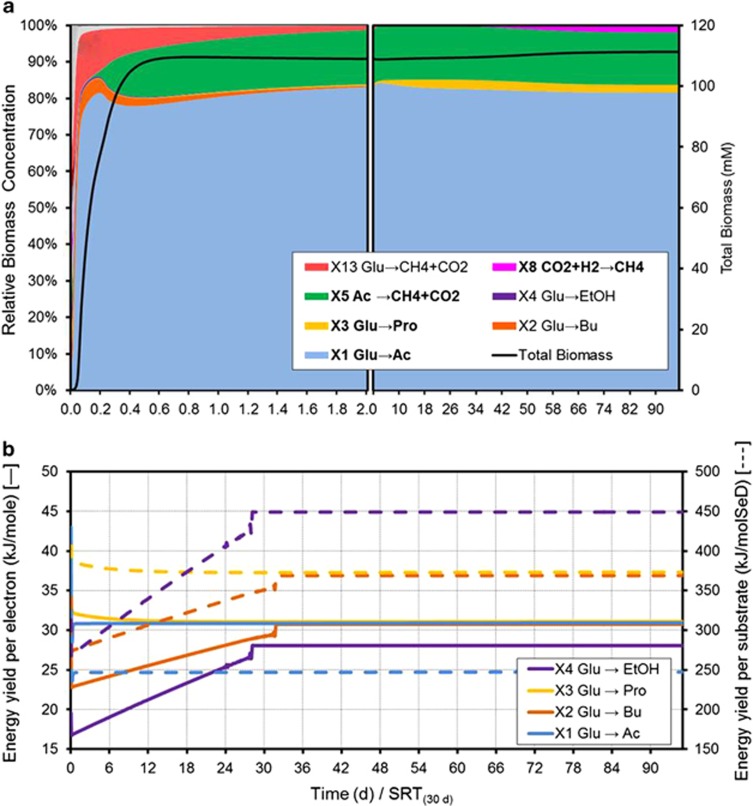
The model simulations (see Figure 1a) predict acetate producers (X₁) and acetate consumers to methane (X₅) as the dominant activities at steady state in line with the experimental observation. These results can be explained because X₁ catabolism involves a smaller quantity of metabolic labour (measured in this model as the number of electrons transferred, N_e) than other glucose consuming metabolisms (Table 1) and that translates into a higher maximum specific substrate uptake rate (q_S^max, see Equation 4). Acetate production catabolism appears as one of the largest energy harvesters per mol of electron transferred (Figure 1b, left axis), advantage that allows this catabolism to dominate over the others under these specific conditions.

Figure 1.

Simulated dynamics of the microbial ecosystem during anaerobic fermentation of glucose to CH₄. (a) Evolution of the microbial population in total biomass and relative abundance terms. (b) Catabolic energy yield per mol of electron transferred throughout the catabolic reaction (solid line) and catabolic energy yield per mol of substrate (dashed line).

Simultaneously to this, acetate-consuming methanogenesis performed by X₅ appear to obtain a very low energy yield from acetate to methane, but it is the large availability of the substrate combined with a high maximum specific uptake rate due to the very low metabolic labour involved (N_e=2, see Table 1) that allows this catabolic activity to also succeed in parallel with acetate producers.

The synergy established between acetate producers and consumers in this system constitutes a division of labour revealed as beneficial for both. The first provides substrate for the second, which, in turn, increases the energy available for the first (ΔG_cat) by removing the reaction product. This collaborative work does not imply a higher total energy yield per unit of substrate over the whole pathway, but it does achieve a higher overall energy harvest rate.

The existing trade-off between yield and rate in energy harvest promotes the abundance of species that consume glucose to produce VFAs in this system. This analysis presents a mechanism for the reasons why a possible microorganism capable of harvesting more overall energy per mol of glucose (by complete conversion into CH₄ and CO₂) may not actually have an overall competitive advantage compared with other organisms converting glucose to only VFAs. The additional energy gained by the final steps of the full pathway would not compensate for the lower metabolic rate associated with the longer metabolic pathway.

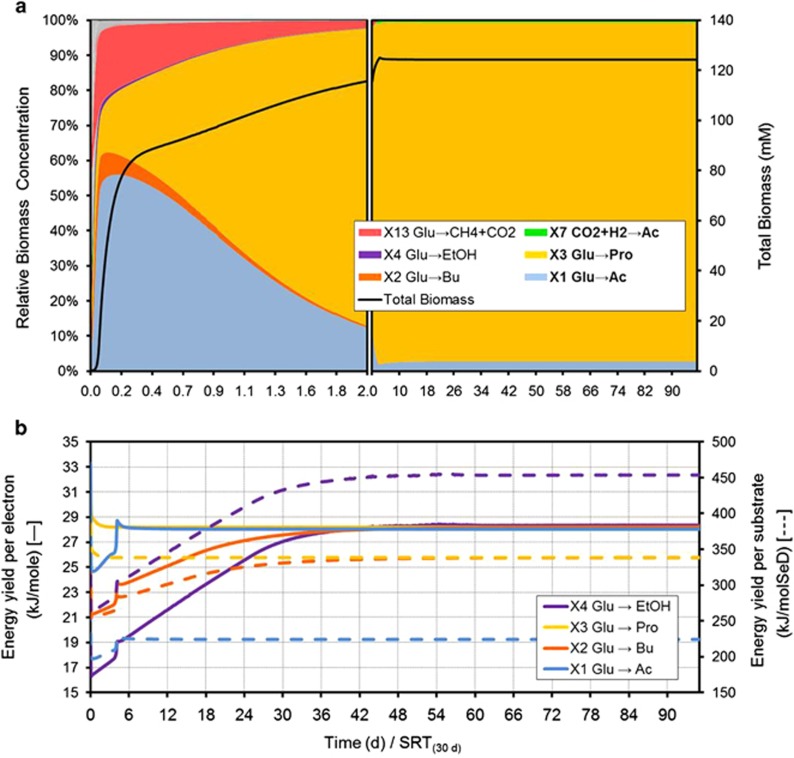
Non-methanogenic glucose fermentation at high H₂ partial pressure

Acidogenic fermentation of glucose by mixed anaerobic cultures is a process well-known to display a large diversity of products (Temudo et al., 2007). Our approach provides a possible explanation to this observation. The diverse catabolic pathways in anaerobic glucose fermentation have indeed very similar values of energy yield per electron mol (that is, acetate X₁, butyrate X₂, propionate X₃, and ethanol X₄ producers, Figures 1b and 2b), which implies that small changes in environmental conditions (concentrations) can easily lead to shifts between the most successful catabolic activities. This, together with the need to allocate electron equivalents into products in a system with no external electron acceptors available, presents a possible explanation for the variability and diversity of products typically observed in these fermentation systems.

Figure 2.

Simulated dynamics of the microbial ecosystem during anaerobic fermentation of glucose at acidic pH and constant high P_H2. (a) Evolution of the microbial population in total biomass and relative abundance terms. (b) Catabolic energy yield per mol of electron transferred throughout the catabolic reaction (solid line) and catabolic energy yield per mol of substrate (dashed line).

In order to test this and in the context of interest in the production of reduced products (propionic or butyric acids and ethanol) for biorefinery applications, the impact of high hydrogen pressure in the non-methanogenic fermentation of glucose was simulated. A simulation case study at constant fixed P_H2 of 1 atm (and a total pressure of 2 atm) and pH 5 was conducted (see Supplementary Table S1 for full details). For the sole purpose to isolate the intended effects, in this simulation, CH₄, CO₂, and H₂ producers (X₅, X₆, and X₈, typically archaea) were manually removed from the ecosystem (as they are fully inhibited in acidogenic fermentation at low pH).

Simulation results are shown in Figure 2. The high P_H2 value allowed the hydrogen-consuming propionate producers (X₃) to overcome other microbial groups that had initially higher growth rates (such as acetic acid producers, X₁). This is caused by the energetic shift that increases the catabolic available energy for X₃ due to the higher P_H2, and that therefore also directs the product formation of the ecosystem towards more reduced products.

Inorganic nitrogen oxidation–reduction

The second microbial ecosystem studied in this work is that performing the conversions from the nitrogen cycle metabolism consisting of the oxidation and reduction of inorganic nitrogen compounds. Winogradsky (1890) did first report about two microbial groups (ammonia oxidizing bacteria (AOB) and nitrite oxidizing bacteria (NOB)) working in syntrophic cooperation on the oxidation of ammonia. The reasons behind nitrification taking place in two stages have been an old question addressed by the kinetic theory of the optimal pathway length (Costa et al., 2006). Authors such as Costa et al. (2006) have hypothesized the possible existence of strains capable of performing complete nitrification in one stage. However, to date, no microorganisms capable of performing complete nitrification have been reported, fact that has been addressed by Pérez et al. (2009) based on the presence of some limitations of physiological nature.

The nitrogen oxidation–reduction microbial ecosystem studied is defined by initially considering the presence of microorganisms that hypothetically could conduct aerobic autotrophic nitrification as well as anoxic heterotrophic and autotrophic nitrogen oxides reduction reactions (Table 2). Both reported and hypothetical but not observed catabolic activities are included based only on combinations of known feasible biochemical reactions.

The operational and environmental conditions applied to this ecosystem are detailed in Supplementary Table S1. This ecosystem is also simulated for a CSTR at high solids retention time. Organic and inorganic carbon supply as well as oxygen presence are adjusted to evaluate three possible scenarios, namely: (i) autotrophic aerobic, (ii) hetrotrophic anaerobic and (iii) autotrophic anaerobic ecosystems. The simulation results are presented in Figure 3 for the autotrophic aerobic case and in Figure 4 for both the heterotrophic and autotrophic anaerobic cases.

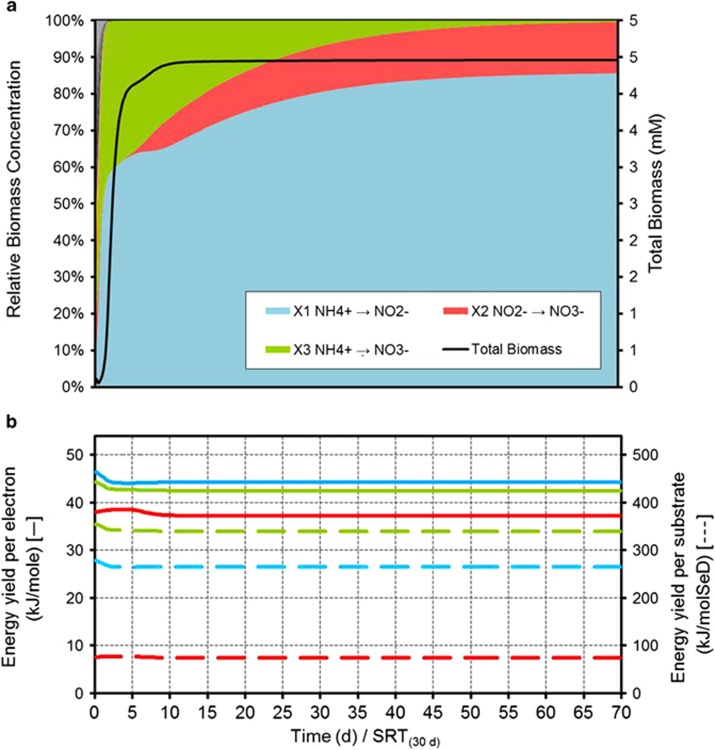
Figure 3.

Simulated dynamics of the microbial ecosystem during autotrophic nitrogen oxidation. (a) Evolution of the microbial population in total biomass and relative abundance terms. (b) Catabolic energy yield per mol of electron transferred throughout the catabolic reaction (solid line) and catabolic energy yield per mol of substrate (dashed line).

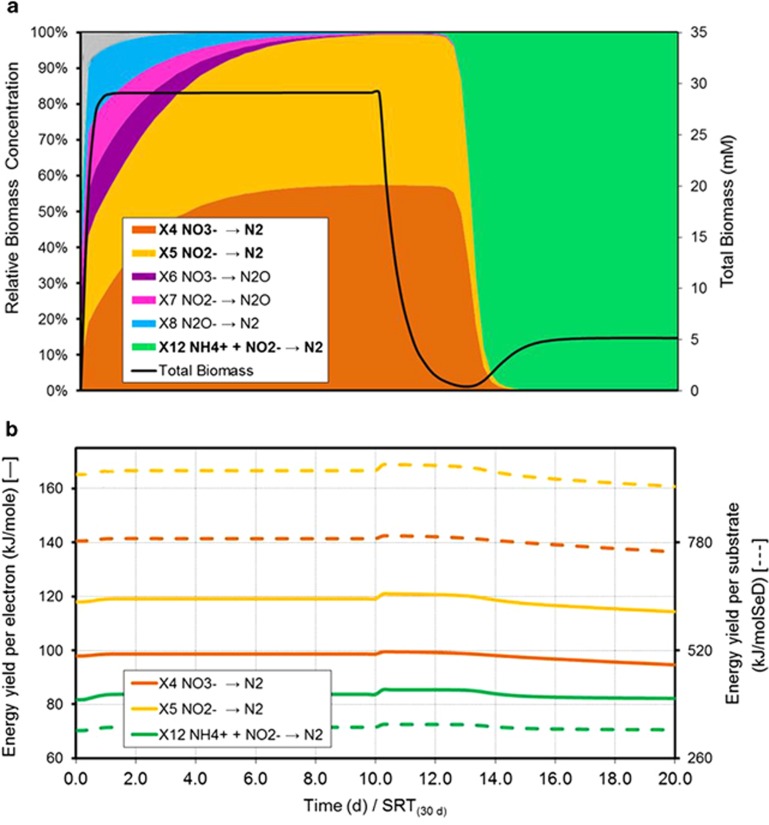
Figure 4.

Simulated dynamics of the microbial ecosystem during nitrogen reduction. (a) Evolution of the microbial population in terms of total biomass and relative abundance. (b) Catabolic energy yield per mol of electron transferred throughout the catabolic reaction (solid line) and catabolic energy yield per mol of substrate (dashed line).

Autotrophic aerobic nitrogen ecosystem

Under aerobic conditions, only X₁, X₂ and X₃ (that is, the aerobic autotrophic metabolic activities) have the necessary substrates to thrive and the others quickly decrease. When looking at the complete nitrification (X₃), although the total energy yield per unit of substrate is higher (Figure 3b), the energy yield per electron is lower than that of the partial nitrifiers to nitrite (X₁). The initially high concentration of ammonium allows for the presence of both partial (X₁) and complete (X₃) nitrifiers (Figure 3a). However as the ammonium concentration decreases over time, the energy yield gained by the one-step nitrifiers (X₃) becomes diminished to a larger extent than that of the partial nitrifiers (X₁). This is due to the latter benefiting from the activity of nitrite oxidizers (X₂), which by removing their reaction product (NO₂⁻) allow them to maintain a high energy yield to outcompete the complete nitrifiers (X₃) in the long run.

Nitrite oxidizers (X₂) become, together with ammonia oxidizers (X₁), the dominant microbial activities in the long term; this is despite their lower yield and partly due to the absence of any other competitors for nitrite in the system. The synergism between the two catabolic activities, analogous to the case of the anaerobic glucose fermentation system, leads to a higher overall energy harvest rate than the one-step nitrification. In both cases, the same overall energy yield per unit of substrate is obtained but, again, this occurs at a higher rate if the process is conducted by two separated microbial groups.

As these results are completely in line with the experimental observation of the well-known AOB and NOB, a possible explanation of the absence of competitive advantage for a microorganism in developing the complete nitrification in one step is hereby provided based on the energetic considerations.

Heterotrophic and autotrophic anaerobic nitrogen ecosystems

In order to explore the system behaviour under anaerobic conditions (Table 2) with an eye on denitrification, a case study is simulated with a mixture of nitrogen compounds (NH₄⁺, NO₂⁻ and NO₃⁻) with roles in denitrification fed to the reactor (Supplementary Table S1). Both heterotrophic (with acetate as carbon source) and autotrophic (with HCO₃⁻ as carbon source) conditions are studied. Simulations were run first with an acetate feed to allow for heterotrophic growth, and after steady state was reached, the feed of acetate ceased and a constant concentration of CO₂ was maintained for autotrophic growth conditions.

Heterotrophic denitrification activities from both NO₃⁻ (X₄) and NO₂⁻ (X₅) are predicted as prevailing metabolisms in line with experimental observations (Ruiz et al., 2006), both displaying similar growth rates and yields. Other postulated metabolisms, such as the two-stage heterotrophic denitrification through N₂O (X₆, X₇ and X₈), and dissimilatory nitrite and nitrate reductions (X₉, X₁₀ and X₁₁) are, however, not predicted as successful in the system.

The energy available in NO_x reduction to N₂O (X₆ and X₇) is smaller compared with the reduction to N₂ (X₄ and X₅, Table 2) while the same amount of electrons are transferred in the process. This explains why denitrification stopping in N₂O appears as not favoured in our simulations. However, NO_x reduction to N₂O has been repeatedly reported to be associated with a competition between the enzymes involved in the four reductive steps of complete denitrification under specific environmental conditions, such as limitation in the carbon and nitrogen ratio or at low ranges of pH (Pan et al., 2012, 2013a, 2013b). These very specific biochemical limitations are out of the scope of our modelling approach, and for this, the presence of N₂O denitrification cannot be predicted.

Dissimilatory nitrite and nitrate reductions are also not predicted as successful metabolisms (even if NH₄⁺ feeding is stopped, data not shown) despite the fact that they have been reported where electron donors other than organic matter (for example, H₂S) (An and Gardner, 2002) and/or specific environmental conditions (Roberts et al., 2014) are present.

Finally, in the absence of organic carbon source, autotrophic anaerobic ammonia oxidizers (anammox, X₁₂) are predicted as successful dominant catabolic activity. This occurs despite the higher energy yields of other denitrification routes (Figure 4b), and it is attributed to the environmental conditions of limited organic carbon source that allow anaerobic ammonia oxidizers to appear (van de Graaf et al., 1996).

Shorter pathway lengths and cross feeding prevail under decreasing average energy yield per electron

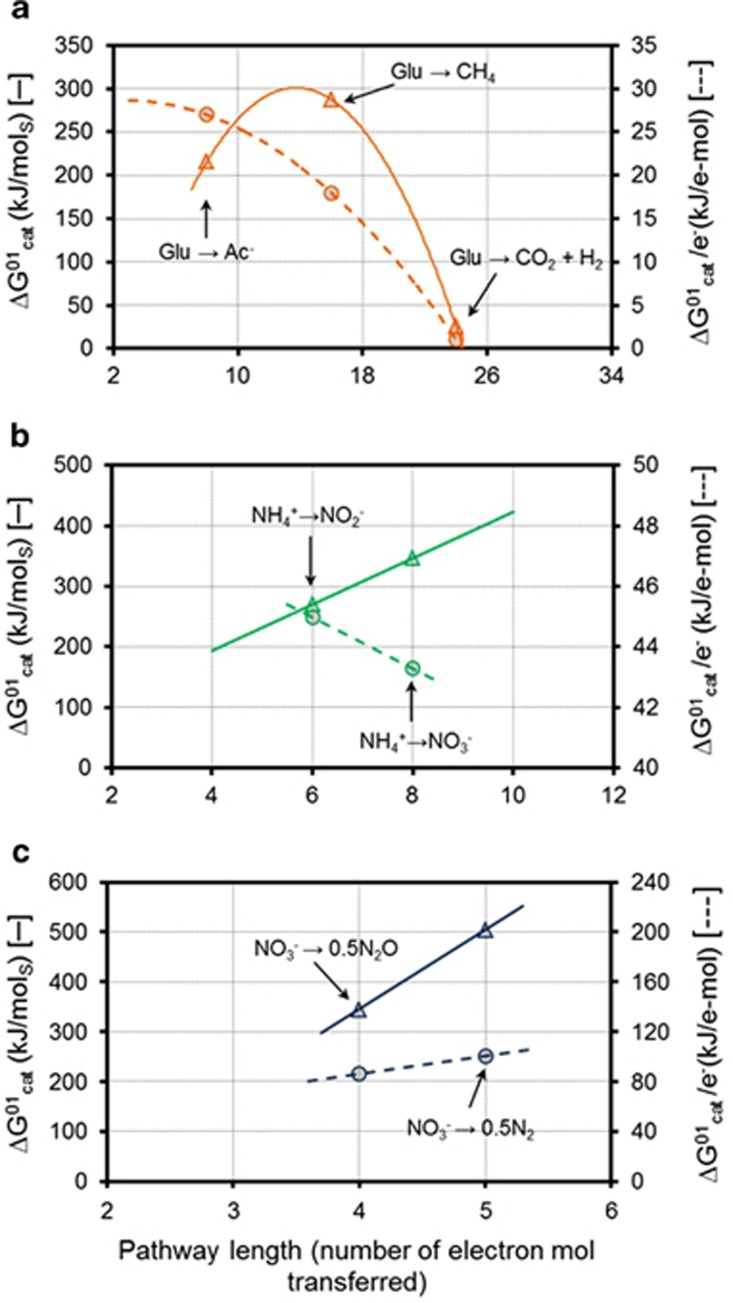
Two-stage autotrophic nitrification as opposite to one-stage heterotrophic denitrification are both predicted by the modelling approach and experimentally observed. An analysis of the energy yields per electron provides a plausible explanation of these observations. Unlike the similar analysis by Costa et al. (2006), any physiological aspects of ATP production are excluded and the total Gibbs energy available of each catabolic process is directly used together with an account of the number of electron transfers in each pathway. The relationship between energy and pathway length is illustrated in Figure 5 by comparing the average Gibbs energy yields per electron transferred with the yields per mol of substrate for the pathways studied above (standard conditions and pH 7 are considered).

Figure 5.

Theoretical energy yield per mol of substrate (triangles) and per mol of electron transferred (circles) with respect to pathway length for (a) glucose fermentation; (b) nitrification and (c) denitrification. (ΔG⁰¹ values are presented in Table 1; for denitrification case, ΔG⁰¹ is referred per mol of NO₃⁻).

The overall analysis of the modelling results suggests that the lengths of the successful pathways predicted above and experimentally reported appear to be defined by the maximum energy harvest rate (which is also affected by the environmental conditions). Stepwise processes appear as more favourable when pathways have decreasing average energy yields per electron transferred (Figure 5b), whereas direct longer pathway conversions are favoured at increasing average energy yields instead (Figure 5c). This is further illustrated in Supplementary Information S2.2.

Conclusions

Through a modelling approach based on the available energy in catabolic reactions and using the number of electron transfers in a pathway as measure of maximum specific metabolic rate, the success of specific microbial catabolic activities as well as syntrophic relations can be predicted in good agreement with experimental observations. The modelling approach provides mechanistic hypotheses, on the basis of bioenergetic considerations, for the reasons behind the success of certain microbial activities in nature versus others.

The analyses are developed by comparing metabolic activities conducted by non-adapted microbial groups, competing under the same conditions for the available energy. Non-differentiated enzymatic rates are assumed by considering the same q_S^max per electron for all microbial groups (Equation 4). Similarly, non-differentiated substrate transport capacities are assumed for Ks calculations by considering the same cell shape and size (Supplementary Information S1.4). These generalized parameter values attempt to reflect the modelling of non-specifically adapted microorganisms, using very limited empirical information. The q_S^max and K_S parameters, for which arguably different numerical values could be used, do not appear to affect the results and conclusions obtained, which are very much in line with the experimentally observed microbial activities. However, it is important to highlight that at the core of the modelling approach presented is the assumption that all the non-adapted microbial groups have non-differentiated physiological characteristics (that is, the same maximum specific rates, half saturation kinetic constants controlled by transport kinetics, cell shape and size, equal maintenance and decay kinetics, fully efficient catabolic energy harvest) and that the hypotheses resulting from this study must be interpreted with these limitations in consideration.

During the simulation of a glucose anaerobic fermentation ecosystem, a multistage microbial conversion from glucose to methane (involving VFA producers in synergy with methanogens) is predicted as successful versus a single-stage microbial conversion. This is a direct consequence of the higher energy yield per electron in the conversion of glucose to VFAs with respect to that of VFAs to methane. In addition, the very similar energy harvest rates displayed by several of the alternative conversions of glucose to VFAs and alcohols potentially explain the variability and diversity of catabolic products observed in (non-methanogenic) glucose fermentation ecosystems under different operational conditions.

Analogously, during the simulation of the nitrogen oxidation–reduction ecosystem, the autotrophic ammonium oxidation in two stages (involving AOB in synergy with NOB) is predicted as favoured versus a single-stage microbial conversion from ammonium to nitrate. This is a direct consequence of the mutually beneficial syntrophic relation between AOB and NOB described by the dynamic model simulations presented. The syntrophic AOB–NOB cooperation is analogous to that existing between acetate producers and consumers in the glucose fermentation case capable of overcoming a hypothetical one-stage nitrification alternative.

The above pathway partitions are not predicted, however, during the simulation of heterotrophic denitrification (NO_x reduction), again in line with experimental observations. This is attributed to the lower energy per electron involved in NO₂⁻ or NO₃⁻ reduction to N₂O than that from N₂O to N₂, leading to an optimum one-stage denitrification to achieve a maximum energy harvest rate.

Overall, the modelling approach provides energy-based mechanistic interpretations to experimental observations, supporting a hypothesis of maximum energy harvest rate as the main selective pressure in some microbial ecosystems.

The dynamic simulation of the hypothetic competition between non-specialized proposed and experimentally observed microbial activities suggests that the evolutionary adaptation of microorganisms towards specific successful catabolic activities is determined by the maximum energy harvest rate under the given environmental conditions. The model is capable of describing the interdependences between the energy available in the system, the environmental conditions and the activity of the microorganisms present, which dynamically affect one another.

Given these results, we advocate for the study of microbial ecosystems as highly efficient energy harvesters and postulate that the quest for energy might have promoted synergetic cooperation between microorganisms and also possibly directed subsequent steps in the evolutionary course towards more complex micro- and macro-organisms.

The authors declare no conflict of interest.