An excitatory basis for divisive normalization in visual cortex

Abstract

Neurons in visual cortex are connected not only locally but also through networks of distal connectivity. These distal networks recruit both excitatory and inhibitory synapses, and result in divisive normalization. Normalization is traditionally thought to result from increases in synaptic inhibition. By combining optogenetic stimulation and intracellular recordings in mouse visual cortex here we show that, on the contrary, normalization is due to a decrease in synaptic excitation.

Distant neurons in primary visual cortex (V1) influence each other through polysynaptic networks of distal intracortical connectivity. These networks involve horizontal connectivity within V1 and feedback from higher areas¹. Their effect depends on the activity of the target region, increasing its firing when it is at rest, but suppressing its firing when it responds to visual input². Arithmetically, these effects are well described by the normalization equation^2,3: distal network activation causes mostly summation at low contrast, and mostly division at high contrast.

Divisive normalization is widespread across neural systems and species⁴, and is often assumed to rely on the level of synaptic inhibition. This assumption has been shown to be correct in some circuits, such as the olfactory system of Drosophila⁵ and zebrafish⁶. In visual cortex, however, the evidence is mixed. For instance, there is disagreement as to whether the level of inhibition does^10,11 or does not¹² underlie the preference of V1 neurons for smaller stimuli, which depends on contrast and is a form of normalization⁴. While some models for normalization in V1 rely on sustained increases in inhibition^7-9, others rest on alternative explanations^4,12-15.

To establish the synaptic basis of normalization mediated by distal network connectivity in mouse V1, we activated source neurons in the binocular zone (BZ) and we recorded from target neurons in the monocular zone (MZ), ~60 deg away in the retinotopic map (~0.8 mm away in cortex). We first used in utero electroporation to express ChR2-venus in layer 2/3 pyramidal neurons of V1 in the left hemisphere. We then recorded from layer 2/3 neurons in the left MZ, under isoflurane anesthesia, while activating the left BZ through antidromic optogenetic stimulation² of its contralateral callosal projections (Figure 1a).

Figure 1.

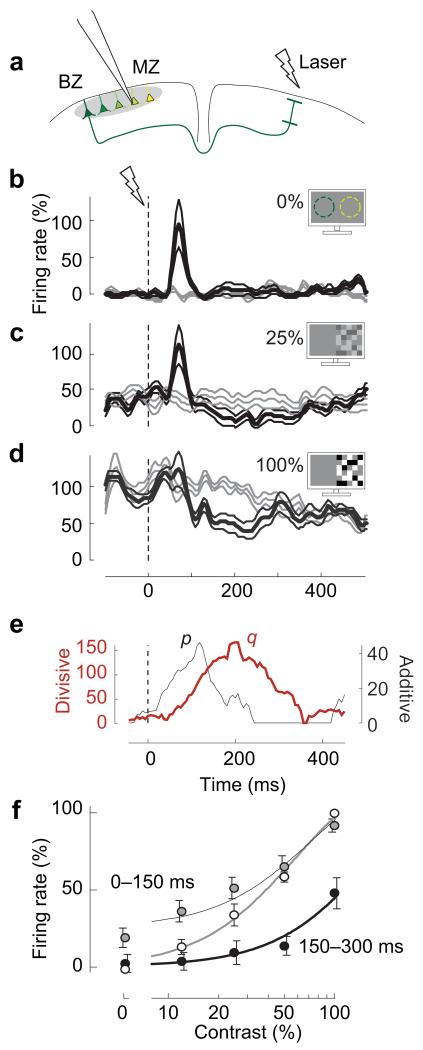
Distal cortical activation causes contrast- and time-dependent summation and division. (a) We recorded extracellularly from L2/3 neurons in the far monocular zone (MZ) while activating the binocular zone (BZ) by laser pulses on the opposite hemisphere. Colors represent different retinotopic positions. (b) Firing rate in the MZ in the absence (gray) and the presence (black) of distal network activation (n=14, mean±s.e.m.). Time 0 is laser onset. Visual contrast is 0%. Dashed circles illustrate receptive fields of BZ (green) and MZ (yellow). (c-d) Same, in the presence of visual stimuli of 25% or 100% contrast. Visual stimulation started 1 s before time 0 and was restricted to the far MZ. (e) Impact of distal network activation on additive term p (gray) and divisive term q (red). (f) Contrast responses (white dots), and effects of distal network activation after 0-150 ms (gray dots, p=24, q=37) or 150-300 ms (black dots, p=0, q=138). Dots are mean±s.e.m.. Curves indicate the fit of the normalization equation.

We first measured MZ firing rates with extracellular recordings, and confirmed that the effects of distal network activation depend markedly on visual stimulation² (Figure 1b-d). If the MZ was not visually stimulated (0% contrast), BZ activation drove MZ spiking 50-150 ms afterwards (Figure 1b). If, instead, the MZ was stimulated with higher contrast (Figure 1c,d), the drive turned into suppression, particularly at later times (150-300 ms).

These effects are well summarized by the normalization equation, where MZ responses depend on local contrast c and on the time t after distal network activation:

$$R\left(t\right)\propto \frac{c^n+p\left(t\right)}{c_{50}^n+c^n+q\left(t\right)}$$

Here, c₅₀ and n determine responses to visual contrast, and p and q determine distal contributions^2,4. These rose after distal network activation, with the additive term p preceding the divisive term q (Figure 1e). This equation provided good fits to the population firing rate, explaining >98% of its variance (Figure 1f). At low contrast (c ⪡ c₅₀), and at short latencies (0-150 ms), distal network activation increases firing rate, (because p>0 and q~0). At high contrast (c ⪢ c₅₀) and longer latencies (150-300 ms), it suppresses firing rate (because p<q).

To study the cellular basis of these effects, we recorded membrane potential (V_m) of MZ neurons using whole-cell somatic patch-clamp recordings (Figure 2a-f). We studied two conditions of visual stimulation, 0% and 100% contrast, as these show, respectively, the largest additive and divisive effects.

Figure 2.

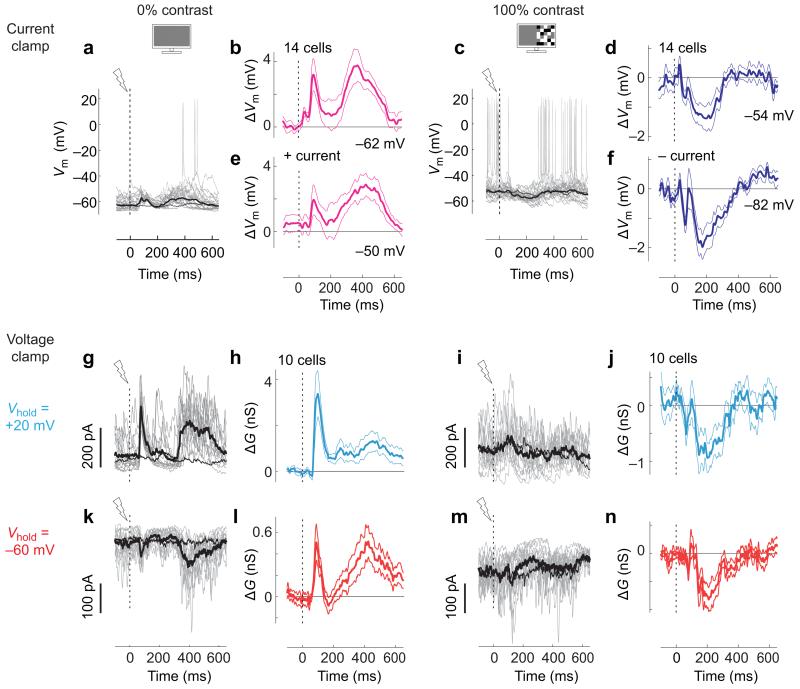
Distal network activation causes context-dependent synaptic effects. (a) Whole-cell patch clamp recordings of V_m in current clamp mode from a single neuron in the absence of visual stimulation. Responses to distal network activation are shown for 20 trials (gray) and on average (thick black). The average trace in the absence of distal network activation (control) is shown for comparison (thin black). (b) Effect of distal network activation on V_m, relative to control condition, averaged over 14 neurons. Traces show mean±s.e.m.. mV values indicate mean potential in the absence of distal network activation. (c,d) Same as a, b, in the presence of visual stimulation (100% contrast). a and c are from the same neuron. (e,f) Same as b,d, during positive (e, +50 pA) or negative (f, −223±16 pA) current injection. (g) Measurements of IPSCs in another neuron in the absence of visual stimulation, obtained in voltage clamp mode at V_hold =+20mV. Same format as in a. Gray traces show 15 individual trials. (h) Difference between activated and control traces, averaged over 10 neurons (mean±s.e.m.). (i-j) Same as g-h, but at 100% contrast. (k-n) Same as g-j measured at V_hold=−60 mV to estimate EPSCs. g,i,k,m are from the same neuron.

In the absence of visual stimulation, distal network activation caused depolarization (Figure 2a,b). In the 450 ms after optogenetic activation of BZ, MZ cells depolarized by 1.9±0.4 mV (Wilcoxon signed rank test, p=0.0006, n=14). Depolarization often involved two phases (Figure 2b), starting with a transient that rose rapidly and reliably within 150 ms (Supplementary Figure 1a-c). In contrast to the effects of local network activation, depolarization was rarely followed by hyperpolarization¹⁶ (Figure 2a), and depended little on the prior¹⁷ level of V_m (Supplementary Figure 1d-f).

In the presence of 100% contrast visual stimulation, instead, distal network activation caused hyperpolarization (Figure 2c,d). Between 150 and 300 ms after optogenetic activation of BZ, MZ cells hyperpolarized by 1.1±0.4 mV (p=0.005, n=14).

How can the same distal network activation have opposite effects on V_m depending on visual contrast? One possibility is that the effects depend simply on baseline V_m, which is ~10 mV more depolarized at 100% contrast than at rest. However, when we depolarized MZ cells by ~10 mV by positive current injection at 0% contrast, BZ activation depolarized them further (Figure 2e, Supplementary Figure 2a,c, 1.4±0.4 mV for 0-450 ms period, p=0.004, n=14). Likewise, when we hyperpolarized them with negative current during visual stimulation, BZ activation hyperpolarized them further (Figure 2f, Supplementary Figure 2b,d,f, −1.4±0.4 mV for 150-300 ms period, p=0.0004, n=14). Therefore, baseline V_m of MZ cells cannot explain why the effects of BZ activation depend on visual contrast.

In fact, the hyperpolarization caused at high contrast by distal network activation seems unlikely to result from increases in the level of GABA_A inhibition^7-9. Indeed, the hyperpolarization due to a GABA_A conductance would decrease in the presence of negative current, which is the opposite of what we observed (Fig.2d,f). Moreover, when we increased internal chloride concentration, which makes GABA_A inputs depolarizing, distal network activation at 100% contrast still hyperpolarized V_m (Supplementary Figure 3). Might the hyperpolarization caused by distal network activation be due instead to a decrease in excitation¹²?

To measure synaptic inhibition and excitation, we performed voltage clamp experiments using a cesium-based internal solution. At zero contrast, distal network activation recruited both inhibitory postsynaptic currents (IPSCs, Figure 2g,h, conductances of 1.15±0.28 nS, 0-450 ms, p=0.002, n=10) and excitatory postsynaptic currents (EPSCs, Figure 2k,l, 0.28±0.08 nS, p=0.002, n=10). Consistent with measurements of V_m, recruitment of EPSCs consisted of two phases, and did not depend on the prior spontaneous activity level (Supplementary Figure 4).

Visual stimulation completely changed these effects: instead of increasing inhibitory and excitatory currents, distal network activation decreased them both (Figure 2i,j,m,n). At 100% contrast, distal network activation decreased both IPSCs (Figure 2i,j, −0.91±0.25 nS, 150-300 ms, p=0.006, n=10, Supplementary Figure5) and EPSCs (Figure 2m,n, −0.34±0.08, p=0.002, n=10, Supplementary Figure 5). Overall, excitation and inhibition remained roughly proportional: following distal network activation, they decreased and increased together (Figure 3a,b).

Figure 3.

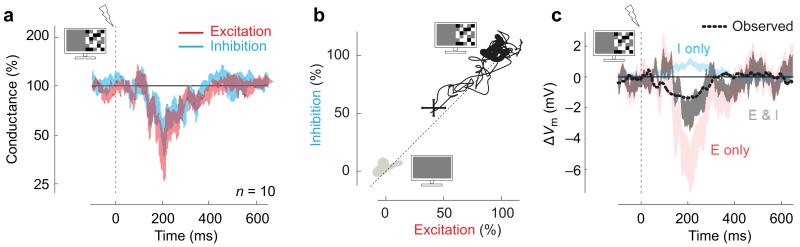
Roles of excitation and inhibition in divisive suppression. (a) Average excitatory and inhibitory conductances, following distal network activation at 100% contrast. Conductances are normalized by their values in the 100 ms before distal network activation. Shaded areas indicate mean±s.e.m. (n=10 neurons). (b) Relationship between inhibition and excitation in the presence of visual stimulation. Thick gray and black lines are the trajectories in the 100 ms before distal network activation at 0% contrast (gray) and 100% contrast (black). When distal network activation arrives in the presence of 100% contrast, it decreases both inputs proportionally (thin black, 0-700 ms). The cross shows mean±s.e.m (n=10). (c) Predictions of V_m based on synaptic conductances, all measured at 100% contrast. The measured V_m averaged over 14 neurons following distal network activation (dashed) is poorly predicted by inhibitory conductance alone (cyan), as inhibition would predict a depolarization. It is better predicted by synaptic excitation (pink) especially in combination with inhibition (black). Shaded areas indicate mean±s.e.m.(n=10 neurons).

This result indicates that the hyperpolarization caused by distal network activation at high visual contrast is due to a decrease in excitation, not to an increase in inhibition. Indeed, in control experiments where we recorded in both current clamp and voltage clamp in the same neurons, the hyperpolarization and the decrease in excitation had similar time courses (Supplementary Figure 6). A simple calculation confirms that the decrease in the level of excitation explains the suppressive effects seen in membrane potential (Figure 3c). Inhibition contributes the opposite effect: by decreasing following distal network activation, it depolarizes the target cells (Figure 3c, cyan). It thus counteracts, rather than enhance the effect of the decreased excitation (Figure 3c, black, pink). Similarly, the additive effects of distal network activation, which are seen when the target region is at rest, are best predicted by increases in both types of synaptic input (Supplementary Figure 7).

These results are consistent with the predictions of models that involve strong recurrent local networks^12,14,15, where suppression arises from a concerted decrease in network activity, i.e. in the level of local excitation and inhibition. Some are based on an inhibition-stabilized network¹⁸, where recurrent excitation is strong enough to destabilize the network in the absence of fast recurrent inhibition. In these networks, the levels of excitation and inhibition are reduced by a transient increase in inhibition, which has been occasionally observed¹². However, our measurements did not reveal a significant transient increase in ISPCs in any of 10 cells (p>0.05, 80–120 ms following distal network activation, Supplementary Figure 8c). Clarifying this discrepancy may require optical methods, to monitor simultaneously the activity of multiple classes of interneurons.

Though our experiments focus on normalization signals originating from distal cortical locations, the results might extend to closer interactions. Indeed, phenomena of normalization occurring within the receptive field of V1 neurons⁷ are immune to blockage of GABA_A receptors¹⁹ and can be enhanced by optogenetic suppression of excitatory inputs³. Further research is required to establish how general the role of recurrent excitatory connections is in cortical normalization, preferably during wakefulness³, and during behaviors that engage top-down signals²⁰.

Our results add to the view that different neural systems use different mechanisms to perform a single computation such as normalization⁴. In systems with few recurrent connections, normalization seems to rely mostly on increases in the level of inhibition^5,6. In cortex, instead, where recurrent excitatory connections are plentiful, normalization seems to operate largely by modulating the level of excitation.

Online Methods

Experiments were conducted according to the UK Animals (Scientific Procedures) Act, 1986 under personal and project licenses issued by the Home Office following ethical review.

In utero electroporation

We expressed ChR2-venus in layer 2/3 pyramidal neurons over visual cortex via in utero electroporation onto C57Bl6 × CD1 mice at embryonic day 15.5. We used the offspring of a cross between CD1 females and C57BL/6 males (Charles River, UK), taking advantage of the fertility and fostering capability of CD1 females. Crossed mice had brown or black coats as described previously¹¹ and showed normal features in the pigmented epithelium of eye, confirmed with fundus images and sectioned images (data not shown). E15.5 timed-pregnant CD-1 mice were anesthetized with 2% isoflurane in oxygen. Up to 1 μl of DNA solution with Fast Green (Sigma, UK) was pressure-injected into left lateral ventricle of embryos. The solution^2,11,21 contained pCAGGS-ChR2-Venus (Addgene 15753, 1.5 μg/μl) and pCAG-mCherry (0.5 μg/μl). Electroporation was achieved with 5 square pulses (50 V, 50 ms, 1 Hz, CUY21, NepaGene, Japan). mCherry fluorescence was used to screen for positive animals at P0 under a fluorescent stereoscopic microscope (MVX10, Olympus). Images showing ChR2-venus expression in a whole brain in vivo and in sectioned slices are available in our previous study (Fig. 1d,e in Ref. 2).

Animals were maintained with a light-dark cycle of 12:12 h, and up to four mice were kept in one cage after weaning.

Initial surgery

At postnatal day 21-28 the electroporated mice were implanted with a cranial window over V1 contralateral to the electroporated hemisphere. Electroporated mice (n=48, both sexes, 3-4 week old) were implanted with a head post and a cranial window (3 hours). Anesthesia was obtained with 2% isoflurane and temperature was maintained at 37°C using a feedback-controlled heating pad (TR-200, FST, Germany). Carprofen (10 mg/kg), atropine (0.3 mg/kg) and dexamethasone (2 mg/kg) were applied to prevent pain, secretions and brain edema. Eyes were covered with ointment (chloramphenical, Martindale Pharmaceuticals, UK). A head-plate was implanted to the skull with black dental cement (Ortho-Jet powder, Lang Dental, USA). A cranial window was embedded at the callosal stimulation side (Fig.1a). Through the window, callosal axon terminals were clearly seen as Venus-labeled band under a microscope (MVX10, Olympus) with a CMOS camera (sCMOS, pco.edge, PCO) (see Fig. 1d in ref ²). The space beneath the window glass was filled with aCSF-agarose (0.25%) rather than using layered glass. Because we needed to align the laser spot onto the callosal band, only mice showing a clear band (48 out of 96 electroporated) were implanted and used for subsequent procedures, as in our previous work². No experimenter blinding was done.

Similarly, for control experiments involving optogenetic stimulation of PV-positive interneurons (Fig.S8) we implanted a head post in mice expressing ChR2-EYFP in PV interneurons²² (Pvalb-IRES-Cre;Ai32, n=7, both sexes, 4-5 week old).

Pre-recording surgery

A pre-recording surgery was performed (2 hours), 3-7 days after implantation of the cranial window. An implanted animal was anesthetized with isoflurane (2%), and was given Carprofen, atropine and dexamethasone as described above. The animal was held with a head-plate holder, and its temperature was maintained at 37°C. The eye for visual stimulation was covered with a contact lens (Pmma 003, Veterinary Specialty Products, UK), and the other eye with a black piece of aluminum foil. The bone over visual cortex was thinned at 2.5 mm lateral and 0.5 mm rostral to lambda (a square of 1 × 1 mm). Then a vessel-free area of 300 μm was identified for a craniotomy (<300 μm) and a durotomy. The chamber was filled with warm HEPES-buffered artificial cerebrospinal fluid (aCSF, 150 mM NaCl, 4 mM KCl, 10 mM HEPES, 1 mM MgCl₂ and 2 mM CaCl₂, pH 7.4) to prevent desiccation and maintain ionic balance. Just before recording, anesthesia was lowered to 0.025 - 0.5%, supplemented with chlorprothixene (1 mg/kg, Sigma, UK).

Electrophysiology

Patch pipettes (4-6 MΩ) were pulled (PC-10, Narishige, Japan) and were mounted in a headstage (Multiclamp 700B, Molecular Devices) on a micromanipulator (Luigs & Neumann, Germany). Before recording, the exposed cortex was covered with thick aCSF-agarose (1%) to prevent pulsation, and the preferred retinotopic position was measured using the local field potential (LFP). Then, standard blind patch clamp recordings were performed under voltage-clamp mode²³ to achieve a gigaohm seal (> 3GΩ) followed by establishment of the whole-cell configuration. Presumed pyramidal neurons with broad spike width²⁴ were analyzed. If stability was compromised, or if the retinotopic position established by LFP recordings was not in the far MZ, the experiment was aborted. Data were successfully collected from 23 out of 48 implanted electroporated mice and 5 out of 7 PV-ChR2 mice.

Based on micromanipulator travel and angle, we estimate our recordings to be from superficial cortical layers, at depth < 330 μm. Receptive field locations were typically ~75 deg from vertical meridian, corresponding in mouse V1 to ~0.8 mm away from the callosal BZ (e.g. see Fig.S2b and Fig. 1c in our previous study²).

We analyzed all of the recorded traces, without post-hoc selection, except that we excluded two neurons with narrow spikes (presumably PV cells, not analyzed here). All our measurements are presumed to originate from somas, thus underestimating synaptic events in dendrites.

For measurements of membrane potential, we placed the amplifier in current-clamp mode and corrected the bridge balance. We aborted the recording if initial series resistance was > 60 MΩ or if action potentials did not overshoot. In experiments with current injection, the injection started 200 ms before and ended 475 ms after the optogenetic stimulation. The amount of injection was 50 pA for depolarization, −250 pA for hyperpolarization in most experiments; in other experiments we used currents ranging from −300 to +100 pA. In most experiments, we used an internal solution based on potassium gluconate (K gluconate 135 mM, KCl 6 mM, HEPES 10 mM, MgATP 4 mM, NaGTP 0.3 mM, EGTA 0.1 mM, phosphocreatine 4 mM, pH 7.3 adjusted with KOH). In some recordings (Supplementary Figure 3), we used an internal solution based on potassium chloride (substituting K gluconate with KCl) to make GABA_A input depolarizing. In some cases, V_m was linearly detrended for slow DC drift²⁵.

For measurements of postsynaptic currents, series resistance (39.1 ± 3.4 MΩ) and membrane capacitance were corrected and compensated by 50-60%. The recording was aborted if series resistance was >50 MΩ. To isolate EPSCs or IPSCs, we selected a holding potential of −60mV or +20 mV. These potentials are around the reversal potential for GABA_A input or glutamatergic input with our cesium based solution. We first measured EPSCs, then IPSCs. In most experiments, we used a solution based on cesium together with internal blockers (cesium methanesulphonate 140 mM, MgATP 4 mM, Na₃GTP 0.3 mM, EGTA 0.3 mM, phosphocreatine 4 mM, TEA-Cl 5 mM, QX314-Cl 4 mM, pH 7.3 adjusted with CsOH) to facilitate measurements of synaptic conductances. In a few experiments (Supplementary Figure 6), we used a solution based on potassium gluconate to achieve both voltage- and current-clamp recordings in the same neurons.

Signals from the amplifier were low-pass filtered at 10 kHz (Multiclamp 200B) and then acquired at 30 kHz with a DAQ board (National Instruments).

Liquid junction potential

In our readings of membrane potential we did not correct for the liquid junction potential, the electrochemical potential generated at the border between two solutions. This junction potential compounds the voltage readings during experiments²⁶. We estimated the junction potential (Clampex, Molecular Probes) to be 12 mV, 13 mV, and 1 mV for the solutions based on potassium gluconate, cesium methansulfonate, and potassium chloride.

Optogenetic stimulation

A blue laser light (SDL-473-200T, DreamLasers, China) was directed into an optical fiber (50μm diameter), and diverging light from the fiber end was collimated and refocused to a 500μm diameter spot using convex lenses. Laser power density at the focused spot was adjusted to 250 mW/mm² (ref. ²) with a rotatable neutral density filter. The laser spot was aligned onto the callosal band. Laser illumination lasted 2 ms and was controlled with a high-speed shutter (LS3T2, Uniblitz, USA). A small fraction of laser output was monitored with a photodiode (PDA100A, ThorLabs, UK). The illumination commenced 1 s after each condition started. The interstimulus interval for laser was > 2.5 s.

Visual stimulation

Visual stimuli were presented on two LCD monitors (E2273HDS, Iiyama, Japan, mean luminance 50 cd/m², refresh rate 60Hz, gamma corrected), covering an angle of 100° horizontal and 65° vertical in the right visual hemifield contralateral to the recording site. We presented dynamic white noise (bright and dark 6° sized-squares, 10.7 frames/s, 1.5 s) stimulating only the far monocular visual field (55-95° azimuth)². The random noise was different across blocks but the same within a block. There were at least 20 blocks for current-clamp measurements and 15 blocks for voltage-clamp measurements. Each block involved 4-16 conditions in a random order, the combination of contrast (0 or 100 %), laser stimulation (absence or presence) and, if in the current-clamp experiments, current injection (3-4 different currents including zero). Interstimulus interval for visual stimulation was >1 s.

Data analysis

Data were analyzed in MATLAB (MathWorks, USA) and were shown as mean ± s.e.m., unless otherwise stated. For statistical pairwise tests, the two-sided Wilcoxon signed rank test was used, unless otherwise stated. The alpha level (0.05) was appropriate for the sample size.

Analysis of current-clamp data

To analyze subthreshold membrane potential (V_m), action potentials were detected as an upstroke in the 1st derivative of V_m and were replaced with an interpolated straight line for 1 ms before and 9 ms after the upstroke. We then smoothed the V_m signal with a 10 ms Gaussian window (SD 2 ms). Mean, SD and s.e.m. were calculated among trials for each condition. To evaluate the impact of distal network activation on V_m, we calculated the difference in V_m with and without the activation, and took the mean and s.e.m. across trials (Fig. 2a,c). This helped remove variability among trials inevitably introduced by dynamic white noise, which was different across trials.

Analysis of synaptic currents

We smoothed the current signal as described for the V_m signal, and calculated the difference between the two conditions. To evaluate the conductances Ge and Gi underlying the EPSC and the IPSC, we first corrected the potential drop at the uncompensated series resistance²⁷

$$\mathrm{V}\left(\mathrm{t}\right)={\mathrm{V}}_{\text{hold}}-\mathrm{I}\left(\mathrm{t}\right){}^{\ast }{\mathrm{R}}_{\text{series}}$$

where V(t) is the holding membrane potential after correction, V_hold is either 20 mV or −60 mV, I(t) is measured current, and R_series is the portion of series resistance that was not compensated during experiments (40-50%). We then derived G_e and G_i from the following equation (ref. ²⁷):

$$\mathrm{I}\left(\mathrm{t}\right)={\mathrm{G}}_{\text{rest}}{}^{\ast }\left(\mathrm{V}\left(\mathrm{t}\right)-{\mathrm{E}}_{\text{rest}}\right)+{\mathrm{G}}_{\mathrm{e}}\left(\mathrm{t}\right){}^{\ast }\left(\mathrm{V}\left(\mathrm{t}\right)-{\mathrm{E}}_{\mathrm{e}}\right)+{\mathrm{G}}_{\mathrm{i}}\left(\mathrm{t}\right){}^{\ast }\left(\mathrm{V}\left(\mathrm{t}\right)-{\mathrm{E}}_{\mathrm{i}}\right)$$

Here, G_rest and E_rest are the resting leak conductance and membrane potential, and E_e (13 mV) and E_i (−63.2 mV, Supplemental Figure. 8f) are the reversal potentials.

For robustness, we chose the values V_hold so that after correction for junction potentials they would be close to the reversal potentials for inhibitory and excitatory inputs. For instance in the case of the Cs-methansulfonate solution, the junction potential of 13 mV means that commanding V_hold = −60 mV resulted in a corrected V_hold = −73 mV, and commanding V_hold = 20 mV means that the corrected V_hold = 7 mV. Nonetheless, using the equation above does not require that the holding values correspond precisely to the actual reversal potentials.

V_m predictions based on conductance measurements

To predict V_m based on derived synaptic conductance (Figure 3c and Supplementary Figure 7b), we used the equation above setting I =0 and G_e(t) and G_i(t) to the measured conductances (Figure 2j,n). E_rest and G_rest were set to −61.9mV and 4.3nS. These values were based on current clamp experiments (Figure 2b,e), not on voltage clamp experiments where many intrinsic conductances were blocked. We set E_e and E_i at 12 mV and −71.4 mV taking into consideration the liquid junction potential for a potassium gluconate solution (Supplementary Figure 9c). V_m traces were predicted for 10 neurons based on their conductance measurements, and then averaged (Figure 3c and Supplementary FIgure7b). V_m prediction was also made based on excitatory conductance alone (G_i = 0, pink) and on inhibitory alone (G_e = 0, cyan).

To test for the robustness of our conclusions, we repeated analysis above with different values for E_i resulting from the potassium gluconate solution (−65 or −75 mV), and for E_i in the equation above (−60 or −70 mV). In all of those cases, the conclusions remained the same (data not shown): the prediction based only on inhibition goes in the wrong direction, while the prediction based only on excitation is too hyperpolarizing. The prediction based on the combination of excitation and inhibition best captures the data.

Confirming the estimates of reversal potential

To compare the results obtained when measuring conductance and those obtained when measuring membrane potential (Fig 3c), we need to estimate reversal potentials for the two experimental conditions: voltage clamp (a cesium methansulfonate solution) and current clamp (a potassium gluconate solution). We established these reversal potentials by estimating the liquid junction potential and the chloride ion concentration outside and inside the cell. There might be errors in these estimates. For instance, the chloride concentration outside the cell is affected both by natural CSF and by our aCSF, and we don’t know which one predominates.

To test our estimates quantitatively, we measured the reversal potentials for directly activated GABA_A inputs in V-clamp and in I-clamp (Supplementary Figure 9). We recorded from PV-ChR2 mice and evoked GABA_A input optogenetically^28,29, while we recorded intracellularly from excitatory neurons. We found that GABA_A input reverses at −63.2 ± 1.3 mV in V-clamp and −71.4 ± 1.5 mV in I-clamp (Supplementary Figure 9), consistent with predicted values for chloride concentrations in our two internal solutions with external aCSF (−62 and −74 mV).

Scaling of different measurements in the same neurons

To facilitate comparison between different measurements within the same neurons (e.g. the EPSG vs the IPSG in Figure 3b and Supplementary Figure 7a, V_m vs EPSCs in Supplementary Figure 6), the traces were normalized to the average visual response measured in the 100 ms before distal network activation. For plots of excitation vs. inhibition (Figure 3b and Supplementary Figure 7a) or V_m vs EPSCs (Supplementary Figure 6i,j), we also subtracted the values measured at rest (0% contrast) so that the normalized average values before distal network activation were 0 in the absence of visual stimulation, and 100% in the presence of visual stimulation.

Trial variability in the absence of visual stimulation

To characterize transient and slow V_m depolarizations in the absence of visual stimulation, we measured the height of the V_m response from the lower boundary in V_m (V_bottom see below), and evaluated its reliability as mean divided by SD (the reciprocal of the coefficient of variation across trials, 1/C.V., Supplementary Figure 1b). If a transient event within 150ms had mean/SD > 2, the response was counted as a significant depolarization. Similarly, if the time-averaged V_m response between 300 and 450 ms had mean/SD > 2 across trials, the response was regarded as a slow V_m depolarization. The same evaluation was adopted for EPSCs and IPSCs (Supplementary Figure 4).

To evaluate the effects of prior V_m onto V_m depolarizations in the absence of visual stimulation (Supplementary Figure 1d), we separated trials into two groups: a more quiescent (hyperpolarized) group and a less quiescent (depolarized) group. We based this separation on averages of V_m taken 0-100 ms before the distal network activation. If this average was below a criterion voltage, we classified the trial as more quiescent, and otherwise as less quiescent. To determine the criterion voltage, we proceeded as follows. First, we determined the upper and the lower boundaries in spontaneous V_m as average of the most depolarized V_m or the most hyperpolarized V_m among trials (V_top and V_bottom). Then we set the criterion voltage at 20% distance from V_bottom to V_top. To compare the size of early and slow depolarizations between the two groups (Supplementary Figure 1f), we measured the V_m response size relative to V_bottom. We adopted the same grouping for EPSCs and IPSCs (Supplementary Figure 4).

Fits of the normalization model

We analyzed the multiunit activity in the superficial layers in the far MZ which was collected in our previous study² (n=14). We first fit the firing rate of the control condition (no activation) with a hyperbolic ratio function⁷:

$$r\left(c\right)=r_0+r_{\mathit{max}}\frac{c^n}{c_{50}^n+c^n}$$

where r₀ is the baseline firing rate, r_max is the maximum rate, c₅₀ is the semisaturation contrast, and n is a constant determining the slope of the function. The values of r₀ and r₁₀₀ were then used to normalize each unit’s response to values R ranging from 0 to 1. We then fitted the control responses together with the responses measured with the activation using the full normalization equation⁴ (given in main text). We imposed the same c₅₀ and n across conditions, and obtained parameters p and q. Model parameters were obtained by weighted least squares fit. To investigate temporal dynamics in additive and divisive contributions (Figure 1e), we used a sliding window of 100ms to measure response and obtain parameters p and q.

To assess fit quality² we measured the percentage of variance in the responses R explained by the model predictions m:

$$v=1-\frac{{\Sigma }_{i=1}^n{\left(R_i-m_i\right)}^2}{{\Sigma }_{i=1}^n{\left(R_i-\stackrel{‒}{R}\right)}^2}$$

where the indices i indicate one of visual contrast and $\stackrel{‒}{R}$ is the mean of the responses.