Abstract
Purpose:
Rapid reconstruction of undersampled multicoil MRI data with iterative constrained reconstruction method is a challenge. The authors sought to develop a new substitution based variable splitting algorithm for faster reconstruction of multicoil cardiac perfusion MRI data.
Methods:
The new method, split Bregman multicoil accelerated reconstruction technique (SMART), uses a combination of split Bregman based variable splitting and iterative reweighting techniques to achieve fast convergence. Total variation constraints are used along the spatial and temporal dimensions. The method is tested on nine ECG-gated dog perfusion datasets, acquired with a 30-ray golden ratio radial sampling pattern and ten ungated human perfusion datasets, acquired with a 24-ray golden ratio radial sampling pattern. Image quality and reconstruction speed are evaluated and compared to a gradient descent (GD) implementation and to multicoil k-t SLR, a reconstruction technique that uses a combination of sparsity and low rank constraints.
Results:
Comparisons based on blur metric and visual inspection showed that SMART images had lower blur and better texture as compared to the GD implementation. On average, the GD based images had an ∼18% higher blur metric as compared to SMART images. Reconstruction of dynamic contrast enhanced (DCE) cardiac perfusion images using the SMART method was ∼6 times faster than standard gradient descent methods. k-t SLR and SMART produced images with comparable image quality, though SMART was ∼6.8 times faster than k-t SLR.
Conclusions:
The SMART method is a promising approach to reconstruct good quality multicoil images from undersampled DCE cardiac perfusion data rapidly.
Keywords: compressed sensing, DCE imaging, multicoil imaging, cardiac perfusion, fast minimization
1. INTRODUCTION
Over 17 million people in the US are affected by coronary artery disease (CAD). Dynamic contrast enhanced (DCE) cardiac perfusion imaging with MRI is a powerful diagnostic tool for detecting CAD and assessing the amount of blood flow to the myocardium. Regions that receive the gadolinium (Gd) based contrast agent that is injected into the patient appear bright in a T1 weighted sequence due to the T1 shortening effect of Gd. Less bright regions or less rapid uptake reflects ischemia, so for accurate diagnosis, high spatiotemporal resolution is desired. One of the current methods for accomplishing relatively high spatial and high temporal resolution is to undersample the k-space data and use the time saved to improve temporal resolution. This approach leads to artifacts in image space, with the type of artifact depending on the point spread function (PSF) of the sampling pattern.
Broadly speaking, two types of approaches have been developed to handle the artifacts that arise due to undersampling k-space: (a) parallel imaging (PI) techniques and (b) compressed sensing (CS) based techniques. PI based techniques use information from multichannel receivers to remove aliasing artifacts and improve image quality. The most common PI techniques are sensitivity encoding (SENSE)1 and generalized autocalibrating partially parallel acquisitions (GRAPPA).2 Techniques based on the principle of CS use sparsifying transforms to improve image quality. In Ref. 3, a combination of CS and non-linear GRAPPA (Ref. 4) was used to achieve high acceleration factors. The types of auxiliary information in SENSE reconstructions and CS reconstructions are different: coil sensitivity information in the case of SENSE reconstructions and sparsity based information in the case of CS reconstructions. Thus, their combination allows for the use of higher acceleration factors than those achieved by either SENSE or CS individually. In Refs. 5 and 6, spatial TV was used as the constraint in conjunction with SENSE, whereas in k-t sparse-SENSE,7 a Fourier transform along the temporal dimension was used as the L1 constraint. In Ref. 8, TV constraints were used along the spatial and temporal dimensions to drive sparsity and the cost functional was minimized using a nonlinear conjugate gradient (CG) implementation. Techniques have also been developed to incorporate motion compensation along with the sparse-SENSE formulation to improve image quality further. In Ref. 9, diffeomorphic motion compensation was performed along with a spatiotemporal TV constraint and the cost functional was minimized using an alternating projection on convex sets technique. All of the above methods, though capable of reconstructing good quality images from undersampled data, suffer from slow reconstruction speeds due to the inherent ill-conditioning of the reconstruction problem.
Recently, several methods have been proposed to accelerate the convergence of CS based methods that employ L1 norm to drive sparsity. The fast iterative shrinkage-thresholding algorithm (FISTA)10 and variable splitting or alternating direction method of multipliers (ADMM) based methods such as split Bregman (SB)11 and augmented Lagrangian (AL)12 are more popular. SB and AL methods have been shown to be nearly equivalent.12 FISTA, SB, and AL use soft-thresholding11 to quickly minimize the L1 norm problem. These methods are sometimes used along with proximal operators13 to make the cost functional easier to minimize. When the multicoil SENSE method is included with the CS method, it can be more challenging to minimize the objective function quickly. Some techniques have been developed to meet these challenges by using a combination of methods; these are detailed in the Appendix after the notation and theory are introduced in Sec. 2.A.
Here we propose to develop a new fast multicoil reconstruction algorithm that makes use of TV along the spatial and temporal dimensions as sparsifying constraints. To achieve rapid reconstructions, the proposed method uses a novel combination of SB- and FISTA-based iterative reweighting. The method is thus termed the split Bregman multicoil accelerated reconstruction technique (SMART). The performance of this type of approach for first pass myocardial perfusion imaging is evaluated.
2. THEORY AND METHOD
2.A. SMART formulation
The basic constrained sparse-SENSE cost functional can be written as
| (1) |
where E is an encoding matrix that includes the sampling pattern and the Fourier transform, C is the complex coil sensitivity maps, k is the measured k-space data, μ is the weight on the multicoil fidelity constraint, is the L1 norm, and is the L2 norm. A single set of images m that satisfies the multicoil fidelity constraint and the sparsity constraint is estimated, instead of estimating a different image for each coil. φ1 and φ2 are constraints that help in driving sparsity of the reconstructed images in some transformation domain.
To utilize the spatial and temporal correlations in the data, we use TV for constraints along the spatial and temporal dimensions.
Hence Eq. (1) can be rewritten as
| (2) |
where ∇xy is the spatial gradient operator and ∇t is the temporal gradient operator. μ, λ1, and λ2 are weights that control the amount of fidelity constraint, spatial regularization, and temporal regularization, respectively. Applying the SB-based variable splitting technique to Eq. (2) by using surrogate variables S, T, and P, such that S = ∇xym, T = ∇tm, and Pi = Cim, allows Eq. (2) to be rewritten as
| (3) |
, and come from optimizing the Bregman distance.11 The image m that is being estimated has been decoupled from the L1 norm terms and is present only in L2 norm based terms. Hence, when trying to minimize Eq. (3) with respect to m, only the L2 norm terms remain,
| (4) |
Similarly, the surrogate variable P is present only in L2 norm terms,
| (5) |
Equations (4) and (5) can be quickly minimized using the acceleration scheme in FISTA.
The FISTA algorithm defines a sequence of weights,
| (6) |
Given any two successive sets of estimates Zn+1 and Zn, FISTA helps to improve the estimate by the following step: to accelerate convergence. The new improved estimate is fed back into the iterative reconstruction algorithm.
The L1 norm terms are given by
| (7) |
| (8) |
The L1 norm terms that contain S and T can be minimized using soft-thresholding.11
, and are minimized using a linear update step.
| (9) |
| (10) |
| (11) |
SMART has been specifically designed to handle reconstruction problems where spatial and temporal constraints have to be used simultaneously. This method uses one fewer substitution compared to Ref. 14 and does not use any of the matrix factorization or inversion techniques used in Refs. 14 and 15. The method developed here is tested on prospectively undersampled radial DCE cardiac perfusion images as opposed to the SB/AL methods developed in Refs. 14 and 15 which were tested on retrospectively undersampled Cartesian data. A regridding technique is used here to interpolate the radial k-space data to a Cartesian grid prior to reconstruction for faster iterations, though the proposed method is compatible with methods using the nonuniform fast Fourier transform (NUFFT) to regrid at every iteration.16
DCE cardiac perfusion images have high correlations along the temporal dimension such that a gradient operator along the temporal direction can be used as a good sparsifying transform. When combined with spatial TV, this has been shown to be effective at reconstructing radial DCE cardiac perfusion data.17 The resolution and correlations along the spatial and temporal dimensions for DCE cardiac perfusion images are generally not the same. Hence it is important to keep the spatial and temporal constraints separate, with separate weightings, instead of using a combined spatiotemporal 3D filtering kernel,18 in order to control how much regularization is performed along each dimension.
2.B. Data acquisition
2.B.1. ECG-gated dog datasets
Cardiac perfusion data have been acquired at rest on a 3T Verio scanner using a saturation recovery turboFLASH sequence with TR/TE = 2.5/1.4 ms, FOV = 260 mm2, 1.8 × 1.8 × 8 mm resolution. One saturation pulse per set of four slices is used, so the saturation recovery time for the readout of the first ray is ∼21 ms. A 30-ray golden ratio radial sampling pattern is used, and 100–120 time frames are acquired using a 32-channel phased array coil. The animal study has been performed for a separate study investigating atrial fibrillation, which did not require perfusion data. The contrast agent gadolinium-BOPTA, 0.05 mmol/kg, is used and the proposed reconstruction method is tested on nine dog datasets. Institutional Animal Care and Use Committee (IACUC) approval has been obtained.
2.B.2. Ungated human data
The SMART method is tested on ten ungated human datasets (seven rest perfusion and three stress perfusion datasets) acquired with Institutional Review Board (IRB) approval. The data have been acquired on a Siemens 3 T Verio scanner using a saturation recovery radial turbo-FLASH sequence with TR/TE = 2.2/1.2 ms, FOV = 280 mm2. One saturation pulse is used per set of 4–5 slices so that the saturation recovery time for the readout of the first ray is ∼26 ms. A 24-ray golden ratio, radial sampling pattern is used to acquire the data, and the acquisition matrix is of size 288 × 24. Four to five slices and 220–250 time frames are acquired using a 32-channel phased array coil with a voxel size of 2.3 × 2.3 × 8 mm resolution. The contrast agent gadoteridol, 0.06 mmol/kg, is used for both rest and stress perfusion.
2.C. Coil compression and k-space data interpolation
Data compression using principal component analysis (PCA)19,20 is first performed on the measured k-space data to compress the data to eight virtual coils. Coil compression reduces the reconstruction time. A regridding technique is applied to interpolate the radial k-space data onto a Cartesian grid,21 and the k-space data in Eq. (1) replaced with these interpolated data. This regridding technique allows for faster iterations compared to an implementation that regrids at every iteration to match the measured k-space data. The reconstruction and analysis discussed below are performed on interpolated k-space data.
2.D. Generation of coil sensitivity maps
2.D.1. ECG-gated datasets
To generate coil sensitivity maps for the ECD-gated dog datasets, reference images for each coil are generated by combining 250 unique rays from the postcontrast frames starting from the final postcontrast time frame. As a golden ratio acquisition is used, these rays are nonoverlapping. The number of rays is chosen to be large enough to give good reference images. The coil sensitivity maps are robust to changes in the number of rays chosen for the reference image. The number of rays can be varied from 200 to 300. An IFT of the interpolated k-space data is used to generate the reference images. These reference images are then used to compute the coil sensitivity maps using an eigenvector method described in Ref. 22.
2.D.2. Ungated human datasets
Unlike the ECG-gated dog datasets where each slice has a consistent cardiac phase, the ungated human datasets have data from different cardiac phases in the same slice acquisition. Additional steps are required to reconstruct the ungated human datasets. Binning the data into near-systolic and near-diastolic frames mitigates motion in the data to some extent, which helps to enforce temporal sparsity as the temporal correlations for the binned data are higher than for the unbinned dataset. This binning process helps in the estimation of coil sensitivity maps and improved image quality.
2.D.2.a. Steps to bin the ungated data into near-systolic and near-diastolic frames.
To segregate the ungated data into near-systolic and near-diastolic frames, an initial reconstruction is first performed using a gradient descent (GD) based implementation of Eq. (2) by treating the entire ungated dataset as ki. A temporary coil sensitivity map is generated by combining several postcontrast time frames, and using the IFT as a reference image. The same coil sensitivity map is used for both near-systolic and near-diastolic frames as no binning information is available at this stage. The data are then binned into near-systolic and near-diastolic frames using the self-gating method described in Ref. 23 using the initial set of reconstructions. The steps for this binning operation are shown in Fig. 1. A small rectangular region is cropped around the heart, and the sum over the region is calculated. The peaks and troughs of the 1D signal thus computed are used to bin data points into near-diastolic and near-systolic time frames, respectively.
FIG. 1.
Flow chart showing the steps followed to bin the data into near-diastolic and near-systolic frames to reduce the effects of motion on image reconstructions.
Alternative binning methods could have been used instead of an initial reconstruction based on a gradient descent implementation for binning as described above. Faster binning of the ungated dataset could have been performed by generating images using the IFT of the interpolated k-space data and combining the images using a square-root-sum-of-squares (SSOS). In order to test whether the binning process helped in improving image quality as compared to performing reconstructions from the unbinned dataset, reconstructions had to be performed on the unbinned dataset based on Eq. (2) from the unbinned data. As the GD images thus generated were available, they were used to bin the data. The binning methods are further discussed in Sec. 4.A.
2.D.2.b. Computing coil sensitivity maps after binning is performed.
After the binning process is performed, reference images for each coil are generated by combining k-space data from multiple postcontrast frames such that the reference frame has 250 unique rays. This process is performed for the near-systolic and near-diastolic frames separately. The eigenvector method described in Ref. 22 is then used to generate the coil sensitivity maps from the multiple reference images. Hence the near-diastolic and near-systolic datasets have their own coil sensitivity maps.
2.E. Implementation of reconstruction
The method has been implemented in matlab and runs on a computer with an Intel Xeon E5620 CPU with a processor base frequency of 2.4 GHZ, 32 cores, a total dedicated memory of 96 GB.
2.E.1. Choosing regularization parameters for SMART
2.E.1.a. Radial datasets.
For the ECG-gated dog datasets, the weights are chosen as λ1 = 0.000 75, λ2 = 0.09, μ = 0.3, α1 = 0.035, α2 = 0.035, and β = 0.09. For the ungated human datasets, the weights for the reconstruction are chosen as λ1 = 0.01, λ2 = 0.35, μ = 0.2, α1 = 0.01, α2 = 0.01, and β = 0.7. The weights are chosen based on a test dataset. The weights chosen allow for rapid convergence and give good image quality. The number of iterations is set to 50. The weights chosen for the ECG-gated dog data and the ungated human data are different because these are quite different types of data. In particular, the amount of motion, and also SNR, number of rays, and resolution are different between the two types of acquisitions. Hence the weights are different for each of the data types.
2.E.1.b. Retrospectively undersampled Cartesian dataset.
For the retrospectively undersampled Cartesian data, the weights μ and λ1 are empirically set as μ = 0.5 and λ1 = 0.025. The reconstructions are repeated for various values of λ2 and the optimal weight λ2 is finally set as the value that minimizes the normalized mean squared error (NMSE) between the fully sampled image and reconstructed image. The optimal weight for λ2 is found to be λ2 = 0.01.
2.E.2. Comparison of reconstruction methods
The proposed reconstruction method is compared with a gradient descent based implementation of Eq. (2) and the multicoil k-t SLR method24 (available at https://research.engineering.uiowa.edu/cbig/content/matlab-codes-k-t-slr). The multicoil k-t SLR method uses a combination of low rank constraints and spatiotemporal TV constraints to drive sparsity. An augmented Lagrangian14 variable substitution method is used to accelerate the convergence of the multicoil k-t SLR reconstructions. SMART and multicoil k-t SLR reconstruction methods are also tested on a fully sampled Cartesian dataset that is undersampled with a 16-ray golden ratio sampling pattern. The normalized mean squared errors are calculated for each method.
2.E.3. Choosing regularization parameters for k-t SLR
There are four weights that are set for k-t SLR. The input data are normalized so that the maximum magnitude of the k-space data is fixed to 2.5 × 10−5. The values of p and α are set to p = 0.1 and α = 4, as in Ref. 24. The other two weights are chosen as follows.
2.E.3.a. Radial datasets.
For the ECG-gated dog datasets, the weights are chosen as λ1 = 10−9 and λ2 = 2 × 10−8. For the ungated human datasets, the weights for the reconstruction are chosen as λ1 = 2 × 10−9 and λ2 = 0.75 × 10−8. The weights are empirically chosen to achieve the best visual image quality.
2.E.3.b. Retrospectively undersampled Cartesian dataset.
For the retrospectively undersampled Cartesian data, the weight λ2 is set to λ2 = 4 × 10−8. For the final free weight, λ1, the reconstructions are repeated for various values of λ1 and the optimal weight λ1 is set as the value that minimizes the normalized mean squared error between the fully sampled image and reconstructed image. The optimal weight for λ1 is found to be λ1 = 5 × 10−9.
The three reconstruction methods are compared in terms of reconstruction speed and image quality based on visual inspection and the use of a blur metric.25 The blur metric is a reference image-free metric that quantifies the amount of blur in the image. The intensity variations (the absolute value of the gradient) between neighboring pixels of a low-pass filtered version of the image are compared with the intensity variations between neighboring pixels of the original image. The greater the difference between the two, the sharper the image. The blur metric is normalized to a range of 0–1, with larger values meaning more blurring in the image. A detailed explanation of the blur metric is in Ref. 25.
3. RESULTS
3.A. Comparison with GD based implementations
3.A.1. Reconstruction of ECG-gated dog datasets
The images reconstructed using the SMART implementation have slightly better texture and image quality compared to the gradient decent based implementation of Eq. (2), which is reflected in lower blur metric values for the SMART reconstructions compared to the GD implementation. The values are reported along with the images. Comparisons are also made with images reconstructed on each coil data independently and combined using SSOS to better assess the effect of infusing coil sensitivity information into the reconstruction algorithm. A comparison of the images in Fig. 2 shows that the multicoil images are better at reconstructing fine structures compared to SSOS reconstructions. The white arrow shows the region where multicoil reconstructions are sharper and the structures are better visualized. Between the two multicoil reconstruction methods, the SMART reconstructions tend to have better texture, and the smoothing of uniform regions that is seen in the gradient descent based reconstructions is generally avoided.
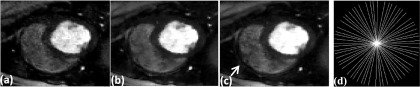
FIG. 2.
Images comparing the effect of including coil sensitivity information in the reconstruction. Reconstructions were performed on a 30-ray per time frame dog dataset. (a) Each coil reconstructed individually and combined using SSOS, (b) multicoil reconstruction using gradient descent, (c) multicoil reconstruction using the proposed SMART method, and (d) one frame of the 30-ray sampling pattern used to acquire the data. The white arrow shows the region where the SSOS image is missing a structure and the multicoil images have performed better at reconstructing the structure more faithfully.
3.A.2. Reconstruction of ungated human datasets
3.A.2.a. Performing reconstructions on unbinned data.
The measured k-space data that are acquired from the scanner using the free-breathing ungated26 acquisition method have time frames of the same slice acquired during different cardiac phases. When reconstructions are performed on the unbinned data, interframe motion in the underlying data causes motion blur in parts of the reconstructed images. Also, in some cases, the excess motion causes a faint false edge to be added to the images due to the use of temporal gradients as constraints. Our experiments show that it is better to perform binning or self-gating to segregate data into near-systolic and near-diastolic frames before reconstruction is performed. An example is shown in Fig. 3. The arrow shows the region where a structure has been smoothed in the unbinned reconstructions whereas the structure has been preserved in the binned reconstructions.
FIG. 3.
The effect of binning to near-diastole and near-systole prior to reconstruction on image quality. (a) Image from unbinned data, reconstructed using GD implementation. (b) and (c) images from binned data using GD and SMART, respectively. The arrow shows the region where there is blurring in the image reconstructed using the unbinned data. Between the SMART image and GD image for binned data, the SMART image has better texture, and smoothing of uniform regions in the image has been avoided. (d) One frame of the 24ray sampling pattern used to acquire the data.
3.A.2.b. Performing reconstruction on binned data.
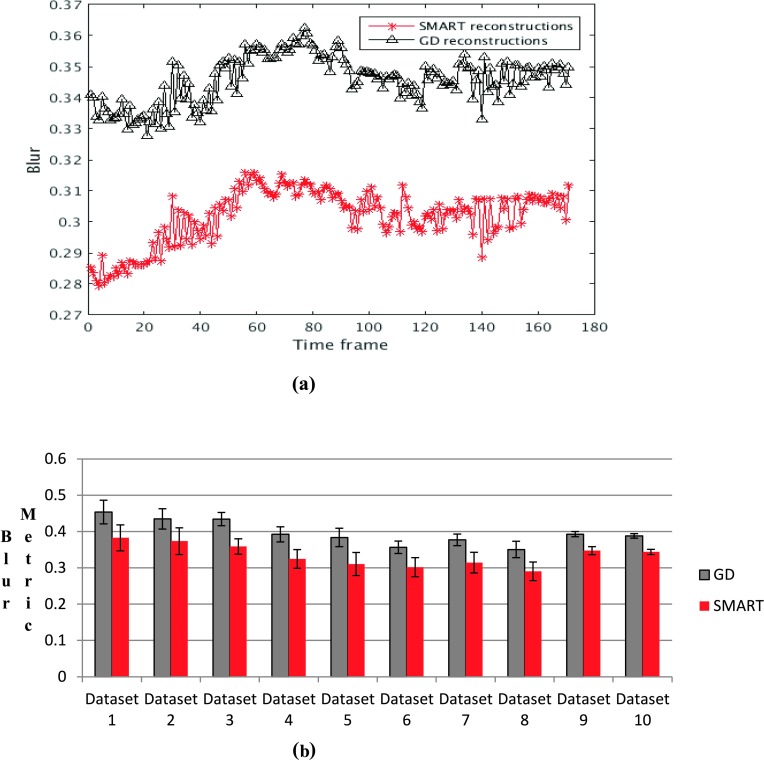
A comparison of the reconstructed images shows that the SMART reconstructions have better texture in uniform regions such as the liver and in the right ventricle (RV) blood pool compared to GD based reconstructions, though overall image quality is similar. An example is shown in Fig. 4. The SMART based images have less blur compared to GD reconstructions, shown by the lower blur metric values reported along with the images. Further comparison using the blur metric is shown in Fig. 5. Figure 5(a) shows a comparison of the blur metric computed from one slice. The black curve, which corresponds to blur metric computed from GD images, is higher for all the time points when compared with the red curve, which corresponds to the blur metric computed using SMART. The blur metric for all ten datasets is shown in Fig. 5(b). GD and SMART have significantly different blur metric, p < 0.05.
FIG. 4.
A comparison of multicoil images reconstructed using GD and SMART methods. A systolic and a diastolic frame are shown for the two reconstructions. The blur metric values are reported along with the images. The SMART reconstructions in (b) and (d) have better texture compared to the GD reconstructions in (a) and (c), which is reflected in the lower blur metric values for SMART images.
FIG. 5.
Blur metric values for the images reconstructed using SMART and GD based methods. A value close to 1 for the blur metric means that the image is highly blurred whereas a value close to 0 means that the image is very sharp. (a) Blur metric comparison between SB and GD computed on a single slice. (b) A comparison of the average blur metric for the ten datasets, and the mean and standard deviation are reported. In both cases, the blur metric calculated from the GD images is higher than the SMART based reconstructions (see color online version).
3.A.3. Reconstruction time
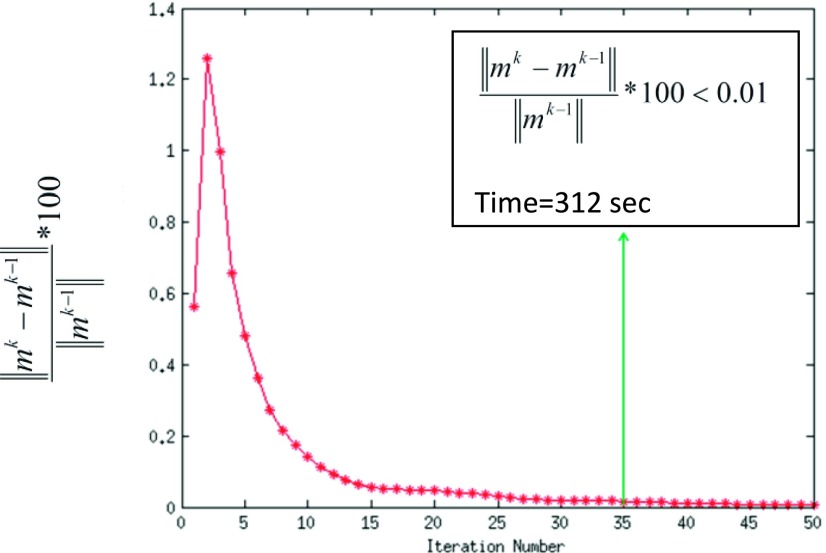
The images reconstructed using the SMART based reconstruction method need ∼35 iterations to meet the convergence criterion . An example is shown in Fig. 6. At the 35th iteration, the curve drops to below 0.01. To be conservative, we set the number of iterations to 50 for all datasets. For a dataset of size (288,288,100), the reconstruction time using the SMART method is ∼(424 ± 18) s, whereas that of a GD based implementation is ∼(2614 ± 77) s. This corresponds to a speedup up of ∼6 compared to the GD based method.
FIG. 6.
Rapid convergence of the SMART based method is shown. At 35th iteration, the relative change in the image between two successive iterations drops below 0.01%. For a dataset of size (288,288) and 100 time frames, the time taken for completing 35 iterations is ∼296 s and for 50 iterations is ∼424 s.
3.B. Comparisons with multicoil k-t SLR
3.B.1. Reconstruction on Cartesian data retrospectively undersampled with a 16-ray golden ratio sampling pattern
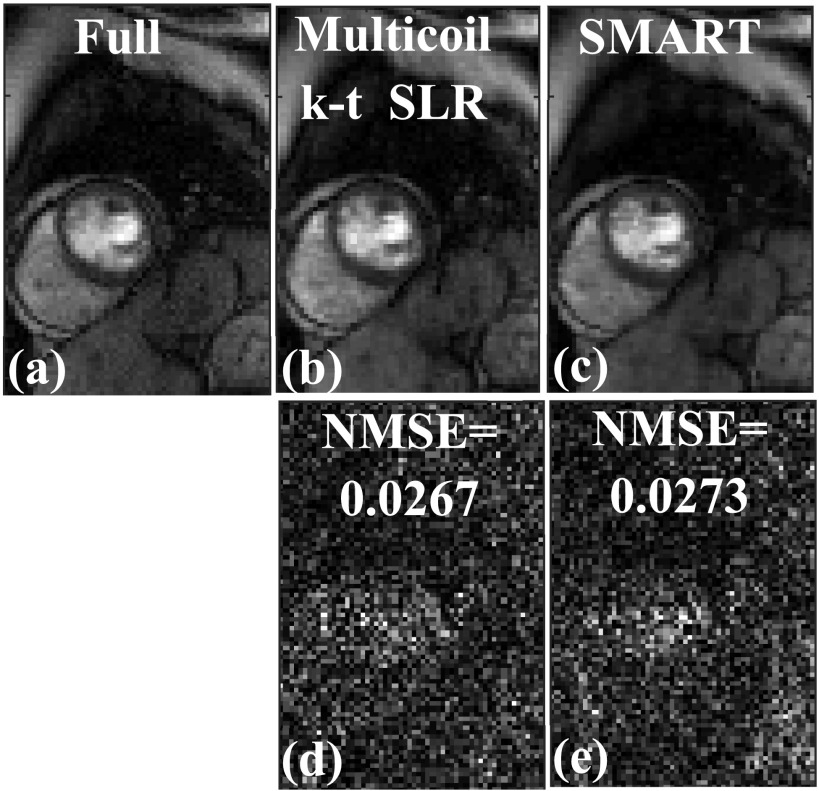
A comparison of images in Fig. 7 shows that both the SMART and multicoil k-t SLR methods perform well at reconstructing the image. Both of these methods are able to reconstruct the different structures faithfully, when compared to the fully sampled image in Fig. 7(a). The magnitude of the image difference shown in Figs. 7(d) and 7(e) appears mostly as noise. The overall image quality of both these methods is similar, as reflected in the NMSE reported in Fig. 7.
FIG. 7.
Comparison of SMART and multicoil k-t SLR on a Cartesian dataset retrospectively undersampled with a 16-ray golden ratio sampling pattern. (a) Truth from the fully sampled Cartesian k-space data, (b) image reconstructed using multicoil k-t SLR, and (c) image reconstructed using SMART. (d) Magnitude of the image difference between multicoil k-t SLR in (b) and the fully sample image in (a). (e) Magnitude of the image difference between SMART in (b) and the fully sample image in (a). The normalized mean squared error (MSE) is reported along with the difference image. Both SMART and k-t SLR performed well at reconstructing the image and had similar image quality.
3.B.2. Reconstruction of gated dog data
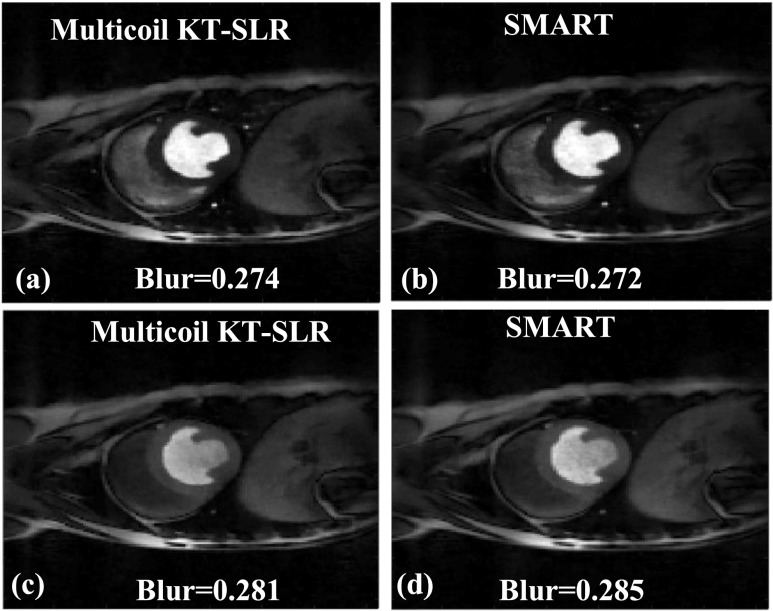
The images in Fig. 8 show two time frames from a gated dog dataset that are reconstructed using multicoil k-t SLR [Figs. 8(a) and 8(c)] and SMART [Figs. 8(b) and 8(d)], respectively. The blur metric values are reported along with the images. There is a very little difference in the blur metric estimated on the images reconstructed by the two methods. Both the SMART and k-t SLR techniques are able to reconstruct high quality images, and the sharpness of the edges in the myocardium is well maintained. For a dataset of size (288,288,100), the reconstruction time using the multicoil k-t SLR method is ∼2879 s, which is ∼6.8 times slower than the SMART technique.
FIG. 8.
Comparison of the proposed SMART with multicoil k-t SLR. The reconstructions were performed on a 30-ray dog dataset; two time frames are shown. [(a) and (c)] Images reconstructed using multicoil k-t SLR. [(b) and (d)] Images reconstructed using SMART. The blur metric values are reported along with the images. The quality of images in (a) and (c), which were reconstructed using multicoil k-t SLR, is similar to the images in (b) and (d), which were reconstructed using SMART. This is reflected in the blur metric.
4. DISCUSSION
A new multicoil reconstruction method that utilizes SB and FISTA to achieve fast convergence is presented. The SMART method is developed for imaging schemes that need to use both spatial and temporal constraints simultaneously. Though the method is developed for the use of total variation along the spatial and temporal domains as the constraints, it is general enough to be used with many sparsifying transforms. The proposed method does not involve any complex matrix inversion or factorization techniques. A SB based variable substitution is used to allow for fast minimization of the optimization problem. Since the SMART method uses one fewer-variable substitution as compared to Ref. 14, the memory footprint of the proposed method is slightly lower. The SMART method has been tested on prospectively undersampled 30-ray radial ECG-gated dog cardiac perfusion data and 24-ray radial ungated human cardiac perfusion data, whereas the existing SB/AL based methods14,15 have been tested only on retrospectively undersampled data.
The SMART formulation has been compared to a steepest descent (GD) based implementation and multicoil k-t SLR in terms of speed and image quality. Overall, the quality of images from the SMART based method and the GD based implementation is similar, though the images reconstructed using the SMART based method have lower blur and better texture in uniform regions, which is seen from the lower blur metric values found with the SMART based method (Fig. 5). Variation in the blur values is mostly due to the use of soft-thresholding in the SB based implementation of SMART as opposed to the use of an approximation to the L1 norm in the GD based implementation. The smooth approximation of the TV term used for GD based implementations is given by , where β2 is a positive constant. By adding a positive constant, the smooth approximation of the L1 norm helps in preventing singularities but becomes a poor approximation of the L1 norm as the positive constant becomes larger.27
The multicoil k-t SLR reconstruction uses an AL based implementation and did not use the smooth approximation of TV. Hence the loss of texture and increase in blur that is seen in GD implementation are not seen in k-t SLR based reconstructions. Both SMART and k-t SLR are able to reconstruct images with good image quality. The k-t SLR method uses a low rank constraint along with a spatiotemporal TV constraint to improve image quality. The SMART technique uses only TV along the spatial and temporal dimensions and does not use any low rank constraints. Though SMART and k-t SLR both use fast minimization techniques, there is a large difference in the reconstruction time. This is mainly due to the use of low rank constraint in the k-t SLR. In time frames where there is contrast in the blood pool-myocardium region, the image quality of k-t SLR and SMART techniques is similar. In some postcontrast time frames, we found small improvements in the texture of uniform regions in areas such as lungs. This resulted in a small change in the blur metric estimated from the k-t SLR reconstructions and SMART reconstructions, as reported in Figs. 8(c) and 8(d).
There is a difference in the way spatiotemporal TV is performed by SMART and k-t SLR. The TV constraint in SMART is implemented as , while the k-t SLR implementation uses . In both these techniques, the amount of spatial and temporal regularizations that is applied can be individually controlled. But these are two different ways of implementing spatiotemporal TV and the overall performance may differ depending on the type of data.
One major problem that multicoil reconstructions face is slow reconstruction speed. The L1 norm based multicoil reconstruction is inherently ill-posed and in general is slow to converge. The proposed method uses variable substitution based on a SB framework to separate the coil sensitivity maps from the fidelity constraint. Similarly, SMART uses the principle of variable substitution in the L1 norm terms to decouple the image being estimated from the coil sensitivity map and also the L1 norm term. The use of soft-thresholding then allows for fast minimization of the L1 norm subproblems. The FISTA based iterative reweighting scheme allows rapid minimization of the rest of the L2 norm based terms. Compared to the GD based implementation, the SMART based formulation has a speedup of ∼6.
Acquiring good quality DCE cardiac perfusion images can sometimes be challenging, especially when the cardiac gating signal is difficult to accurately detect.23,26 Challenges with good gating signals at 3 T has led to the development of ungated23,26 acquisition methods that do not use the cardiac gating signal but instead use self-gating23 to bin the data into near-systolic and near-diastolic time frames postacquisition. More details of the ungated DCE cardiac MR acquisition technique are given in Ref. 23. Though the SMART formulation has been tested on ten human ungated DCE cardiac perfusion datasets and high quality images have been reconstructed, the acquisition of ungated DCE cardiac perfusion images is relatively new and the SMART reconstruction method for ungated DCE data can likely be improved by including motion or using temporally varying weights. That is, there are temporal correlations in the underlying images that can be utilized to drive sparsity. The presence of motion in the data hinders this process. For the ungated human datasets, the best results are obtained when binning is performed prior to reconstruction to segregate the data into near-systolic and near-diastolic frames, which mitigates the effects of cardiac motion. Instead of using only two bins to segregate ungated data into near-systolic and near-diastolic frames, using multiple bins to separate data that are parts of different cardiac cycles could mitigate the problem further without the explicit use of motion compensation techniques.9,28–30 Motion compensation techniques9,28–30 have been shown to perform well in reconstructing good quality images, but using these methods adds an additional level of computational complexity and greatly reduces the reconstruction speed. Another improvement to the SMART technique could be the use of temporally varying weights instead of a constant weight for all time points. As the shape of the heart and the amount of motion change from frame to frame, it might be better to use temporally varying weights that are data dependent. An initial reconstruction could also be used as a reference image to estimate these weights. Similar approaches based on spatially varying weights have been used in Refs. 31 and 32 and have shown improvements in image quality.
4.A. Faster prereconstruction binning strategies
To bin or self-gate the ungated data into near-systolic and near-diastolic frames for improved reconstructions, an initial set of images is generated using a GD implementation of Eq. (2). Faster methods can be used to bin the data. For example, the IFT of the k-space data followed by SSOS can be used as an initial estimate to bin the ungated dataset instead of GD images. A comparison is shown in Fig. 9; diastolic and systolic time frames are shown. The images in Figs. 9(a) and 9(c), which are generated using SMART after the binning process is performed using GD images, are similar in image quality to the images in Figs. 9(b) and 9(d), which are generated using SMART after the binning process is performed using IFT SSOS images. As the main focus of this paper is not the binning process, other binning techniques such as using the center of k-space for binning or using the sinograms are not investigated.
FIG. 9.
Effect of binning using IFT SSOS as the initial estimate instead of using GD implementation of Eq. (2). The IFT SSOS images take less time to compute compared to multicoil GD images. (a) and (c) show SMART reconstructions with the binning process being performed using the GD implementation of Eq. (2). (b) and (d) show SMART reconstructions with the binning process being performed using IFT SSOS images. The image quality for both the binning methods is similar, which shows that using IFT SSOS as the initial estimate for binning is a viable option.
4.B. Improvements using “adding noise back step”
The “adding noise step” derived in Ref. 11 using the application of Bregman distance has been shown to improve image sharpness for some applications such as image denoising. The multicoil version of this adding noise back step is given by
| (12) |
| (13) |
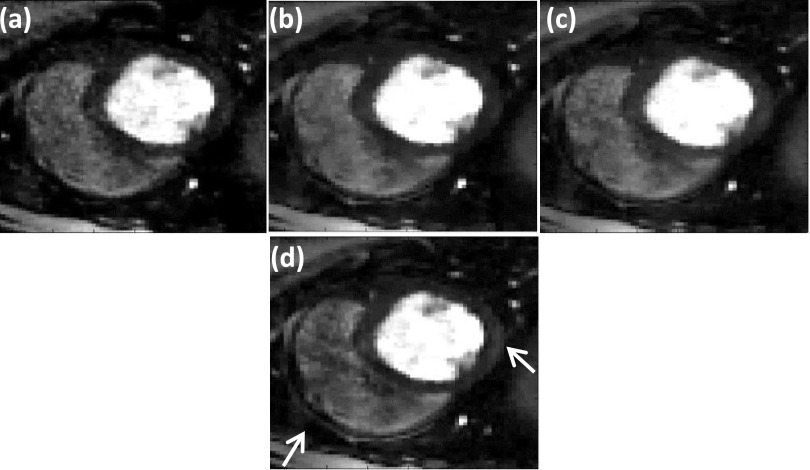
Equation (13), where the difference between the estimated image m and the measured k-space di0 is added back to the measured k-space, is called the adding noise back step. This step helps to maintain fine texture and sharp features, which could be lost by using TV. We applied this step to the SMART formulation to test the effect on image quality. An example of SMART with the adding noise back step applied to a gated dataset is shown in Fig. 10. A comparison of the images shows that the use of this adding noise back step improves the sharpness of features of some regions [white arrow in Fig. 10(d)]. When the SMART formulation with the adding noise back step is applied to ungated human datasets, the change in image quality is minimal. As compared to the gated dog datasets, the ungated human datasets have lower resolution, lower SNR, and fewer rays. In addition, the ungated human datasets have a lot of motion. Since these are quite different types of data, the effect of the adding-noise-back step is different on the two types of data.
FIG. 10.
Improving image quality by using “adding noise back” step (Ref. 11). The reconstructions were performed on a 30 ray dog dataset. Reconstructions using (a) SSOS, (b) GD, (c) SMART method, and (d) SMART with the additional adding noise back step. The white arrow shows the region where the adding noise back step has helped to improve image sharpness beyond that achieved by SMART alone.
4.C. Limitations
The proposed SMART method uses variable substitution to decouple the image being estimated from the L1 norm term. As the method uses variable substitution in the two L1 norm terms and also in the fidelity norm term, the method tends to be memory intensive as compared to the GD based implementation. Cost and availability of computers with large memory are generally not an issue, but still should be considered before choosing a reconstruction algorithm.
5. CONCLUSION
A new fast multicoil reconstruction method is developed and presented. The proposed SMART based technique demonstrates a new framework to apply SB based variable substitution for rapid multicoil image reconstruction. Compared to the standard GD based method, the SMART implementation is able to reconstruct images rapidly, with a speedup of ∼6. The method has been developed for 2D multislice DCE cardiac perfusion images, though the SMART method is applicable to 3D+time acquisition methods or any other type of accelerated data acquisitions that use L1 norm based reconstruction methods to drive sparsity. Further investigation is needed to build on these initial results which show that the new SMART based method is a promising approach to reconstruct multicoil images rapidly.
ACKNOWLEDGMENTS
This work is supported by No. R01HL113224. The authors thank the anonymous reviewers whose suggestions helped greatly to improve the paper.
APPENDIX: COMPARISON OF RAPID MULTICOIL RECONSTRUCTION TECHNIQUES
SB is a popular technique which has been used to accelerate TV based image denoising11 and image restoration.33 The principle of SB-based variable substitution is also useful at accelerating single coil MR reconstructions. For example, in Ref. 34, a SB-based technique is used to accelerate reconstruction of cine images. A spatiotemporal TV constraint combined with a motion compensation technique that uses a free-form deformation (FFD) model is used to mitigate the effects of motion in the acquired data. The formulation is then minimized with a combination of soft-thresholding and a biconjugated gradient stabilized (BiCGSTAB) method. The focus of this paper is on developing a rapid minimization technique for TV based multicoil reconstructions. Hence the comparisons made in the Appendix are limited to techniques that have been developed to accelerate sparse-SENSE type reconstructions.
1. Existing methods for accelerating multicoil reconstructions
In order to put the methods proposed here in context, we examine published methods for minimizing the constrained sparse-SENSE cost functional given in Eq. (1). In this section, the approaches from six groups that have proposed methods for rapidly minimizing Eq. (1) or a similar cost functional are summarized.
a. Method developed by Bilen et al.
In Ref. 35, temporal TV and temporal wavelets are used as sparsifying constraints φ1 and φ2. A version of FISTA (Refs. 35 and 36) is used to minimize the cost functional. This method has been tested on retrospectively undersampled cardiac perfusion data. Though the method is tested only with temporal constraints, spatial TV constraints can also be included in this framework.
b. Variable splitting based method developed by Ye et al.
In Ref. 37, TV and wavelets applied along the spatial dimension are used as sparsifying constraints φ1 and φ2. To accelerate reconstruction, an auxiliary variable is used to decouple the image term from the sparsity constraints by adding an L2 norm squared penalty between the new auxiliary variable and the image term. By using this variable splitting step, the minimization problem is reduced to a combination of a least squares problem and an L1 norm denoising/filtering problem.
Using the method developed in Ref. 37, by enforcing m = v, where v is the auxiliary variable, Eq. (1) can be rewritten as
| (A1) |
| (A2) |
Equation (A2) is minimized in Ref. 37 by using the SB approach of variable substitution followed by soft-thresholding, while Eq. (A1) is minimized using the iterative reweighting scheme used in FISTA.37 The method has been tested on retrospectively undersampled brain data. Though not used in Ref. 37, the variable splitting could have been performed by using a SB-based formulation, instead of using an L2 norm squared based penalty. Unlike SMART, this method does not make a surrogate variable based substitution for Cim. The surrogate variable based substitution m = v is made using a least squared constraint and not AL/SB.
c. Proximal operator based method developed by Montefusco et al.
An alternate approach is developed in Ref. 18 for fast reconstruction of 3D MR images. This approach is based on the use of a proximal operator to make the reconstruction problem in Eq. (1) easier to minimize using the following steps:
| (A3) |
The update step is given by
| (A4) |
| (A5) |
Here the sparsity constraint φ is composed of gradients applied in 3D, using an 18-neighbor structure to calculate the gradients. *T is the conjugate-transpose operator. Equation (A5) is minimized using a recursive median filter.18 A FISTA-based iterative reweighting scheme is used to accelerate convergence. That is, here no substitution is made to Cim and the constraints are applied to a 3D block, unlike SMART, which is designed to handle constraints along the spatial and temporal dimensions separately.
d. Fast composite splitting algorithm (FCSA) based method developed by Jiang et al.
A third group developed a fast minimization algorithm38 by using a composite splitting method.39 The reconstruction method in Ref. 38 has two sparsity constraints like the variable splitting method in Ref. 37, but uses FCSA to reduce Eq. (1) to a combination of two simpler subproblems,
| (A6) |
| (A7) |
In Ref. 38, φ1 and φ2 are spatial gradients and spatial wavelets, respectively. Equations (A6) and (A7) are individually minimized using FISTA and the final solution is computed using a linear combination of the solution of the two subproblems (A6) and (A7). Although this method uses spatial constraints, the framework can easily be extended to include temporal constraints.
The methods mentioned above either do not utilize the SB/AL framework or do not utilize it completely, likely reducing the efficiency of these fast minimization techniques. These methods do not make any substitutions to the fidelity constraint term, which is unlike the methods discussed below which utilize the SB/AL framework to accelerate convergence.
e. SB/AL based methods
Methods have been developed based on the SB/AL framework in Refs. 15 and 14. In Ref. 14, multiple auxiliary variables are used in a SB/AL framework (named as P2 in Ref. 14) with the following substitutions: x = m, Pi = Cim, and v = φx,
| (A8) |
Efficient closed-form solutions were developed for computing terms such as , , and . The method has been tested on retrospectively undersampled MRI brain data using a Poisson-disk based sampling pattern. The method is developed only for reconstruction problems that use spatial constraints and will need to be extended and tested for dynamic data, where utilizing correlations in time is necessary.
The method developed in Ref. 15 to minimize Eq. (1) uses fewer substitutions compared to Ref. 14. The steps are as follows:
Enforcing x = m and v = φx to Eq. (1) using SB,
| (A9) |
Minimization of Eq. (A9) involves computing (α2I + μ(EC)TEC)−1 and . Methods based on the use of singular value decomposition (SVD) have been developed to quickly compute . When constraints such as wavelet transform or Fourier transforms are used for φ, efficient closed-form solutions are available for computing , whereas CG can be used for constraints such as temporal TV.15 A similar algorithm was also developed for synthesis prior based reconstruction.15 The method has been tested on retrospectively undersampled cardiac data, undersampled with a variable density undersampling pattern. It is to be noted that the method was developed only for Cartesian sampled data. For data acquired on non-Cartesian grid points, the method would have to be modified. The speed of this algorithm depends on how quickly the matrix inverses can be calculated. Efficient methods have been developed for Cartesian sampled data, though for radial data, conjugate gradient type methods would have to be used.
f. SMART formulation
Start from Eq. (1), given by
| (1) |
The SMART formulation makes the following substitutions: Pi = Cim, v1 = φ1m, and v2 = φ2m. Enforcing the variable substitutions using SB, Eq. (1) can be rewritten as
| (A10) |
A comparison of Eq. (A10) [or Eq. (3)] with Eqs. (A8) and (A9) shows that the SB based formulation developed here is different from the SB/AL based formulation developed in Ref. 14 [Eq. (A8)] and Ref. 15 [Eq. (A9)]. Unlike Ref. 14, the SMART implementation does not use a surrogate variable to approximate m and does not require methods to invert large matrices such as those used in Refs. 14 and 15.
The SMART method uses few SB based variable substitutions and is compatible with both Cartesian and radial data. The implementation of SMART does not require inversion of large matrices.
REFERENCES
- 1.Pruessmann K. P., Weiger M., Scheidegger M. B., and Boesiger P., “SENSE: Sensitivity encoding for fast MRI,” Magn. Reson. Med. 42, 952–962 (1999). [DOI] [PubMed] [Google Scholar]
- 2.Griswold M. A., Jakob P. M., Heidemann R. M., Nittka M., Jellus V., Wang J., Kiefer B., and Haase A., “Generalized autocalibrating partially parallel acquisitions (GRAPPA),” Magn. Reson. Med. 47, 1202–1210 (2002). 10.1002/mrm.10171 [DOI] [PubMed] [Google Scholar]
- 3.Yihang Z., Yuchou C., Dong L., and Ying L., Presented at the 9th IEEE International Symposium on Biomedical Imaging (ISBI), 2012.
- 4.Chang Y., Liang D., and Ying L., “Nonlinear GRAPPA: A kernel approach to parallel MRI reconstruction,” Magn. Reson. Med. 68, 730–740 (2012). 10.1002/mrm.23279 [DOI] [PubMed] [Google Scholar]
- 5.Block K. T., Uecker M., and Frahm J., “Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint,” Magn. Reson. Med. 57, 1086–1098 (2007). 10.1002/mrm.21236 [DOI] [PubMed] [Google Scholar]
- 6.Ying L., Liu B., Steckner M. C., Wu G., Wu M., and Li S.-J., “A statistical approach to SENSE regularization with arbitrary k-space trajectories,” Magn. Reson. Med. 60, 414–421 (2008). 10.1002/mrm.21665 [DOI] [PubMed] [Google Scholar]
- 7.Otazo R., Kim D., Axel L., and Sodickson D. K., “Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI,” Magn. Reson. Med. 64, 767–776 (2010). 10.1002/mrm.22463 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Feng L., Grimm R., Block K. T., Chandarana H., Kim S., Xu J., Axel L., Sodickson D. K., and Otazo R., “Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI,” Magn. Reson. Med. 72, 707–717 (2014). 10.1002/mrm.24980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Adluru G. and DiBella E. V., “Reconstruction with diffeomorphic motion compensation for undersampled dynamic MRI,” Proc. SPIE 8858, Wavelets and Sparsity XV, 88581X (September 26, 2013). 10.1117/12.2024046 [DOI] [Google Scholar]
- 10.Beck A. and Teboulle M., “A fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM J. Imaging Sci. 2, 183–202 (2009). 10.1137/080716542 [DOI] [Google Scholar]
- 11.Goldstein T. and Osher S., “The split Bregman method for L1-regularized problems,” SIAM J. Imaging Sci. 2, 323–343 (2009). 10.1137/080725891 [DOI] [Google Scholar]
- 12.Wu C. and Tai X., “Augmented Lagrangian method, dual methods, and split Bregman iteration for ROF, vectorial TV, and high order models,” SIAM J. Imaging Sci. 3, 300–339 (2010). 10.1137/090767558 [DOI] [Google Scholar]
- 13.Combettes P. and Wajs V., “Signal recovery by proximal forward-backward splitting,” Multiscale Model. Simul. 4, 1168–1200 (2005). 10.1137/050626090 [DOI] [Google Scholar]
- 14.Ramani S. and Fessler J. A., “Parallel MR image reconstruction using augmented Lagrangian methods,” IEEE Trans. Med. Imaging 30, 694–706 (2011). 10.1109/TMI.2010.2093536 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bilen C., Wang Y., and Selesnick I. W., “High-speed compressed sensing reconstruction in dynamic parallel MRI using augmented Lagrangian and parallel processing,” IEEE J. Emerging Sel. Top. Circuits Syst. 2, 370–379 (2012). 10.1109/JETCAS.2012.2217032 [DOI] [Google Scholar]
- 16.Bagchi S. and Mitra S. K., The Nonuniform Discrete Fourier Transform and its Applications in Signal Processing (Kluwer Academic, Norwell, MA, 1999). [Google Scholar]
- 17.Adluru G., Whitaker R. T., and DiBella E. V., Presented at the 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro (ISBI), 2007.
- 18.Montefusco L. B., Lazzaro D., Papi S., and Guerrini C., “A fast compressed sensing approach to 3D MR image reconstruction,” IEEE Trans. Med. Imaging 30, 1064–1075 (2011). 10.1109/TMI.2010.2068306 [DOI] [PubMed] [Google Scholar]
- 19.Adluru G. and DiBella E., “Compression2: Compressed sensing with compressed coil arrays,” J. Cardiovasc. Magn. Reson. 14, 1–2 (2012). 10.1186/1532-429X-14-S1-P24222226320 [DOI] [Google Scholar]
- 20.Zhang T., Pauly J. M., Vasanawala S. S., and Lustig M., “Coil compression for accelerated imaging with Cartesian sampling,” Magn. Reson. Med. 69, 571–582 (2013). 10.1002/mrm.24267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Adluru G., McGann C., Speier P., Kholmovski E. G., Shaaban A., and DiBella E. V. R., “Acquisition and reconstruction of undersampled radial data for myocardial perfusion magnetic resonance imaging,” J. Magn. Reson. Imaging 29, 466–473 (2009). 10.1002/jmri.21585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Walsh D. O., Gmitro A. F., and Marcellin M. W., “Adaptive reconstruction of phased array MR imagery,” Magn. Reson. Med. 43, 682–690 (2000). [DOI] [PubMed] [Google Scholar]
- 23.Likhite D., Adluru G., Hu N., McGann C., and DiBella E., “Quantification of myocardial perfusion with self-gated cardiovascular magnetic resonance,” J. Cardiovasc. Magn. Reson. 17, 1–15 (2015). 10.1186/s12968-015-0109-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lingala S. G., DiBella E., Adluru G., McGann C., and Jacob M., “Accelerating free breathing myocardial perfusion MRI using multi coil radial k-t SLR,” Phys. Med. Biol. 58, 7309–7327 (2013). 10.1088/0031-9155/58/20/7309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Crete T. D. F., Ladret P., and Nicolas M., “The blur effect: Perception and estimation with a new no-reference perceptual blur metric,” Proc. SPIE 6492, 64920I (2007). 10.1117/12.702790 [DOI] [Google Scholar]
- 26.Harrison A., Adluru G., Damal K., Shaaban A. M., Wilson B., Kim D., McGann C., Marrouche N. F., and DiBella E., “Rapid ungated myocardial perfusion cardiovascular magnetic resonance: Preliminary diagnostic accuracy,” J. Cardiovasc. Magn. Reson. 15, 26 (2013). 10.1186/1532-429X-15-26 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tai X.-C. and Wu C., “Augmented Lagrangian method, dual methods and split Bregman iteration for ROF model,” in Scale Space and Variational Methods in Computer Vision, edited by Tai X.-C., Mørken K., Lysaker M., and Lie K.-A. (Springer, Berlin, Heidelberg, 2009), Vol. 5567, pp. 502–513. [Google Scholar]
- 28.Lingala S. G., DiBella E., and Jacob M., “Deformation corrected compressed sensing (DC-CS): A novel framework for accelerated dynamic MRI,” IEEE Trans. Med. Imaging 34, 72–85 (2015). 10.1109/TMI.2014.2343953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen X., Salerno M., Yang Y., and Epstein F. H., “Motion-compensated compressed sensing for dynamic contrast-enhanced MRI using regional spatiotemporal sparsity and region tracking: Block low-rank sparsity with motion-guidance (BLOSM),” Magn. Reson. Med. 72, 1028–1038 (2014). 10.1002/mrm.25018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Usman M., Atkinson D., Odille F., Kolbitsch C., Vaillant G., Schaeffter T., Batchelor P. G., and Prieto C., “Motion corrected compressed sensing for free-breathing dynamic cardiac MRI,” Magn. Reson. Med. 70, 504–516 (2013). 10.1002/mrm.24463 [DOI] [PubMed] [Google Scholar]
- 31.Strong D. M., Blomgren P., and Chan T. F., “Spatially adaptive local-feature-driven total variation minimizing image restoration,” Proc. SPIE 3167, Statistical and Stochastic Methods in Image Processing II, 222 (October 14, 1997). 10.1117/12.279642 [DOI] [Google Scholar]
- 32.Iyer S. K., Tasdizen T., and DiBella E., “Edge-enhanced spatiotemporal constrained reconstruction of undersampled dynamic contrast-enhanced radial MRI,” Magn. Reson. Imaging 30, 610–619 (2012). 10.1016/j.mri.2011.12.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Osher S., Burger M., Goldfarb D., Xu J., and Yin W., “An iterative regularization method for total variation-based image restoration,” Multiscale Model. Simul. 4, 460–489 (2005). 10.1137/040605412 [DOI] [Google Scholar]
- 34.Abascal J. F. P. J., Montesinos P., Marinetto E., Pascau J., and Desco M., “Comparison of total variation with a motion estimation based compressed sensing approach for self-gated cardiac cine MRI in small animal studies,” PLoS One 9, e110594 (2014). 10.1371/journal.pone.0110594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bilen C., Selesnick I. W., Wang Y., Otazo R., Kim D., Axel L., and Sodickson D. K., “On compressed sensing in parallel MRI of cardiac perfusion using temporal wavelet and TV regularization,” in IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX (IEEE, 2010), pp. 630–633. 10.1109/ICASSP.2010.5495163 [DOI] [Google Scholar]
- 36.Beck A. and Teboulle M., “Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems,” IEEE Trans. Image Process. 18, 2419–2434 (2009). 10.1109/TIP.2009.2028250 [DOI] [PubMed] [Google Scholar]
- 37.Ye X., Chen Y., Lin W., and Huang F., “Fast MR image reconstruction for partially parallel imaging with arbitrary k space trajectories,” IEEE Trans. Med. Imaging 30, 575–585 (2011). 10.1109/tmi.2010.2088133 [DOI] [PubMed] [Google Scholar]
- 38.Jiang M., Jin J., Liu F., Yu Y., Xia L., Wang Y., and Crozier S., “Sparsity-constrained SENSE reconstruction: An efficient implementation using a fast composite splitting algorithm,” Magn. Reson. Imaging 31, 1218–1227 (2013). 10.1016/j.mri.2012.12.003 [DOI] [PubMed] [Google Scholar]
- 39.Huang J., Zhang S., and Metaxas D. N., “Efficient MR image reconstruction for compressed MR imaging,” Med. Image Anal. 15(5), 670–679 (2011). 10.1016/j.media.2011.06.001 [DOI] [PubMed] [Google Scholar]