Cause-effect relationship between vocal fold physiology and voice production in a three-dimensional phonation model

Zhaoyan Zhang

doi:10.1121/1.4944754

. 2016 Apr 1;139(4):1493–1507. doi: 10.1121/1.4944754

Cause-effect relationship between vocal fold physiology and voice production in a three-dimensional phonation model

Zhaoyan Zhang ^1,^a)

PMCID: PMC4818279 PMID: 27106298

Abstract

The goal of this study is to better understand the cause-effect relation between vocal fold physiology and the resulting vibration pattern and voice acoustics. Using a three-dimensional continuum model of phonation, the effects of changes in vocal fold stiffness, medial surface thickness in the vertical direction, resting glottal opening, and subglottal pressure on vocal fold vibration and different acoustic measures are investigated. The results show that the medial surface thickness has dominant effects on the vertical phase difference between the upper and lower margins of the medial surface, closed quotient, H1-H2, and higher-order harmonics excitation. The main effects of vocal fold approximation or decreasing resting glottal opening are to lower the phonation threshold pressure, reduce noise production, and increase the fundamental frequency. Increasing subglottal pressure is primarily responsible for vocal intensity increase but also leads to significant increase in noise production and an increased fundamental frequency. Increasing AP stiffness significantly increases the fundamental frequency and slightly reduces noise production. The interaction among vocal fold thickness, stiffness, approximation, and subglottal pressure in the control of F0, vocal intensity, and voice quality is discussed.

I. INTRODUCTION

Phonation results from the self-sustained vibration of the vocal folds, which modulates the glottal airflow and produces sounds. Although voice control is ultimately achieved through laryngeal and respiratory muscle activation, the vibration pattern of the vocal folds and the resulting voice depend on the geometry and biomechanical properties of the vocal folds, with different vocal fold conditions leading to different voice characteristics (Hirano, 1974). An important goal of voice research is to understand the cause-effect relation between biomechanical properties of the vocal folds and the acoustics of the produced voice and identify the biomechanical properties required to produce different voice types. Clinically, such improvement in understanding would allow us to determine the mechanical adjustments to the vocal folds that we wish to achieve to restore or improve voice and predict the outcome of such mechanical adjustments. This knowledge would also allow us to better understand how we use and control our voice. As a step toward this goal, this study investigates changes in vocal fold vibration and the resulting acoustics of the produced voice due to systematic and parametric changes in vocal fold stiffness, medial surface thickness in the vertical direction, resting glottal opening, and subglottal pressure in a large range of conditions, using a computational model of phonation.

Despite many previous research studies on voice production, there have been few systematic studies on the effect of vocal fold biomechanical properties on phonation. Due to limited access to the larynx, human subject experiments (e.g., Isshiki, 1964; Hirano et al., 1969; Hirano et al., 1970; Gay et al., 1972; Stathopoulos and Sapienza, 1993; Holmberg et al., 1988; Henrich et al., 2005) are often limited to observation and measurements of vocal fold vibration and acoustic output (e.g., closed quotient, fundamental frequency, vocal intensity, and various voice spectral measures) and laryngeal muscle activity in different voice conditions or tasks. Although these studies are able to reveal how different vibratory and acoustic measures vary with each other, they are unable to explain why such relationships occur and what biomechanical properties are required to produce the observed voice and vibration patterns. Experiments using physiological larynx models, either excised larynges (e.g., van den Berg and Tan, 1959; Isshiki, 1989) or in vivo models (e.g., Moore and Berke, 1988; Chhetri et al., 2012; Berke et al., 2013), have provided valuable insight toward the physics and control of voice production. However, manipulation of the larynx in these models, either mechanical or through nerve/muscle stimulation, often leads to complex and simultaneous changes in vocal fold stiffness, geometry, and glottal opening, which were often not monitored or measured. For example, elongation of the vocal folds is known to also thin and stiffen the vocal folds. Vocal fold adduction, depending on the specific muscles involved and their activation levels, may also change medial surface shape and/or vocal fold stiffness in addition to vocal fold approximation (Hirano and Kakita, 1985). So far, these experiments have yet to provide a systematic understanding of the effects of individual and combined effects of vocal fold stiffness, geometry, and resting glottal opening. Finally, physical models allow direct and systematic manipulations of vocal fold biomechanical properties. However, except for a few recent studies (e.g., Murray and Thomson, 2012; Xuan and Zhang, 2014), most physical models have yet to incorporate the nonlinear anisotropic material properties of the vocal folds.

Due to these experimental difficulties, computational models have been developed and used for systematic investigations of the influence of vocal fold properties on phonation. The very first such investigation was conducted by Ishizaka and Flanagan (1972), which investigated the effects of vocal fold stiffness and the resting glottal area on the fundamental frequency, vibration amplitude, and glottal closure in the original two-mass model. Similar lumped-mass models were also used in later studies by Story and Titze (1985), Steinecke and Herzel (1995), and Sciamarella and d'Alessandro (2004). Titze and Talkin (1979) used a finite element three-dimensional model of the vocal folds to investigate the effects of vocal fold stiffness, viscosity, geometry, resting glottal opening, and subglottal pressure on vocal fold vibration, fundamental frequency, average glottal flow, output acoustic power, and vocal efficiency. A more detailed analysis of the effect of vocal fold geometry was reported in Pickup and Thomson (2011) using a two-dimensional vocal fold model. One important limitation of these and other similar modeling studies is that they often focused on vocal fold vibration and the glottal flow but seldom included the acoustics of the produced voice (other than the fundamental frequency and vocal intensity).

In this study, the effects of vocal fold properties on vocal fold vibration and the resulting acoustics are investigated using a three-dimensional reduced-order continuum model of phonation (Zhang, 2015). To facilitate linking vocal fold biomechanics to the acoustics of the produced voice, this study focuses on the glottal closure pattern and various voice spectral measures and how they can be regulated by changes in vocal fold stiffness and medial surface thickness, the resting glottal opening, and the subglottal pressure. Glottal closure within each vocal fold oscillation cycle creates abrupt flow cessation and has important effects on the low-frequency harmonic structure and the excitation of higher-order harmonics in the voice spectrum (Fant, 1980, 1982; Fant et al., 1985; Stevens, 1998), both of which are perceptually important features of normal voice production. Despite this importance in linking vocal fold physiology and voice acoustics, the physical mechanisms of glottal closure control still remain unclear. It is generally assumed that glottal closure is achieved by vocal fold approximation through arytenoid adduction with varying degrees of arytenoid adduction leading to changes in voice from a breathy to a pressed quality (Klatt and Klatt, 1990). However, it has been observed that some excised larynges vibrate with incomplete glottal closure despite that the arytenoids are tightly sutured together (Zhang, 2011). This indicates that vocal fold approximation alone does not guarantee glottal closure during phonation. On the other hand, although it is generally accepted that stiffness conditions in the different layers of the vocal fold are important in determining the actual vibration pattern (Hirano et al., 1969; Hirano, 1974, 1981; Titze and Talkin, 1979; Hirano and Kakita, 1985), the effect of vocal fold stiffness on the glottal closure pattern remains unclear. In their experiment with excised larynges, van den Berg and Tan (1959) showed that the glottal closure was reduced or disappeared completely with increasing longitudinal tension of the vocal folds. However, it is not clear whether this change in glottal closure was due to the increased longitudinal tension itself or the geometric changes induced by the increased longitudinal tension. Indeed, in a later paper, van den Berg (1968) argued that increased thickness of the vocal folds would lead to a large vertical phase difference between vibrations in various horizontal planes and allow the glottis to remain closed longer. Increased thickness may also facilitate longer glottal closure by improving the vocal folds' capability to maintain adductory position against the subglottal pressure (Zhang, 2009). In summary, although previous excised larynx experiments (van den Berg and Tan, 1959; Isshiki, 1989, 1998) showed that glottal closure and the resulting voice are highly dependent on the balance among vocal fold stiffness/tension, geometry, initial glottal opening, and subglottal pressure, a clear picture of how glottal closure is controlled by such interaction is still missing.

It is possible that this balance between vocal fold properties and the subglottal pressure is monitored and maintained through laryngeal adjustments during phonation to achieve specific communication goals. For example, although many studies have shown that various laryngeal adjustments have only a slight effect on vocal intensity (Tanaka and Gould, 1983; Titze, 1988; Tanaka and Tanabe, 1986; Zhang, 2015), human subjects experiments show that as vocal intensity increases, the increasing subglottal pressure is often accompanied by a proportional increase in the glottal resistance, particularly at low pitch voice production (Isshiki, 1964; Hirano et al., 1969; Tanaka and Tanabe, 1986; Holmberg et al., 1988; Stathopoulos and Sapienza, 1993). It has been hypothesized that the observed increase in the glottal resistance accompanying vocal intensity increase is due to laryngeal adjustments required to maintain sufficient glottal closure and certain acoustic goals (Isshiki, 1964; Zhang, 2011). Understanding the effects of individual mechanisms (i.e., vocal fold stiffening, tighter approximation, and increased vocal fold thickness) and their interaction on glottal closure and the produced acoustics would identify such goals and elucidate the individual roles of laryngeal muscles in vocal control.

In the following, the computational model and data analysis are first described in Sec. II. The effects of vocal fold thickness, vocal fold stiffness, resting glottal opening, and subglottal pressure on vocal fold vibration and the acoustics of the produced voice are then discussed in Sec. III, followed by a general discussion in Sec. IV.

II. METHOD

A. Numerical model

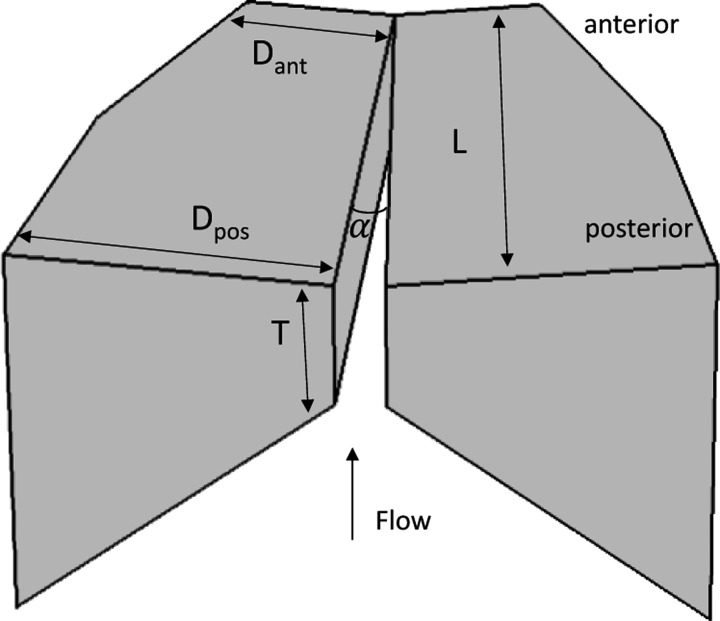
Figure 1 shows the three-dimensional vocal fold model used in this study. For simplicity, left-right symmetry in vocal fold geometry and vibration about the glottal midline is imposed so that only one vocal fold is considered in this study with the contralateral fold exhibiting mirror-image motion. The vocal fold is 17 mm long along the anterior-posterior direction. The posterior cross-sectional geometry of the vocal fold model is similarly defined as in Zhang (2009, Fig. 2), with a depth (dimension along the medial-lateral direction) of 7.5 mm and a variable medial surface thickness T in the vertical direction. The vocal fold cross-section tapers quadratically toward the anterior direction with the depth reduced to 3.75 mm at the anterior surface of the vocal fold. The medial surfaces of the two vocal folds form an angle α, which controls the resting glottal opening. The vocal fold model is fixed at the lateral surface and the two side surfaces at the anterior and posterior ends. To avoid possible source-tract interaction, no sub- or supra-glottal tracts are included in this study. The effects of source-tract interaction will be addressed in a subsequent study.

FIG. 1. — The three-dimensional vocal fold model.

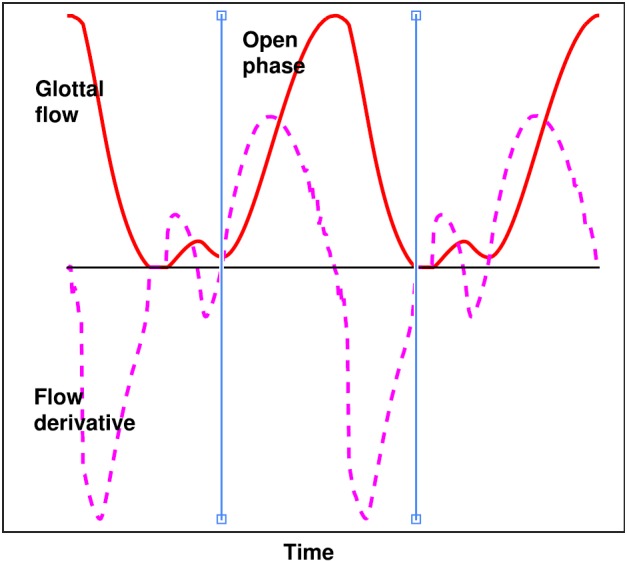
FIG. 2. — (Color online) Definition of the closed quotient (CQ) used in this study. The solid and dashed curves are the normalized glottal flow waveform and its time derivative. The two vertical lines indicate the instant of glottal opening and glottal closing, which define the open phase of the glottal cycle. The CQ is calculated as one minus the ratio between the open phase and the period of the glottal cycle.

Modeling the three-dimensional glottal fluid-structure interaction is computationally expensive. Considering the large number of conditions to be investigated, the reduced-order three-dimensional phonation model described in Zhang (2015) is used. The reader is referred to the Zhang (2015) paper for details of the model. The Zhang (2015) model is computationally efficient due to the following three major simplifications. First, linear elasticity is assumed for vocal fold mechanics, neglecting both material and geometric nonlinearities. Thus the material moduli (discussed in the following text) used in this study should be interpreted as the tangent moduli around specific vocal fold posturing conditions with different stiffness values representing different posturing conditions (e.g., different degrees of elongation). The use of a linear elastic material implicitly assumes small-strain deformations, which may not be valid for very large-amplitude vocal fold vibrations. Second, the glottal flow is modeled as a one-dimensional quasi-steady potential flow until it separates from the glottal wall at a location downstream of the minimum glottal constriction where the glottal area is 1.2 times the minimum glottal area. Downstream of the flow separation point the pressure is assumed equal to atmospheric pressure. Finally, the use of vocal fold eigenmodes as basis functions in Zhang (2015) significantly reduces the degrees of freedom of the system governing equations. The eigenmodes can be pre-computed prior to phonation simulations instead of at every single time step, which further improves computational efficiency.

Despite these simplifications, our previous studies using similar computational models have been able to reproduce experimental observations regarding sound production by confined pulsating jet flows (Zhang et al., 2002), dependence of phonation threshold pressure on vocal fold properties (Zhang, 2010; Mendelsohn and Zhang, 2011), and vocal fold vibration patterns in different vibratory regimes and transitions between regimes (Zhang and Luu, 2012; Zhang, 2014). Therefore it is reasonable to conclude that this model captures the essential features of the glottal fluid-structure interaction. Nevertheless, study is under way to validate this model by comparison to experiments.

Although the vocal fold is physiologically a multi-layered structure and often simplified as a body-cover two-layer structure, Yin and Zhang (2013) showed that activation of the cricothyroid (CT) and the thyroarytenoid (TA) muscles generally led to varying difference between the anterior-posterior (AP) and transverse stiffnesses but not much stiffness difference between the body and cover layers. In other words, the vocal folds behaved mechanically as a one-layer structure for most activation conditions of the CT/TA muscles except for conditions of strong TA activation and weak CT activation. In this study, to further reduce the number of parametric conditions to be investigated, a one-layer vocal fold structure is assumed. The vocal fold is modeled as a one-layer transversely isotropic, nearly incompressible, linear material with a plane of isotropy perpendicular to the AP direction, as in previous studies (Titze and Talkin, 1979; Itskov and Askel, 2002; Zhang, 2011, 2015). The material control parameters for the transversely-isotropic vocal fold include the transverse Young's modulus E_t, the AP Young's modulus E_ap, the AP shear modulus G_ap, and density. The longitudinal Poisson's ratio is assumed to be 0.495.

B. Simulation conditions

To limit the number of conditions to be investigated, parametric variations are considered only for the medial surface thickness, vocal fold stiffness along the AP direction, resting glottal angle, and the subglottal pressure, which are known to vary significantly during phonation and can be controlled through activation of laryngeal and respiratory muscles. To further reduce the number of conditions to be investigated, E_ap = 4 G_ap is also assumed in this study. All other control parameters are kept constant. A total of 19 008 conditions are investigated as summarized in Table I. For each condition, the simulation was run for 0.5 s with the subglottal pressure linearly increased from zero to a target value in 30 time steps and then kept constant.

TABLE I.

Simulation conditions. For all conditions, the vocal fold density is 1.2 kg/m³, the AP Poisson's ratio is 0.495, the transverse Young' modulus is 4 kPa, and the length is 17 mm; 19 008 conditions in total with each condition 0.5 s long.

Vocal fold thickness	T = [1, 2, 3, 4.5] mm
AP shear modulus	G_ap = 4 – 50 kPa in a step of 2 kPa
AP Young's modulus	E_ap = 4G_ap
Initial glottal angle	g₀ = 0–4° in a step of 0.4°
Subglottal pressure	P_s = [50, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1200, 1400, 1600, 1800, 2000, 2200, 2400] Pa

Open in a new tab

The medial surface of realistic vocal folds is more rounded, unlike the idealized geometry as in Fig. 1. Thus the medial surface thickness in this study should be interpreted as an approximate measure of the thickness of the most constricted portion of the glottis in the flow direction. Four values of the vocal fold medial surface thickness are considered in this study, from 1 to 4.5 mm, which roughly covers the range as used in previous studies (Titze and Talkin, 1979; Alipour et al., 2000; Scherer et al., 2001; Thomson et al., 2005; Luo et al., 2009) and estimated from reported experimental data (Sidlof et al., 2008). The initial glottal angle is varied in a range between 0° and 4°, which corresponds to a resting glottal opening of 0–10.1 mm². This range is slightly larger than that investigated in Titze and Talkin (1979) and the range of normal phonation in Isshiki (1998).

Although laryngeal muscle activation affects vocal fold stiffness in all directions, Yin and Zhang (2013) showed that stiffness along the AP direction exhibited the largest variation with varying CT/TA activations, whereas changes in the transverse stiffness was much smaller. Thus in this study, the transverse stiffness is kept constant at 4 kPa, similar to previous studies (Titze and Talkin, 1979; Berry et al., 1994; Chhetri et al., 2011). The AP shear modulus G_ap on the other hand is varied in a large range to encompass possible physiological range. Note that the minimum value of G_ap in Table I is 4 kPa below which no phonation is observed for the subglottal pressure range investigated (up to 2.4 kPa). Examination of vocal fold deformation in these conditions (i.e., G_ap < 4 kPa, corresponding to isotropic or a small degree of anisotropy) showed large static deformation, which may have violated the small-strain assumption, and these conditions are thus not included in the discussion in the following text.

C. Data analysis

Data analysis is performed using the last 0.25 s of each simulation by which time vocal fold vibration has reached steady state or nearly steady state. In addition to the mean glottal area Ag₀ and mean glottal flow rate Q_mean, the glottal area amplitude Ag_amp is calculated as half of the difference between maximum and minimum glottal areas. The mean and amplitude of the medial-lateral (ML) and superior-inferior (SI) displacement at the lower margin of the medial surface in the coronal plane are similarly calculated. The vertical phase difference (VPD) is calculated as the phase difference in the ML motion between the upper and lower margins of the medial surface in the coronal plane.

The closed quotient is generally defined as the fraction of the cycle that the glottis remains completely closed (i.e., a zero glottal area) and thus will be zero for large initial glottal angles even though glottal closure is present in the anterior portion of the glottis. In the following, closed quotient thus defined is referred to as CQ0. To take into account partial glottal closure, in this study, another measure of the closed quotient (CQ) is calculated as one minus the ratio between the open phase and the period of the glottal cycle, with the beginning and end of the open phase within each cycle defined as illustrated in Fig. 2. The beginning of the open phase is defined as the instant the waveform of the time derivative of the glottal flow last crosses zero before the curve reaches its positive peak. The end of the open phase is defined as the instant when the waveform of the time derivative of the glottal flow first crosses zero after the curve reaches its negative peak. This process is automated using a matlab script subject to manual inspection and correction if necessary. Unlike CQ0, which quantifies the duration of complete glottal closure, CQ quantifies the duration of vocal fold contact, no matter whether the contact closes the glottis completely or partially. The CQ may be large for vibrations with incomplete glottal closure but a long period of partial vocal fold contact and small if glottal closure is complete but brief.

The sound pressure level (SPL) is calculated as the root-mean-square value of the produced sound 30 cm away from the glottal exit, assuming a simple monopole sound source at the glottal exit. To calculate the relative perceived loudness, the A-weighted SPL is also calculated. Because the A-weighted and un-weighted SPLs are generally similar, only the A-weighted SPL is discussed in the following text. A similar measure (un-weighted) is also calculated for the noise component of the voices (Zhang, 2015) from which the un-weighted harmonic-to-noise ratio (HNR) is calculated. The spectra of the time derivative of the glottal flow waveform are calculated using fast Fourier transform with a Hanning window, from which the spectral amplitude difference between the first harmonic and the second harmonic (H1-H2), the fourth harmonic (H1-H4), the harmonic nearest 2 kHz (H1-H2k), and the harmonic nearest 5 kHz (H1-H5k) are extracted. These spectral measures have been shown to be perceptually important (Klatt and Klatt, 1990).

III. RESULTS

A. Phonation threshold pressure

Figure 3 shows the phonation threshold pressure as a function of the vocal fold medial surface thickness, the AP stiffness, and the resting glottal angle. Note that regions in the figure without data indicate conditions at which no phonation is observed. The resting glottal angle has the largest effect on phonation threshold pressure with the phonation threshold pressure generally increasing with increasing resting glottal angle, particularly for conditions with T > 1 mm. The AP stiffness appears to have the smallest effect on phonation threshold pressure, similar to the observation in Zhang (2015). Note that the transverse stiffness, which is expected to have a large effect on phonation threshold pressure, is kept constant in this study.

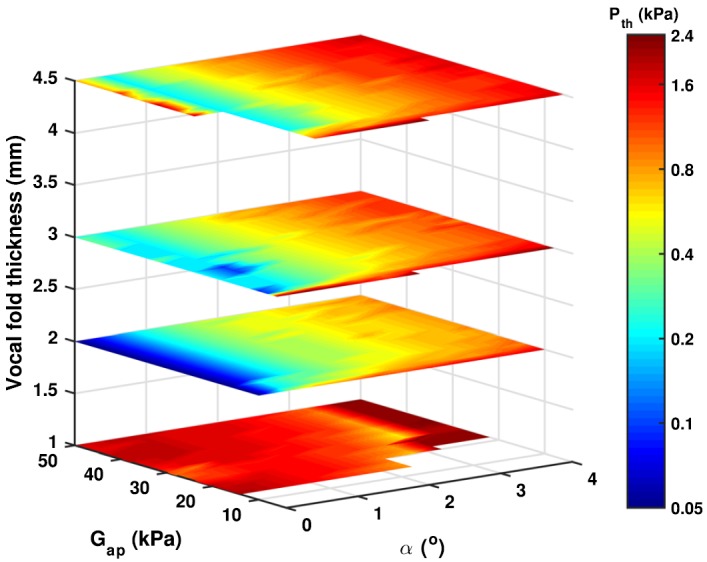
FIG. 3. — (Color online) Phonation threshold pressure as a function of the medial surface thickness T, the AP stiffness (*G_ap*), and the resting glottal angle (α).

With increasing medial surface thickness, the phonation threshold pressure first decreases and reaches the minimum for T = 2 mm and then increases with further increase in the medial surface thickness. The trend for conditions of large medial surface thickness (T > 1 mm), i.e., phonation threshold pressure increases with increasing medial surface thickness, is consistent with our previous computational and experimental observations (Zhang, 2010; Mendelsohn and Zhang, 2011). The significant increase in phonation threshold pressure for very thin vocal folds is most likely due to the inability of the vocal folds to maintain the resting glottal opening against the subglottal pressure (Fig. 4, as discussed in the following text), which leads to a prephonatory glottal opening much larger than the resting glottal opening and reduces the fluid-structure coupling strength.

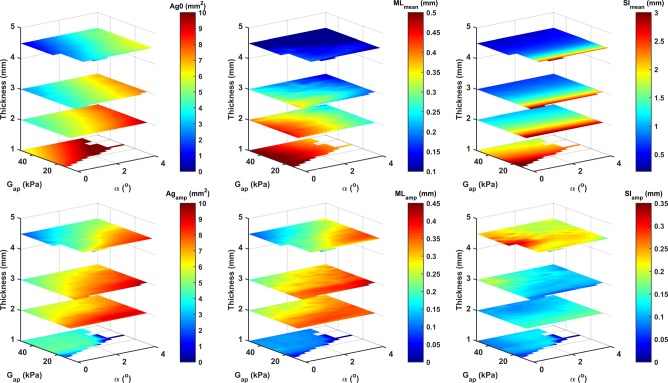
FIG. 4. — (Color online) The mean (upper) and amplitude (bottom) of the glottal area (left panels), the medial-lateral (ML; middle panels) and superior-inferior (SI; right panels) displacements of the lower margin of the medial surface in the coronal plane, as a function of the medial surface thickness, the AP stiffness (*G_ap*), and the resting glottal angle (α), for *P_s* = 2 kPa. Positive values of the mean ML and SI displacement indicate lateral and upward motion, respectively.

B. Vocal fold vibration, glottal closure, and CQ

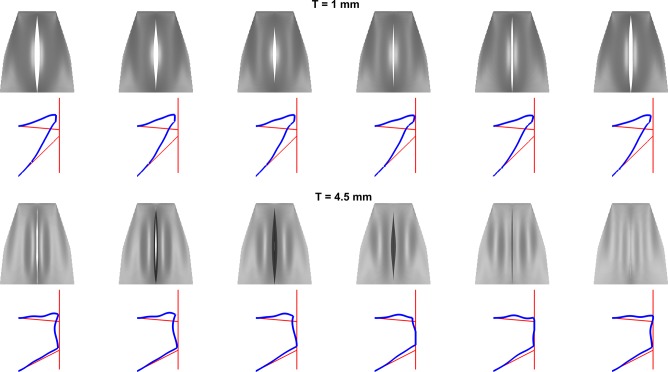
Figure 4 shows the mean glottal opening Ag₀ at different vocal fold conditions for a subglottal pressure of 2 kPa (this high subglottal pressure is chosen so that phonatory data are available for all thickness conditions because of the high phonation threshold pressure associated with the thinnest vocal folds). Vocal folds with a medial surface thickness greater than 2 mm are better able to maintain the resting glottal opening, with the mean glottal area either similar to or slightly smaller than the resting glottal opening. For thinner vocal folds, the prephonatory glottal opening is much larger than the resting glottal opening. This improved ability of thick vocal folds to maintain their resting position against airflow is due to that increasing medial surface thickness significantly reduces the mean ML displacement of the vocal fold ML_mean but has a relatively smaller effect on the ML vibration amplitude ML_amp, as shown also in Fig. 4. As a result, increasing medial surface allows the vocal fold to vibrate with improved glottal closure as illustrated in Fig. 5, which compares the vibratory pattern during one oscillation cycle between T = 1 and 4.5 mm. Despite zero resting glottal angle (i.e., glottis completely closed at rest), the thinner vocal fold is unable to maintain its resting position against the subglottal pressure and vibrates with a persistent glottal opening throughout the entire oscillation cycle. In contrast, the thicker fold (T = 4.5 mm) is able to maintain its position and vibrates with a considerably long period of complete glottal closure.

FIG. 5. — (Color online) Vocal fold vibration over one cycle for T = 1 mm and T = 4.5 mm. For each condition, the first panel shows the superior view of vocal fold vibration during one oscillation cycle, and the second panel shows the vocal fold surface shape in the coronal plane during one oscillation cycle (the thin lines indicate the resting vocal fold surface shape and glottal midline).

Figure 4 also shows that the vocal fold exhibits a very large mean vertical displacement at conditions of small vertical thickness (see also Fig. 5) or small AP stiffness; this is consistent with experimental observation in isotropic physical models of the vocal folds (Thomson et al., 2005; Zhang et al., 2006; Murray and Thomson, 2012). This large vertical deformation is suppressed with an increase in either the AP stiffness (or increasing anisotropy) or medial surface thickness. For most conditions, the ML vibration amplitude is larger than the vertical vibration amplitude (Fig. 4).

As expected, complete glottal closure in this study is achieved only for conditions of a zero resting glottal angle. Figure 6 shows CQ0, which quantifies the degree of complete glottal closure, as a function of the medial surface thickness, AP stiffness, and subglottal pressure, for conditions of α = 0°. In general, complete glottal closure is achieved for conditions of large AP stiffness and large medial surface thickness, except for conditions of very low subglottal pressures in which a vocal fry-like vibration is observed as discussed further in the following text.

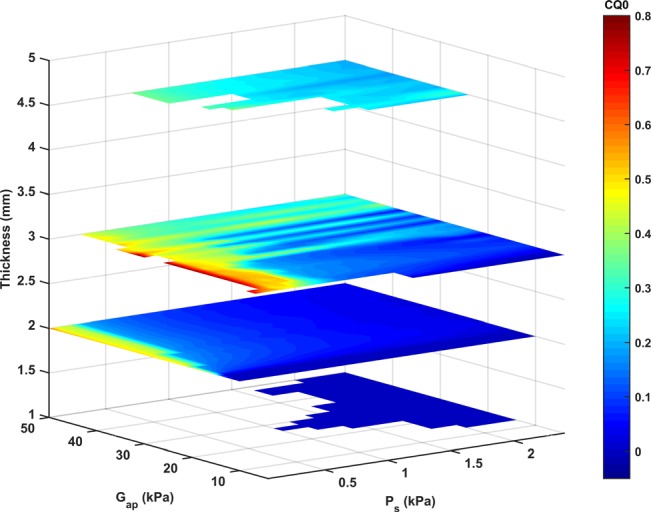
FIG. 6. — (Color online) The closed quotient CQ0, which quantifies the degree of complete glottal closure, as a function of the medial surface thickness, the AP stiffness (*G_ap*), and the subglottal pressure (*P_s*), for α = 0°.

Figure 7 shows the CQ as a function of the medial surface thickness, the AP stiffness, and the resting glottal angle, for a subglottal pressure of 2 kPa. Note that CQ quantifies the duration of vocal fold contact, which is not necessarily related to complete glottal closure. A large CQ value may occur with an incomplete (i.e., CQ0 = 0) but a long period of partial vocal fold contact. Figure 7 shows that the CQ is primarily determined by the medial surface thickness with some secondary effects of the resting glottal angle and AP stiffness. The reason underlying this strong dependence of CQ on the medial surface thickness is that for the same vocal fold condition, a larger medial surface thickness generally leads to a larger vertical phase difference (VPD) in vocal fold motion between the upper and lower margins of the medial surface, as shown in Fig. 7 (bottom panel). A non-zero VPD means that when the lower margins of the medial surface start to open, the glottis would continue to remain closed until the upper margins start to open. The larger the VPD, the longer the closed phase or the CQ (van den Berg, 1968). Indeed, the VPD and CQ exhibit high similarity in their dependence on the control parameters in Fig. 7, both of which depend primarily on the medial surface thickness. Similar results have also been observed in the original two-mass model (Ishizaka and Flanagan, 1972).

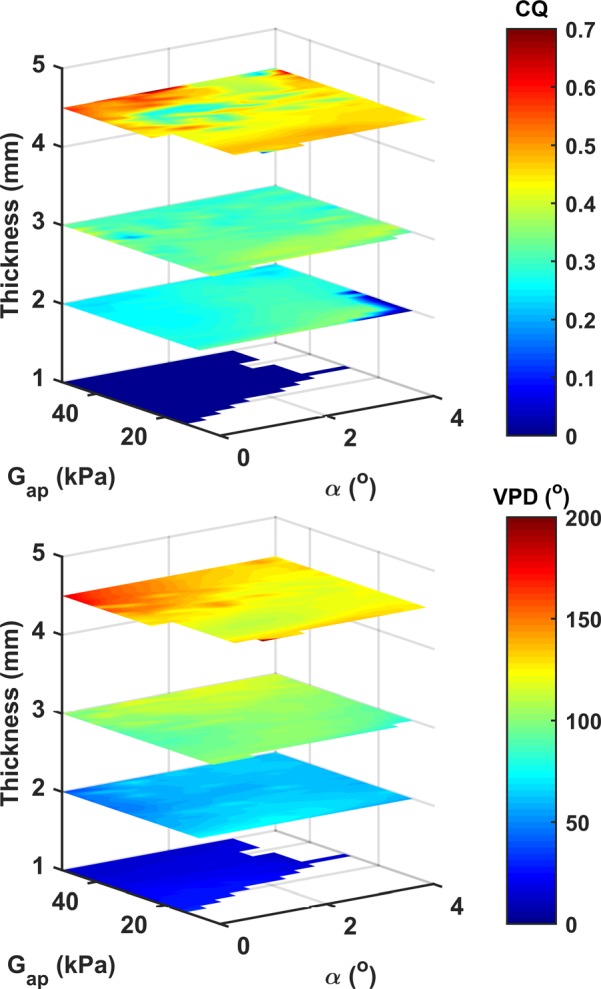
FIG. 7. — (Color online) The closed quotient CQ and vertical phase difference VPD as a function of the medial surface thickness, the AP stiffness (*G_ap*), and the resting glottal angle (α), for *P_s* = 2 kPa.

Although it is generally assumed that increased CQ can be achieved through tighter vocal fold approximation (Isshiki, 1964; Klatt and Klatt, 1990), Fig. 7 shows that neither the resting glottal angle, a measure of vocal fold approximation, nor AP stiffness has any large and consistent effect on the CQ. In this study, the overall effect of increasing vocal fold approximation is only a slight increase in the CQ, mostly for thin vocal folds (T < = 2 mm) under low subglottal pressures (Figs. 8, and 9, as discussed later). The effect of increasing AP stiffness on the CQ is generally small except for conditions of very low AP stiffness and low subglottal pressure (Fig. 10), as discussed further in the following text.

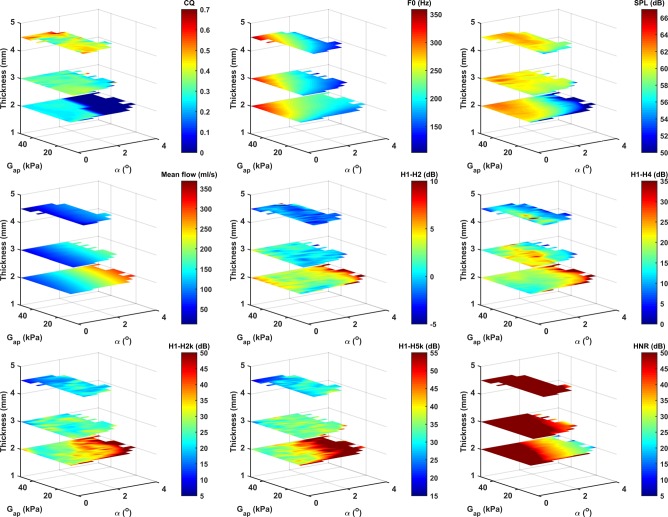
FIG. 8. — (Color online) Effects of the medial surface thickness, vocal fold AP stiffness *G_ap*, and the resting glottal angle (α). *P_s* = 800 Pa. See Sec. II for definitions of different measures. The region without data indicates conditions at which no phonation is observed. For clarify, the upper color scale for HNR is clipped at 50 dB.

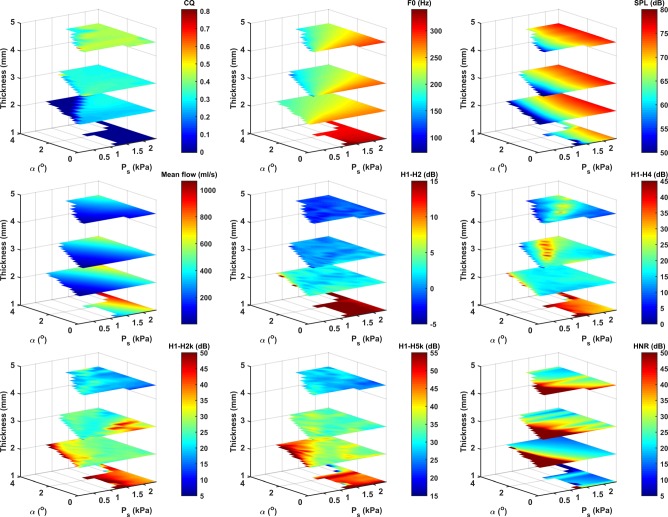
FIG. 9. — (Color online) Effects of the medial surface thickness, resting glottal angle (α), and subglottal pressure (*P_s*). G_ap = 20 kPa. See Sec. II for definitions of different measures. The region without data indicates conditions at which no phonation is observed.

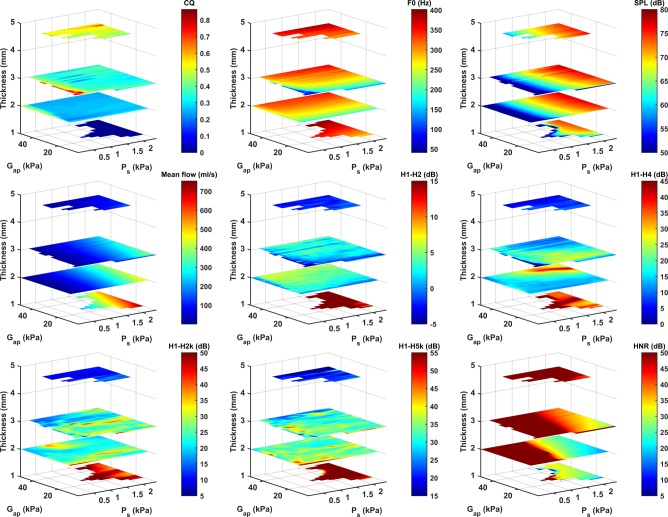
FIG. 10. — (Color online) Effects of the medial surface thickness, vocal fold AP stiffness *G_ap*, and subglottal pressure (*P_s*). α = 0°. See Sec. II for definitions of different measures. The region without data indicates conditions at which no phonation is observed.

Although Fig. 7 only shows the data for a subglottal pressure (2 kPa) much higher than the typical values observed in speech, the general pattern does not appear to change much with the subglottal pressure, as further discussed in Sec. III D 4.

It is worth noting that the highest CQ in this study is obtained for thick vocal folds (T = 3 and 4.5 mm) when the vocal folds are tightly approximated and both the AP stiffness and subglottal pressure are very low (Fig. 10). In these conditions, the vocal fold exhibits a vocal fry-like vibration and sound quality, with the CQ as high as 0.85 and the F0 as low as 41 Hz. The required degree of approximation for this vibration mode decreases slightly with increasing thickness. This mode of vibration is very sensitive to the stiffness and the subglottal pressure and disappears with an increase in either parameter.

C. F0, SPL, and mean glottal flow

Figures 8–10 also show various aerodynamic and acoustic measures as a function of vocal fold thickness, AP stiffness, resting glottal angle, and the subglottal pressure for selected conditions. These figures show that the F0 increases with increasing AP stiffness, increasing subglottal pressure, and decreasing resting glottal angle. Because of the linear material assumption of the vocal folds, the effect of the subglottal pressure and resting glottal angle on F0 is probably related to changes in the degree of vocal fold contact, which effectively stiffens the vocal folds. The F0 generally decreases with increasing medial surface thickness (T = 1–3 mm) and then slightly increases for T = 4.5 mm. Note that, in general, the highest F0 is reached for the thinnest vocal fold T = 1 mm (Figs. 9 and 10).

The A-weighted SPL depends mainly on the subglottal pressure, particularly for subglottal pressures way above phonation onset, consistent with previous observations (Tanaka and Gould, 1983; Titze, 1988; Tanaka and Tanabe, 1986; Zhang, 2015). The effects of the AP stiffness, resting glottal angle, and medial surface thickness become important only for subglottal pressures close to phonation onset in which case the SPL slightly increases with either increasing AP stiffness or decreasing resting glottal angle (Fig. 8).

The mean glottal flow increases with increasing subglottal pressure and resting glottal angle and decreases with increasing medial surface thickness and AP stiffness (Figs. 8–10). Note that increasing medial surface thickness is similarly effective as, if not more than, decreasing the resting glottal angle in reducing the glottal flow (Fig. 9). In other words, the glottal resistance (the ratio between the subglottal pressure and mean glottal flow) increases with increasing medial surface thickness, decreasing resting glottal angle, and to a lesser degree with increasing AP stiffness.

D. Voice spectral characteristics

Figures 8–10 show that the harmonic structure of the voice spectra depends primarily on the medial surface thickness and, to a much lesser degree, on the resting glottal angle and the AP stiffness. Noise production is mainly controlled by the subglottal pressure and the resting glottal angle and to a lesser degree by the medial surface thickness and the AP stiffness. Strong interactions between the stiffness, thickness, resting glottal opening, and subglottal pressure in the control of the voice spectra are observed. In the following, the effects of individual control parameters on the glottal flow waveform and its time derivative and acoustics are described in detail.

1. Effects of vocal fold thickness

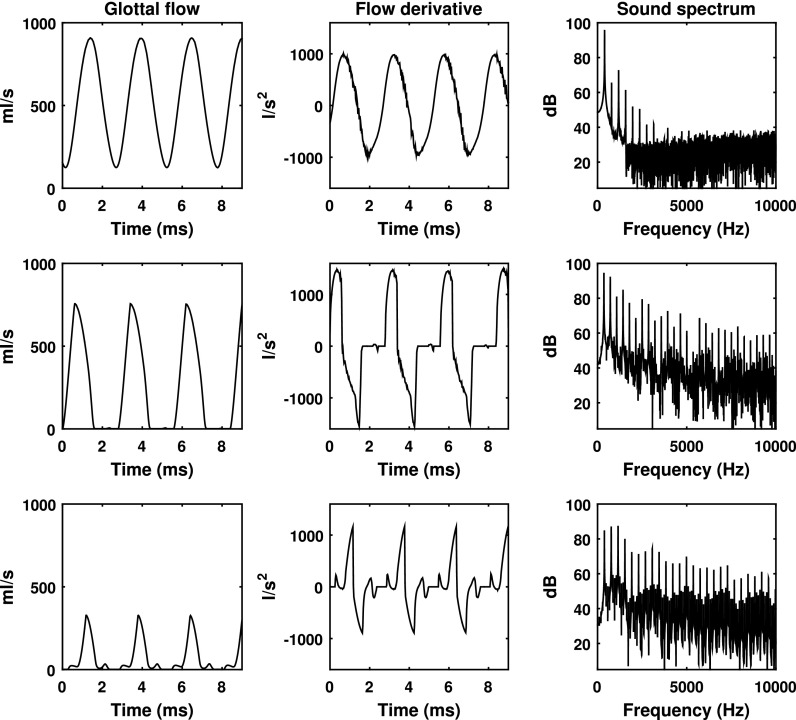
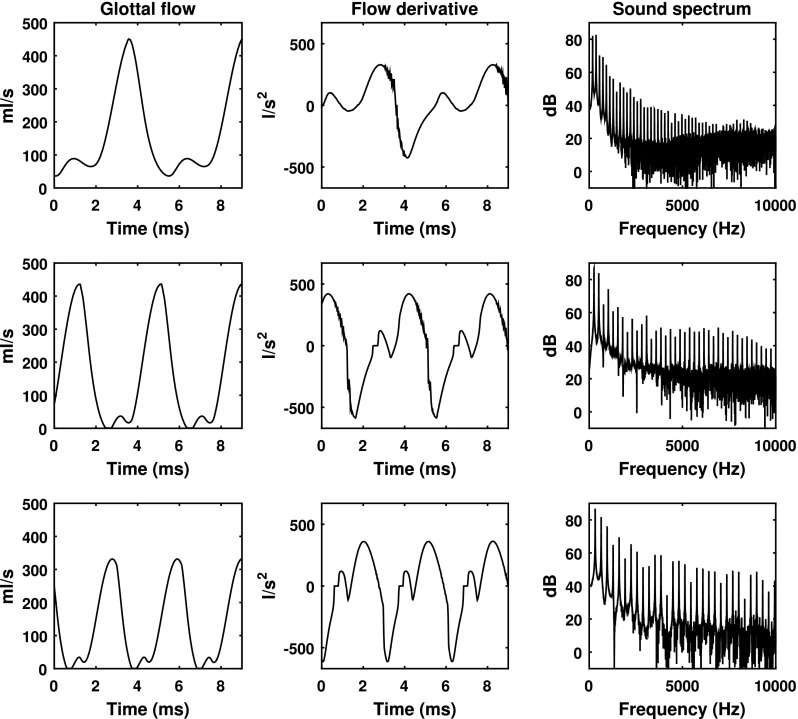
Figure 11 shows the glottal flow waveform, the time derivative of the glottal flow, and the corresponding sound spectrum for three different medial surface thicknesses. For the thinnest vocal folds, due to the reduced capability to maintain the resting glottal position, vocal fold contact is minimal, and there is a non-zero minimal glottal flow throughout the entire oscillation cycle. As a result, the glottal flow waveform and its time derivative are smooth and almost sinusoidal. This leads to a sound spectrum with only a few lower-order harmonics excited. The persistent glottal opening also leads to significant noise production, which can be observed in both the glottal flow time derivative and the sound spectrum.

FIG. 11. — The effect of the medial surface thickness on the glottal flow waveform, its time derivative, and the corresponding voice spectrum. T = 1 mm (top), 3 mm (middle), and 4.5 mm (bottom). α = 0°, *G_ap* = 50 kPa, *P_s* = 2.4 kPa.

Increasing medial surface thickness leads to improved vocal fold contact and complete shutoff of the glottal flow and thus discontinuity in both the glottal flow waveform and its time derivative. The acoustic consequences are twofold. First, the change from incomplete to complete glottal closure introduces discontinuity in the time derivative of the glottal flow waveform and leads to strong excitation of higher-order harmonics (compare the top row of Fig. 11 to the other two rows and also Figs. 8–10). Second, the increasingly longer period of glottal closure (or CQ) leads to a local peak in the low-frequency portion of the sound spectra, with the peak frequency slightly higher than the F0 and increasing roughly with CQ (Fant, 1980; Henrich et al., 2001). In other words, increasing medial surface thickness reduces H1-H2, with a large positive value for the thinnest vocal folds and a negative value for the thickest vocal folds (Figs. 8, 9, and 11).

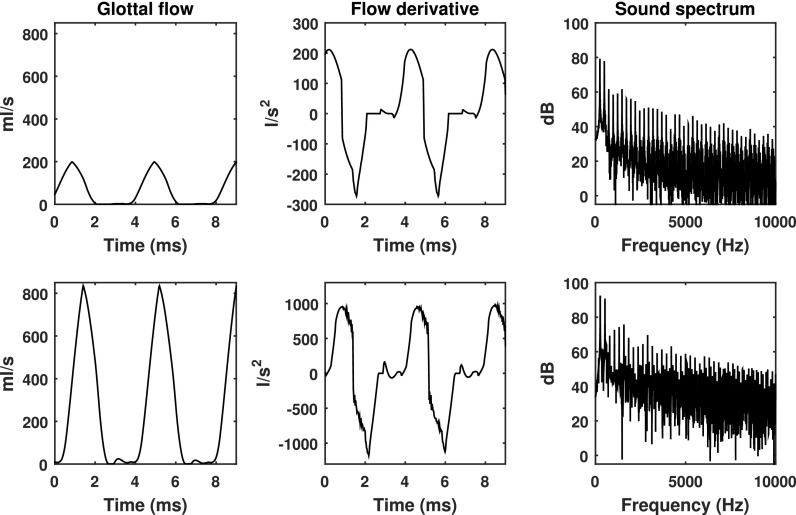
2. Effects of resting glottal opening

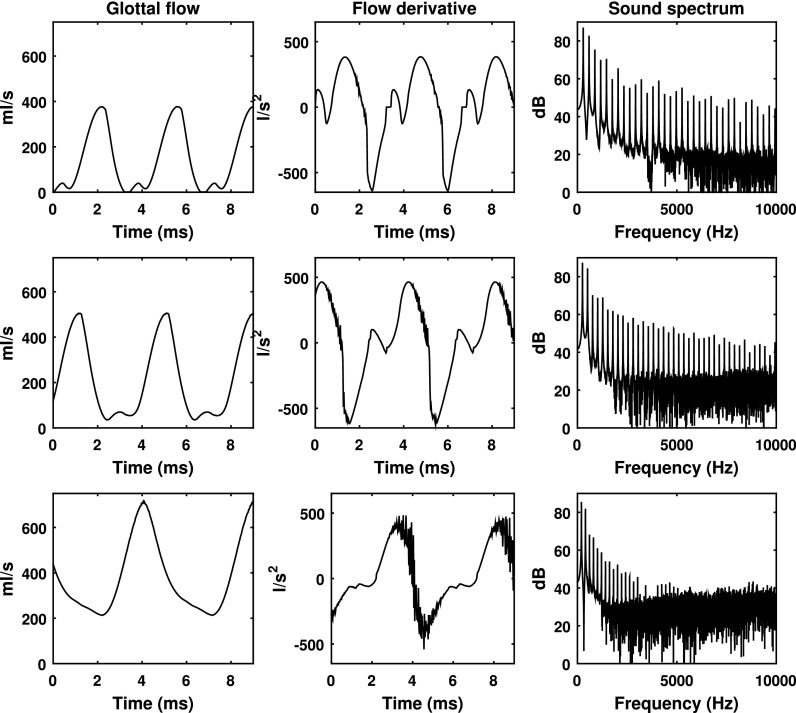
Figure 12 shows the effect of the resting glottal angle on the glottal flow waveform, its time derivative, and the resulting sound spectrum. Two major effects can be observed. First, increasing the resting glottal angle increases the minimum flow through the glottis and thus noise production. Second, for large resting glottal angles (third row in Fig. 12), because the posterior portion of the vocal folds needs to travel a farther distance than the anterior portion to reach glottal midline, there is considerable AP phase difference in glottal closure as closure often starts from the anterior and spreads to the posterior end. As a result, glottal closure takes longer and is much less abrupt with increasing resting glottal angle, leading to an increasingly smoother waveform of the time derivative of the glottal flow, particularly in the closing phase after the instant of negative peak in the flow derivative waveform (third row in Fig. 12). Acoustically, this reduces excitation of higher-order harmonics. Overall, increasing resting glottal angle leads to a voice with reduced higher-order harmonics and increased noise production at high frequencies, particularly for large resting glottal angles (Figs. 8, 9, and 12). In contrast, increasing the resting glottal angle alone has only small effect on the low-frequency portion of the voice spectra (mostly H1-H4, Fig. 9) except for conditions of large resting glottal angle and subglottal pressures close to phonation onset (Figs. 8 and 9) in which the effect can be relatively large.

FIG. 12. — The effect of the resting glottal angle on the glottal flow waveform, its time derivative, and the corresponding voice spectrum. α = 0°, (top), 0.6°, (middle), and 2°, (bottom). T = 2 mm, *G_ap* = 30 kPa, *P_s* = 1.2 kPa.

3. Effects of vocal fold stiffness

The effect of vocal fold stiffness on the voice spectrum is generally small. In addition to an increased F0, increasing AP stiffness slightly reduces the noise (Fig. 13, right column) and improves the HNR (Figs. 8 and 10) although the effect is smaller compared with the other controls.

FIG. 13. — The effect of the AP stiffness on the glottal flow waveform, its time derivative, and the corresponding voice spectrum. *G_ap* = 10 kPa (top), 20 kPa (middle), and 40 kPa (bottom). T = 2 mm, α = 0°, *P_s* = 1.2 kPa.

For conditions of very small AP stiffness and not so thick vocal folds under low to medium subglottal pressure, increasing the AP stiffness may increase the excitation of higher-order harmonics. Figure 13 illustrates such effects for a vocal fold condition with T = 2 mm. For very small AP stiffness, the vocal fold vibrates with incomplete glottal closure with a persistent leak flow through the middle glottis throughout the entire oscillation cycle, similar to observations in physical vocal fold models with isotropic material properties (Zhang, 2011; Mendelsohn and Zhang, 2011; Xuan and Zhang, 2014). As a result, the time derivative of the glottal flow is rather smooth, which leads to weak excitation of higher-order harmonics. Increasing the AP stiffness leads to brief complete glottal closure (Fig. 6; but not much change in CQ) and relatively faster changes in the time derivative of the glottal flow waveform (Fig. 13), which improves excitation of higher-order harmonics in the resulting voice spectra (Figs. 8, 10, and 13). However, further increase in AP stiffness does not appear to produce any further improvement.

4. Effects of subglottal pressure

Increasing subglottal pressure increases the vibration amplitude and the glottal flow amplitude, which leads to significant increase in the produced noise and a reduction in HNR. Despite the increased vibration amplitude with increasing subglottal pressure, there appears to be little effect on the CQ (Figs. 9 and 10), the glottal flow wave and the waveform of its time derivative (Fig. 14). As a result, the effect of the subglottal pressure on the spectral shape and the harmonic structure is generally small, as shown in Figs. 9 and 10.

FIG. 14. — The effect of the subglottal pressure on the glottal flow waveform, its time derivative, and the corresponding voice spectrum. *P_s* = 0.8 kPa (top) and 2 kPa (bottom). T = 3 mm, α = 0°, *G_ap* = 20 kPa.

Two exceptions are observed in which the effect of the subglottal pressure on the voice spectra is no longer small, both of which occur when the subglottal pressure is slightly above phonation onset. The first exception is when the vocal fold is not too thick (T $< =$ 2 mm) and the resting glottal angle is relatively large (Fig. 9) in which case the vocal fold vibrates with minimum contact. Increasing the subglottal pressure in this case leads to vocal fold contact during vibration and significantly increases the higher-order harmonics excitation. The second exception occurs when the vocal fold has a low AP stiffness and is tightly approximated and vibrates in a vocal fry-like mode (a large CQ, a negative H1-H2, and a very low F0, as discussed earlier; Fig. 10). Increasing the subglottal pressure in this case would cause the vocal fold to leave this vibration mode, significantly reducing the CQ and increasing the F0 and H1-H2.

E. Multiple linear regression between physiological controls and output variables

Stepwise multiple linear regression is conducted to predict the vibration and acoustic measures from the four control parameters (thickness, AP stiffness, resting glottal angle, and subglottal pressure). Table II shows the regression coefficients and the corresponding R² values. Interpretation of Table II requires consideration of both the absolute values of the coefficients and the ranges of variation of the corresponding control and output variables. Consider H1-H2 as an example. Table II shows a coefficient of −4.3104 for the medial surface thickness, which indicates a change in the medial surface thickness from 1 to 4.5 mm (the range of variation of this study) will reduce the H1-H2 by 15.1 dB. In contrast, for changes in the resting glottal angle (from 0° to 4°), AP stiffness (10–50 kPa), and subglottal pressure (0.5–1.5 kPa), Table II would predict much smaller changes in H1-H2 (0.5, 3.6, and 1.9 dB, respectively). Thus in the case of H1-H2, the medial surface is the dominant determining factor. In Table II, similarly identified dominant determining factors are highlighted. In general, the identified main relationships correspond to primary cause-effect relations that are observed consistently across a large range of conditions.

TABLE II.

Regression coefficients between physiological controls and vibration and acoustic output measures and the corresponding R² values. Numbers in bold indicate large effect as determined by consideration of the coefficient value and the range of variation of the corresponding physiological and output variables. For SPL, the numbers in parenthesis are values obtained when log₁₀ (P_s) is used. For H1-H4, the AP stiffness does not enter the regression equation.

	T (mm)	α (°)	G_ap (kPa)	P_s (kPa)	Intercept	R²
F0 (Hz)	−12.8862	−24.4709	2.7912	44.8626	171.7038	0.80
SPL (dB)	1.5617 (1.3493)	−0.3605 (−0.8373)	0.1049 (0.1056)	13.0858 (34.3627)	39.1633 (56.0832)	0.70 (0.77)
CQ	0.1054	−0.0247	−0.0003	0.0283	−0.0135	0.61
H1-H2 (dB)	−4.3104	−0.1248	0.0888	1.9427	10.8227	0.44
H1-H4 (dB)	−5.2865	0.4156		2.6273	30.3599	0.41
H1-H2k (dB)	−6.2679	1.4282	−0.1352	−2.1378	50.0072	0.52
H1-H5k (dB)	−5.3545	1.3718	−0.0963	−3.7513	57.0543	0.47
HNR (dB)	11.4960	−28.1858	0.7802	−111.2251	241.6140	0.62

Open in a new tab

The R² values in Table II are about 0.8 for F0 and SPL (with log₁₀ P_s as input), but vary from 0.4 to 0.6 for the CQ and spectral measures, indicating a moderately nonlinear relationship between the control parameters and these output variables. Considering the strong interaction between control parameters observed in this study, a more complex nonlinear regression may be required to accurately predict the acoustic consequence of changes in vocal fold physiology or to recover the control parameters from the output acoustic measures. However, the relatively high correlations do suggest the possibility for a rough and fast estimation of vocal fold properties and the glottal configuration from output acoustic measures.

IV. DISCUSSION AND CONCLUSIONS

This study shows that vocal fold approximation has a dominant effect on phonation threshold pressure and thus is essential to achieving phonation at low subglottal pressures and reducing respiratory effort of phonation. With properly approximated vocal folds, the VPD, CQ, and voice spectral shape (both low frequency and high frequency) are largely controlled by the medial surface thickness. In general, thin vocal folds tend to vibrate with small vertical phase difference between the lower and upper margins of the medial surface, no or brief glottal closure, relatively high glottal flow rate, a smooth or nearly sinusoidal flow waveform, a large and positive H1-H2, and a small number of harmonics excited. In contrast, thick vocal folds vibrate with large vertical phase difference between the upper and lower margins of the medial surface, long closure of the glottis, relatively small flow rate, a small or negative H1-H2, and strong harmonics excitation in the voice spectra. This large impact of medial surface thickness on voice acoustics and voice quality indicates that control of medial surface thickness plays an importance role in voice quality control. Clinically, this also suggests that one of the goals of phonosurgery should be to maintain or establish a reasonable medial surface thickness, e.g., by medializing or augmenting the inferior portion of the medial surface.

In contrast, the main acoustic effect of changes in the AP stiffness, resting glottal angle and subglottal pressure that is consistently observed in a large range of conditions, other than F0 control and vocal intensity control (for subglottal pressure), is on noise production, which decreases with increasing AP stiffness, decreasing resting glottal angle, and decreasing subglottal pressure. For some limited range of conditions (mostly for large resting glottal angle, small AP stiffness, and/or small subglottal pressure), increasing AP stiffness and subglottal pressure and decreasing resting glottal angle may improve vocal fold contact and thus increase the excitation of high-order harmonics.

It may appear surprising that vocal fold approximation has only a slight effect on the CQ in this study. However, it is noted that the phonation threshold pressure is very sensitive to the resting glottal angle. For subglottal pressures typical of speech, phonation is only possible for very small resting glottal angles (less than 4° in this study). Similarly high sensitivity of phonation onset to the resting glottal opening was also observed in Titze and Talkin (1979) and Isshiki (1989). Therefore the possible range of variation for the resting glottal opening while still maintaining phonation is quite limited. Within this small range of variation, it is not surprising that changes in the resting glottal angle only have small effect on the CQ, particularly for a triangle-shaped glottis for which vocal fold contact will occur at least for some portion of the glottis. Thus starting from the resting configuration of the glottis, the main purpose of vocal fold approximation is to bring down the phonation threshold pressure to initiate phonation. Further increase in vocal fold approximation only serves to reduce noise production and increase fundamental frequency and has little effect on the CQ.

Although it is generally assumed that the CQ can be increased through increased vocal fold adduction as one changes voice from breathy to pressed, the results of this study indicate that in addition to vocal fold approximation, vocal fold adduction must also increase the medial surface thickness to increase the CQ significantly. In humans, vocal fold adduction is achieved through stimulation of the recurrent laryngeal nerve (RLN), which innervates the lateral cricoarytenoid (LCA) muscle, the interarytenoid (IA) muscle, and the TA muscle. It is generally assumed that activation of the LCA and IA muscles leads to rotation and translation of the arytenoid cartilage, which approximates and slightly thins the vocal folds (Hirano and Kakita, 1985). Activation of the TA muscle, on the other hand, has been hypothesized to be able to approximate the lower portion of the medial surface toward the glottal centerline, thus changing the medial surface contour. If these hypotheses hold, it would indicate that the thyroarytenoid muscle, instead of the LCA/IA muscles, plays an exclusive role in the control of the CQ and the low-frequency portion (e.g., H1-H2) of the resulting voice spectra as voice quality changes within a breathy/pressed continuum.

This study shows that the effect of the medial surface thickness on F0 is relatively small so that adjustment of the medial surface thickness by itself is not critical to F0 control (although Figs. 9 and 10 do show that the highest F0 is reached for the thinnest vocal fold, indicating a thin vocal fold is preferred for very high-F0 voice production). In humans, however, the medial surface thickness often co-varies with the AP stiffness and the resting glottal angle. Control of the AP stiffness is achieved through activation of the CT muscle, which has been generally assumed to also reduce the medial surface thickness and in some conditions increase the resting glottal angle (van den Berg, 1968; Hirano and Kakita, 1985). On the other hand, activation of the TA muscle is also known to reduce AP stiffness, decrease the resting glottal opening, and increase medial surface thickness (Hirano and Kakita, 1985). Thus if one attempts to increase F0 by increasing vocal fold approximation alone (with or without simultaneous increase in the subglottal pressure), the vocal folds are likely to have a large medial surface thickness and probably low AP stiffness, which, according to the results of this study, will produce a chest-like voice with large phase difference along the medial surface, long closure of the glottis, small flow rate, and strong harmonic excitation. In this study, the maximum F0 that can be reached in this way is around 250–300 Hz, depending on the values of other control parameters. In contrast, if one attempts to increase F0 by increasing the AP stiffness alone (with or without increase in the subglottal pressure), the vocal folds, with a small medial surface thickness, are likely to produce a falsetto-like voice with incomplete glottal closure and a nearly sinusoidal flow waveform, high flow rate, very high F0, and a very small number of harmonics. This antagonistic role of the CT/TA muscles in the control of vocal fold posturing has been hypothesized by Van den Berg (1968) to be a possible origin of vocal registers and their transitions; this is supported by the results of this study.

Similar to previous studies (Tanaka and Gould, 1983; Titze, 1988; Tanaka and Tanabe, 1986; Finnegan et al., 2000; Zhang, 2015), the SPL (both un-weighted and A-weighted) in this study depends primarily on the subglottal pressure. The effect of vocal fold properties (thickness, AP stiffness, and resting glottal angle) on the SPL is generally small except near phonation onset. Increasing subglottal pressure also leads to significant noise production, which can be counterbalanced by decreasing the resting glottal angle, increasing the thickness, and/or increasing AP stiffness, all of which increase the glottal resistance, to maintain a desirable HNR. This may explain why vocal intensity increase in humans, particularly at the low-middle pitch range, is often accompanied by simultaneous increases in both the subglottal pressure and the glottal resistance (Isshiki, 1964; Hirano, 1981; Holmberg et al., 1988; Stathopoulos and Sapienza, 1993) despite the relative small effect of laryngeal adjustments on vocal intensity. Additionally, this study also shows that at conditions close to phonation onset, increasing AP stiffness or decreasing resting glottal angle can increase the SPL by a few decibels. Thus the glottal resistance may be increased at conditions of low subglottal pressures (and most likely a relaxed vocal fold) to take advantage of this additional gain in vocal intensity.

The main limitation of this study, in addition to model simplifications as discussed earlier, is that only one-layer vocal fold conditions are considered. Physiologically, the vocal folds are multi-layered structures, and it has been hypothesized that this layered structure may have dynamical importance. Limiting our focus to a one-layer vocal fold structure in this study is necessary to reduce the number of conditions to be investigated and makes it easier to sort out the effects of the already complex interaction between different control parameters on voice production. However, future work is required to extend this study to a multi-layered vocal fold model. Also the transverse stiffness and vocal fold length in this study are kept constant. Variation of the transverse stiffness is expected to have a significant effect on phonation threshold pressure, the vertical phase difference, and possibly the CQ and the spectral shapes. It is possible that in a multi-layered model, vocal fold stiffness, both in the AP direction and the transverse plane, may have a more important impact on the voice spectra than observed in the present study. Finally, inclusion of a subglottal and supraglottal tract is expected to interact with the glottal flow and its effect will be reported in a future study.

ACKNOWLEDGMENTS

This study was supported by research Grant Nos. R01 DC009229 and R01 DC011299 from the National Institute on Deafness and Other Communication Disorders, the National Institutes of Health.

References

1. Alipour, F. , Berry, D. A. , and Titze, I. R. (2000). “ A finite-element model of vocal-fold vibration,” J. Acoust. Soc. Am. 108, 3003–3012. 10.1121/1.1324678 [DOI] [PubMed] [Google Scholar]
2. Berke, G. , Mendelsohn, A. , Howard, N. , and Zhang, Z. (2013). “ Neuromuscular induced phonation in a human ex vivo perfused larynx preparation,” J. Acoust. Soc. Am. 133(2), EL114–EL117. 10.1121/1.4776776 [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Berry, D. A. , Herzel, H. , Titze, I. R. , and Krischer, K. (1994). “ Interpretation of biomechanical simulations of normal and chaotic vocal fold oscillations with empirical eigenfunctions,” J. Acoust. Soc. Am. 95, 3595–3604. 10.1121/1.409875 [DOI] [PubMed] [Google Scholar]
4. Chhetri, D. , Neubauer, J. , and Berry, D. (2012). “ Neuromuscular control of fundamental frequency and glottal posture at phonation onset,” J. Acoust. Soc. Am. 131(2), 1401–1412. 10.1121/1.3672686 [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Chhetri, D. K. , Zhang, Z. , and Neubauer, J. (2011). “ Measurement of Young's modulus of vocal fold by indentation,” J. Voice 25, 1–7. 10.1016/j.jvoice.2009.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
6. Fant, G. (1980). “ Voice source dynamics,” STL-QPSR 21, 17–37. [Google Scholar]
7. Fant, G. (1982). “ Preliminaries to analysis of the human voice source,” STL-QPSR 23(4), 1–27. [Google Scholar]
8. Fant, G. , Liljencrants, J. , and Lin, Q. (1985). “ A four-parameter model of glottal flow,” STL-QPSR 26(4), 1–13. [Google Scholar]
9. Finnegan, E. , Luschei, E. , and Hoffman, H. (2000). “ Modulations in respiratory and laryngeal activity associated with changes in vocal intensity during speech,” J. Speech Lang. Hear. Res. 43, 934–950. 10.1044/jslhr.4304.934 [DOI] [PubMed] [Google Scholar]
10. Gay, T. , Hirose, H. , Strome, M. , and Sawashima, M. (1972). “ Electromyography of the intrinsic laryngeal muscles during phonation,” Ann. Otol. Rhinol. Laryngol. 81, 401–409. 10.1177/000348947208100311 [DOI] [PubMed] [Google Scholar]
11. Henrich, N. , d'Alessandro, C. , and Doval, B. (2001). “ Spectral correlates of voice open quotient and glottal flow asymmetry: Theory, limits and experimental data,” in Proceedings of EUROSPEECH, Scandinavia, pp. 47–50. [Google Scholar]
12. Henrich, N. , d'Alessandro, C. , Doval, B. , and Castellengo, M. (2005). “ Glottal open quotient in singing: Measurements and correlation with laryngeal mechanisms, vocal intensity, and fundamental frequency,” J. Acoust. Soc. Am. 117(3), 1417–1430. 10.1121/1.1850031 [DOI] [PubMed] [Google Scholar]
13. Hirano, M. (1974). “ Morphological structure of the vocal fold and its variations,” Folia Phoniatr. 26, 89–94. 10.1159/000263771 [DOI] [PubMed] [Google Scholar]
14. Hirano, M. (1981). Clinical Examination of Voice: Disorders of Human Communication ( Springer, New York: ), Vol. 5, Chap. 3. [Google Scholar]
15. Hirano, M. , and Kakita, Y. (1985). “ Cover-body theory of vocal fold vibration,” in Speech Science: Recent Advances, edited by Daniloff R. G. ( College-Hill Press, San Diego: ), pp. 1–46. [Google Scholar]
16. Hirano, M. , Ohala, J. , and Vennard, W. (1969). “ The function of laryngeal muscles in regulating fundamental frequency and intensity of phonation,” J. Speech, Hear. Res. 12, 616–628. 10.1044/jshr.1203.616 [DOI] [PubMed] [Google Scholar]
17. Hirano, M. , Vennard, W. , and Ohala, J. (1970). “ Regulation of register, pitch and intensity of voice: An electromyographic investigation of intrinsic laryngeal muscles,” Folia Phoniatr. 22, 1–20. 10.1159/000263363 [DOI] [PubMed] [Google Scholar]
18. Holmberg, E. , Hillman, R. , and Perkell, J. (1988). “ Glottal airflow and transglottal air pressure measurements for male and female speakers in soft, normal, and loud voice,” J. Acoust. Soc. Am. 84, 511–529. 10.1121/1.396829 [DOI] [PubMed] [Google Scholar]
19. Ishizaka, K. , and Flanagan, J. L. (1972). “ Synthesis of voiced sounds from a two-mass model of the vocal cords,” Bell Syst. Tech. J. 51, 1233–1267. 10.1002/j.1538-7305.1972.tb02651.x [DOI] [Google Scholar]
20. Isshiki, N. (1964). “ Regulatory mechanism of voice intensity variation,” J. Speech, Hear. Res. 7, 17–29. 10.1044/jshr.0701.17 [DOI] [PubMed] [Google Scholar]
21. Isshiki, N. (1989). Phonosurgery: Theory and Practice ( Springer-Verlag, Tokyo: ), Chap. 3. [Google Scholar]
22. Isshiki, N. (1998). “ Mechanical and dynamical aspects of voice production as related to voice therapy and phonsurgery,” J. Voice 12, 125–137. 10.1016/S0892-1997(98)80031-3 [DOI] [PubMed] [Google Scholar]
23. Itskov, M. , and Aksel, N. (2002). “ Elastic constants and their admissible values for incompressible and slightly compressible anisotropic materials,” Acta Mech. 157, 81–96. 10.1007/BF01182156 [DOI] [Google Scholar]
24. Klatt, D. H. , and Klatt, L. C. (1990). “ Analysis, synthesis and perception of voice quality variations among male and female talkers,” J. Acoust. Soc. Am. 87, 820–856. 10.1121/1.398894 [DOI] [PubMed] [Google Scholar]
25. Luo, H. , Mittal, R. , and Bielamowicz, S. (2009). “ Analysis of flow-structure interaction in the larynx during phonation using an immersed-boundary method,” J. Acoust. Soc. Am. 126, 816–824. 10.1121/1.3158942 [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Mendelsohn, A. , and Zhang, Z. (2011). “ Phonation threshold pressure and onset frequency in a two-layer physical model of the vocal folds,” J. Acoust. Soc. Am. 130, 2961–2968. 10.1121/1.3644913 [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Moore, D. M. , and Berke, G. S. (1988). “ The effect of laryngeal nerve stimulation on phonation: A glottographic study using an in vivo canine model,” J. Acoust. Soc. Am. 83, 705–715. 10.1121/1.396113 [DOI] [PubMed] [Google Scholar]
28. Murray, P. R. , and Thomson, S. L. (2012). “ Vibratory responses of synthetic, self-oscillating vocal fold models,” J. Acoust. Soc. Am. 132, 3428–343. 10.1121/1.4754551 [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Pickup, B. , and Thomson, S. L. (2011). “ Identification of geometric parameters influencing the flow-induced vibration of a two-layer self-oscillating computational vocal fold model,” J. Acoust. Soc. Am. 129(4), 2121–2132. 10.1121/1.3557046 [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Scherer, R. , Shinwari, D. , De Witt, K. , Zhang, C. , Kucinschi, B. , and Afjeh, A. (2001). “ Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees,” J. Acoust. Soc. Am. 109(4), 1616–1630. 10.1121/1.1333420 [DOI] [PubMed] [Google Scholar]
31. Sciamarella, D. , and d'Alessandro, C. (2004). “ On the acoustic sensitivity of a symmetrical two-mass model of the vocal folds to the variation of control parameters,” Acta Acust. 90, 746–761. [Google Scholar]
32. Sidlof, P. , Svec, J. , Horacek, J. , Vesely, J. , Klepacek, I. , and Havlik, R. (2008). “ Geometry of human vocal folds and glottal channel for mathematical and biomechanical modeling of voice production,” J. Biomech. 41, 985–995. 10.1016/j.jbiomech.2007.12.016 [DOI] [PubMed] [Google Scholar]
33. Stathopoulos, E. , and Sapienza, C. (1993). “ Respiratory and laryngeal function of women and men during vocal intensity variation,” J. Speech Hear. Res. 36, 64–75. 10.1044/jshr.3601.64 [DOI] [PubMed] [Google Scholar]
34. Steinecke, I. , and Herzel, H. (1995). “ Bifurcations in an asymmetric vocal fold model,” J. Acoust. Soc. Am. 97, 1874–1884. 10.1121/1.412061 [DOI] [PubMed] [Google Scholar]
35. Stevens, K. N. (1998). Acoustic Phonetics ( MIT Press, Cambridge, MA: ), Chap. 2. [Google Scholar]
36. Story, B. H. , and Titze, I. R. (1985). “ Voice simulation with a body-cover model of the vocal folds,” J. Acoust. Soc. Am. 97, 1249–1260. [DOI] [PubMed] [Google Scholar]
37. Tanaka, S. , and Gould, W. (1983). “ Relationships between vocal intensity and noninvasively obtained aerodynamic parameters in normal subjects,” J. Acoust. Soc. Am. 73(4), 1316–1321. 10.1121/1.389235 [DOI] [PubMed] [Google Scholar]
38. Tanaka, S. , and Tanabe, M. (1986). “ Glottal adjustment for regulating vocal intensity, an experimental study,” Acta Otolaryngol. 102, 315–324. 10.3109/00016488609108682 [DOI] [PubMed] [Google Scholar]
39. Thomson, S. L. , Mongeau, L. , and Frankel, S. H. (2005). “ Aerodynamic transfer of energy to the vocal folds,” J. Acoust. Soc. Am. 118, 1689–1700. 10.1121/1.2000787 [DOI] [PubMed] [Google Scholar]
40. Titze, I. R. (1988). “ Regulation of vocal power and efficiency by subglottal pressure and glottal width,” in Vocal Physiology: Voice Production, Mechanisms and Functions, edited by Fujimura O. ( Raven, New York: ), pp. 227–238. [Google Scholar]
41. Titze, I. , and Talkin, D. (1979). “ A theoretical study of the effects of various laryngeal configurations on the acoustics of phonation,” J. Acoust. Soc. Am. 66, 60–74. 10.1121/1.382973 [DOI] [PubMed] [Google Scholar]
42. Van den Berg, J. W. (1968). “ Register problems,” Ann. NY Acad. Sci. 155(1), 129–134. 10.1111/j.1749-6632.1968.tb56756.x [DOI] [PubMed] [Google Scholar]
43. Van den Berg, J. W. , and Tan, T. S. (1959). “ Results of experiments with human larynxes,” Pract. Otorhinolaryngol. 21, 425–450. [DOI] [PubMed] [Google Scholar]
44. Xuan, Y. , and Zhang, Z. (2014). “ Influence of embedded fibers and an epithelium layer on glottal closure pattern in a physical vocal fold model,” J. Speech Lang. Hear. Res. 57, 416–425. 10.1044/2013_JSLHR-S-13-0068 [DOI] [PMC free article] [PubMed] [Google Scholar]
45. Yin, J. , and Zhang, Z. (2013). “ The influence of thyroarytenoid and cricothyroid muscle activation on vocal fold stiffness and eigenfrequencies,” J. Acoust. Soc. Am. 133, 2972–2983. 10.1121/1.4799809 [DOI] [PMC free article] [PubMed] [Google Scholar]
46. Zhang, Z. (2009). “ Characteristics of phonation onset in a two-layer vocal fold model,” J. Acoust. Soc. Am. 125, 1091–1102. 10.1121/1.3050285 [DOI] [PMC free article] [PubMed] [Google Scholar]
47. Zhang, Z. (2010). “ Dependence of phonation threshold pressure and frequency on vocal fold geometry and biomechanics,” J. Acoust. Soc. Am. 127, 2554–2562. 10.1121/1.3308410 [DOI] [PMC free article] [PubMed] [Google Scholar]
48. Zhang, Z. (2011). “ Restraining mechanisms in regulating glottal closure during phonation,” J. Acoust. Soc. Am. 130, 4010–4019. 10.1121/1.3658477 [DOI] [PMC free article] [PubMed] [Google Scholar]
49. Zhang, Z. (2014). “ The influence of material anisotropy on vibration at onset in a three-dimensional vocal fold model,” J. Acoust. Soc. Am. 135(3), 1480–1490. 10.1121/1.4863266 [DOI] [PMC free article] [PubMed] [Google Scholar]
50. Zhang, Z. (2015). “ Regulation of glottal closure and airflow in a three-dimensional phonation model: Implications for vocal intensity control,” J. Acoust. Soc. Am. 137, 898–910. 10.1121/1.4906272 [DOI] [PMC free article] [PubMed] [Google Scholar]
51. Zhang, Z. , and Luu, T. (2012). “ Asymmetric vibration in a two-layer vocal fold model with left-right stiffness asymmetry: Experiment and simulation,” J. Acoust. Soc. Am. 132(3), 1626–1635. 10.1121/1.4739437 [DOI] [PMC free article] [PubMed] [Google Scholar]
52. Zhang, Z. , Mongeau, L. , and Frankel, S. H. (2002). “ Experimental verification of the quasi-steady approximation for aerodynamic sound generation by pulsating jets in tubes,” J. Acoust. Soc. Am. 112(4), 1652–1663. 10.1121/1.1506159 [DOI] [PubMed] [Google Scholar]
53. Zhang, Z. , Neubauer, J. , and Berry, D. A. (2006). “ The influence of subglottal acoustics on laboratory models of phonation,” J. Acoust. Soc. Am. 120(3), 1558–1569. 10.1121/1.2225682 [DOI] [PubMed] [Google Scholar]

[c1] 1. Alipour, F. , Berry, D. A. , and Titze, I. R. (2000). “ A finite-element model of vocal-fold vibration,” J. Acoust. Soc. Am. 108, 3003–3012. 10.1121/1.1324678 [DOI] [PubMed] [Google Scholar]

[c2] 2. Berke, G. , Mendelsohn, A. , Howard, N. , and Zhang, Z. (2013). “ Neuromuscular induced phonation in a human ex vivo perfused larynx preparation,” J. Acoust. Soc. Am. 133(2), EL114–EL117. 10.1121/1.4776776 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c3] 3. Berry, D. A. , Herzel, H. , Titze, I. R. , and Krischer, K. (1994). “ Interpretation of biomechanical simulations of normal and chaotic vocal fold oscillations with empirical eigenfunctions,” J. Acoust. Soc. Am. 95, 3595–3604. 10.1121/1.409875 [DOI] [PubMed] [Google Scholar]

[c4] 4. Chhetri, D. , Neubauer, J. , and Berry, D. (2012). “ Neuromuscular control of fundamental frequency and glottal posture at phonation onset,” J. Acoust. Soc. Am. 131(2), 1401–1412. 10.1121/1.3672686 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c5] 5. Chhetri, D. K. , Zhang, Z. , and Neubauer, J. (2011). “ Measurement of Young's modulus of vocal fold by indentation,” J. Voice 25, 1–7. 10.1016/j.jvoice.2009.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c6] 6. Fant, G. (1980). “ Voice source dynamics,” STL-QPSR 21, 17–37. [Google Scholar]

[c7] 7. Fant, G. (1982). “ Preliminaries to analysis of the human voice source,” STL-QPSR 23(4), 1–27. [Google Scholar]

[c8] 8. Fant, G. , Liljencrants, J. , and Lin, Q. (1985). “ A four-parameter model of glottal flow,” STL-QPSR 26(4), 1–13. [Google Scholar]

[c9] 9. Finnegan, E. , Luschei, E. , and Hoffman, H. (2000). “ Modulations in respiratory and laryngeal activity associated with changes in vocal intensity during speech,” J. Speech Lang. Hear. Res. 43, 934–950. 10.1044/jslhr.4304.934 [DOI] [PubMed] [Google Scholar]

[c10] 10. Gay, T. , Hirose, H. , Strome, M. , and Sawashima, M. (1972). “ Electromyography of the intrinsic laryngeal muscles during phonation,” Ann. Otol. Rhinol. Laryngol. 81, 401–409. 10.1177/000348947208100311 [DOI] [PubMed] [Google Scholar]

[c11] 11. Henrich, N. , d'Alessandro, C. , and Doval, B. (2001). “ Spectral correlates of voice open quotient and glottal flow asymmetry: Theory, limits and experimental data,” in Proceedings of EUROSPEECH, Scandinavia, pp. 47–50. [Google Scholar]

[c12] 12. Henrich, N. , d'Alessandro, C. , Doval, B. , and Castellengo, M. (2005). “ Glottal open quotient in singing: Measurements and correlation with laryngeal mechanisms, vocal intensity, and fundamental frequency,” J. Acoust. Soc. Am. 117(3), 1417–1430. 10.1121/1.1850031 [DOI] [PubMed] [Google Scholar]

[c13] 13. Hirano, M. (1974). “ Morphological structure of the vocal fold and its variations,” Folia Phoniatr. 26, 89–94. 10.1159/000263771 [DOI] [PubMed] [Google Scholar]

[c14] 14. Hirano, M. (1981). Clinical Examination of Voice: Disorders of Human Communication ( Springer, New York: ), Vol. 5, Chap. 3. [Google Scholar]

[c15] 15. Hirano, M. , and Kakita, Y. (1985). “ Cover-body theory of vocal fold vibration,” in Speech Science: Recent Advances, edited by Daniloff R. G. ( College-Hill Press, San Diego: ), pp. 1–46. [Google Scholar]

[c16] 16. Hirano, M. , Ohala, J. , and Vennard, W. (1969). “ The function of laryngeal muscles in regulating fundamental frequency and intensity of phonation,” J. Speech, Hear. Res. 12, 616–628. 10.1044/jshr.1203.616 [DOI] [PubMed] [Google Scholar]

[c17] 17. Hirano, M. , Vennard, W. , and Ohala, J. (1970). “ Regulation of register, pitch and intensity of voice: An electromyographic investigation of intrinsic laryngeal muscles,” Folia Phoniatr. 22, 1–20. 10.1159/000263363 [DOI] [PubMed] [Google Scholar]

[c18] 18. Holmberg, E. , Hillman, R. , and Perkell, J. (1988). “ Glottal airflow and transglottal air pressure measurements for male and female speakers in soft, normal, and loud voice,” J. Acoust. Soc. Am. 84, 511–529. 10.1121/1.396829 [DOI] [PubMed] [Google Scholar]

[c19] 19. Ishizaka, K. , and Flanagan, J. L. (1972). “ Synthesis of voiced sounds from a two-mass model of the vocal cords,” Bell Syst. Tech. J. 51, 1233–1267. 10.1002/j.1538-7305.1972.tb02651.x [DOI] [Google Scholar]

[c20] 20. Isshiki, N. (1964). “ Regulatory mechanism of voice intensity variation,” J. Speech, Hear. Res. 7, 17–29. 10.1044/jshr.0701.17 [DOI] [PubMed] [Google Scholar]

[c21] 21. Isshiki, N. (1989). Phonosurgery: Theory and Practice ( Springer-Verlag, Tokyo: ), Chap. 3. [Google Scholar]

[c22] 22. Isshiki, N. (1998). “ Mechanical and dynamical aspects of voice production as related to voice therapy and phonsurgery,” J. Voice 12, 125–137. 10.1016/S0892-1997(98)80031-3 [DOI] [PubMed] [Google Scholar]

[c23] 23. Itskov, M. , and Aksel, N. (2002). “ Elastic constants and their admissible values for incompressible and slightly compressible anisotropic materials,” Acta Mech. 157, 81–96. 10.1007/BF01182156 [DOI] [Google Scholar]

[c24] 24. Klatt, D. H. , and Klatt, L. C. (1990). “ Analysis, synthesis and perception of voice quality variations among male and female talkers,” J. Acoust. Soc. Am. 87, 820–856. 10.1121/1.398894 [DOI] [PubMed] [Google Scholar]

[c25] 25. Luo, H. , Mittal, R. , and Bielamowicz, S. (2009). “ Analysis of flow-structure interaction in the larynx during phonation using an immersed-boundary method,” J. Acoust. Soc. Am. 126, 816–824. 10.1121/1.3158942 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c26] 26. Mendelsohn, A. , and Zhang, Z. (2011). “ Phonation threshold pressure and onset frequency in a two-layer physical model of the vocal folds,” J. Acoust. Soc. Am. 130, 2961–2968. 10.1121/1.3644913 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c27] 27. Moore, D. M. , and Berke, G. S. (1988). “ The effect of laryngeal nerve stimulation on phonation: A glottographic study using an in vivo canine model,” J. Acoust. Soc. Am. 83, 705–715. 10.1121/1.396113 [DOI] [PubMed] [Google Scholar]

[c28] 28. Murray, P. R. , and Thomson, S. L. (2012). “ Vibratory responses of synthetic, self-oscillating vocal fold models,” J. Acoust. Soc. Am. 132, 3428–343. 10.1121/1.4754551 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c29] 29. Pickup, B. , and Thomson, S. L. (2011). “ Identification of geometric parameters influencing the flow-induced vibration of a two-layer self-oscillating computational vocal fold model,” J. Acoust. Soc. Am. 129(4), 2121–2132. 10.1121/1.3557046 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c30] 30. Scherer, R. , Shinwari, D. , De Witt, K. , Zhang, C. , Kucinschi, B. , and Afjeh, A. (2001). “ Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees,” J. Acoust. Soc. Am. 109(4), 1616–1630. 10.1121/1.1333420 [DOI] [PubMed] [Google Scholar]

[c31] 31. Sciamarella, D. , and d'Alessandro, C. (2004). “ On the acoustic sensitivity of a symmetrical two-mass model of the vocal folds to the variation of control parameters,” Acta Acust. 90, 746–761. [Google Scholar]

[c32] 32. Sidlof, P. , Svec, J. , Horacek, J. , Vesely, J. , Klepacek, I. , and Havlik, R. (2008). “ Geometry of human vocal folds and glottal channel for mathematical and biomechanical modeling of voice production,” J. Biomech. 41, 985–995. 10.1016/j.jbiomech.2007.12.016 [DOI] [PubMed] [Google Scholar]

[c33] 33. Stathopoulos, E. , and Sapienza, C. (1993). “ Respiratory and laryngeal function of women and men during vocal intensity variation,” J. Speech Hear. Res. 36, 64–75. 10.1044/jshr.3601.64 [DOI] [PubMed] [Google Scholar]

[c34] 34. Steinecke, I. , and Herzel, H. (1995). “ Bifurcations in an asymmetric vocal fold model,” J. Acoust. Soc. Am. 97, 1874–1884. 10.1121/1.412061 [DOI] [PubMed] [Google Scholar]

[c35] 35. Stevens, K. N. (1998). Acoustic Phonetics ( MIT Press, Cambridge, MA: ), Chap. 2. [Google Scholar]

[c36] 36. Story, B. H. , and Titze, I. R. (1985). “ Voice simulation with a body-cover model of the vocal folds,” J. Acoust. Soc. Am. 97, 1249–1260. [DOI] [PubMed] [Google Scholar]

[c37] 37. Tanaka, S. , and Gould, W. (1983). “ Relationships between vocal intensity and noninvasively obtained aerodynamic parameters in normal subjects,” J. Acoust. Soc. Am. 73(4), 1316–1321. 10.1121/1.389235 [DOI] [PubMed] [Google Scholar]

[c38] 38. Tanaka, S. , and Tanabe, M. (1986). “ Glottal adjustment for regulating vocal intensity, an experimental study,” Acta Otolaryngol. 102, 315–324. 10.3109/00016488609108682 [DOI] [PubMed] [Google Scholar]

[c39] 39. Thomson, S. L. , Mongeau, L. , and Frankel, S. H. (2005). “ Aerodynamic transfer of energy to the vocal folds,” J. Acoust. Soc. Am. 118, 1689–1700. 10.1121/1.2000787 [DOI] [PubMed] [Google Scholar]

[c40] 40. Titze, I. R. (1988). “ Regulation of vocal power and efficiency by subglottal pressure and glottal width,” in Vocal Physiology: Voice Production, Mechanisms and Functions, edited by Fujimura O. ( Raven, New York: ), pp. 227–238. [Google Scholar]

[c41] 41. Titze, I. , and Talkin, D. (1979). “ A theoretical study of the effects of various laryngeal configurations on the acoustics of phonation,” J. Acoust. Soc. Am. 66, 60–74. 10.1121/1.382973 [DOI] [PubMed] [Google Scholar]

[c42] 42. Van den Berg, J. W. (1968). “ Register problems,” Ann. NY Acad. Sci. 155(1), 129–134. 10.1111/j.1749-6632.1968.tb56756.x [DOI] [PubMed] [Google Scholar]

[c43] 43. Van den Berg, J. W. , and Tan, T. S. (1959). “ Results of experiments with human larynxes,” Pract. Otorhinolaryngol. 21, 425–450. [DOI] [PubMed] [Google Scholar]

[c44] 44. Xuan, Y. , and Zhang, Z. (2014). “ Influence of embedded fibers and an epithelium layer on glottal closure pattern in a physical vocal fold model,” J. Speech Lang. Hear. Res. 57, 416–425. 10.1044/2013_JSLHR-S-13-0068 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c45] 45. Yin, J. , and Zhang, Z. (2013). “ The influence of thyroarytenoid and cricothyroid muscle activation on vocal fold stiffness and eigenfrequencies,” J. Acoust. Soc. Am. 133, 2972–2983. 10.1121/1.4799809 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c46] 46. Zhang, Z. (2009). “ Characteristics of phonation onset in a two-layer vocal fold model,” J. Acoust. Soc. Am. 125, 1091–1102. 10.1121/1.3050285 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c47] 47. Zhang, Z. (2010). “ Dependence of phonation threshold pressure and frequency on vocal fold geometry and biomechanics,” J. Acoust. Soc. Am. 127, 2554–2562. 10.1121/1.3308410 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c48] 48. Zhang, Z. (2011). “ Restraining mechanisms in regulating glottal closure during phonation,” J. Acoust. Soc. Am. 130, 4010–4019. 10.1121/1.3658477 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c49] 49. Zhang, Z. (2014). “ The influence of material anisotropy on vibration at onset in a three-dimensional vocal fold model,” J. Acoust. Soc. Am. 135(3), 1480–1490. 10.1121/1.4863266 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c50] 50. Zhang, Z. (2015). “ Regulation of glottal closure and airflow in a three-dimensional phonation model: Implications for vocal intensity control,” J. Acoust. Soc. Am. 137, 898–910. 10.1121/1.4906272 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c51] 51. Zhang, Z. , and Luu, T. (2012). “ Asymmetric vibration in a two-layer vocal fold model with left-right stiffness asymmetry: Experiment and simulation,” J. Acoust. Soc. Am. 132(3), 1626–1635. 10.1121/1.4739437 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c52] 52. Zhang, Z. , Mongeau, L. , and Frankel, S. H. (2002). “ Experimental verification of the quasi-steady approximation for aerodynamic sound generation by pulsating jets in tubes,” J. Acoust. Soc. Am. 112(4), 1652–1663. 10.1121/1.1506159 [DOI] [PubMed] [Google Scholar]

[c53] 53. Zhang, Z. , Neubauer, J. , and Berry, D. A. (2006). “ The influence of subglottal acoustics on laboratory models of phonation,” J. Acoust. Soc. Am. 120(3), 1558–1569. 10.1121/1.2225682 [DOI] [PubMed] [Google Scholar]

PERMALINK

Cause-effect relationship between vocal fold physiology and voice production in a three-dimensional phonation model

Zhaoyan Zhang

Abstract

I. INTRODUCTION

II. METHOD

A. Numerical model

FIG. 1.

FIG. 2.

B. Simulation conditions

TABLE I.

C. Data analysis

III. RESULTS

A. Phonation threshold pressure

FIG. 3.

FIG. 4.

B. Vocal fold vibration, glottal closure, and CQ

FIG. 5.

FIG. 6.

FIG. 7.

FIG. 8.

FIG. 9.

FIG. 10.

C. F0, SPL, and mean glottal flow

D. Voice spectral characteristics

1. Effects of vocal fold thickness

FIG. 11.

2. Effects of resting glottal opening

FIG. 12.

3. Effects of vocal fold stiffness

FIG. 13.

4. Effects of subglottal pressure

FIG. 14.

E. Multiple linear regression between physiological controls and output variables

TABLE II.

IV. DISCUSSION AND CONCLUSIONS

ACKNOWLEDGMENTS

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases